在气象、地理等学科中利用计算机解决与图形有关的问题时, 经常会遇到要在一个给定区域内进行某种特定处理, 而在此区域外不进行该种处理的情况。在这种情况下首先需要确定哪些点位于区域内, 哪些点位于区域外。对于人脑而言, 这是很容易解决的问题。然而, 这种解决方法是建立在人脑的感知意识和逻辑分析、判断能力基础之上的, 是一种主观判别方法, 很难在计算机上直接实现。要在计算机上通过“ 数”的变化来解决这类问题, 如果给定区域的边界能用一种比较简单、确定、规则的数学模型来描述, 相对较为容易; 但倘若无法用这种数学模型来描述这条边界, 如某个不规则行政区域的范围, 处理起来就会困难得多。在计算机图形学中有的处理技术(如相交判别、区域填充等)可以用来解决这个问题, 但其解决方法与过程会相当复杂。
这个问题在涉及到图形图像分析的各个领域中都存在。用几何语言描述, 实际上就是如何确定一个给定点与一个由闭合曲线(位于二维平面上, 下同)围成的区域之间的关系:给定点是在该区域内, 还是在该区域外? 本文将给出一个非常简单的客观判别方法。
1 基本判断方法从理论上讲, 一条闭合曲线是由无数个连续的几何点构成的, 有的闭合曲线可以用数学函数来描述, 有的则不能。但无论前者还是后者, 在实际的数学描述中, 都可将其看成为是由有限多个点构成的、在点与点之间有直线相连的折线, 也就是可以用首尾相连的有限条线段来拟合闭合曲线。
设闭合曲线L 由点集Pi(Xi, Yi), i=1, …, n, 构成, Pi(Xi, Yi)∈曲线L, 其所在的二维平面上, 有一个给定点P 0(X 0, Y 0) , 则上述问题可表述为如何确定点P
在闭合曲线所在的二维平面中, 连接P 0 和Pi, 该连线与X 轴有一夹角, 可由
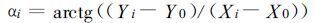
|
(1) |
求出。沿闭合曲线的某一方向(顺时针或逆时针)逐点计算给定点和曲线上点的连线与X 坐标轴形成的角度, 并累加相邻边界点角度的增量, 令其为β, 即
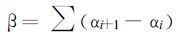
|
(2) |
直到全部边界点计算完毕。注意闭合曲线的起点同时也是它的终点, 应该参与两次计算。根据给定点和闭合曲线的关系, 可以得出给定点在闭合区域内部和外部时β 有不同的数值。
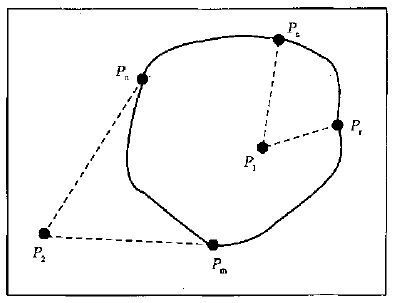
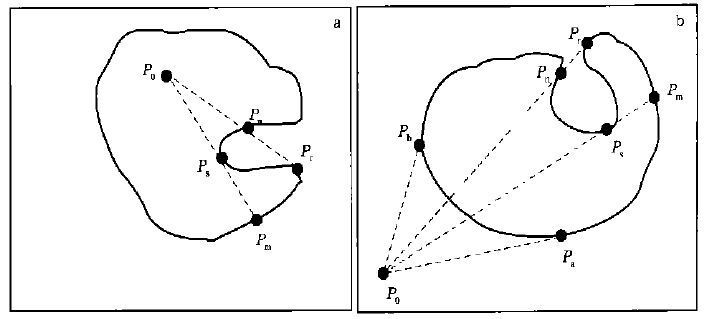
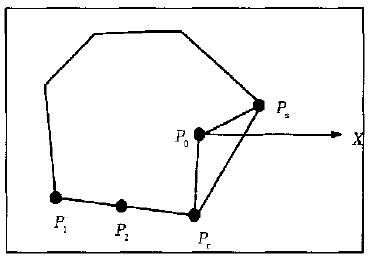
如图 1 所示, 当给定点P 1 位于闭合曲线所围区域内, 且闭合曲线的走向(Pr 到P s 或P s 到Pr)不改变方向(一直保持顺时针或逆时针方向)时, 闭合曲线上任意相邻两点间角度的增量αi+1 -αi 将始终保持符号不变。当计算到终点(也就是闭合曲线的起点)时, 从点P 1到闭合曲线上点的连线必然扫过一个360°的圆周角, 即 β=360°。当曲线走向为顺时针方向时, 为-360°; 当曲线走向为逆时针方向时, 为+360°。如果闭合曲线在中途改变走向, 如图 2a 中的Pr 到Ps 段, 由原来的逆时针走向变为顺时针走向, 必然会存在另外两段曲线(Pm 到Pr 与P s 到P n), 其角度增量的量值正好与Pr 到P s 段的角度增量量值相同, 但由于曲线的走向正好与Pr 到Ps 段相反(这是由闭合曲线的性质所决定的), 从而角度增量的符号是相反的。因此, 两者抵消后, 还将保留一个在原来方向上的增量不变, 从而使得计算完整条曲线时, 给定点与曲线上点的连线所扫过的角度仍然是360°。
|
|
| 图 1. 给定点与闭合曲线(不改变走向)所围区域的关系 | |
当给定点位于不改变走向的闭合曲线所围区域外时(图 1 中的点P 2) , 从Pn 到Pm段和从Pm 经Pr、Ps 到Pn 段的角度增量正好是大小相等, 方向相反的, 从而使得总的角度增量之和为0 。当给定点位于改变走向的闭合曲线所围区域外时, 如图 2b 中的点P 0, 与给定点处于闭合曲线所围区域中的情况一样, 从Pr 到Ps 段曲线走向发生变化, 但从Pm 到Pn 段的角度增量之和正负抵消之后, 实际上仍只相当于从Pm 到Pr 段的角度增量。因此, 从Pb 到Pa 段的角度增量与Pa 经Pm 到Pb 段的角度增量仍然是大小相等, 方向相反的, 其累计之和依然为0 。如果给定点位于Ps 附近的闭合曲线所围区域外时, 那就与图 1 中点P2 的情况实际上是相同的。
|
|
| 图 2. 给定点与闭合曲线(改变走向)所围区域的关系 (a)点在区域内; (b)点在区域外 | |
根据以上讨论, 可以得出以下结论:相对于闭合曲线围成的区域, 如果给定点与曲线上点的连线相对于X 轴所形成的角度增量的累计值的数值等于360°, 则该点必位于该区域的内部; 如该累计值为0, 则该点必位于该区域的外部。如此可得
判据1:β =360°时, 给定点在闭合曲线所围区域内
β =0°时, 给定点在闭合曲线所围区域外
2 特殊点的判别方法当闭合曲线上相邻两点的位置特殊时, 如果仅仅考虑数学运算结果, 在式(2) 中有可能出现增量|(αi+1-αi)| ≥180°的情况。此时, 应当按照本问题的几何含义来确定合理的角度增量。
如图 3 所示, 当闭合曲线上点的延伸方向为逆时针方向(笛卡尔坐标系中角度的正方向)时, 相对于给定点P0, 从点Pr 到Ps 的角度增量如果纯粹按数学方法计算, 应当是绝对值大于180°的负值。但从本问题的几何含义来讲, 实际上应当是从点Pr 到Ps 逆时针转过的角度, 是小于180°的正值, 可用
|
|
| 图 3. 特殊点的处理 | |
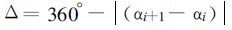
|
来确定。再考虑到(αi+1 -αi)>180°时的情况, 可以将这类情况下的判据定义为:
判据2:当|(αi+1 -αi)| >180°时,
如(αi+1 -αi)>0, 则取角度增量为:Δ=-(360°- |(αi+1 -αi)|)
如(αi+1 -αi)<0, 则取角度增量为:Δ=360°- |(αi+1 -αi)|
对于自身位于闭合曲线上相邻两点间连线上的给定点(即给定点在闭合曲线上, 但又不属于该曲线的数学描写模型所用到的点的子集, 如图 3 中的P2) , 则可自由定义其是在图 3 特殊点的处理所围区域内还是在所围区域外。可使用
判据3:当(αi+1 -αi)=180°,
如需将其定义为在区域内, 角度增量恒取为:Δ=| (αi+1 -αi)|
如需将其定义为在区域外, 则角度增量恒取为:Δ=- |(αi+1 -αi)|
与闭合曲线上的点重合的给定点(图 3中的P1) 可以根据角度为0或距离为0来判定, 可根据具体应用情况直接选择将其定义为在区域内或者在区域外。只是要注意与使用判据3的点保持一致。
3 应用实例气象上最常见的等值线描绘问题在很多情况下需要仅在一个行政区域内进行。例如成都市气象局在为地方政府提供气象服务产品时经常要绘制雨量分布图, 图上不仅要标出各个站点的降雨量, 还需要绘制出雨量等值线, 但这些等值线只能局限在成都市的范围内而不能延伸到其外。一般情况下, 这种等值线绘制工作是借助于将不规则站点上的数据通过客观分析方法拓展到一个二维网格区域上来完成的。绘图工具可以根据网格点上的数据判定该网格点是否进入分析范围。因此, 只要能区分出行政区域内外的两类网格点, 就能把绘制的等值线局限在行政区域范围内。
将成都市的行政边界数值化后(考虑到应用领域, 数值化的精度并不高)获得了一个代表边界的闭合曲线上点的子集, 用它可以绘制出成都市行政区域地图的简图(图 4) , 该简图可用来作为雨量图的底图。取一个能全部包含成都市的矩形区域, 并将其设置为N×M 的网格区, 其内部就有N ×M 个网格点。其中一部分网格点位于成都市范围内, 一部分位于其外。将每一个网格点视为已知点, 运用公式(1) 、(2) 和判据1、2、3进行计算和判别, 可以在计算机上迅速确定该网格点位于成都市范围内还是在其外。将在内的网格点赋值为0, 在外的网格点赋值为1, 两种不同数值网格点的交界线可以清楚地勾画出成都市的轮廓。当然, 网格格距越小, 轮廓就越逼真。
|
|
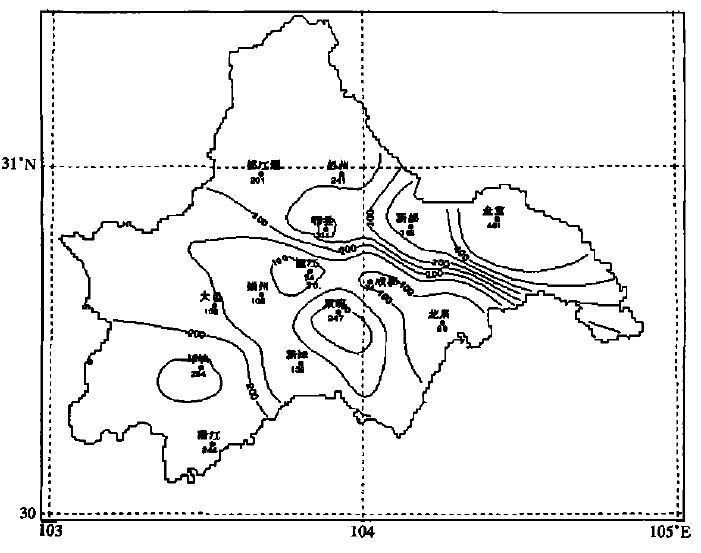
| 图 4. 运用本方法确定区域后绘出的成都市雨量图 (单位:mm, 等值线间距:50 mm) | |
以这种网格点的数据为基础, 在进行客观分析时, 就可只计算位于成都市范围内的网格点处的分析值, 然后利用绘图功能将有分析值部分的等值线绘制出来, 如图 4 所示, 即可达到预期目的。
该方法是以平面几何原理为基础, 构造出判断一个已知点是否位于由闭合曲线所围成的区域内的客观方法, 原理清楚, 计算简单, 判别条件明确, 充分利用了计算机运算的特点, 是在计算机上处理该类图形问题的有力助手。这种方法可以用于任意闭合曲线, 对于不规则的、近似于由点构成的闭合曲线特别适用。
 2003, 14 (1): 125-128
2003, 14 (1): 125-128

