气候的可预报性研究是对气候变化研究的一个重要方面, 随着短期气候预测逐渐引起人们的重视, 有关短期气候预测可预报性问题的研究也不断地广泛和深入。国内外在可预报性方面有很多研究, 如Shukla、Trenberth等[1~4], 这些研究针对不同的气象要素, 分析了可预报性的时空分布特征及其可能影响机制。我们知道, 实际大气是一个非线性系统, 可预报性则是这个非线性系统的一种性质, 实际大气的可预报性反映了真实大气的实际可预报能力; 若我们建立一种模式, 利用一组方程来描述这个非线性系统的演变, 那么我们所描述出来的非线性系统也是具有可预报性的, 这就是模式大气的可预报性。模式大气是对实际大气的近似, 由于受模式性能的限制, 两种大气之间存在偏差, 两种大气的可预报性之间也存在偏差, 这种差异在一定程度上反映了模式描述实际大气能力的高低。从这一观点出发, 本文将分别利用观测资料与动力模式的资料, 研究月尺度实际大气与模式大气的可预报性, 在此基础上, 对这两种可预报性, 进一步分析不同空间尺度的大气运动对整体运动可预报性的影响, 并找出影响最大的部分。通过对实际大气与模式大气的可预报性的对比分析, 检验动力模式描述实际大气的能力, 并为提高动力模式的预报性能探求新的思路。
1 资料与分析方法 1.1 资料分析所用的资料为欧洲数值天气预报中心 (ECMWF) 提供的1979~1993年500 hPa高度场12:00(U TC, 下同) 的逐日再分析资料。
模式资料包括两部分, 首先是ECMWF的T63模式提供的500 hPa高度场冬、夏季的模拟资料, 这部分资料以实测SST强迫T63模式, 以1979~1992年每年11月22~30日12:00的观测大气作为9个初始场分别对模式进行积分, 从12月1日起积分120 d, 以每10 d平均的输出结果作为一个旬的平均, 得到冬季资料; 以1979~1993年每年5月23~31日12:00的观测大气作为9个初始场分别对模式进行积分, 从6月1日起积分120d, 以每10 d平均的输出结果作为一个旬的平均, 得到夏季资料。由于本文分析的是月尺度可预报性, 所以仅分析了前3个旬的资料, 即1979~1992年12月、1979~1993年6月的逐旬资料。第二部分模式资料为国家气候中心月动力延伸预报的500 hPa高度场预报资料, 以对SST距平的持续性预报得到的SST强迫T63模式, 以1990年及1995~1999年每年5月19、20日00:00、06:00、12:00、18:00共8个时次的观测场为8个初始场, 分别对模式进行45 d积分而获得, 本文取前30 d的积分结果进行分析。
上述所有资料均为网格点资料, 经纬度网格距均为2.5°×2.5°。
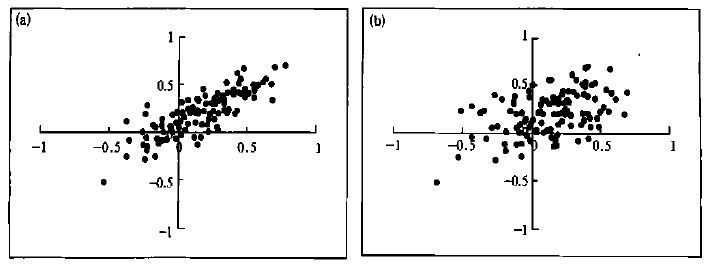
1.2 不同尺度波对月预报的影响在下文研究可预报性之前, 我们通过比较ECMWF模式模拟的500 hPa高度场在不同波数上与实况的距平相关系数 (ACC), 先对不同尺度的波在月预报中的作用进行一下讨论。图 1为模拟的1979~1992年共14年9个初始场126个个例12月月平均500 hPa高度场与相应的实况的距平相关系数。横坐标为1~3波 (或4~9波) 模拟与实况的ACC, 纵坐标为全波模拟与实况的ACC, 图中的实心点的位置是由一对ACC确定的。可以看出, 图 1a中实心点的分布是很集中的, 且基本上分布在一条穿过坐标原点的斜率为正的斜线附近。表明, 若1~3波模拟得好, 则全波的模拟也较好, 两者之间存在很好的线性相关, 而图 1b中实心点的分布比较分散, 表明4~9波的模拟效果与全波的模拟之间则没有很好的相关性。为了更清楚地说明这一问题, 我们以1~3波或4~9波模拟与实况的ACC为自变量, 以全波模拟与实况的ACC为因变量, 对图中的离散点进行拟合, 建立线性回归方程。发现图 1a中拟合的线性方程斜率为0.69, 表示分散程度的拟合率为0.01, 而图 1b中相应的斜率与拟合率分别为0.37与0.04, 可见, 1~3波的ACC与全波的ACC之间的相关性明显好于4~9波与全波的情况, 清楚地说明了若超长波模拟效果好, 则整体模拟效果相应也好, 超长波的预报效果对月预报具有重要的作用, 而天气尺度波对月预报的作用明显减小。这一结论与李维京[5]利用其它资料的研究结果是一致的。下面我们将进一步从可预报性的角度对超长波在月预报中的作用进行说明。
|
|
| 图 1. 全球12月平均全波与1~3波 (a), 4~9波 (b) 模拟与实况的距平相关系数分布 (纵坐标:全波模拟与实况的ACC, 横坐标:1~3波 (a)、4~9波 (b) 模拟与实况的ACC) | |
1.3 分析方法
可预报性分析普遍采用的是方差分析方法, Shukla (1983) [1]、T renberth[2]等用观测资料分析可预报性以及Shukla (1981) [3]、赵彦[4]用模式资料分析可预报性均采用了这种方法。方差分析方法的主旨是检验气候信噪比, 即认为影响短期气候变化的因素主要有两种[6]:一种是由海表面温度 (SST) 异常等下边界条件变化引起的影响, 即热流入量的影响; 另一种是由大气内部的动力不稳定及其非线性相互作用所产生的影响。由此, 在研究可预报性时, 相应地把大气变化总的变率分为年际变率和由上述内部动力原因引起的自然变率两部分, 并认为前者作为气候信号, 是可预报的, 而后者作为气候噪音, 是不可预报的, 通过对气候信号与气候噪音的比值进行方差检验来反映大气的可预报程度。
对于观测资料, 按照T renberth[2, 7]等的方法, 在分析可预报性之前, 需要先将观测资料去掉年循环。计算年循环的具体方法是:将所用资料的气候值按365 d的长度进行时间上的谐波分析, 求得该气候值波数为0~4的谐波, 此谐波即为年循环。
假定φi, j为去掉年循环后的第i天、第j年的500 hPa高度场的观测值, J为所取资料的年数, N为所取资料的天数。对于全球144 ×73个格点, 在每一个格点上, 计算
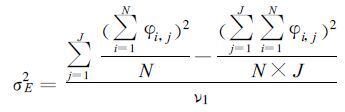
|
(1) |
式 (1) 中, 分子为每一年的平均值对总体平均值的离差平方和, ν1为J-1, 表示自由度。该式即组间方差, 或称外部方差, 这是由外强迫的年际变化而引起的, 为年际变率; 计算
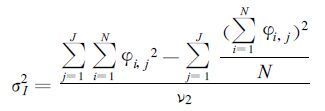
|
(2) |
在式 (2) 中, 分子表示每年某个月的各个值对该年平均值的离差平方和, ν2为J ×[(N/T 0)-1], 同样表示自由度。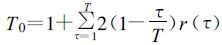
计算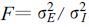
对模式资料的分析方法与此类似, 这里不再赘述。
本文用该方法分析了上述观测资料与模式资料12月、6月 (为了叙述方便, 将上述国家气候中心资料的日期描述为6月) 的月尺度可预报性, 并进一步对上述500 hPa高度场的资料进行谐波分析, 用同样的方法分别研究了波数分别为0~3的波 (纬向平均场和超长波) 以及4波以上波的可预报性。目的是通过对不同空间尺度大气运动可预报性的对比研究, 找出对实际大气或模式大气整体运动可预报性影响最大的部分。
2 结果分析 2.1 实际大气可预报性图 2自上而下分别为ECMWF观测资料1979~1993年12月500 hPa高度场的全波、0~3波以及4波以上波的F值分布情况, 阴影区表示具有可预报性的区域; 图 3与图 2类似, 表示6月的情况。可以看出, 不论是12月还是6月, 对于全波而言, 热带地区的可预报性都是全球最大的, 热带外地区的可预报性明显减小, 可预报性呈带状分布; 12月F值普遍较6月大, 可预报区域的面积也明显比6月大。这与Shukla等[1]的研究结论是一致的。另外, 从图 2、3中均可以看出, 0~3波可预报的区域面积最大, 全波次之, 且全波F值的大小与分布基本与0~3波类似; 与0~3波以及全波相比, 4波以上的波可预报区域的面积小了很多, 可预报区域内的F值也明显减小。
|
|
| 图 2. ECMWF资料1979~1993年12月500 hPa高度场全波 (a)、0~3波 (b) 以及4波以上 (c) 的F值分布 (阴影区表示具有可预报性 (信度97.5 %下的F-检验)) | |
|
|
| 图 3. ECMWF资料1979~1993年6月500 hPa高度场全波 (a)、0~3波 (b) 以及4波以上 (c) 的F值分布 (阴影区表示具有可预报性 (信度97.5 %下的F-检验) | |
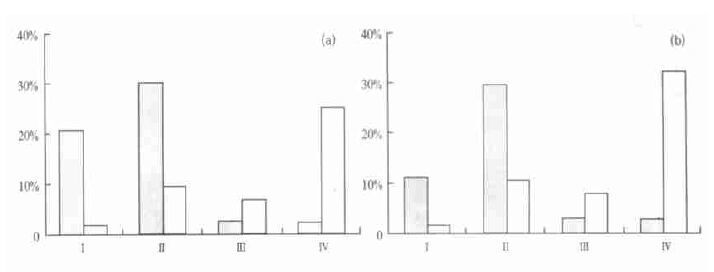
为了更清楚地说明波数为0~3的大尺度大气运动以及其它尺度大气运动对全波可预报性的相对影响, 本文根据三种波段的波能否预报的情况, 对全球区域进行4种划分 (下文将对各种划分的意义进行详细说明), 按照不同划分的面积占全球总面积比例的相对大小, 对这一问题进行分析。图 4a和图 4b分别为500 hPa高度场12月、6月不同划分的面积占全球总面积的比例图。
|
|
| 图 4. 1979~1993年12月 (a)、6月 (b) 实际大气4种划分的全球总面积的百分比 | |
图 4中, 第Ⅰ分类表示0~3波以及4波以上的波均可预报, 第Ⅱ分类表示0~3波可预报而4波以上的波不可预报, 第Ⅲ分类表示0~3波不可预报而4波以上的波可预报, 第Ⅳ分类表示0~3波以及4波以上的波均不可预报; 图中的灰框表示上述不同分类意义下全波可预报的面积比例, 白框则表示全波不可预报的面积比例。从图 4a中可以看出, 对于第Ⅰ分类, 当0~3波、4波以上的波均可预报时全波可预报的面积占全球总面积的20 %, 而此时全波不可预报的面积仅占全球总面积的1.7 %, 从理论上讲, 后者是不合理的, 所占的比例也很小, 可以视为由不可避免的计算误差所引起。第Ⅱ分类中, 当4波以上的波不可预报时, 全波可预报的面积比例反而有所增加, 为30 %, 全波不可预报的面积比例增至9.5 %。从第Ⅰ、Ⅱ分类可以看出, 在0~3波可预报时, 不论4波以上的波能否可预报, 全波可预报的面积比例, 即Ⅰ、Ⅱ分类中灰框表示值的和, 达到50 %, 明显大于此时全波不可预报的面积比例。
第Ⅲ、Ⅳ分类中, 全波可预报的面积比例都很小, 分别为2.6 %与2.7 %, 其中后者从理论上讲也是不合理的, 同样视为由不可避免的计算误差引起; 这两种分类中, 全波不可预报的面积比例较大, 分别为7.2 %与25 %。从这两种分类可以看出, 0~3波不可预报时, 不论4波以上的波能否可预报, 全波不可预报的面积比例, 即Ⅲ、Ⅳ分类中灰框表示值的和, 明显大于此时全波可预报的面积比例。
总之, 若波数为0~3的大气运动可预报, 则全波可预报的面积比例明显大于全波不可预报的比例; 若波数为0~3的大气运动不可预报, 则全波可预报的面积比例很小。可见, 波数为0~3的大气运动对全波可预报性的影响最大, 而其它尺度大气运动的影响则很小。对实际大气整体运动可预报性的贡献主要来自波数为0~3的大尺度大气运动。图 4b同样体现了上述特征。
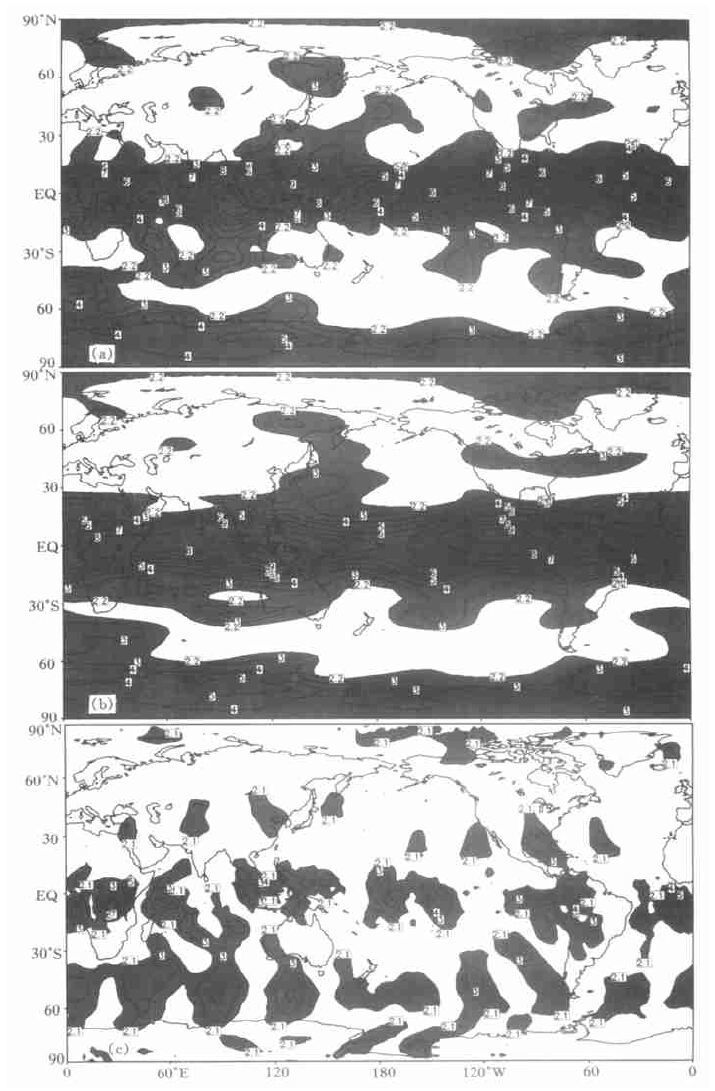
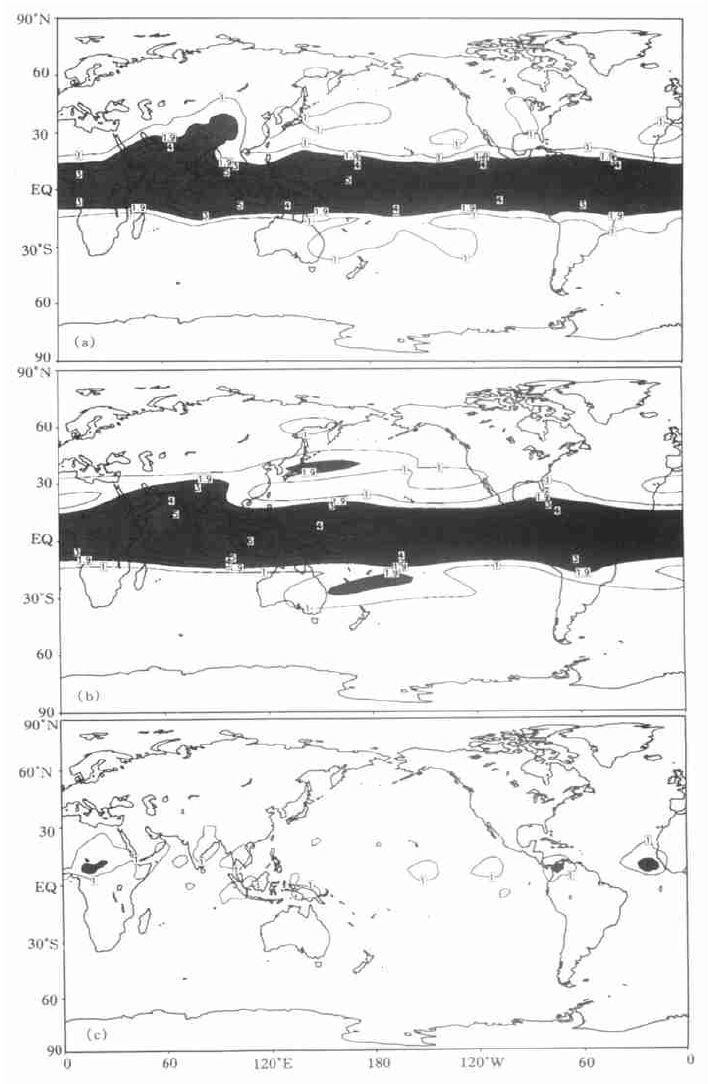
2.2 模式大气可预报性图 5为ECMWF的T63模式模拟1979~1993年500 hPa高度场12月的可预报性, 自上而下分别为全波、0~3波以及4波以上波的情况。可以看出, 与图 2相比, 不论是何种波段的波, 模式大气可预报区域面积明显比实际大气少; 全波与0~3波仅热带地区具有可预报性, 可预报性区域呈狭窄的带状分布, 且0~3波与全波不论是可预报的区域分布还是F值的大小分布都十分接近; 而4波以上的波几乎不存在可预报性。图 6与图 5类似, 为6月的情况, 反映了同样的特征。此外, 模式大气可预报性12月与6月的差异很小, 而不象图 2、3所表现的实际大气12月可预报性明显较6月大。

|
|
| 图 5. T63模式1979~1992年12月500 hPa高度场全波 (a)、0~3波 (b) 及4波以上 (c) 的F值分布 (阴影区表示具有可预报性 (信度97.5 %下的F-检验)) | |
|
|
| 图 6. T63模式1979~1993年6月500 hPa高度场全波 (a)、0~3波 (b) 以及4波以上 (c) 的F值分布 (阴影区表示具有可预报性 (信度97.5 %下的F-检验)) | |
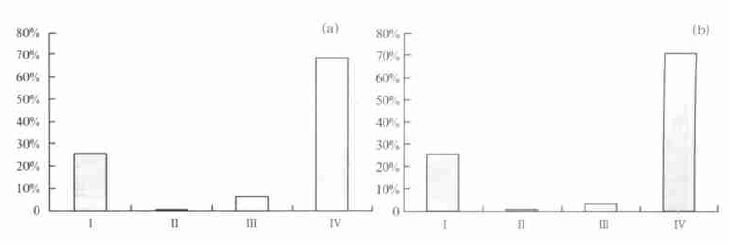
图 7为根据ECMWF的T63模式大气全波、0~3波能否可预报的情况, 将全球区域划分为4类, 不同划分的面积占全球面积的比例图 (由于4波以上的波几乎不存在可预报性, 该图仅分析了对全波和0~3波的情况)。图 7a、图 7b分别表示1979~1992年12月、1979~1993年6月的情况。图 7中, 第Ⅰ分类表示全波与0~3波均可预报, 第Ⅱ分类表示全波可预报而0~3波不可预报, 第Ⅲ分类与第Ⅱ分类意义相反, 表示全波不可预报而0~3波可预报, 第Ⅳ分类表示全波与0~3波均不可预报。可以看出, 不论12月还是6月, 第Ⅱ、Ⅲ分类所占的面积比例非常小, 说明0~3波与全波可预报的区域面积几乎相等, 进一步对全波可预报性最大的贡献来自0~3波; 第Ⅰ、Ⅳ分类中, 0~3波与全波均可预报的面积比例 (近似于全波可预报的比例) 为25 %左右, 均不可预报的面积比例 (近似于全波不可预报的比例) 接近70 %。
对比图 7与图 4发现, 此模式大气的可预报性远小于同一时期实际大气的可预报性。进一步分析对全波可预报性影响最大的0~3波部分, 发现实际大气中0~3波可预报的面积比例, 即图 4中第Ⅰ、Ⅱ分类的总和, 在12月与6月分别为61 %与51 %, 而模式大气中, 0~3波可预报的面积比例, 即图 7中第Ⅰ、Ⅲ分类的总和, 12月与6月分别为31 %与28 %, 不同月份均降低了30 %左右。可见, 在对全波可预报性影响最大的0~3波部分, 模式大气的可预报性与实际大气差异较大。
|
|
| 图 7. ECMWF模式大气1979~1992年12月 (a)、6月 (b)4种划分的面积占全球面积的百分比 | |
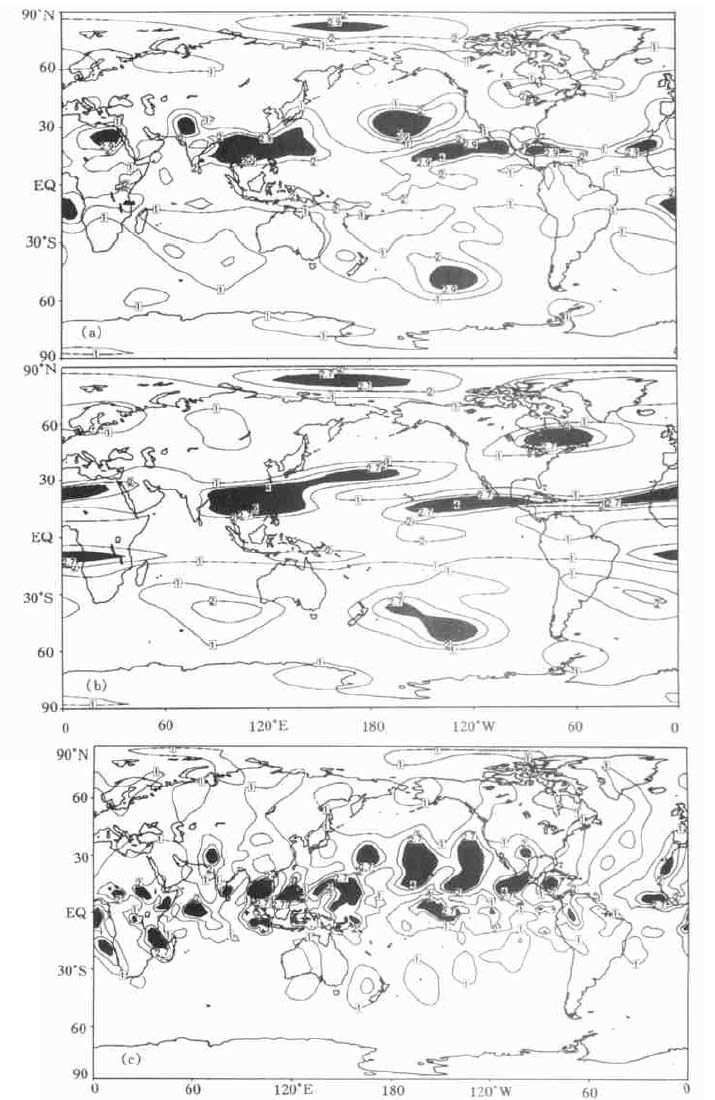
对国家气候中心月动力延伸预报的模式大气, 由于缺乏足够的资料, 这一部分的结论仅做为参考。图 8为1990、1995~1999年6月全波、0~3波以及4波以上的波的F值分布图, 非常明显, 尽管其F值在热带地区最大, 表现出一定的带状分布性质, 但由于此模式应用持续性预报的SST强迫动力模式等原因, 各波段的波可预报性均很小。
|
|
| 图 8. 月动力延伸预报模式6月500 hPa高度场全波 (a)、0~3波 (b) 以及4波以上 (c) 的F值分布 (阴影区表示具有可预报性 (信度97.5 %下的F-检验)) | |
3 小结与讨论
(1) 从可预报性的全球分布来看, 不论12月还是6月, 对于全波和0~3波, 实际大气的可预报性在热带地区最大, 热带外地区可预报性明显减小, 可预报性呈带状分布; 4波以上的波可预报性较小, 呈杂乱的零星分布; 各种波段的大气运动, 12月可预报性明显较6月大; 0~3波的可预报性最大, 全波的可预报性次之, 4波以上波的可预报性最小。
(2) ECMWF模拟的模式大气, 其全波与0~3波的可预报性在热带地区最大, 而热带外地区基本不存在可预报性, 可预报性呈带状分布, 而4波以上的波几乎没有可预报性; 此模式大气12月与6月的可预报性相似, 没有明显的时间变化; 0~3波的可预报性稍大于全波的可预报性。国家气候中心月动力延伸预报模式大气, 尽管F值表现出一定的带状分布性质, 但具有可预报性的区域很少。
(3) 不论是哪一种波段的波, 不论12月还是6月, 模式大气的可预报性均远远低于实际大气的可预报性, 在对全波可预报性影响最大的0~3波部分, 模式大气的可预报性与实际大气的可预报性差别较大。
综上所述, 不论模式大气还是实际大气, 对全波可预报性最大的影响都是波数为0~3的大尺度大气运动, 其可预报性的大小决定着全波可预报性的大小。然而, 就所研究的两个模式而言, 它们均存在一定的缺陷, 不能较好地描述实际大气状况, 模式大气与实际大气之间, 特别是在0~3波部分, 存在较大的差异, 这也是模式大气可预报性落后于实际大气可预报性的一个主要原因。因此, 抓住大尺度大气运动的特征, 提高动力模式性能还有充足的发展空间。已有研究[9~10]证明, 从不同的角度提高动力模式对超长波的预报能力, 能提高模式大气与实际大气的近似程度, 进一步提高动力模式性能, 这一方面还有待更多、更深入的研究。
致谢 ECMWF 和国家气候中心提供了本文可预报性分析的相关资料, 特此感谢!| [1] | Shukla J, Gutzler D S. Interannual variability and predictability of 500mb geopotential heights over the northern hemisphere. Mon. Wea. Rev., 1983, 111: 1273~1279. |
| [2] | Trenberth K E. Potential predictability of geopotential heights over the southern hemisphere. Mon. Wea. Rev., 1984, 113: 54~64. |
| [3] | Shukla J. Dynamical predictability of monthly means. J. Atmos. Sci., 1981, 38(12): 2547~2572. |
| [4] | 赵彦, 郭裕福, 袁重光, 等. 短期气候数值预测可预报性问题. 应用气象学报, 2000, 11, (增刊): 64–71. |
| [5] | 李维京. 月尺度动力延伸预报进展. 李维京,纪立人主编. 月动力延伸预报研究. 北京:气象出版社, 2000. 1~9. |
| [6] | 李崇银. 气候动力学引论(第二版). 北京: 气象出版社, 2000. |
| [7] | Trenberth K E. Persistence of daily geopotential heights over the Southern Hemisphere. Mon. Wea. Rev., 1984, 113: 38~53. |
| [8] | Leith C E. The standard error of time-average estimates of climatic means. J. Appl. Meteor., 1973, 12: 1066~1069. |
| [9] | 龚建东. 统计与动力相结合改进月动力延伸预报的研究: [博士论文]. 甘肃: 兰州大学, 1999. |
| [10] | 陈伯民. 改进动力延伸月预报的一种新方法: [博士论文]. 北京: 中国科学院大气物理研究所, 2000. |
 2003, 14 (1): 49-60
2003, 14 (1): 49-60

