2. 中国气象科学研究院 北京 100081;
3. 北京敏视达雷达有限公司 北京 100085
2. Chinese Academy of Meteorological Sciences , Beijing 100081;
3. Beijing Metstar Radar Company , Limited , Beijing 100085
天气雷达探测气象信息, 主要是通过雷达发射电磁波, 接收目标后向散射波的幅度、相位, 并对这些信息进行分析和处理来实现的。常规天气雷达只利用了某种单一偏振状态下回波的幅度信息, 推导雷达的反射率因子、降水强度等, 常用的偏振方式是水平偏振。
脉冲多普勒天气雷达通过对回波信号相位信息的分析, 获得气象目标的速度和谱宽分布, 从而了解大气的热力学和动力学结构。双线偏振天气雷达可以发射和接收水平、垂直两种不同偏振状态的电磁波, 由于散射粒子一般是非球形的, 根据散射粒子对两种偏振波的散射能力不同, 得到差反射率因子ZDR=10lg (ZHH/ZVV), 其中ZHH为雷达发射和接收水平偏振波时的反射率因子, ZVV为雷达发射和接收垂直偏振波时的反射率因子。当散射粒子为非球形且其对称轴空间取向偏离垂直和水平方向时, 粒子不仅散射与入射波偏振方向相同的电磁波, 还散射与入射波偏振方向垂直的电磁波, 这样, 就可以得到线性退偏振比LDR=10lg (ZHV/ZHH), 其中ZHV、ZHH分别为雷达发射水平偏振波, 接收其后向散射波垂直、水平偏振分量时的雷达反射率因子。由于水平偏振波和垂直偏振波在介质中的传播常数不同, 差相移率常数定义为:KDP=Re (kH-kV)(180/π)(单位:°/km), 其中kH、kV分别为水平和垂直偏振波的传播常数, Re表示取复数的实部。另外一个双线偏振雷达可测量的参量为ρHV(0), 定义为水平偏振回波信号与垂直偏振回波信号的零延迟相关系数。利用这些参数不仅能提高降雨估测精度, 还能判断降水粒子的形状、尺寸和相态, 为天气预报和大气科学研究提供丰富的气象信息。
国外对线偏振雷达的研究主要是针对S波段的, M.Sachidananda[1]计算得到, KDP=5°/km、相应的雨强为80 mm/h时, σKDP=0.5°/km产生10 %的雨强估测误差, 而KDP的测量误差与KDP的大小无关, 因此, 雨强小时相对误差将会更大。Ryzhkov[2]认为, σKDP=0.05°/km产生3 mm/h的雨强估测误差, 而且与雨强大小无关。目前, 美国准备在其布网雷达WSR-88D上增加偏振功能。
我国对双线偏振雷达的研究起步较晚, 第一部双线偏振雷达是原中国科学院兰州高原大气物理研究所在测雨雷达713的基础上改装而成的, 由于没有多普勒功能和技术水平的限制, 该雷达只能测量ZH和ZDR, 因此以前主要是对ZH、ZDR在降水估测、识别云中粒子相态等方面进行了研究[3~5], 而没有开展KDP等方面的研究。现在, 北京市气象局的C波段双线偏振多普勒天气雷达即将投入试运行, 中国气象局的车载C波段双线偏振多普勒天气雷达也正在筹建中, 在多普勒雷达系统上增加双线偏振功能必将大大增加该系统的探测能力, 与之相应的基础性研究工作也刚刚开始, 本文打算在双线偏振多普勒天气雷达探测误差方面做一点工作。
我国研制的双线偏振多普勒天气雷达以交替发射水平和垂直线偏振波为机制, 除了能得到强度和多普勒相移信息, 还能获取差反射率因子ZDR、差相移率常数KDP、零延迟相关系数ρHV(0) 和线性退极化比LDR等参数。雷达的基本用途之一是定量测量降水, 反射率因子、差反射率因子和差相移率常数都可以用来反演降水, 而差相移率常数反演降水有其自身的优越性, 因为差相移率常数和降雨强度之间几乎存在线性关系。差相移率常数的估值精度是能否利用其反演降水强度的关键, 其测量误差包括雷达系统引起的系统偏差和天气信号统计特性引起的估计误差, 通过标定和补偿, 可以消除系统偏差。本文主要考虑天气信号统计特性引起的差相移率常数测量误差, 并以均方差表示误差的大小。
1 差相移率常数KDP的估值精度的计算方法到达雷达有效照射体积内某一粒子上的电磁波不仅包含雷达发射的电磁波, 还包含它的上游粒子的前向散射分量, 非球形降水粒子对水平和垂直偏振波的前向散射分量是不同的, 这种差异是电磁波传播引起的称为传播相移。差传播相移ΦDP(Differential Propagation Phase Shift)=ΦH-ΦV, 其中ΦH、ΦV分别是水平、垂直偏振时的传播相移, ΦDP表示水平、垂直偏振波在传播一定距离后散射回来, 其散射信号的相位差, 但它不包括散射过程本身引起的相位变化。ΦDP和差相移率常数KDP(Specific Differential Phase) 之间存在这样的关系:ΦDP(r)=2∫orKDP(r) dr, 式中KDP(r) 是径向距离r的函数。若在降水区中相邻距离r1、r2处测得的双程差传播相移分别为Φ(r1) 和Φ(r2), 则KDP=[Φ(r2)-Φ(r1)] /[2(r2-r1)], 若r1与r2是降水区中任意两点的距离, 则上式求得的KDP就代表在r2~r1这降水区间的平均差相移率常数。雷达在实际观测中就是根据这个原理得到KDP的, 因此, 要计算KDP的测量精度就要先计算ΦDP的测量精度。
1.1 差传播相移ΦDP测量精度的计算ΦDP的估值通常采用改进的脉冲对处理方法, 这个方法是Mueller[6]提出的, 其原理如下:当雷达交替发射和接收水平、垂直偏振波时, 假设它从降水目标后向散射获得的电压时间序列分别用H2i和V2 i +1(i=1, 2, ..., M) 表示, M为样本对数 (相邻样本HV或VH为一对样本), 总的样本数目为2M。
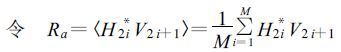
|
(1) |
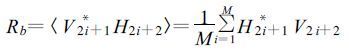
|
(2) |
式中“〈〉”代表期望值, 上标*代表取共轭。如果不考虑偏振系统引起的相位差, 则式 (1)、(2) 中包含着多普勒相移ΦD和双程差传播相移ΦDP两种信息。
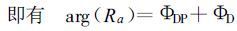
|
(3) |
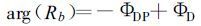
|
(4) |

|
(5) |
式中arg表示取复数的幅角, 由式 (1)~(5) 可直接求出差相移率常数。
Sachidananda和Zrnic[1]利用扰动分析法推导出ΦDP方差的表达式, 原理如下:假设样本Hi、Hi +m(m个脉冲延迟) 的相关系数或V i、Vi +m之间的相关系数为r(m), 则有

|
(6) |
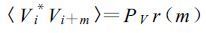
|
(7) |
这里PH、PV分别为水平偏振与垂直偏振回波信号的平均功率。
若以rHV(m)表示样本Hi、Vi +m之间的相关系数, 则有
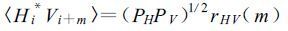
|
(8) |
影响rHV(m)的因素有:①降水粒子之间的相对运动, ②粒子形状和倾斜角度分布。这两个因素可以看成是统计独立的, 因此, 式 (8) 可以写成
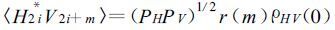
|
(9) |
天气信号一般为高斯功率谱分布, 如果信噪比很大 (≥20 dB), 就可以不考虑信噪比的影响, 则相关系数的大小为[7~9]
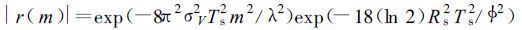
|
(10) |
其中, Ts代表脉冲重复周期, σV代表谱宽, λ表示波长, φ代表波束宽度, R s为天线转速。
ΦDP的估计值可以看成平均值和其相对于平均值的一个微小的扰动之和
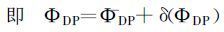
|
(11) |
根据扰动分析法得到ФDP的方差表达式
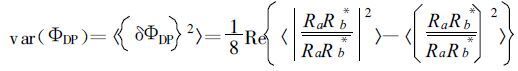
|
(12) |
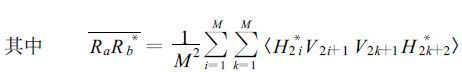
|
(13) |
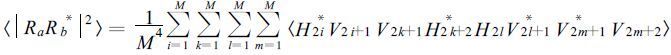
|
(14) |
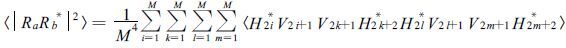
|
(15) |
将式 (6)、(7) 和 (9) 代入式 (12)~(15), 得到
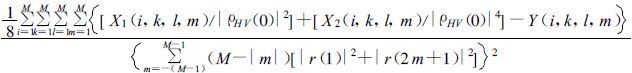
|
(16) |
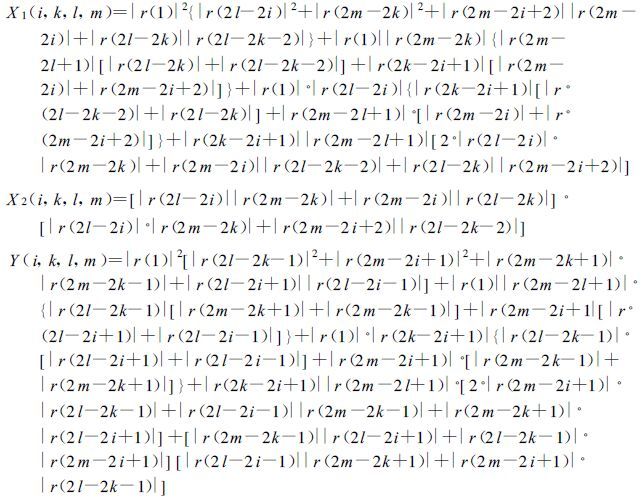
|
则以度为单位的ΦDP的均方差表示为:
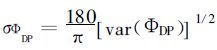
|
(17) |
在以上各式中, M为样本对数, “||”代表取复数的模, ρHV(0) 为发射波分别为水平和垂直线偏振波时的零延迟相关系数的模。
1.2 差相移率常数KDP测量精度的计算如果已知降水区中距离r1、r2(与雷达的径向距离) 之间各距离库的ΦDP, 有几种不同的方法可以得到r1与r2之间的平均KDP, 每种方法KDP的测量误差是不同的, 下面分别进行讨论。
(1) 方法一
若降水区中距离r1、r2之间包含N个距离库, 每个库都测得一个ФDP, 对这N个ФDP用最小二乘法进行线性回归, 拟合直线的斜率就是r1、r2之间的平均KDP。其表达式可以写成[10]
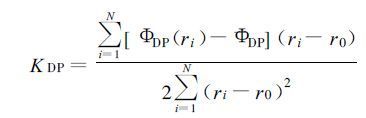
|
(18) |
式中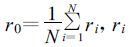
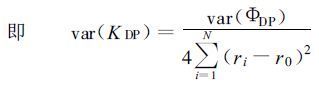
|
(19) |
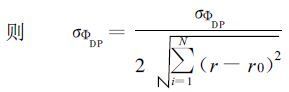
|
(20) |
(2) 方法二
若降水区中距离r1、r2之间包含N个距离库, 且库长为H, 根据每个距离库的ΦDP, 先求出每个库的KDP, 然后对N个库的KDP求平均值, 得到r1和r2之间的平均KDP。其表达式为:
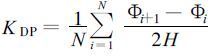
|
(21) |
求每个距离库的KDP时, KDP的均方差可表示成

|
(22) |
对N个距离库的KDP求平均值时, KDP的均方差是未平均时的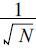
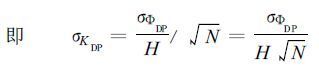
|
(23) |
(3) 方法三若降水区中距离r1、r2之间包含N个库长为H的距离库, 先分别对L个库的ΦDP平均, 即ΦDP的距离分辨率为LH, 再求出N/ L个KDP值并对其进行平均, 得到r1与r2之间的平均KDP。计算方法基本与方法二相同, 如果平均区间是不重叠的, 可以得到KDP的均方差。
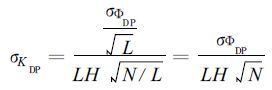
|
(24) |
本文中, 计算所用的参数主要是参考C波段新一代天气雷达的参数, 取λ=5.5 cm, =1.0°, Ts=1 ms, Rs=2周/min, 通常气象回波信号的ρHV(0) 接近于1, 降雨的ρHV(0) 较大, 降雪和降雹的ρHV(0) 较小, 这里取ρHV(0)=0.995, 一般情况下, 层状云降水的速度谱宽较小, 约为1 m/s, 而对流性降水σV≥4 m/s, 计算中分别取为1、2、3、4、5、6 m/s, 将这些参数代入式 (10)、(16)、(17), 计算出不同的样本对数M所对应的ΦDP的均方差。
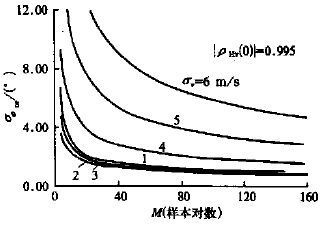
图 1给出了不同谱宽σΦDP随样本对数M的变化曲线, 从图中可以看出, 对于所有的谱宽, ΦDP的取样误差都随着M的增大而减小, 且M较小时, 减小的幅度很大, 随着M的增大减小的幅度逐渐变小, 当σV=3 m/s, M=8时σΦDP=2.791°, M=64时, ΦDP的测量精度就已达到0.823°, 说明对ΦDP的取样信号进行方位平均是减小ΦDP的测量误差的重要手段。从图中还可以看出, 谱宽σV越大, 则ΦDP的测量误差越大, 只有σV=1 m/s时除外, 这是因为, 谱宽很小时对应于层状云降水, 降水粒子之间的相对运动较小, 相关性较大, 因而等效独立样本数减少了。
|
|
| 图 1. σΦDP与谱宽以及样本对数的关系 | |
从式 (16) 可以看出, 其他参数一定时, 零延迟相关系数的模|ρHV(0)|越大, ΦDP的测量误差就越小。因此降雨时ΦDP的测量误差较小, 而降雹时的误差较大。
从σΦDP的计算公式可以看出, 波长λ是通过影响r(m) 来影响σΦDP的, 通过计算发现, 其他参数相同时, 谱宽σV≤3 m/s时, 波长为10 cm的σΦDP比波长为5.5 cm的大, σV>4 m/s时, 情况相反。因此, 仅从理论计算的ΦDP的测量误差上考虑, 对于层状云降水和混合型降水, 用C波段测量KDP的效果比S波段好。提高脉冲重复频率可以改善ΦDP的测量。另外, 减小波束宽度和增大脉冲重复频率效果一样。
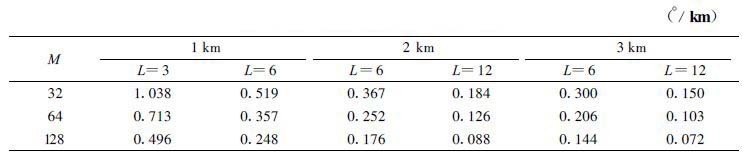
对ΦDP进行距离平均能进一步减小ΦDP的测量误差, 若距离平均区间包含N个距离平均脉冲数, ΦDP的均方差将减小N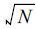

|
|
表 1 不同的距离平均区间对σΦDP的影响 |
用方法一和方法二计算KDP时, 取σV=3 m/s、|ρHV(0)|=0.995、τ=1 μs, 距离平均区间ΔR(=r2-r1)=1、2、3 km, 将这些参数分别代入式 (20)、(23) 可以得到相应的σKDP, 结果如表 2所示。
|
|
表 2 方法一和方法二计算KDP时产生的测量误差 |
从表 2中可以看出, 样本对数M越大、距离平均区间ΔR越大, KDP的测量误差就越小, 方法二的σKDP比方法一的σKDP大几倍甚至上十倍, 方法一明显优于方法二。当距离平均区间ΔR=3 km, M=64时KDP的测量精度已接近于0.1°/km, 而方法二的σKDP均在0.8°/km以上, 很难达到精度要求。如果谱宽增大、零延迟相关系数减小, KDP的测量误差将会增大, 可以通过增大样本对数、距离平均区间或脉冲重复频率来减小KDP的测量误差。
用方法三计算KDP时, 其均方差的大小与L的取值有关, 计算中其他参数与表 2中相同, L分别取3、6、12, 根据式 (24) 可求出σKDP, 结果如表 3所示。
从表 3中可以看出, σKDP与L成反比关系, σKDP随L的增大而减小, 当距离平均区间ΔR=2、3 km, L=12, M<128时KDP的测量精度就可以达到0.1°/km, 比较表 2和表 3, 可以看出, 当距离平均区间ΔR=2、3 km, L=12时, 方法三的σKDP比方法二的小, L=6时刚好相反, 当距离平均区间ΔR=1 km, L=6时, 方法三的σKDP比方法二的小, L=3时, 方法二的σKDP比方法三的小。
|
|
表 3 方法三计算KDP时产生的测量误差 |
3 结论
(1) 本文以谱宽为参数, 计算了不同样本对数M所对应的ΦDP的测量误差, 计算结果表明:σΦDP随M的增大而减小, 随谱宽的增大而增大 (σV=1 m/s时除外), 同时根据ΦDP方差表达式和相关系数的模|r(m)|表达式, 分析了|ρHV(0)|、脉冲重复频率和波束宽度等参数对σΦDP的影响, |ρHV(0)|、脉冲重复频率越大, 波束宽度越小, σΦDP则越小。
(2) 本文还计算了波长分别为5.5 cm和10 cm时的样本对数M所对应的KDP的取样误差, 结果说明:仅从理论计算的ΦDP的测量误差上考虑, 对于层状云降水和混合型降水, 取样时间相同时, 用C波段测量KDP的效果比S波段好。
(3) 本文总结了三种由ΦDP计算KDP的方法, 并对这三种方法的测量误差进行了比较, 结果表明:方法二的测量误差最大, 方法三的σKDP与L的大小有关, L达到一定值时, 其测量效果优于方法一。
以上结果可为双线偏振多普勒雷达系统的设计提供依据。另一方面, 这些结果可以用雷达定点观测的资料进行检验, 检验的方法为:雷达定点观测一降水云体, 在一段时间内获取同一方位、同一距离库的一定量的KDP, 假设在这一段时间内降水区KDP本身不变, 则
| [1] | Sachidananda M, Zrnic D S. Differential propagation phase shift and rainfall rate estimation. Radio Sci., 1985, 20(2): 235~247. |
| [2] | Ryzhkov A, Zrnic D S. Assessment of rainfall measurement that uses specific differential phase. J. Appl. Meteor., 1996, 35: 2080~2090. |
| [3] | 楚荣忠, 徐宝祥, 贾伟, 等. 双线偏振雷达测量精度的统计分析与降水估测. 高原气象, 1995, 14, (1): 47–54. |
| [4] | 刘黎平, 钱永甫, 王致君. 双线偏振雷达测量降雨效果的对比分析. 大气科学, 1996, 20, (5): 613–619. |
| [5] | 刘黎平, 钱永甫, 王致君. 用双线偏振雷达研究云中粒子的相态和大小的空间分布. 气象学报, 1996, 54, (5): 590–599. |
| [6] | Mueller E A. Calculation procedure for differential propagation phase shift. 22nd Conference on Radar Meteorology. Zurich, Switzerland. Boston, U.S.A.: American Meteorological Society, 1984. 397~399. |
| [7] | Sachidananda M, Zrnic D S. ZDR measurement considerations for a fast scan capability radar. Radio Sci., 1985, 20(4): 907~922. |
| [8] | 刘黎平, 徐宝祥. 雨区衰减和雷达取样误差对713型双线偏振雷达测量精度的影响. 高原气象, 1989, 8, (2): 181–188. |
| [9] | Ray P S, Zrnic D S, Doviak R. Time, angle and range averaging of radar echoes from distributed targets. J. Appl. Meteor., 1980, 19(3): 315~323. |
| [10] | Doviak R J, Zrnic D S, Doppler radar and weather observations. San Diego : Academic Press, Inc, 1993: 154-155. |
 2003, 14 (1): 30-38
2003, 14 (1): 30-38