双多普勒雷达同步观测是利用两部多普勒天气雷达对同一降水目标进行同步观测,以获取两个方向的径向速度,这样利用这两个径向速度和质量连续方程就可以得到降水系统风场的三维结构,而不需要更多的假设[1]。另外,这些资料也可以用于雷达资料的同化中,使同化得到的风场更加符合实际。自从1970年Lhermitte第1次对双多普勒雷达观测进行描述后[2],该技术已经成为研究台风、暴雨、冰雹等强风暴过程三维风场结构的重要手段[3, 4]。
我国雷达气象专家对双多普勒雷达观测技术很重视, 并进行了理论研究[5], 1998年在淮河流域能量和水分循环试验和研究项目的外场试验中, 利用日本3部X波段多普勒雷达在淮河流域进行了双多普勒雷达降水系统的观测。当我们的新一代天气雷达投入业务运行后, 我国也开始了使用自己的多普勒天气雷达进行双多普勒雷达观测试验, 2001年在长江中下游开展的973“中国暴雨”外场试验中, 中国科学家第1次利用我国生产的多普勒天气雷达进行了双多普勒雷达观测, 以获取梅雨锋暴雨风场的三维结构, 为研究梅雨锋暴雨发生发展的机理和提高暴雨的预测能力提供高质量的暴雨中尺度资料, 这一观测技术的成功与否是该973项目外场试验的关键。在合肥、马鞍山、宜昌和荆州这两对双多普勒中, 其中有3部雷达是2001年刚投入使用的, 在双多普勒雷达同步观测技术、资料的质量等方面有许多有待进一步解决的问题。为此, 很有必要对我国首次开展的双多普勒雷达同步观测资料进行较为严格的质量控制, 以保证所得到的风场有较高的可信度, 从理论上研究双多普勒雷达这种配置下反演风场的精度和误差。
本文的主要目的就是研究双多普勒雷达资料的质量控制方法, 并以这两对双多普勒同步观测资料为例, 进行对比分析和质量控制试验, 并给出相应的结论, 并从理论上探讨了雷达测量径向速度的误差对风场反演的影响。这一工作为充分使用这些资料以及今后开展双多普勒雷达观测都具有重要意义。
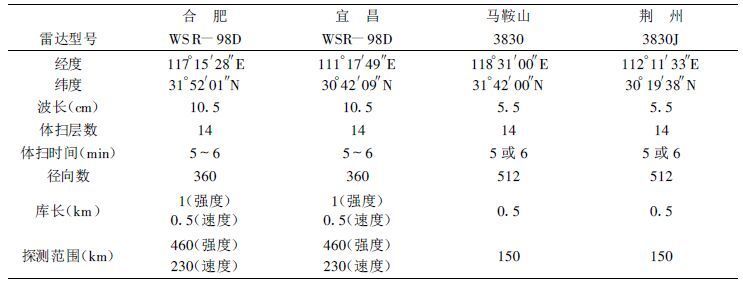
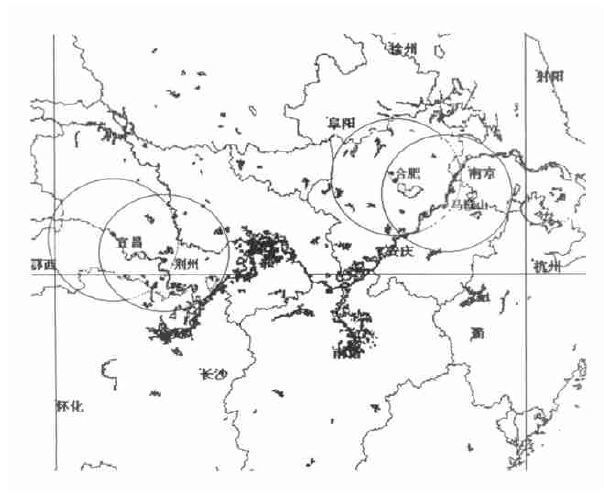
1 双多普勒雷达站点的设置和同步观测技术在973“中国暴雨”的双多普勒雷达观测外场试验中, 在合肥和宜昌已布设S波段WSR-98D型号的多普勒雷达的基础上, 在马鞍山和荆州分别布设了C波段3830型固定多普勒雷达和3830J可移式多普勒雷达, 构成了两对双多普勒雷达观测系统。图 1给出了两对双线偏振雷达的位置分布, 合肥与马鞍山和宜昌与荆州两对配对的双多普勒雷达之间的距离分别为120 km和96 km。表 1给出了两种雷达观测期间的主要参数。
|
|
| 图 1. 双多普勒雷达观测示意图 | |
|
|
表 1 多普勒雷达系统主要参数 |
1.1 雷达设点的考虑
从纯粹的双多普勒雷达观测理论和国外的经验考虑, 根据双多普勒雷达反演三维风场的精度的考虑, 两站之间的距离在60~80 km范围内比较合适。距离太近, 虽然共同覆盖区大, 但有一定反演精度的区域比较小; 距离太远, 两个雷达共同覆盖的区域比较小, 而且不适合探测低层的风场。在实际设站中其它因素如地形、电力、通讯、交通等方面的因素也要考虑。这次双多普勒雷达观测是兼顾业务和科研两方面的要求, 在与合肥配对的多普勒雷达选址过程中, 我们考察了合肥周围桐城、巢湖、马鞍山等地, 考虑到马鞍山已经建成了雷达塔楼以及它还可以与南京的雷达配对观测等原因, 最后将C波段3830多普勒雷达设置在马鞍山。同样可移式多普勒雷达系统设在荆州也主要是兼顾科研和气象业务防洪的需要。
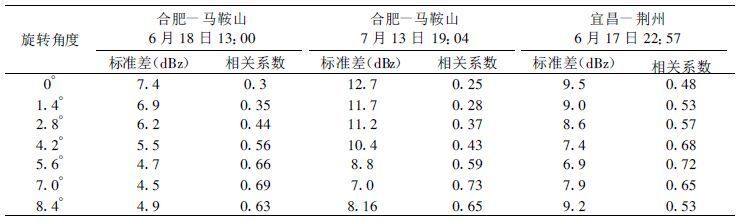
1.2 双多普勒雷达同步观测方法从理论上讲, 双多普勒雷达最理想的观测模式是同时观测得到同一散射体的两个径向速度, 并以最快的速度完成体积扫描。由于降水系统是在不断发展变化中, 结构和位置不断改变, 即使做不到“同时”观测, 也要尽量减小时间差。比较理想的观测方法是共面观测, 即两部雷达同时在不同角度的通过两个雷达的平面内进行观测, 以获取降水系统的三维风场结构资料, 这样可以最大限度地减小时间差造成的反演误差。但这种作法非常困难, 雷达必须同时改变方位和仰角, 以保证雷达的扫描线在一个平面上, 目前, 我国新一代天气雷达系统还没有这种功能。实际上我们采用了如下同步方法:由于配对的两部多普勒雷达系统的型号不同, 其中合肥和宜昌雷达由北京敏视达公司生产, 马鞍山和荆州雷达由“38”所生产, 配对的两部雷达的观测模式的控制方法、天线扫描速度、径向数、距离库数和库长也不尽相同。为了缩短每个体扫的观测时间, 增加体扫的层数, WSR-98D雷达的现行模式以VCP11最适合双多普勒雷达观测, 一个VCP11体扫平均时间为5.5 min, 14层扫描; 马鞍山和荆州雷达也采用14层的体扫资料, 体扫时间采用5 min和6 min相间的方法。当降水系统处在共同观测区时, 进行双多普勒雷达同步观测, 每小时进行一次同步, 每4 h通过010-117电话进行计算机时间校准, 如误差大于1 min, 修改计算机时间。这样就保证了最大限度地减小了两部雷达观测时间的差异。
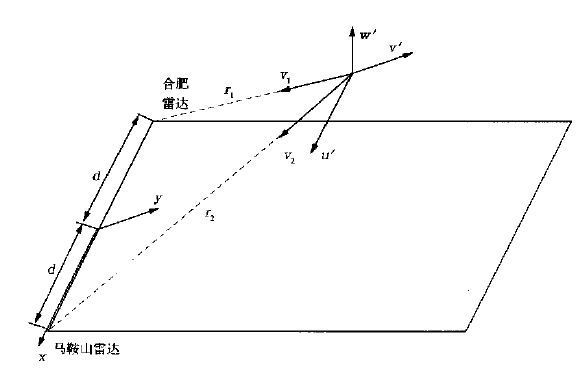
1.3 双多普勒雷达合成风场的误差分析双多普勒雷达采用共面方法反演风场的方法如图 2所示, 所分析的风场的位置和两个雷达3点组成一个平面, 在该平面上建立坐标系, 坐标点在两个雷达的中点, X轴通过两个雷达。将风场在该坐标系上进行分解, 即将风场分解为平行于X轴的分量u′和平行于Y轴分量v′, 这两个分量可以直接用两个雷达探测的径向速度直接计算得到, 垂直于该平面的分量可以通过对质量连续方程进行积分并假设第1层 (通常距地面高度为1 km左右) 的垂直速度为零而计算得到。为了简单起见, 我们只讨论两对双多普勒雷达如此配置情况条件下, 其探测接近地平面的u′、v′的精度, 因为这两个分量可以直接转换为水平风场。设两个雷达探测径向风场的标准差误差分别为σ1和σ2, 这样u′、v′的标准差误差σx、σy分别为[6]:
|
|
| 图 2. 双多普勒雷达反演风场示意图 | |
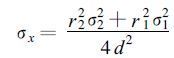
|
(1) |

|
(2) |
其中:r1、r2分别为任意点 (x, y) 距两个雷达的距离, d为两个雷达距离的一半。在该平面风场的大小和方向的误差σH、σθ分别为:
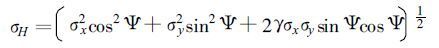
|
(3) |
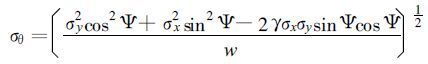
|
(4) |
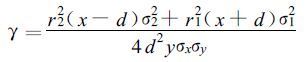
|
(5) |
其中Ψ是风场与雷达连线的夹角, w为速度的大小。
根据新一代天气雷达的技术要求, 合肥、马鞍山、荆州、宜昌4部雷达的探测径向速度的标准差应小于为1 m/s, 假设两部雷达测量径向速度的标准差为1 m/s, 我们计算了两对双多普勒雷达探测u′、v′的误差。
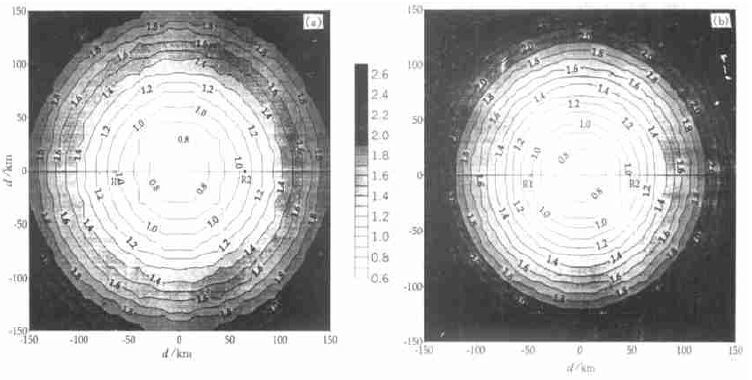
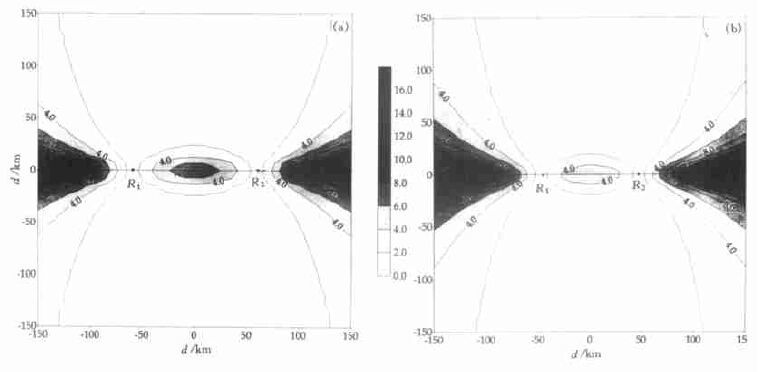
图 3、图 4分别给出了合肥、马鞍山双多普勒雷达和荆州、宜昌双多普勒雷达的σx、σy。从图中可以看出:双多普勒雷达反演平行于雷达连线的风场分量的误差随距雷达连线中点的距离的增大而增大, 当距离是两个雷达距离一半时, 其反演误差为雷达探测径向速度的误差, 在雷达150 km覆盖范围内, σx的范围在1.5倍的雷达取样误差以内。对于垂直于雷达连线的分量来讲, 在雷达连线附近反演误差比较大。基本规律是:两个雷达探测的径向速度的夹角接近0°或180°时, 反演误差比较大, 当远离这两个角度时反演误差比较小, 两个径向速度的夹角在40°~140°范围内, 其反演雷达连线垂直分量的误差在两倍雷达取样误差范围内。在两个雷达共同覆盖区内, 垂直于雷达连线的风场分量的反演误差一般大于平行于雷达连线分量的误差。根据这两对双多普勒雷达位置, 我们可以认为:两对雷达反演东西方向的风的误差小于反演南北方向的风。
|
|
| 图 3. 雷达测量径向速度的统计误差引起的合肥、马鞍山双多普勒雷达 (a) 和宜昌、荆州双多普勒雷达 (b) 的σx(单位:m/ s) | |
|
|
| 图 4. 雷达测量径向速度的统计误差引起的合肥、马鞍山双多普勒雷达 (a) 和宜昌、荆州双多普勒雷达 (b) 的σy(单位:m/s) | |
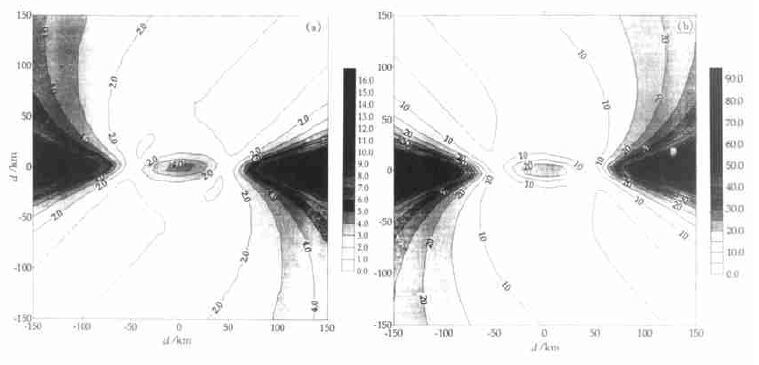
对于实际风场的大小和角度的误差来讲, 从式 (3)~(5) 中可以看出:除与σx、σy有关外, 还与风场的方向有关, 当风场方向与雷达连线平行时, 其风场大小的反演误差与σx相同, 同样, 当风场方向垂直于雷达连线时, 其大小的反演误差与σy一样。风场方向的反演误差除以上因素外, 还与风速大小本身有关, 风速越大, 风场角度的误差越小。图 5以宜昌荆州双多普勒雷达为例, 给出了风场方向与雷达连线夹角为45°、风速为10 m/s时, 风速大小和角度的反演误差。在两个雷达探测的径向速度的夹角40°~140°范围的大部分范围, 风速大小的误差在3 m/s内, 风方向的反演误差在20°以内。
除雷达探测径向速度的统计误差外, 雷达探测径向速度的系统误差也能引起合成风场的误差。设两部雷达探测风场的系统误差分别为ΔV 1、ΔV 2, 则因雷达系统误差造成的合成风场的两个分量的误差ΔV x、ΔV y分别为:
|
|
| 图 5. 在Ψ=45°, V=10 m/s时, 风速大小 (a) 和方向 (b) 的反演误差 (单位:风速—m/s, 方向—°) | |
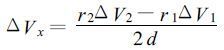
|
(6) |
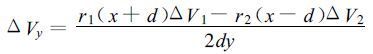
|
(7) |
从式 (6)、(7) 可以看出:当计算的风场坐标点与雷达距离在2d范围内, 雷达的系统误差引起的平行于雷达连线的风场分量的误差小于雷达系统误差。而对于垂直于雷达连线的风场分量误差来讲, 情况就复杂些。还以宜昌、荆州雷达为例, 图 6给出了ΔV 1=1 m/s, ΔV 2=0时, 风场垂直分量的误差, 与图 4相似, 该误差也与两个径向速度的夹角有关。

|
|
| 图 6. 雷达测量径向速度的系统误差造成的垂直于雷达连线的速度分量的反演误差 (m/ s) | |
值得注意的是:以上讨论的风场反演误差只涉及在共面上的风场分量, 影响因素只包括雷达测量径向速度的统计误差和系统误差, 而垂直速度的误差直接与以上两个风场分量的误差有关。在实际高层水平风场和垂直风场反演中, 还涉及到降水粒子本身下落速度、质量连续方程的积分以及资料的插值。另外, 由于两个径向速度观测时间的不同而引起的降水系统本身变化所造成的误差、雷达方位、仰角定位误差等因素引起的反演误差比较复杂, 在这里不再一一讨论。
2 双多普勒雷达观测资料质量控制的方法和结果从以上分析可以看出:配对的两部多普勒天气雷达探测的径向速度和反射率因子如果存在比较大的误差, 它可能导致风场反演的误差。为了保证双多普勒雷达资料分析结果的准确性, 研究双多普勒雷达资料的控制方法, 并对两对双多普勒雷达资料进行对比分析是很必要的。
2.1 双多普勒雷达观测资料的对比方法回波强度Z、径向速度V和速度谱宽W的对比方法如下:首先将两部多普勒雷达以球坐标方式存储的原始资料, 经水平面上的双线性插值、垂直方向的线性插值等处理后, 转化以雷达为中心的直角坐标的资料, 该资料的水平和垂直分辨率均为1 km。然后, 根据两个雷达的相对位置, 将这两种直角坐标下的资料转化到同一坐标上。在进行回波强度比较时, 尽量选择与两个雷达距离相近的回波区进行对比; 而径向速度除雷达连线附近的区域外, 其它区域两个雷达探测的径向速度方向不一致, 无法对比, 同样速度谱宽也与方向有关, 所以, 两个雷达探测的径向速度和速度谱宽只在雷达连线上方1~2 km的等高面上进行对比。
由于雷达信号本身的涨落、两部雷达方位和距离的微小误差以及降水系统的演变和移动等原因, 使得点对点的对比时两个回波强度差值的变化范围很大。为此我们提出了回波强度的概率比较法, 即在同一块回波面积中, 将两部雷达探测的回波强度按大小进行概率分布计算, 然后根据概率分布曲线确定两个雷达探测的回波强度之间的关系。如果一部雷达探测的某一回波强度的概率与另一雷达探测的另一回波强度的概率相同, 则这两个强度是对应的。这样可以得到两部雷达探测的不同回波强度之间的关系, 从而对回波强度进行订正等处理。
2.2 对比结果下面以2001年973“中国暴雨”外场试验的双多普勒雷达资料为例进行资料对比试验。在2001年6月10日至7月20日的外场试验期间, 长江中游和下游的双多普勒雷达分别获取到5次和3次降水过程, 中游5次过程的时段为:6月16日14:00(北京时, 下同)~18日20:00、6月27日20:00~29日12:00、7月6日18:00~7日22:00、7月12日12:00~23:00、7月14日18:00~23:00, 下游3次过程的时段为:6月16日20:00~19日08:00、6月22日20:00~24日14:00、7月11日14:00~15日08:00。
利用2001年两对双多普勒雷达的观测资料, 对比了回波强度、径向速度的观测结果。我们以6月18日13:00、7月13日19:04、7月14日03:22合肥、马鞍山双多普勒雷达观测结果为例, 讨论长江下游双多普勒雷达对比结果; 以6月17日22:17的体扫资料为例讨论长江中游双多普勒雷达观测资料的对比结果。
首先, 比较6月18日13:00个例的回波强度。从合肥、马鞍山两个雷达观测的4 km高度上的等高显示CAPPI图上 (略) 可以看出:两个雷达观测的同一降水区回波的位置、强度变化趋势等宏观特征较为一致, 但位置有一定的误差。考虑到马鞍山和荆州雷达未采用太阳法精确确定方位, 所以我们对马鞍山和荆州雷达资料进行方位旋转处理, 在一定的回波范围内求出每一次旋转时配对的两个雷达的1 km ×1 km格点的回波强度的相关系数和标准差 (表 2)。从结果可以看出:将马鞍山和荆州雷达资料沿逆时针旋转7.0°和5.6°后 (雷达方位分别减去7.0°和5.6°), 两对双多普勒雷达资料的相关明显增大, 标准差减小。同时, 我们也分析了观测时间的不同对误差的影响, 用相隔6 min的两个体扫的资料进行对比发现, 3个个例相关系数在0.6~0.8之间, 标准差在4.8~8.3 dBz之间。
|
|
表 2 马鞍山、荆州雷达不同旋转角度时配对雷达1 km×1 km格点上回波的标准差和相关系数 |
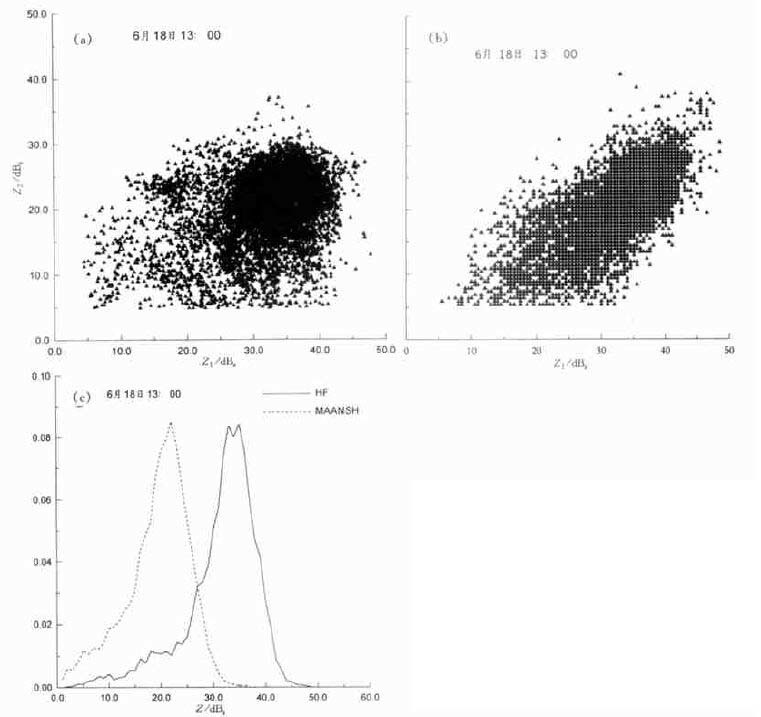
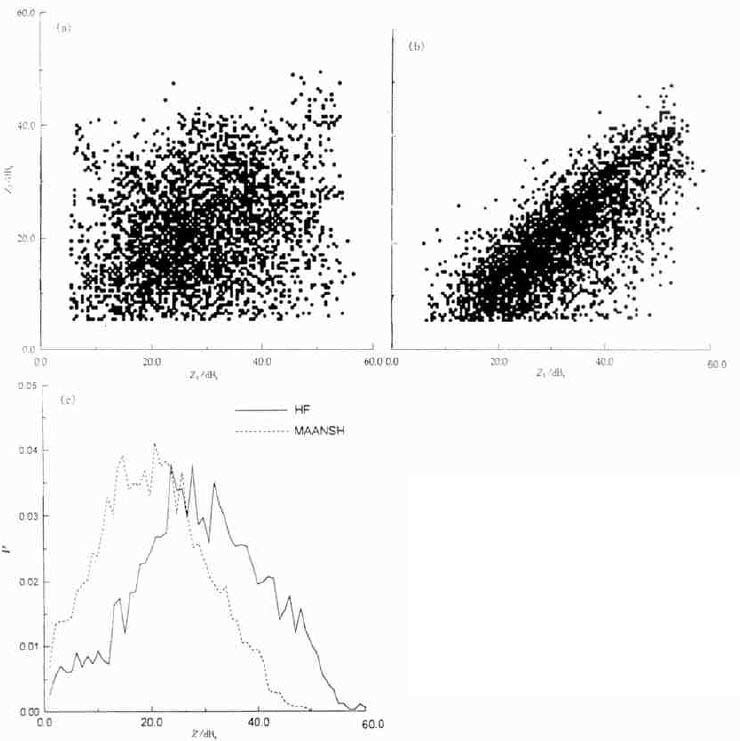
图 7中给出了90 km ×90 km范围内旋转前和旋转后点对点的对比结果及不同强度的概率分布图。马鞍山和合肥雷达观测的回波强度有明显的差异, 从概率分布来看, 除两个雷达的灵敏度不同和观测的距离不同而引起的弱回波区的变化趋势有所区别外, 两个曲线变化规律很一致, 只要将马鞍山雷达对应的概率分布曲线向右移11 dBz, 它就和合肥的曲线基本重合。旋转后7.0°, 马鞍山和合肥雷达回波强度对应关系明显改善。同样, 有较强回波强度的7月13日19:03的个例 (图 8) 也一样, 两个雷达观测的回波强度相差也约为11 dBz, 雷达方位旋转后, 回波强度对应关系也明显改善。从这两个例我们可以初步得出结论:合肥马鞍山双多普勒雷达观测强回波和弱回波的强度全部相差11 dBz, 而且马鞍山雷达方位定位偏离7.0°。造成这一差别的原因可能是雷达在标定的计算中有误。
|
|
| 图 7. 2001年6月18日13:00合肥雷达、马鞍山雷达观测的回波强度 (Z) l km×1 km格点在方位旋转前(a) 和旋转后(b) 一对一的对比和不同回波强度的概率(P)分布图 (c)(Z1为合肥雷达观测的回波强度,Z2为马鞍山雷达观测的回波强度) | |
|
|
| 图 8. 2001年7月13日19:04合肥雷达、马鞍山雷达观测的回波强度l km×1 km格点在方位旋转前(a) 和旋转后(b) 一对一的对比和不同回波强度的概率分布图 (c)(Z1为合肥雷达观测的回波强度,Z2为马鞍山雷达观测的回波强度) | |
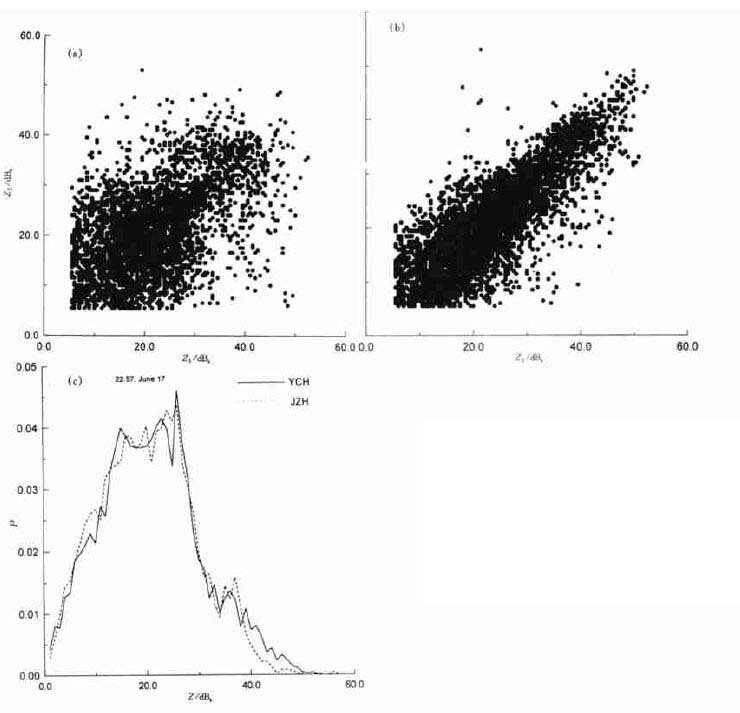
我们也分析了长江中游宜昌和荆州多普勒雷达观测的回波强度的对比结果, 图 9给出了6月17日22:57两个雷达观测的回波强度的对比, 从这一结果可以看出:宜昌和荆州雷达观测的回波强度的概率分布曲线很吻合。也就是说:这两个雷达探测的回波强度比较一致, 不需要订正, 但雷达的方位定位存在5.6°左右的误差。
|
|
| 图 9. 2001年6月17日22:57宜昌、荆州雷达观测的回波强度l km×1 km格点在方位旋转前(a) 和旋转后(b) 的对比及不同回波强度的概率分布图 (c)(Z1为宜昌雷达观测的回波强度,Z2为荆州雷达观测的回波强度) | |
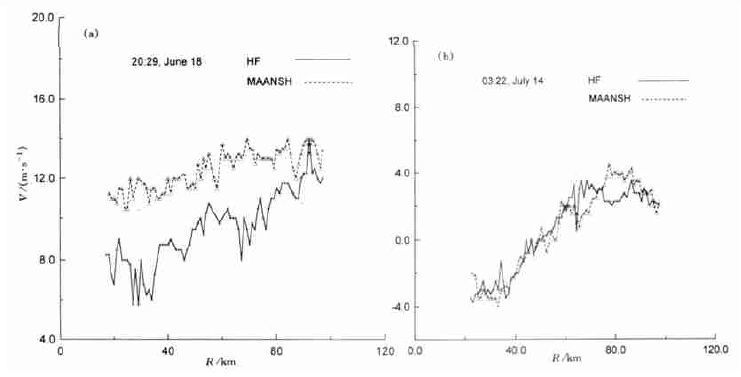
对于合肥、马鞍山雷达观测的径向速度, 我们比较了经方位旋转后6月18日13:00和7月14日03:22两个个例 (图 10), 两个个例给出的结果也不尽相同。其中第1个个例的径向速度值比较大, 马鞍山观测的径向速度的绝对值比合肥的大2~3 m/s左右; 另一个个例径向速度的值比较小, 两个雷达观测的径向速度不管是变化趋势还是数值都相当一致。
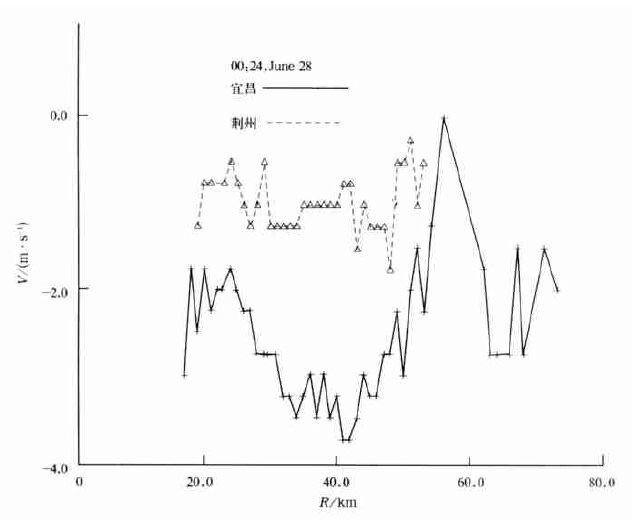
对应长江中游的观测情况, 2001年处于两个雷达连线的过程不多, 从6月28日的结果 (图 11) 可以看出:雷达观测的径向速度的变化趋势比较一致, 两者相差1~1.5 m/s。
|
|
| 图 10. 2001年6月18日13:00 (a) 和7月14日03:22 (b) 合肥、马鞍山雷达连线上方2 km等高线上的径向速度的对比 (其中将马鞍山的径向速度改变了符号以方便比较) | |
|
|
| 图 11. 2001年6月28日00:28宜昌、荆州雷达连线上方2 km等高线上的径向速度的对比 (其中将荆州的径向速度改变了符号以方便对比) | |
两个雷达观测的径向速度不同的一个原因是两个雷达观测的径向速度的时间不相同, 降水系统的移动和演变会造成误差。我们比较了相差5 min的同一雷达的资料, 发现5 min的间隔速度差0.3~1.0 m/s。径向速度的对比比较复杂, 它不像回波强度那样可以在比较大的范围内对比, 只能在雷达连线上1~2 km的等高线上对比, 应有比较多的个例才能进一步说明问题。
3 结论通过以上分析, 我们可以得到如下结论:
(1) 双多普勒雷达反演的共面上的速度与雷达探测径向速度的统计误差和系统误差有关外, 还与速度的大小和方向有关, 两个径向速度的夹角在40°~140°范围内, 反演径向速度的标准差误差不超过雷达探测径向速度的标准差的2倍。
(2) 两对双多普勒雷达观测的回波强度的宏观特征比较一致, 合肥、马鞍山的雷达的回波强度相差11 dBz, 宜昌、荆州雷达回波强度很吻合。马鞍山和荆州雷达在方位定位上可能存在比较大的误差, 将这两个雷达资料的方位分别减去7.0°和5.6°后, 双普勒雷达资料的对应关系明显改善。在试验双多普勒雷达资料时, 必须进行严格的资料对比, 以保证结果的可靠性。
(3) 两对双多普勒雷达观测的雷达连线上的径向速度变化趋势比较一致, 但在数值上有一定差异, 这种差异除雷达系统本身的测量误差外, 实际观测的时间差也是造成这一现象的主要原因。这一问题仍有待进一步研究。
(4) 从分析结果看, 双多普勒雷达观测与单多普勒雷达观测相比, 对雷达的探测精度和定位精度要求更高, 很小的系统误差有可能导致分析结果的很大误差。
致谢 感谢安徽省气象局、湖北省气象局、马鞍山气象局、宜昌市气象局、荆州市气象局等参加外场试验观测的气象工作者为雷达观测付出的辛勤劳动。| [1] | Larry A. A theory for the determination of wind and precipitation velocity with Doppler radars. J. Atmospheric Science, 1969, 26: 570~573. |
| [2] | Lhermitte R M. Dual Doppler radar observation of convective storm circulation. Preprints of 14th Radar Meteorology Conference, Tucson, American Meteor. Society, 1970. 139~144. |
| [3] | Ray P S, Ziegler C L, Bumgarner W, Single-and multiple-Doppler radar observations of tornadic storms. Monthly Weather Review, 1980, 108: 1607–1625. DOI:10.1175/1520-0493(1980)108<1607:SAMDRO>2.0.CO;2 |
| [4] | Mewes J J, Shapiro A, Dual-Doppler analysis using the anelastic vertical vorticity equation. 29th International Conference on Radar Meteorology, 1999: 33–36. |
| [5] | 张沛源, 何平, 宋春梅, 等. 三部多普勒天气雷达联合测量大气风场的误差分布及最佳布局研究. 气象学报, 1998, 56: 94–103. |
| [6] | Doviak R J, Ray P S. Error estimation in wind fields derived from dual-Doppler radar measurement. J. Applied. Meteor., 1976, 15: 868~878. |
 2003, 14 (1): 17-29
2003, 14 (1): 17-29