多普勒天气雷达所探测到的风场信息存在噪声、缺测和速度模糊问题,这成为多年来一直影响风场信息应用的棘手问题。
国外从20世纪70年代末开始研究速度扩展问题。最简单的方法就是单径向上“点-点"对比法[1],这个方法对噪声和缺测点敏感,如一个单点错误,可以引起径向上其余点的速度扩展的连续不正确或判别终止。80年代初有人改进了这种单径向法[2],虽然这些技术减少了噪声等的敏感性,但是在正交方向的连续性仍被忽略了。1984年Merrit提出了一个较为有力的二维方法[3],后经Boren(1986),Bergen和Albers(1988)进一步发展完善[4, 5]。该方法利用了雷达在一个仰角扫描下的完整的二维数据,其缺点是必须使用一个风场模型来消除大区域的整体模糊,而相对于小区域的整体模糊区则不十分有效,另一方面需要花费大量的计算时间。1990年Eilts和Smith使用“双径向"方法[6]进行了速度扩展,对正确率和计算时间都有所改善。但是这种方法并非总是可靠,因在切向上利用的仅是两点间的信息,对噪声的敏感性虽然降低了,但在距离和方位上的误差叠加却出现了。与国外相比,国内在这一方面的研究成果还不多。目前主要采用手工的或人机结合的方法对径向上单点资料进行处理,这样的方法效率低,不能适应科学研究和实际业务工作的需要。
为了降低噪声和缺测值的影响,本文提出了一种物理意义较明确的“K-邻域频数法"的物理统计方法进行预处理,在此基础上设计了用“双径向-双切向"的二维方法进行速度扩展,并在WINDOWS环境下建立起有效的“交互"式的消除整体速度模糊的新方法。
1 多普勒天气雷达速度模糊与噪声问题由于采样的离散性,在多普勒雷达的探测中,常常出现速度模糊现象。多普勒雷达所探测到的速度值被限制在一个有限的动态范围内,称为Nyquist速度VN。多普勒雷达的最大可测径向速度VN与雷达波长λ和脉冲重复频率Fr有如下关系:
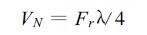
|
通常,若多普勒速度测量值为V,我们只知道实际的径向速度V′是:
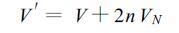
|
(1) |
这里,n是一个整数。这是由于真实速度超出了±VN的范围,而被“折叠"限定在正、负Nyquist速度之间。
速度扩展的目的就是对每一个速度测量值寻找出一个正确的n值,从而获得真实的径向速度值V′。
从广义上讲,在多普勒雷达速度扩展中的关键问题是“噪声"。如果数据无噪声并且连续,又有可预测的边界范围,那么一个非常简单的处理就会得到一个好的结果。影响速度扩展的因素包括数据尖点,数据的缺测,数据不连续和非自然的突变,地物杂波,飞机反射,二次回波,旁瓣等等,另外也与多普勒天气雷达性能密切相关。一个实用的速度扩展算法必须对各种“噪声"做合适的处理。“噪声"使得速度扩展变得更加困难,因为在一定程度上使通常的数据连续性假定变得无效。相反,如果有一个合适的“噪声"处理方法,则速度扩展技术一般不会出现大的问题。下文就介绍一种新的滤波方法。
2 K-邻域频数法速度扩展之前,在保留有效速度信息下尽可能多地剔除噪声是非常必要的。这有两方面的原因:一是要剔除非自然的大梯度,它影响到算法对数据的识别;二是要减少速度扩展算法的计算要求。Boren等人提出了5点双向中值滤波器来处理孤立点、缺测点和剔除一些脉冲噪声。该方法是对传统中值滤波器(medianfilter)的一个改进,具有其优越性。但是在试用中,经进一步试验分析,我们发现补缺测点时所依据的邻点具有不可靠性,因为往往在缺测点附近出现较多的噪声,因此会出现噪声的扩大;剔除噪声所依据的有效数据点可能本身就是噪声,缺乏衡量数据是否有效的一个尺度。
本文经过反复的试验和对比分析,提出了一种物理意义较明确的统计方法来进行资料的预处理。以下简称为“K-邻域频数法"。
在M×N的窗口中,属于同一物体(回波)的像素,它们的灰度值高度相关,噪声则普遍是一些孤立的、不相关或不连续的奇异点(域),是统计叠加在图像上的。因此,对窗口内像素灰度的分布统计具有其物理意义。我们把±Nyquist速度范围分成不同的P个等距Np(p=1,2,…,P),区间间隔为Δd,另外窗口中心点的值Vij±Δd/2列为第P+1个区间N′,然后统计在M×N窗口内的点分布在不同区间出现的频数χp(p=1,2,…,P)和χ′,令xmax是χp(p=0,1,2,…,P)、χ′中的最大值,取xmax所对应的区间的中点值为Vp,那么,窗口中心点新值V′ij可以表示为:
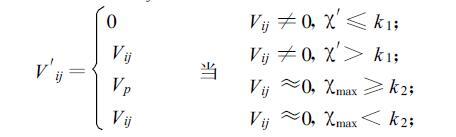
|
(2) |
式中,k1是剔噪声阈值,k2是补值阈值,“0"代表无回波,在式(3)、(4)中相同。
这是一个空间二维的统计方法,其过程可分为三步:
第一步,统计以Vij为中心的M×N窗口内的M×N个点分布在不同区间的频数χp(p=1,2,…P)、χ′,寻找出最大的频数xmax。
第二步,剔除孤立点、孤立小区域和连续区域中的奇异点。Vij可表示为:
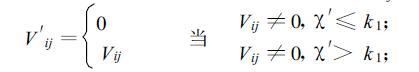
|
(3) |
如果Vij不为0,当χ′≤k1时,即该点出现的次数很少,以至于小于k1次,则把该点剔除,认为是无效的噪声点;当χ′>k1时,即出现的次数足够多,则认为该点具有统计属性,是“真实"的点。
第三步,补缺测点。Vij可表示为:
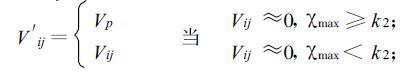
|
(4) |
如果Vij为0,并且满足条件xmax≥k2,即在以该点为中心的窗口内,出现次数最多的点所出现的次数足够大,以至大于给定的阈值时,表明该窗口区域具有统计属性,以xmax所对应区间的中点值Vp补充该缺测点是满足统计特征的,取Vij=Vp而使该点也具有了这个窗口的共同属性,这是具有物理意义的;若不满足条件xmax≥k2,则认为该点无回波,表明其所在的窗口区域内无回波或很少有回波。
为保持空间不变性,对一个点的处理,不影响任何一个相邻点的处理。经分析比较,“K-邻域频数法"是一种物理意义明确,省时有效,既处理了噪声,又保持了原有数据结构的较好方法:
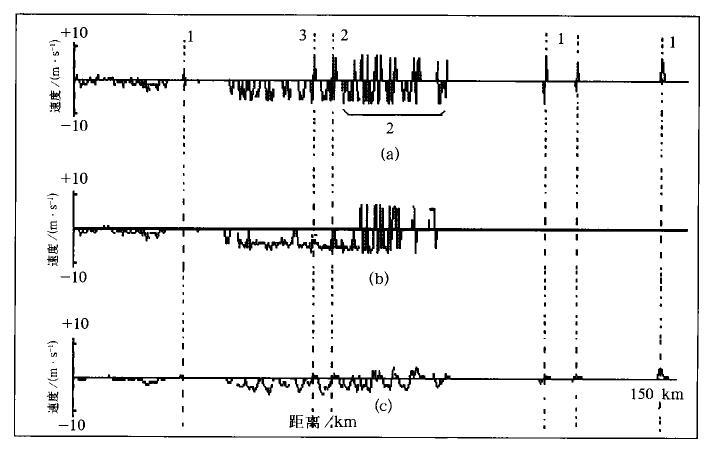
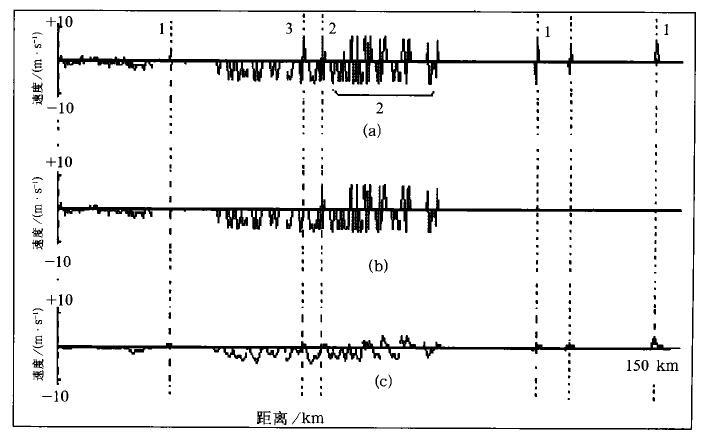
(1) “K-邻域频数法"的处理结果与参数P、M、N、k1和k2有关。P与Nyquist值相关,经试验整数P在数值上约取VN大小较合适。如果窗口M×N取得太大,则对数据过于平滑,保持细节不好。k1和k2与M、N有关,一般不应小于M×N窗口内的点分布在所有P个区域的平均数χ=(M×N)/P,试验表明k1和k2应大于χ。k1是噪声阈值,k1越大越容易剔除噪声,但k1过大会产生误剔除。k2是补值阈值,对不同的目的,可通过调整k2达到不同的效果。k2越小,填补点越多,反之填补点减少。图 1和图 2是在k1不变时,分别取k2=1/6(M×N)和k2=1/3(M×N)的对比试验。由图可见,在取相同的k1时孤立点1作为噪声均被剔除;点2在图 2中相对图 1填补值较少,保持较好;点3是M×N窗口内负值区里的一个正值,被当作奇点修正为正值。
|
|
| 图 1. “K-领域频数法”处理径向速度示例K2=1/6(M×N) | |
|
|
| 图 2. K-领域频数法”处理径向速度示例K2=1/3(M×N) | |
(2) 抑制或消除噪声比较有效,保持回波原有结构效果理想。图 1和图 2中的上图(a)是原始数据廓线,中图(b)是经该方法预处理后的数据廓线,下图(c)是经平滑处理后的数据廓线。图 1、图 2的中图(b)中的噪声点1被很好地消除,图 2中图(b)的点2保持了原有的细节。下图(c)在平滑处理后的数据中虽然噪声得到了抑制,但数据间的差别在很大程度上被抹杀了。
(3) 对于回波区内的缺测点、奇值点,可以作较好的填补。图 2中图(b)的点3得到了修正。图 4和图 5的A区和D区对边缘的填补既保持了原状,又对边缘作了修剪。

|
|
| 图 4. CAMS多普勒天气雷达PPI径向速度图像 | |
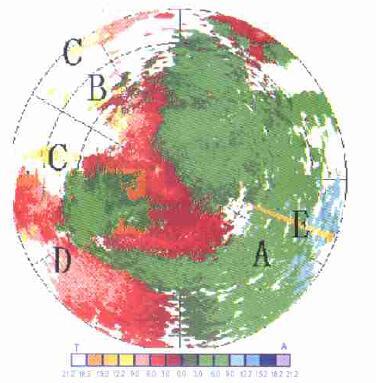
|
|
| 图 5. 对图4K-领域频数法”和单径向退模糊 | |
(4) CAMS的雷达观测中,我们取M×N为5×5是合适的。这有两方面的原因:一是从统计效果来考虑,二是从反演算法的计算网格考虑。国产714SD多普勒雷达的方位分辨率是1°,径向分辨率是300m, 在15km处的5×5窗口相当于1.5km×1.5km, 在50km处的5×5窗口相当于1.5km×4.3km。统计这样大小的回波体,足以表示出它的共同属性。在本文的算法中计算网格取为1.5km, 所以统计窗口和计算网格是一致的。
同一物体的像素点是高度相关的,噪声则是叠加其上的离散点或缺测点。K-邻域频数法正是利用了物体(像素)的相关性,物理意义是明确的。K-邻域频数法处理的点具有其所在邻域的共同的统计属性,包含二维风场的信息。在进行“点-点"相比较时,实质上是对点所在区域共同属性的比较,这样就大大降低了速度扩展时对缺测点和噪声的敏感性。
3 速度扩展算法设计采用“K-邻域频数法"极大地抑制或消除了噪声,填补了空缺,从而大大地降低了噪声等对速度扩展的影响。在此,我们设计了单径向的速度扩展算法,并提出“双径向-双切向"的二维速度扩展算法。
第一步,运用K-邻域频数法沿径向对雷达资料作预处理。
包括补充缺测点,消除尖点,抑制噪声,平滑数据。这样,凡是经过处理的点,包含了其邻域内二维风场的统计信息,具有了共同的特征;未经处理的点,则被认为是正确的点,它包含有正常速度值、模糊速度值和未被消除或受到抑制的噪声。
第二步,自雷达原点沿径向速度扩展。
此时,径向上第一点被认为是正确的。以该点为基准,对该径向上的每一有效点i与其后不超过k个有效点作比较,比较顺序是从雷达原点方向到远处,若有一点满足条件,则对i点后的第一点退模糊。
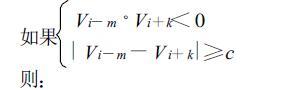
|
(5) |
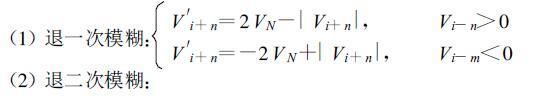
|
(6) |
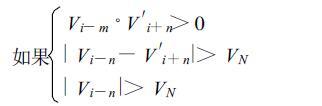
|
(7) |
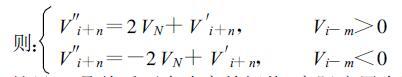
|
(8) |
这里,c是前后两点速度差阈值,实际应用中取小于2倍的VN;i是径向数据点序号,以此点为参考点对其后的i+n点退模糊,通常n取1,但当数据“跳跃"或“缺测"严重时可取2或3;m和k是整数,k≥1,m≥0且m,k<M′,M′是在i点处取同径向邻近点个数的阈值;本文中取k≥1,m≥0的含义是在i点附近存在无回波区时向前或向后寻找若干点检验是否满足公式(5),其实质是取消了速度退模糊的数据连续性假定(如图 3);V′i+n是速度扩展后的值,VN是Nyquist速度。

|
|
| 图 3. 多普勒速度场分布示意图 | |
双径向速度扩展算法。在选择双径向的方法时,则在上述速度扩展的过程中,对每一个“已扩展的点"作上标记,当在扩展下一个径向速度时,参考其前一个径向在方位上相对应的点或其邻点。当一个径向上的数据有较多的不连续点时,常不能满足条件式(5),此时式(5)改写为:
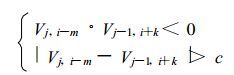
|
(5′) |
式中,Vj-1是Vj的前1个径向速度值。这里需注意Vj-1,i+k是未经速度扩展的值,它具有一个标记f{0,1},当f=0表示该点不是速度模糊值,当f=1时表示该点是模糊值。因此,双径向速度扩展算法的判别式是:
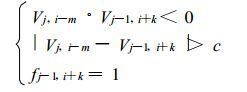
|
(5′′) |
式(5″)的含义是,当某点不满足式(5)时,即考查其前一径向对应的相邻点,如果邻点满足式(5)且是模糊点,则将该点作速度扩展处理。
风场数据不连续是影响单径向速度扩展效果的一个重要原因,双径向法使得数据不连续在一定程度上得到了改善。
第三步,沿切向整体模糊区的速度扩展。
通常的速度扩展算法均有两个假定,一是假定风场数据是连续的,二是假定初始的参考点是正确的。如果速度场被很好地取样,以致于可以满足上述条件时,速度扩展则很少成为问题。在风场连续的速度模糊区,点-点间的联系是明确的,ΔV是一个可知量。这种连续区域内与点-点间风速差有关的模糊被称为相对模糊。借助于ΔV的差别,数据连续的相对模糊区通常能够被正确地速度扩展。其实,在雷达原点附近且远离地物回波的点都可用于初始化参照。当第一点接近雷达时,通常具有很好的参考意义,当初始参照点离雷达较远时,就有可能出现整体模糊,即径向和(或)切向连续的区域数据均是速度模糊的。
在本文的速度扩展中,我们取消了第一条假定,即连续性假定,认为风场相对孤立的回波区存在彼此间的联系,如在公式(5)中取k≥1,m≥0且m,k<M′。如图 3,A位置的数据是一片相对于雷达原点孤立的回波区,A区通常缺乏真实的参考点(或线),我们只能以第二条假定为基础,以区域边缘为初始参照点。因此,A区可能出现整体模糊。C区靠近雷达原点,通常取原点附近的值为初始参照是可行的。B位置相对C位置是孤立的回波区,B区和C区之间的联系有多大是不确定的。由于B区的速度扩展是以C区为参考的,也存在可能整体模糊问题。
由上述可知,经过第二步速度扩展处理,相对模糊能够被很好地识别并处理,留下的问题是有些区域出现整体模糊。这些区域既是相对独立的,有其自身的属性,又是相互联系的。本文正是利用其既相互区别,又相互联系的辩证关系,从区分各个区域的平均属性差ΔV来识别整体模糊的。
本文消除整体模糊的方法是以起始选择的假定正确的数据为参照,沿切向(方位)进行区域速度扩展,取双切向上同一方位两点周围的有效点的平均值表示其属性,通过减少切向上近邻点-点之间的差别,直至小于Nyquist速度为止。双切向法与双径向法不同处是以两点的平均值代替单点值,这是由于整体模糊区内的点具有同是正值或同是负值的特点。
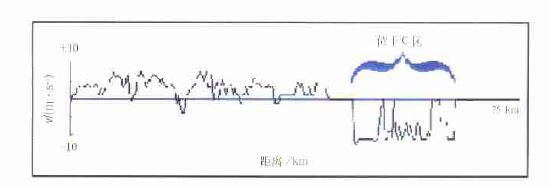
图 4是北京地区的一次强降雹过程的多普勒风场,取自CAMS的10cm多普勒雷达1995年6月22日15:00(北京时,下同)的观测资料。在A区的风场资料严重缺测,径向上模糊和不模糊的数据排列无序。B区存在许多孤立噪声,消除这些噪声是非常必要的。C区是数据模糊区域,需要作速度扩展处理。图 6是取自图 4穿过C区的一个径向上的速度廓线,明显看出C区速度是模糊的。CAMS多普勒雷达的Nyquist速度范围为±10.6m/s, 这样低的Nyquist速度意味着退模糊存在更大的难度和低成功率。这有两方面的原因,一是低Nyquist速度使得出现更多的速度模糊,二是大的风切变和噪声使低Nyquist速度模糊识别造成困难。
|
|
| 图 6. 取自图4穿过C区的方位为281度的径向速度廓线 | |
图 5是对图 4经预处理后的图像。经K-邻域频数法处理噪声后,A区的噪声得到了极大的抑制,补充了这一区域的风场缺测资料。补充后的风场,不但没有改变原有风场区域内的共同属性,而且使新补充的数据正表现了原有数据的特征。在B区,噪声被很好地消除。C区速度得到扩展。D区是一个边缘杂乱的区域,经处理后,不但得到了修正,而且保持着原有形状和结构。
在这个例子中,共有125000个速度数据,存在模糊的数据约5500个,经单向的速度扩展处理,已消除了绝大多数的数据模糊区。在E区出现整体模糊,占模糊数据的10%,再经切向速度扩展可以达到90%以上的准确率。这表明该方法是可行的,基本能够满足实际工作的需要。
径向速度扩展法一般是可靠的,但是当出现大的风切变,又在低Nyquist速度下,各种速度扩展方法都会遇到难以克服的困难。为了达到接近100%的处理结果和满足有些科学研究的需要,本文提供了一种界面十分友好、省时有效的交互方法作为自动速度扩展方法的一个补充。
4 交互式速度扩展方法多普勒天气雷达的风场信息是复杂多变的,各种速度扩展方法总有其局限性,无法做到尽善至美,而往往是在最需要的时候出现速度扩展不正确。本文面对复杂多样的数据,对无法自动进行速度扩展的整体模糊部分,采用了一种界面十分友好的、直观形象的人机交互式方法。
人机交互包括两个层次的内容:
(1) 一维的数据交互。在扫描前或扫描后,用户可以用鼠标拖动“橡皮筋"显示任意径向和切向上的速度廓线图。这些廓线图使用户透过屏幕图像在交互窗口内直接观察到多普勒速度数据。在交互窗口内,除完成每一个径向和切向上的速度廓线图显示外,还可以编辑数据,选择速度扩展参数,校正径向速度扩展的数据。
(2) 二维的数据交互。二维的数据交互是整体速度扩展的有力补充。在完成径向速度扩展之后,必要时有两种选择来消除整体模糊,一种是沿切向整体速度扩展,另一种就是二维的数据交互。所谓二维的数据交互就是用户在显示有整体模糊区的速度图像上,用鼠标单击一下,程序就把这个屏幕像素点转换到雷达速度数据中定位,根据定位点周围数据的平均属性来确定具有这一相同属性的区域,然后确定本区域与其相邻区域的差别,从而根据这些差别达到速度扩展的目的。这种交互方式十分快捷准确,操作灵活方便,只要用户用鼠标在屏幕上轻轻一点,就能把整体模糊区域识别出来,然后在屏幕上以“色标"重新表示,给人的感觉就象在调和颜色一样轻松。二维的数据交互能够处理自动速度扩展遗留下的全部速度模糊区,这在科学研究中完成约90%以上的速度扩展在一定条件是必要的,尤其在低Nyquist速度和出现大的风切变情况下就显得更为重要了。这样的人机交互式速度扩展方法改变了传统的人机结合的方法,极大地提高了效率。
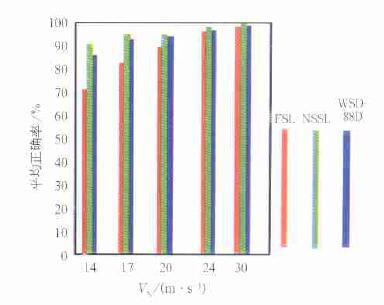
5 效果分析与算法应用1993年,Zittle等对WSR-88D、NSSL和FSL的速度扩展算法进行了对比分析[7],表明在低Nyquist速度下(14m/s)的速度扩展正确率约为70%~90%,如图 7所示。
|
|
| 图 7. 美国“预报系统实验室(FSL)”,“国家强风暴实验室(NSSL)”和“WSD-88D雷达”速度扩展正确率比较 | |
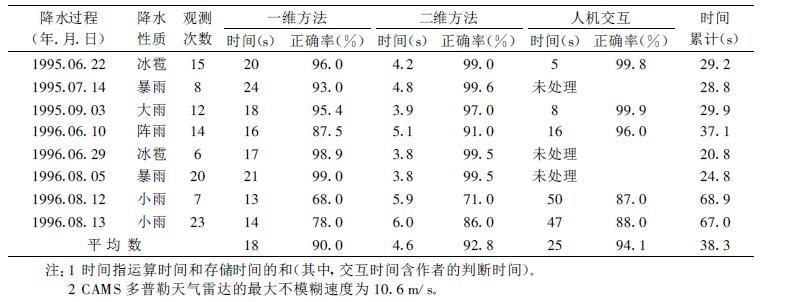
以上介绍的速度扩展算法在中国气象局强风暴实验室得到试验应用,对京津冀中尺度探测基地1995~1996年的不同降水性质的探测资料进行了分析比较,结果如表 1。
|
|
表 1 CAMS多普勒天气雷达速度资料退模糊试验表 |
本文采用了Zittle文中的方法,正确率PC(Percent Correct)表示为:
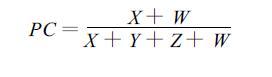
|
式中X、Y、Z和W的含义如表 2。如果“真实"场的数据与算法处理过的数据的差小于1m/s且大于Nyquist速度VN,那么该点记为“X-对";如果算法退模糊过的值大于VN,而“真实"值小于VN,则记为“Z-错";如果两个值均小于VN且小于1m/s的门限,则记为“W-无";其它情况时,记为“Y-失"。
|
|
表 2 速度扩展后的可能情况 |
从表中可知:①在降水量级偏小时,速度扩展的正确率相对于出现冰雹、大(暴)雨等强烈天气时的正确率偏低,当出现强烈天气现象时其正确率比较高。而在强烈天气现象出现时,保证高的速度扩展正确率正是我们所期望的。当降水量级小时,雷达的信噪比降低,增加了区别有用信号与噪声的难度,从而影响到速度扩展的正确率。②一维(或二维)的速度扩展算法的平均正确率约为90%(最大不模糊速度10.6m/s),与美国WSR-88D、NSSL和FSL的速度扩展正确率相当,本文所采用的“K-邻域频数法"和速度扩展算法是可行的。③当需要更高的正确率时可以使用人机交互的方法,在处理质量和处理时间上做出选择。
本方法在国产多普勒天气雷达714SD上普遍使用,在1998年华南暴雨试验多普勒天气雷达资料处理中得到很好的应用。实践证明,该方法基本上能够满足实际工作的需要,是目前所采用的一种行之有效的较好的方法。在微机上进行数据预处理,降低了硬件成本。
6 结语多普勒天气雷达的数据预处理是一个复杂的难题,不同性能和参数的雷达,不同的测站环境,不同的天气现象等都会影响数据处理的效果。随着单部多普勒天气雷达风场反演方法的发展和使用,数据预处理的方法和处理效果越来越显得重要,其效果的好坏直接影响风场反演的结果。今后在多普勒天气雷达数据预处理的实时性和处理效果方面有待于进一步的提高,对各种影响因素的适应性也需要改善。另外,有了风场信息预处理的有效方法,也将有利于促进多普勒天气雷达风场反演方法的业务使用。
| [1] | Ray P, Ziegler C. De-aliasing first-moment Doppler estimates. Appl.Meteorol, 1977, 16: 563–564. DOI:10.1175/1520-0450(1977)016<0563:DAFMDE>2.0.CO;2 |
| [2] | Bargen D W, Brow n R C. Interactive radar velocity unfolding. Boston, 1980: 278–283. |
| [3] | Merrit M W. Automatic velocity dealiasing for real-time application. Soc.,Boston, 1984: 528–533. |
| [4] | Boren T A, Cruz J R, Zrnic D S. An artificial intelligence approach to Doppler radar velocity dealiasing.23rd Conferenceon Radar Met eorology,Snowmass,Colo.,American Meteor. Soc.,Boston, 1986: 107–110. |
| [5] | Bergen W R, Albers S C. Two- and three- dimensional dealiasing of Doppler radar velocity. And Oceanic Tech., 1988, 5: 305–319. DOI:10.1175/1520-0426(1988)005<0305:TATDDA>2.0.CO;2 |
| [6] | Eilts M D, Smith S D. Efficient Dealiasing of Doppler Velocities Using Local Environmental Constraint s,FAA Report,1988. FAA Report, 1988. |
| [7] | Zittle W D, O' Bannon T. On the performance of three velocity dealiasing techniques over a range of Nyquist velocities :Preliminary findings.25th Conference On Radar Meteorology,AMS,Paris,France,American Meteor. Soc.,Boston, 1991: 53–55. |
 2002, 13 (5): 591-599
2002, 13 (5): 591-599