近些年来,科学家们用全球海气耦合模式研究人类活动对气候影响有了进一步的发展。与以前不同的是更多的考虑了人类活动对近百年全球气候变化的影响。即在模式做近百年气候变化的模拟中加入了二氧化碳等温室气体和硫化物气溶胶的作用,从而用模式模拟的近百年气候变化与观测的气候变化作对比,一方面可以分析模式的可靠性,另一方面可以检测人类活动对近百年气候变化的影响[1~4]。
本文将对由IPCC数据中心 (DDC) 提供的5个全球模式的模拟结果在东亚地区进行检测。这5个模式包括ECHAM4[5] (德国马普研究所),HADCM2[6] (英国Hadly气候预测与研究中心),GFDL-R15[7] (美国普林斯顿大学地球物理流体动力实验室),CGCM1[8](加拿大气候模式与分析中心),CSI RO-MK2[9, 10] (澳大利亚科学与工业研究所)。这些模拟是为目前正在进行的IPCC第三次气候变化评估报告的编写而进行的。众所周知,利用全球模式模拟区域气候变化是有较大的局限性和不确定性,过去不少人曾进行过检验,但自从IPCC第二次评估报告出版以来,全球海气耦合模式得到了一定的改进,我们所用的这5个模式模拟结果是目前可以获得的最新的模拟结果,因而检验它们在东亚地区模拟的准确性是十分必要的。
1 气候模式资料的处理和检测方法 1.1 资料用于检测的5个模式及其试验设计的简介和输出变量情况如表 1,从表中可以看出,5个模式的运行中都包括了1900~1990年的时段,且分别考虑了CO2等温室气体 (下面简称方案1) 和考虑CO2等温室气体与硫化物气溶胶 (下面简称方案2) 的实际排放情况。各个模式输出的变量不太一致,在以后进行的检测评估中,我们重点对≥3个模式都有的变量进行评估,且各变量的值都是模拟的30年 (1961~1990年) 的平均。按照IPCC的要求,评估与检测时模拟的各变量一律同最近30年 (1961~1990年) 实际观测的气候场进行比较; 实际观测资料是用IPCC数据分发中心 (DDC) 提供的全球分辨率为0.5 ×0.5的30年 (1961~1990年) 月平均格点资料。
|
|
表 1 5个全球海气耦合模式及数值试验设计简介 |
1.2 评估与检测的方法
由于各模式的输出结果分辨率不同,为了更好的与观测场进行比较,我们在这里将各个模式和观测场资料都用线性内插的插值方法统一插值到标准格点2.5 ×2.5上。评估与检测区域为东亚地区 (主要是中国) (70°~140° E,15°~60° N)。对只有CO2等温室气体的情况和既考虑CO2等温室气体又考虑加入硫化物气溶胶的影响两种情况下的模拟场和观测场除了进行直接的比较外,还分别计算了各自的均值、误差值、各模拟场与观测场的均方误差及相关系数,其计算方法采用国际通用方法[11],其中均值统计量用于两个场平均值差异的度量; 各模拟场与观测场的均方误差可用来度量两个场之间的绝对差异; 相关系数度量两个场分布形势的相似程度。为了节省篇幅,本文大部分比较都是在5个模式的平均与实际观测之间,并且只给出各个量进行各季和年平均的比较。
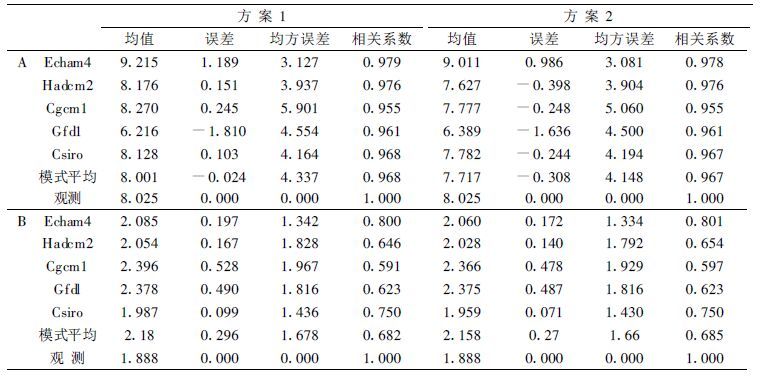
2 东亚和中国区域的近30年气候变化的检测 2.1 近30年全球平均的检测在分析对东亚地区气候变化的检测前,首先简单分析并给出5个全球海气耦合模式对近30年 (1961~1990年) 全球气候的检测。表 2给出检测近30年观测的和5个全球海气耦合模式模拟的全球年平均气温与降水量,从表中注意到,5个模式平均的气温与观测的差值在加入CO2等温室气体时为-0.024℃,而在既考虑CO2等温室气体又考虑硫化物气溶胶时差值为-0.308℃。尚需指出的是,5个模式在未加入温室气体与硫化物气溶胶时 (简称方案0),模式模拟的全球年平均气温与观测的差值为0.4~0.5℃ [12~14],由此表明,方案1和方案2都更接近于观测的实况。对应气温的其他检测值及降水的检测,也都表明这点。例如,两个方案中5个模式模拟与观测的气温的相关系数大致在0.96到0.98之间,降水的相关在0.6到0.8之间。
|
|
表 2 近30年 (1961~1990年) 观测的和5个全球海气耦合模式模拟的全球年平均表面气温 (A, 单位: ℃) 与降水量 (B, 单位: mm/d) 统计分析表 |
2.2 近30年东亚区域平均的检测
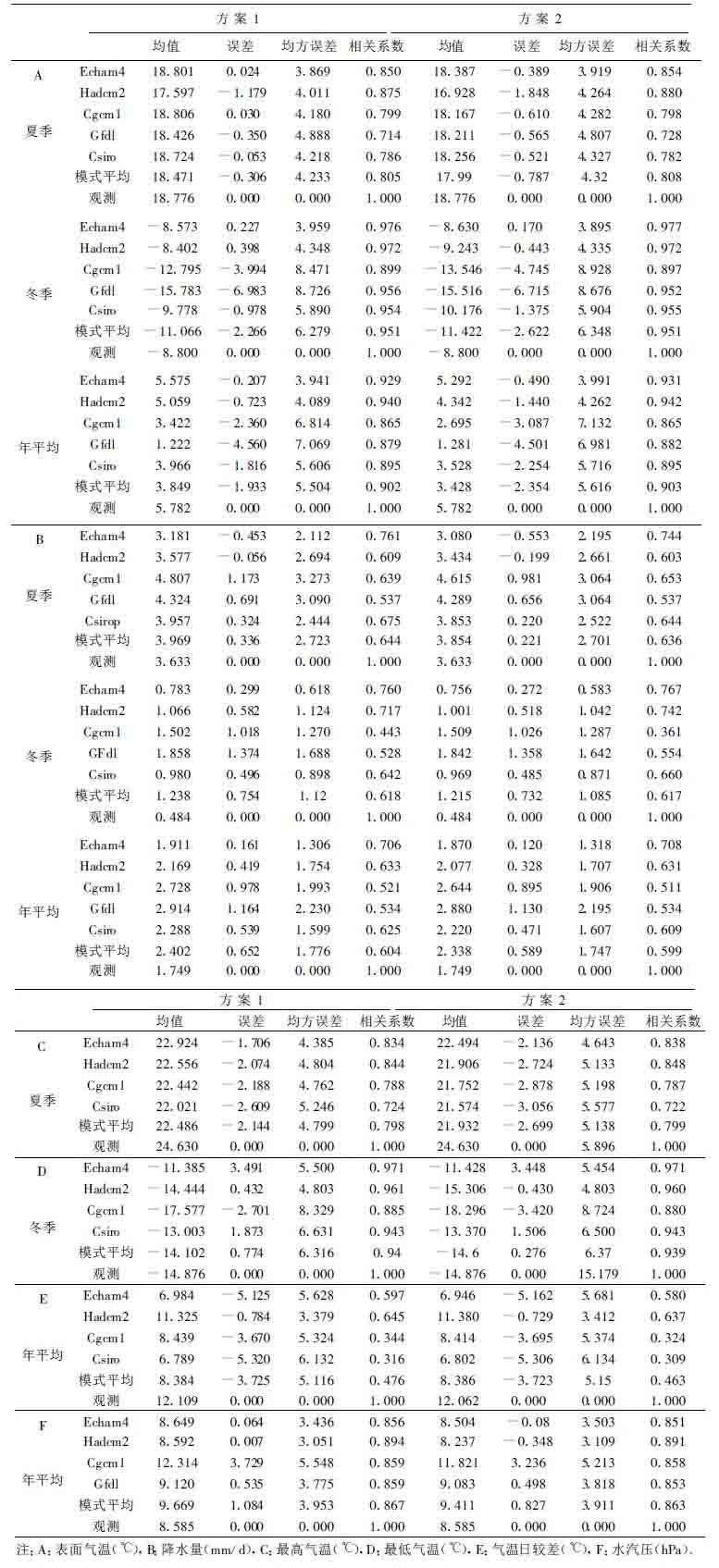
我们对近30年人类活动对东亚地区气候的影响进行检测,表 3为5个全球海气耦合模式的区域评估的统计分析结果。由表可见,对表面温度而言,方案1,5个模式温度的平均误差夏季为-0.306℃,冬季为-2.266℃,年平均为-1.933℃。各个模式的区域平均误差在各个季节各不相同,有的偏高,有的偏低。5个模式中,ECHAM4、CGCM1和CSIRO在夏季误差最小,比观测值分别偏高0.024℃,0.030℃和偏低0.053℃,HADCM2模式的误差最大,偏低1.179℃,冬季的误差比夏季大; 方案2,模拟的气温比方案1更偏低,误差增大。从各个模式来看,冬季则是ECHAM4模式的误差最小,偏高0.227℃,GFDL最大为-6.983℃,即加入硫化物气溶胶的影响后各个季节的温度误差均比只考虑CO2等温室气体的影响时大,5个模式的平均与观测值相比则是更加偏低,说明硫化物气溶胶在气候变化当中的冷却作用是明显的。
|
|
表 3 5个全球海气耦合模式模拟东亚区域的评估与检测结果 |
降水量的模拟结果是5个模式年区域平均误差为0.652 mm/d,冬季误差为0.754mm/d,比夏季大,几个模式中HADCM2模式的误差最小。加入硫化物气溶胶的影响后,降水量在夏季、冬季和年平均的误差都有所减少。
最高温度模拟的区域平均值各个模式都比实际区域平均值偏低,如在夏季模式平均偏低2.144℃,加入硫化物气溶胶的影响后,则偏低2.699℃; 对最低温度,冬季各模式的区域平均值大部分偏高,模式平均误差为0.774℃,考虑硫化物气溶胶的影响后,误差明显减小0.5℃; 而日较差的模式区域平均值比观测值偏低,误差最小的模式是HADCM2,在方案2时,误差值有所减小; 在方案1,模式模拟的水汽压区域平均值比实测值偏高1.084 hPa, 5个模式中ECHAM4和HADCM2的模拟效果最好,误差仅为0.064 hPa和0.007 hPa; 考虑硫化物气溶胶的影响后,水汽压的误差降低0.257 hPa。
从模拟和观测的空间变化的均方误差来看,方案1,夏季温度的均方误差小于冬季的; 而降水则是冬季的比夏季的小,说明温度的模拟在夏季较好,冬季差一些,降水则相反。方案2,年平均温度的均方误差小于方案1,降水的均方误差在各个季节也都比方案1时小。
从模拟和观测场的相关系数来看,在只考虑CO2等温室气体的影响和加上硫化物气溶胶的影响后,温度场的模拟都是比较令人满意的,尤其是冬季,尽管误差值相对大一些,但各模式的相关系数除CGCM1模式外,其余都在0.95以上,这表明模式模拟和观测的温度是非常相似的。从相关系数的数值上看,方案2比方案1与观测场更为相似; 夏季的5个模式平均的相关系数在两种情况下分别为0.805和0.808,年平均相关系数大部分模式也都达到了0.86以上; 从最高温度和最低温度的相关系数来看,模式平均的最高温度的夏季相关系数在方案1和方案2分别为0.798和0.799,冬季的最低温度的相关系数分别为0.940和0.939;降水量的模拟场和观测场的相关虽然比温度差一些,但在两种情形下,模式平均的相关系数,也都超过了0.50,夏季分别为0.644和0.636,冬季分别为0.618和0.617,年平均为0.604和0.599。对各个模式来说,降水相关最好的模式是ECHAM4,夏季、冬季和年平均,它的相关系数都达到了0.70以上; 日较差的模拟和观测场之间的相关系数最低,尤其是CSIRO模式模拟的日较差,相关系数仅有0.316和0.309,另外从空间相关性还可看出,冬季的情况大部分比夏季好。
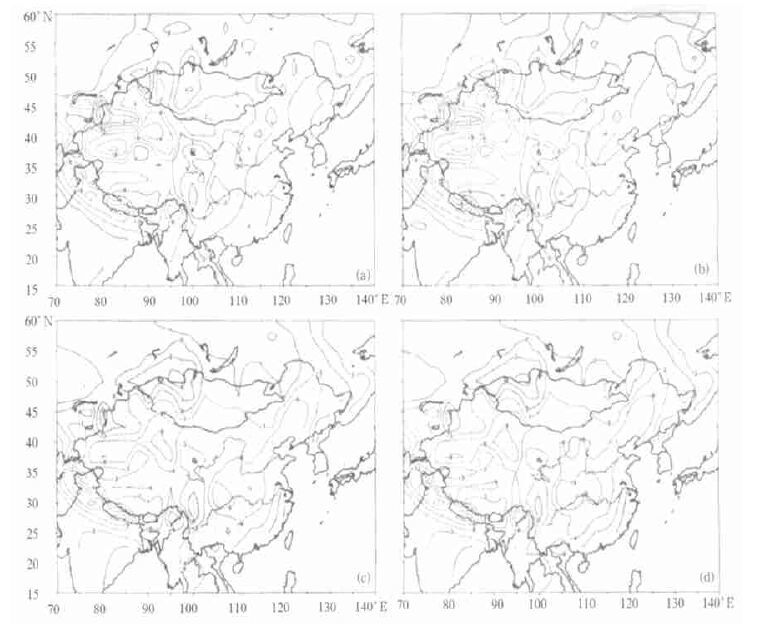
2.3 各季、年平均表面气温的空间分布从图 1所示的5个模式平均的模拟场中看出,与观测场相比,5个模式平均的年平均温度场在两种情况下虽然在数值上系统性偏低,但分布形势都与观测场非常一致,基本上模拟出了温度场的主要特征,即区域北部冷,南部与东南部暖,青藏高原上有冷中心; 从图 1中的模式平均的误差场分布图中也可看出,误差场的分布在两种方案下,以100° E为界,西部模式平均温度比实际观测场偏低5~10℃,我国新疆的北部误差最大,100° E以东误差较小,一般小于3℃; 对各个季节而言,模式平均的春季和冬季的误差在西部最大,误差最大的新疆地区达15℃; 夏季和秋季在西部的误差相对较小。

|
|
| 图 1. 年平均温度的观测场(a)和方案1、方案2模式平均场(b)(c)及其与观测场的误差(d)(e) | |
作为2个例子,图 2给出夏季和冬季模式平均与实际观测场的误差场。从图中可以看出,夏季的情形与年的类似,仍为东部误差小,西部误差大; 而冬季在整个中国范围内,都存在误差,但相对来说,东部沿海地区的误差最小。就方案1和方案2两种情形而言,它们的误差空间分布相差不大,两方案之间的误差仅相差百分之几,在图中反映不明显。
|
|
| 图 2. 方案1和方案2夏季 (a、b)、冬季 (c、d) 平均温度与观测温度的误差场 (单位: ℃) | |
2.4 季与年平均降水场
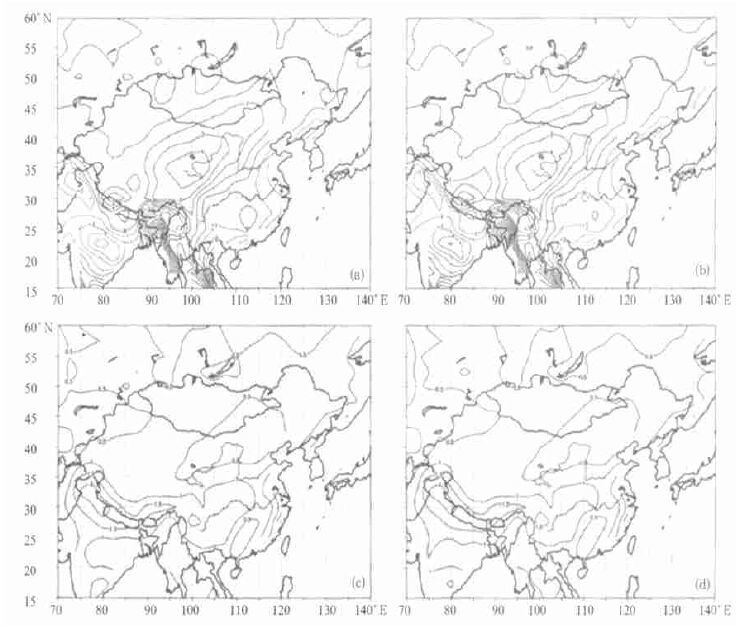
5个模式平均的年平均降水分布型与观测场相比基本一致,只是数值上大部分偏多,这从图 3所示的年平均降水实际观测场和模式平均分布图中可以看出,在30° N以北,无论方案1还是方案2,模拟场都为降水偏少区,与观测场一致,尤其是西北地区降水最少,30° N以南为降水偏多区,也与实际观测场的分布一致; 从误差分布图中可知,模拟场的降水比实测场系统性偏高,在我国北方大部地区模拟场和实测场的误差在1~2 mm/d,最大误差区在高原东部和黄河上游地区,110° E以东的大部地区误差小于1 mm/d,而在高原南部与印度相邻的地区模拟值比实测值偏少3 mm/d。

|
|
| 图 3. 年平均降水观测场(a)和方案1、方案2模式平均场(b)(c)及其与观测场的误差(d)(e) | |
从各个季节的误差分布图来看,在方案1和方案2两种情况下,春季 (图略) 模拟的降水在长江一带及其以北地区偏多,误差值在2~3 mm/d,东南沿海地区降水偏少1 mm/d左右; 夏季的误差较大 (如图 4),长江以北及黄河和我国的北方大部地区误差值在1~4mm/d之间,且误差分布呈东北-西南向,最大误差区在黄河的上游,约偏多4 mm/d,长江流域一带误差较小,东部沿海和东南沿海地区降水比实测场偏少1~2 mm/d,东亚地区的西南和高原南部误差最大,比实测值偏少3~8 mm/d; 冬季的误差,主要集中在35° N以南和115° E以西的地区,这是由于冬季降水除低纬外,大部分地区偏少。与平均温度场的模拟相比,平均温度场的模拟效果比降水好。
|
|
| 图 4. 方案1和方案2夏季 (a, b)、冬季 (c, d) 平均降水与观测值的误差场 (单位: mm/ d) | |
2.5 各季最高、最低温度场及日较差
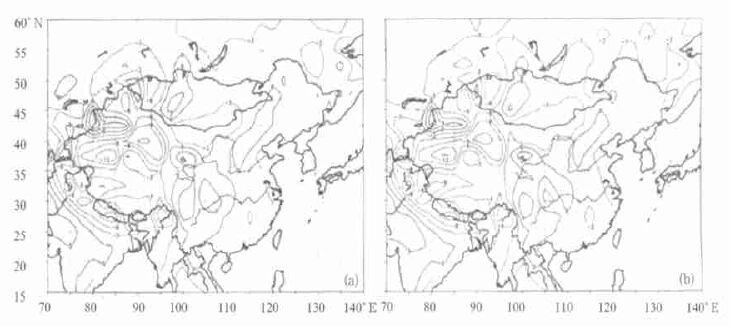
本文讨论的最高温度和最低温度是对4个模式的平均,为了节省篇幅,只给出夏季最高温度与冬季最低温度和年日较差的图。对于各个季节最高温度场来说,与平均温度的误差分布基本类似,秋季、夏季、年平均的空间分布场也是100° E以西误差较大,100° E以东误差小,这种情况可以从图 5给出的最高温度夏季误差分布图中看出,图中表明,在方案1和方案2两种情况下,100° E以东地区的误差都非常小,100° E以西的误差范围在5~10℃,主要位于青藏高原及新疆地区; 春季和冬季误差较大,误差范围最大的为冬季,冬季在整个东亚范围内模拟值都比实测值偏低,误差值在5~15℃。
|
|
| 图 5. 模式平均夏季最高温度与观测值的误差场 (单位: ℃)(a) 方案1, (b) 方案2 | |
而对最低温度来说,误差分布不同于最高温度场,在方案1和方案2两种情形下,各个季节模拟场与实测场相比情况都不太一样,夏季和秋季在黄河上游和长江上游地区有一个偏高5℃左右的误差中心,在我国105° E以东的范围误差很小,几乎为零,但对于整个东亚区域来说,高纬 (50° N以北) 和西南部的误差却较大,误差范围在5~10℃之间; 冬季的情况如图 6所示,与夏季和秋季相比,冬季在长江中游一带误差大一些,比实测值偏低5℃左右,我国东北和东南地区的误差较小,与其他各季相同,东亚地区的高纬和西南部的误差大一些。

|
|
| 图 6. 模式平均冬季最低温度与观测值的误差场 (单位: ℃)(a) 方案1, (b) 方案2 | |
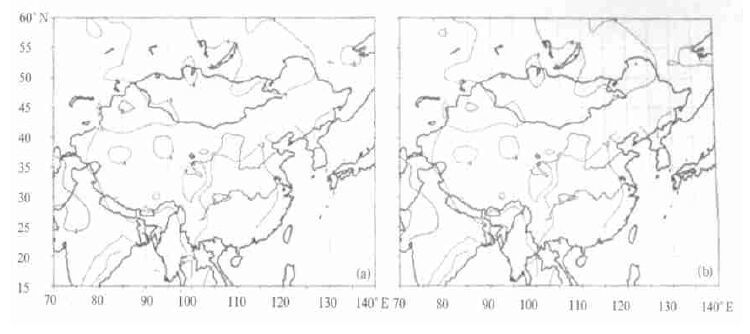
从由图 7给出的日较差的年平均误差分布图中可知,在方案1和方案2两种情形下,模拟的日较差的年平均值大多偏低,35° N以南和100° E以东的地区与实测值相比,误差最小,其他大部地区均比实测值偏低3~6℃,这与前面分析的模拟的最高温度偏低,最低温度偏高相一致,误差最大区集中在高纬和我国的西部地区。
|
|
| 图 7. 模式平均日较差年平均与观测值的误差场 (单位: ℃)(a) 方案1, (b) 方案2 | |
2.6 其他几个变量误差的分析
由于所获得的各个模式的变量不一致,因此,我们在这里只简单的讨论下面几个变量的误差分布情况,对水汽压 (4个模式的平均) 的年平均分布 (图 8),在方案1和方案2两种情况下,模式平均误差场以105° E为界,105° E以东水汽压误差很小,误差值基本为0,但在105° E以西,我国的高原地区比实测值偏多3~6 hPa, 东亚地区的西南却偏少3~6 hPa,另外,东亚的高纬地区误差也相对较小; 对云量的模拟,只有HADCM2一个模式有该变量的输出,总体来说,模拟场的分布形势与实测场基本一致,但整个东亚地区数值系统性偏低,45° N附近的误差相对小一些,我国东南沿海地区误差相对大一些; 对风场的模拟,在方案1时只有3个模式的结果,方案2仅有两个模式的结果,从这2~3个模式的结果来看,在两种方案下,我国东南沿海地区和西部的误差较大,方案2的误差更大一些,45° N附近误差较小。由于各个模式输出的辐射场的定义不一致 (有的是净辐射,有的是长波辐射),无法进行比较,本文不加讨论。

|
|
| 图 8. 模式平均水汽压年平均与观测的误差场 (单位: hPa)(a) 方案1, (b) 方案2 | |
3 结论与讨论
(1) 5个海气耦合模式都有一定的模拟东亚气候的能力,在方案1和2两种情形下,对平均温度场、最高、最低温度场和降水的主要分布特征都能进行较好的模拟,但它们也都有各自的系统误差。尤以高原地区模拟的效果较差,但却优于以前的模式。5个模式平均的模拟效果比单独用某一个模式要好一些。
(2) 误差的空间分布表明,在整个东亚地区,以100° E为界,西部误差大于东部,对平均温度的模拟系统性偏低,降水大部偏多,但总的来说,温度的模拟优于降水。
(3) 统计分析的结果表明,对各个变量,模拟效果最好的是温度 (包括平均、最高、最低温度),其次是水汽压,然后是降水,最差的是日较差。从区域平均的误差值来看,温度和降水的误差都是夏季小于冬季。从各个季节的相关系数来看,则是对同一个变量,模拟与观测场的相关系数最好的是冬季,春季和秋季次之,夏季最差。
(4) 对各个模式,模拟效果相对较好的是ECHAM4和HADCM2,它们对年平均温度的模拟的相关系数分别为0.929和0.940,年平均降水的相关系数分别为0.706和0.633。
(5) 对比方案1与方案2在东亚地区的模拟结果表明,计算的模式平均与观测相关系数一般是方案2略优于方案1;
(6) 模式平均与观测的误差和均方误差计算表明,除气温外,一般也是方案2优于方案1,尤以最低温度最明显。由此提示我们,近30年东亚地区的气候变化是否也与大气中温室气体与硫化物气溶胶的增加有一定联系,模式模拟的气温方案2差于方案1,可能是由于方案1多数模式模拟低于观测值,因此,再加入硫化物气溶胶后,其气温值更低于观测值所致。
本研究是建立在IPCC数据中心 (DDC) 提供的模式计算结果的基础上,因此计算与分析受到局限性,我们准备用国家气候中心的海气耦合模式计算1900~1990年的全球与东亚区域的气候自然变化,分别考虑方案1与方案2时的人类活动引起的气候变化情况,这样用3个数值试验与近百年观测的气候变化作对比,将能更好的检测与估计气候变化的原因。
致谢 感谢I PCC资料分发中心 (DDC) 提供的5个全球海气耦合模式模拟结果及5个模式组。| [1] | Houghton J T, Jenkins G J, Ephraum J J. Climate Change:the IPCC Scientific Assessment. Cambridge University Press, 1990: 365. |
| [2] | Houghton J T, Callander B A, Varney S K. Climate Change 1992 :the Supplement Report to IPCC Scientific Assessment. Cambridge Universit y Press, 1992: 200. |
| [3] | Houghton J T, Meira Filho L G, Callander B A, et al. Climate Change 1995 :the Science of Climate Change. Cambridge University Press, 1995: 285. |
| [4] | Barnett T P, Hasselmann K, Chelliah M, et al. Detection and attribution of recent climate change:a status report. Bulletin of the American Meteorological Society, 1999, 80, (12): 2631–2659. DOI:10.1175/1520-0477(1999)080<2631:DAAORC>2.0.CO;2 |
| [5] | Roeckner E L, Bengtsson J Feichter, Lelieveld J, et al. Transient climate change simulations with a coupled atmosphereocean GCMincluding the tropospheric sulfur cycle. Submitted to J.of Climate, 1998. |
| [6] | Mitchell J F B, Johns T C. On modification of global warming by sulphate aerosols. J Climate, 1997, 10, (2): 245–267. DOI:10.1175/1520-0442(1997)010<0245:OMOGWB>2.0.CO;2 |
| [7] | Haywood J M, Stouffer R J, Wetherald R T, et al. Transient response of a coupled model to estimated changes in greenhouse gas and sulphate concentrations. Geophys.Res.Let t., 1997, 24: 1335–1338. DOI:10.1029/97GL01163 |
| [8] | Boer G J, Flato G M, Reader MC, et al. Transient climate change simulation with historical and projected greenhouse gas and aerosol forcing. submitted to Climate Dynamics., 1999. |
| [9] | Gordon H B, Farrell S P O. Transient climate change in the CS IRO coupled model with dynamic sea ice. Mon thly Weather Review, 1997, 125, (5): 875–907. DOI:10.1175/1520-0493(1997)125<0875:TCCITC>2.0.CO;2 |
| [10] | Hirst A C, Gordon H B, O'Farrell S P. Global warming in a coupled climate model including oceanic eddy-induced advection. Geophysical Research Letters, 1996, 23: 3361–3364. DOI:10.1029/96GL03234 |
| [11] | Hulme M, Crossley J, Lister D, et al. Climate Observations and GCMValiclation, Interim Annual Report to the Department of the Environment, Transport and the Regions, Apr. CRU, Norwich, UK, 2000. |
| [12] | 赵宗慈. 模拟人类活动影响气候变化的新进展. 应用气象学报, 1993, 4, (4): 468–475. |
| [13] | 赵宗慈, 丁一汇, 李晓东, 等. 海气耦合模式在东亚地区的可靠性评估. 应用气象学报, 1995, 6, (增刊): 9–18. |
| [14] | 高学杰, 黄荣辉, 丁一汇.人类活动对中国气候变化影响的数值检测研究:[博士学位论文].北京:中国科学院大气物理研究所, 2000. |
 2002, 13 (5): 513-525
2002, 13 (5): 513-525