从20世纪60年代以来,双或三或多部多普勒天气雷达联合探测大气风场技术有了很大发展。先后发展了双或三或多部地基多普勒天气雷达联合探测大气风场技术、双机机载多普勒雷达联合探测大气风场技术、机载双波束多普勒天气雷达大气风场探测技术、双机机载双波束多普勒天气雷达联合探测大气风场技术,90年代中又研制成功了地基单点发射多点接收的多普勒天气雷达大气风场探测系统。随着以上各种探测系统的发展,双多普勒天气雷达大气风场探测的算法也有了很大发展。1969年Larry Armijo在笛卡尔坐标下提出了双和三多普勒天气雷达联合探测大气风场的原理并给出求解方程[1]。1970~1974年Lhermit te和Miller等人提出并发展了双多普勒天气雷达大气风场探测的共面技术 (coplan)[2~3]。1983年Ray和Sang ren提出ODD技术[4],1996年Chong和Campos又提出了EODD技术[5],在此基础上,1998年Bousquet和Chong发展了多部多普勒天气雷达合成和连续调整技术 (MUSCAT)[6]。试验表明同一资料不同处理方法反演出的风场是有差异的,有时差异还是很大的,这将引起人们对其反演的真实性提出怀疑。因此开展双多普勒天气雷达风场探测可靠性研究是必要的。
1 反演的基本假定及与实际观测的差异 1.1 双或三或多部多普勒天气雷达联合探测大气风场的基本假定通过了解各种算法的推导过程,可以清楚看到双或三或多部多普勒天气雷达联合探测大气风场不是没有假定条件的。并不是用3部雷达测量3个不同方向的径向速度就可以求得大气风场的,也不是用2部雷达测得2个不同方向的径向速度再加上连续方程就可以求解大气风场的,而是在以下基本假定条件下才能反演出大气风场:
a.假定雷达波束是直线传播;
b.地球表面是几何平面;
c.双或三或多部雷达同时探测到大气空间中的各个点的径向速度;
d.对于双多普勒天气雷达还假定大气中各点的降水粒子的下落末速度是已知的。
只有在以上假定下,Larry Armijo给出的在笛卡尔坐标系中的求解公式才成立:

|
(1) |
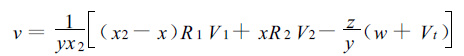
|
(2) |
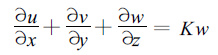
|
(3) |
其中第1部雷达在原点 (0,0,0),第2部雷达在X轴上,其坐标为 (x2,0,0),测点坐标为 (x,y,z),R1为第1部雷达到测点的距离,R2为第2部雷达到测点的距离,即
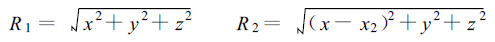
|
u,v是风在x,y坐标上的分量,w是垂直方向的分量,Vt为降水粒子的下落末速度。式 (3) 为连续方程,其中
Lhermitte和Miller在共面柱坐标下,给出的以下求解公式:
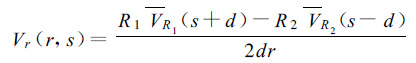
|
(4) |
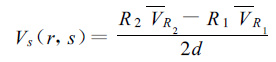
|
(5) |
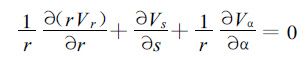
|
(6) |
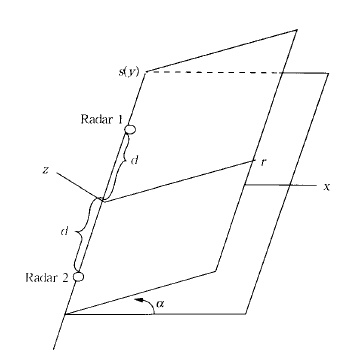
r,s,α是柱坐标中的3个分量,s是两部雷达的连线,做为柱坐标的轴,r是柱坐标中的半径,α是柱坐标中的方位角,d是两雷达之间距离的一半。它与笛卡尔坐标之间的关系见图 1。VR2和VR1为两部雷达测得的径向速度,R1,R2是s-r平面上的一点到雷达1、雷达2的距离。

|
式 (6) 为柱坐标中的连续方程,由此方程积分求得Vα。
|
|
| 图 1. 共面坐标的选取 | |
以上求解公式也只有在上述基本假定条件下才成立。同样ODD、EODD和MUCAT技术也是在上述基本假定下推导出来的。除此而外,在实际求解过程中,不同方法还有不同的要求。
1.2 实际观测与基本假定的差异在实际观测中上述基本假定是得不到满足的。其原因是:
a.地球表面是一个球面。
b.地球大气的压、温、湿随高度增加而减小,上下密度不同,雷达波束在这种非均匀介质中是以曲线形式传播,传播路径不是直线。而且大气压、温、湿随高度的分布随时间变化,造成雷达波束在大气中的传播路径的曲率也随时间变化。
c.雷达扫描一圈大概需要30 s,一般一个立体扫描16圈,需要花费8 min。因此一部雷达同时把空间所有点的径向速度测量出来是不可能。
d.由于雷达观测扫描方式所限,在实际工作中双多普勒天气雷达或三多普勒天气雷达观测不可能同时观测所有点的径向速度,也不能保证所有点都有双 (或三) 多普勒天气雷达观测资料。有双 (或三) 多普勒天气雷达观测资料的点,也不能保证这些资料是同时采集到的。
2 具体问题及解决途径 2.1 波束非直线传播及地球表面的非几何平面问题 2.1.1 引起的困难由于雷达波束在地球大气中的非直线传播,在双多普勒天气雷达联合探测大气风场中将引起以下困难。
a.确定径向速度的方向问题 由于波束的非直线传播,不能单纯根据天线的仰角和方位确定每点后向散射的方向,而需要根据波束传播路径上的每点的切线方向确定。因此为了确定径向速度的方向,必须知道传播路径。这是很困难也很复杂的一件事。
b.雷达定位问题 在风场反演过程中,需要由一部雷达先确定空间某一点,然后通过换算找出另一部雷达波束通过这一点的发射仰角、方位和路径长度。由于波束的弯曲,给这一换算造成很大困难,而且波束的弯曲情况又随大气垂直结构的变化而变化,使得问题更加复杂。
c.地球曲率给地基多普勒天气雷达大气风场探测的反演工作造成坐标选取上的困难 在双多普勒天气雷达风场反演中,不但把波束路径看成直线,而且把地球表面作为几何平面处理的。
2.1.2 解决方法在我们的编程过程中,以上问题采用以下方法解决。
a.为了处理方便,把波束走过的路径拉成一条直线,那么相应的地球曲率也要跟着变化,本来地球半径r=6400 km,由于波束的弯曲情况与大气层结有关,在标准大气折射条件下,把波束拉成直线后,地球半径将做为8500 km处理,即
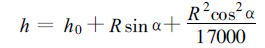
|
(7) |
R为目标物到天线的距离 (单位用km),α为雷达天线仰角,h0为天线的海拔高度,h为目标物的海拔高度。
b.地球坐标与大气风场反演中选取的笛卡尔坐标或柱坐标的坐标关系不是一个简单的关系。一般在笛卡尔坐标中选取两雷达的连线为x轴,其中一部雷达位于原点。如果地球表面为水平面则可使用以下公式从雷达坐标转到笛卡尔坐标。
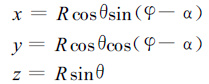
|
(8) |
其中x,y,z是笛卡尔坐标系的坐标,R,θ,φ是雷达坐标系的斜距、仰角和方位。α为笛卡尔坐标系中的y轴与地面正北线之间的夹角。
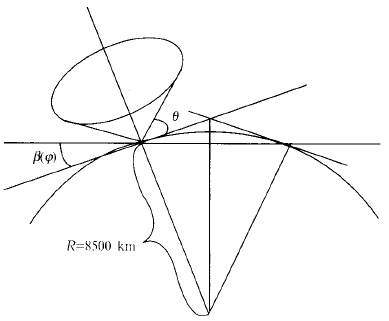
如果考虑地球曲率,仍以两雷达连线为x轴,则从雷达坐标转换到笛卡尔坐标将采用以下公式 (见图 2)(推导过程略):
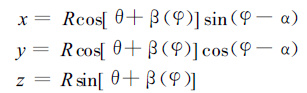
|
(9) |
其中β(φ) 是仰角订正函数,它与方位有关,
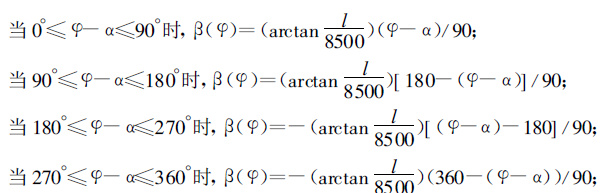
|
l为两雷达之间的地面距离,当l=80 km时,仰角的最大订正值为0.36°。对于Coplan中的极坐标,可以用类似的方法加以订正。
|
|
| 图 2. 雷达坐标与风场反演中的笛卡尔坐标之间的关系 | |
c.坐标的选取及转换问题:雷达测得的径向速度的方位、仰角是由雷达本身的坐标确定的。双多普勒天气雷达大气风场探测时,两部雷达各用各的坐标系进行观测,在反演过程中首先需要把各自测得的径向速度转化到统一坐标中,这个统一坐标是人们自己选取的。反演公式需要在这个坐标系中推导得到,如果反演出的风向、风速需要进入模式和做天气分析,还需要把这个坐标系中的量转换到模式或天气分析的坐标系中。需要特别指出的是雷达坐标系中的90°~270°的概念与经纬度坐标系中的90°~270°的概念不同,即东西概念不同。雷达坐标系中的90°~270°线是与以地球中心为圆心的过雷达天线的大圆相切的线,经纬度坐标系中的东西概念是与纬度圆相切的线,因此在具体处理过程中应引起注意。在推导反演公式时,径向速度应满足以下关系:

|
(10) |
其中VR是径向速度,V表示风矢量,
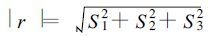
|
S1,S2,S3是r在正交坐标系中的3个分量。
2.2 有关同点同时问题 2.2.1 问题的提出a.天气雷达通过天线扫描进行观测完成一个立体扫描一般需要5~8 min,不同的空间点观测到的时间不同。也就是说天气雷达这种观测方式本身就不能满足反演中的同时性要求。采用这套反演方法,只对那些相对稳定的系统是有效的,也就是只能对定常中尺度系统进行反演。
b.对空间某一点而言,两部雷达可能同时观测到这一点,也可能一先一后观测到这一点 (或这一小区域),也可能一部雷达观测到了这一点而另一部雷达没有观测到这一点,也可能两部雷达都没有观测到这一点。第1种情况为同点同时,第2种情况为同点不同时,这两种情况又称共点,即在这一点有两部雷达的观测资料。第3种情况只有一部雷达的观测资料,第4种情况是在这一点没有观测资料。对于定常天气系统应该说第1种情况,第2种情况都是有用的反演点,第3种情况、第4种情况是需要处理的。
如果两部雷达都采用现行的雷达立体扫描观测方法,只在开始时间上进行统一,那么两部雷达30 s扫完一个PPI后,在这30 s内只有一条曲线上的点是两部雷达都扫到的,即:
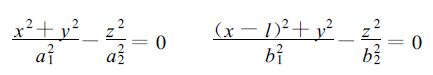
|
(11) |
两个锥面的交线,其中l是两部雷达之间的距离 (两部雷达的连线为x轴,一部雷达在原点上;另一部雷达在x=l处);a1为z=a2时锥面与水平面相交的圆的半径;b1为z=b2时锥面与水平面相交的圆的半径。
因此在扫描空间中,对很多观测点,两部雷达不是同时测到观测值的。如果一个立体扫描需要8 min,则两部雷达在同一点的观测时间可能相差8 min。使用这种观测资料反演大气风场,反演结果的可靠性需要通过讨论确定。如果这时的大气流场是准定常的,那么反演结果是可信的;如果这时大气流场变化很快,那么反演结果也许毫无意义。
“中国暴雨试验研究”的主要对象是中尺度强暴雨对流系统,根据实际观测和数值模拟可知,这种系统的发展演变是很快的,同时性问题必须考虑。
2.2.2 可能的解决办法该问题是很难解决的问题。目前世界上已研究出解决该问题的方法有以下几种:
a.双基地多普勒雷达网
20世纪90年代中,美国研制了一点发射、三点接收的多普勒天气雷达系统[7]。该系统在一点发射雷达波束,同时在这一点利用粒子的后向散射接收回波,另外两点利用粒子的侧向散射接收回波,三点接收的同步问题用GPS中的原子钟的时间进行解决。这种方法可以解决同点同时问题,但不同点观测时间还是不同的。
b.共面技术
这种技术要求两部雷达,同时在同一平面中扫描。为此要求两部雷达的仰角和方位角之间都满足以下关系:
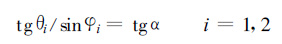
|
(12) |
其中θi为雷达仰角,φi为雷达方位角,α为斜面与水平面之间的两面角 (图 1)。i=1表示第1部雷达,i=2表示第2部雷达。两面角的轴线为两部雷达的连线,α可选12~16个不同的角度。两部雷达在每个角度上扫描都要满足式 (12),12~16个平面扫完的时间应小于3 min。这种方法在20世纪70年代曾经在一些雷达上实施[3]。由于10 cm或5 cm雷达天线较大,在实际观测中有一些困难,因此只是采用它的数据处理方法。
两部雷达各自进行立体扫描,每个立体扫描各层仰角是已知的,公式 (12) 可以确定两部雷达在一个共面上的观测数据。利用这些数据,对风场进行反演。
所以采用共面技术的数据处理方法,其原因是风在共面平面中的两个分量可以用两部雷达在这个平面内同时测到的径向速度直接计算出来,即公式 (4)、(5) 中不包括Vα分量,这样就可以把三维问题首先简化成二维问题处理。
2.3 粒子下落末速度的求算 2.3.1 目前求算方法及存在问题双多普勒雷达风场反演中,要求降水粒子的下落末速度已知。目前解决的办法是根据回波强度利用下式计算求得[8]:
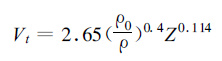
|
(13) |
其中Z为反射率因子,该公式是在假定粒子谱为Marshall-palmer分布条件下,通过统计得出的。但在自然界,不同降水类型、不同降水过程,降水粒子的谱分布都可能有很大变化。因此对某一具体过程和某一观测时刻有可能计算出来的V t(单位:m/s) 与实际值有较大差别。
2.3.2 解决途径a.为了避免以上公式带来的误差,可采用三多普勒天气雷达探测技术,三多普勒天气雷达风场探测求解公式中水平风u,v的计算与粒子降落速度无关。在我们的反演程序中,有三多普勒天气雷达风场探测反演程序。
b.利用双线偏振技术,增加雷达测量参数,在一定假定条件下求得粒子大小的谱分布,然后利用粒子的大小与下落末速度的定量关系,求出粒子的平均下落速度。该项工作以后将有专文论述。
2.4 照射体积的非一致性问题 2.4.1 两部雷达的照射体积不一致两部雷达同时或先后扫描到空间某一点时,由于两部雷达相对这一点的位置不同,因此这两部雷达的有效照射体积不同。雷达接收到的回波功率是照射体积内的全部粒子的后向散射能量的总和。一部雷达的照射体积的大小可用以下公式表示:
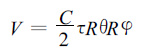
|
(14) |
其中C是光速,τ是脉冲宽度,R是距离,θ是水平波束宽度,φ是垂直波束宽度。对于一部雷达来说,照射体积随距离的增加以几何级数增大。
我国新一代天气雷达测速的脉冲宽度为1 μs,水平波束宽度和垂直波束宽度都是1°。在这种情况下,照射体积的径向长度为150 m,水平切向和垂直切向宽度在10 km处为175 m,在100 km处为1746 m。
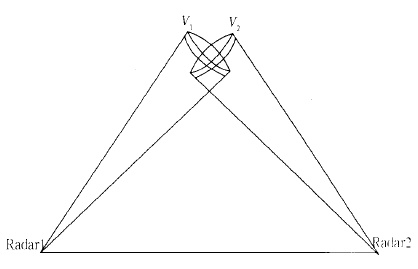
理想的双多普勒天气雷达大气风场探测要求两部雷达测量出同一时刻的同一照射体积内的两个不同方向的径向速度,然后利用这两个量才能反演大气风场。但在实际观测中,这是不可能的。图 3是两部雷达对应的照射体积,V1是雷达1的照射体积,V2是雷达2的照射体积。如果照射体积距雷达100 km,它的径向厚度只有150 m,而切向宽度可达1746 m,形状实际上是一个小薄片。两个照射体积的重叠部分只占照射体积的1/2。
|
|
| 图 3. 两部雷达照射体积示意图 | |
2.4.2 可采用的解决方案
由公式 (14) 可知,照射体积随距离的增大而几何增大,但其中的径向厚度是不变的,只是垂直切向和水平切向范围在变大。对新一代天气雷达来说,当R=9 km时,径向厚度与切向宽度相当。R每增加9 km,切向宽度就增加一个径向厚度的大小,因此通过合并距离库的方法,使两部雷达的照射体积尽量达到一致。具体方法将在程序中表现出来,不同距离采用不同大小的照射体积。
2.5 外场雷达布局对双多普勒天气雷达风场探测的影响有关外场试验的布局对反演结果的影响,作者在文献[9]中已进行过一些讨论,为了使反演误差最小,要求两部雷达的间距为雷达最大可测距离的0.55倍。
5 cm车载多普勒天气雷达,当脉冲重复频率取1000 Hz时,测速范围为±12.5 m/s,最大可测距离为150 km,这时雷达相距应为82 km;当脉冲重复频率取1300 Hz时,测速范围为±16.25 m/s,最大可测距离为115 km,这时两部雷达之间的距离应为63 km。
首先,两部雷达相距不能太远。越远,两部雷达的重叠探测区域就越小,可进行双多普勒天气雷达反演的区域就越小。如果两部雷达远到无重叠区,根本谈不上双多普勒天气雷达观测。
两部雷达也不能太近,太近,计算的基线太短,将造成较大误差。
双多普勒天气雷达风场探测中存在有盲区,这也是值得注意的。有关反演误差以及布局中的其他问题可参阅文献[10, 11]。
这里想进一步说明的是两部雷达最好南北方向放置,以便两部雷达能同时观测到从西向东移动的天气系统。
3 多普勒天气雷达风场探测的可靠性分析图从以上论述可知,双多普勒天气雷达探测大气风场并不是简单的事情。其中很多因素严重影响反演结果的可靠性。尽管我们已有办法消除某些因素的影响,但同时性问题和同点问题至今没有好的解决办法,因此对每次反演结果进行可靠性分析是非常必要的。
3.1 同点的可靠性分析由于电磁波在大气中的非直线传播,以及地球表面的曲率问题,要使两部雷达发射的波束都通过空间某一固定点,并不是一个简单的事情。假定大气为标准大气,地球曲率通过4/3订正后,可以认为电磁波在大气中的传播路径是直线,地球曲率半径
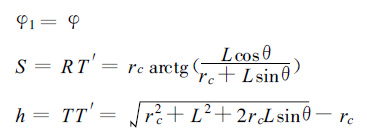
|
(15) |
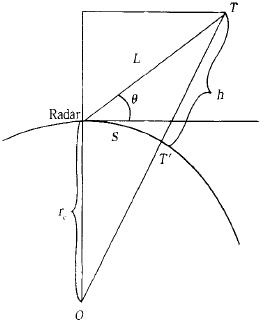
φ为雷达观测的方位角,φ1为空间某一点相对于雷达的方位角。S为空间某一点到雷达之间的地面距离,h为空间某一点的高度。L是空间某一点到雷达之间的斜距,θ为雷达天线的仰角。
|
|
| 图 4. 雷达坐标与地球坐标之间的转换关系 | |
在地球为圆球体假设条件下,根据雷达天线所在经纬度 (α0,β0) 和φ1、S值,可以推导出以下计算目标物所在经纬度 (α,β) 的计算公式 (推导过程略):
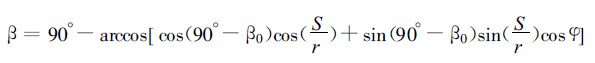
|
(16) |
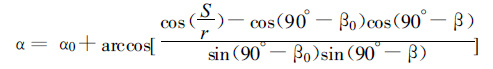
|
(17) |
通过以上公式计算可以判断反演使用的数据是否是同一点的数据。
一般来说,大气层结的变化造成的地面距离误差小于150 m,在200 km之内造成的高度误差小于800 m (具体计算过程略)。
3.2 同时性分析同时性问题是在同一点问题已解决的基础上进行讨论的。在这种情况下,同时性问题除受外场试验设计和外场试验指挥的影响外,还与探测对象,即探测的天气系统有关。如果天气系统很稳定,同时性问题将不会给反演结果造成很大影响。
天气系统很稳定的含义是在两部雷达先后观测到这一点的时间间隔之内,这一点的风向、风速变化不大。有3种情况可能使这一点的风向风速有很大变化:一是系统本身发展演变很快;二是系统在这一点的风向、风速的梯度很大;三是系统在大气中的移动速度很快,因此同时性分析与天气系统及天气背景有关。一般说来强对流天气在初生阶段,发展演变很快,双多普勒天气雷达对这一阶段的风场探测的可靠性较差。对强风切变区探测的可靠性有可能较差,因此需要认真分析。对移动速度>30 km/h的强风暴,两部雷达观测到同一点的时间最好不要超过2 min。
同时性分析还涉及到连续方程的积分问题,从地面到顶部的积分也要求是同一时刻的。不管是采用笛卡尔坐标还是采用共面的柱坐标,这一问题并没有解决,它的可靠性应认真分析。
3.3 雷达观测误差分析3.1和3.2的可靠性分析是在假定雷达观测无误差的情况下做出的。事实上雷达观测不可能不存在观测误差,这些误差也将影响风场反演的可靠性。
3.3.1 时钟误差两部雷达之间的时钟误差将影响到观测的同时性。为此要求双多普勒天气雷达联合探测中的时钟,应该经常对时。一般多普勒天气雷达30 s水平扫描一圈 (360°),每秒钟扫描12°,按理说天线每运行1°要1/12 s,因此对时精度应高于1/12 s,但由于技术上的困难,在“我国重大天气灾害形成机理与预测理论研究”外场试验中,对时精度要求到秒。
3.3.2 定标误差雷达天线电轴指北线的定标误差,天线座的水平调整和天线电轴0°仰角的定标误差,以及方位、仰角的同步误差,量化误差等对两部雷达取的是否是同一点数据都有直接影响。尤其天线指北线的定标和天线底座水平调整中的失误将造成系统误差,它严重影响双多普勒天气雷达风场反演的可靠性。
雷达各种参数测量及定标,将影响雷达回波强度和径向速度的测量值。回波强度值影响降水粒子下落末速度的计算;径向速度测量值的正确与否,直接影响风场反演的可靠性。
有关定标中的误差问题,将另有文章进行专门分析,这里不再论述。
3.3.3 观测过程中可能引起的不可靠问题观测过程中某些环节出现问题,都可能造成风场反演结果的不可靠。如两部雷达之间的观测不同步,或某部雷达在观测过程中出现故障或异常。
4 方案设计及编程中需要注意的问题从以上论述可以看出双多普勒天气雷达风场探测的可靠性与很多环节和处理方法有关。因此在方案设计和编程过程中需要多考虑一些问题,多研究一些处理方法以便提高反演的可靠性。
国家重大基础研究项目“我国重大天气灾害形成机理与预测理论研究”将开展外场观测试验,在外场观测试验中将采用双多普勒天气雷达联合观测,这是我国科学家在国内第一次进行的中小尺度天气三维风场探测研究活动,它具有重要的科学意义。为了更好地处理外场观测试验数据,在编制的双多普勒天气雷达风场反演系统中包含有以下功能。
4.1 参数设置由于外场试验将采用车载多普勒天气雷达,每次具体观测地点及地理条件是可变的。而在双多普勒天气雷达风场反演中需要知道各部雷达的经纬度、海拔高度、雷达参数、定标参数等,这就要求双多普勒天气雷达风场反演系统具有参数设置功能。
4.2 观测方法选择不同的观测方法在双多普勒天气雷达风场反演中处理方法不同,为了正确反演出大气风场,双多普勒天气雷达风场反演系统中需要包括对各种观测方法的数据处理程序,每次反演时需要告诉系统这些数据是采用什么观测方法获取的,例如立体扫描、共面扫描等。不同扫描方式,数据处理方式不同。
4.3 软件系统中包含有多种风场反演方法由于外场试验的设计可能有多种多样,为了适应多种需要,在风场反演软件系统中包含有:
a.双多普勒天气雷达的共面扫描的风场反演软件。
b.双多普勒天气雷达立体扫描的风场反演软件。
c.三多普勒天气雷达风场反演软件。
d.单多普勒天气雷达风场反演软件。
4.4 方案设计中包含有可靠性分析反演结果是否可靠是需要认真分析的,否则利用它去分析研究强暴雨系统的结构和机理就可能导致错误。可靠性分析除以上列出的内容外,还包括计算误差,边值条件的合理性等等。
5 结论从以上分析可以得到以下结论:
(1) 双多普勒天气雷达风场探测并不像人们想象的那样可靠,还存在不少有待解决的问题。
(2) 双多普勒天气雷达风场探测中两部雷达获取资料的同时性问题有待进一步研究。所谓同时性有两种含义,一是所有资料都是在同一时刻采集到的,二是两部雷达同时采集到空间某一点的数据,而不同点采集数据的时间不同。前一种情况是最理想化的,但实际上是不可能实现的;第二种情况是放宽条件的一种,这对一些点是可以实现的,但不是对所有点都能实现的。在双多普勒天气雷达风场反演中,对第二种情况要求天气系统为准定常,也就是要求各点的
(3) 使用双多普勒风场探测反演结果时,必须进行可靠性分析,不同天气过程反演出的可靠性不同。同一天气过程观测方法不同,反演出的可靠性也不同。同一观测方法采用不同的数据处理技术反演结果也可能不同。除此以外,雷达工作状况的好与坏,都会影响反演结果。因此分析人员必须高度重视可靠性分析,并清楚反演结果中,哪些数据是比较真实可靠的,哪些数据可能存在问题,尽量避免引导出错误概念。
(4) 建议外场试验时,两部雷达的间距不要超过80 km,在60~70 km之间为宜,两部雷达应南北放置。
| [1] | Larry Armijo, A theory for determination of wind and precipitation velocities with Doppler radars. J. Atmos. Sci., 1969, 26: 570–573. DOI:10.1175/1520-0469(1969)026<0570:ATFTDO>2.0.CO;2 |
| [2] | Lhermitte R M, Dual-Doppler radar observation of convection storm circulation. Preprints, 14th Radar Meteor. Conf., 1970: 153–156. |
| [3] | Miller L J, Strauch R G, A dual-Doppler radar method for the determination of wind velocities within precipitating weather systems. Remote Sensing Environ., 1974, 3: 219–235. DOI:10.1016/0034-4257(74)90044-3 |
| [4] | Ray P S, Sangren K L, Multiple-Doppler Radar network design. J. Climate Appl. Meteor., 1983, 22: 1444–1454. DOI:10.1175/1520-0450(1983)022<1444:MDRND>2.0.CO;2 |
| [5] | Chong M, Testud J, Three-dimensional air circulation in a squall line from airborne dual-beam Doppler radar data: A test of coplane methodology software. J. Atmos. Oceanic Technol., 1996, 13: 36–53. DOI:10.1175/1520-0426(1996)013<0036:TDACIA>2.0.CO;2 |
| [6] | Bousquet O, Chong M, A multiple-Doppler synthesis and continuity adjustment technique (MUSCAT) to recover wind components from Doppler radar measurements. J. Atmos. Oceanic Technol., 1998, 15: 343–359. DOI:10.1175/1520-0426(1998)015<0343:AMDSAC>2.0.CO;2 |
| [7] | Wuman J, Randall M, Burghart C, Read time vector winds from a bistatic Doppler radar network. Preprints, 27th Conference on Radar Meteorology, AMS, Vail, Colorado, USA, 1995: 725–728. |
| [8] | Doviak R J, Zrnic D, Doppler Radar and Weather Observations. Academic Press Inc., 1984: 249–253. |
| [9] | 张沛源, 何平, 宋春梅, 等. 三部多普勒天气雷达联合测量大气风场的误差分布及最佳布局研究. 气象学报, 1998, 56: 94–103. |
| [10] | Robert P, Jones D, Dual-Doppler radar coverage area as a function of measurement accuracy and spatial resolution. J. Appl. Meteor., 1979, 18: 1229–1233. DOI:10.1175/1520-0450-18.9.1229 |
| [11] | Doviak R J, Ray P S, Error estimation in wind fields derived from dual-Doppler radar measurement. J. Appl. Meteor., 1976, 15: 868–878. DOI:10.1175/1520-0450(1976)015<0868:EEIWFD>2.0.CO;2 |
 2002, 13 (4): 485-496
2002, 13 (4): 485-496

