2. 中国气象科学研究院, 北京 100081;
3. 中国气象局培训中心, 北京100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081;
3. CMA Training Center, Beijing 100081
在微分方程数值计算中, 差分格式对于其精确度与有效性都是极其重要的。在天气预报中, 有多种时间积分格式被研究和采用过[1, 2]。半隐格式可以说是效果较好的一种, 用于动力-热力方程的某些项有较高的精确度和相对大的时间步长。半拉格朗日格式因为可以取较大的步长, 对计算机的设备要求较低, 而计算机精确度却有所增加, 近年来日益引起人们的兴趣。
王斌等[3]在一维偏微分方程中运用特征方向法, 对完全平方守恒显式差分格式进行了改进, 得到了理论上无条件稳定的格式。应用理想化的Rossby-Haurwit z波对正压浅水方程波进行了计算, 结果表明, 该格式可以节省计算时间。但是对时间积分格式的改进仅停留在传统的无记忆框架中。
许多差分格式都是以一些物理量 (如能量、角动量等) 守恒为基础设计的。Egger[4]曾研究了一种在相空间中容积守恒的数值积分格式; 对可逆流问题严格地要求容积守恒进行了论证。他认为这种流的总体预报的初始分布所占有的相空间容积是不随时间改变的。他设计了一个相应的对容积守恒的检验方法并对平流方程的格点表示和一维非粘性浅水流进行了检验。
曹鸿兴等[5, 6]提出并发展了大气记忆动力学, 他们的基本观点是考虑大气有记忆能力, 可以由多个时次的初始场而不仅是一个时次的初始场来求得大气运动的数值解。本文中的回溯时间积分格式也是基于类似的想法, 即利用多时间层次资料, 建立一种新的时间积分格式。这种格式与传统的格式很不一样, 可以包含三个以上不同的时间层次, 可以从过去的多时次场中得到更多的信息。这种格式在数值计算中还能自动起过滤作用, 可以平滑预报场中的虚假值。
事实上, 也曾有人在时间积分格式中有过类似的想法。Rivest等[7]提出对n+1, n和n-1时次的观测值选定适当的系数, 以调节不同时次观测值的作用。本文从介绍回溯时间积分格式的基本理论入手, 对大气记忆动力学也作了简介, 给出了回溯格式和它的稳定性表达式, 最后以回溯时间积分格式对平流方程进行了计算, 并与蛙跃格式进行了比较。由于平流方程在如海洋、水文、环境、航空等多种学科中使用, 本文提出的方法在计算数学中也是一个贡献。
1 基本理论对微分方程

|
(1) |
可以用不同的差分格式进行运算, 例如中央差分格式
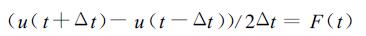
|
(2) |
上式 (2) 亦可改写为:
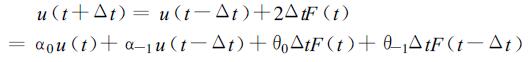
|
(3) |
式中α0=0, α-1=1, θ0=2, θ-1=0。式 (2) 是在数值计算基础上得出的, 遗憾的是, 实际上由于α0=0和θ-1=0, 这样的计算略去了包含于u (t)和F(t-Δt) 等项中的信息。而这些信息正巧是对预报u(t+Δt) 很有用的。也就是说, 在作u(t+Δt) 预报时希望用到t和t-Δt间的变量u和源函数F的全部信息。
对式 (3) 作一个推广, 得出
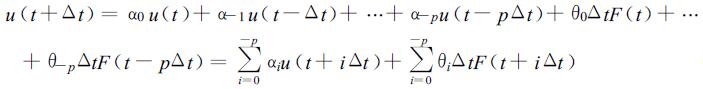
|
(4) |
式 (4) 就称之为数值模式中具有p阶 (p≥2) 的时间积分回溯格式。对于这个格式, 关键问题是如何决定系数αi和θi。如果把u值看作系统中的一个状态变量, 把函数F看作是系统的外界变量, 式 (4) 正是系统辨识中的一般性方程。所以式 (4) 中的系数可以由系统辨识中的种种方法来确定[8]。如随机近似, 松弛算法, 经典的最小二乘法乃至遗传算法等。以下计算中用的是最小二乘法。
实际上, 数值天气预报已使用了多时次的观测资料, 只不过是包含了两个步骤, 即时间积分和时间过滤。我们引用ECMWF (欧洲中期天气预报中心) 模式作如下论证。在ECMWF谱模式[9]中, 时间积分格式为
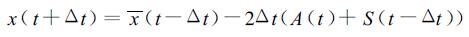
|
(5) |
式中A, S分别代表绝热和非绝热项。那里有3个时间层次p=p+2=3, x(t) 是时刻t的滤波值, 即
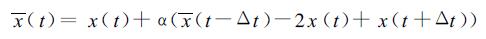
|
(6) |
同样地有
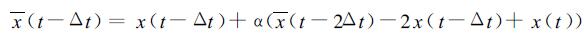
|
(7) |
从式 (5)~(7) 可以看出, 式 (5) 中x(t+Δt) 包含了x(t-2Δt) 的信息, 因为权重α值比较小, α=0.06, 由x(t-2Δt) 得到的信息也是比较少的。它启发了我们, 要设计一个新的时间积分格式, 使能包含更多的时间层次, 例如:t+Δt, t, t-Δt, t-2Δt, …, t-pΔt, 即p≥2, 且不在积分过程中作时间过滤。这意味着新的格式至少具有两个功能:时间积分和时间过滤。由于积分过程中没有进行时间过滤, 大气波就不会减弱。这样的大气方程的解可以更精确。
2 记忆动力学要决定式 (4) 中系数αi和θi的值, 可以有两种途径。一种是直接的, 即前面已经提到过的, 以最小二乘法或随机近似等方法由观测资料求得; 另一种是间接的, 由记忆动力学[5]演绎而得。下面将对此进行介绍。
一般地说, 大气动力-热力方程可写作
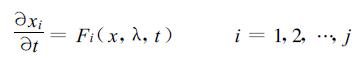
|
(8) |
其中j是整数, xi是第i个物理变量, λ是物理参数。为简单起见, 以下只考虑一个物理量x, 在Fi(x, λ, t) 中略掉x和λ。这样式 (8) 只表示x的一个局地变化和一个源函数F的关系。显然, x是在空间r和时间t的纯量函数。引入权重β(r, t) 作为记忆函数, 式 (8) 从t0至t的加权积分为
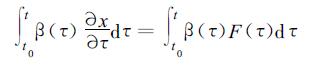
|
(9) |
其中因为空间点r是固定的, β(r, t) 中的r可以省写。对式 (9) 左侧运用分部积分得
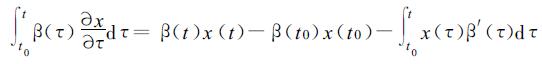
|
(10) |
式中β′(τ)=∂β(τ)/∂τ。应用中值定理计算式 (10) 右侧的第三项, 即得
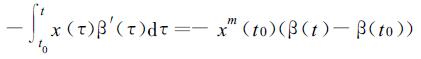
|
(11) |
其中, 中值xm(t0)≡x(tm), t0<tm<t。把式 (10) 和 (11) 代入式 (9) 并进行代数运算, 得到
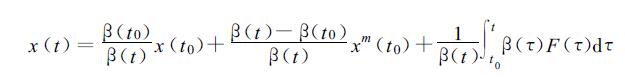
|
(12) |
式 (12) 的前两项, 是在固定的r点, 只与在初始时刻t0和中间时刻tm的x有关, 所以称之为自记忆项。式中第三项称为有效项, 即在时间段[t0, t]内其它空间点对固定点r的总有效贡献。对于多时次即ti, i=-p, -p+1, …, t0, t类似于式 (10) 推导, 可以记作:
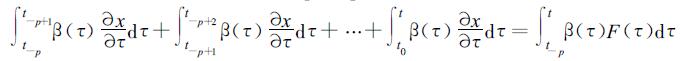
|
(13) |
消去相同的项β(ti)x(ti), i=-p+1, -p+2, …, 0, 得出
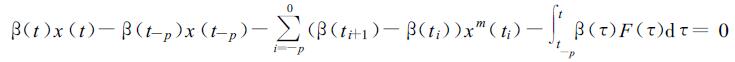
|
(14) |
这是一个差分-积分方程, 称为回溯阶p的自忆性方程, 这也就是将要讨论的基本方程。
令p=0, 则时间仅有t和t0, 式 (14) 变成式 (12), 称为0阶自忆性方程。若p=1, 则有时间t, t0和t-1, 式 (14) 成为
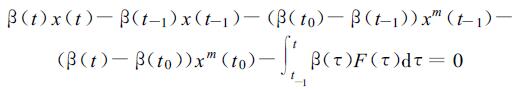
|
(15) |
称式 (15) 为1阶自忆性方程。例如一维平流方程
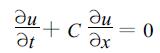
|
(16) |
即
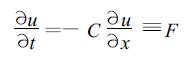
|
(17) |
其中x表示空间坐标, C为常定平流速度。对空间r点, 与式 (14) 相类似, 自忆性方程为
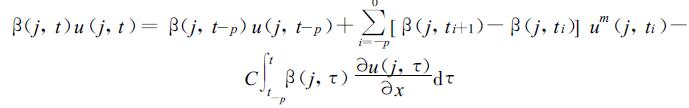
|
(18) |
若以式 (14) 作预报, 要用到t时刻以前的u(ti) 的p个值和F(ti) 的p个场。所以, 在式 (14) 中, β(ti) 的作用是记忆p+1的u值和p+1的F场。这是我们称这为记忆函数的原因, 也是提出记忆动力学的数学基础[5, 6]。
3 平流方程的回溯格式采用在差分格式中使用的符号, 即令
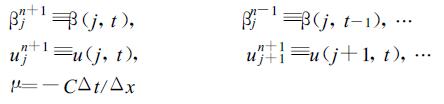
|
对n-p至n+1的积分以求和来代替, 空间则采用中央差分, 回溯阶为p, 式 (17) 的回溯格式为
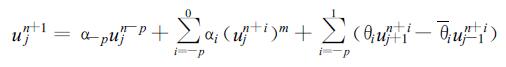
|
(19) |
其中:
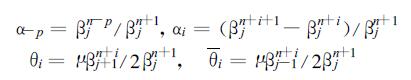
|
令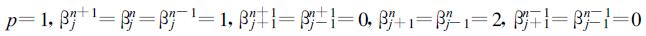
则式 (19) 为
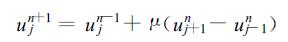
|
(20) |
这就是蛙跃差分格式[10]。如果取定不同的αi, θi, θi和 (ujn+i)m就可以得到种种不同的差分格式, 这可能是构造回溯格式的一个丰富多彩的结果。若令
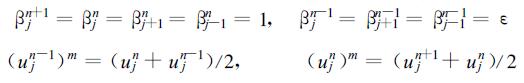
|
式 (19) 成为

|
(21) |
其中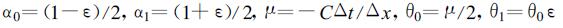
令ε=1, 则
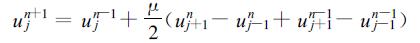
|
(22) |
这就是Grank-Nicolson差分格式。
令ε=1/2, 则
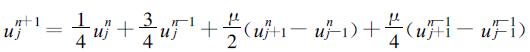
|
(23) |
如果以蛙跃差分格式与之比较, 明显地看到在对ujn+1的预报中包含了ujn, uj+1n-1和uj-1n-1的信息。
令ε=0, 则
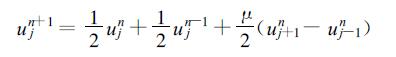
|
令ε=-1, 则
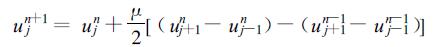
|
(24) |
从式 (21) 至式 (24) 可以看出, 给定不同的记忆函数, 差分格式即有相应的变化。
4 回溯格式的稳定性众所周知, 蛙跃格式 (20) 的稳定条件为|ωΔt|≤1, 如果|ωΔt|>1, 格式必定是不稳定的。在对式 (21) 格式的稳定性进行研究时, 先观察式 (21) 与式 (20) 有何差异。显而易见, 两者的差异在于式 (21) 比式 (20) 更多地包含有在n和n-1时刻观测得到的信息。
令
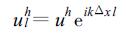
|
(25) |
其中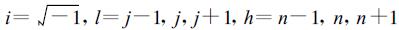
把式 (25) 代入式 (21), 得到
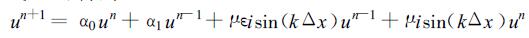
|
(26) |
其中sin (kΔx)=(eikΔx-e-ikΔx)/2i, 同类项合并后, 得到
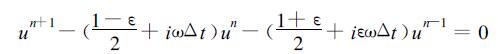
|
式中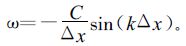
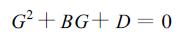
|
(27) |
其中B=-((1-ε)/2+iωΔt), D=-((1+ε)/2+iεωΔt), 式 (27) 的两个解为
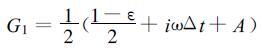
|
(28a) |
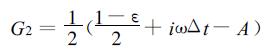
|
(28b) |
其中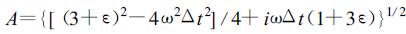
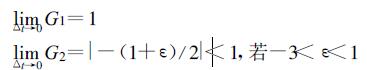
|
对于真解必定有G=1, 所以式 (28a) 与物理波相联, 而式 (28b) 则与计算波相联。令u1n=G1nu10, u2n=G2nu20, 则

|
(29) |
以下计算还需要两个初始值, 一个物理的u10和一个计算的u20, a与b为常量。从式 (29) 可得出
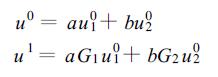
|
式 (29) 可改写为

|
(30) |
以下讨论一些特例:
(1) 若ωΔt=0, 且-3<ε<1, 则G1=1, |G2|=|-(1+ε)/2|<1, 这种情况下的差分格式是稳定的。
(2) 若ωΔt≠0, 当Im (A)=0, 则 (1+3ε)=0, ε=-1/3。令
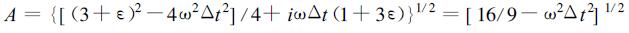
|
(a) 若A>0, 即|ωΔt<4/3, 则
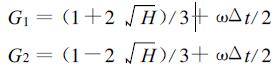
|
其中H=(1-9 ω2Δt2/16)。显然, |G1≤1|, |G2|≤1, 其数值计算是稳定的。相角为
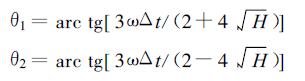
|
则有
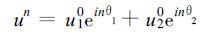
|
(31) |
(b) 当A=0, 即|ωΔt|=4/3
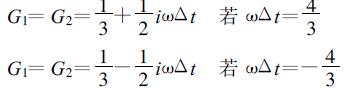
|
可得出|G1|<1, |G2|<1

|
所以得出的表达式为

|
(32) |
(c) 若A<0, 即ωΔt>4/3,
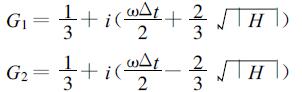
|
如果ωΔt>4/3则|G1|>1;如果ωΔt<-4/3则|G2|>1。容易看出, 格式 (21) 总是不稳定的。如上所述,
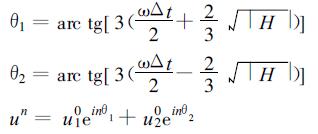
|
(33) |
格式 (21) 与蛙跃格式有相同的特点, 即周期为4Δt的波是不稳定的。
(3) 令E=(3+ε)2/4-ω2Δt2, F=ωΔt(1+3ε), 方程
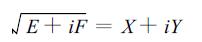
|
(34) |
成立。分别对式 (34) 两侧平方, 把实数部分与虚数部分对应, 可得
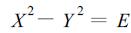
|
(35a) |
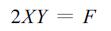
|
(35b) |
联立方程 (35) 的解为
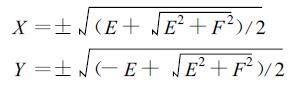
|
(a) E≥0
通过推导, 得出
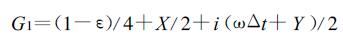
|
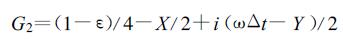
|
假定|ε|<1, 按照E≥0, 即|ωΔt|≤(3+ε)/2取
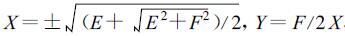
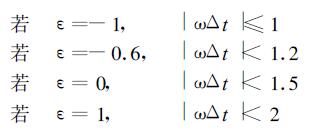
|
(36) |
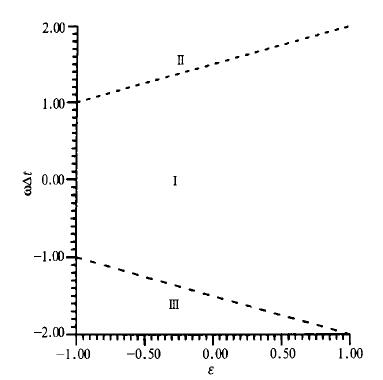
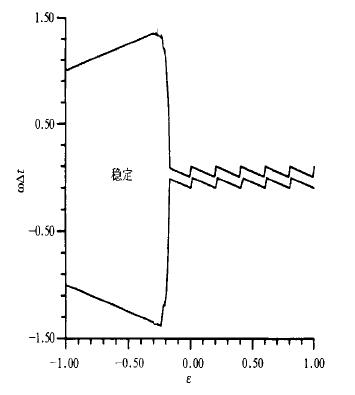
式 (36) 的图示在图 1中给出, 图中区域Ⅰ满足式 (36)。在这个区内满足|G1|≤1和|G2|≤1的稳定区域在图 2中表示。由图可以看出以下特征:
|
|
| 图 1. 稳定区域Ⅰ与不稳定区域Ⅱ、Ⅲ (纵坐标ωΔt, 横坐标为ε, ω是频率, ε是式 (21) 中的一个记忆参数) | |
|
|
| 图 2. ε≥0, E=(3 +ε)2/ 4-(ωΔt)2时的稳定域 (说明同图 1) | |
若ε∈ [-1, -0.269754]且|ωΔt|≤(3+ε)/2, 则|G1|≤1, |G2|≤1, 格式 (21) 是稳定的; 若ε∈[-0.269754, -0.1800]且|ωΔt|≤1.415, 则|G1|≤1, |G2|≤1, 格式 (21) 是稳定的; 若ε∈[-0.1800, 1]且|ωΔt|≤0.10, 则|G1|≤1, |G2|≤1, 格式 (21) 是稳定的, 这个稳定区域的边界好象一个双波运动。
(b) E<0
即|ωΔt>(3+ε)/2, 取
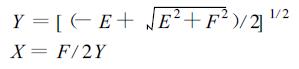
|
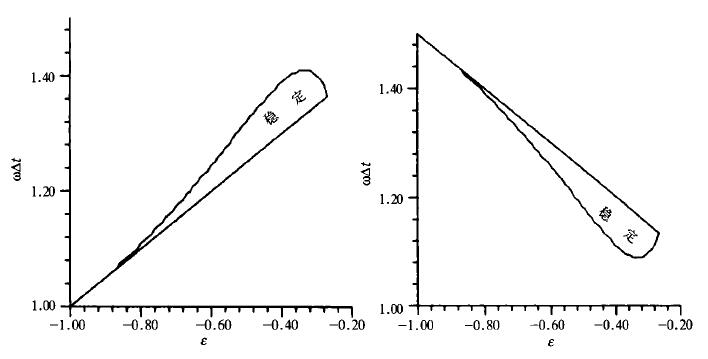
这就是图 1中的区域Ⅱ和区域Ⅲ。这两个区域中满足|G1|≤1和|G2|≤1的面积都很小, 如图 3所示。从图 3可以看到它们的稳定区域图形好象两个快速下坠中的流星。
|
|
| 图 3. 区域Ⅱ和Ⅲ中的稳定区域 | |
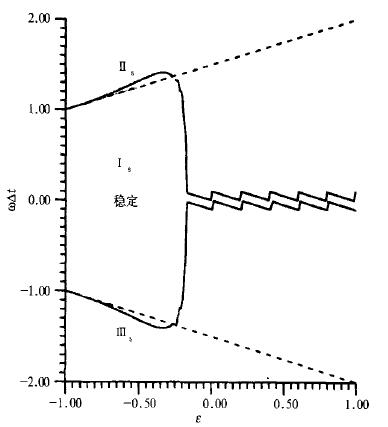
为了对稳定区有一个总体概念, 图 4给出了各稳定区的综合。
|
|
| 图 4. Ⅰ、Ⅱ和Ⅲ三个区中稳定域的合并 (Ⅱs和Ⅲs是图 3中相应部分的缩小) | |
5 平流方程的计算
根据式 (4), 可以把式 (17) 的蛙跃格式写作:
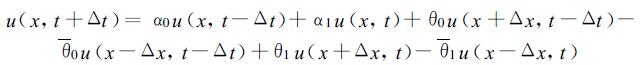
|
(37) |
取α0=1, α1=0, θ0=θ0=0, θ1=θ1=μ。且采用在差分格式中常用的符号, 式 (37) 就成为式 (20)。因为假定了α1=θ0=θ0=0, 所以在t时刻的单点观测资料和t-Δt时刻的场资料都没有得到利用。
作为一个实例, 假定有3个时间水平, 在t和t-Δt时刻的资料全都用上, 以式 (21) 回溯格式进行计算, 式中的系数α0, α1, θ0和θ1不是由给定β(r, t) 一个特定值来决定, 而是由一个理想场资料以最小二乘法来确定, 由理想流

|
(38) |
计算得出, 式中
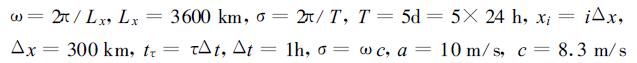
|
显然, 式 (38) 是正弦和余弦项的组合。如果x为已知, u随时间t而变, 首先计算120 h时间序列, 称为实时序列。这序列是由式 (38) 假定x=1800, 2000, 2400 km产生的。随后是48 h序列, 是设定了p=1, 以式 (20) 和 (21) 预报得出的。在积分中, 对于蛙跃格式时间步长为10 min, 回溯格式时间步长为1 h。所用的依赖样本120个, 独立样本48个。若取定x=1800 km, 通过计算, 得出回溯时间积分方程为
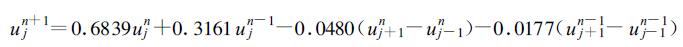
|
(39) |
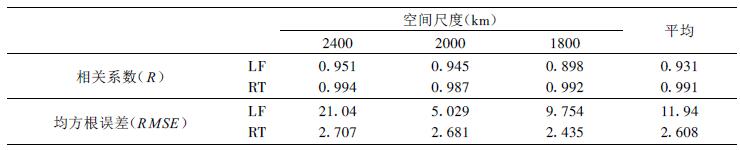
在表 1中可以明显地看到回溯积分比蛙跃格式好得多。虽然用蛙跃格式 (LF) 或回溯格式 (RT) 预报得出的时间序列与用式 (38) 生成的时间序列的相关系数都是显著的 (R0.01=0.37), 但是RT的相关系数都比LF的大, 特别是RT的均方根误差 (RMSE) 比LF的小得多。平均相差5倍 (11.94/2.608=4.6), 在x=2000 km时, 至少也有2倍。这足以证明RT格式计算是比较精确的。此外, 在计算中RT格式所取步长为1 h, 它是LF格式计算的6倍, 所以效率也大大高于LF格式。
|
|
表 1 蛙跃格式 (LF) 与回溯格式 (RT) 在时间积分中的精确度的比较 |
6 结论
在各种不同的预测预报领域, 如海洋、水文、气象、地震乃至经济等, 对提高预报准确度和效率给予了极大的关注, 本文提出的回溯时间积分格式比传统采用的积分格式包含更多的信息, 使观测所得的点和场资料能得到充分利用, 而且在计算中所用记忆系数本身能起到时间平滑的作用, 避免了在积分过程中进行时间平滑。可见, 回溯格式对提高数值预报准确度和计算速度有可靠的效果, 是一个有前途的新方法。当然, 任何新的方法都需要经历逐步提高与完善的过程, 回溯格式也不例外。从数学上充分证明回溯格式的稳定性是很困难的, 本文针对记忆函数的特定的取值来加以讨论, 是否对所有情况都有普适性, 有待于继续研究。
| [1] | Robert A, A stable numerical integration scheme for the primitive meteorological equations. Atmos-Ocean, 1981, 19, (1): 35–46. DOI:10.1080/07055900.1981.9649098 |
| [2] | O′Brien J J, Time integration schemes, Advanced Physical Oceanographic Numerical Modeling. J.J.O′Brien ed.NATO ASI Series, Reidel, 1986: 155–164. |
| [3] | Wang Bin, et al. A time-saving explicit scheme for numerical integration. Chinese Science Bulletin, 1993, 38, (3): 230–234. |
| [4] | Egger J, Volume conservation in phase space:a fresh look at numerical integration schemes. Mon.Wea.Rev, 1996, 124, (9): 1955–1964. DOI:10.1175/1520-0493(1996)124<1955:VCIPSA>2.0.CO;2 |
| [5] | Cao Hongxing, Self-memorization equation in atmospheric motion. Science in China, series B, 1993, 36, (7): 845–855. |
| [6] | Cao Hongxing and Zhu Zhengxing.Self-memorization and predictability of atmospheric motion.WMO/TD-No.652, 1995. |
| [7] | Rivest C, Staniforth A, Robert R, Spurious resonant response of semi-Lagrangian discretization to orographic forcing. Mon.Wea.Rev., 1994, 122: 366–376. DOI:10.1175/1520-0493(1994)122<0366:SRROSL>2.0.CO;2 |
| [8] | 蔡季水. 系统辨识. 北京: 北京理工大学出版社, 1989. |
| [9] | ECMWF.ECMWF forecast model.Reading:ECMWF Research Department, 1987. |
| [10] | Haltiner G J.Numerical Weather Prediction.New York:John Wiley & Son Inc.1971. |
 2002, 13 (2): 207-217
2002, 13 (2): 207-217