高空气象台站目前已使用计算机对高空探测资料进行处理,而工厂提供的探空仪气压特性仍然是手工绘制在方格纸上的校准曲线。这使得台站不得不再从校准曲线上取点,换算成高次方程输入计算机,以此查算信号的对应气压值。台站迫切希望工厂能直接提供数字化校准曲线,以便从根本上消除手工绘制过程中引起的各种误差。
GZZ2-1 型探空仪是目前高空站网正式大量使用的探空仪。它把随气压p 变化的空盒中心位移Z转换成电码Ma 而形成气压和电码的关系特性。本文将对空盒特性(p~Z),空盒中心位移转成电码的转换特性(Ma-Z)以及探空仪气压特性(p-Ma)进行回归拟合和分析,最终给出最适宜的统一的拟合方程,实现GZZ2-1 型探空仪气压校准曲线的数字化。
1 空盒特性回归空盒膜片是由钢模压延加工的。以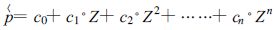
|
|
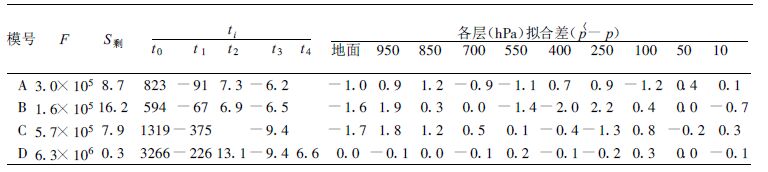
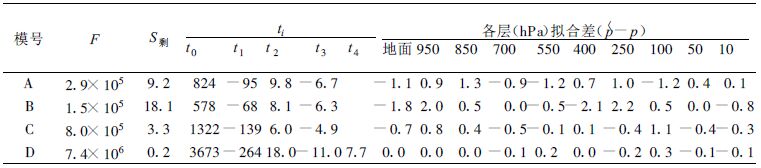
表 1 空盒特性的最优拟合方程 |
表 1 中F 是F 检验值,ti 是t 检验值,S剩是剩余平方和。空盒中心位移单位是0.01 mm,电码单位是码(下同)。α=0.01 时临界值F(2,7)=9.5,F(3,6)=9.8,F(4,5)=11.4,t(7)=3.5,t(6)=3.7,t(5)=4.0。可见,对各种典型的空盒(这里A 模行程大,D 模行程小,A,B 模特性凸起,C,D 模特性凹下) F 检验值和ti 检验值都大于其临界值,可以用4 次方以下的方程很好地拟合。
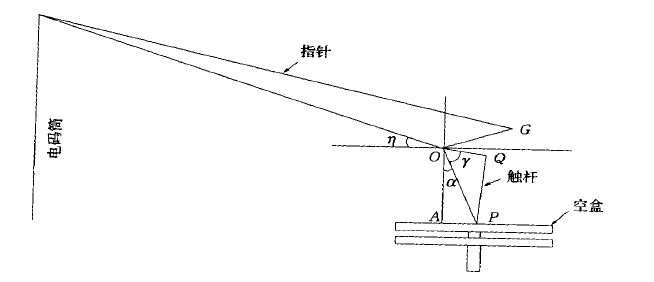
2 转换特性回归将空盒中心位移转换成电码的转换结构如图 1。
|
|
|
图 1. GZZ2-1 型探空仪气压部件结构示意图
|
|
图中,点P 是空盒中心,点O 是指针转动轴。QP =24.2 mm,OQ =9.196 mm,AP =6.7 mm,OG=16.132 mm,GE =83 mm。气压下降,P 点上升,角γ和α增加,η减少,指针GE 绕O 轴转动,针尖在电码筒上划出电码值,从而完成转换。
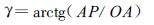
|
(1) |
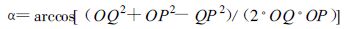
|
(2) |
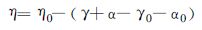
|
(3) |
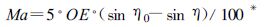
|
(4) |
设初始值:地面气压时η0 = 0.367 rad,Ma0 =7,OA0 =26.8 mm。由此可算出γ0 = 0.245 rad,α0 =1.029 rad,OE =68.78 mm。
根据中心位移,可以算出对应的γ,α,η,Ma。计算结果列于表 2。
|
|
表 2 A 模转换特性的回归拟合方程 |
Ma-Z 的关系特性就是转换特性。为可比较,这里将气压按电码线性化,即按式(5)转换成pm
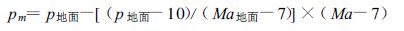
|
(5) |
以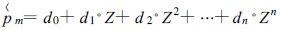
其实,转换特性是探空仪气压部件结构的特性,与空盒无关,这里只是借用A 模的数据而已。由表 2 可知,转换特性是偶次方程,其中2 次方程拟合效果最好。
3 空盒特性+转换特性回归将表 1 中的4 种钢模加工的空盒实测特性按前述方法转换成p-Ma 的关系特性,再以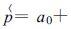
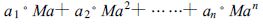
|
|
表 3 空盒特性+转换特性的最优拟合方程 |
显然,总的最优拟合方程是空盒特性+转换特性最优拟合方程的叠加。
4 探空仪气压特性回归探空仪气压特性回归拟合到什么程度才是好的呢? 首先,作为产品特性的回归,拟合曲线必须符合产品标准,回归方程必须高度显著。GZZ2-1 型探空仪标准SJ2468 对气压特性拟合的要求是“首末两校准点偏离曲线应不大于1 hPa,其余点应不大于1.5 hPa。超过该极限即为超差点。超差点不得多于两点,且不允许在首末两校准点、950 hPa 校准点、50 hPa 校准点和任何相邻两校准点上出现”。其次,应是“最优”回归方程。但如果“最优” 和符合产品标准产生矛盾,则应是“次优”,即不强求所有的而要求更多的拟合因子高度显著,还要求拟合差基本上由操作误差引起。
对探空仪气压特性进行回归拟合就可得到数字化校准曲线。统计100 台探空仪数据列于表 4。
|
|
表 4 100 台探空仪气压特性回归拟合数据统计 |
还可用重复校准求得误差平方和,用误差平方和S 误对失拟平方和S lf 进行F 检验,以进一步确定回归方程拟合程度的好坏。对全部校准点重复校准两次,选出两次电码值全部相同的探空仪共5 台。用4 次方程回归拟合,F 1 值均小于临界值F(5,10)。如用3 次方程,F1 值就有3 台大于临界值F(6,10)。表 5 列出其中两台的数据。
|
|
表 5 重复试验拟合的S误、Slf和F1 |
由表 4 和表 5 可知,4 次方程是最适宜统一的回归方程。用4 次方程回归,F 检验值均大于临界值F(4,5),回归方程全部高度显著;拟合曲线全部符合产品标准;且半数以上的拟合因子ti 检验值大于临界值 t(5)而高度显著;重复试验的F1 检验值均小于临界值F(5,10)表明拟合差基本上由操作误差引起。
5 外延部分误差估计虽然GZZ2-1 型探空仪标准规定气压校准曲线外延部分(外延到5 hPa)的误差不作规定,但由于用无形的拟合方程替代有形的手工绘制曲线,尤其是外延3 次方以上的拟合曲线有可能产生很大的误差,因此有必要来估计外延部分的误差。
任选10 台探空仪从1050~5 hPa 共校准13 点。令p1 表示以1050~15 hPa 共12 个校准点求得的拟合方程计算出外延的第13 点气压值;p2 表示以1050~10 hPa 共13 个校准点求得的拟合方程拟合的第13 点的气压值;p 3 表示第13 点的实测气压值。于是(p1 -p3)就是外延部分的误差,经计算列于表 6。由表 6 可见,这10 台探空仪外延部分最大误差仅为0.56 hPa。如果按标准将最后一点拟合差(p2 - p 3)控制在±1 hPa 内,那么外延部分的误差将被控制在±1.5 hPa 内。因为表 6 显示(p1 -p 3)近似为(p2 - p 3)的1.5 倍,这个误差并不大。
|
|
表 6 外延部分误差和拟合差比较 |
气压校准曲线虽然在整体上是4 次曲线,但在250~5 hPa 范围内几乎成了一根直线。表 7 列出其中两台电码刚好在5 hPa 过渡的探空仪在12 个校准段内的实测和拟合后的灵敏度(即斜率)就足以证实这一点。而直线的外延是不会产生很大的误差的,何况只外延了约2%(5 hPa)。因此现在仍然可以按照标准校准到15 hPa 再外延到5 hPa。
|
|
表 7 各校准段灵敏度(即斜率) |
6 校准方案设计
实际操作中总存在各种误差。据测量,校准点出现±2.0 hPa 范围内操作误差的概率约95 %,这是目前的较好水平。用户当然希望回归方程对校准点±2.0 hPa 范围内的误差能高概率拟合成功(符合产品标准),而对超过±3.0 hPa 的操作误差则应以高概率拟合失败即对拟合差规定一个界限(如产品标准),一旦超过这个界限就予以剔除从而确保回归拟合曲线的准确。这就要求我们根据用户需求来设计校准方案。
对首末校准点外的其他校准点,操作误差基本上会同步反映在拟合差上。例如,950 hPa 校准点出现±3.0 hPa 的偏离,那该点就会出现 1.8 hPa 的拟合差,相邻点会出现±1.1 hPa 的拟合差。显而易见,只要规定任何两相邻点拟合差差值的绝对值之和大于2.9 hPa 时便予以剔除,就可以确保任何点的操作误差将被限制在±3.0 hPa 范围内(这个要求严于现行产品标准)。
对首末校准点,由于其前后不再有校准点,操作误差较大时拟合差仍较小。如首点1050 hPa 校准点,操作误差为±6.0 hPa,拟合差仅为 1.0 hPa,相邻点950 hPa 校准点的拟合差也仅为±1.5 hPa。解决这个问题的办法是增加校准点。如增加1000 hPa 校准点,增加后,1050 hPa 校准点操作误差为±3.0 hPa 时,拟合差就为 1.0 hPa,1000 hPa 校准点的拟合差为±1.2 hPa。至此,再规定首点拟合差的绝对值大于1.0 hPa 时便予以剔除,就可以确保首点的操作误差也将被限制在±3.0 hPa 范围之内。
7 灵敏度检查高空台站施放前需对控空仪进行灵敏度检查以判定其是否合格,为此还需给出Ma-p 的拟合方程供台站查算电码符号。
由上所述,Ma-p 的拟合方程应该是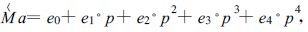
|
|
表 8 p-Ma 和Ma-p 拟合结果比较 |
显然,两个拟合的F 值大致相等,S 剩经换算后也大致相等(因为平均灵敏度为4 hPa/Ma 故气压p的S 剩大致是电码Ma 的S剩的16 倍)说明这两个拟合是等效的。
 2002, 13 (1): 125-128
2002, 13 (1): 125-128