在过去的近一个世纪里,尤其是最近的20~30 年以来,数值天气预报取得了迅速的发展,数值预报模式技术的发展经历了从L.F.Richardson 的“原始方程模式”[1]至Charney,Fjörtof t 和Von Neumann 的“滤波简化模式”[2]再到改进的“原始方程模式” 的过程[3]。模式水平分辨率由60~70 年代的300~400 km 提高到目前的几公里至几十公里,数值预报模式可以提供十几小时的短时天气预报、1~3 天的短期天气预报、3~10 天的中期天气预报以及月季年短期气候预测,利用数值预报模式预报台风、暴雨已完全成为可能,数值预报模式和物理过程参数化方案不断完善,数值预报水平在不断提高。当今,美、英、法、欧洲共同体诸国、加拿大、日本、中国、澳大利亚、印度等世界上许多国家先后建立了数值天气预报中心,数值天气预报已成为每天气象预报的制作不可缺少的重要基础和手段。
然而,在数值预报的模拟研究和业务应用的实践中,人们发现,一方面,“单一的”确定性数值预报水平的再提高变得越来越困难,以欧洲中心中期数值预报业务发展为例,过去的20~30 年里,中期数值预报的可用时效(以500 hPa 的距平相关系数达0.6 为标准)平均每10 年才提高1 天,而且可用时效的再延长,困难越来越大;另一方面,“单一的” 确定性数值预报结果也很不稳定,即有时同一次天气过程,不同气象中心的业务数值预报系统的预报结果相差很大,或者对于同一次天气过程、同一套业务数值预报系统,该数值预报系统提前5 天作出的预报准确率可能比提前2 天的预报准确率还高! 集合数值预报正是针对“单一的”确定性数值预报的这一“可预报性”问题而提出来的一种新的预报理论。
集合预报思想首先由Epstein(1969)[4]和Leith(1974)[5]提出,经历了70~80 年代的研究探索和数值试验后,至90 年代初,美国国家环境预报中心(NCEP)[6, 7]和欧洲中期天气预报中心(ECMWF)[8]于1992 年12 月先后建立了各自的集合数值预报业务系统,这标志着集合数值预报已进入了实际业务应用的成熟阶段;经过90 年代中后期的研究开发,集合数值预报得到了进一步的完善和应用拓宽,在美国、欧洲等发达国家的数值预报业务体系中,集合数值预报已占据了非常重要的位置(如ECMWF 的集合数值预报产品已占所有数值预报产品的60 %以上),而且集合数值预报产品已在气象台站得到了广泛应用[9~13],对于提高业务天气预报水平发挥了越来越重要的作用,受到了预报员的欢迎。我国的集合数值预报起步较晚,有关的文献也不多[14]。本文在简述集合数值预报基本概念的基础上,侧重对国家气象中心集合数值预报系统的发展及应用情况作一介绍。同时,本文还将讨论集合数值预报的未来发展以及在我国的研究与应用推广的问题。
1 集合数值预报的基本概念 1.1 数值预报存在不确定性在数值预报领域中常说的模式初值指的是离散化大气模式三维空间的、规则分布格点上的气象要素值。它主要是利用非均匀分布的、稀疏的观测网点的气象观测值,通过近似的客观插值分析方法而获取。由此获得的模式初始场仅仅是真实大气状态的一个近似,因此实际大气的真正初始状态永远也不可能被精确地分析估计出来。因此,以这种初始场作为初值的数值模式解也仅仅是实际情况的一个可能解。
数值预报中的关键部分---大气模式是一个离散化的数值模型,它存在物理意义和数学意义上的近似。数值预报模式所描述的大气过程并非“真实” 的大气过程,“模式大气”与真实大气存在“误差”,而这种数值模式的预报误差随着模式积分时间的延长而增加。资料误差、模式误差以及大气系统本身的混沌特性(高度非线性)使得数值预报存在不确定性。
1.2 解决“单一”数值预报存在不确定性问题的途径---集合数值预报高度非线性的数值模式对微小初值误差的敏感性,必然会导致所谓的确定性(determinist ic)唯一解很有可能是错误的。著名的气象学家Lorenz (1965)[15]曾指出,引起数值模式预报误差的主要原因在于大气是一个混沌系统,这种“混沌”特性使得从两个相差很小的初始状态起步的模式预报,在积分4 至8 天以后可能变得面目全非。
要找出数值预报模式所有可能的解(或预报结果),首先要估算初值中误差的可能分布范围,或者误差的概率分布。为了减少由于资料误差、模式误差和大气系统混沌特性引起的数值预报的不确定性,根据某种误差概率分布生成的一组初值数据集,制作出与之相对应的一组预报集合。这一方法就是所谓的集合预报方法。它同传统的“单一”确定性数值预报不同,集合预报的初值不是“一个”,而是满足某一误差概率分布的初值数据集,因此,它的预报结果也不仅仅是“一个”,而是“一组”(或“一集”)预报结果。这就为解决“单一”数值预报存在不确定性的问题提供了一条新的途径。
1.3 集合数值预报的关键---扰动初值初值的生成是集合数值预报关键的第一步,通常是采用某种扰动方法,生成一系列小扰动量分别叠加到初始场上,形成模式初值数据集,并由此制作集合数值预报。集合数值预报系统的难点是初始扰动的生成方法,扰动初值的质量好坏直接影响模式的预报质量。初始扰动生成方法的基本原则一般是:
(1) 扰动场的特征大致与实际分析资料中可能的误差分布一致,以保证所叠加的每个初值都有同样的可能性代表大气的实际状态;
(2) 扰动之间在模式中的演变方向尽可能大地发散,以保证其预报集合最大可能地包含了实际大气所能出现的状况。
对于初值扰动场的生成目前大致有4 种方法:① 随机扰动法,即经典的蒙特卡罗法,扰动量由一个随机函数给出。② 时间滞后法(Lagged Average Forecast,LAF)[16],即用“滞后的”不同时间初值作模式预报,把同一预报时段的预报结果加起来取平均,此即为集合预报;由于计算机资源的限制,集合预报中的成员数目不能无限地增多。为了更有效地满足设计的第二个条件(即成员间的发散程度尽可能地大),人们又提出了能生成包含有动力学结构扰动场的数学方法,这就是③ 奇异向量法(Singular Vector,SV),它是通过求解伴随数值预报模式得到的,因此需要花费大量的计算时间。④ 增长模繁殖法(Breeding of the Grow ing Mode),此法模拟了气象资料分析处理的过程,既考虑了实际资料中可能出现的误差,同时又考虑了快速增长的模式大气动力学结构。
2 国家气象中心集合数值预报系统开发的简要回顾早在20 世纪70~80 年代,集合数值预报(最初称为“随机动力预报” ---Stochastic Dy namic Forecasting)的研究已在国外受到广泛重视,1980 年欧洲中期天气预报中心(ECMWF)举办了第一次较大的针对集合数值预报的国际学术研讨会(ECMWF Wo rkshop on Stochastic Dynamic Forecasting)。至1992 年12 月,集合数值预报业务系统正式在美国国家环境预报中心(NCEP)和ECMWF 先后建立。随后,法国、英国、日本、澳大利亚、加拿大、南非等国也先后建立了各自的集合数值预报业务系统。
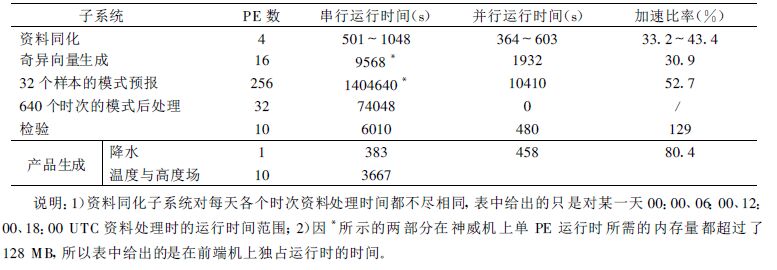
相比之下,我国开展集合数值预报研究与业务的时间就晚多了,一个很重要的客观原因是集合数值预报需要很大的计算机资源。以ECMWF 为例,其中期集合数值预报系统所需计算机资源比其资料四维变分同化与模式预报两者之和还多(参看表 1):
|
|
表 1 ECMWF 各业务系统所需计算机资源比较 |
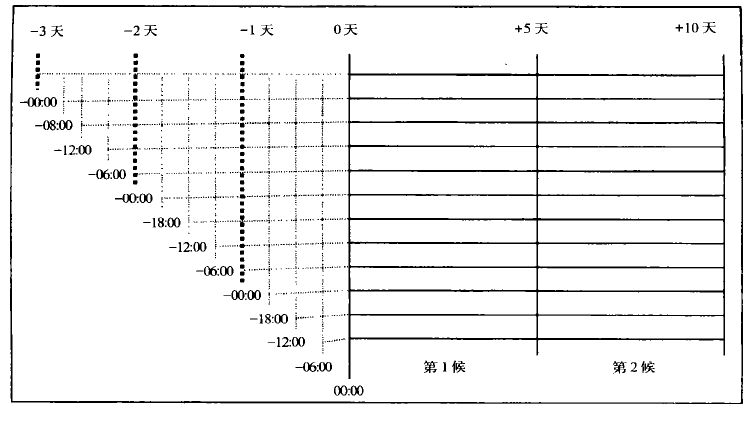
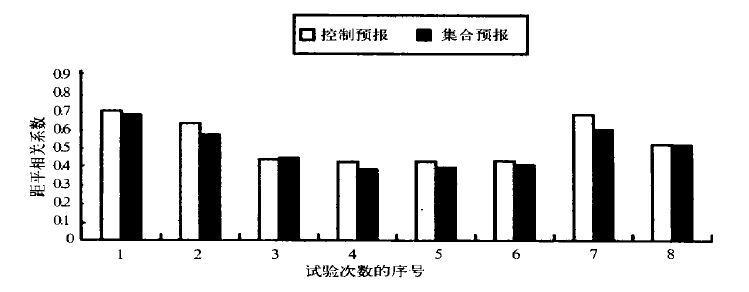
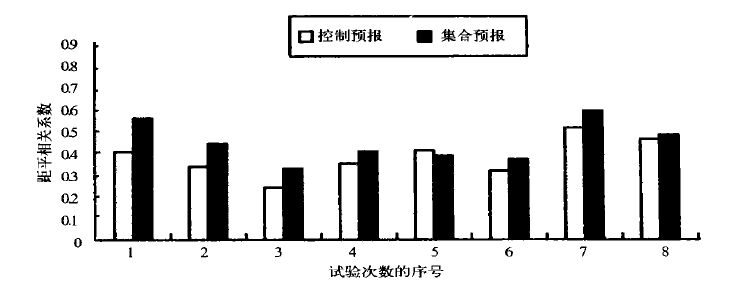
1995 年,国家气象中心安装了从美国进口的IBM/SP2 巨型并行计算机(32 个节点,浮点运算峰值速度达80 亿次/s),这为我们开展集合数值预报提供了必要的客观条件。为了充分利用IBM/SP2 巨型并行计算机的资源,国家气象中心于1996 年5 月下旬开始,以原有的动力延伸预报为基础,着手在IBM/SP2 巨型并行计算机上开发建立一套中期集合数值预报系统。该系统以T63L16 为基础,采用时间滞后平均法生成扰动初值(图 1)[17],即以过去3 天、每天4 个时次(00:00,06:00,12:00 和18:00UTC,下同)的分析场为初值,模式往前积分10~13 天,由此组成包含有12 个成员的集合预报。该系统已于1996 年9 月投入试验运行,结果提供给中央气象台中期天气预报参考。以“00:00”时刻的10 天预报作为“控制预报(CRL)”,与其余11 个成员取平均形成“集合预报”,两者的预报检验比较见图 2 和图 3。由图可以看出,对于第一候的预报,“控制预报”仍优于“集合预报”,而第二候的情况却几乎完全相反,“集合预报”明显优于“控制预报”。
|
|
|
图 1. 利用时间滞后方法生成集合预报模式初值
(虚线表示“过去” 时刻,生成初值;实线表示“未来” 时刻,集合预报) |
|
|
|
|
图 2. 国家气象中心第一代中期集合数值预报试验系统T63L16/ LAF 第1~5 天
(第1 候)预报平均北半球500 hPa 距平相关系数(1996 年9 月下旬~11 月,8 次个例过程) |
|
|
|
|
图 3. 国家气象中心第一代中期集合数值预报试验系统T63L16/ LAF 第6~10 天
(第2 候)预报平均北半球500 hPa 距平相关系数(1996 年9 月下旬~11 月,8 次个例过程) |
|
由于现有的数值预报模式存在“模式预报准确率与预报时效长度成反比” 的系统误差,即预报时效越长,预报准确率越低,所以,出现图 2 的结果(对于第一候的预报,“控制预报”仍优于“集合预报”)就不足为奇了。为此,借鉴ECMWF 集合预报系统,以奇异向量法(Sing ular Vecto r,SV)[18]取代时间滞后法,对原有集合预报系统的扰动初值生成方法进行改进。这样一来,所有的集合预报成员的起报时间点都一样(如图 1 中的0 天00:00时刻),所不同的是“控制预报”为初值不加上任何扰动的预报,“集合预报”为“控制预报”的初值加上不同小扰动后所形成的“新初值”的预报。以T21L16 为奇异向量生成模式、以 T63L16 为集合预报模式、集合成员为11 个的第二代中期集合数值预报试验系统于1999 年2 月在IBM/SP2 上建立,并将初步结果提供给中央气象台中期天气预报会商参考。
在第二代中期集合数值预报试验系统的基础上,国家气象中心与北京北方计算中心合作,在国产高性能计算机神威-I 上建立了第三代中期集合数值预报系统。该系统以 T106L19 全球模式为基础,水平分辨率约120 km,垂直分辨率19 层(约0.5~2 km),采用奇异向量法生成扰动初值,成员有32 个,系统增加了预报检验和产品加工子系统。该系统于1999 年年底投入准业务运行,并在不断改进完善之中。
3 国家气象中心基于神威计算机的集合数值预报业务系统 3.1 集合数值预报系统的组成与功能神威集合数值天气预报系统以神威巨型计算机为运行平台,以中国气象局业务运行的中期数值天气预报模式为基础,并与国家气象中心业务所用的数据库、通信等支持系统相连接,形成一套完整的集合数值天气预报业务系统。该系统采用奇异向量法产生初始扰动,产生奇异向量的模式为T21L19,集合预报模式为T106L19,集合预报成员为32 个。
在并行软件研制中,紧密结合集合数值预报计算量、资料量很大和神威并行机计算能力强的特点,分别采用了并行任务创建与过程唤醒相结合、数据分布加消息传递以及SPMD( Single Prog ram Multiple Data)等并行方法,提高并行计算效率,缩短运行时间,满足了实际预报的时效要求。该系统的主体部分由下列7 个子系统组成:
前处理子系统 将接收的二进制格式的报文进行数据转换,经过解码、探空报合并以及报文重排序等步骤生成观测资料AOF 文件,供资料同化系统使用。
资料同化子系统 利用观测资料中提取的信息、初估场(前一次6 h 模式预报场)和前一次分析的误差增量场产生当前时刻的初始场,供集合预报初始场生成系统使用,并用当前时刻的初始场做6 h 模式预报,生成下一次的分析初估场。
集合预报初始场生成子系统 在资料同化所得到的初始场的基础上,用T21L19 模式产生奇异向量,从而构造初始扰动,得到32 个样本的初始场,供32 个样本的10 天模式预报系统使用。另外,目前正在将生成初始扰动的T21L9 模式升级为T42L19(包括“正模式”和伴随模式的升级),T42L19 模式程序在作进一步优化。
模式预报子系统 利用集合预报初始场生成子系统所产生的32 个初始场,做32 个成员的10 天模式预报,预报模式为T106L19,水平分辨率约120 km,垂直分辨率19 层(约0.5~2 km),每个成员按每天间隔12 h 输出一次结果,32 个成员共输出640 个时次的结果。
模式后处理子系统 将32 个成员共640 个时次的输出结果处理成对数据用户更为方便和标准的格式,分辨率为1.125°,供数据库存档和产品生成子系统使用。
产品生成子系统 根据后处理结果,生成所需的预报产品,即未来10 天逐日的中国范围的降水概率预报,日降水预报,850 hPa 日温度距平的概率预报、500 hPa 高度场集合平均,以及500 hPa 高度场10 天平均。数值预报产品达100 种以上。
可视化运行监控子系统 具有每天定时自动启动运行集合预报系统,为系统运行提供可视化监测、控制、出错处理选择,与所用T106L19 业务系统无缝连接运行、查看机器资源等功能。
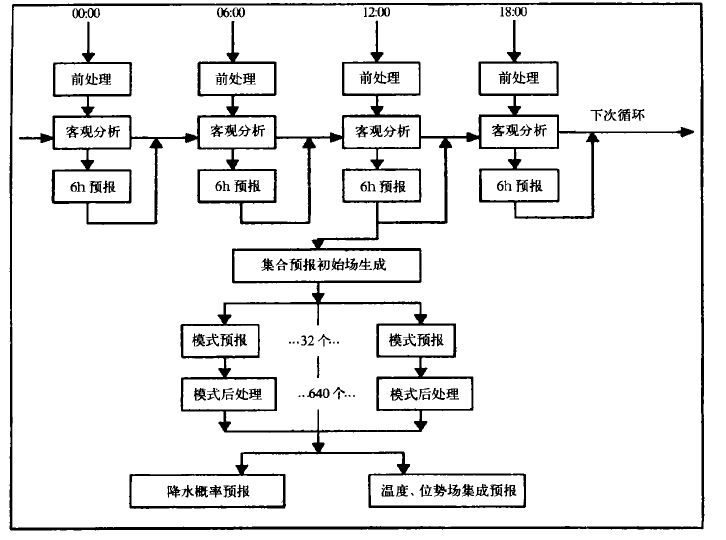
该系统使用了神威计算机中的264 个PE(处理器),存储总量达120 GB,程序总量达36 万行。每天定时从4 个时次的资料滚动开始,依次做前处理、资料同化、集合预报初始场的生成、模式预报、模式后处理,最后制作出集合预报的产品。图 4 给出了神威集合数值预报系统的总体运行流程结构。
|
|
|
图 4. 神威集合预报系统运行流程结构图
|
|
3.2 主要技术特点
(1) 数值预报模式集合数值预报系统中的核心部分为大气模式,主要包括大气运动方程、大气质量守恒方程、大气热力学方程、大气状态方程等。本集合数值预报系统采用已在国家气象中心业务运行的T106L19 全球谱模式作为集合预报系统的核心预报模式,即截断波数为106 个(相当于水平分辨率约为120 km),垂直分层为19 层,垂直坐标取混合坐标(低层为σ坐标,高层为p 坐标)。物理过程参数化方案包括辐射过程、垂直湍流扩散过程、次网格尺度降水过程(深对流、浅深对流)、大尺度降水过程、陆面过程等参数化方案。
(2) 初始扰动方法集合数值预报系统中,初始扰动方法是关键的技术。基于神威巨型计算机的集合数值预报系统采用奇异向量法生成模式初始扰动场。
a) 奇异向量生成的基本原理
对某一数值天气预报模式:
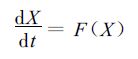
|
(1) |
它的切线性模式为:
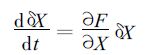
|
(2) |
称式(2)为预报模式(1)的切线性模式,其中X 为状态变量。将模式方程(1)写成转移矩阵形式:
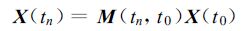
|
(3) |
也可以将切线性方程(2)写成矩阵形式:
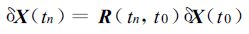
|
(4) |
同时,在Hilbert 空间中存在映射规律:设X 为Hilbert 空间H 中的任一元素,Y 为 Hilbert 空间F 中的元素,T 为从空间H 到空间F 的连续线性映射算子,若存在一从空间 F
利用该性质,对式(4)作“点内积”有:
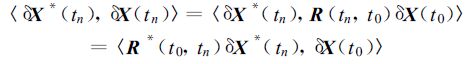
|
(5) |
称
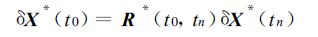
|
(6) |
为切线性模式的伴随形式,即为伴随模式。
对t0 时刻预报初值中的初始误差(用扰动δX(tn)表示)增长幅度,可以用二次范数形式表示tn 时刻的扰动大小:
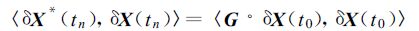
|
(7) |
b) 奇异向量矩阵的特殊求解方法一般求矩阵特征值和特征向量的方法只适用低阶的方阵,对1000 阶以下的方阵较为有效,而求矩阵G 的特征值和特征向量时,很难写出它们的具体矩阵形式及其矩阵元素。且矩阵的阶数如此之大,用常规的方法求其特征值和特征向量非常困难。数学家Lanczos 在20 世纪50 年代提出了一种迭代方法,人们称其为Lanczos 方法,该方法有助于求解大型稀疏对称矩阵的特征值和特征向量。它不需要知道矩阵元素,对于只求少数几个(相对于矩阵的阶数)极端特征值的问题是非常有效的方法。
(3) 并行计算原理和方法在神威机上,解决科学计算和工程应用课题时,采用的并行方式通常有两类:一是功能并行,也可称为任务并行或MPMD(Multiple Program Multiple Data),即多个处理器在同一时间内执行不同的运算;二是数据并行,也可称为SPMD(Single Prog ram Multiple Data),即多个处理器在同一时间内执行同一指令。
在神威集合数值天气预报系统中主要对占用资源大,数据文件交换量大、运行时间长的6 个部分进行了并行化处理,即资料同化、奇异向量生成、模式预报、模式后处理、产品生成和检验子系统。集合数值天气预报在计算机软件实施上遇到的主要困难是:样本数多、计算量和数据传输量都很大。我们充分发挥神威计算机并行机制的强大优势,围绕多样本并行计算与控制这一核心,针对各部分技术特点,采用不同的并行方法,或并行任务创建与过程唤醒相结合,或数据分布加消息传递以及SPMD 等,尽力加大并行度,不断优化程序设计,从而提高了系统的并行解算效率,缩短了运行时间,最终使得软件系统在功能实现、计算时效、日常运行等各个方面都满足了业务运行的需求。
在神威巨型机上,对集合数值预报系统各部分的并行化效率进行测试,其测试结果列于表 2。从表 2 中可以看出,并行化后系统的各部分时效有了较大程度的提高,其中检验子系统并行效率最高,达到129 %,奇异向量生成部分稍低,但也达30.9 %,而32 个样本的模式预报的并行规模最大,串行运算的CPU 时间为1 404 640 s (390 h),经并行化后其 CPU 时间仅为10 410 s (2 h 53 min)。另外,从表中还可以看出,大规模、多处理器的巨型机在集合预报这样多样本、多任务应用的并行化计算方面有着很大的优势,模式后处理子系统就利用了多处理器同时计算,实现了与模式预报子系统的同步运算,从而在整个系统的运行过程中几乎不占用任何时间。
|
|
表 2 并行效率表 |
(4) 检验方法和原理集合数值预报的成员很多,不能简单地直接引用传统的“单一”确定性数值预报的检验方法对集合预报的每一个“成员”进行检验,因为要归纳出这样的“成员检验”结果是非常困难的,因此必须开发出针对集合数值预报的检验方法。目前,国际上具有集合数值预报业务系统的先进国家和地区,如美国国家环境预报中心,欧洲中期天气预报中心等,已研究出了一系列有效的集合数值预报检验评价方法。参考其它国家气象中心的成功经验,本集合数值预报系统开发应用的集合预报检验方法[19]有① Talag rand 分布:O.Talagrand[20]认为一个“好”的集合预报的标准应是每个预报成员几乎以同样的概率发生;换言之,观测实况也应以相同的概率落在它们附近。② 离散度(或分散度):各扰动预报与控制(未扰动)预报之间的平均距离,也即离散度越小,可预报性越大,集合预报要比控制预报好。③ 概率预报检验方法之一:Brier 评分(Brier Score,简称BS),即平均平方概率误差,评分的取值范围是0~1,且BS 越小越好。④概率预报检验方法之二:相对作用特征(Relative Operating Characteristic,简称ROC),这是信号探测理论(Signal Detection Theory)在数值天气预报中的一种应用,即对二分类要素序列进行检验,表示集合预报的命中率和假警报率情况,命中率越高、假警报率越低,预报效果越好。
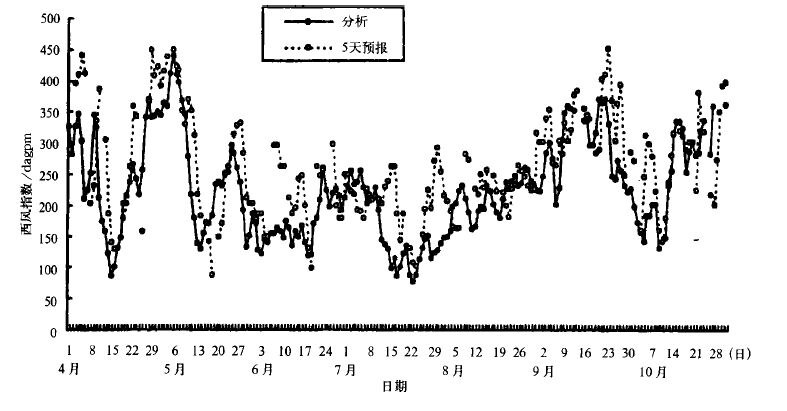
4 集合数值预报产品的初步检验与解释应用 4.1 集合数值预报产品的初步检验基于神威巨型计算机的中期集合数值预报系统于2000 年12 月投入准业务运行,经过一年的运行后,于2001 年1 月正式投入业务运行,并对预报结果进行了初步检验。图 5 给出了亚洲中高纬度区域西风指数演变的预报情况。从2000 年4~10 月中高纬度西风指数演变图可以看出(图中粗黑线表示分析场,即实况;细点虚线表示集合数值预报),集合数值预报结果与实况(即分析场)演变过程非常接近,而且能提前5 天预报出西风指数的变化,这就为预报员提供了很好的参考价值。
|
|
|
图 5. 2000 年4~10 月逐日西风指数的分析与5 天集合预报比较
|
|
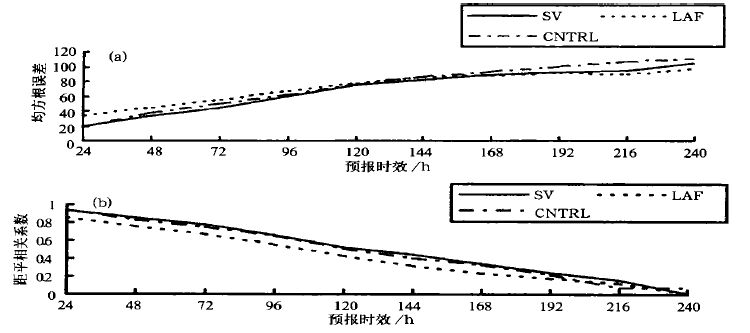
图 6给出了时间滞后法(LAF)和奇异向量法(SV)初值生成方案的集合预报比较试验结果,即北半球500 hPa 高度场的距平相关系数、均方根误差的对比检验,检验时段为2000 年9 月21 日~10 月11 日的20 天平均。对距平相关系数来说,SV 集合预报的效果除第9 、10 天外都比LAF 和控制预报好;对均方根误差RMSE 来说,SV 集合预报的均方根误差都比控制预报的要小,只是第9 、10 天SV 比LAF 稍微大了一点。由此看来,SV的总体效果要比LAF 好。
|
|
|
图 6. 集合数值预报(平均)和控制预报北半球500 hPa 高度场检验:均方根误差(a)距平相关系数(b)
(SV 为奇异量的预报,LAF 为时间滞后的预报,CRL 为控制预报) |
|
4.2 主要集合数值预报产品的解释应用
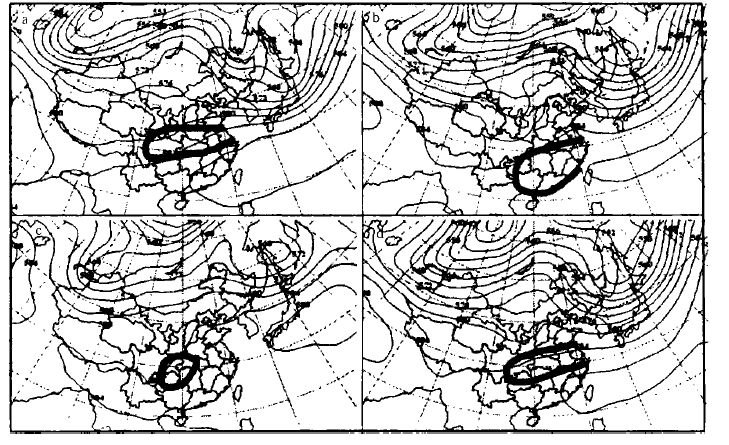
集合数值预报所能提供的信息量是“单一”确定性预报的十到几十倍,因此,集合数值预报产品解释应用的开发就显得尤其重要。目前已开发出的产品有500 hPa 高度预报场分簇(类)图;500 hPa 预报特征等高线图(又称“面条图”);定点气象要素的概率预报图;定点850 hPa 温度概率烟羽图;温度演变趋势图;500 hPa 集合成员简单平均环流形势图;西风指数演变图;降雨量的概率预报图等等(这些集合数值预报产品解释应用的图例将在本期刊中的其它文章有专门介绍)。图 7 给出了500 hPa 集合成员简单平均环流形势图的例子。从2000 年6 月1 日500 hPa 环流形势图可以看出(粗黑线所包围的区域表示主要降雨区位置和分布),集合预报可以较准确地提前4~5 天预报出副高的位置和主要雨带的落区、分布。与之相比,业务数值预报对这次天气过程的预报效果要差一些。
|
|
|
图 7. 500 hPa 高度场(粗实线表示降雨区域)
(a)2000 年6 月1 日实况,(b)4 天集合预报,(c)4 天业务预报,(d)5 天集合预报 |
|
5 集合预报的未来发展趋势 5.1 各国现有集合数值预报业务系统简介
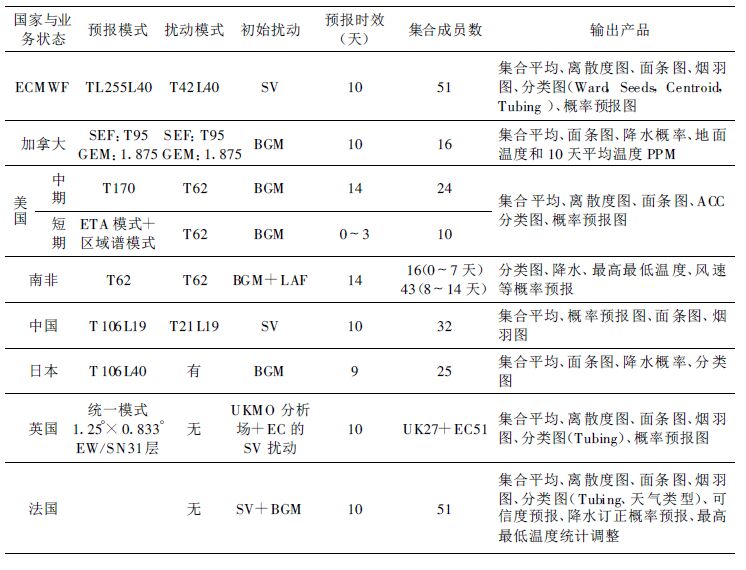
随着数值预报和高性能计算机技术的发展,集合数值预报不仅已成为数值预报的一个重要发展趋势,而且日趋成熟,集合数值预报的应用也越来越受到重视,越来越显示出它在日常天气预报与短期气候预测方面不可替代的作用和优势。表 3 简要归纳了 ECMWF 、美国、加拿大等国[21]气象中心集合数值预报系统的基本技术要点。从表中可见,集合数值预报的动力模式多为全球谱模式;扰动初值生成的模式分辨率比预报模式的分辨率稍低;扰动初值生成的方法多采用增长模繁殖法(BGM)和奇异向量法(SV);预报时效多为中期(10 天左右);集合成员最多的为ECMWF 、英国和法国。在实际应用中,ECMWF 的产品应用最广泛,且ECMWF 的集合数值预报系统的分辨率也最高;美国 NCEP 是目前唯一开展了短期集合数值预报业务的气象中心,且其中期集合数值预报系统的预报时效已达14 天。
|
|
表 3 ECMWF、美国和加拿大等国集合预报业务系统 |
5.2 未来集合数值预报的研究与业务发展
集合数值预报的初值扰动理论仍将是一个焦点研究问题。目前业务上常用的增长模繁殖法(BGM)和奇异向量法(SV)较随机扰动法、时间滞后平均法,具有发散度大、预报效果好等优点,但也存在“先天之不足”。增长模繁殖法具有一定的模式动力物理意义,但缺乏严格的理论推导予以支持,而奇异向量法具有严格的数学理论推导予以支持,但却难于确保奇异向量法给出的扰动发展方向就必然是模式大气的可能发展方向。另外,现有的初始扰动法只限于中高纬度地区,在热带地区的初始扰动理论还不是很成熟,有待完善和提高。在热带地区,非绝热加热过程对模式初始扰动起到至关重要的作用和影响。如 ECMWF 将非绝热过程引入模式和伴随切线模式中,用线性化的非绝热过程[22],考虑湿度场,计算热带地区的初始奇异向量,用类似方法对西太平洋两次台风路径和强度作了集合预报试验[23]这些研究试验都取得了“正”的影响结果。另外,从已有的研究看,扰动模式物理过程参数化方案[24]的方法可以增加成员间的发散度,提高较小尺度天气事件的预报概率。
我们知道,对于数值预报来说,预报结果不仅取决于模式初值,而且其影响因素还包括动力模式差异、同一动力模式采用的物理过程方案不同、分析同化方案不同(客观分析插值方法、观测资料)。这就把初值不确定性的集合数值预报问题提为“多因素”不确定性的集合数值预报问题,也即“超级集合预报问题”。多动力模式、多物理过程方案、多分析初值的“超级”集合预报的方法,可很容易地增加集合预报成员数和发散度,更全面考虑“单一”数值预报的不确定性因素,从而提高集合预报效果。有科学家(朱跃建,个人联系)将世界上各气象业务中心的中期数值模式业务运行结果作简单的算术平均,形成“多业务数值预报模式系统平均集合预报”,发现后者的月检验评分(500 hPa 距平相关系数)优于任何“单一”中期数值模式业务运行的结果。
一个集合数值系统所能提供的产品信息量是非常大的,可以是“单一”数值预报的几十倍,预报员要在极有限的时间内对如此大量的信息进行分析,并用于制作日常天气预报与服务是很困难的,因此,集合数值预报产品的解释应用技术研究也显得同等重要。目前在用的产品释用方法和技术主要有:简单集合平均图、邮票图、烟羽图(plumes charts)、面条图(spag hetti chart),要素概率图、聚类分类法(clustering)、500 hPa 环流形势分型法等。聚类分类法又可分为Ward 聚类法(Ward algorithm)、重心聚类法(Cent roid algorithm)、种子分类法(Seeds clustering)、中央聚类法(Cent ral clustering)和管形聚类法(Tubing clustering)等[25, 26]。近年来,也有科学家开展了集合数值预报的PPM 、MOS 、神经元网络等方法的研究与业务应用(如美国用MOS 方法,加拿大用PPM 方法,瑞士则用神经元网络)。集合数值预报产品的释用应与预报员紧密结合,这点非常重要。另外,集合数值预报的多维产品(如三维动画)、物理概念模型产品等的释用技术开发仍有待加强。
集合数值预报的业务应用最初只限于全球中期数值预报,近年来,集合数值预报领域不断拓宽,已在有限区域短期天气预报、月季年短期气候预测等方面的业务中得到应用。同时,在台风(飓风)路径预报[27]、中小尺度极端天气预报[28, 29]等方面开展了集合数值预报的研究,也得到了令人鼓舞的结果。集合数值预报甚至在一些专业气象预报中也得到了应用,如用ECMWF 集合预报与海浪预报模式耦合,每天发布海浪集合预报[30];用大气和海浪集合预报一起制作横渡大西洋的船舶航线预报,船舶航行成本与海浪和风有很大关系、法国气象局用污染模式与ECMWF 集合预报模式耦合,预报海面石油泄漏形成的污染物漂移过程;将集合数值预报产品应用到未来1~10 天电力需求的预报中[31],等等。
6 结束语世界气象组织(WMO)已明确地把资料同化、耦合模式、高分辨率模式和集合预报等列为未来数值预报领域的4 个发展战略,西方发达国家也把集合数值预报系统的研究开发与下一代数值预报系统的研究开发置于同样重要的地位。
国家气象中心虽然在集合数值预报方面起步较晚,但自1996 年起,经过4~5 年的研究开发与应用实践,以国产神威巨型计算机为运行平台、以国家气象中心业务运行的中期数值天气预报模式为基础,已经建立了我国的全球中期集合数值天气预报业务系统。该系统采用奇异向量法产生初始扰动,产生奇异向量的模式为T21L19,预报模式为 T106L19,集合预报成员为32 个。该系统使用了神威计算机中的264 个PE 处理器,存储总量达120 GB,程序总量达36 万行。每天定时从4 个时次(00:00 、06:00 、12:00 、18:00 UTC)的资料滚动开始,依次做前处理、资料同化、集合预报初始场的生成、模式预报、模式后处理,最后做出集合预报的产品。整个系统自1999 年12 月实时运行以来,系统运行稳定、效率高,预报应用效果得到了中央气象台预报员的肯定。
然而,集合数值预报无论是理论研究还是业务应用都未能引起我国科学家的足够重视。事实上,集合数值预报产品很值得在我国的气象台站推广应用。我们以中期数值预报为例进行讨论。大家都知道,人们通常所说的中期数值预报有效预报天数为5 天,指的是一个月(或一个季度、一年)的平均情况。但是,对于某一天的中期数值预报有效预报天数可能小于5 天(如4 天,甚至3 天),也可能大于5 天(如6 天,甚至7 天),而这种中期数值预报的逐日可预报性不稳定问题是普遍存在的。在每天的天气预报制作中,充分利用集合数值预报的结论,可以较好地解决业务中期数值预报的逐日可预报性不稳定问题,在实际应用中“延长”中期数值预报的有效预报天数(如由平均的5 天“延长” 为实际的6天),以便有限地提高业务中期数值预报的水平。要知道,根据ECMWF 过去20 多年的中期数值预报的发展水平,ECMWF 平均每10 年才把其中期数值预报的有效预报天数延长1 天,可见集合数值预报是数值预报领域中具有广阔开发研究前景的课题,中期集合数值预报产品在业务台站中的推广应用非常必要和具有实际意义。对于其它短期、长期集合数值预报,其道理也相同。
| [1] | Richardson L F. Weather Prediction by Numerical Process. Cambridge University Press, reprinted Dover, 1922. 236. |
| [2] | Charney J G, Fjörtoft R, Von Neuman J, Numerical integration of the barotropic vorticity equation. Tellus, 1950, 2: 237–254. |
| [3] | Haltiner G J, Williams R T. Numerical Prediction and Dynamic Meteorology. John Wiley & Sons Press, reprinted in USA, 1980. 1-3. |
| [4] | Epstein E S, Stochastic dynamic prediction. Tellus, 1969, 21: 739–759. |
| [5] | Leith C S, Theoretical skill of Monte Carlo forecasts. Mon. Wea. Rev., 1974, 102: 409–418. DOI:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2 |
| [6] | Tracton M S, Kalnay E, Operational ensemble prediction at the National Meteorological Center. Weather and Forecasting, 1993, 8, (3): 379–398. DOI:10.1175/1520-0434(1993)008<0379:OEPATN>2.0.CO;2 |
| [7] | Tracton M S, Du J. Short range ensemble forecasting (SREF) at the National Center for Environmental Prediction. WMO Workshop on the Use of Ensemble Prediction, Beijing, 2000. |
| [8] | Molteni E, Buizza R, Palmer T N, The ECMWF ensemble prediction system: Methodology and validation. Q. J. R. Meteor. Soc., 1996, 122: 73–119. DOI:10.1002/(ISSN)1477-870X |
| [9] | Cavalcanti I F A, Bonatti J P, Coutinho M, et al. Weather forecasts and climate prediction at CPTEC: The ensemble prediction system. WMO Workshop on the Use of Ensemble Prediction, Beijing, 2000. |
| [10] | Kusunoki Shoji. Dynamical long-range forecasting activities at the Japan Meteorological Agency (JMA). WMO Workshop on the Use of Ensemble Prediction, Beijing, 2000. |
| [11] | Wilson L J. Canadian Meteorological Center for ensemble prediction system. WMO Workshop on the Use of Ensemble Prediction, Beijing, 2000. |
| [12] | Mylne K R. Quasi-operational multi-model multi-analysis ensembles on medium-range time scale. WMO Workshop on the Use of Ensemble prediction, Beijing, 2000. |
| [13] | Zhang Z, Krishnamurti T N, Ensemble forecasting of Hurricane Tracks. Bull. Amer. Meteor. Soc., 1997, 78: 2785–2795. DOI:10.1175/1520-0477(1997)078<2785:EFOHT>2.0.CO;2 |
| [14] | 毛恒青, 王建捷. 集合预报业务使用现状和趋势. 气象, 2000, 26, (6): 24–29. |
| [15] | Lorenz E N, A study of the predictability of a 28 - variable atmospheric models. Tellus, 1965, 17: 321–333. |
| [16] | Brankovic C, Extended-range prediction with ECMWF models: Time-lagged ensemble forecasting. Q. J. R. Meteor. Soc., 1990, 116: 863–912. |
| [17] | 李小泉, 刘金达, 汪迎辉. 集合预报及其在中期时间尺度预报中的应用问题. 国家气象中心科技年报(A类), 1997, 16-26. |
| [18] | 刘金达. 集合预报开创了业务数值天气预报的新纪元. 气象, 2000, 26, (6): 21–23. |
| [19] | Stansk H R, Wilson. L. J, Burrows W R. Surrey of common verification methods in meteorology. WMO/TD, No. 358, 1989. |
| [20] | Talagrand O, Vautard R. Evaluation of probabilistic prediction systems. Workshop on Predictability, ECMWF, 1997, 20-20, 10. |
| [21] | WMO. Numerical Weather Prediction, Progress Report for 1992-1998, WMO/TD, 1993. |
| [22] | Barkmeijer J, Buizza R, Palmer T N, et al. Tropical singular vectors computed with linearized diabatic physics. ECMWF Technical Memorandum 297, 1999. |
| [23] | Puri K, Barkmeijer J, Palmer T N. Ensemble prediction of tropical cyclones using targeted diabatic singular vectors. ECMWF Technical Memorandum 298, 1999. |
| [24] | Stensrud D J, Bao J, Warner T, Using initial condition and model physics perturbation in short-range ensemble simulations of meso-scale convective systems. Mon. Weather Rev., 2000, 128: 2077–2107. DOI:10.1175/1520-0493(2000)128<2077:UICAMP>2.0.CO;2 |
| [25] | Atger F, Tubing: An alternative to clustering for the classification of ensemble forecast. Weather and Forecasting, 1999, 14, (5): 41–757. |
| [26] | Nicolau J. Use of Ensemble Forecasting at Meteo-France. WMO Workshop on the Use of Ensemble Prediction, Beijing, 2000. |
| [27] | Zhang Z, Krishnamurti T N, A perturbation method for hurricane ensemble predictions. Mon. Wea. Rev., 1999, 127: 447–469. DOI:10.1175/1520-0493(1999)127<0447:APMFHE>2.0.CO;2 |
| [28] | Petroliagis T, Buizza R, Lanzinger A, et al. Extreme rainfall prediction using the ECMWF ensemble prediction system. http://www.ecmwf.int/pressroom.1997. |
| [29] | Palmer T N, Barkmeijer R, et al. The future of ensemble prediction. ECMWF Newsletter No 88, summer/autumn, 2000. |
| [30] | Janssen P. Potential benefits of ensemble prediction of waves. ECMWF Newsletter, No. 86, winter, 1999/2000. |
| [31] | Buizza R, Palmer T N, The singular-vector structure of the atmospheric general circulation. J. Atmos. Sci., 1995, 52: 1434–1456. DOI:10.1175/1520-0469(1995)052<1434:TSVSOT>2.0.CO;2 |
 2002, 13 (1): 1-15
2002, 13 (1): 1-15