目前国内外, 季尺度短期气候预测多以统计学方法为主要依据。利用气候的历史资料, 通过相关分析, 选取具有一定物理内容的预测因子建立起预测对象随时间变化的统计关系式, 从而对未来的气候特征做出预测。研究表明, 预测因子如何选择是十分重要的, 相同的预测因子, 不同的统计模型, 预测结果的差异并不十分显著, 但在实际工作中, 寻找物理意义明确而相关又显著的预测因子并不容易。目前较普遍的方法是, 确定了预测对象后, 对前期的高度场、海温场及其他环流特征量进行相关普查, 从中选取相关系数达到一定置信度的作为备选预测因子。这样就存在两个问题, 一是对高度场和海温场的相关普查, 一般对逐个网格点计算相关系数, 挑选成片的通过一定置信度的区域平均值作为备选因子, 这样某些有较好物理意义的因子因相关系数偏低不能入选, 而一些入选的因子却缺乏明确的物理内容, 似乎有些随机性; 其次是入选的预测因子大部分是前期某个月的, 缺乏连续性, 不符合短期气候预测的尺度对应原理[1], 同时这种“小原因, 大效果” (用前期某个时间尺度短的大气过程表现, 来预测后期时间尺度长的大气过程变化), 令人感到有些偶然性。本文旨在针对这些问题, 对预测因子的如何选择, 综合处理进行试验, 使入选因子在天气气候学上有较好的解释又提高与预测对象之间的相关程度, 达到提取强信号的目的, 并将此方法应用于长江三角洲汛期的旱涝趋势预测中, 取得了明显效果。
1 预测对象和预测因子的选取处理 1.1 预测对象的选取取1952~1996年长江三角洲的上海龙华和崇明、江苏的东山、南通、东台、常州、南京、溧阳及浙江的杭州和乍浦等10个站5~9月、6~8月期间的降水量, 作EOF分解。由于它们的第一特征向量的方差贡献已达63%, 前3个特征向量的累积方差贡献超过83%, 已能表示长江三角洲汛期旱涝空间分布特征, 并且前几个特征向量场有较好的稳定性。本文的预测对象转化为前3个特征向量所对应的时间系数, 将时间系数的预测结果与相应的特征向量相乘, 可得到旱涝趋势分布预测场。
1.2 预测因子的选取、综合处理研究和实践表明, 影响我国汛期旱涝的因子主要有:北太平洋海面温度和西北太平洋副热带高压的异常; 夏季风活动异常、南海高压、越赤道气流强弱的影响; 中高纬度环流 (阻塞高压、极涡等) 的影响, 还须考虑各种气候要素背景, 北半球大气环流各种遥相关模型指数的异常等等。这些因子都具有一定的天气气候学意义或物理内容, 对我国不同区域所起的作用也有差异。本文将上述有关的已有物理基础的各种因子指数化, 取上年6月至当年2月的资料, 计算预测对象与各月因子序列的相关系数。结果表明, 各种指数因子与预测对象的相关性绝大部分并不好, 更值得注意的是各因子序列与预测对象之间逐月的相关性质呈非一致性, 同一个因子即使是相邻的两个月亦存在正负两种相反关系。
前期的气候和环流背景的连续变化, 对后期的气候和环流状况必然有一定的影响。根据尺度对应原理, 任何尺度的初始值都只能对应本阶次尺度的预测量, 超出一定的范围, 就应当改变初始量的阶次。例如我国流传的天气谚语“久晴必久雨”, 就十分明确地表达了尺度对应原理。“久晴”是初始过程, “久雨”是预测过程, 或是相反也可以, 重要的是前后两个“久”在时间尺度上应当是对应的。汛期旱涝 (降水) 的时间尺度为3~5个月, 因此它的预测因子的初始量也应大致在这个时间尺度上。为了获得相应时间尺度上预测因子的综合信息, 常规的处理方法是计算前期相应时段的累计值或平均值, 但由于逐月的因子序列与预测对象序列相关性质的非一致性, 造成处理后的序列与预测对象序列相关系数大幅度下降, 破环了因子和对象之间的对应关系, 影响了因子的挑选。
现在引入相关系数权重概念, 采用以下公式计算预测因子序列的时段累积 (平均) 值。
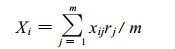
|
(1) |
式中Xij为某月的因子序列, i=1, 2, …n为样本数, j=1, 2 …m为月份个数, rj为某月因子与预测对象的相关系数。将上年6月至当年2月分为两个时段, 6~9月 (m=4) 表示前期夏季背景状况, 10月至翌年2月 (m=5) 表示前期秋冬季背景状况。由公式 (1) 计算得到的预测因子新序列, 含有某时间段内该因子的综合信息, 称为因子综合指数。这种综合方法, 避免了选择前期单月因子造成信息缺乏和常规的累计 (平均) 值引起相关性下降的缺点, 最大程度保留了前期各月可用的预测信息, 排除了逐月之间由于相关不一致带来的干扰, 物理意义也更明确。得到的因子综合指数和预测对象之间的相关系数均有不同程度的增大。
2 两种方法预测应用试验第一种方法为先对前面所述的影响我国汛期旱涝的具有一定的天气气候学意义的因子资料按公式 (1) 进行处理, 再相关普查, 选取相关系数最大的前12个为备选因子, 采用最优子集回归方法, 用双评分准则[2]确定最优子集回归, 考虑到预测方程的稳定性, 最终进入方程的因子不超过8个。
第二种方法是对所有的因子按常规的累积平均方法处理, 划分的时段亦同样为上年6月至9月, 上年10月至当年2月。备选因子数、建立预测方程的方法及最终进入方程的因子数均与第一种方法相同。
用1952~1989年历史资料为建立方程的样本, 预测1990年的长江三角洲汛期降水场; 用1952~1990年样本预测1991年的降水场, 以此类推, 共进行10年的独立预测, 对预测试验结果用4种评估参数进行检验[3], 以作比较。
从表 1可见, 无论是距平相关系数、距平同号率还是预测评分和技巧评分, 由公式 (1) 处理得到的综合指数方法 (方法1) 均比常规方法 (方法2) 有明显的提高, 汛期 (5~9月) 的预测评分和技巧评分提高19分和25分。
|
|
表 1 两种因子处理方法的10年预测评估对比 (1990~1999年) |
图 1为采用方法1建立的预测模型对1999年夏季 (6~8月) 降水场预测和实况的对比。从实况图看, 1999年夏季长江三角洲大部分地区降水异常偏多, 特别是南部地区各站降水量均在1000 mm以上, 发生了百年未遇的特大涝灾。对照预测和实况图可看出, 降水预测场南多北少的分布与实况场较一致, 尤其是南部几个站的降水距平百分率预测值超过100%, 虽然与实况相比, 强度上还有差距, 但对于一个统计模型来说, 能有如此高的极值预测是很不容易的。评估1999年夏季的预测效果, 距平相关系数0.82, 距平同号率90%, 预测评分和技巧评分分别为98分和82分, 效果令人满意。

|
|
| 图 1. 1999年长江三角洲6~8月降水距平百分率预则 (a) 与实况 (b) 分布图 | |
3 结语
统计预测模型的可靠性、稳定性决定于预测因子是否具有物理意义或天气气候学意义, 预测因子应充分体现预测对象的成因。挑选预测因子, 应先选择有物理意义的因子, 再相关普查。对于汛期旱涝趋势短期气候预测, 由于预测对象时间尺度较长, 根据尺度对应原理, 挑选预测因子时, 应注意综合前期相应时间尺度上的各种背景信息, 这样才能有利于提高预测准确性。如何综合前期各种因子信息, 以提取预测强信号, 需要我们进一步深入研究。
| [1] | 张家诚. 长期天气预报方法论概要. 北京: 农业出版社, 1981: 12-16. |
| [2] | 魏凤英, 曹鸿兴. 长期预报的数学模型及其应用. 北京: 气象出版社, 1990: 22-48. |
| [3] | 陈桂英, 赵振国. 短期气候预测评估方法和业务初估. 应用气象学报, 1998, 9, (2): 178–185. |
 2001, 12 (2): 251-254
2001, 12 (2): 251-254


