18世纪中叶, 人们发现雨量器安装高度不同测得的值不一样, 后来认识到, 这是由于自然风场受高出于地面的雨量器的干扰而变形所造成的, 这一误差称之为风场变形误差。一般认为, 由于风场变形, 普通雨量器对雨和雪的收集率分别偏少2%~10%和10%~50%[1]。为了消除这一误差, 最初人们把注意力集中在研制各种各样的防风圈上, 但最终未能把问题解决。之后找到了坑式雨量器, 它能收集到最大的降水量, 但由于坑内积水不易排出和观测不便, 加之解决不了测雪中的吹雪问题, 因此坑式雨量器未能应用于台站业务, 而只能用它来作为对比标准。后来人们又把注意力投放在降水资料的订正上。国际气象组织和国际水文科学协会从1955年开始先后组织过多次雨量器的国际对比, 以便找到降水资料的订正方法。在订正方法的研究上, 经过各国的共同努力, 虽然取得了可喜的进展, 但由于引起风场变形误差的作用机制复杂, 至今未能开发出适合于业务订正的方法。在雪量测量上, 目前的测雪仪器均不理想。本文从分析风场变形误差的物理机制出发, 得出风场变形误差与横向降水量相关, 并设计出了用来测量横向降水量的横向雨量器。经全国不同地理气候的30个站7年对比观测, 证实了降水量测量的绝对差值与横向降水量相关, 且相关系数很高。
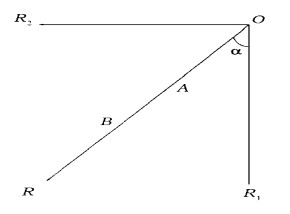
1 横向降水量和横向雨量器的设计从大气中降落到地面的各种液态或固态的水粒子在其降落的过程中具有矢量的特征, 用矢量OR的方向表示水粒子的降落方向, 矢量OR的长度OR表示水粒子的水量 (如图 1)。我们称矢量OR的水平分量OR2在降水方向上的投影大小OA为横向降水量, 用式表达为:
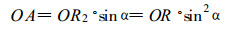
|
(1) |
|
|
| 图 1. 水粒子的矢量图 | |
式中α为水粒子的降水角度。
同样, 我们称垂直分量OR1在降水方向上的投影大小OB为纵向降水量, 用式表达为
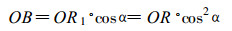
|
(2) |
由式 (1) 和式 (2) 可得
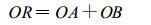
|
(3) |
式 (3) 表明, 水粒子的降水量为横向降水量与纵向降水量之和。
实际降水中, 降水是由形状、大小各异的水粒子组成, 降水角度各不相同, 并随时间变化而变化, 因此具有普遍意义的公式应为
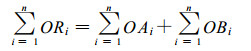
|
(4) |
式中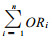
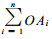
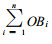
我们称一个能够测量横向降水量的仪器为横向雨量器。横向雨量器所收集到的水量应为
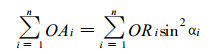
|
(5) |
由于水粒子的大小、形状各异, 加上自然界的风向和风速随时都在发生变化, 因此各水粒子的降落方向和降落角度不但不同时刻不会一样, 即令同一时刻也不会一样, 这就要求雨量器能同时接收来自全方位 (0°~360°) 和不同降水角度 (0°~90°) 的水粒子。
如果能设计出一种仪器, 这种仪器收集降水面积随着横向降水量占整个降水量的比例的变化而变化, 对每一特定的降水角度α, 且能满足

|
(6) |
进而在降水角度0°~90°的范围内, 上式也能成立, 那这种仪器就是我们所要设计的横向雨量器。要能够设计出一个完全满足方程 (6) 的仪器是非常困难的, 但我们却可以近似地做到, 这只要在普通雨量器收集口的上方的某一高度上安上一个一定尺寸大小的圆形遮雨板 (如图 2), 就能达到我们的设计目的。
|
|
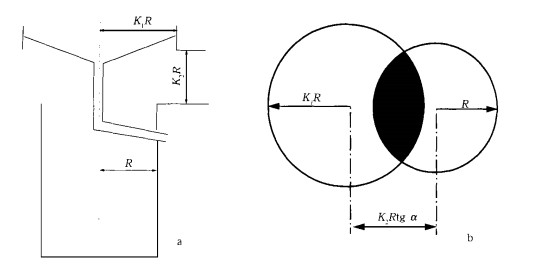
| 图 2. 横向雨量器 (a) 及其投影计算图 (b) | |
图 2中的R为普通雨量器的器口半径, K1R为遮雨板的半径, K1为遮雨板的尺寸系数, K2R为遮雨板离普通雨量器器口的高度, K2为遮雨板的安装高度系数。
通过计算图 2投影圆中R圆非黑影部分的面积与R圆面积的比值, 我们可以得到下列方程
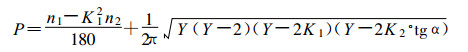
|
(7) |
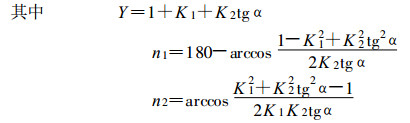
|
式中P为有遮雨板时, 仪器的接水面积 (即R圆非黑影部分的面积) 与普通雨量器的器口面积 (即R圆的面积) 之比值。
通过求取积分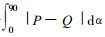
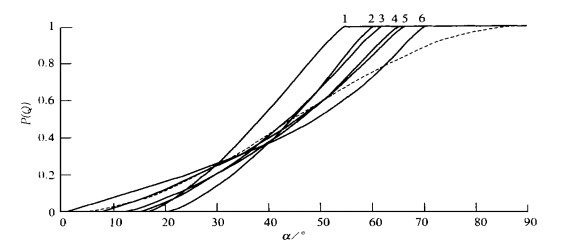
图 3给出了P与α的关系曲线组 (实线) 和Q与α的关系曲线 (虚线)。表 1给出了在确定K1值时的最佳K2值。
|
|
| 图 3. 横向雨量器的理论设计线Q (虚线) 与实际设计线P (实线) (图中1、2、3、4、5、6线的K1、K2值分别为 (1.0, 0.7)、(1.1, 0.9)、(1.2, 1.0)、(1.3, 1.2)、(1.5, 1.73)、(1.5, 1.4), α为降水角度) | |
|
|
表 1 确定K1值时的最佳K2值表 |
2 风场变形的物理机制
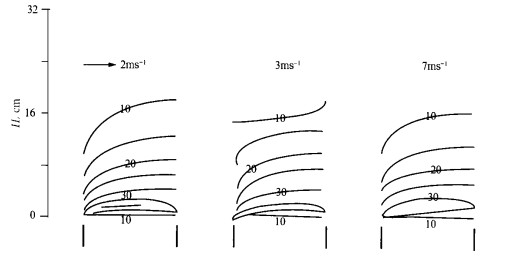
雨量器的风洞实验表明[2], 雨量器收集口上方处的风速明显地高于其它地方的风速。在收集口上方的同一高度上, 收集口上方处的下风方向的风速又比上风方向的风速大, 两者绝对差值随着风速的增大而增大 (图 4)。雨量器收集口上方处的这一不对称的变形风场是造成雨量器收集率偏少的原因。
|
|
| 图 4. 雨量器风洞试验图 (图中曲线中的数字为风速的百分增量, H是距雨量器的器口高度) | |
由于在高出于地面的雨量器的器口上方, 下风方向的风速要比上风方向的大, 对同样大小的水粒子而言, 下风方向的水粒子的降落角度比上风方向的大, 因而, 在雨量器收集口处, 水粒子的降落迹线形似喇叭口。由于迹线发散, 雨量器器口上方的水粒子密度比其它地方的要稀, 故而高出于地面的雨量器所收集到的降水量和与地面齐平的雨量器相比其收集量要少。风速越大, 水粒子越小, 则雨量器上方的水粒子迹线愈发散, 雨量器所收集的降水量越少, 即由风场变形所引起的误差越大。
从式 (6) 可知, 横向降水量与降水量的比值是水粒子降落角度的函数。风速越大, 水粒子越小, 则降水角度愈大, 横向降水量所占比例也愈大。由于降水量测量的绝对差值与降水量的比值也取决于风速与水粒子的大小, 且风速越大, 水粒子越小, 这个比值也越大, 故横向降水量与降水量测量的绝对差值存在着某种确定关系, 这一关系可以通过实验对比求得。
3 降水量测量的绝对差值与横向降水量的实验关系为了确定风场变形误差与横向降水量的相关关系, 我们在不同的气候区域和不同的海拔高度上组建了30个实验对比站。这些站址分布在20°02′~47°26′N, 81°20′~126° 58′E的广大区域, 各站海拔高度差异很大, 最低的4.8 m, 最高的3837.0 m。各站的年平均气温、年平均风速和年平均降水量均有很大差异。
对比实验站的仪器是这样设置的:1台坑式雨量器, 2台台站雨量器, 1台横向雨量器。各仪器间的安装距离均为5~7 m。4台雨量器的器口面积均为314 cm2, 台站雨量器与横向雨量器的安装高度同为70 cm。表 1中的最佳值是假定降水角度均匀地发生在0°~90°的范围内求得的, 考虑到我国的降水角度多数情况是在0°~60°的范围内发生的, 我们采用横向雨量器遮雨板的尺寸系数K1=1.5, 遮雨板的安装高度系数K2=1.73。此设计满足降水角度为30°时, 横向雨量器测定的横向降水量没有误差。坑式雨量器的防溅网采用标准设计。
用坑式雨量器作为对比标准, 以它的测值作为降水量的真值。用横向雨量器测定横向降水量。由于降水量在空间分布上是随机性较大的气象要素, 这种空间分布的不均匀性, 会使得安装在不同地点的雨量器带来采样差, 另外还存在着其它测量随机差, 为了确定随机性的大小, 故安装了两台同样型式的台站雨量器, 用两台台站雨量器的测量差值来确定降水测量中的随机差。用两台台站雨量器的测值的平均值作为台站雨量器的测值。
在有吹雪出现时, 坑式雨量器所收集到的雪量往往很大部分是由吹雪引起的, 这是一个伪误差, 在作统计时, 必须予以剔除。由人工和其它原因所造成的伪误差也应予以剔除。
对比实验从1992年开始, 资料统计到1998年底, 历时7年。整个试验期间, 有降水测次29276次。其中由于坑内积水排不出造成坑式雨量器缺测284次, 365测次无横向降水量, 总缺测率为2.2%。取得完整对比测次28627次, 剔除雨的伪误差81测次, 雪54测次, 雨和雪实际有效对比测次分别为26260次和2232次, 合计28492测次。就降水日而言, 雨和雪的有效对比降水日分别为16319日和1665日, 合计17984日。
为了滤除随机差的影响, 我们用分段平均值来求相关。区间的大小要根据每区间段内原始样本数的多少来决定。每区间段内的原始样本数越多, 区间段越多, 所求取的相关关系越能反映实际。因为雨和雪为不同形态的降水, 故分别进行统计。为了比较按测次统计与按日统计的优劣, 还分别进行了按测次统计与按日统计。
从30个站的统计结果看, 不管是雪还是雨, 不管是按测次统计还是按日统计, 降水量的测量差值都明显地与横向降水量相关。在各种一元函数的相关统计中, 以下列幂函数的相关系数为最高:
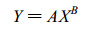
|
(8) |
式中Y为降水量测量的绝对差值 (mm), X为横向降水量 (mm)。
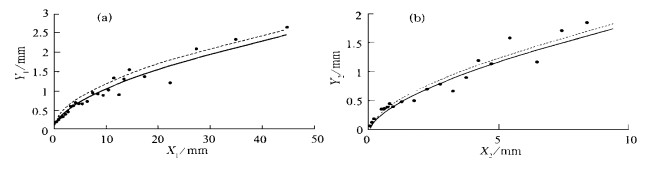
表 2列出了由对比试验得出的雨量器口径为314 cm2、安装高度70 cm时的A、B值、样本数N及相关系数r。图 5给出了式 (8) 的关系曲线。不同口径和不同安装高度的雨量器的A、B值应通过实测对比确定。
|
|
| 图 5. 降水测量的绝对差值 (Y) 与横向降水量 (X) 的实验关系图 (a) 横向降雨量 (b) 横向降雪量 (图中实线为按测次订正, 虚线为按日订正) | |
|
|
表 2 降水测量差值Y与横向降水量X的关系式 (Y=AXB) 的系数值 |
从表 2可知, 降水量的测量差值与横向降水量呈幂函数相关, 其相关系数为0.99, 采样次数越多, 相关系数越高。雪的相关曲线的斜率比雨的要大, 故雨和雪的测量要按不同的系数进行订正。从按测次统计和按日统计的结果看, 两组相关曲线几乎一致, 因而实际订正中可以随意选择按测次订正或按日订正。由于降水量测量差值是绝对差, 而不是相对差, 只要测出横向降水量, 就可知道降水量的测量差值, 而不需要知道降水量的大小, 这就使得订正的计算极其简便。
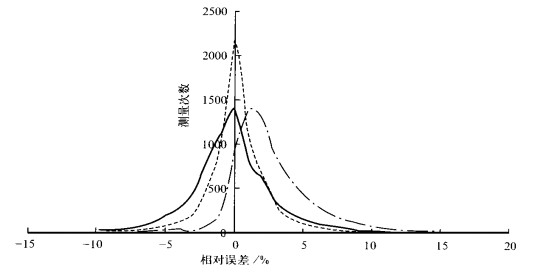
4 订正效果用横向降水量按上面实验关系逐次订正30个站的台站雨量器的测值, 将订正后的值与坑式雨量器的测值进行比较, 得出了雨量订正前后误差的分布 (图 6), 用两台台站雨量器的测量差值所表示的随机误差的分布也一并给出。由于降水量测量的读数精度为0.1 mm, 为避免读数误差的影响, 对小于5 mm降水不作相对误差统计。从图 6可以看出, 订正前的误差分布带明显地偏在中轴线的右侧, 这表明台站雨量器的测值比坑式雨量器的小。从图中还可以看出, 订正后的误差分布基本上都在中轴线两侧成对称正态分布, 与随机误差分布带基本吻合, 说明订正有效。
|
|
| 图 6. 降雨量测量的相对误差分布图 (图中点划线为订正前, 实线为订正后, 虚线为随机差) | |
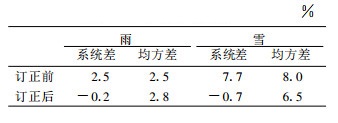
从30个站7年统计结果 (见表 3) 看, 测雨的系统差和均方差均为2.5%。测雪的系统差为7.7%, 均方差为8.0%。不管是雨还是雪, 均方差与系统差值接近, 这说明要检验订正的有效性, 必须要有足够的样本数。从30个站的综合取样看, 用两台同样型式的台站雨量器测量, 不管是雨或雪, 随机差的平均值均趋近于零, 这说明样本数足够。订正前后的均方差值没有变化, 说明均方差不可能通过订正来提高。而两台同样型式的台站雨量器测量的均方差, 雨为1.8%, 雪为2.8%。订正后的系统差比订正前的系统差小了1个数量级, 表明用测定横向降水量来订正降水测量中的风场变形误差极其有效。各站降水量测量的系统差和均方差有很大差异。
|
|
表 3 30个站平均误差 |
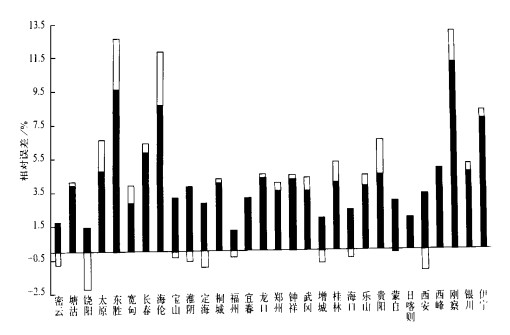
30个站合计, 坑式雨量器测得的降水总量为157810.7 mm, 而台站雨量器为152115.6 mm订正前平均误差为3.6%, 订正后为0.2%。各站降水总量订正前后的相对误差见图 7。
|
|
| 图 7. 各站降水总量订正前后的相对误差 (图中黑条为订正前, 白条为订正后) | |
5 结论
(1) 经2.8万多次的坑式雨量器、台站雨量器和横向雨量器的对比观测, 不管是测雨还是测雪, 坑式雨量器与台站雨量器测量的绝对差值均与横向降水量成幂函数相关, 相关系数很高, 均为0.99。采样次数越多, 相关系数越高。从按测次统计和按日统计结果看, 两组相关曲线几乎一致。但雪的相关曲线的斜率比雨的要大。这种相关是在不同地理气候条件下求得的, 因而具有广泛的普遍性。
(2) 按照试验求得的相关关系, 用横向降水量对台站雨量器的测值进行逐次订正, 不管是雨或雪, 订正后的误差分布带均落入到正常的误差带内。订正后的精度基本上接近坑式雨量器的测量精度。
(3) 在现行的台站观测业务中, 仅仅只要增加与普通雨量器一样简单的横向雨量器的并行观测, 就可按测次或按日对台站雨量器测量的降水量进行订正。订正方法简单易行, 订正精度高。用测定横向降水量订正降水测量中的风场变形误差的方法, 解决了大气探测中降水量测不准的长久难题, 具有广泛的实用价值。订正实施后, 必将大大地提高降水量的测量精度。
| [1] | Sevruk B. Correction of precipitation measurements. WMO/TD, No.104, 1985. 13~23. |
| [2] | Sevruk B, Klemm S. Instruments and observing methods report No.39. WMO/TD, 1989, No.313, 1989.16. |
 2001, 12 (2): 188-195
2001, 12 (2): 188-195