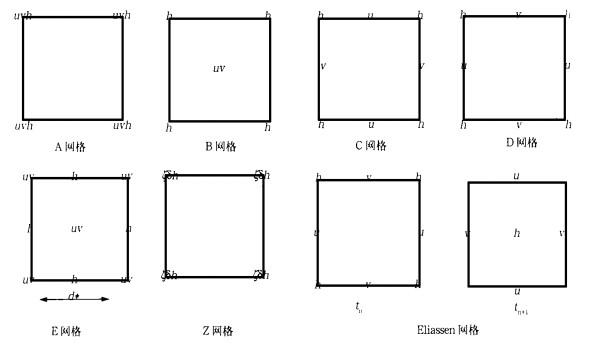
Winninghoff[1]和Arakawa[2]在Arakawa A—E网格上对模拟惯性重力波的情况进行过讨论, 认为在可分辨 (λ/d > 1) 的情况下, C网格效果较好些, 而在λ/d < 1的情况下, 虽然B网格效果较好, 但有小尺度噪音。后来David A Rondall[3]提出了一种Z网格 (见图 1), Z网格风的辐散部分分量象在C网格一样趋于跳点, 而风的旋转部分分量象在D网格上一样趋于跳点。因此Z网格从设计的角度来讲, 是比较先进的。另外Eliassen还提出了一种时间水平跳点网格———Eliassen网格 (见图 1), 这种网格可消除由于时间取中央差而造成的计算波。
|
|
|
图 1. 各种网格的变量配置图
( |
|
一般而言, 大气模式的Rossby半径 (约为1000 km) 比海洋模式的Rossby半径 (对于第一斜压模态约为50~100 km) 大, 本文为分别讨论大气模式和海洋模式的网格对惯性重力波的模拟情况, 大气模式取为λ/d=2, 而海洋模式λ/d=0.5。
本文为完整地比较这7种网格, 给出线性浅水方程组的解析频散方程和解析群速; 给出Arakawa A—E网格、Z网格和Eliassen网格的频散方程和群速, 同时给出出现错误群速的水平尺度范围; 对这7种网格进行综合讨论。
1 微分情况在f平面上惯性重力波的线性浅水方程组为:
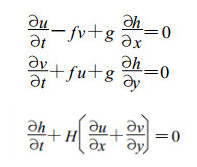
|
(1) |
其中 (u, v) 是水平速度分量, h是离开定常深度H的位移。
设h~ei(kx+ly-wt)可得解析频散关系:
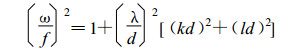
|
(2) |
这里 (k, l) 分别为纬向和径向的水平波数, 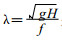
由式 (2) 可导出群速, 由于惯性重力波是各向同性的, 因此我们只给出x方向的群速 (以下6种网格的群速也只取x方向的, 为简便以后简称为群速):
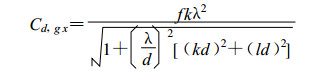
|
(3) |
由式 (3) 可以看出, 在各种水平尺度范围内, 群速始终是正的。
2 水平网格的计算频散性(1) A网格:变量分布如图 1所示, 各变量分布在同一个格点上。线性浅水方程组在A网格上离散后, 用Shuman算符表示的形式为:
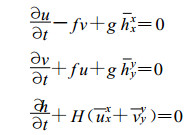
|
(4) |
其中若α代表u、v或h则
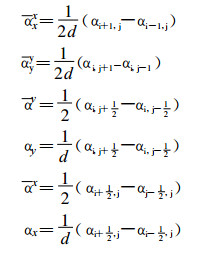
|
其频散方程为:
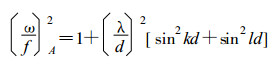
|
(5) |
群速为:
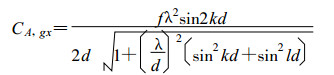
|
(6) |
群速的符号取决于sin2kd的符号, 对于波长L > 4d而言, 群速为正。而在区间2d < L < 4d群速为负, 就是说, 波长处于这个范围内, 群速是错误的。并对波长2d和4d群速为零, 使得这些波动无法移动。
(2) B网格:变量配置如图 1所示, 其离散方程为:
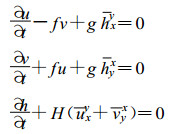
|
(7) |
其中若α代表u、v、h则
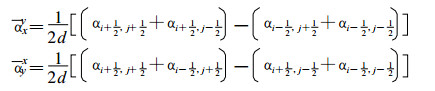
|
频散方程为:
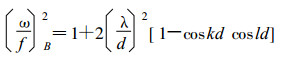
|
(8) |
群速为:
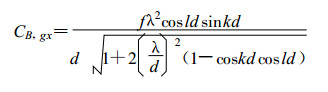
|
(9) |
群速的符号取决于sinkd×cosld的符号, 当λ/d > 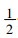
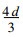
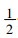
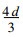
(3) C网格:变量配置如图 1所示, 其离散方程为:
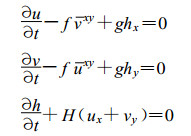
|
(10) |
其中若α代表u、v、h则
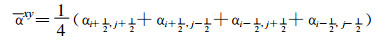
|
频散方程为:
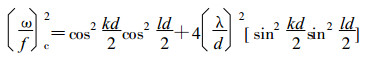
|
(11) |
群速为:
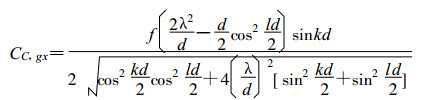
|
(12) |
群速的符号取决于sinkd的符号, 对于波长L > 2d而言, 群速为正。而在区间d < L < 2d群速为负, 就是说, 波长处于这个范围内, 群速是错误的。并也有使群速为零的波长。
(4) D网格:变量配置如图 1所示, 其离散方程为:
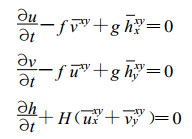
|
(13) |
其中若α代表u、v、h则
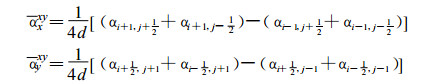
|
频散方程为:
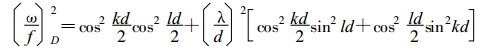
|
(14) |
群速为:
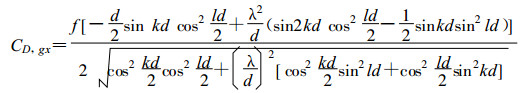
|
(15) |
当λ/d < 0.5时对于波长d < L < 2d和λ/d > 0.5时波长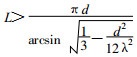
(5) E网格:变量配置如图 1所示, 其离散方程为:
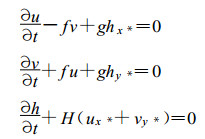
|
(16) |
这里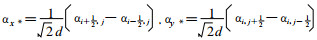
则频散方程为:
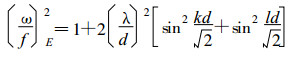
|
(17) |
群速为:
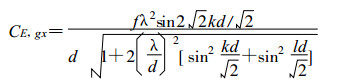
|
(18) |
对于波长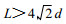
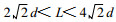
(6) Z网格:变量配置如图 1所示, 就是将涡度、散度和位势高度放在同一个格点上。
首先从式 (1) 根据涡度和散度可导出下列方程组:
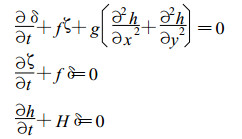
|
(19) |
再根据变量配置方法, 写出其离散方程组为:
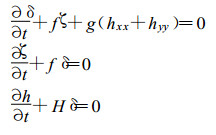
|
(20) |
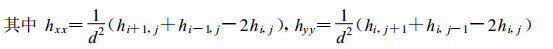
|
则频散方程为:
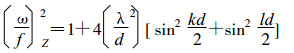
|
(21) |
由以上频散关系可求得群速为:
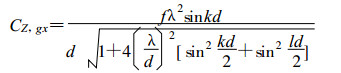
|
(22) |
群速的符号取决于sinkd的符号, 对于波长L > 2d而言, 群速为正。而在区间d < L < 2d群速为负, 就是说, 波长处于这个范围内, 群速是错误的。并也有使群速为零的波长。
(7) Eliassen网格:实际上是时间跳点的Arakawa D网格, 变量配置如图 1所示。
其离散方程组为:
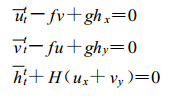
|
(23) |
则频散方程为:
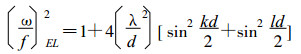
|
(24) |
由以上频散关系可求得群速为:
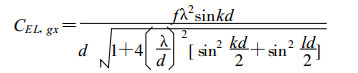
|
(25) |
群速的符号取决于sinkd的符号, 对于波长L > 2d而言, 群速为正。而在区间d < L < 2d群速为负, 就是说, 波长处于这个范围内, 群速是错误的。并也有使群速为零的波长。
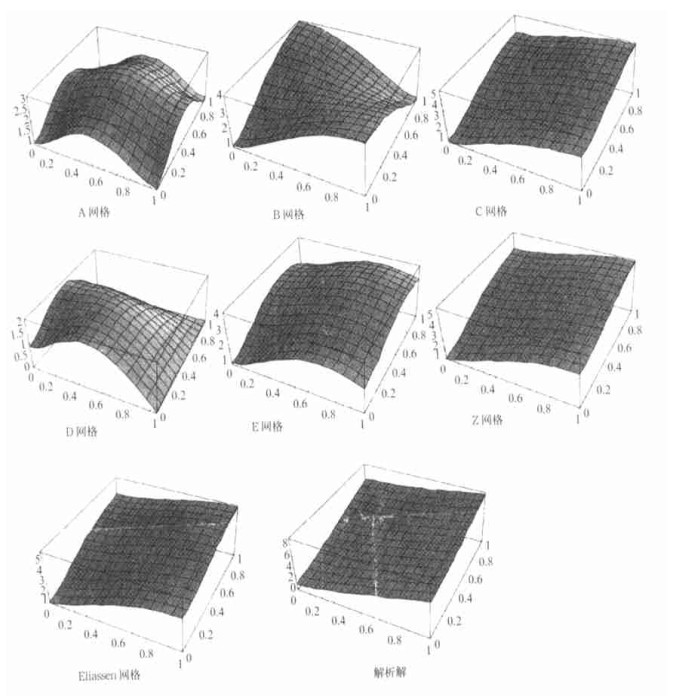
3 讨论图 2给出了λ/d=2 (图 2a) 和λ/d=0.5 (图 2b) 情况下7种数值频散关系和解析频散关系图, x方向的坐标为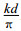
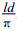
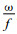
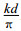
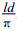
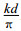
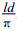
|
|
图 2a. 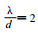 |
|
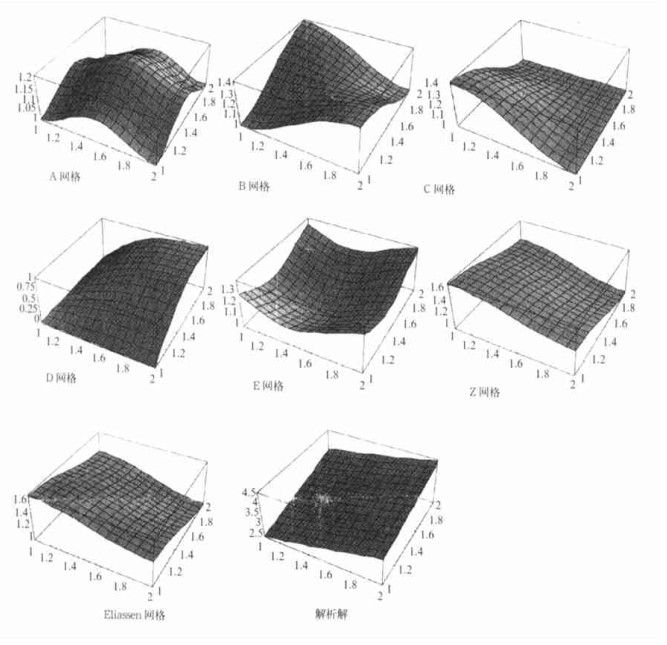
|
|
图 2b. 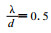 |
|
由频率图可以看出:在可分辨的情况下 (λ/d=2) 模拟地转适应C、Z和Eliassen网格在6种网格中最好, 而B、D网格在不可分辨的情况下 (λ/d=0.5) 比较好。并给出了7种网格的群速特征。从中可以看出, 只有C、Z和Eliassen网格在所有可分辨的尺度范围内是大于零的。其它网格在可分辨的尺度范围内, 群速都有负的情况。也就是说, 这些网格在可分辨的尺度范围内都要采用合适的滤波器来控制噪音; 在不可分辨的尺度范围内, 只有B网格的群速是大于零的, 而其它网格在此不可分辨的尺度范围内, 均为负的。因此从群速的角度来看:在可分辨的情况下, C、Z和Eliassen网格较好, 而在不可分辨的情况下, B网格较好。
从频率和群速综合起来看, 在可分辨的情况下, C、Z和Eliassen网格较好地模拟惯性重力波, 而在不可分辨的情况下, 仅有B网格能较好地模拟惯性重力波。
下面分析一下各种网格出现偏差的原因:
(1) Arakawa A网格:它是非跳点的, 因此讨论起来也比较简单。由于u和v定义在同一个格点, 故动量方程的科氏项计算精度较高。但那些空间导数项必然要涉及到平均。例如, 要考虑A网格上一个u点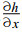
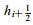
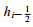
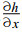
(2) B网格:象在A网格上一样, 科氏项容易计算, 因为u、v定义在同一个格点上不要平均。而气压梯度力又象在A网格上一样必须平均, 但有一点不同:在A网格上, 用来近似气压梯度力x分量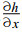
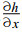
(3) C网格:因为定义的h点东西为u点, 南北为v点, 所以气压梯度力不需要平均。类似地, 连续方程的质量辐合和辐散项不需要平均风场也能算出。但由于u、v定义在不同点上, 求科氏项则需要平均。对于小尺度惯性重力波, 科氏项可以忽略, 这意味着如果模式的水平分辨率足够高, 以至于能在网格上表示出的最小波动对科氏力不敏感, C网格用起来就比较好。更确切地说, 当网格距比变形半径λ小时, C网格较好。
(4) D网格:它可进行地转风的简单计算, 从大尺度运动的地转平衡重要性来看, 似乎是一个引人注意的特征。但很明显的是, 在气压梯度力、质量辐合辐散, 甚至在科氏项也需要平均。因此频散关系较差。
(5) E网格:它本质上是一个旋转的B网格, E网格格距为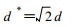
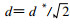
(6) Z网格:此网格风的辐散部分分量像在C网格一样, 趋于跳点, 而风的旋转部分分量像在D网格一样趋于跳点, 这意味着Z网格不与Arakawa A—E网格中任一种对应, 用Z网格也不需要平均。方程组中出现的唯一空间差分算子为▽2, 它出现在散度方程中并作用于h, 用通常的中央有限差分法, ▽2h的有限差分近似被定义在h格点上。因此不需要平均。
(7) Eliassen网格:这种网格不仅在水平方向上是跳点的, 而且在时间上也为跳点, 同时也不需要任何平均, 由于下一时间层某一格点上的变量置于其它格点上了, 这样时间取中央差也不会产生计算波。因此是一种理想的网格。
4 结论从以上的分析可以得到以下结论:
(1) 这7种网格中, 在可分辨的情况下, Z、C和Eliassen网格的效果最好, 在不可分辨的情况下, B网格的效果最好。
(2) 只有C、Z和Eliassen网格在可分辨的尺度范围内, 群速符号才是正确的, 其它网格都会出现错误符号的群速。而在不可分辨的尺度范围内, 只有B网格群速符号才是正确的, 其它网格都会出现错误符号的群速。
(3) 大气模式一般是λ/d > 1, 因此设计大气模式时, 应采用Z、C或Eliassen网格; 而海洋模式一般是λ/d < 1, 因此设计海洋模式时, 应采用B网格。
如果设计的模式的网格距比网格上能反映出来的重要物理模态的变形半径大, 那么这种模态就不可能用C、Z或Eliassen网格模拟好, 应选择用B网格, 因为B网格的频散关系对λ/d值不敏感。
在一些模式中习惯采用涡度散度方程, 因为位涡和位涡拟能守恒原理容易实现, 重力波容易用阻尼散度来控制, 另外, 涡度和散度是真正的标量, 而不像动量方程中的水平速度分量是矢量而难以处理。因此Z网格更适合用在采用涡度散度方程的模式中。
Eliassen网格是一种时间水平跳点网格, 其频散特征很好, 与Z网格相同。但用在实际模式中, 编写程序较复杂, 同时水平边界和上下边界处理也较困难, 因此实际应用比较复杂。
| [1] | Winninghoff F J. On the adjustment toward a geostrophic balance in a simple primitive equation model with application to the problems of initialization and objective analysis: [Ph.D.thesis]. Los Angeles: University of California, 1968. |
| [2] | Arakawa A and Lamb V R. Computational dynamical processes of the UTLA general circulation model. In: Chang J.Ed.Methods in Computational Physics. Academic Press, 1997. 173~265. |
| [3] | David A Rondall. Geostrophic adjustment and the finite difference shallow water equations. Monthly Weather Review, 1994, 122: 1371–1377. DOI:10.1175/1520-0493(1994)122<1371:GAATFD>2.0.CO;2 |
 2001, 12 (2): 140-149
2001, 12 (2): 140-149

