2. 湖北省气象科学研究所, 武汉 430074
NOAA卫星资料包含着丰富多彩的信息, 水体是其中一种重要的信息, 它是监测洪涝灾害所必需的信息.将NOAA卫星图像中有关的水体信息从其他信息中区分出来, 即进行水体识别, 是NOAA卫星遥感监测洪涝灾害的前提.常规的水体识别方法有目视解译法和阈值法.目视解译法是最为准确的办法, 但在水体信息分布状态的描述和时效上存在问题, 难以自动在计算机上实现.实际处理时多用阈值法[1, 2], 但阈值法往往只注意水体在某些波段的光谱特征而忽略其他波段, 实际上水体在所有的波段上都有一定的区别于其他信息的光谱特征, 另外将众多阈值同时都调整到恰当点既费时又存在着很多人为的因素.由于这些原因, 阈值法的识别精度和效率无法得到更大的提高.可以预见, 随着将来卫星通道的增加, 阈值法的不足之处将会更加明显, 因此, 有的气象卫星遥感工作者开始寻找在卫星通道增加的情况下新的水体识别方法[1].
近年来迅速发展起来的人工神经网络理论 (简称神经网络) 为NOAA卫星图像的水体识别提供一条新的途径.由于神经网络是模拟生物神经网络的人工智能技术, 具有并行处理、非线性、容错性、自适应和自学习的特点, 因而广泛应用于模式识别、信号处理和自动控制以及遥感图像的分类[3~5].到目前为止, 已经出现许多种神经网络模型及相应的学习方法, 其中反向传播神经网络模型 (简称BP模型) 是应用较广泛的一种.本文探讨了利用BP神经网络实现NOAA卫星图像的水体识别的基本原理和技术方法.
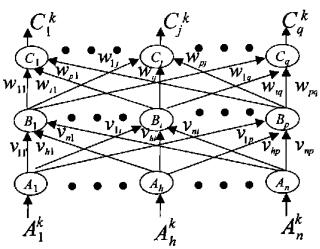
1 基本原理和技术方法 1.1 BP神经网络的基本原理[6]20世纪80年代Rumelhart和Webb等人建立了BP (Back Propagation Learning Algorithm) 反向学习算法, 该算法针对前馈型神经网络, 其典型代表是多层感知机.常用的BP模型由3个神经网络元层组成, 其最下层为输入层, 中间层为隐含层, 最上层为输出层, 相邻层次的神经元之间用连接权系数作相互连接, 而各层内的神经元之间没有连接, 如图 1所示.
|
|
| 图 1. BP网络的拓扑结构 | |
BP神经网络的数学模型是:

|
(1) |
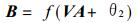
|
(2) |
这里A, B, C分别是输入层, 隐含层和输出层矢量 (节点向量), V, θ1和W, θ2表示隐含层与输出层, 输入层与隐含层之间的连接权和阈值, f (x) 为网络激活函数, 这里采用S型函数, 即
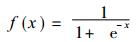
|
(3) |
通过对样本的学习和训练, 不断调整各节点的连接权和阈值, 进而得到样本输入输出的非线性关系.在BP神经网络中, 引入代价函数 (也称能量函数)
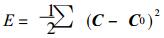
|
(4) |
这里C0是期望输出矢量.BP神经网络通过代价函数的最小化过程来完成输入到输出的映射.它的基本思想是如果利用已有权重和阈值正向传播得不到期望的输出, 则反向传播学习, 反复修改 (迭代) 各节点的权重和阈值, 逐步减少代价函数, 直到代价函数达到预先设定的要求, 一般以代价函数小于某一相当小的正数或迭代时不再减少而反复振荡为止, 此时完成BP网络的训练, 输入与输出映射的确立.
根据文献[6], 若BP网络中隐含节点可根据需要自由设定, 那么3层BP神经网络可实现任意连续函数的任意精度逼近.
1.2 BP神经网络的算法实现[6]设n、p和q分别为BP网络的输入层、中间层和输出层的神经元 (节点或单元) 个数, m为样本模式对的个数, Ak和Ck分别为第k组样本模式对的输入和输出, 那么BP神经网络的算法如下:
(1) 随机给出输入层单元到隐含层单元的连接权vhi, h=1, 2, … n, i=1, 2, … p, 隐含层单元到输出层单元连接权wij, i=1, 2, … p, j=1, 2, … q以及隐含层单元的阈值θi, 输出层单元的阈值rj.一般地赋予 (-1, +1) 区间内的随机数.
(2) 对于样本模式对 (Ak, Ck) (k=1, 2, … m) 进行下列操作:
①将Ak送到输入层单元, 计算隐含层单元的激活值
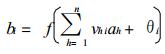
|
(5) |
式中ahk为输入层第h单元的输入, i=1, 2, …, p, f为式 (3) 所表达S型函数.
②计算输出层单元的激活值

|
(6) |
③计算输出层单元和一般化误差
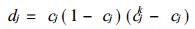
|
(7) |
式中j=1, 2, …, q; cjk为输出层单元j的希望输出.
④计算隐含层单元对于每个dj的误差

|
(8) |
式中j=1, 2, …, p; 上式相当于将输出层单元的误差反向传播到隐含层.
⑤调整隐含层到输出层的连接权

|
(9) |
式中i=1, 2, …, p和j=1, 2, …, q; λ为学习率0 < λ < 1.
⑥调整输入层到隐含层的连接权

|
(10) |
式中h=1, 2, …, n且i=1, 2, …, p; U为学习率0 < U < 1.
⑦调整输出层到隐含层的阈值

|
(11) |
⑧调整隐含层单元的阈值

|
(12) |
(3) 重复步骤 (2), 直到对于k=1, 2, …, m误差dj (j=1, 2, …, q) 变得足够小或变为零为止.
1.3 BP模型用于NOAA卫星图像水体识别的步骤NOAA卫星图像水体信息神经网络的识别方法是:将图像各波段数据作为神经网络的输入; 将像元所属的类型作为神经网络的输出; 选择样本来训练网络; 用训练好的网络对图像各像元进行归类, 提取其中水体像元的分布信息.具体步骤是:
(1) NOAA/AVHRR各波段数据的归一化处理 为了加快收敛, 需要对各波段数据进行归一化处理, 表达式如下:

|
(13) |
Xmax和Xmin分别是原像元的灰度最大值和最小值; X是原像元的灰度值; S是归一化后像元的灰度值.
(2) BP模型的设计 按照BP网络设计方法[6], 输入层神经元数目应与NOAA/AVHRR的波段数一致; 为了简单起见, 只设一个隐含层, 其神经元数目应略大于输入层神经元个数; 输出层的神经元个数应与像元类型个数一致, 从减少误差积累和缩短训练时间考虑, 输出层神经元个数应尽量少, 于是将像元类型分为水体和非水体两类, 即将图像中除水体像元以外的所有像元 (如陆地、云等) 都归结为非水体类型, 这样输出层的神经元个数为2.
(3) BP模型的训练 在假彩色合成图上, 利用目视解译法就每一种像元类型选取一些像元样本, 作为网络的学习模式, 提取各像元样本在各个波段的值 (已归一化), 以这些值作为网络的输入模式, 并以对应的像元类型作为输出模式, 这样就建立了网络学习模式对.按照BP神经网络的算法, 对网络进行反复训练.
(4) 水体信息的提取 利用训练好的神经网络, 将图像所有像元在各个波段的值输入到网络中, 根据网络的输出值确定每个像元所属的类型, 并将属于水体类型的像元提取出来, 完成NOAA卫星图像的水体识别.
2 应用实例 2.1 试验情况本文所用的资料是1998年8月4日接收到的NOAA/AVHRR数据, 对其进行投影变换、几何校正后, 生成了4个波段数据集 (AVHRR有5个波段, 这里只用了4个波段).选取220×300大小子区间作为研究对象, 该区间包括的地理范围是洞庭湖以及湖北省东南地区, 这些地区当时正发生特大洪涝灾害.
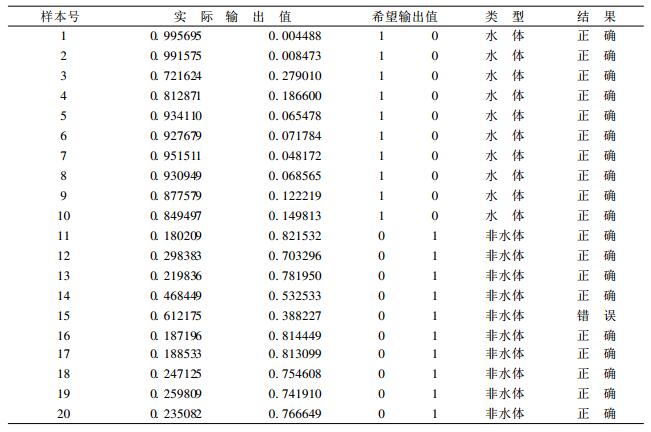
按上述方法, BP网络模型的拓扑结构设计为 (4, 5, 2), 即输入层、隐含层和输出层的神经元个数分别为4、5和2, 水体和非水体的输出模式分别为 (1, 0) 和 (0, 1).选取水体样本68个, 非水体样本69个.训练时选取学习率λ=U=0.1.随着训练的进行, 代价函数稳定减少, 当迭代963次以后, 代价函数已稳定, 训练结束.表 1给出了20个训练样本的希望输出模式与网络稳定后的实际输出模式.由表 1可见, 经训练后的网络已经记忆了各像元类型在不同波段的光谱特性, 具备了将水体像元从非水体像元中区分出来的能力.
|
|
表 1 训练样本的特性输出表 |
2.2 试验结果
利用训练好的神经网络完成NOAA卫星图像的水体识别.图 2 (a) 为1998年8月4日NOAA卫星3个通道 (通道4、2和1分别作为图像的黑、灰和白阶) 合成图, 图 2 (b) 为经神经网络处理后的水体分布图.

|
|
| 图 2. 经神经网络处理前后的1998年8月4日NOAA卫星图像 (a) 处理前3个通道 (1, 2, 4) 合成图 (b) 处理后水体分布图 (黑色为水体) | |
2.3 精度分析
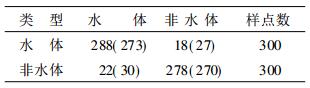
为了检验用神经网络进行水体识别的精度和效率, 本文按文献[1]介绍的阈值法对该次图像进行水体识别, 经反复调整, 得出水体判别4个必要条件是:通道1、2和4在图像合成后的灰度值分别小于83, 102和52, 并且比值植被指数 (R) 为50× (通道2灰度值/通道1灰度值).就每一像元类型各随机选取300个样点进行分析, 以目视解译法的识别结果为标准, 得到两种方法的水体识别结果的混淆距阵, 如表 2所示.表 2中第1列的类型表示用目视解译法所判定的类型, 第1行的类型表示神经网络和阈值法所判定的类型, 括弧里的值为阈值法的判别结果.由表 2可算出水体和非水体的识别精度 (算法为判定正确的样点数除以该类型的总样点数).神经网络的水体精度为96%, 非水体精度为92.7%, 平均精度达94.3%, 而阈值法的水体精度为91%, 非水体精度90%, 平均精度为90.5%.
|
|
表 2 水体识别结果的混淆矩阵表 |
2.4 效率分析
神经网络和阈值法在识别水体时, 都要通过人机交互选择一定的有代表性的样本.不同的是, 阈值法寻找样本的极值 (最大值或最小值) 作为水体和非水体的界限, 因此在取样过程中, 误取 (将非水体当水体) 和漏取 (漏过能成为极值的水体) 将扩大和缩小水体的范围, 必须重新取样; 而神经网络更注意从所有样本总结出水体和非水体的不同特征, 由于神经网络的容错性, 少量误取不影响其整体效果, 漏取也不致于前功尽弃, 可以边训练网络, 边补充样本.本文例子里, 阈值法花费时间5 min, 而神经网络只需1.5 min.
3 结论通过上述研究表明, 神经网络可用于识别NOAA卫星图像的水体信息, 并能得到比阈值法较高的精度和效率.因此, 当洪水发生时, 可以用神经网络技术从NOAA卫星图象中快速准确地提取水体的分布信息, 并以此为基础进行洪涝灾害滥测.
另外, 神经网络在进行水体识别时, 充分考虑了水体在所有通道的光谱特性, 因此它能适应以后卫星通道数的增加 (到时候只需增加输入神经元数目即可).无论现在和将来, 神经网络都是NOAA卫星图像水体识别的一个重要工具.
| [1] | 盛永伟, 肖乾广, 陈维英, 等.气象卫星大范围洪涝灾害快速宏观动态监测方法研究.气象卫星遥感技术为农业服务应用研讨会文集, 北京:气象出社版, 1996.51~62. |
| [2] | 孙涵, 居为民, 汤志成.江苏省洪涝灾害气象卫星遥感监测, 气象卫星遥感技术为农业服务应用研讨会文集, 北京:气象出社版.1996.45~48. |
| [3] | Paola J D, Schowengerdt R A. A detailed comparison of backpropagation neural network and maximum likelihood classifiers for urban landuse classification. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33, (4): 81–995. |
| [4] | Bernard A C, Wilkinson G G, Kanellopoulos I. Training strategies for neural network soft classification of remotely-sensed lmagery, Int. J.Remote Sensing, 1997, 18, (8): 1851–1856. DOI:10.1080/014311697218160 |
| [5] | Benediktsson J A, Sveinsson J R. Feature extraction for multisource data classification with a rtifical neural networks. Int.J.Remote Sensing, 1997, 18, (4): 727–740. DOI:10.1080/014311697218728 |
| [6] | 李学桥, 马莉. 神经网络·工程应用. 重庆: 重庆大学出版社, 1996: 37-44. |
 2001, 12 (1): 85-90
2001, 12 (1): 85-90