应用气象学报  2001, 12 (1): 61-69   PDF    
引用本文
李延兴, 徐宝祥, 胡新康, 何平. 应用地基GPS技术遥感大气柱水汽量的试验研究[J]. 应用气象学报, 2001, 12(1): 61-69.
Li Yanxing, Xu Baoxiang, Hu Xinkang, He Ping. TEST AND STUDY OF THE EARTH-BASED GPS TECHNIQUE FOR REMOTE SENSING OF ATMOSPHERIC PRECIPITABLE WATER[J]. Journal of Applied Meteorological Science, 2001, 12(1): 61-69  
应用地基GPS技术遥感大气柱水汽量的试验研究
李延兴1, 徐宝祥2, 胡新康1, 何平2     
1. 中国地震局第一地形变监测中心, 天津 300180;
2. 中国气象科学研究院, 北京 100081
1999-06-17 收到, 1999-11-25 收到修改稿.
资助项目: 本文由科技部攀登专项95-专-3以及国家重点基础研究发展规划项目资助    
摘要: 从理论上分析了AN (Aske and Nordius) 大气柱总水汽量 (W) 计算模型的偏差, 探空试验结果证实了理论分析的结论.作者经过推导, 建立了新的W计算模型, 与探空方法获得的W值具有很好的一致性. 1998年进行了一次“GPS暴雨观测试验”.试验结果发现:可降雨量的高值时段与降雨过程高度相关; 大的降雨过程, 在降雨前, 可降雨量一般都有一段递增过程, 在降雨结束过程中, 可降雨量一般都有一个递减过程, 在突发暴雨事件发生前往往发生可降雨量突然大幅度递增现象; 在大暴雨事件发生前, 存在一个长时间的十分明显的孕育阶段.
关键词: 水汽遥感    地基    GPS    降雨试验    
TEST AND STUDY OF THE EARTH-BASED GPS TECHNIQUE FOR REMOTE SENSING OF ATMOSPHERIC PRECIPITABLE WATER
Li Yanxing1, Xu Baoxiang2, Hu Xinkang1, He Ping2     
1. First Crustal Deformation Monitoring Center, China Seismological Bureau, Tianjin 3000180;
2. Chinese Academy of Meteorological Sciences, Beijing 100081
Abstract: The deviation of AN (Askne and Nordius) model for calculating PW value has been analyzed theoretically and the conclusion drawn from the theoretical analysis has been confirmed by the results from the sounding test. Through the derivation, a new precipitable Water (PW) calculation model has been established and the calculated results are well consists with the PW values obtained by the sounding method. In 1998, a "GPS Storm Observation Test" was car ried out. It has been discovered from the test results that the high-value time interval of PW generally has an increasing period before the rainfall and a decreasing period in the process when the rainfall is ended; before the occurrence of a sudden storm event, unexpected large-scale increase of PW often occurs; before the occurrence of a large storm event, there is a very clear pregnancy period lasting for a long time.
Key words: Water vapor remote sensing     Ground-based GPS     Rainfall experiment    
引言

在精密GPS定位计算中, 需要精确估计大气折射对GPS信号传播路径的增量.在大气中包含有干空气 (这是主要成分) 和水汽.在GPS数据处理中, 可以精确计算出由于大气中的水汽折射产生的路径增量, 从而可计算出大气柱总水汽量, 其变化与实际降雨过程密切相关, 由此产生了一门新的学科——GPS气象学. GPS气象学是近十年来蓬勃发展起来的一门边缘学科.发源于美国, 在20世纪80年代, 美国的Davis、Herring、Askne, Nordius等人[1]在该领域做了许多理论上的研究并进行了多次试验, 为其发展奠定了理论基础.后来, Bevis和Businger等人[2]进行了较全面的研究, 他们的研究成果促进了GPS气象学的新发展. 1998年5~6月份, 在周秀骥院士主持下, 进行了一次“华南暴雨试验”, 作者主持了其中的“GPS暴雨试验”.这次试验获得了大量的GPS与气象同步观测的数据, 为深入研究GPS气象学奠定了基础.

1 对现有计算W公式的分析

在GPS气象学中, 大气柱总水汽量的计算, 国际上一般都采用如下AN模型[1]

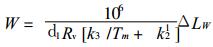
(1)

式中W代表GPS观测站附近单位面积上, 大气中水汽凝结成水时, 水柱的高度, Askne等称其为可降水量 (Precipitable Water).ΔLW代表在GPS观测站附近天顶方向上, GPS卫星发射的无线电信号传到GPS接收机上, 途经大气对流层时, 受大气中水汽的折射影响产生的距离增量.d1代表液水的密度, Rv代表水汽气体常数, Tm代表温度的加权平均值[3]

式中Mv和Md是水汽和干空气的分子量. k1、k2、k3是大气折射指数N计算公式[4]中的物理常数.

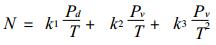
(2)

式中Pd和Pv分别代表大气中干空气和水汽的分压.

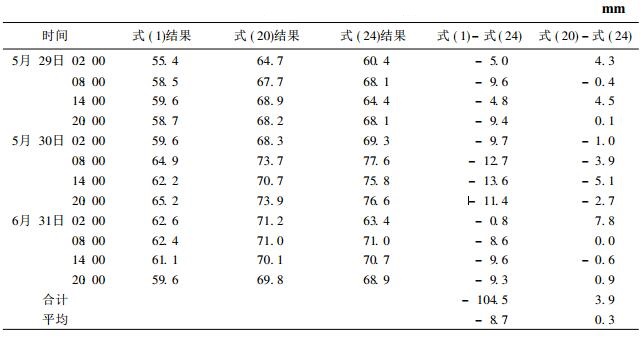
在研究中发现由公式 (1)~(5) 计算的可降雨量与由探空气象数据计算的可降雨量相比存在较大的系统误差.从表 1中可以看出, 由上述式 (1) 计算的可降雨量与实际探测的结果相比数值平均偏小9 mm.这表明AN模型可能不严密, 使计算结果产生了较大的系统误差.为此作者对上述模型重新推导如下:

根据气体状态方程有

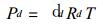
(3)
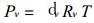
(4)

式中dd代表干空气的密度, dv为水汽密度, Rd代表干空气气体常数, 把式 (3)、 (4) 代入式 (2) 得到

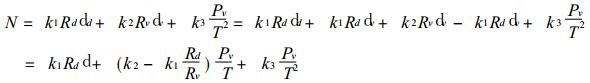
(5)

式中d为大气层总的空气密度.

令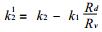, 式 (5) 可改写为Davis (1985) 之结果

(6)

根据气体状态方程 (3) 有

(7)

GPS接收机天顶方向的GPS信号, 由于大气折射产生的路径增量可表示为

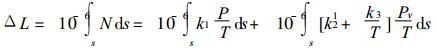
(8)

令:

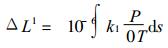
(9)

式 (9) 中, P=Pd+Pv, 在P中已含有水汽成分的作用, 不只是干空气的作用, 这正是公式 (1) 的不严密之处.

式 (8) 右边的第二项是大气中水汽对GPS信号折射产生的路径增量ΔLW, 因此有

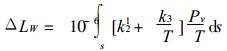
(10)

用Tm代替上式右边括号中的T, 并考虑到式 (4), 上式可改写为

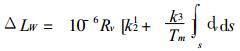
(11)

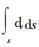
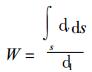
在上式中表示地面上单位面积上空大气柱内水汽的质量, 根据W的定义有

(12)

把式 (12) 代入 (11) 得到

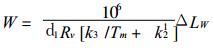
(13)

由式 (8)、 (9) 和 (11) 得到

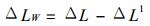
(14)

上式右边的第1项ΔL是大气层对GPS信号折射产生的总路径增量.第2项ΔL1是大气层对GPS信号折射产生的静力路径增量.从式 (9) 可以看出, 计算ΔL1使用的是大气层的总气压P, 在总气压P中含有水汽分压的贡献, 因为P > Pd, 所以用式 (9) 计算的ΔL1 > ΔEd (干空气产生的增量), 用式 (14) 计算的ΔLW必将比它的真值小.由于计算的ΔLW小于其真值, 所以用式 (13) 计算得到的W值也必将比它的真值要小, 这就是用AN模型计算的W值比实测值系统偏小的原因.

上述推导的结果与探空试验的结果都证明, 目前国际上通用的计算可降雨量的AN模型是不严密的, 近似的, 其计算结果比实际值偏小.

2 计算W值新公式的推导

由公式 (2) 可得到

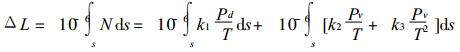
(15)

上式中的第一项为ΔLd, 第二项为ΔLW, 因此上式可改写为

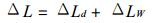
(16)
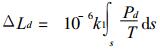
(17)
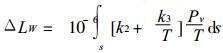
(18)

用Tm代替上式等号右边括号中的T, 则上式可改写为

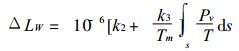
(19)

将式 (4) 和 (12) 代入上式可得到

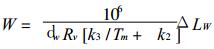
(20)

ΔL表示天顶方向的总增量, 由式 (17) 计算的ΔLd表示天顶方向干空气产生的增量, 由式 (19) 计算的ΔLW表示天顶方向水汽产生的增量.

在计算式 (17) 时, 所用的气压值是干大气的分压, 它可由在GPS观测站上观测得到的总大气压和水汽分压由下式计算得到

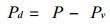
(21)

ΔL通常是作为未知参数在GPS数据处理中解出.ΔLd用地面观测的气温T、大气压P和水汽分压Pv计算得到.ΔLW由下式计算

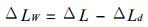
(22)

在传统气象学中, 可降雨量是用大气层探空数据计算的, 其计算公式如下:

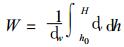
(23)

根据式 (4)、 (23) 可改写为

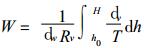
(24)

在上式中h0、H分别代表GPS观测站和对流层顶的高程.赤道地区H=16 km, 从赤道向两极逐渐减小.实际上, 在12 km以上的大气层中, Pv已趋近于零.因此, 取H=16 km可适用于所有地区.

由式 (21) 和式 (17) 计算得到的ΔLd是纯粹由干大气产生的增量, 由ΔL-ΔLd得到的ΔLW就是纯粹由水汽产生的增量.由式 (15) ~ (22) 组成的计算W值的计算模型是一套严密的计算模型.表 1给出了用公式 (20) 计算的结果, 这个结果与用探空数据计算的结果 (式 (24) 结果) 十分接近, 二者之间不存在系统误差.这个统计结果也证明了新计算模型是严密的和精确的.

表 1 可降雨量计算结果统计

3 华南GPS暴雨观测试验 3.1 GPS观测与数据处理

这次GPS暴雨观测试验在汕头气象站、阳江气象站各选建了一个GPS连续观测站.两个台站上安装的都是Rogue-8100型双频GPS接收机. GPS观测工作从1998年5月5日开始, 到6月26日结束, 历时53天.在GPS观测期间, GPS接收机的采样时间间隔为15 s, 接收GPS卫星的截止高度角5°.为了配合这次试验, 在海口、天津两地的GPS跟踪站也同步进行观测.

GPS观测数据的处理分两个阶段进行.第1阶段, 解算出汕头、阳江两个GPS观测站精确的地心坐标.第2阶段, 估计每个GPS观测站天顶方向的湿延迟量.在第1阶段, 为了求出汕头、阳江两个GPS观测站的精确地心坐标, 选择国际地球参考系ITRF96作为计算的参考框架, 选择我国海口、上海、武汉、天津、拉萨以及日本的TSKB和Usuda, 俄罗斯的IRKT和乌兹别克斯坦的Kitab 9个GPS跟踪站作为参考基准, 采用基准技术, 求解汕头、阳江两个GPS站的地心坐标.解算结果表明, 这两个站地心坐标的定位误差小于3 cm.在第1阶段的基础上, 取时段长度为2 h, 按时间序列精确估计每个GPS站天顶方向的湿延迟量.湿延迟量的估计误差小于10 mm.

汕头、阳江GPS站观测过程中的气象数据由这两个气象站观测提供.气象数据的采样间隔为2 h.利用地面观测的气象数据和GPS计算中得到的天顶湿延迟量, 使用作者研究的模型计算逐时 (每2 h计算一次) 的可降雨量.可降雨量的计算误差小于2 mm.

3.2 可降水量的时空变化

表 2是由天津、汕头、阳江、海口4个站GPS观测数据计算的结果.从表 2可以看出W值随时间和空间变化的总貌.在同一个GPS观测站上, W值每天每时都在变化着. W值随时间的变化是非常明显的.例如, 天津站W的最低值为11.3 mm, 最高值为64.7 mm, 变化幅度为53.4 mm; 阳江站W的最低值为37.9 mm, 最高值为82.0 mm, 变化幅度为44.1 mm.从图 1~2可以看出, 有时候W值一天之内最大的变化可达到40 mm, 一小时的最大变化可达到7 mm.W值随空间的变化也是十分明显的.从表 2可以看出, 1998年5~6月的W平均值, 天津为33.4 mm, 汕头为62.6 mm, 阳江为63.5 mm, 海口为67.3 mm.在同一时期北方 (天津) 与南方 (海口) 相比W的平均值相差33.9 mm.W值随空间和时间的变化十分显著, 应用GPS技术可实时监测W值的时空变化, 为降雨预报提供及时可靠的依据.

表 2 1998年5～6月份W值统计表

3.3 可降雨量与实际降雨量的关系

(1) 大气中存在高可降雨量是降雨的必要条件.汕头气象站5月5日到6月26日期间的资料统计表明, 这个地区非降雨天可降雨量的平均值为59.3 mm (见图 1).降雨过程的总时段长624.8 h, 其中可降雨量在低于59.3 mm条件下降雨的时段长为44.2 h, 占降雨总时段长的7%.而且这7%的降雨都是小降雨过程.可降雨量在高于59.3 mm条件下降雨的时段长580.6 h, 占降雨总时段长的93%.若把非降雨天可降雨量的平均值作为基准值, 在此值之上的可降雨量称为高值, 在此值之下的可降雨量称为低值.上述的统计结果表明, 可降雨量的高值时段与降雨过程高度相关.这就是说, 可降雨量在数值上超过基准值以后, 才具备降雨条件.换言之, 大气中存在高可降雨量是降雨的必要条件, 这是一条基本规律.据此, 可判断天气有没有降雨的可能.若可降雨量在此基值线以下, 不可能降大雨, 降小雨的概率也只有7%.

图 1. 汕头可降雨量 (W) 与降雨量 (R) 对应关系图

(2) 可降雨量的变化过程与实际降雨过程密切相关同步变化.大的降雨过程, 在降雨前, 可降雨量一般都有一段递增过程, 在降雨结束的过程中, 可降雨量一般都有一个递减过程.例如, 汕头市从5月17日10:00到5月20日12:00是一个较大的降雨过程 (见图 1).在降雨前, 从5月16日16:00开始到5月17日10:00, 可降雨量逐渐增大, 从45 mm增加到65 mm.从5月20日08:00可降雨量开始降小, 到20日20:00已递减了8.9 mm, 降至基准值之下.雨在递减的过程中, 在20日14:00结束.从6月22日10:00到6月24日20:00, 有一个大降雨过程 (见图 1).在降雨前, 从6月21日16:00开始到6月22日10:00有一段可降雨量的递增过程, 从62.4 mm增加到72.4 mm。从6月24日14:00, 可降雨量从82.5 mm开始递减, 到20:00递减到67.8 mm, 降低了14.7 mm, 雨随之也停止.一个降雨过程是:孕育—降雨—结束, 与其对应的可降雨量的演变过程是:可降雨量递增升到高值—保持在高值—可降雨量递减降到低值.降雨前, 可降雨量的递增并超过基准值, 可作为降雨预报的一个重要判据.而可降雨量的连续递减接近或低于基准值可作为结束降雨预报的一个重要依据.仔细观察图 1和图 2, 一个个降雨过程清晰可见, 按时间排列, 5月15日、5月17~21日、5月23~26日、5月31日~6月6日、6月8~13日、6月17~21日、6月22~25日是7个完整的降雨过程.

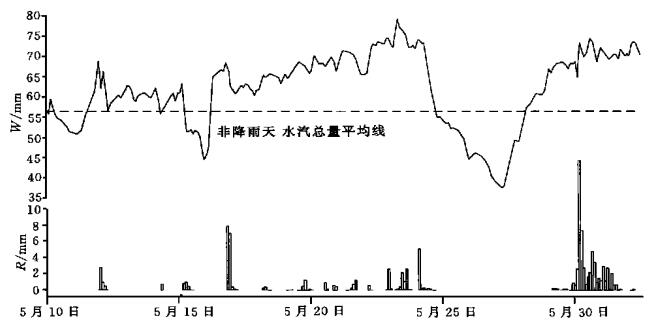
图 2. 阳江总水汽量 (W) 与降雨量 (R) 对应关系图

(3) 在突发暴雨事件发生前, 往往发生可降雨量突然大幅度递增现象.例如, 5月15日04:00~06:00集中降雨16.9 mm.在此之前, 从15日00:00到02:00, 可降雨量突然递增了15.8 mm.6月19日12:00到14:00, 突然集中降雨12.8 mm.在此之前, 从19日04:00到12:00, 可降雨量连续递增了12.8 mm.可降雨量大梯度的递增, 可作为暴雨预测的重要依据之一.

(4) 在大暴雨事件发生前, 存在一个比较长时间的十分突出的孕育阶段.在这个阶段, 可降雨量先由高值连续下降到极小值, 然后由极小值连续递增到高值.在可降雨量的图上出现一个十分突出的大凹槽 (详见图 2).例如, 阳江市在5月30日、31日有一个大暴雨过程.30日总降雨量为433.1 mm, 31日总降雨量160.0 mm, 这是一次少见的大暴雨过程.在这次暴雨发生前, 5月24日10:00, 可降雨量从73.7 mm开始连续下降, 24日17:00下降到平均值后继续下降, 到27日08:00下降到极小值后开始上升, 28日22:00上升到平均值后仍继续上升, 29日04:00上升到较高值66.9 mm, 开始出现降雨, 30日发展到大暴雨.从可降雨量的图上看, 这次大暴雨的孕育过程十分突出.5月17日有一个较大的暴雨过程, 一天集中降雨166.9 mm, 在降雨前也出现了一个相似的过程, 只是规模小一些.如果这两个例子能代表大暴雨孕育的一般规律, 那么GPS技术在灾害性的大暴雨预报中将发挥重要作用.

4 初步结论

理论分析证明, AN模型不够严密, 用此模型计算的W值比理论值偏小.本文建立的计算W的新模型理论推导严密, 计算结果与探空试验结果具有很好的一致性.

GPS暴雨试验的结果证明, 用GPS技术可以精确测量大气柱中的总水汽量, 其变化过程与降雨过程密切相关, 达到高值是降雨的孕育过程, 连续递减将结束降雨.GPS技术为降雨预测开创了新的技术途径.必须指出, 总水汽量增加, 只是产生降雨的必要条件, 不是充分条件, 可降水量与降雨的关系还有待于进一步探索.

参考文献
[1] Askne J, Nordius H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci, 1987, 22: 379–386. DOI:10.1029/RS022i003p00379
[2] Bevis M S, Businger T, Anther A, et al. GPS meteorology:Remote sensing of atmospheric water vapor using the global positioning system. J.Geophys.Res, 1992, 97: 15787–15801. DOI:10.1029/92JD01517
[3] Boudouris G. The index of refraction of air, absorption and dispersion of centimeter waves by gases. J.Res.Natl.Bur.Stand., 1963, 67D: 631–684.
[4] Davis J L, Herring T A, Shapiro I I, et al. Geodesy by radio interferometry:Effects of atmospheric modeling errors on estimates of bas eline length. Radio Sci, 1985, 20: 1593–1607. DOI:10.1029/RS020i006p01593