2. 南京大学大气科学系, 南京 210093
2. Department of Atmospheric Science, Nanjing University, 210093
预报理论和方法的研究一直是人们关注的问题.近年来, 在中、长期天气和短期气候预测中出现了许多有效的预报方法, 如模糊数学方法、灰色系统理论和各种动力-统计模型, 但基于统计理论的相关分析和回归方法在气候资料分析和气象要素预测中仍发挥着十分重要的作用[1].由于大多数统计预报方法是建立在线性相关基础之上的, 因此在处理比较复杂的非线性问题时具有较大的局限性, 而相当多的气象问题恰恰又都是非线性的, 因此探索和寻求一些新的预报方法就显得十分必要.人工神经网络是近年来发展较快的应用研究学科之一, 特别是自本世纪80年代以来许多重要问题的解决和快速有效算法的出现, 使得它在各学科中的广泛应用成为可能.金龙等人[2]利用神经网络同统计回归相结合的方法来进行预报集成的研究, 取得了较单纯统计回归和集成方法先进和可靠的预报效果.
太平洋副高是一个复杂且重要的天气系统, 对它的预报人们一直非常关心, 但至今尚未取得满意结果.符淙斌等人研究发现[3, 4], 西太平洋副热带高压的强度和西伸程度与热带太平洋海温 (SST) 距平之间存在着明显的时滞耦合振荡, 赤道东太平洋海温增高 (降低) 时, 西太平洋副高就会增强 (减弱), 两者之间最大的滞后相关为6个月左右.陈烈庭[5]、藏恒范等[6]也陆续发现和揭示出了低纬东、西太平洋海温同太平洋副高之间存在的许多相关特征和影响机制.龚道溢、王绍武最近研究指出[7]:全球副热带高压强度与超前3个月的低纬SST正相关最为显著.黄荣辉等人[8]的动力学研究和数值试验表明, 热带西太平洋地区的海温异常通过其产生的定常波列的传播也会影响西太平洋以及东亚大陆上空的500 hPa位势高度场, 从而制约该地区的副热带高压活动.最近, 吴国雄等人[9]的研究强调了赤道印度洋同赤道东太平洋海温年际变化的正相关, 表明赤道印度洋海温的变化对西太平洋副高同样具有影响作用和预报意义.
基于上述观测分析和研究结果, 本文引入人工神经网络的BP模型及其优化算法, 建立赤道海温与西太平洋副高之间的映射关系和预报模型, 并对模型的拟合、预报效果以及与统计回归方法的比较等问题作相应的计算和讨论.
1 人工神经网络与BP网络的基本算法人工神经网络是由人工建立的以有向图为拓扑结构的动态系统, 通过对连续或者断续的输入作状态响应而进行信息处理[10].人工神经网络是一个非线性动力系统, 其特色在于信息的分布式存储和并行协同处理, 它是由许多并行运算的被称作神经元的简单单元构成, 这些单元类似于生物神经系统的细胞, 虽然单个神经元的结构非常简单, 功能有限, 但大量神经元构成的网络系统却具备了一定的人工智能特征, 能够描述和模拟许多复杂的行为, 可实现函数逼近、数据聚类、优化计算、模式识别和非线性预测等功能.目前常用的人工神经网络模型主要有:感知器, Madaline网络、Hopfield网络、BP网络、径向基函数网络、自组织网络、回归网络等.
BP网络是当前应用最为广泛的一种多层非线性神经网络模型, 它结构简单、状态稳定、计算条件易于满足, 可用于非线性函数逼近和针对一些不规则的数据结构的复杂系统仿真.
令某一训练输入矢量为Xk=(xk1, xk2, …, xkn) T, 网络实际输出为Yk=(yk1, yk2, …, ykn) T, 对应于输入Xk的理想输出Y′k, 则输出误差为:
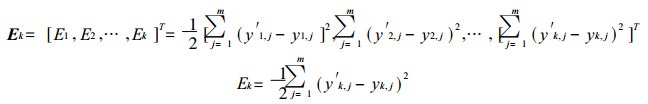
|
(1) |
j为输出层的第j个神经元.由快速下降法知各层神经元的权重系数 (权值) 的迭代方程为[10]:
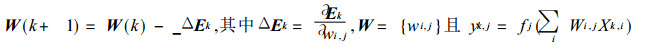
|
(2) |
有
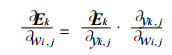
|
(3) |
对于输出层有:
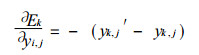
|
(4) |
将式 (2) 代入式 (3) 可得:
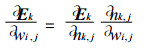
|
其中
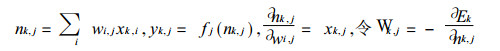
|
(5) |
则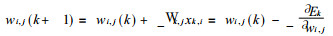

|
因
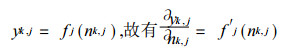
|
(6) |
若是输出层, 那么
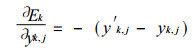
|
则Wk,j=(y′k,j-yk,j) f′j (nk,j)=(y′k,j-yk,j) fj (nk,j) (1-fj (nk,j))
其中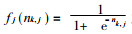
若是隐层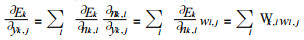
则
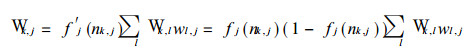
|
(7) |
所以网络权值为:
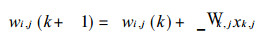
|
(8) |
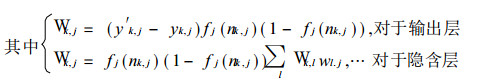
|
这就是包含隐层的多层神经网络的δ法则, 即BP算法.对于某一训练样本, 用上面算法, 通过误差反传调整各层神经元的权值.反复输入所有训练模式样本序列, 重复以上步骤, 直至误差权值不再改变, 输出误差限定于规定范围之内.所有训练样本的误差平均值E (W), 称为网络的均方误差函数: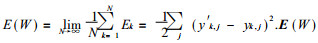
资料为美国国家环境预报中心和大气科学研究中心 (NCEP/NCAR) 的再分析计划及美国综合大气资料集 (COADS) 的1963年1月~1990年12月全球月平均海温场时间序列.预报对象为国家气候中心预测室提供的范围为110°E~180°, 10°N以北区域的西太平洋副热带高压500 hPa月平均面积指数.预报因子取:(1) 赤道东太平洋 (160°~90° W, 10°S~0°区域平均) 海温; (2) 热带西太平洋 (120°~140°E, 20°~30°N区域平均) 海温; (3) 赤道印度洋 (50°~90°E, 0~15°N区域平均) 海温; (4) 前期副高面积指数.
预报因子和预报对象之间的时滞相关分析表明, 平均情况下, 副高面积指数与超前3个月的海温因子之间存在较好的相关性.基于相关分析和预报意义上考虑, 拟建模式中, 预报对象取当前时刻的副高面积指数; 预报因子则分别取超前预报对象3个月的东、西太平洋海温、印度洋海温和前期副高面积指数.这样选择的理由是:(1) 物理意义清楚, 有观测事实和相关研究成果支持; (2) 网络模型的映射和相空间的拓扑结构有一定的相关依据; (3) 由于预报因子超前于预报对象, 因此所建立的模型具有实际的预报意义.
为便于比较网络模型预报效果, 我们将数据资料分为独立的两部分.第1部分用于模型的建立和拟合检验:预报对象 (副高面积指数) 时段为1963年4月~1977年12月; 预报因子 (海温等) 时段为1963年1月~1977年9月, 均为15年共177个月.第2部分用于网络模型预报效果的评估, 为充分检验实际预报效果, 取不连续的两个时段.时段1:预报对象为1978年4月~1982年12月, 预报因子为1978年1月~1982年9月; 时段2:预报对象为1986年4月~1990年12月, 预报因子为1986年1月~1990年9月.两时段均为5年共57个月.
2.2 模型的预报原理和网络结构网络模型的建立过程, 即是通过预报因子输入序列和预报对象输出序列之间对应关系的反复学习和训练, 不断调整网络输入层与隐层、隐层与输出层之间的连接权值和阈值, 找出其传递函数的最佳权值矩阵和阈值矩阵, 从而建立起两者之间的映射关系和预报模型.从理论上讲, 取较多的预报因子及较长的训练数据时间序列, 对模型预报效果会有所提高, 但建模难度会加大; 反之, 若所建模型的神经元少、时间序列短, 则建模比较容易, 但预报效果相对较差.
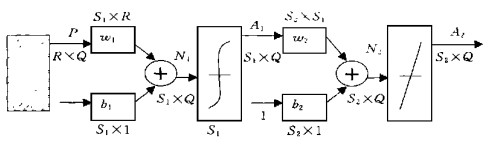
根据可用资料和计算条件, 本文拟采用两层BP网络模型结构 (如图 1) 和动量-自适应学习率调整算法. BP网络中采用的传递函数均为可微的单调递增函数, 其中输入层与隐层之间采用sigmoid型传递函数 (取logsig函数), 隐层与输出层之间采用线性传递函数 (purelin函数).
|
|
| 图 1. 两层BP网络模型结构, 其中S1为隐层神经元 | |
2.3 预报模型的建立
建模过程中, 输入目标 (预报因子) 分别取赤道东太平洋SST (记为Te)、热带西太平洋SST (记为Tw)、赤道印度洋SST (记为Tid) 和前期副高面积指数 (记为Ha) 时间序列的当前值和其延后的3个值, 共计4×4=16个输入值, 即每一时次网络输入层有16个神经元, 输入矩阵为:P=[delaysig (Te, 0, 3); delaysig (Tw, 0, 3); delaysig (Tid, 0, 3); delaysig (Ha, 0, 3)]是一个16×177阶矩阵; 输出目标 (预报对象) 为滞后3个月的副高面积指数时间序列 (记为Hb), 每一时次有1个输出值, 即输出层为一个神经元, 输出矩阵为T=[Hb], 是一个1×177阶的矩阵.网络训练和模型建立的过程即是在每一时刻, 用预报因子的16个输入神经元通过网络隐层传递函数映射去逼近预报对象的1个输出神经元, 找出该两者之间传递函数的最佳权值矩阵和阈值矩阵, 建立起两者间尽可能准确的拟合模型和预报方程.
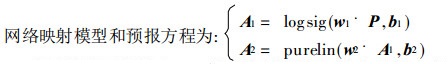
|
其中A1为网络隐层的输出, A2为网络预报输出.本文建模中取隐层神经元S1=20, 则每一时刻输入层和隐层之间传递函数的权值w1为一个20×16阶矩阵, 阈值b1为一个20×1阶矩阵; 隐层和输出层之间传递函数的权值w2为一个1×20阶矩阵, 阈值为b2一个1×1阶矩阵, 矩阵参数值在网络计算和训练过程中经过优化调整, 在误差达到最小值后求出.
模型的学习、训练和仿真基于第2节所述算法, 用Matlab语言编程, 在Neural Network Toolbox中的仿真环境中实现[11], 大致步骤为:
1) 载入输入矩阵P和输出矩阵T.为使网络误差减小和收敛速度加快, 对数据进行必要调整或标准化处理 (本文对副高指数作距平处理并除以20以使其接近海温的距平数值).
2) 对网络进行初始化, 求取隐层和输出层的初始权值矩阵 (w1, w2) 和阈值矩阵 (b1, b2).
3) 采用BP网络优化算法训练网络, 调整和优化网络权值矩阵 (w1, w2) 和阈值矩阵 (b1, b2).
4) 仿真网络模型, 检验模型计算输出同预报目标的拟合程度和独立预报效果.
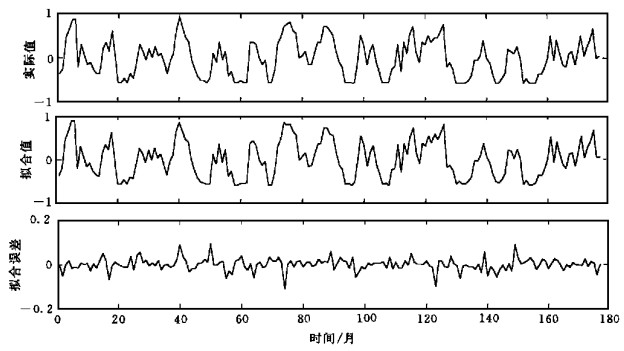
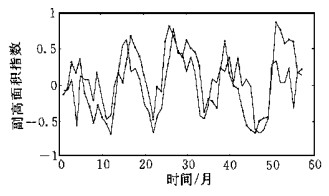
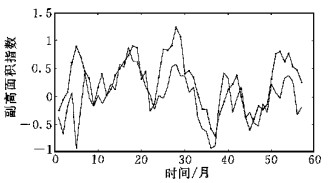
2.4 网络模型的拟合程度和预报效果BP网络的动量-自适应学习率调整算法 (记为BPx) 是基于梯度下降的一种快速有效的训练方法, 图 2是采用BPx算法进行5000次训练迭代后所建立网络模型的计算值与实际值之间的比较.结果表明, 两者间达到了很好的拟合程度, 主体趋势和大部分细节都被较好地描绘了出来, 拟合误差基本控制在10%以内.网络模型较好地建立起了预报因子和预报对象之间的映射关系.图 3、图 4是基于所建网络模型, 通过独立的第2部分数据资料所作副高面积指数预报值与实际值的对比.可以看出, 尽管预报结果对细节的描述还不完善, 还存在一定的疏漏和部分位相偏移, 对峰、谷值的预测幅度也有所欠缺, 但副高面积指数时间序列变化的主要趋势, 主要的升降过程和大部分转折点基本上被正确地反映和预报了出来.考虑到副高变化的复杂性和网络模型3个月的预报时效, 预报结果从中、长期天气和短期气候意义上说是可以接受的, 也具有一定的预报意义.
|
|
| 图 2. 1963年4月~1977年12月副高面积指数网络模型拟合效果比较 | |
|
|
| 图 3. 1978年4月~1982年12月副高面积指数网络模型预报效果比较 (个例1) (实线为实际值, 带点线为预报值) | |
|
|
| 图 4. 1986年4月~1990年12月副高面积指数网络模型预报效果比较 (个例2) (实线为实际值, 带点线为预报值) | |
3 统计回归方法的预报效果比较
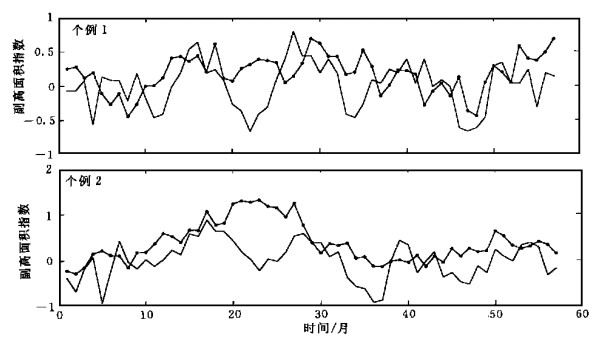
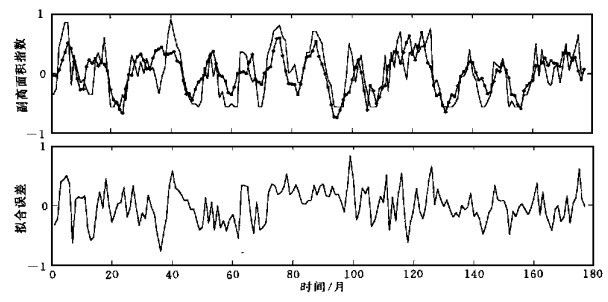
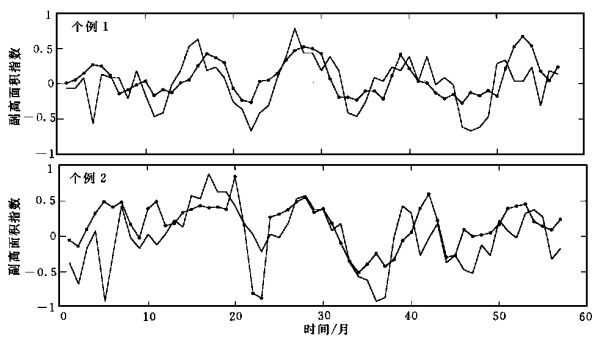
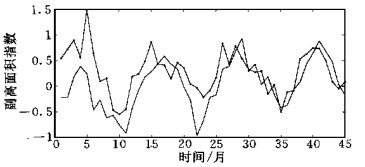
统计回归方法是中、长期天气和气候预测研究中经常使用的一种重要方法和工具, 为检验神经网络建模预报方法在处理副高这样复杂问题时是否有独到的特点和优势, 我们用同样的数据资料建立了统计回归的预报模型, 通过对其拟合程度和预报效果的分析比较, 对两种方法的预报效率作一评估.首先, 用线性回归方法建立了副高面积指数同超前3个月的海温因子和前期副高面积指数之间比较简单的一个预报模型, 图 5是该回归模型基于第2部分资料所作的两个时段的独立预报效果比较.由图中可见, 预报结果难以正确地描述实际情况, 主要的变化趋势和转折过程均不能把握, 预报误差太大, 基本上没有预报价值, 表明这种简单的线性回归模型在处理非线性复杂问题时有较大的局限性.为充分比较统计回归与神经网络两种方法的预报效率, 基于网络模型完全相同的资料处理和选择, 我们分别采用标准回归、逐步回归和向后剔除变量3种方法建立起3个预报子方程, 然后对该3个子系统再进行回归集成, 建立起一个基于3种回归方法的统计集成预报模式.图 6是该统计集成模式的拟合效果和拟合误差情况.由图中可见拟合值基本上可以表现实际的主要动态和趋势, 大部分走向和转折也基本正确, 但对细节的描述和峰、谷的逼近仍不完善 (拟合值与实际值的相关系数为0.73), 同网络预报模型的拟合效果 (图 2, 拟合值同实际值的相关系数为0.97) 相比尚存在较大差距.图 7是用该统计集成模式所作的两个时段预报效果比较.可以看出其预报效果较图 5的线性模式有了较大提高, 时间序列中几个主要的变化趋势和升降过程大体上可以识别和描述出来, 但是对过程中一些略小波动起伏的描述仍表现欠佳, 尤其对峰、谷预测的逼近幅度还很不到位.比较图 3 (预报值与实际值的相关系数为0.65) 和图 7 (上) (预报值与实际值的相关系数为0.54) 及图 4 (预报值与实际值的相关系数为0.63) 和图 7 (下) (预报值与实际值的相关系数为0.51), 应该说网络预报模型对预报对象的总体把握和描述较统计集成模型要更加恰当和准确一些.进一步的网络模型预报结果 (1992年4月至1995年12月, 副高面积指数已订正) 也同样能够正确表现副高面积指数的基本趋势和转折变化 (图 8), 预报值与实际值的相关系数达0.642.因此, 在类似的非线性问题预测中, 神经网络预报方法具有一定的优势.
|
|
| 图 5. 个例1, 个例2线性回归模式的预报效果比较 (实线为实际值, 带点线为预报值) | |
|
|
| 图 6. 1963年4月~1997年12月统计集成模式的拟合效果比较 (上图中实线为实际值, 带点线为拟合值, 下图为拟合误差) | |
|
|
| 图 7. 个例1, 个例2副高面积指数统计集成模式的预报效果比较 (实线为实际值, 带点线为预报值) | |
|
|
| 图 8. 1992年4月~1995年12月网络模型预报效果比较 (实线为实际值, 带点线为预报值) | |
4 存在问题和改进办法
网络预报模型既有上述一些优点和长处, 但也存在许多不足, 如:预报结果对细节描述欠佳, 存在一定的位相偏移, 对峰、谷值预测幅度把握不好等.究其原因, 主要可归结为以下3个方面:
(1) 预报对象本身比较复杂.据模型拟合时段15年177个月的西太平洋副高面积指数的功率谱分析, 除存在比较明显的年变化和准4年变化特征外, 还存在多个连续功率谱峰值, 即存在多种变化周期.显然, 这是类似于混沌系统的非线性复杂时间序列.
(2) 预报因子的选择尚不是最佳.就预报效果而言, 预报因子与预报对象之间相关性愈好, 则所建模型预报效果愈好.我们所取预报因子与预报对象的相关系数基本上在0.5左右, 尚偏小, 其结果导致网络相空间的拓扑结构比较复杂, 建模中非线性映射逼近和误差控制均比较困难.
(3) 业已证明, BP网络可以逼近任意的非线性函数和对任意的复杂系统进行仿真[10], 但实际应用中则要受许多因素制约.一般而言, 预报因子愈多、神经元愈多、训练数据时间序列愈长, 则愈可能有效地接近目标, 同时随着训练中信息量的加大, 网络模型对预报对象变化规律和映射关系的学习把握也愈好, 相应的预报效果就愈好.但是, 这就对计算条件提出了较高的要求.基于资料和计算条件限制, 本文这方面尚有所不足.
综上所述, 改进网络模型的办法主要有:①首先要有一个物理图像比较清晰的模型框架; ②充分进行相关分析普查, 选择最优预报因子; ③根据预报对象的尺度特征, 对原始数据进行必要的滤波, 以减小建模过程的处理难度; ④计算条件允许情况下, 适当多选相关预报因子、增加建模资料的时间序列和隐层神经元数目; ⑤对资料进行初始化或者标准化处理, 尽量减小各因子之间的量级差异和与所取传递函数的值域差异.
此外, 采用其它的先进网络模式 (如具有反馈环节的动态回归网络模型和径向基函数网络模型) 和其它优化算法 (如BP网络中的模拟退火法和遗传算法) 以及设计多层网络和网络集成等方法也是值得尝试的提高预报效率的有效途径.
| [1] | 叶笃正, 曾庆存, 郭裕福. 当代气候研究. 北京: 气象出版社, 1991: 164-177. |
| [2] | 金龙, 陈宁, 林振山. 基于人工神经网络的集成预报方法研究和比较. 气象学报, 1999, 57, (2): 198–207. |
| [3] | Fu C B, Zeng Z M. Ten years experioment on long range prediction of the Northwest Pacific high according to sea surface temperature anomalies. Proceedings of first WMO Conference on long-range forecasting, the practical problems and future prospects. WMO/TD. No.147, 1986. 77~86. |
| [4] | 符淙斌, 叶笃正. 热带海洋对副热带高压长期变化的影响. 科学通报, 1977, 21: 313–317. |
| [5] | 陈烈庭. 北太平洋副热带高压与赤道东部海温的相互作用. 大气科学, 1982, 6: 148–156. |
| [6] | 藏恒范, 王绍武. 赤道东太平洋水温对低纬大气环流的影响. 海洋学报, 1984, 6, (1): 16–24. |
| [7] | 龚道溢, 王绍武. 南北半球副热带高压对赤道东太平洋海温变化的响应. 海洋学报, 1998, 20, (5): 44–53. |
| [8] | 黄荣辉, 李维京. 夏季热带西太平洋上空的热源异常对东亚上空副热带高压的影响及物理机制. 大气科学特刊, 1988: 107–116. |
| [9] | 吴国雄, 孟文. 赤道印度洋-太平洋地区海气系统的齿轮式耦合和ENSO事件. 大气科学, 1998, 22, (4): 470–479. |
| [10] | 沈清, 胡德文, 时春. 神经网络应用技术. 北京: 国防科技大学出版社, 1993. 3~33, 77~86. |
| [11] | 施阳, 李俊. MATLAB语言工具箱——TOOLBOX实用指南. 西安: 西北工业大学出版社, 1998: 124-209. |
 2000, 11 (4): 474-483
2000, 11 (4): 474-483

