2. 扬州大学理学院物理系, 扬州 225009
2. College of Mathematics and Physics, Yangzhou University, Yangzhou 225009
从大气热力-动力方程出发, 运用自忆原理, 曹鸿兴等构建了一个温度、降水和高度3变量的区域气候预测模式[1, 2].该模式包含了两个主要学术观点.一是认为长时间的气候过程中热力作用占主导地位.因此, 模式是以非绝热加热率的热流量方程为基本出发方程.二是考虑大气记忆特性, 从区域气候场历史演变中提取预报信息代替从单一时次全球气候场中提取信息, 即以“时间”信息代替“空间”信息, 充分利用了气候状态的统计特征.因此, 模式运用了含有多时次气候场的自忆性方程, 在求记忆系数过程中将长时间观测资料中的有价值信息提取出来.由此可见, 这一气候预测模式与目前通行的数值模式的基本思想是很不相同的.初步计算实例表明, 该模式具有较高的预报能力, 它为短期气候预报开辟了一条新途径.
上述工作系基础性研究, 其研究目标为区域的年代预测.本工作从制作中国汛期降水分布预报的实际需要出发, 对模式的边界条件及计算格式进行了一定的调整.本文讨论了模式中记忆系数的线性趋势及周期变化等特征.用本模式进行了1988~1997年10年汛期 (6~8月) 降水距平百分率的预报试验, 并对结果进行了分析.同时, 给出了1998年汛期的实际预报结果.
1 模式概况和计算 1.1 模式方程组由地表气温距平T′s方程、500 hPa高度距平h′方程和降水距平百分率R′方程构成了预报区域气候的闭合方程组[1], 即
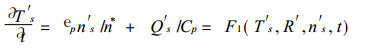
|
(1) |
式中n′s和n′分别表示地面和高空云量距平.n*为经验常数. Cp为空气的定压比热, Q′s为地面非绝热加热率距平, R′为气体常数距平, 式中ep为
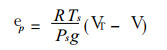
|
其中Ps为地面气压, VT干绝热大气直减率, V为大气直减率, g为重力加速度.
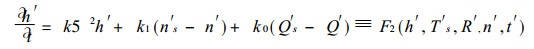
|
(2) |
式中k为Adem大型湍流交换系数, 52为水平拉普拉斯算子, k1=-gep/Vn*, k0=g/VCp.
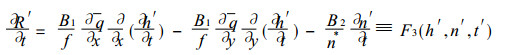
|
(3) |
式中B1和B2为物理参数, f为柯氏参数, q为比湿气候值.
1.2 自忆性方程引进记忆函数U (t), t=t0, t-1, …, t-p, t0为初始时刻, t-p为回溯阶时刻, p为回溯阶.将模式方程组 (1)~(3) 变换为差分-积分形式的自忆性方程组.为书写方便, 以下将T′s记为T, h′记为h, R′记为R.将T, h, R用经验正交函数 (EOF) 展开, 并将自忆性方程离散化, 通过复杂推导得到预报地面气温、500 hPa高度和降水距平百分率的离散化自忆性方程.
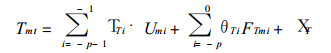
|
(4) |
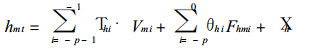
|
(5) |
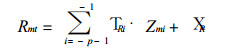
|
(6) |
式中t为预报时刻, m=1, 2, …, M, M为EOF截断数.T.i和θ.i (下标中的“·”表示方程 (2)~(4) 中任一有关变量) 为用实测资料求得的记忆系数, 它们代表了从初始时刻到回溯时刻间观测场对未来值的影响程度. Umi, Vmi, Zmi和Fmi是与地表气温、500 hPa高度和降水距平的EOF时间系数值相联系的变量.X为误差项, 包括方程简化和EOF截断带来的误差.公式详细表达式见文献[1].
1.3 计算和资料计算时, 方程 (4)~(6) 中的一阶和二阶空间差分采用三次样条函数插值格式.根据试算确定回溯阶p=5.用预报年份前N年资料以最小二乘法求 (4)~(6) 式中记忆系数T.i和θ.i.
由于缺少云量资料, 实际计算时简单假定在回溯期p+1时间内云量距平有正有负, 求和时相互抵消, 即假设云量距平之和近似为零.在计算时我们取p=5, 即回溯期为6年, 考虑云量的2~3年周期, 在此期间内云量距平有正有负, 加之系数均为小量, 求和时有抵消之趋势.因此, 假定云量距平之和近似为零是有实际依据的.模式中的物理参数和常数参考前人有关工作并符合我国实际情况事先给定, 带有一定任意性.
模式中所用的资料取为15°~54°N, 70°~133°E范围, 格距为3°×3°.用国家气候中心预测室的160站降水和温度资料, 用文献[2]中的客观分析程序算得1951~1998年的格点资料.高度从北半球500 hPa格点资料中获取.为适应我国汛期降水预报的实际需要, 降水量用6~8月总量, 温度、高度则用6~8月的平均.为了与业务预报一致, 最终输出的降水预报结果为降水距平百分率.具体计算时, 在所取范围的308个格点中, 凡在中国界内的格点 (109点) 取实测值, 界外格点均赋予109点的平均值.
2 记忆系数的特征预报方程 (4)、(5) 和 (6) 中的记忆系数T.i和θ.i表示第i时次观测对预报的贡献大小, 其中T.i代表某预报量的贡献, θ.i则代表整个场的贡献.我们取1951~1992年降水、温度、高度的实测格点资料进行模拟计算.回溯阶p取为5, 这样可以得到逐年的记忆系数TTi, Thi, TRi, θTi, θhi, i=0, 1, 2, 3, 4, 5.
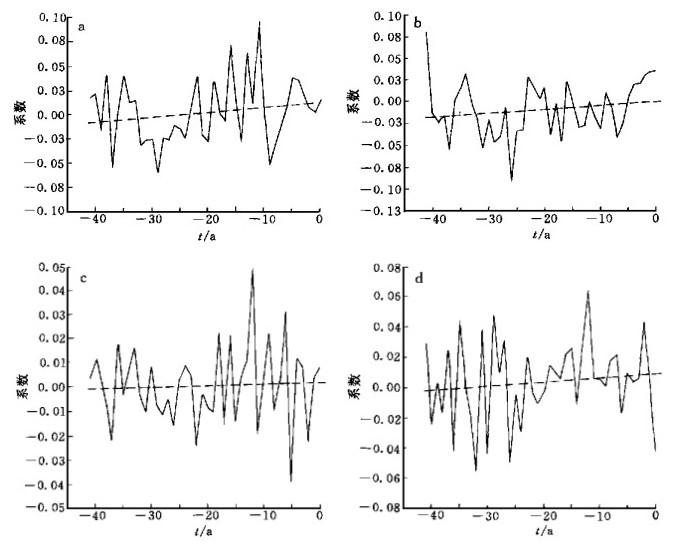
2.1 记忆系数的变化趋势.图 1 (a) 和 (b) 给出温度记忆系数TT0和TT1随时间的变化曲线.横坐标为时间t, 其中t=-41, -40, …, 0, 它们分别对应的年份为1951, 1952, … 1992.图中虚直线为系数序列的线性趋势.从理论上讲, 由于我们采用了距平方程, 记忆系数的线性趋势应呈水平直线.但图 1显示, 系数TT0和TT1随时间的变化呈明显上升趋势.而TT2, TT3, (图略) 则呈下降趋势.表明, 存在着其它物理因素影响着中国区域气候的变化.
|
|
| 图 1. 温度和降水系数随时间的变化 (a) TT0 (b) TT1 (c) TR0 (d) TR1 | |
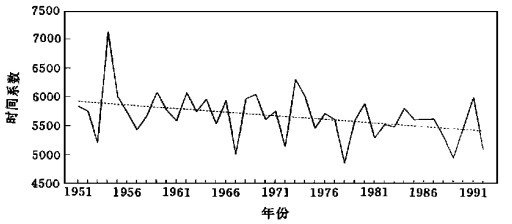
图 1 (c) 和 (d) 为降水记忆系数TR0和TR1随时间变化曲线, 它们略呈上升趋势.近40年来, 中国大范围夏季降水是呈显著下降趋势的.这一点从1951~1992年中国160站夏季降水总量E0F1的线性趋势图 (图 2) 中可以看出.系数的上升趋势可能是由其它物理因素的影响造成的, 并不完全反映降水场本身的趋势变化.高度场的记忆系数 (图略) 的变化亦呈现出一定的上升趋势, 但与温度、降水不同的是, 它们的周期变化更显突出.
|
|
| 图 2. 中国大范围夏季降水线性趋势 (—时间系数…线性趋势) | |
2.2 记忆系数的周期变化
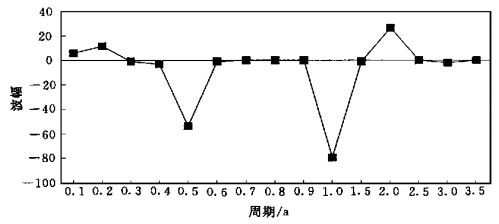
如上所述表示对变量场贡献的系数T.i变化表现出某种上升或下降倾向.而表示整个场贡献的系数θ.i的变化则主要呈现振荡现象.记忆系数的谐波分析结果表明, 不同回溯阶的系数θTi和θhi存在长度大致确定的周期变化.这里仅以高度场系数θh0为例来说明.图 3为θh0的谐波分析结果.从图中可以看出, 周期的谐波分量出现在2.0年处谐波分量呈最大值.这说明θh0主要存在准两年左右的周期变化.准两年的周期变化是大家所熟知的气候振荡的反映.
|
|
| 图 3. 高度场系数θh0谐波分析 | |
3 预报试验
利用区域气候自忆预报模式进行了我国范围内的1988~1997年汛期降水预报试验.具体做法是:取1951~1987年实测资料, 用最小二乘法确定出记忆系数, 回溯阶p取为5, 采用有限记忆递推法向前作一步预报, 即作出1988年汛期的降水预报.再取1952~1988年实测资料, 重新确定记忆系数, 再作一步预报, 即作出1989年的预报, 如此继续下去, 共作出10年预报.从统计学意义上讲, 进行了10年独立样本的预报试验, 是实际意义上的预报.在1998年4月, 我们取1952~1997年实测资料作出了当年汛期的降水预报.在计算距平值时, 平均值取1961~1990年的平均.
预报效果的检验采用距平相关系数.其计算公式为:
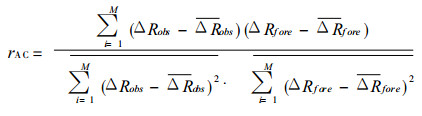
|
其中ΔRobs、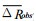
距平相关系数 (rAC) 可以反映降水距平的预报水平, 是国际上通用的检验气候模式预报效果的指数.由于降水气候预报的难度, 就跨季度汛期降水 (时效为2至3月) 而言, 业务预报近20年距平相关系数的平均值仅为0.03. [3]
表 1给出1988~1998年观测值与预报值之间的距平相关系数 (rAC) 及距平符号一致率 (Pa).
|
|
表 1 1988~1998年预报效果检验 |
从表 1第2行看出, 就年际汛期降水预报 (时效为12个月) 而言11年距平相关系数平均为0.07, 最高年份1992年rAC=0.41, 而最差的年份是1994年和1996年rAC=-0.13, 其中1988、1991、1992、1993、1998年的预报技巧得分是相当不错的.第3行表示距平符号实况与预报一致的个数占格点总数 (109) 的百分率.其中1988、1991、1993、1996、1998年距平符号一致率超过了50%.说明本模式有一定的年际气候预报能力.
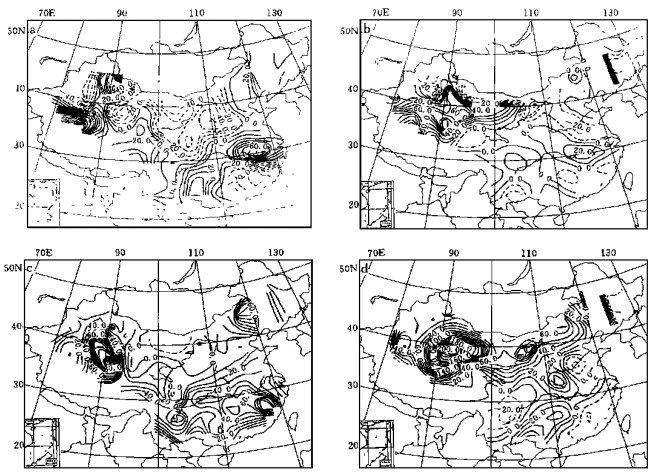
大范围汛期降水的短期气候预测更注重降水分布的趋势特征, 尤其是检验将出现多雨或少雨区的位置报得是否准确. 1991年夏季江淮流域出现了特大洪涝, 洪涝程度严重但范围不广, 主要集中在江淮中下游地区, 降水距平百分率高达50%以上, 而江南东部、华北大部及西北地区降水偏少, 呈中间降水多、南北降水偏少的分布型式, 国家气候中心确定为Ⅱ类雨型 (图 4 (a)).自忆预测模式基本上将这种降水异常分布趋势报出来了 (图 4 (b)), 尽管东部降水偏多、偏少的程度远不及实况那么强, 但是中间多, 南北少的分布格局还是接近实况的. 1996年实况与预报场之间距平相关系数rAC=-0.13, 是11年预报中rAC最低的一年, 但距平符号一致率比较高Pa=0.54, 所以主要多雨区的位置预报还是与实况比较吻合. 1996年夏季主要多雨区集中在长江沿岸及其以南地区, 属Ⅲ类雨带类型.这一年的预报, 北方的降水趋势基本与实况反了, 但是淮河、长江以南大范围的降水偏多趋势还是正确的, 当然强度仍偏弱 (图略). 1998年夏季我国大部地区降水偏多, 多雨中心位于长江流域和东北西部、内蒙古东部地区 (图 4 (c)).长江出现了全流域性的特大洪水; 嫩江、松花江的洪涝亦是超历史记录的.自忆预测模式的预报 (图 4 (d)) 与实况虽有不小的差距, 但在长江中下游、东北和内蒙古部分地区降水是呈现偏多趋势的.
|
|
| 图 4. 中国夏季降水距平百分率 (a) 1991年实况 (b) 1991年预报 (c) 1998年实况 (d) 1998年预报 | |
4 小结
温度和降水场记忆系数随时间变化呈较明显上升或下降趋势.表明它们的变化可能受气候长期振荡作用及外强迫诸多因素的影响.高度场记忆系数的变化呈准两年周期变化, 这可能是短期气候振荡的反映.
1988~1997年中国汛期降水分布预报检验及1998年实际预报表明, 区域气候自忆模式具有一定的预报技巧, 对降水异常分布有时也能作出较好的预报.当然, 象其它气候数值模式和统计预测模型一样, 本模式在预报汛期降水分布方面效果还不够稳定, 甚至出现某些地区的预报与实况距平符号完全相反的情况.这些都有待今后从物理以及计算上进行改进.
| [1] | 曹鸿兴, 封国林, 魏凤英. 一种区域气候预测模式的构建. 气象学报, 2000, 58, (2): 159–167. |
| [2] | 魏凤英, 曹鸿兴. 我国月降水和气温网格点资料的处理和分析. 气象, 1994, 20, (10): 26–30. |
| [3] | 赵振国, 陈桂英. 短期气候预测评估方法和业务的初估. 应用气象学报, 1998, 9, (2): 178–185. |
 2000, 11 (4): 467-473
2000, 11 (4): 467-473


