1922年Richardson首先提出了数值天气预报 (NWP) 的概念. Charney等[1]以正压涡度方程第一次成功地作了24小时数值天气预报, 至今已有半个多世纪的历史.目前NWP的可用预报可达到7~8天, 超过这些天数的数值预报技巧是比较差的.早些年, 数值天气预报时效的进展大约是每10年延伸2天.但是自20世纪90年代以来计算机技术发展迅速, 与其相比, NWP的进展, 是比较慢的.一般说来, 10~30天平均预报评分基本上依赖于逐日预报的水平.理论上说, 逐日预报的可预报性上限为2~3周.为此, 我们面对的任务是除了改进预报模式的空间分辨率和有关物理过程的处理外, 还要继续探索新的数值天气预报技术. 20世纪50年代以来, 许多中国学者[2, 3]作过多种尝试, 他们的基本思路是找出一个实际可行的方法, 在模式中应用多时次空间场, 代替单一的初始场.
近几年来, 曹鸿兴等[4, 5]基于大气运动是一个不可逆过程的事实, 构造了大气自忆方程, 它是一个差分-积分方程.现已从数学上证明, 给定记忆函数以某些特殊值就可以从此方程推导出一些现存的差分格式.若干多时次数值预报模式可以纳入这个自忆性方程的框架中.
本文基于大气自忆性原理, 导出了以T42谱模式为动力核的全球自忆谱模式, 用这个模式进行了积分试验.目的在于改进逐日天气预报, 延长预报时效, 提高中期环流预报技术.在对差分-积分方程的数学处理上与文献[6]有相当大的差异, 后者的动力核为美国的AFGL模式.
1 自忆性原理的谱表达式在数值天气预报中谱模式有很多长处, 为此被广泛采用.世界上许多著名的数值天气预报模式是谱模式.谱模式中的球谐系数直接反映了大气波的特性, 并有全球效应.在应用自忆性原理时, 谱模式的全局效应可以减少局地记忆误差.
在谱空间, 大气运动方程可以表示为:

|
(1) |
式中J为整数, m和n分别为经向和纬向波数, xm, n和Fm, n为复数变量.在谱模式中, 通常以涡度和散度方程来代替水平运动方程.所以xi可表示涡度、散度、温度、比湿或地面气压.对xim, n定义一个复记忆函数U (m, n) (t), 根据自忆性原理[4], 可导出
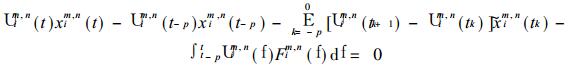
|
(2) |
它是大气自忆方程的谱表达式, 是一个以谱系数为变量的差分-积分方程.式中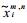
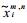
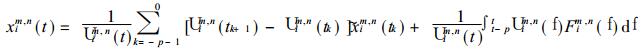
|
(3) |
(3) 的右侧第1项为自忆项, 第2项为他效项, 它表示动力核的作用.离散化第2项, 积分用求和替代, 则有
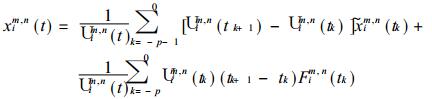
|
(4) |
令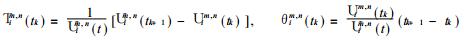
得到
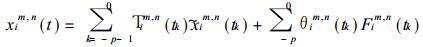
|
(5) |
式中记忆系数Tim, n (t) 和θim, n是复记忆函数Uim, n (t) 的组合.求解 (5) 的目的是要得到这些系数.一旦记忆系数Tim, n (t) 和θim, n (t) 被确定, 即可用 (5) 预报下一个时次的xim, n (t1).
2 自忆T42谱模式 2.1 自忆模式方程原则上, 任何动力模式都可以用作自忆模式的动力核[6].但是, 谱方法可能减少计算量和局地记忆误差, 为此建立自忆谱模式是更有效的.为了便于比较, 构造了一个全球自忆谱模式, 简称SMT42.它以移植来自ECMWF (欧洲中期天气预报中心) 的国家气象中心的T42业务模式为动力核.模式方程为[7]:

|
(6) |

|
(7) |
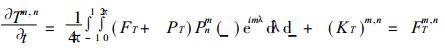
|
(8) |
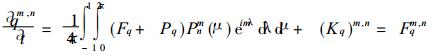
|
(9) |
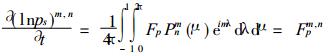
|
(10) |
其中Y为涡度, D为散度, T为温度, q为比湿, ps为地面气压, a为地球半径, 其他符号见文献[7]、[8].令FYm, n, FDm, n, FTm, n, Fqm, n和Fpm, n分别代表式 (6)~(10) 右端各项, 则 (6)~(10) 有类似于 (1) 的形式
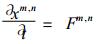
|
(11) |
按照第一节的步骤, 可以从 (6)~(10) 式得到SMT42模式的离散方程
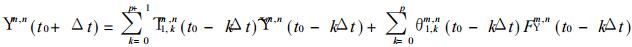
|
(12) |
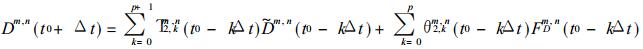
|
(13) |
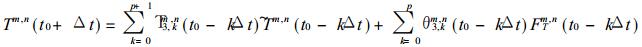
|
(14) |
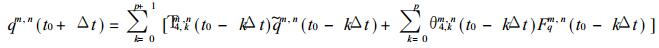
|
(15) |
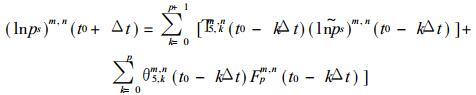
|
(16) |
其中t0是初始时刻, Δt是取样时间间隔, t=t0+Δt为预报时刻, t0-iΔt (i=1, 2, …, p) 为t0前的时刻, 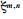
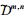
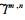
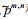
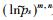
(12)~(16) 和离散的 (6)~(10) 的差异在于前者在预报进行中应用了t0前的p个场的资料.若p=0, 则 (12)~(16) 蜕化为离散的 (6)~(10) 式, 它是众所熟识的仅有一个场的数值模式.
2.2 数值试验以观测资料应用格谱转换技术计算出谱系数Y, D, T, q和lnps, 然后基于 (6)~(10) 式就可以计算得出FYm, n, FDm, n, FTm, n, Fqm, n, Fpm, n.实际上, 如果直接用T42常规产品计算则更为方便.简单地, 把 (12)~(16) 的中值取作:

|
(17) |
计算出N个样本的xm, n, 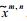
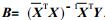
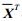
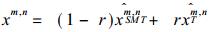
|
(18) |
其中, 
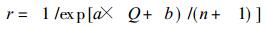
|
(19) |
确定.式中Q是预报步数: Q=0, 1, 2, …, 15.随着Q增加, r则变小.这意味着当Q增加, SMT42对xm, n的贡献增大.另一个参数n是波数, 当n增加时, r也增加; 这意味着对组合xm, n的贡献主要来自T42而不是SMT42.n愈大, T42的贡献愈大; 反之, SMT42的贡献愈小.通过一些实际计算, 确定取经验系数a=2.2, b=2.83, 也就是说, 为了改进预报, 用的是SMT42与T42的混合方法, 作为动力核的模式似乎在起作“顶梁柱”的作用.
求解中对样本量N和回溯阶p的确定, 先根据天气学原理定一个数, 然后通过多次试算来确定.由于天气变化中的季节性差异很大, 因此不宜像数理统计理论确定的那样, 样本量需大于30.我们一般取样本量10~20, 回溯阶p取1~5.不同的预报时效有不同的样本量和回溯阶.预报时效长所取样本量大, 回溯阶也长.从物理上讲, 就是短期预报取决于1~2个初始场, 而中期预报取决于3~5个初始场, 这和通常的预报经验相符合.
3 中期天气预报分别计算了1990年1、4、7、10月上半月的全球预报, 发现在各个季节SMT42的预报效果都比T42有很大提高.图 1给出了两种模式500 hPa高度预报的均方根误差, 明显地SMT42均方根误差的都比T42的小, 尤其在7天以后, 差异更为显著.

|
|
| 图 1. 以T42谱模式 (虚线) 与SMT42谱模式 (实线) 所作的 500 hPa高度预报的均方根误差 (S) 全球平均 | |
这4个月500 hPa高度预报, 从第1天开始SMT42模式的均方根误差就比T42的小且7天以后SMT42的均方根误差增长是缓慢的.例如1月SMT42模式第7天预报的均方根误差为60.3 gpm, 到第15天, 增至78.1 gpm, 其增长速度为2.22 gpm/d ((78.1-60.3)/8).但是T42的相应增长速度为3.05 gpm/d.7月份的结果是, 在上述同样情况下, SMT42的增长速度为1.28 gpm/d, 而T42为2.8 gpm/d, 4月和10月的情况与7月基本相同.由此可见, 自忆模式对全年中期预报的改进都是相当显著的.
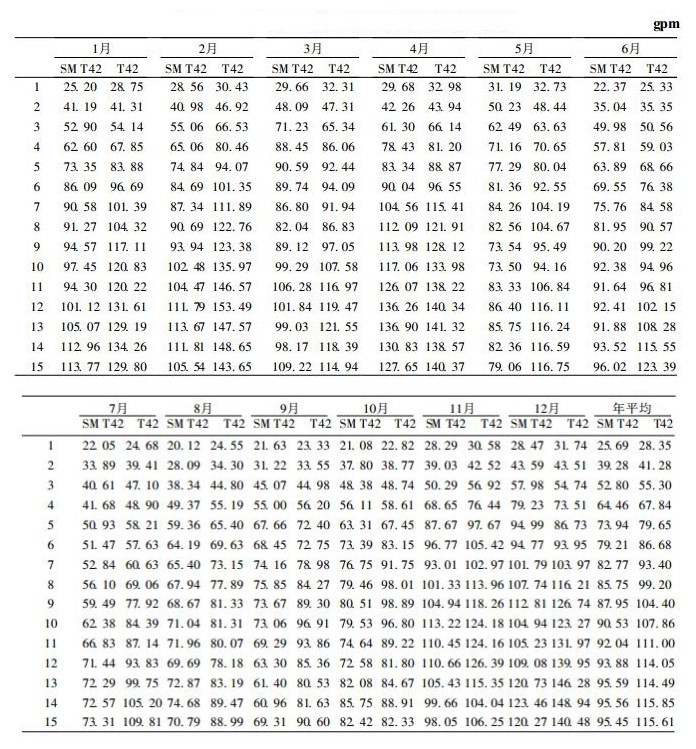
为了进一步检验SMT42的预报功能, 以1990年为实例, 对北半球地区20°~90°N区域全年12个月500 hPa高度进行了计算 (表 1), 并对比了同期T42的计算结果.得出第1天预报年平均均方根误差为25.7 gpm, 第7天为82.8 gpm, 增长速度还是比较迅速的.但是从第7天起, 它比T42的增长慢得多.第7天SMT42的均方根误差与T42相比其减少约为11% ((93.4-82.8)/93.4).到第15天, 两者差异变大, SMT42的为均方根误差95.5 gpm, 其增长速度为1.59 gpm/d, 此时T42的均方根误差为115.6 gpm, 两者相差17% ((115.6-95.5)/115.6).夏季的差异比冬季更为明显.统观表 1的全部, 容易看到绝大部分SMT42都优于T42, 仅有个别月份的极少天数例外.具体地说, 也就是全年只有10天SMT42比T42差, 占总数的5%, 而且没有出现在6~8月份.这个结果增强了我们对SMT42的信心, 特别是在夏季中期预报中SMT42的准确性的提高.
|
|
表 1 北半球20°~90°N 500 hPa高度的均方根误差 |
表 2和表 3分别给出SMT42和T42在南半球20°~90°S和热带20°S~20°N 500 hPa预报的均方根误差值.由表可见, 在南半球1月份SMT42模式在第7天预报的均方根误差与T42相比减少了22%, 第15天减少23%.对于年平均, 第7天的减少为17%, 第15天是24%.在热带, 1月份SMT42第7天预报的均方根误差减少为36%, 第15天为37%; 7月份, 第7天为20%, 第15天为24%; 全年平均, 与T42相比, SMT42的第7天预报的均方根误差的减少为28%, 第15天为35%.
|
|
表 2 南半球20°~90°S 500 hPa高度的均方根误差 |
|
|
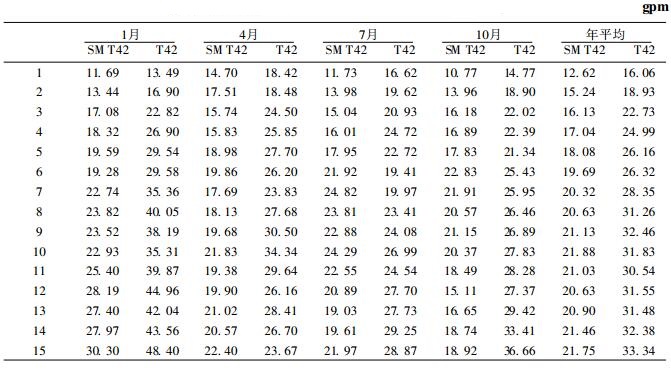
表 3 热带20°S~20°N 500 hPa高度的均方根误差 |
细观北半球、南半球和热带全年各月500 hPa高度预报, SMT42的均方根误差比T42的都小得多, 而且随着预报日数的增加, SMT42的均方根误差的增大速度变慢, 使得两者的差异也就越来越大.全年只有7月份第6和第7天在热带地区SMT42的均方根误差比T42的大, 这可能是由于夏季异常天气形势所引起.
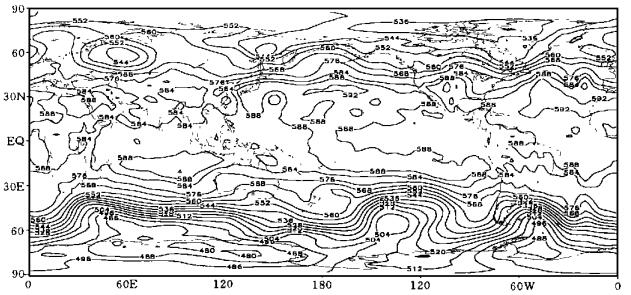
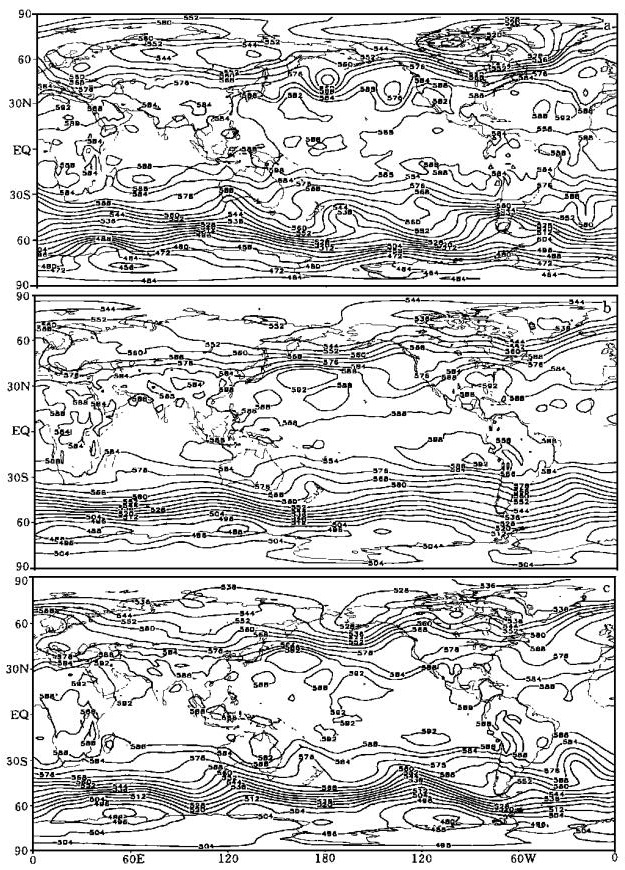
图 2是1990年8月31日500 hPa高度的初始场.由此出发分别用T42和SMT42作了以后1~15天的预报.图 3和图 4分别给出5天和10天的预报结果.虽然两个模式预报的大气环流系统都不能令人满意, 但是, 第5天SMT42与T42预报的均方根误差分别为64.4 gpm和78.6 gpm; 第10天, 前者为71.9 gpm, 后者为93.1 gpm, 两者的差异为22.8% ((93.1-71.9)/93.1), 可以说差异是比较大的.
|
|
| 图 2. 1990年8月31日500 hPa高度的初始场 | |

|
|
| 图 3. 1990年9月5日500 hPa高度 a) 观测结果; b) T42谱模式的预报; c) SMT42谱模式的预报 | |
|
|
| 图 4. 1990年9月10日500 hPa高度场 (说明同图 3) | |
总之, 用SMT42作500 hPa预报, 其RMSE相对于T42的减少是十分显著的, 在南半球使用效果又比北半球的好, 更有意义的是, 通常认为数值预报难以预测的热带地区, 用SMT42也能得到较好的改进.
在数值预报中通常使用距平相关系数 (ACC) 来表征两个场之间图像的相似程度.当今, 一个常用的标准是, 在中短天气预报中, 当观测场与预报场之间的距平相关系数d达到0.6, 则认为该预报达到可用预报水平.用此标准, 我们检验了谱模式T42和自忆谱模式SMT42的全球距平相关系数d≥0.6的天数, 见表 4.由表可见, 就全年而言, SMT42的可用预报为3.4天, 而T42的可用预报为3天.如本文引言所述, 10年才能延伸可用预报2天.而我们仅采用自忆技术, 就延伸了可用预报0.4天.可以推测, 若我们采用更高分辨率的谱模式为动力核, 有可能将可用预报延伸得更长.
|
|
表 4 观测场与预报场之间距平相关系数ρ≥0.6的天数 |
从1至12月1~15天的距平相关系数的计算结果来看, 自忆谱模式SMT42对谱模式T42的预报也有改进, 但没有均方根误差的改进那么显著, 表 5列出了12个月1~15天的距平相关系数的平均值.显然, 11天以后的改进最明显, 这是十分令人鼓舞的, 因为当今10天以后预报的改进十分缓慢.其中, 最大改进为第12天, 相对改进率为38% ((0.279~0.202)/0.202), 最小改进为第7天, 相对改进率为3% ((0.365~0.353)/0.353), 15天平均改进率为15%, 可以说SMT42对T42的改进也相当可观.
|
|
表 5 逐日距平相关系数的12个月平均值及改进率 |
4 结束语
数值预报已是业务天气预报以及有关研究的主要工具.人们期望借助于现代数学和物理理论以及现代计算技术的发展使之进一步完善.在某些方面来说, 就是要使数学模式不仅能逼近真实大气, 有实际预报功能, 既减少计算机资源的负担, 又能提高计算速度.数值预报的准确度极大地受到初始条件、模式方程和计算技术的影响.本文提出的基于自忆性原理建立的自忆谱模式 (SMT42) 在预报过程中可以不必进行时间平滑, 有利于提高计算精度.SMT42在计算量上比常用的T42模式只增加1/20.已有实例计算表明, 它比传统的谱模式的预报评分有很大提高.它可为数值天气预报, 特别是中期数值预报开辟一个有潜在前景的新途径.
致谢 本文的资料准备和计算, 得到陈国范、魏凤英女士和马建中先生的协助, 丑纪范教授对此项研究给予了极为有益的指导, 在此特致感谢.另外, 我们还要对国家自然科学基金会给予的支持表示感谢.| [1] | Charney J G, Fjortoft R, von Neumann J. Numerical in tegration of the barotopic vorticity equation. Tellus, 1950, 2: 237–254. |
| [2] | 顾震潮. 作为初值问题的天气形势数值预报与用地面天气历史演变作预报的等值性. 气象学报, 1958, 29, (2): 176–186. |
| [3] | Chou Jifan. The problem of using past data in numerical weather prediction. Scientia Sinica, 1974, 1, (6): 635–644. |
| [4] | Cao Hongxing.Self-memorization equation in atmospheric motion, Science in China, series B, 1993, 26 (7): 845~855. |
| [5] | Cao Hongxing, Zhu Zhengxin.Self-memorization and predictability of atmospheric motion.In ternational Workshop on Imbalances of Slowly Varying Components of Predictable Atmospheric Motion, 1995, WMO/TD No.652, 13~18, Beijing, China, 7~10 March. |
| [6] | 曹鸿兴, 蒋维东, 哥道夫斯基. 自忆谱模式及其初步应用. 大气科学, 1998, 22, (1): 119–126. |
| [7] | ECMWF.ECMWF forecast model.Research Manual 2 and 3, 1987, 1988, ECMWF, Reading, England. |
| [8] | Bourke W. A Multi-level spectral model: (Ⅰ), Formulation and hemispheric integration. Mon.Wea.Rev, 1974, 102: 688–701. |
| [9] | 谷湘潜.全球大气自忆谱模式及其数值试验.[博士论文].兰州:兰州大学, 1998. |
 2000, 11 (4): 455-466
2000, 11 (4): 455-466