ENSO循环的变化规律及形成机制是ENSO动力学研究的关键问题. ENSO的模式研究从80年代初开始至今已取得了令人注目的进展.从热带太平洋区域的简单距平模式 (如Zebiak & Cane, 1987) [1]到全球范围的完善海气耦合模式 (CGCM, 如Philander等, 1992; Lau等, 1992) [2, 3], 其中已有不少能较好地模拟类似于实际ENSO结构3~7年周期的热带太平洋海洋、大气振荡现象.对此Neelin等 (1992, 1998) [4, 5]已有很好的总结.同时, 人们也讨论了ENSO循环可能的动力学机制, 其中比较有名的是“时滞振子”假说 (Battisti & Hirst, 1988; Suarez& Schopf, 1989) [6, 7], 即ENSO循环的负反馈机制 (回复机制) 可归结为太平洋西边界波反射产生的时滞效应.
考虑到简单海气耦合模式不受“气候漂移”困扰 (因为多为距平模式) 但无法直接模拟或预报热带海温异常引起的热带外气候异常, 而完善海气耦合模式虽可直接进行热带外的气候异常模拟或预报但又一般存在“气候漂移”, 作者用一个全球大气环流模式与一个热带太平洋简单距平模式进行耦合, 构成一种新型的ENSO模式——混合海气耦合模式.用此模式, 作者已进行了ENSO的预报试验[8].本文将讨论的重点放在模式ENSO循环及其形成机制上.
1 模式简介耦合模式在文献[8]中已有详细说明, 这里仅作简要介绍.大气模式为垂直方向具有9层σ面、水平菱形截波为15的全球大气环流谱模式.为减小地形谱截断产生的误差, 吴国雄等引入了层结参考大气[9].观测SST强迫下AGCM多年模拟结果的平均将作为大气模式自身的气候态.海洋模式是一个简单的两层距平模式[10], 模式范围仅限于热带太平洋, 以线性约化重力模态为动力学基础.表层海温距平倾向方程中包括三维的温度平流, 由给定的平均流和计算出的异常流共同确定.大气模式通过风应力异常影响海洋, 海洋模式通过海温异常影响大气加热场, 将两者进行同步耦合.参与耦合的风应力距平是扣除大气模式自身气候态的结果, 即两者实际上是通过距平量进行耦合, 这样就有效地避免了“气候漂移”.
将上述耦合模式进行连续45年的积分.具体做法是:选定一个初始时刻 (如, 1982年5月31日), 大气模式的初始场取AGCM模拟积分 (用1979~1994年观测SST强迫AGCM, 进行16年的积分, 事先已完成) 保留下来的该天的谱场; 海洋模式的初始场这样得到:用AGCM模拟的风应力距平从1979年1月开始强迫海洋模式, 一直运行到1982年5月为止, 再让两者进入耦合阶段, 并连续积分45年 (不外加其它异常强迫).模式运行的头7个月的结果不参加本文的分析, 将第8个月作为第一模式年的第一个月.
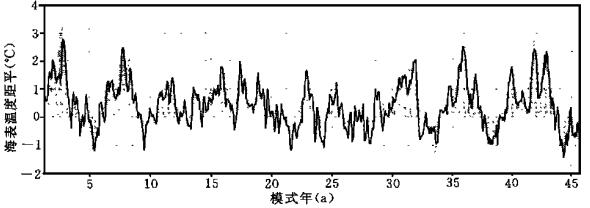
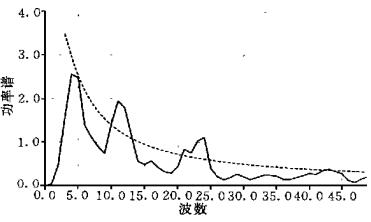
2 模式ENSO循环的基本特征 2.1 时间变化及其谱图 1给出Niño3指数 (150°~90°W, 5°N~5°S范围内SSTA的平均) 的时间变化.可见, 赤道太平洋海温有不规则的年际振荡, SST最大增幅超过+2 ℃, 最大负距平为-1 ℃左右.暖 (冷) 事件在强度上不尽相同, 冷 (暖) 事件间的时间间隔也不完全相同, 显示出较显著的“不规则性”, 负SSTA维持的时间、出现的强度均不及暖事件; 在一次较长的冷 (暖) 过程中还伴随着短时间的扰动, 表明多时间尺度的共存.图 1中阴影表示TW2指数 (180°~140°W, 5°N~5°S内海表纬向风距平的平均) 的时间变化 (已经过5个月的滑动平均).可见, 纬向风也显示明显的年际振荡, 其不规则的形状显示着大气风场变化包含多种时间尺度; 纬向风异常与SSTA有明显的对应关系, 西 (东) 风异常对应于正 (负) SSTA. TW2指数的功率谱如图 2所示, 第一显著周期为50~60个月, 次周期为23.3个月 (准两年), 10.7个月周期上出现第三个峰值 (通过95%红噪声检验).Niño3指数的功率谱也有类似的结果 (图略).
|
|
| 图 1. 耦合模式模拟的Niño3指数 (实线, 单位: ℃) 和TW2指数 (经5个月滑动平均, 阴影, 单位: m/s) 随时间的变化 | |
|
|
| 图 2. TW2指数的功率谱分布 (虚线为95%红噪声水平, 周期T=256/k, k为波数 ) | |
2.2 时空分布
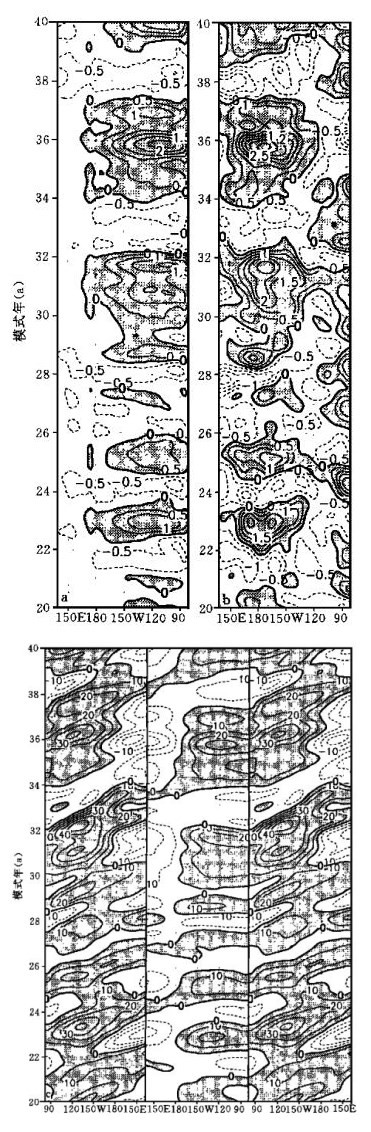
图 3a给出了模式第20至39年SSTA沿赤道 (5°N~5°S内平均) 的时间-经度剖面, 已滤掉周期为11个月以下的信号 (阴影区为正).可以看到, 赤道太平洋正负海温异常随时间不规则交替出现, 正SSTA主要分布在中东太平洋 (日界线以东), 中心位于120°W附近, 最强可达2.5 ℃; 西太平洋地区大部分时间维持负距平, 强度较弱, 负SSTA中心在90°W附近, 最强仅-1.0 ℃左右, 冷暖位相具有显著的不对称性.另外, 图中海温异常的纬向传播特征不明显.
|
|
| 图 3. 第20~39模式年沿赤道的 (5°N~5°S内平均) (a) SSTA (单位: ℃), (b) 海表纬向风异常 (单位: m/s), (c) 沿赤道 (5°N~5°S内平均, 中间图) 及沿10°S (7°N~13°S内平均, 两侧图) 斜温层深度距平 (单位: m) 的时间-经度剖面 (阴影表示正区) | |
图 3b给出表层纬向风距平沿赤道的时间-经度剖面 (阴影区为西风异常).可以看到, 纬向风异常与SSTA的分布在时间上完全对应, 西 (东) 风异常对应于正 (负) SSTA.西风异常出现在异常暖水中心的西侧, 暖水中心的东侧是东风异常, 正距平主要分布在赤道中西太平洋, 但西风异常范围向东仅达120°W.
图 3c给出斜温层深度扰动沿赤道 (5°N~5°S内平均) 及沿10°S (7°~13°S内平均) 的时间-经度剖面, 为看清波动的传播及反射, 把沿10°S的剖面东西向对调.沿赤道, 斜温层深度的变化与海温距平完全对应: El Niño期间, 中东太平洋地区 (180°以东) 斜温层深度为正距平 (加深), 西太平洋地区为负距平 (抬升), La Niña期间情况与此相反, 即斜温层东、西部呈“跷跷板”式的变化.同时, 斜温层扰动具有明显的东传性, 正距平从西边界到东边界约需不到1年的时间, 并在东传过程中得到维持和增幅; 负距平在西太平洋地区基本上呈驻波振荡.在赤道南北两侧, 斜温层扰动有更为明显的西传性, 从东边界到达西边界大致需1~2年.另外, 东部赤道两侧的扰动 (Rossby波) 主要是Kelvin波在东边界反射所致, 反射后在赤道两侧向西传播, 正Rossby波到达西边界后可反射成赤道正Kelvin波, 负Rossby波在西传过程中大多衰减消亡.但在El Niño发展过程中, 在中西部激发的赤道两侧的负Rossby波可西传到达西边界.然而, 仔细观察图 3c中赤道西太平洋地区的负距平的位相, 可以看到, 它超前于到西边界的负Rossby波的位相, 而和中东部的正距平同位相, 因此图 3C赤道西太平洋地区的负距平并不能理解为赤道两侧西传的Rossby波遇西边界反射而成, 而应理解为El Niño发展过程中中西部西风异常所激发的Kelvin驻波.
2.3 合成分析类似于Rasmusson & Carpenter (1982) [11], 采用位相合成的方法, 将一次ENSO过程分成8个位相, 取Niño3指数出现负极大值的时间为第1位相, 出现正极大值的时间为第5位相, 其间由负转正的时间为第3位相, 第1、3位相的中间时间为第2位相, 第3、5位相的中间时间为第4位相.对称地, 取其后Niño3指数由正转负的时间为第7位相, 第5、7位相的中间时间为第6位相; 第7位相与下一次负极大值 (即下一次ENSO第1位相) 出现时间的中间时间为第8位相.按此方法, 将45年内的ENSO事件进行位相划分, 然后按位相进行合成平均, 得出一个平均ENSO过程及它的8个位相.
(1) 冷态成熟期 (位相1)
图 4a给出8个位相的SSTA分布.位相1时, 整个热带太平洋全为负距平, 最大负中心出现在大洋东部的赤道两侧.此时, 东太平洋斜温层深度为负距平 (超过-10m), 沿赤道呈舌状向西伸展, 中西部赤道两侧及西太平洋地区为正扰动 (图略).海表风应力异常分布如图 4b所示 (阴影区表示显著辐合), 此时110°W以西全为东风异常, 受其影响, 赤道太平洋出现向西的表面异常流, 冷水上翻也随之加强 (图略).

|
|
| 图 4. 位相合成后ENSO8个位相的SSTA水平分布 (单位: ℃) 和海表风应力异常的水平分布 (图a中阴影表示正区, 图b中阴影区表示显著辐合区) | |
(2) 冷态的衰减及消亡 (位相2、3)
位相2时, 热带太平洋仍维持海温负距平 (图 4a), 但中东部的负SSTA已明显减弱.位相3时, 该地区的冷水区已经被较弱的异常暖水取代, 东部赤道两侧的负SSTA有所减弱, 但依然维持.与此同时, 东部斜温层负深度距平开始减弱, 至位相3时, 赤道西太平洋地区已被负深度距平控制, 中东太平洋出现小块正深度距平区 (图略).图 4b显示, 位相2时, 赤道东风异常明显减弱, 西太平洋地区已出现西风异常, 异常辐合区出现在日界线附近.之后, 西风异常进一步加强并向东扩展, 原先的东风异常减弱并东退, 辐合区相应东移.位相2时, 西太平洋赤道地区出现向东的海表异常流以及向赤道辐合的经向异常流, 这样赤道中西太平洋出现异常下沉运动, 其两侧出现异常上升运动以作补偿 (图略), 之后, 西太平洋地区下沉运动不断加强并沿赤道向东扩展, 但东部赤道地区仍为异常上升, 其两侧为异常下沉.
(3) 暖态的建立与发展 (位相4)
赤道中东太平洋的正SSTA继续发展, 范围扩大, 向西越过日界线, 向东在南美沿岸形成1 ℃左右中心, 西太平洋地区则为较弱的负距平.至此, 一个典型的El Niño已形成 (图 4a).与之相对应, 东太平洋斜温层明显加深, 西太平洋地区明显变浅, 强度均在10 m以上 (图略).海表西风距平不断加强并向东扩展至125°W附近, 辐合区继续东移 (图 4b).受其影响, 向东的异常海表流进一步增强, 并扩展到120°W以东, 西太平洋地区向赤道的经向辐合流也不断增大 (图略), 与之相对应的赤道异常下沉运动及其两侧的补偿上升运动也继续增强、向东扩展, 东部的赤道上翻流异常向东退至120°W以东.
(4) 暖态成熟期 (位相5)
热带中东太平洋正SSTA已发展到鼎盛时期, 异常暖水的范围达最大, 向西到日界线以西, 东部中心强度达2 ℃以上, 西太平洋地区为负SSTA (图 4a).斜温层在赤道东太平洋地区加深达20 m以上, 西太平洋赤道地区抬升近30 m.低层西风异常亦达最强 (图 4b), 125°W以西为西风距平, 以东为东风距平, 125°W附近为明显的辐合中心 (位于异常暖水中心的西侧).另外, 向东的异常海表流几乎遍及整个赤道太平洋, 强度达25 cm/s; 西太平洋地区向赤道的经向辐合流进一步加强, 并向东扩展到150°W.120°W以西的赤道地区为强的异常下沉, 其两侧为强的异常上升, 以东赤道地区为异常上翻, 其两侧为异常下沉, 但东部的变化强度远不及西部.
(5) 暖态的衰减及消亡 (位相6、7)
海温异常达最强后将开始衰减.由图 4a可见, 赤道中东太平洋异常暖水的强度已明显减弱, 位相7时, 仅东部残存弱暖水区, 且其南北两侧均出现了负SSTA分布, 表明El Niño正趋于消亡.位相6时斜温层在东部的加深明显减弱, 赤道两侧的正深度距平有西传迹象, 西太平洋地区的负深度距平区范围减小.至位相7时, 东太平洋赤道地区已被弱的负深度距平取代, 赤道两侧的加深信号继续西传, 西太平洋地区负距平进一步减弱.赤道太平洋中、西部的西风异常开始减弱西撤, 东部的东风异常加强并向西扩展, 辐合区的范围明显减小 (图 4b).相应地, El Niño成熟期时向东的海表异常流的范围向西缩小, 强度减弱, 随着东部东风的加强, 东太平洋出现向西的异常流, 并不断加强, 向西扩展.位相7时, 向西的异常流已控制整个赤道太平洋.同时, 赤道西太平洋地区的经向辐合及东部的经向辐散明显减弱, 这又导致中西部赤道异常下沉及东部异常上升的减弱 (图略).上述变化表明, El Niño正逐步减弱并趋于消亡.
(6) 冷态的发展与建立 (位相8)
图 4a显示, 位相8时热带太平洋大部分地区又重新被海温负距平覆盖, SSTA的分布类似于位相2, 东部两侧又出现负SSTA中心.东部斜温层深度负距平进一步加强 (超过-10 m), 赤道两侧的正距平继续西传, 西太平洋斜温层加深 (图略).赤道太平洋上的西风异常已经消失, 取而代之的是东风异常 (图 4b).受其影响, 赤道太平洋向西的海表异常流进一步增强, 原西太平洋赤道上的经向辐合变为弱的经向辐散, 赤道太平洋中西部的异常下沉也被异常上翻取代, 东部的异常上升仍维持, 即整个赤道地区均为异常上翻, 有助于负SSTA的发展, 至此, 一次新的La Niña已经建立.
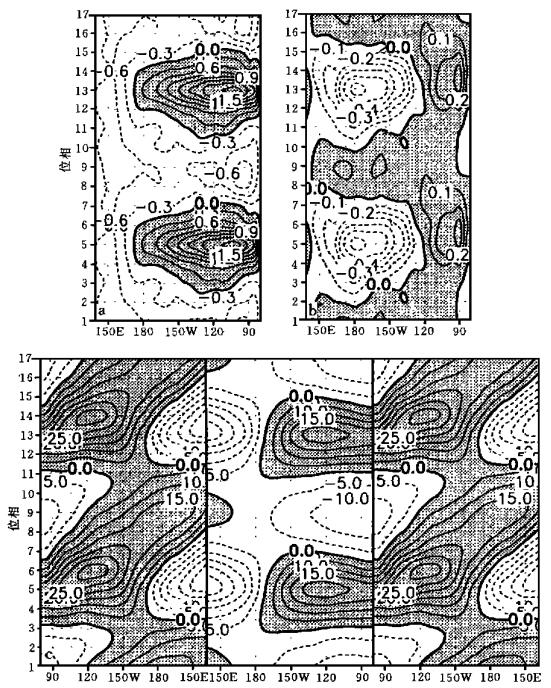
3 模式ENSO循环的负反馈机制图 5a、b、c分别给出沿赤道的SSTA、海流垂直速度异常、斜温层扰动的位相-经度剖面 (图 5c还给出沿10°S的剖面, 东西向对调).这里给出两个周期的变化, 9~16位相实际上是1~8位相的重复.有两点值得指出: (1) 图 5b的异常下沉运动完全对应于中东太平洋的正SSTA, 但其范围仅在120°W以西, 其东部基本上是异常上升区, 且其强度随正SSTA的发展而加强, 这与暖水中心东部东风异常的加强有关 (图 4b).如此强的上升运动对暖态的消亡可能起重要作用; (2) 正Kelvin波在东边界可反射成在赤道两侧西传的正Rossby波, 在西边界又反射成赤道正Kelvin波.正Kelvin波的东传可能是冷态消亡、暖态产生的触发机制.尽管El Niño发展过程中中西太平洋赤道两侧激发的负Rossby波可到达西边界, 但图 5c中西太平洋赤道地区的负距平在位相上超前于到达西边界的Rossby波, 因而不能认为是Rossby波反射所致.因此暖态消亡的负反馈机制不能由“时滞振子”假说去解释.
|
|
| 图 5. 位相合成后沿赤道 (5°N~5°S内平均) 的 (a) SSTA (单位: ℃), (b) 垂直速度异常 (单位: cm/s), (c) 沿赤道 (5°N~5°S内平均, 中间图) 及沿10°S (7°N~13°S内平均, 两侧图) 的斜温层深度距平 (单位: m) | |
海洋模式[10]中, SSTA变化倾向方程如下:
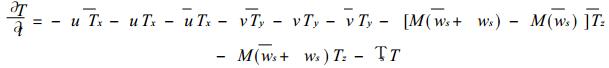
|
(1) |
右端共9项.其中带`-’的为气候平均值, 不带‘-’的为距平值.函数M (x) 有以下形式:
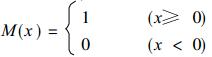
|
(2) |
分析前8项对总的海温变化倾向的贡献:
(1) 冷态的消亡 (位相2、3) 总海温倾向 (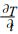
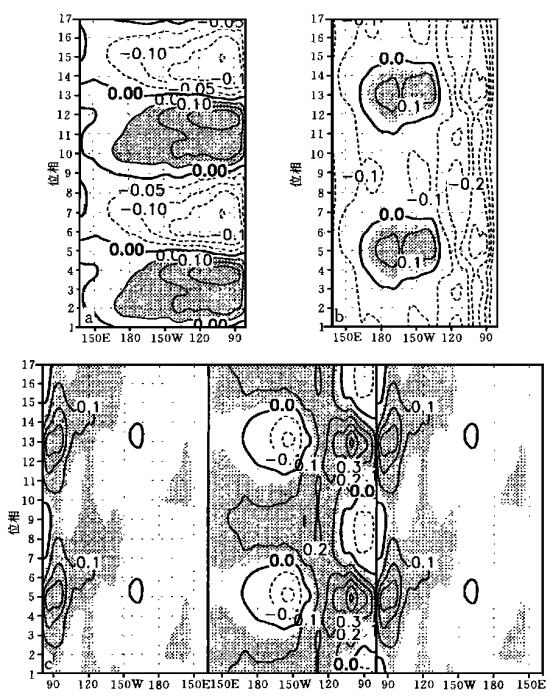
|
|
| 图 6. 位相合成后的 (a) SSTA总倾向, (b) 倾向方程中第7项贡献, (c) 倾向方程中第 8项贡献沿赤道 (5°N~5°S内平均, 中间图) 及沿10°S (7°N~13°S内平均, 两侧图) 的位相-经度剖面 (阴影区表示 ≥ 0.05 ℃/月) | |
(2) 暖态的消亡 (位相6、7) 图 6a表明, 在6、7位相时, 赤道中东太平洋呈显著的降温趋势, 降温率达-0.15~-0.2 ℃/月.通过比较可知, 对赤道中太平洋降温起作用的是第1、2项 (第2项量值为-0.1~-0.2 ℃/月), 而东太平洋地区主要是第7项的贡献 (图 6b).由图 4b可以看到, 在ENSO暖位相期, 热带太平洋东部有较强的东风异常, 它的存在加强了东部赤道上翻运动, 使得该处的异常上翻始终维持, 并随着El Niño的发展而增强, 由此带来的冷水上涌并向西平流使得成熟期之后的暖态逐渐减弱并趋于消亡.注意到图 6b与图 5b有很好的一致性, 而由图 6c看不到斜温层负距平信号东传并促使暖态消亡的现象, 因此, 暖位相位消亡与El Niño发展过程中太平洋东部不断增强的东风异常所产生的冷水上翻的加强以及纬向向西的冷平流有关, 而非“时滞效应”所致.
4 总结与讨论(1) 该模式能较好地再现热带太平洋ENSO年际变化的基本特征, 如赤道中东太平洋几年一次不规则的海水增暖, 与之伴随的大气风场、洋流、斜温层变化等.其时间变化、空间分布及水平结构演变均与观测比较相符.
(2) 模式ENSO循环的主周期为4~5年, 在准2年及年循环尺度上也有显著变化, 即模式可再现ENSO循环的多时间尺度特征.
(3) 模式ENSO循环中, 暖态的消亡与El Niño发展过程中东太平洋 (120°W以东) 不断增强的东风异常所产生的冷水上翻的加强以及纬向向西的冷平流有关; 冷态的消亡与冷态发展中赤道两侧西传的正Rossby波遇西边界反射形成的正Kelvin波的东传有关, 即“时滞效应”所致.
关于ENSO循环形成的机制, Suarez& Schopf (1989) 的结果[7]认为冷、暖态的消亡均是由西边界波反射效应造成, 而Battisti& Hirst (1988) [3]认为暖态的消亡主要由波反射效应引起, 冷态的消亡主要受热力衰减过程的作用, 可见, 本文的结论与他们有明显的差别.尽管如此, 可以肯定的是“时滞振子”假说在ENSO循环, 至少在ENSO循环的某一阶段承担着负反馈机制的作用, 这种作用在简单的海气模式中有, 在本文的混合海气系统中也有.此外, 我们用全球范围的大气环流模式与热带太平洋简单海洋模式进行耦合, 从理论上讲, 它比简单的海气模式多引入了热带外大气过程, 这对真实再现ENSO变化过程是十分重要的.对此, 我们将做进一步的探讨.
| [1] | Zebiak S, Cane M. A model El Niño-Southern Oscillation. Mon.Wea.Rev, 1987, 115: 2262–2279. DOI:10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2 |
| [2] | Philander S, Pacanowski R, Lau N, Nath M. Simulation of ENSO with a global atmospheric GCM coupled to a high-resolution tropical Pacific ocean GCM. J.Climate, 1992, 5: 308–329. DOI:10.1175/1520-0442(1992)005<0308:SOEWAG>2.0.CO;2 |
| [3] | Lau N, Philander S, Nath M. Simulation of ENSO phenomena with a low-resolution coupled GCM of the global ocean and atmosphere. J.Climate, 1992, 5: 284–307. DOI:10.1175/1520-0442(1992)005<0284:SOELPW>2.0.CO;2 |
| [4] | Neelin J, et al. Tropical air-sea interaction in general circulation models. Climate Dyn, 1992, 7: 73–104. |
| [5] | Neelin J, Battisti D, Hirst A, et al. ENSO theory. J Geophys.Res, 1998, 103, (c7): 14261–14290. DOI:10.1029/97JC03424 |
| [6] | Battisti D S, Hirst A C. Interannual variability in a tropical atmosphere-ocean model: Influence of the basic state, ocean geometry and nonlinearity. J.Atmos.Sci, 1989, 46: 1687–1712. DOI:10.1175/1520-0469(1989)046<1687:IVIATA>2.0.CO;2 |
| [7] | Suarez M J, Schopf P S. A delayed action oscillator for ENSO. J.Atmos.Sci, 1988, 45: 3283–3287. DOI:10.1175/1520-0469(1988)045<3283:ADAOFE>2.0.CO;2 |
| [8] | Wu Aiming, Ni Yunqi. A hybrid coupled ocean-atmosphere model and ENSO prediction study. Adv.Atmos.Sci, 1999, 16, (3): 1–12. |
| [9] | Wu Guoxiong, Liu Hui, et al. A nine-layer atmosphere general circulation model and its performance. Adv.Atmos.Sci, 1996, 13: 1–18. DOI:10.1007/BF02657024 |
| [10] | Zebiak S E.Tropical Atmosphere-Ocean interaction and El Nino/Southern Oscillation Phenomenon.Ph.D thesis, MIT, 1984, 261. |
| [11] | Rasmusson E, Carpenter T. Variations in the tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/El Niño. Mon.Wea.Rev, 1982, 110: 354–384. DOI:10.1175/1520-0493(1982)110<0354:VITSST>2.0.CO;2 |
 2000, 11 (4): 419-429
2000, 11 (4): 419-429

