随着气候模式的不断改进, 实现业务化指日可待.国家气候中心的T63动力延伸预报为我们提供了有一定预报技巧的月平均环流形势预报, 但通过检验分析, 其第2、3旬的预报仍有相当误差[1, 2], 所以必须对其进行解释应用, 对形势预报进行误差订正, 并转化为要素预报, 进而为短期气候预测提供指导产品.本文采用卡尔曼滤波法对500 hPa月平均高度预报场进行误差订正, 将订正后的预报场用于基于天气系统特征相似的预报模型, 制作东北区51个站点的定量的月降水预报.
1 资料的选用国家气候中心的T63动力延伸预报模式每旬旬末制作之后3个旬和1个月的平均高度预报.选取1996年1~12月、1997年1~9月逐旬T63动力延伸预报产品 (分辨率2.5°×2.5°) 及对应的500 hPa旬平均高度实况资料建立卡尔曼滤波误差订正模型.选取1951~1996年7、8月北半球500 hPa月平均高度资料 (分辨率10°×5°) 及对应的东北区51个站点的月降水资料建立降水预报模型.
2 用卡尔曼滤波法对T63动力延伸预报产品进行误差订正卡尔曼滤波法是一种统计估算方法, 通过处理带有误差的实际量测数据得到物理参数的最佳估算.它由前一次预报的误差根据递推公式对预报方程系数进行调整, 以提高本次预报精度, 所以能够适应模式的变化及季节的变化.卡尔曼滤波递推模型的建立不需太长的样本, 我们运用50个样品, 在20°~70°N, 60°~150°E范围内逐点建立递推模型, 逐点进行订正得到新的预报场.
2.1 订正公式[3]本文采用的订正公式为:
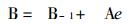
|
(1) |

|
(2) |
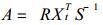
|
(3) |
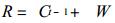
|
(4) |
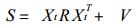
|
(5) |
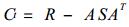
|
(6) |
其中Bt是t时刻的预报方程系数; e是预报误差; Yt是t时刻实况; Xt是t时刻预报因子; Ct-1是Bt-1的误差方差阵; W是动态噪声的方差; V是测量噪声的方差.
利用上面的递推关系, 根据前一步的参数和新增加的Yt, 就可推算出本步的Bt, 不断更新预报方程系数.
2.2 订正因子为充分考虑预报的系统误差 (包括时间和地理系统误差), 我们初选了8个预报因子, 它们分别为被订正格点及其周围最近4点的月高度预报值、被订正格点当月3个旬的预报值.根据相关性检验, 最后确定被订正格点月预报值、其右边一点月预报值、第2、3旬预报值作为订正因子.
2.3 递推初始参数的确定由订正公式, 卡尔曼滤波递推模型的建立需确定4个初始参数: B0、W、C0、V.
(1) B0的确定
B0是起步预报方程系数.根据50个样品, 建立线性逐步回归方程, 以其系数作为B0向量.
(2) W的确定
W是动态噪声方差.由白噪声假定, W是对角矩阵, 我们这里选取4个因子, 所以是5阶对角矩阵.将50个样品分为两组, 分别建立线性回归方程得到B0和B1向量, 由式 (7) 得到W各对角元素估计值.
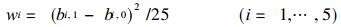
|
(7) |
式中25为两样本的时间间距.
(3) C0的确定
C0是B0的误差方差阵, 递推起步时, 可认为B0是精确的, C0为零矩阵.
(4) V的确定
V是量测噪声的方差, 由于只有一个预报量, 所以V是一个数值, 以回归方程的剩余标准差作为V值.
2.4 业务试验情况确定初始参数后, 根据卡尔曼滤波递推公式就可进行误差订正.我们对1996~1997年逐旬的月预报进行了误差订正.为检验订正效果, 我们计算了订正前后预报场的均方根误差、距平符号一致率、距平相关系数和副热带高压指数与实况的偏差.
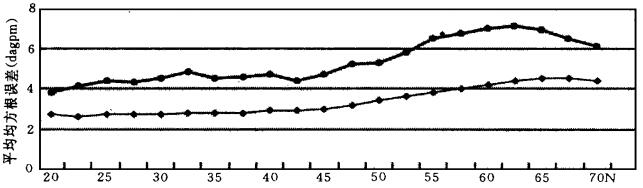
图 1为订正前后平均均方根误差随纬度的分布曲线.可以看出订正后的误差明显小于订正前的误差; 随着纬度的增加, 两条曲线的误差都逐渐增大, 而订正后的曲线变化更为平缓; 误差最大值都出现在天气系统转换频繁的65°N附近.图 2为1996、1997年7、8月逐旬月预报订正前后副热带高压指数与实况的偏差.可以看出T63动力延伸月预报副热带高压预报明显偏强, 订正后的强度略偏弱, 但绝对偏差明显减小.从订正前后准确率对比 (表 1) 可以看出, 经误差订正后3项准确率指标均明显改善, 平均均方根误差由5.09 dagpm下降为2.95 dagpm; 平均距平符号一致率由59.7%上升为79.3%;平均距平相关系数由0.368上升为0.777.另外我们对每个个例订正前后的预报场和实况场进行了对比, 发现订正后的天气系统不论是位置还是强度更接近实况, 订正效果非常明显.
|
|
| 图 1. 卡尔曼滤波误差订正前后平均均方根误差随纬度的分布 (圆点表示订正前, 菱形表示订正后) | |
|
|
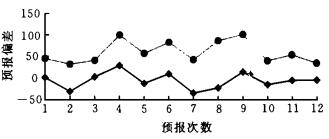
| 图 2. 1996、1997年7、8月逐旬月预报订正前后副热带高压指数与实况的偏差 (说明同图 1) | |
|
|
表 1 卡尔曼滤波误差订正前后准确率平均值对比 |
3 由同期500 hPa月平均环流建立月降水模型
动力气候模式为我们提供了未来一个月的平均环流场, 所以我们从相关性更好的同期500 hPa月平均环流建立月降水模型.采用EOF展开分析法对东北区夏季月降水分布进行分型, 分析各降水型500 hPa天气系统特征, 运用天气系统自动识别技术定性判断订正后的预报场所属降水型, 结合相似离度指数的计算, 定量确定各特征向量的时间系数, 进而得到各站点的定量降水.由于国家气候中心的T63动力延伸预报模式每旬末制作下1个月的预报, 所以在释用中也是制作相应时段的降水预报.
3.1 对东北区夏季降水场进行EOF展开对气象要素场进行EOF (自然正交函数) 展开, 不但能够得到其客观分型, 而且能够通过对时间系数的预报作出对气象要素场的预报.通过对1951~1996年东北区夏季7、8月降水距平百分率的EOF展开分析表明, 特征值最大的前两个特征向量的累积方差贡献占全部51个特征向量总方差贡献的53.9%, 前4个占66.5%, 其余特征向量的方差贡献很小且很分散.第1特征向量分布特征为全区同符号, 第2特征向量分布特征为南北符号相反.这样我们根据前两个特征向量将东北区夏季降水分布划分为5型:全区一致多、全区一致少、南多北少、南少北多、正常.同时我们还能得到各降水型的平均时间系数和各个例的时间系数.
3.2 各降水型500 hPa天气系统特征分析月平均环流反映了该时段大气平均运动状况, 其平均槽区反映了该地区为低槽活动的高频率区域, 在相当程度上也反映了该时段非绝热过程的影响.我们首先从月平均环流与东北降水区降水距平百分率的同期相关分析入手, 结合预报经验, 发现东北区夏季降水与同期平均环流场的副热带高压、乌拉尔山以东地区系统 (西槽)、东北区及其上游系统 (东槽) 关系最为密切, 而与印缅低压、极涡中心位置关系不太显著[4].
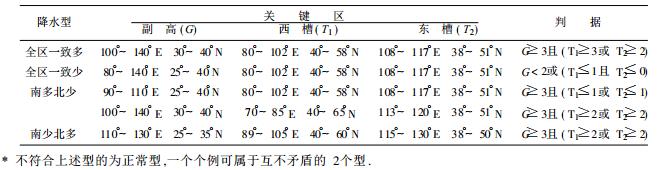
根据EOF展开时间系数, 结合降水距平百分率, 得到各降水型的典型个例.对各型典型个例的500 hPa月平均环流场从以上3方面进行分析, 得到各型的天气系统特征.副热带高压由关键区的面积指数G (> 5880 gpm点数) 表示, 低槽由关键区的强度T (与标准等值线的交点数) 表示, 这样不但反映了系统的位置, 也反映了系统的强度.
从表 2可以看出:全区一致多环流特征为副热带高压偏北、偏强, 欧亚中高纬关键区有低槽配合; 全区一致少环流特征为副热带高压偏弱, 欧亚中高纬关键区无低槽; 南多北少环流特征为副热带高压偏西、偏北, 蒙古东部维持低槽; 南少北多环流特征为副热带高压偏南, 东北区多冷涡影响.
|
|
表 2 各降水型天气系统关键区位置及判据 |
为检验历史拟合情况, 我们根据上述判据对1951~1996年7、8月份降水进行反算, 拟合率达99.0%, 其中典型个例完全正确, 只有2个属于正常型的个例判断错误.为保证业务系统完全客观自动, 我们运用天气系统自动识别技术, 对订正后的预报场的高低压、槽脊进行自动识别, 这样根据前面各降水型的环流特征, 就可定性判断预报场所属环流型.
3.3 用相似离度指数定量确定预报时间系数相似离度指数既能反映两个场“形”的相似程度, 又能反映“数”的相似程度.为得到预报场的时间系数, 我们在前面定性判定降水型的基础上, 进一步采用相似离度指数定量确定预报场与所属环流型的相似程度.
设i, j两个场有相同的元素分布, 经极值标准化处理后, 其元素分别为xik (k=1, …, m), xjk (k=1, …, m), m为元素个数
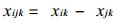
|
(8) |
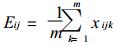
|
(9) |
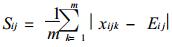
|
(10) |
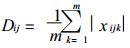
|
(11) |
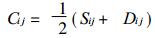
|
(12) |
Cij为i, j两个场的相似离度指数.
若天气系统特征预报场符合一个降水型, 则由式 (8)~(12) 计算预报场与该型逐个例的相似离度指数cj, 由式 (13) 确定各个例的权重系数Wj, 由式 (14) 得到各特征向量的预报时间系数Ti; 若符合多个降水型, 则计算预报场与它们的平均环流场的相似离度指数, 由式 (2) 确定各型的权重系数Wj, 由式 (14) 得到预报时间系数.最后把预报场的时间系数回代EOF展开模型, 得到东北区51个站定量的降水预报.
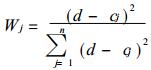
|
(13) |
d为常数, 可取为cj中最大值与最小值之和; n为个例 (或型) 数.
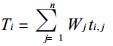
|
(14) |
ti, j为第i特征向量、第j个例 (或型) 的时间系数.
4 业务预报流程应用前面的方法, 我们建立了完全客观、自动的月降水预报流程.
(1) 根据建立的卡尔曼滤波递推模型, 对T63动力延伸预报产品进行误差订正.
(2) 采用天气系统自动识别技术 (由于篇幅, 本文未介绍), 对订正后的500 hPa月平均高度预报场进行系统识别.主要包括高空槽及副热带高压的识别.
(3) 根据前面总结的各降水型500 hPa天气系统特征及订正后预报场系统特征, 判断预报场所属降水型.
(4) 若预报场符合一个降水型, 则计算预报场与该型逐个例的相似离度指数, 确定各个例的权重系数, 得到各特征向量的预报时间系数; 若符合多个降水型, 则计算预报场与它们的平均环流场的相似离度指数, 确定各型的权重系数, 得到预报时间系数.
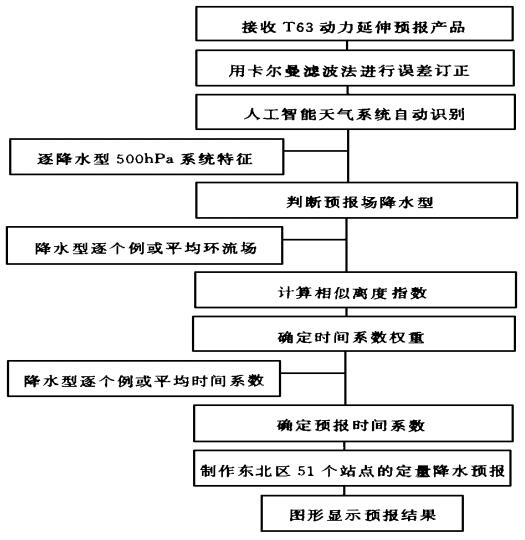
(5) 将预报场的时间系数回代EOF展开模型, 得到东北区51个站定量的降水预报.图 3是系统预报流程图.
|
|
| 图 3. 东北区夏季降水释用方法预报流程图 | |
5 预报试验分析
运用1996~1998年6、7月下旬的T63动力延伸预报产品, 对东北区7、8月降水进行了预报试验, 并采用目前长期预报业务评分标准, 对预报结果进行了TS评分.
TS=(预报正确站数/总预报站数)×100%
表 3为对预报试验结果进行的TS评分, 可以看出都超过了60%, 最高达73%, 略高于日常业务预报, 所以预报试验效果还是比较好的.
|
|
表 3 1996~1998年预报试验TS评分表 |
6 结语
(1) 运用卡尔曼滤波法对T63动力延伸预报产品进行误差订正可取得很好的效果, 均方根误差明显下降, 环流形势更接近实况.
(2) 动力气候模式产品的应用, 使我们只需从相关性更好的同期500 hPa环流场出发建立预报模型.我们采取的天气系统特征定性判断与相似离度指数定量相似相结合的降水型判别方案, 不但能够从宏观上把握天气形势, 物理意义更为明确, 而且使预报结果定量化、定点化.
(3) 由于当前气候模式的预报水平所限和提供产品的单一性, 单独对其解释应用很难达到理想的预报结果, 所以综合运用各种资料建立预报模型是提高预报精度的重要途径.
致谢 李维京博士为本项研究提供了资料和技术指导, 谨表谢意!| [1] | 李小泉, 李维京. 500 hPa平均环流形势月预报的水平的评估. 应用气象学报, 1994, 5, (4): 69–75. |
| [2] | 张存杰, 董安祥. 对T63L16所作延伸预报准确率的评估. 气象, 1998, 24, (10): 38–39. |
| [3] | 陆如华, 何于班. 卡尔曼滤波在天气预报中的应用. 气象, 1994, 20, (9): 41–43. |
| [4] | 朱其文.东北地区夏季冷暖的环流型客观预报方法.东北短期气候研究.北京:气象出版社, 1998.88~98. |
 2000, 11 (3): 348-354
2000, 11 (3): 348-354