2. 中国气象科学研究院, 北京 100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081
早在70年代初期, Madden和Julian[1]就利用1957~1967年Canton岛的10年观测资料, 通过谱分析的方法首先发现热带大气风场和气压场变化中存在着40~50天周期的低频振荡.后来广泛而深入的研究又证实在全球热带地区都存在着40~50天周期的低频振荡.
中高纬度地区低频振荡的存在最早可见于Anderson等[2]关于角动量输送的研究中, 后来, Krishnamurti等[3]指出30~60天的周期振荡是一种全球大气变化现象.广泛的研究[4]表明:中高纬度大气的低频振荡具有正压结构, 且呈现二维波列的特征.
1 基本方程组考虑青藏高原存在地形高度hs (x, y)、摩擦和非绝热加热Q, 浅水模式方程组可以写为:
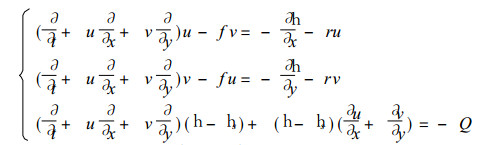
|
(1) |
式中假设摩擦为Rayleigh摩擦, 即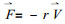
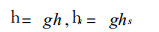
|
分别表示自由面高度h (x, y, t) 和地形高度hs (x, y) 上的重力位势.
方程组 (1) 的获得已经应用了含地形的下边界垂直运动Ws的条件, 即z=hs (x, y) 有
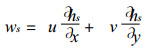
|
上式右端第1项主要表征大地形的气流爬坡作用.在中高纬度的自由大气, u > 0, 则在大地形的西侧 (迎风坡), 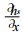
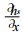
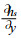
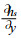
对于青藏高原的大地形, 通常认为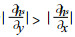
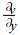
大量的观测事实表明:青藏高原在夏季是热源, 高原的温度高于附近空气的温度.正由于此, 夏季的高原有利于水平辐合抬升.
基于上述分析, 我们把方程组 (1) 中的非绝热加热Q表示为:
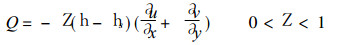
|
其中Z为加热强度系数
这样, 包含地形坡度、摩擦和加热的浅水模式方程组 (1) 可以写为:
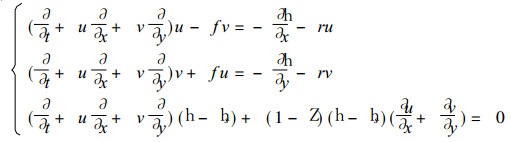
|
(2) |
该方程组的准地转模式方程组为:
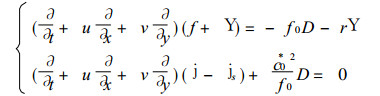
|
(3) |
其中
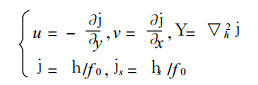
|
D为一级近似的水平散度, c0*2=(1-Z)c02, c02=g (H-Hs), H和Hs分别为自由面和大地形的平均高度.
方程组 (3) 的两个方程消去D, 得到
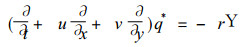
|
(4) |
其中
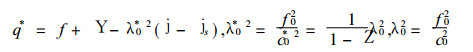
|
方程 (2)、(3) 和 (4) 就是我们分析青藏高原大地形动力、热力作用与低频振荡的基本方程.
2 缓变波包分析假定物理量分解为沿纬圈平均的基本部分 (记为“-”) 和扰动部分 (记为“′”), 即
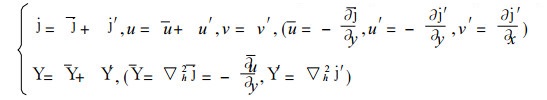
|
上式代入方程 (4), 得到线性化的扰动方程为
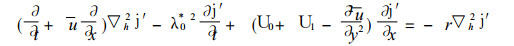
|
(5) |
其中U0为Rossby参数的特征值, 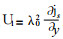
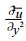
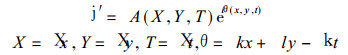
|
(6) |
X为小参数, k和l分别是x和y方向上的波数, k为圆频率, θ为位相函数.式 (6) 代入方程 (5), 再应用小参数方法, 令
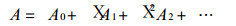
|
这里A0, A1, A2, …分别表示A的零级、一级、二级……近似.
这样, 我们求得 (5) 的零级近似方程为
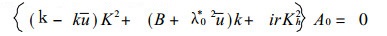
|
因A0≠0, 则求得频散关系为
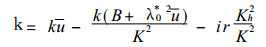
|
(7) |
其中:Kh2=k2+l2; K2=Kh2+λ0*2
由式 (7) 看到, 摩擦明显地起耗散的作用, 若忽略摩擦, 则式 (7) 化为:
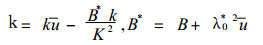
|
由此求得x方向上的相速度cx为
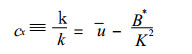
|
x和y方向上的群速度cgx和cgy分别为
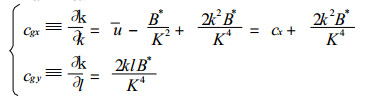
|
(8) |
由式 (8) 我们求得

|
其中: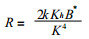
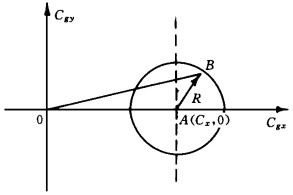
在 (cgx, cgy) 的平面图上, 上式表示以A (cx, 0) 为圆心, 半径为R的圆, 见图 1.在图中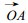
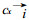
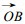
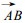
|
|
| 图 1. 方程 (8) 的几何解释 | |
式 (5) 的一级近似方程为:
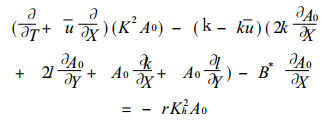
|
(9) |
引入Rossby波的波能密度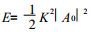
则方程 (9) 可以化为
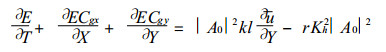
|
(10) |
而且不难求得
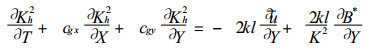
|
(11) |
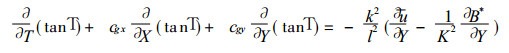
|
(12) |
其中: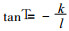
对于有限区域E内的扰动, 设扰动在区域边界上为零, 则式 (10) 积分得到
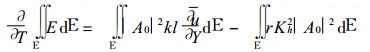
|
由此便知, 摩擦恒使有限区域内的扰动能量减小, 而Rossby波的螺旋结构和纬向基流的配置决定了扰动能量的变化.对此, 曾庆存[5]已作了详尽的研究, 这里不再叙述, 我们重点阐述大地形对Rossby波的影响.
考虑到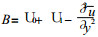
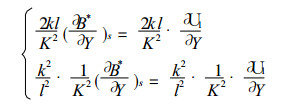
|
由于大地形南坡U1 > 0, 北坡U1 < 0, 因而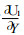
利用式 (6), 我们不难求得动量的经向输送能量的零级近似为
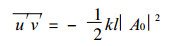
|
因而在低纬的风速的低频变化可以通过向北的动量输送, 形成中高纬度风速的低频变化.
3 低频振荡分析我们应用方程组 (2) 来分析高原对低频振荡的影响.为了滤去高频波, 我们引进滤波参数W, 又不考虑摩擦, 则方程组 (2) 化为
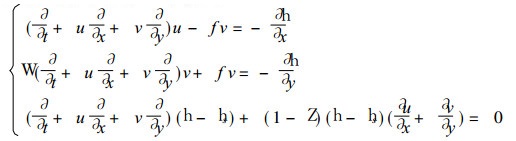
|
(13) |
W=0称为低频近似或长波近似, 令
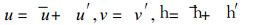
|
(14) |
显然有

|
在上式中, 取f=f0, u=常数, 
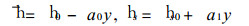
|
其中h0和hs0为y=0处的h和hs, 且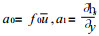
式 (14) 代入方程组 (13), 得到线性化的方程组:
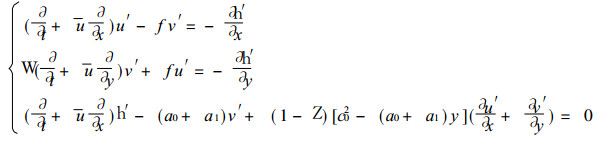
|
(15) |
其中c02=h0-hs0≈g (H-Hs).
方程组 (15) 的头两式消去h′, 得到
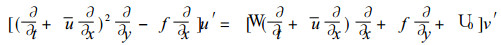
|
(16) |
方程组 (15) 的第一、第三两式消去h′, 得到
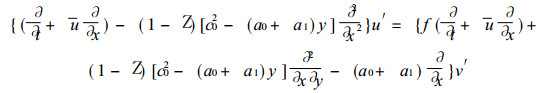
|
(17) |
(16) 和 (17) 两式消去u′, 得到
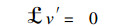
|
(18) |
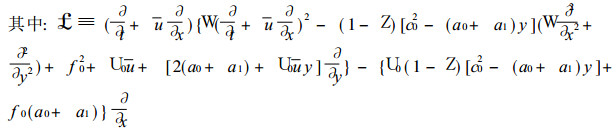
|
(19) |
为了滤去高频波, 我们取W=0, 则式 (19) 化为
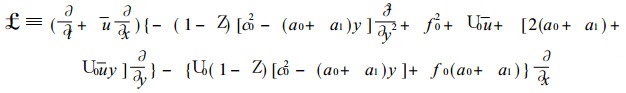
|
(20) |
由此可见, W=0也就是低频近似或者x方向的长波近似.
下面, 我们求解方程 (18), 其中算子£为式 (20).分两种情况说明:
(1) u=0
此时的式 (20) 化为
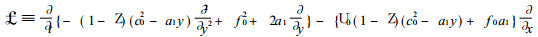
|
(21) |
① 若不考虑a1y和
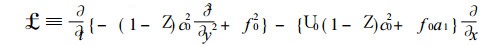
|
(22) |
此时的方程 (18) 为常系数方程, 可令
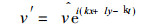
|
(23) |
其中k和l分别是x和y方向上的波数, k为圆频率.
式 (23) 代入方程 (18) (算子用 (22)) 求得
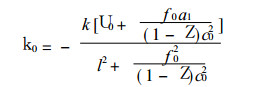
|
(24) |
这就是含地形、地形坡度和地形加热的长Rossby波的圆频率.
在无地形 (c02=gH≡c002)、无地形坡度 (a1=0) 和无地形加热 (Z=0) 时, 式 (24) 化为
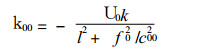
|
这就是一般长Rossby波的圆频率.
若考虑平均地形, 即a1=0, 但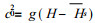
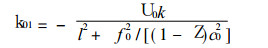
|
(25) |
因为 (1-Z) c02«c002, 因而
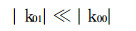
|
由此可见, 地形本身和地形加热有利于低频波的形成.
至于地形坡度a1, 由式 (24) 知, 它影响k0的大小.不过通常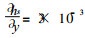
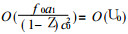
② 若不作简化, 此时可令

|
代入方程 (18) (应用算子 (21)) 得到
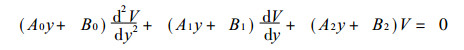
|
(26) |
其中
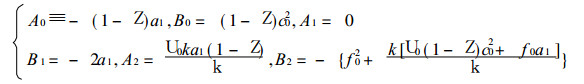
|
若无地形坡度, a1=0则A0=B1=A2=0, 方程 (26) 化为
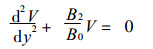
|
若B2/B0=l2, 则得到式 (25).
考虑地形坡度, 方程 (26) 为Laplace型方程, 若令
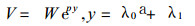
|
其中
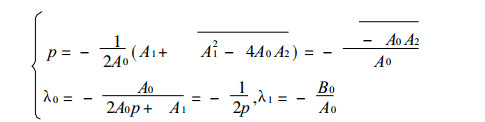
|
则方程 (26) 化为下列合流超比方程
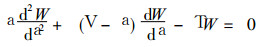
|
(27) |
其中
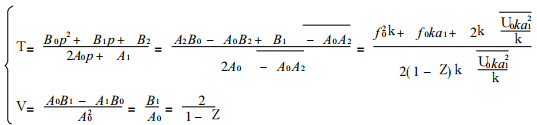
|
(28) |
方程 (27) 满足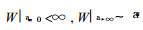
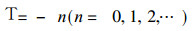
|
(29) |
相应的本征函数为
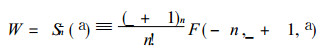
|
其中
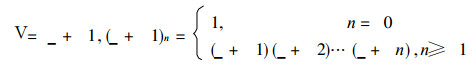
|
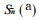
式 (28) 中的T代入到式 (29) 得到
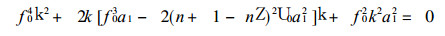
|
由此求得
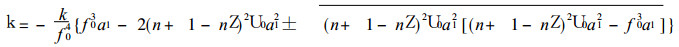
|
从上式看到, 考虑了地形坡度和地形加热不但会改变k的数值, 而且会影响Rossby波的稳定性.地形加热强度越小, Rossby波越易稳定, 北坡 (a1 < 0) 一定是稳定的, 南坡 (a1 > 0) 只有满足条件
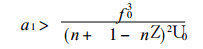
|
才是稳定的, 而且a1的数值越大, Rossby波越稳定.
(2) u≠0
此时, 若不考虑 (a0+a1) y和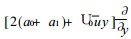
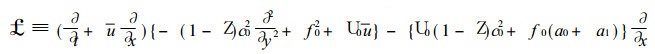
|
此时的方程 (18) 为常系数方程, 以式 (23) 代入, 求得
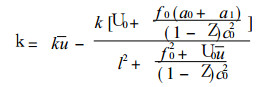
|
这就是存在基本气流的情况下, 含地形、地形坡度和地形加热的长Rossby波的圆频率, 而波的周期为
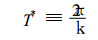
|
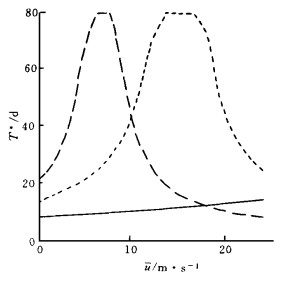
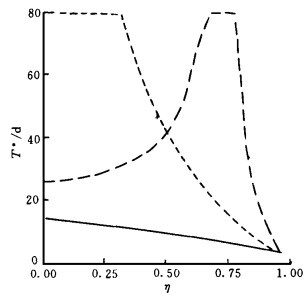
由此, 我们可知T随u, a1和Z的变化而变化.图 2, 图 3和图 4分别给出了T*随u, T随a1和T*随Z的变化.从图 2可看出, 在一般加热情况 (取Z=0.5), a1=0.01 m·s-2, 纬向2波在u=10~15 m·s-1, 纬向3波在u=5~10 m·s-1有利于季节内振荡.从图 3可看出:在一般加热 (取Z=0.5) 和一般西风 (取u=10 m·s-1) 情况下, 地形坡度均有利于季节内振荡的形成, 特别是南坡的3波情况更是如此.从图 4看出:在一般西风 (取u=10 m·s-1) 和平均地形坡度 (取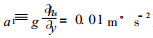
|
|
| 图 2. T*随u的变化 (u > 0) (实线、点线、虚线分别表示纬向波数1, 2, 3, 周期超过80天的点均取为80天) | |
|
|
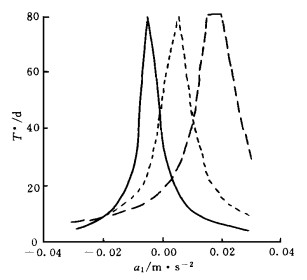
| 图 3. T*随a1的变化 (说明同图 2) | |
|
|
| 图 4. T*随Z的变化 (说明同图 2) | |
| [1] | Madden R D, Julian P. Detection of 40-50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci, 1971, 28: 702–708. DOI:10.1175/1520-0469(1971)028<0702:DOADOI>2.0.CO;2 |
| [2] | Anderson J R, Rosen R D. The latitude height structure of 40-50 day variations in atmospheric angular momentum. J. Atmos. Sci, 1983, 40: 1584–1591. DOI:10.1175/1520-0469(1983)040<1584:TLHSOD>2.0.CO;2 |
| [3] | Krishnamurti T N, et al. On the structure of the 30-50 day mode over the global during FGGE. Tellus, 1985, 37, (A): 336–360. |
| [4] | 李崇银. 大气低频振荡. 北京: 气象出版社, 1993. |
| [5] | Zeng Qingcun (曾庆存). On the evolution and interaction of disturbances and zonal flow in rotating banotropic atmosphere. J. Meteor. Soc. Japan, 1982, 60:24~31. |
| [6] | 叶笃正, 高由禧. 青藏高原气象学. 北京: 科学出版社, 1979: 278. |
 2000, 11 (3): 312-321
2000, 11 (3): 312-321

