2. 兰州大学大气科学系, 兰州 730000
在对微分方程初值问题的数值计算中, 当采用前向或后向差分格式时有两个时间层次, 而当用中央差分格式时则有3个时间层次.由于把预报问题提为初值问题, 因此只有一个初始场的信息被利用.本文从扩展信息源的角度出发, 对微分方程的时间积分提出了一种新格式——回溯时间积分格式, 并对在大气、海洋、水文等常用的平流方程进行了实例计算.
制约动力系统的微分方程可以写为:
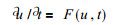
|
(1) |
其中, u为状态变量, F为除局地变化项外的所有项, 称为源函数, 设时间间隔为△t, 式 (1) 的时间中央差格式为:
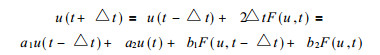
|
(2) |
其中a1=1, a2=0, b1=0, b2=2△t, 式 (2) 从计算流体力学来看是很自然的, 但从信息论来看, 系数a2、b1取为0是很可惜的, 等于抛弃了u (t) 和F (u, t-△t) 中对预报有用的信息.所以, 我们将时间层次p′推广到p′=p+1=3以上, 即有回溯时间积分格式
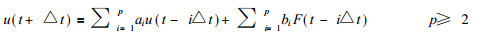
|
(3) |
式中p为回溯阶, 系数ai、bi可以半理论半经验确定, 也可用观测数据藉最小二乘、遗传算法等确定.
平流方程为:
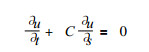
|
(4) |
其中s表示空间坐标, C为常定平流速度.
其回溯格式为
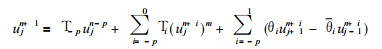
|
(5) |
式中T-p, Ti, θi和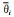
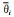
当对系数取随回溯时次 (t-i△t) 呈指数衰减形式时, 运用经典的von Neumann方法, 我们从数学上证明了当取p=2时回溯格式的稳定性, 其稳定域比蛙跃格式要大.
数值计算是对由正弦和余弦组成的理想场进行的.结果表明, 回溯格式比蛙跃格式其精度要高2~5倍.回溯阶p取3~5为宜.
理想气流场由
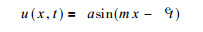
|
(6) |
计算得出, 式中

|
其中m为波数, c为波速.
取△t=1 h, 先用式 (6) 计算48 h作为样本场, 即取样本量N=48.用最小二乘法求出系数Ti, θi和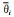
|
|
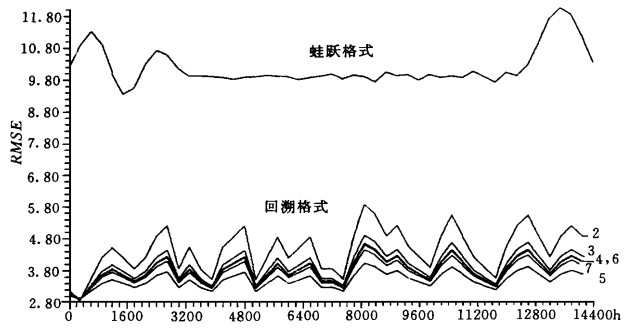
| 图 1. 积分流场与理想流场之间误差随积分时间的变化 (回溯格式中2表示回溯阶p=2, 其中p=4和6的RMSE曲线几乎重合, 以p=5的RMSE最小) | |
 2000, 11 (2): 249-250
2000, 11 (2): 249-250

