气候变化研究的基础是均一性的长序列数据.然而由于仪器变动, 站址迁移, 观测方法改变, 常会使序列数据产生非均一.国外许多气候学家在研究判断非均一的方法并应用于具体气候数据方面做了大量工作[1~3], 取得了重要进展[4].我国气候学工作者近年来在降水、气温、探空资料的均一性检验方面也做过一些探讨[5-7].
风是重要的气候要素之一, 它不但可以反映大气环流的特征, 也是各地气候资源的主要项目.交通运输、城市建筑、桥梁水库建设、市政规划设计、风能资源开发均需要风的统计数据.解放以来我国已积累了长时期风速观测数据.风的观测仪器在近40年间发生过重大变化, 其对风的均一性产生多大影响, 是许多学者及实际应用者关注的问题.年平均风速是逐年振动很小的气象要素, 检验其逐年平均记录, 更容易检查出由于台站迁移、周围环境变化引起的非均一[8].因此, 年平均风速均一性检验不仅能给风要素做出质量评估, 也为测风仪器换型提供参考.
1 检验方法在通过观测形成的气候资料序列中, 包含有气候变化、气候趋势的有关信息, 这些气候变化、气候趋势的信号可能会导致错误的结论, 因此作非均一性检验时, 应首先对原始序列进行“过滤”, 以便删除序列中气候变化或趋势的信号.有关“过滤”的方法, 国外许多学者进行过深入的研究, 其中有差值法、比值法、回归法等, 即选取邻近站作为参照序列, 利用被检验站与参照站序列, 经过处理, 形成新的被检序列, 然后通过非均一性检验方法, 显露被检站序列的非均一.
本文采用的SNHT (Standard Normal Homogeneity Test) [9]方法.是利用邻近站作为参照站, 用被检站与参照站的比值作为被检序列来检验非均一的参数检验法.
产生风速非均一的重要原因是仪器的变化.在我国1967~1970年间风的观测仪器发生过重大变化, 为了避免被检站与参照站同时换型的影响, 本文从每个被检站邻近的30个站中挑选5个与被检站相关系数最高的站, 用其加权平均值作为参照序列.这5个站在同一年份换型的机率很小, 避免了由于换型造成间断的情况.
1.1 资料序列的预处理对于被检验站年平均风速序列xi作如下处理:
f (xi)=xi/x, x为被检验站风速的平均值.
对于参照站函数g (yi), 用k个参照站的加权平均求取, 本文采用相关系数平方作为加权因子.即
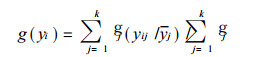
|
其中gj=rj2, rj为被检验站与第j个参照站之间的相关系数. 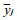
由年平均风速序列, 求出其比值序列qi:
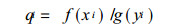
|
对qi序列进行标准化处理, 形成zi序列:
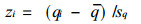
|
其中q为比值序列qi的算术平均值, sq为该序列的标准差.
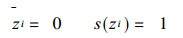
|
(1) |
即zi序列呈平均值为0, 标准差为1的正态分布.
1.2 序列假设检验(1) 如果{zi}序列无间断点, 统计检验为:零假设Ho:z∈N (0, 1)∀i
(2) 如果{zi}序列有一间断点且出现在序列ν处, 统计检验为:
H1:对某些1≤ν≤n和μ1≠μ2有
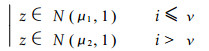
|
(2) |
这里z∈N (0, 1) 为正态分布, μ1和μ2分别为间断点ν前后两个序列的平均值, ν为假设的间断点, n为样本数.
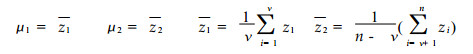
|
(3) |
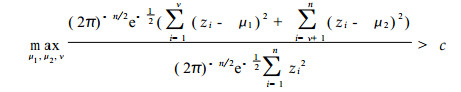
|
(4) |
将式 (3) 代入式 (4)
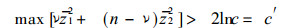
|
(5) |
令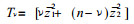
可构造检验统计量
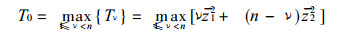
|
(6) |
根据式 (6) 可计算出检验统计量T序列, T0为该序列的最大值.当T0大于某临界值水平T95, 则该序列为该水平上的非均一, 临界值与序列长度 (n) 有关. SNHT方法中给出了T0的临界值表, 其n值从25到600, 本文为适应我国资料长度, 采用内插方法列出了n从25到41的T90、T95值 (表 1), 选用临界值T95检验非均一.
|
|
表 1 不同N值下的T90、T95值 |
2 检验前的数据处理 2.1 正态转换建立初始序列
使用比值法进行风速序列非均一性检验, 要求原序列必须服从正态分布, 但是许多研究表明, 风速并不服从正态分布, 而是正偏态分布[10], 其在统计性质上有两个明显特征, 一是它的取值在一端是有界的, 如风的最低值是零, 即静风.二是它的频率分布具有明显的不对称性, 它的概率分布通常为韦布尔分布.本文采用文献[9, 11, 12]的方法, 对原始序列进行正态转换.
2.2 正态检验根据变量分布检验方法[13], 对某一变量作正态检验.首先假设其遵从正态分布, 计算序列的偏态系数及峰态系数, 在显著性水平α=0.05下若偏态系数和峰态系数
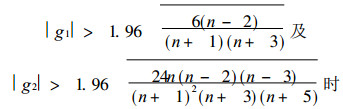
|
则拒绝假设, 认为变量不服从正态分布, 否则可认为遵从正态分布.
根据以上检验方法, 对建立的初始序列进行正态检验.
3 检验过程(1) 选用参照站 对每一个被检验站, 首先计算其与邻近30个站的相关系数, 从中选出5个相关系数最高的站.每个站均通过了相关系数的显著性检验 (T=0.05).
(2) 形成被检验序列 用这5个站的平均值作为参照序列, 根据检验方法, 求出检验系列与参照序列的比值并进行标准化处理后作为被检验原始系列.
(3) 正态转换 计算被检验原始序列的偏态系数及峰态系数, 并进行正态检验, 如通过检验, 则认为被检验序列基本为正态分布, 可不进行转换而直接检验.否则, 则用以上3种正态转换方法分别进行转换, 用具有最小偏态系数的序列作为被检验序列.
(4) 淘汰非正态序列 如果经过转换及正态检验仍未通过, 则认为该序列为非正态, 不作该站的检验.
(5) 均一性检验 对被检验序列进行检验, 当检验统计量超出临界值水平时, 认为该系列为该水平上的非均一, 找出间断点, 即间断年份.
(6) 查找间断原因 根据间断年份, 查阅台站历史沿革, 判断产生间断的原因及间断的真实性.
4 检验结果对全国690个站1951~1990年年平均风速数据进行了检验, 结果如下:
(1) 690个站中, 通过3种转换仍为非正态分布的站有343个, 占总数49.7%, 即有约一半的站未检验.
(2) 在已检验的347个站中, 原始序列服从正态分布的站有171个, 占被检验站的49.3%, 经过指数转换而为正态的站有111个, 占32.0%, 经平方根转换为正态分布的站有13个, 占3.7%, 经韦布尔分布转换为正态站有52个, 占15.0%.
(3) 347个被检验站有70个站有间断, 占被检验站的20.1%, 有277个站为均一, 占80%.
(4) 70个有间断的站中, 由于仪器变化而间断的站有47个, 占67.1%, 因迁站而间断的有11个, 占15.7%, 原因不明的有12个, 占17.1%,
(5) 在47个由于仪器变化而间断的站中, 由于换型造成间断的站有8个, 占17.0%, 由于更换仪器造成间隔的站有25个, 占53.2%, 由于仪器高度变化而间断的站有14个, 占29.8%.
5 检验结果分析(1) 风速分布特征 根据有关研究[14], 风速的概率分布是二元正态分布、韦布尔分布、瑞利分布, 且三者紧密联系.本次检验中, 相当多的站近似于正态分布, 或通过韦布尔分布转换后成为正态分布.对于不服从正态分布的站, 没有做检验.这部分站的检验有待于寻找一种更适合的方法.
(2) 平均风速质量 本文共检验343个站, 分布于全国各省, 具有一定的代表性.基本能反映我国年平均风速的质量情况.在已检验的343个站中, 约有80%的站是均一的.这说明虽然我国在风观测中仪器发生过重大变化, 但对大部分站未造成大的影响.平均风速资料质量基本是可靠的.
(3) 方法的适用性 在已找出间断年份的站中, 约有82%的站有明显的原因.说明已判断出的间断年基本是可靠的.同时说明该方法能较好的找出序列的非均一.在平均风速的均一性检验中此方法是适用的.
(4) 仪器变化是平均风速序列非均一的主要原因 国外研究表明, 台站历史沿革 (metadata) 在气候变化研究及判断系列非均一性中有着重要作用[15].因而WMO特别强调各国建立metadata的档案.本研究借助我国积累的台站地面气象记录月报 (即气表 1) 中较详细的原始记录, 查阅了每一个产生非均一台站每一个间断年的当年及其前、后一年各月仪器栏、备注栏、台站高度、地理环境等有关信息, 分析判断产生系列非均一的原因.结果表明, 本次查找产生非均一的站, 有67.1%的站是由于仪器变化引起.说明仪器变化是平均风速非均一的主要原因.风速对仪器变化及迁站很敏感, 尤其是仪器变化, 这与国外有关研究检验结果是一致的[15], 同时也进一步反映了metadata的重要性.
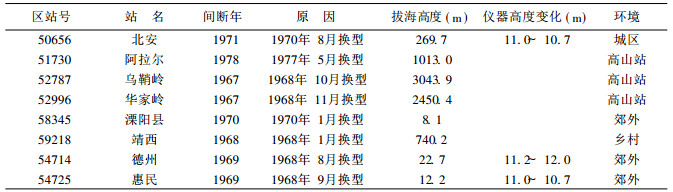
(5) 仪器换型与台站类型的关系 我国在1967~1970年间由风压板换型为EL型电接风, 所造成的非均一仅占仪器变化的17.0%.仪器换型引起的非均一站多为高山、高原或山区站 (表 2).其原因[16]是我国风压板是根据1010.6 hPa (气温15 ℃) 情况下的空气密度将风压转换成风速的.风压板指针全国统一, 并无高山平原之别.而在高山上的空气密度显著比平原小.我国高山、高原并未对风速进行密度订正, 造成风速误差.同时风压板在山区气流非水平时, 所测风速也偏大.因为风压板的齿针位置依据水平气流设计, 在山区气象站迎风坡上, 沿坡而上的气流带着向上分量抬起风压板, 发生偏差, 坡度大于10°的地形偏大得更多.风速越大, 偏差也越大.本次由于换型引起中断的8个站中有3个站为高山站, 占37.5%, 另有3个站在换型中高度发生了变化.
|
|
表 2 换型站间断情况 |
(6) 仪器更换的影响 在长期观测中, 虽然仪器没有换型, 但同一型号的仪器更换也易造成非均一.这部分台站占仪器变化引起非均一台站的53.2%.其原因是在更换仪器前, 原仪器已发生了故障, 所测数据偏差较大.在日常观测中, 应随时注意仪器的维护, 按规范要求检查仪器.
(7) 仪器高度变化的影响 检验结果表明, 虽仪器高度变幅不大, 但其变化也不容忽视.根据研究[17], 在平坦开阔地区, 风速随高度变化近地层垂直分布可采用对数律模式, 即
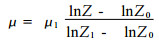
|
式中μ为Z高度处的风速, μ1为Z1高度处的风速. Z0为下垫面的粗糙度, 在平坦地面最低Z0=0.001 cm, 而在城市最高Z0=200 cm, 次高在市镇Z0=100 cm.
由于风速与高度及粗糙度有关, 因此, 测风仪高度变化, 在不同地区变化幅度不同.在市镇和城市, 变幅在11%~16%.根据我国地面气象观测规范[18], 距地高度10~12 m时, 风速器感应高度为允许范围.但“规范”未规定变化范围, 根据公式, 当Z0=0.001 cm时, 仪高由10 m变化12 m时, 变化幅度为0.2%.在城镇, Z0=100 cm, 变化幅度为7%.在城市Z0=200 cm, 变化幅度达11%.
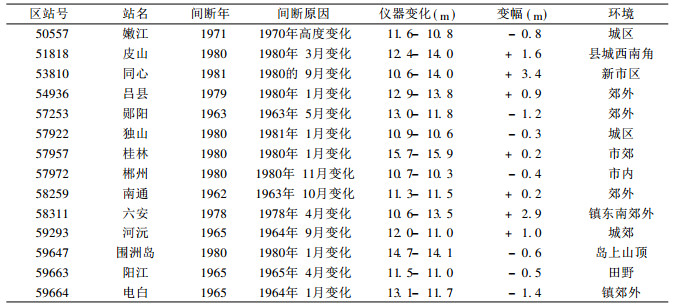
由表 3可看出, 在14个站中有4个站其环境为“城区”, 且变幅最小在0.2 m, 最大变幅达3.4 m.在7个非城区但超过`规范’规定的仪器高度范围的站中, 仪器高度的变幅最大达2.9 m. 14个站平均变幅达1.1 m.说明仪器高度及高度变幅的影响不容忽视.
|
|
表 3 仪器高度变化站间断情况 |
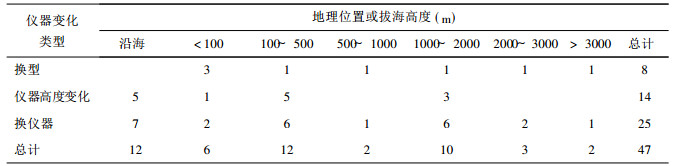
(8) 沿海及高山站对仪器变化的敏感性 分析由于仪器变化产生非均一的台站的地理分布 (图略), 发现沿海台站及海拔高度为1000 m以上的台站对仪器变化更敏感 (表 4).在47个由于仪器变化引起非均一的台站中, 沿海站占25.5%, 1000 m以上的台站占31.9%, 两者共占57.4%.即在因仪器变化产生非均一的台站中, 约有6成站位于沿海或海拔高度较高处.东南沿海地区为我国年平均风速最大的3个地区之一[19], 年平均风速在2m/s以上.高山站也是风速较大地区.显而易见, 测风仪器变化对风速大的地区更敏感, 因此高山站及沿海台站更应注意测风仪器的维护.
|
|
表 4 仪器变化站地理分析 |
6 结语
(1) 采用SNHT方法, 对1951~1990年我国690个站平均风速进行均一性检验.结果表明, 该方法对平均风速有较好的适用性. SNHT方法适用于正态分布, 因此对于非正态的序列必须通过转换, 使其服从正态分布.
(2) 对于检验出的间断年份, 必须通过台站历史沿革查找产生间断的原因, 以判断间断的真实性.在气候观测数据积累的同时, 台站历史沿革的建立也是同等重要的.
(3) 在检验的343个站中, 约有80%的序列是均一的.其具有一定的代表性, 反映我国平均风速数据的质量基本可靠.
(4) 仪器变化及迁站是造成非均一的主要原因.其中仪器变化对年平均风速序列的非均一性影响最大.
(5) 60年代中后期我国风观测仪器换型对少数高山、高原及山坡台站造成影响.
(6) 观测仪器的日常维护及检查至关重要, 尤其是沿海及高山台站.仪器安装高度应在规定范围内.在“规范”中对风仪器高度的变化幅度, 最好应有进一步的规定.
| [1] | Potter k W. Illustration of a new test for detecting a shift in mean precipitation series. Mon. Wea. Rev, 1981, 109: 2040–2045. DOI:10.1175/1520-0493(1981)109<2040:IOANTF>2.0.CO;2 |
| [2] | Easterling D R, Peterson T C. Techniques for Detecting and Adjusting for Artificial Discontinuities in Climatological Time Series:A Review. In:Fifth International Meeting on Statistical Climatology, 1992. 28~32. |
| [3] | Easterling D R, Peterson T C. A new method for detecting undocumented discontinuities in climatological time series. Int. J. Climatol, 1995, 15: 369–377. DOI:10.1002/(ISSN)1097-0088 |
| [4] | Herzog J, Muller W G. Homogenization of Various Climatological Parameters in the German Weather Service. In:Proceedings of the First Seminar for Homogenization of Surface Climatological Data, 1996. 101~111. |
| [5] | 刘小宁, 孙安健. 年降水量序列非均一性检验方法探讨. 气象, 1995, 8: 3–6. DOI:10.11676/qxxb1995.001 |
| [6] | 宋超辉, 刘小宁, 李集明. 气温序列非均一性检验方法的研究. 应用气象学报, 1995, 6, (3): 289–296. |
| [7] | 翟盘茂. 中国历史探空资料中的一些过失误差及偏差问题. 气象学报, 1997, 55, (5): 563–572. DOI:10.11676/qxxb1997.055 |
| [8] | 么枕生, 丁裕国. 气候统计. 北京: 气象出版社, 1990: 270. |
| [9] | Alexandersson H A. Homogeneity test applied to precipitation data. J. Climatol, 1986, 6: 661–675. DOI:10.1002/joc.v6:6 |
| [10] | 朱瑞兆. 应用气候手册. 北京: 气象出版社, 1991: 42–44. |
| [11] | 张开斗. 航空气候学. 北京: 气象出版社, 1997: 15. |
| [12] | 曲建和. 华北平原旱涝气候特征的研究. 山东气象, 1989, 5, (增刊): 21–24. |
| [13] | 黄嘉佑. 气象统计分析与预报方法. 北京: 气象出版社, 1990: 133. |
| [14] | 么枕生, 丁裕国. 气候统计. 北京: 气象出版社, 1990: 283. |
| [15] | Raino H. Metadata and Their role in Homogenization. In:Proceedings of the First Seminar for Homogenization of Surface Climatological Data, 1996. 7. |
| [16] | 谭冠日, 严济远, 朱瑞兆. 应用气候. 上海: 上海科技出版社, 1985: 101. |
| [17] | 郭英起, 段英. 大气环境影响评价实用技术. 北京: 气象出版社, 1993: 23. |
| [18] | 中央气象局. 地区气象观测规范. 北京: 气象出版社, 1979. 52. |
| [19] | 张家诚. 中国气候总论. 北京: 气象出版社, 1991: 171. |
 2000, 11 (1): 27-34
2000, 11 (1): 27-34