2. 北京大学地球物理系暴雨监测与预测国家重点实验室, 北京 100871
2. Department of Geophysics, Peking University, Beijing 100871
多普勒天气雷达与常规天气雷达相比主要的优点是可以提供回波区的风场信息, 因而是监测和研究中尺度强对流天气的有力工具.发展多普勒雷达的主要目的是获取中尺度风场信息, 但多普勒雷达只能测得风矢量在径向方向上的分量.为了要获得完整的中尺度风场, 必须发展风反演方法, 因为在业务天气预报中实现多部雷达协同观测是难以做到的.
从单多普勒速度场反演风场的方法有三类.第一类是统计拟合方法, 如早期提出的VVP (Volume Velocity Processing) 方法 (Waldteufel等1979) [1].它是用最小二乘法拟合线性风场.理论分析表明只有在样本数量非常大的情况下才可能达到必要的精度, 因此其空间分辨率不能满足中尺度分析的要求.实践还表明 (Koscielny等, 1982) [2], VVP方法的反演效果也不够好, 因此已很少使用.第二类方法是基于风矢量和径向分量之间的数学关系, 在一定的假定下反演风矢量.如Person和Anderson (1987) 提出UW (Uniform Wind) 方法[3]和陶祖钰 (1992) 提出的VAP (Velocity Azimuth Processing) 方法[4].其中UW方法在瑞典和德国[5]得到了应用, VAP方法也在中国的有些多普勒雷达上试用.这类方法的缺点是对多普勒速度的变化很敏感, 计算误差较大, 因此还未得到业务应用.第三类方法是动力学方法.它是用大气数值模式的同化方法来反演风场.如Sun J Z等人 (1991年) 提出四维同化方法 (SDPR) [6], 吴绍荣等 (1996年) 提出的平面同化 (PAR) 方法[7]和邱崇践等人 (1992, 1994a, b) 提出简化共轭方法 (SA) [8, 9, 10]等.这类方法所依据的控制方程组都是对大气不同程度的近似, 而且普遍存在计算时间长、需要连续观测资料等问题, 目前还处于研究阶段.由上可见, 其中的第二类方法如能减小其计算误差是可望在近期内成为风场反演的基础.为此, 本文提出了一个用二维滤波方法对原始多普勒速度资料进行预处理以减小VAP方法的计算误差.
1 VAP方法及资料的预处理VAP方法的基本假定是同一距离圈上相邻方向角的两点风矢量相等, 在此前提下, 风速的大小和风向与向径之间的夹角就决定了多普勒速度随方位角的变化.反过来, 就可以根据各距离圈上多普勒速度随方位角的分布廓线计算出风向、风速, 其计算公式为
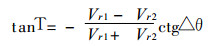
|
(1) |
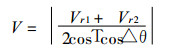
|
(2a) |
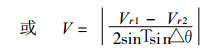
|
(2b) |
其中T为径向风Vr与风矢量的夹角, θ为方位角.局地均匀风的假定是指与计算点相邻△θ的两点的风矢量相等, 由此可见, VAP方法反演的风场的切向分辨率为2△θ.
由于VAP方法在△θ很小的情况下对Vr的变化非常敏感, 特别是当△θ很小时, 如2°左右, 2 m/s左右的速度涨落会产生10 m/s的风速变化, 对反演结果产生严重干扰.例如韩国Soon-Hee Choi (1997) [11]等用TOGA-COARE的多普勒雷达资料对VAP方法和双多普勒雷达的反演作了比较.他们发现, 对层状云, VAP方法得到的风向和风速几乎和双多普勒雷达一样.但对对流云, 两种方法虽然都反演出与阵风锋相联系的风向不连续现象, 但是VAP方法估计出的风速和风向变化都明显的比双多普勒雷达大, 因此VAP方法可用于作强对流系统的快速考查.吴绍荣等 (1996) [7]也认为VAP方法虽然误差较大, 但可用它的反演结果作为动力学方法反演的初始场.
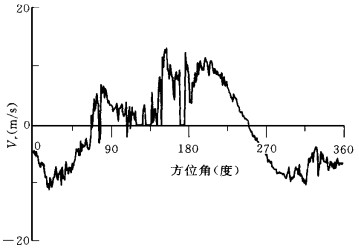
瞬时风场中包括了各种尺度的大气运动, 从水平尺度为数千公里的大尺度运动到1 km以下的小尺度和微尺度运动.如果我们将风场的反演限定尺度为数十公里以上的中-U尺度系统, 即略去尺度在几公里以下的中-V尺度系统, 则可以略去几公里内的风场不均匀性.但是, 多普勒雷达观测到的速度中, 包括了各种尺度的大气运动信息.如图 1所给的速度-方位廓线, 其简谐曲线的整体分布特征是大尺度运动信息的反映.其上叠加的一些小波动是中-T和中-U尺度运动信息的反映.廓线上相邻点的速度涨落则是更小尺度大气运动的反映.对于所要反演的中-U尺度以上的风场, 它们是必须过滤掉的噪音.要想用VAP方法从多普勒风场中反演出中尺度风场, 就必须将微尺度和小尺度系统所造成的速度脉动过滤掉, 这是VAP技术在业务中得到应用的关键问题.
|
|
| 图 1. 在一个距离圈上原始的多普勒速度随方位角分布的廓线 | |
以前的过滤方法是采用一维线性平滑方法.这样做可以部分滤掉速度脉动, 但从反演结果看, 依然存在比较严重的风向摆动现象.为此我们设计了一种二维区域滑动低通滤波方法.具体做法如下:
在雷达扫描范围内取大小为Wmn={(i, j); i, j∈Wmn}的滤波窗口.根据要过滤掉的是中-V尺度 (及以下) 的系统, 窗口的大小可取为5 km.在窗口Wmn内做二维滑动滤波, 过滤掉短波分量.滤波函数为:
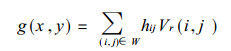
|
(3) |
其中hij为滑动权重系数.在滑动区间中的权重系数满足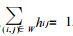
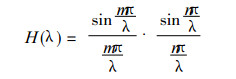
|
(4) |
其中波长λ=m/p或λ=n/p (p=1, 2, 3, …).由上式可以看出波长较大时, 即λ→∞, 波长响应函数H (λ)→1, 滤波后无任何削弱.对于波长等于滑动间隔m或n时, H (λ)=0, 表示这种波长的振动全部削弱.对于大于m和n的波长, 波长响应函数总小于1, 这类波长的振动则有不同程度的削减, 波长越长, 削弱程度越弱.如果选择5 km×5 km的窗口, 对于尺度为10 km的系统, H (λ)=0.9, 削弱程度很弱, 基本保留了其特征, 小于10 km的系统都被过滤掉, 10 km与30 km之间的系统受到不同程度的削弱.
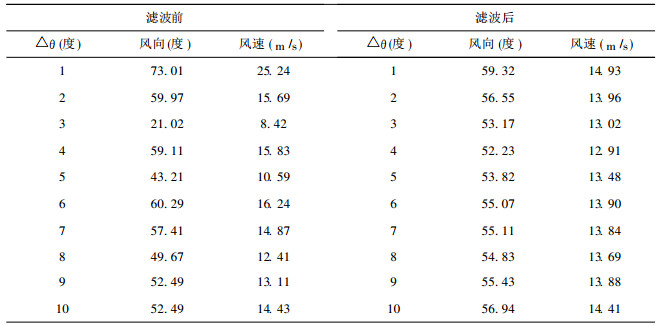
为了选取一个合适的△θ值作为滤波窗口, 我们做了多组对比实验, 表 1为其中一组实验数据, 第100圈 (径向距离20 km) 的以方位角120°为中心、△θ从1°~10°, 所反演出的风向风速结果对比.从表中可以看出, 滤波前计算出的风向风速随△θ的变化很大.如△θ为1°和3°时计算出的风向相差52°, 风速相差3倍.它显示出在△θ很小的情况下, VAP方法的计算结果不稳定.但是当△θ大于7°时, 计算结果比较稳定, 风向的变化只有10°左右、风速的变化只有2 m/s左右, 但这样的分辨率已不能满足中-β尺度分析的要求.表 1还表明, 经过滤波后, 在△θ为2°~5°时计算出的风速和风向的差别相当小, 只有不到1 m/s和几度的差别, 是中尺度风场分析可以接受的.
|
|
表 1 反演风向和风速随△θ的变化 |
考虑到近距离圈廓线上相邻两点的距离较近, 远距离圈廓线上相邻两点的距离较远, 故对不同的距离圈应选取不同的△θ.按照反演风场水平分辨率为5 km的要求, 我们取△θ=5/(2×r), 其中r为距离圈的半径.对于远距离圈, 当△θ < 3°时, 取△θ=3°, 对于近距离圈, 当△θ > 6°时, 取△θ=6°.图 2为图 1的廓线二维滤波后的结果.从图可见, 廓线上的小尺度和微尺度脉动均已被过滤掉.特别值得指出的是, 经过二维区域滑动低通滤波后的廓线上中-U尺度系统的特征非常清楚, 它表现为廓线上的几个方位张角为数十度的小波动.而且, 与原始廓线相比, 它们的振幅和位相并未因滤波而改变, 也就是说, 经过二维区域滤波后, 原始多普勒速度资料中的中-U尺度以上的信息相当完整地保留下来.因此, 经过滤波后的数据可用来做中尺度流场的反演.

|
|
| 图 2. 经二维滤波后的多普勒速度方位角廓线 | |
另外从式 (2) 可看出当T→(2k+1)·π/2, k=0, 1时, 式中分母将趋于零.为了避免计算溢出, 可对式 (2) 进行变形, 得到另外一种风速计算公式.
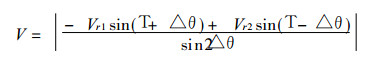
|
(5) |
用式 (5) 计算风速的另一个优点是分母变成△θ的倍角形式, 可一定程度的减小计算误差.
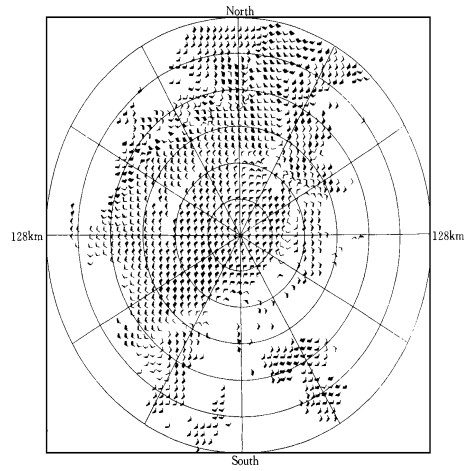
图 3给出了从首都机场多普勒雷达速度资料经滤波后反演出的1997年7月19日一次强对流暴雨过程的中尺度风场.图中强对流暴雨所产生的偏北风外流边界和它与偏南风暖湿气流之间的阵风锋在反演出的风场中非常清晰.图 2所示的风场和Lemon等 (1979) [12]所归纳的中尺度强风暴低空流场模式非常相象.我们将在另文中用立体扫描资料对这个个例的三维流场作详细的分析并与每小时一次的单站地面资料、中尺度地面分析和高空风观测进行仔细的对比.
|
|
| 图 3. 1997年7月19日16:00的反演风场 | |
2 总结
本文首先讨论了单多普勒雷达反演风场的三类方法, 认为VAP方法是近期可望在业务中应用的方法, 并指出VAP方法反演风场的效果依赖于能否将原始资料中的中-U (及以上) 尺度的风场信息过滤出来, 以消除中-V尺度 (及以下) 风场信息对反演结果的影响.为此文中提出了二维区域滑动低通滤波方法.个例反演试验结果表明, 用这种方法处理过的数据可清晰地反演出中-U尺度系统.本文还对VAP方法的风速计算公式进行了改进, 减小了计算误差.
致谢 首都机场气象中心的顾雷工程师为本文提供了部分资料, 在此表示感谢.| [1] | Waldteufel P, Corbin H. On the analysis of single-Doppler radar data. J. Appl. Meteor, 1979, 18: 532–542. DOI:10.1175/1520-0450(1979)018<0532:OTAOSD>2.0.CO;2 |
| [2] | Albert J, et al. Statistical considerations in the estimation of divergence from single-Doppler radar and application to prestorm boundary-layer observations. J. Appl. Meteor, 1982, 21: 197–210. DOI:10.1175/1520-0450(1982)021<0197:SCITEO>2.0.CO;2 |
| [3] | Ola P, Persson G and Tage Anderson. Automatic Wind Field Interpretation of Doppler Radar Radial Wind Components. In: Pennsylvania Uni., USA. SMHIPROM IS REPORTS, 1987. |
| [4] | 陶祖钰. 从单Doppler雷达速度场反演风矢量场的VAP方法. 气象学报, 1992, 50, (1): 81–90. |
| [5] | Hagen M. Retrieval of Wind from Doppler Measurements of a Single Radar and Application on a Cold Front with Narrow Rain Band: [PHD Thesis ]. Munchen: University Munchen, 1989. |
| [6] | Sun J Z, Flicker D W, Lilly D K. Recovery of three-dimensional wind and temperature fields from simulated single-Doppler radar data. J. Atmos. Sci, 1991, 48: 876–890. DOI:10.1175/1520-0469(1991)048<0876:ROTDWA>2.0.CO;2 |
| [7] | 吴绍荣. 单多普勒雷达资料水平风场反演方法的研究: [硕士论文]. 北京: 中国气象科学院, 1994. |
| [8] | Qiu C J, Xu Q. A simple adjoint method of wind analysis for single-Doppler data. J. Atmos. Ocean Technol, 1992, 9: 588–598. DOI:10.1175/1520-0426(1992)009<0588:ASAMOW>2.0.CO;2 |
| [9] | Xu Q, Qiu C J, Yu J X. Adjoint-method retrievals of low-altitude wind fields from single-Doppler reflectivity measured during Phoenix-Ⅱ. J. Atmos. Ocean. Technol, 1992a, 11: 275–288. |
| [10] | Xu Q, Qiu C J. Simple adjoint method for single-Doppler wind analysis with a strong constraint of mass conservation. J. Atmos. Ocean. Technol, 1992b, 11: 289–298. |
| [11] | Choi S H, Park S G, Kim K E. Estimations of horizontal wind fields by VAP method. J. Meteor. Soc. Korea, 1997, 33: 535–551. |
| [12] | Lemon L R, Doswell C A. Severe thunderstorm evolution and mesocyclone structure as related to tornadogenesis. Mon. Wea. Rev, 1979, 107: 1184–1197. DOI:10.1175/1520-0493(1979)107<1184:STEAMS>2.0.CO;2 |
 2000, 11 (1): 21-26
2000, 11 (1): 21-26