Synchronous control of dual travelling wheels for transmission line clearance flying robot
-
摘要: 传统架空输电线路异物清除作业无人机易受环境影响，作业困难且存在较多扰动等问题。基于此本文设计一种高空作业无人机挂线行走控制机构解决该问题。首先，根据输电线路环境与无人机作业模式，设计挂线行走机构，减弱高空作业时对无人机所受飞行作业扰动的影响；其次，针对清障机器人双行走轮转速同步存在误差问题，提出一种基于反向传播–比例积分微分（back propagation-proportional-integral-differential，BP-PID）主从融合偏差耦合的电机同步控制策略。通过仿真与实物实验验证表明，本文提出的挂线作业无人机双行走轮同步控制算法可有效解决电机因负载导致的转速不稳定以及高空作业无人机受环境扰动的问题。Abstract: Traditional foreign object removal operations from overhead transmission lines by drones are easily affected by environmental factors. The operations are difficult and there are many disturbances. This paper proposes a solution to solve this problem by designing a high-altitude operation drone hanging-wire walking control mechanism. Firstly, based on the environment of the power transmission line and the operating mode of the drone, a hanging-wire walking mechanism is designed to reduce the impact of flight operation disturbances on the drone during high-altitude operations. Secondly, in response to the problem of synchronization errors in the dual-wheeled walking speed of the obstacle-clearing robot, a motor synchronization control strategy based on back propagation-proportional-integral- differential (BP-PID) master-slave fusion deviation coupling is proposed. Through simulation and physical experiments, it is demonstrated that the dual-wheeled walking synchronization control algorithm proposed in this paper can effectively solve the problem of motor speed instability caused by load and the disturbance of the high-altitude operation drone due to environmental factors.
-
电力系统是国民经济发展的重要因素，确保电力安全平稳运行极为重要[1]。输电线路的定期检修维护需要极大人力和物力[2]，线路的巡检与作业机器人代替人工作业已成为保障电网安全运行的主流模式[3]。输电线路作业机器人在国内外已有一定研究，如通过控制实现巡检作业等任务。许昌亮等[4]设计的新型多旋翼作业型空中机器人，廖禄伟等[5]研发的悬挂伸缩刀具的树障清理空中机器人，该类机器人以多旋翼无人机为平台，携带作业工具完成相应任务[6-7]。本研究设计的输电线路清障飞行机器人用于清除输电线路上挂载的风筝线、气球等异物，设计亮点在于机器人可飞行挂载到输电线路上，通过行走机构运动至异物前方，用作业机构完成异物清除。
输电线自然形成坡度，为实现机器人稳定上下坡，考虑机器人自重，论证分析后选择双行走轮方案。双行走轮均用同型号无刷直流电机驱动，以满足水平行走与上下坡需求。同时，因机器人在行走过程中受负载变化影响，存在两电机转速不完全同步现象，进而出现行走轮打滑、磨损及行走效率降低等问题。多电机同步控制属于非线性系统，主要有耦合控制与非耦合控制2种[8]。非耦合控制对象之间不存在耦合，会因扰动产生较大同步误差，控制精度较低，无法满足高精度同步控制需求；耦合控制可减弱扰动对多电机同步系统的影响，有效提高多电机系统同步精度。针对机器人电机及多电机系统同步控制已有一定研究，如李捷文等[9]设计的树障清理机器人刀具系统自抗扰控制器，解决了作业过程中力矩变化及参数摄动对刀具系统的影响，但存在参数不可在线调节的不足；留若宸[10]的多电机伺服系统控制研究，提出了一种改进自抗扰控制算法，优化了二阶观测器，提高了同步控制精度，但内环参数无法自适应导致动态性能不佳；吴鑫煜[11]的多电机同步驱动伺服系统控制器，设计了一种新的滑模速度控制器，但系统响应和抗扰能力不足。
基于此，本文提出一种基于反向传播（back propagation，BP）神经网络[12]的主从融合偏差耦合双行走轮驱动电机同步控制算法。该算法将BP神经网络、偏差耦合及主从控制相结合，主电机以反馈信号、自身跟踪误差及其微分作BP神经网络输入，动态调节比例积分微分(proportional-integral-differential，PID)控制器参数，从属电机采用PID控制器（给定控制参数），通过负反馈与一个惯性前馈环节实现速度跟踪控制，解决了传统PID多电机控制易受扰动与负载影响、参数调节缺乏自适应及控制精度低的问题，提高了电机同步系统的同步性能与抗扰性。最后，通过MATLAB/Simulink仿真及实物验证，证明了该算法的可行性与有效性。
1. 行走机构设计与驱动电机建模
1.1 行走轮设计
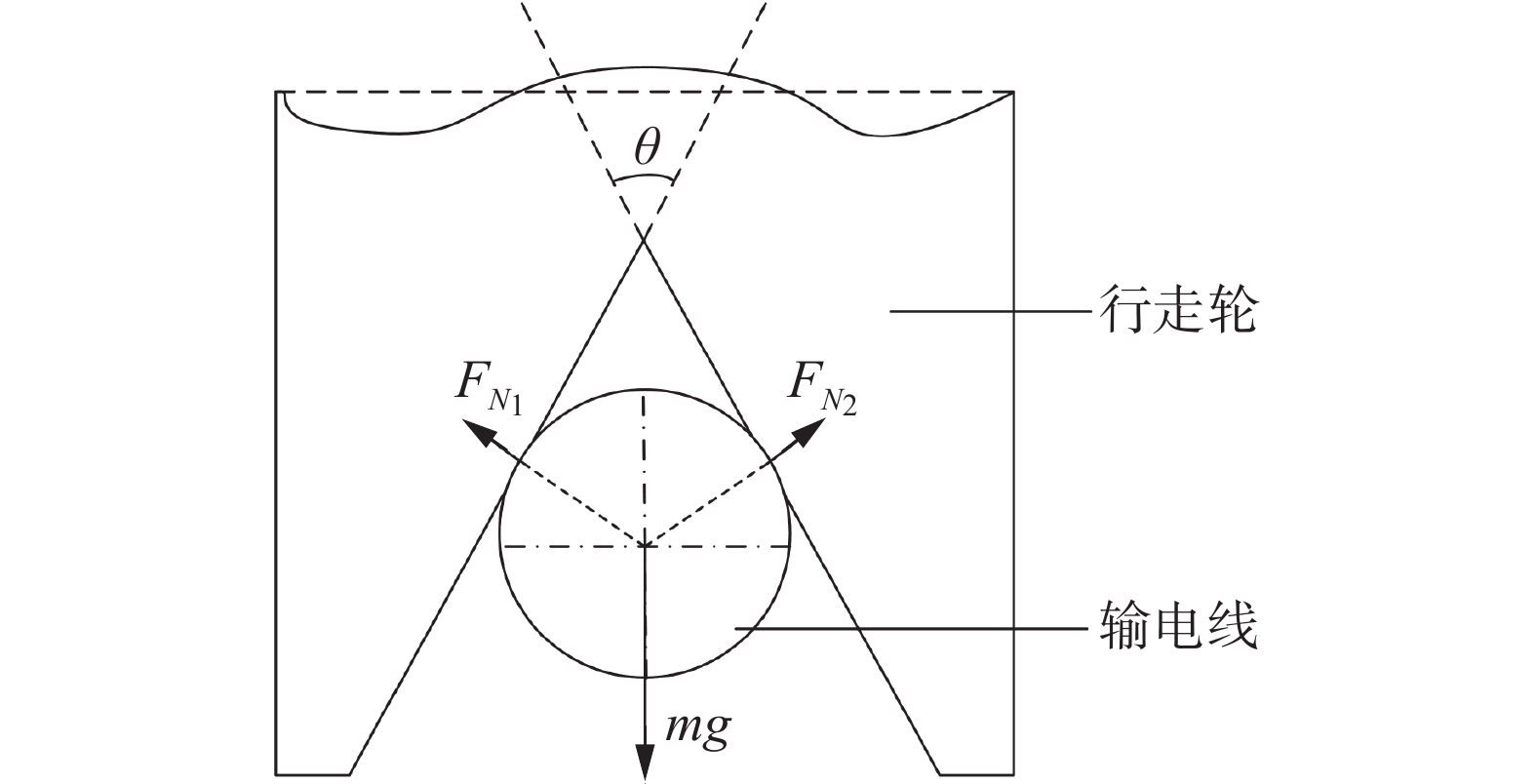
针对输电线路这一特殊作业环境，为提高行走作业效率，将行走轮机械结构设计为V型[13]，力学分析如图1所示，
$mg$ 为机器人总重力，$\theta $ 为行走轮内斜面夹角，${F_{N_1}}$ 与${F_{N_2}}$ 为行走轮斜面所受正压力。
图 1 V型行走轮力学分析
下载:
全尺寸图片
通过力学分析可知，行走轮所受摩擦力为
$$ {f^{'}} = \mu ({F_{N_1}} + {F_{N_2}}) = 2\mu \cdot \dfrac{{\dfrac{1}{2}mg}}{{\sin \dfrac{\theta }{2}}} = \pm \dfrac{{\mu \cdot mg}}{{\sqrt {\dfrac{{1 - \cos \theta }}{2}} }} $$ (1) 由式（1）可知，要增大机器人的行走、爬坡能力，需尽可能选择与导线摩擦系数
$\mu $ 较大的材料；同时行走轮的夹角越小越好。基于上述分析，本文行走轮夹角设计为60°，使用轻质复合材料做轮毂、复合橡胶做表皮（设计有防滑花纹）结合的形式[14]，保证了行走轮的机械强度与大摩擦力，设计的行走轮实物如图2所示。
图 2 机器人V型行走轮下载:
全尺寸图片
1.2 行走机构设计
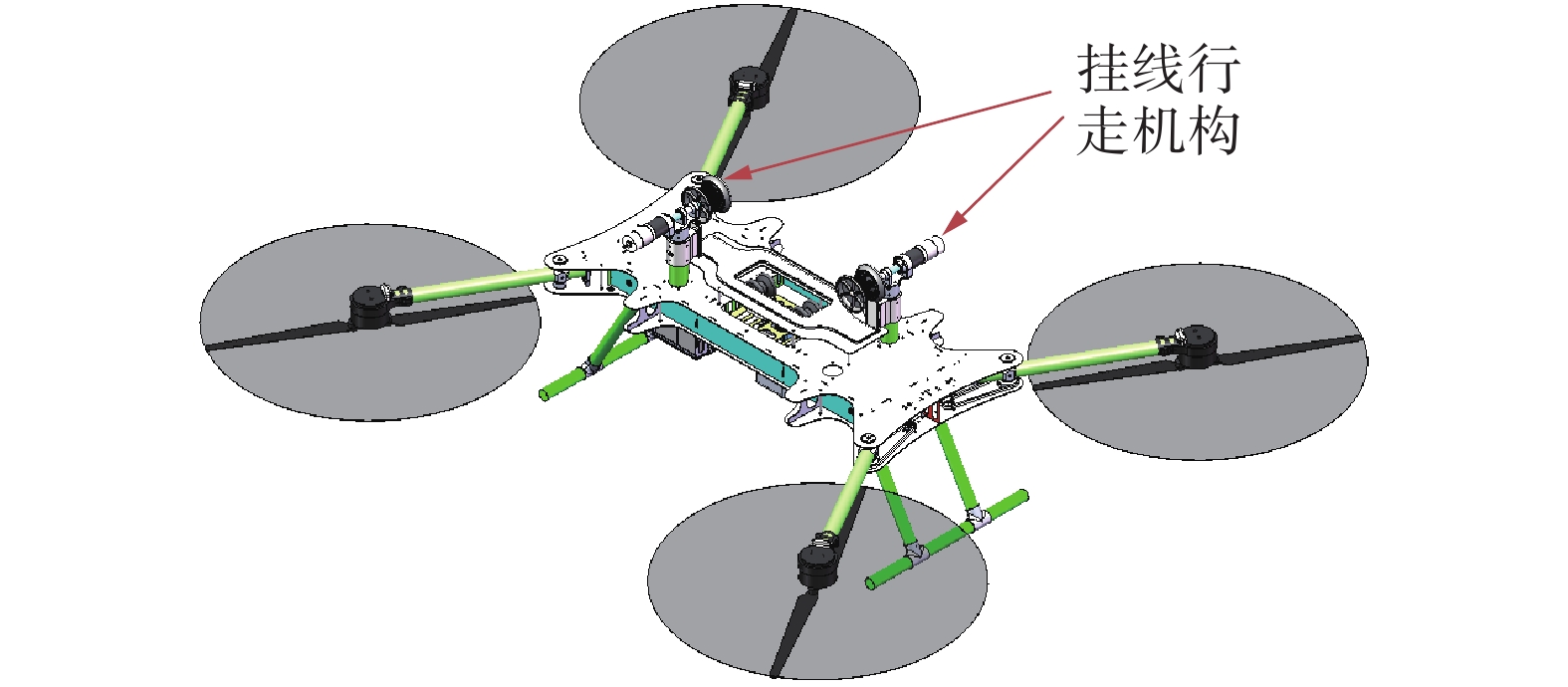
为实现机器人在输电线路环境下的安全稳定作业，在四旋翼飞行平台上设计挂线行走机构，挂线行走机构采用分布交错式布局，如图3所示。
图 3 机器人挂线行走机构下载:
全尺寸图片
该机构由挂线连杆与双行走轮组成，挂线部分设计为交错式布局，同时考虑机器人控制系统与输电线的安全距离，防止高压击穿。机器人通过视觉导航——轨迹跟踪偏航90°的方式挂线，飞行上下线时需与线路接触，机器人与线路接触部分必须具有绝缘性能；因此，挂线连杆采用尼龙材料，不仅保证了机器人的安全，且减轻了机器人的本体质量。
该结构有效分散了挂线行走机构所受载荷，确保了机器人的机械强度，同时解决了行走过程中可能因摆动导致的机器人脱线问题。
1.3 行走轮驱动电机建模
建立机器人行走轮驱动电机数学模型，基于此模型对双行走轮做同步控制仿真。实际系统中，电机受负载及其他因素影响，模型可能发生改变，考虑影响因素对电机建模，以提高同步系统控制精度。电机运动控制基本方程为
$$ \left\{ \begin{gathered} \frac{{{\text{d}}(J{\varOmega _{\text{m}}})}}{{{\text{d}}t}} = {T_{\text{m}}} - {T_{\text{L}}} - D{\varOmega _{\text{m}}} - K{\theta _{\text{m}}} \\ \frac{{{\text{d}}{\theta _{\text{m}}}}}{{{\text{d}}t}} = {\varOmega _{\text{m}}} \\ \end{gathered} \right. $$ (2) 式中：
$J$ 为转动惯量，kg·m2；${\varOmega _{\text{m}}}$ 为转子角速度，rad/s；${\theta _{\text{m}}}$ 为转子转动角，rad；${T_{\text{m}}}$ 为电磁转矩，N·m；${T_{\text{L}}}$ 为负载转矩，N·m；$D$ 为转矩阻尼系数；$K$ 为扭转弹性转矩系数。忽略扭转弹性转矩与阻尼转矩，将电机运动方程简化为
$$ \left\{ \begin{gathered} J\frac{{{\text{d}}({\varOmega _{\text{m}}})}}{{{\text{d}}t}} = {T_{\text{m}}} - {T_{\text{L}}} \\ \frac{{{\text{d}}{\theta _{\text{m}}}}}{{{\text{d}}t}} = {\varOmega _{\text{m}}} \\ \end{gathered} \right. $$ (3) 采用工程单位制，将式(3)改写为
$$ \frac{{G{D^2}}}{{375}}\frac{{{\text{d}}(n)}}{{{\text{d}}t}} = {T_{\text{m}}} - {T_{\text{L}}} $$ (4) 式中：
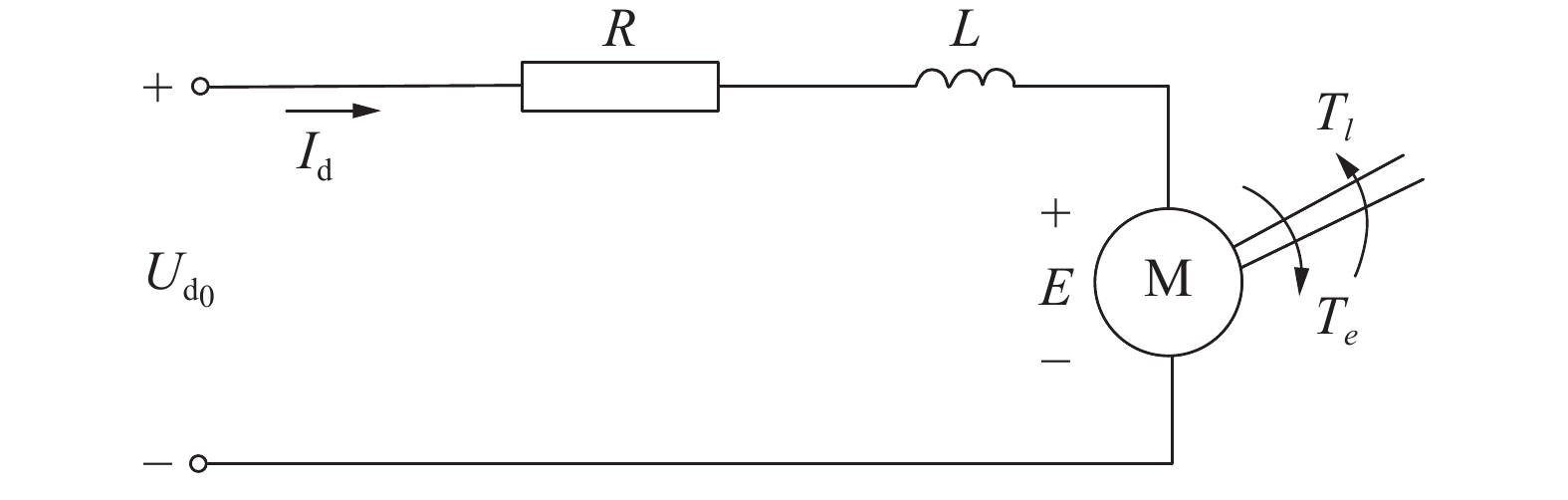
$G{D^2}$ 为转动惯量，N·m2，$G{D^2} = 4\;gJ$ ；$n$ 为电机转速，r/min；$n = 60\;{\varOmega _{\text{m}}}/2{\text{{\text{π}} }}$ 。无刷直流电机等效电路如图4所示。
图 4 直流电机等效电路下载:
全尺寸图片
电机动态电压方程为
$$ {U_{{{\text{d}}_{\text{0}}}}} = R{I_{\text{d}}} + L\frac{{{\text{d}}{I_{\text{d}}}}}{{{\text{d}}t}} + E $$ (5) 式中：
${U_{{{\text{d}}_{\text{0}}}}}$ 为空载额定电压，$R$ 为电枢回路等效电阻，$L$ 为电枢回路等效电感，${I_{\text{d}}}$ 为电枢回路电流，$E$ 为电机感应电动势。定义电磁时间常数为
${T_1}$ ，电机拖动时间为${T_2}$ ，则有：$$ \left\{ \begin{gathered} {U_{{{\text{d}}_{\text{0}}}}} - E = R\left({I_{\text{d}}} + {T_1}\frac{{{\text{d}}{I_{\text{d}}}}}{{{\text{d}}t}}\right) \\ {I_{\text{d}}} - {I_{{\text{d}}_L^{}}} = \frac{{{T_2}}}{R}\frac{{{\text{d}}E}}{{{\text{d}}t}} \\ \end{gathered} \right. $$ (6) 式中
${I_{{{\text{d}}_L}}}$ 为负载电流。无刷直流电机绕组回路电压方程为
$$ u(t) = L\frac{{{\text{d}}i(t)}}{{{\text{dt}}}} + Ri(t) + E $$ (7) 式中电机反电动势E由电机绕组匝数、永磁体磁通量、转子转速决定，且E与转速
${\varOmega _{\text{m}}}$ 成反比。由式(7)及安培定则可得电磁转矩
${M_{\text{m}}}(t)$ 为$$ {M_{\text{m}}}(t) = {C_{\text{m}}} \cdot i(t) $$ (8) 电机轴转矩平衡方程为
$$ J\frac{{{\text{d}}{\varOmega _{\text{m}}}(t)}}{{{\text{d}}t}} + {f_{\text{m}}} \cdot {\varOmega _{\text{m}}}(t) = {M_{\text{m}}}(t) - {M_L}(t) $$ (9) 式中
${f_{\text{m}}}$ 为电机轴上的黏性摩擦系数。以绕组电压
$u(t)$ 为输入，角速度${\varOmega _m}(t)$ 为输出，将式(7)~(9)进行拉氏变换得到：$$ \left\{ \begin{gathered} U(s) = L \cdot s \cdot I(s) + R \cdot I(s) + {C_e} \cdot \varOmega (s) \\ {T_{\text{m}}}(s) = {C_{\text{m}}} \cdot I(s) \\ J \cdot s \cdot \varOmega (s) + {f_{\text{m}}} \cdot \varOmega (s) = {M_{\text{m}}}(s) - {M_L}(s) \\ \end{gathered} \right. $$ (10) 消去式(10)的中间变量
$I(s)$ ，并由式(2)~(6)进行系数替换可得：$$ {T_{\text{m}}}s\varOmega (s) + \varOmega (s) = {K_{\text{m}}}U(s) - {K_L}{M_L}(s) $$ (11) 根据式(11)得行走轮驱动电机模型传递函数为
$$ G(s) = \frac{{\varOmega (s)}}{{U(s)}} = \frac{{{K_{\text{m}}}}}{{{T_{\text{m}}}s + 1}} $$ 代入电机相关参数，得到电机模型传递函数为
$$ G(s) = \frac{{142.94}}{{1.0{s^2} + 7.6s}} $$ 至此，输电线路清障飞行机器人行走轮驱动电机数学模型建立完毕。
2. 双行走轮同步控制
2.1 主从控制及偏差耦合控制
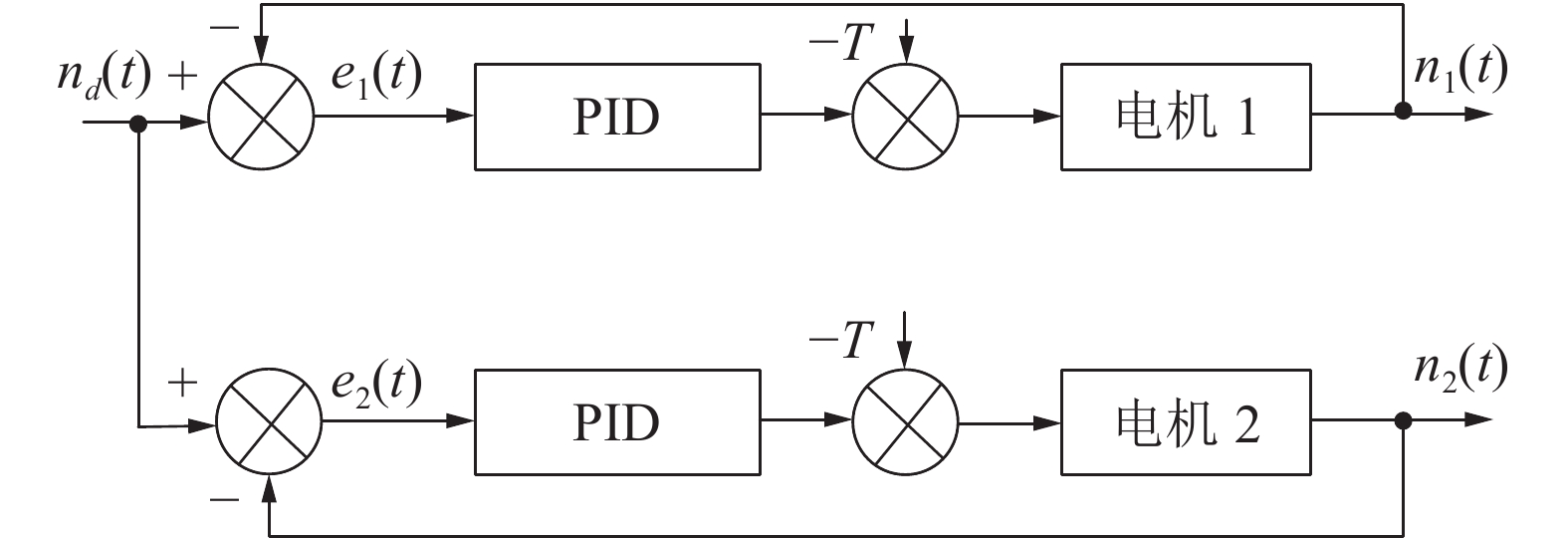
主从控制为多电机同步控制传统方法之一，以从属电机跟随主电机运动为基本原理，跟随实现电机同步控制。该方法存在同步系统抗扰性较差的问题，如主电机受外界扰动，从属电机同样跟随主电机受扰动；从属电机受外界扰动，主电机无法感知扰动，同步性能变差。故传统电机同步控制仅使用主从控制，易受外界扰动影响，无法达到稳定同步。
多个电机共同完成某项任务时，因不同电机本身存在误差，该误差会耦合到其他电机的控制中[15]，造成互相干扰，进而导致任务效果下降。偏差耦合控制通过实时测量电机间偏差，引入反馈，采用高级控制算法调节控制器参数，有效去除多电机间的耦合，实现多电机同步控制。
传统多电机主从同步控制方法以PID为控制器，通过速度反馈实现电机同步，如图5所示。
图 5 双电机主从控制下载:
全尺寸图片
偏差耦合控制结构如图6所示，其提高了多电机系统的同步性能，但存在同步系统抗扰性较差的不足。
图 6 偏差耦合控制下载:
全尺寸图片
2.2 主从结合偏差耦合控制
针对输电线路清障飞行机器人行走轮驱动电机不同步，导致机器人行走轮打滑、磨损及行走效率低等问题，本文提出一种主从融合偏差耦合的同步控制算法。主从控制通过神经网络动态调节控制器参数，提高系统的抗扰动性能；偏差耦合控制将同步误差进行前馈补偿，提高系统的同步性能。本文将上述2种方法结合起来，使系统的抗扰性与同步性都得到明显提升。
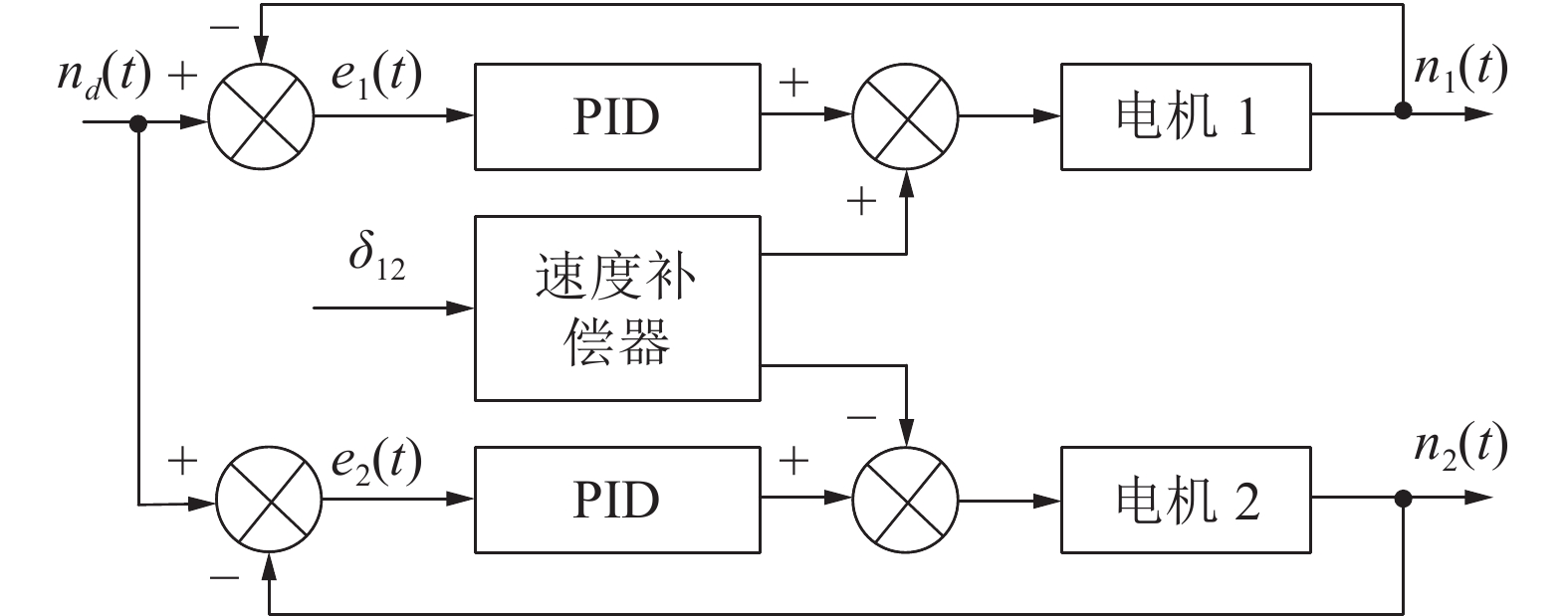
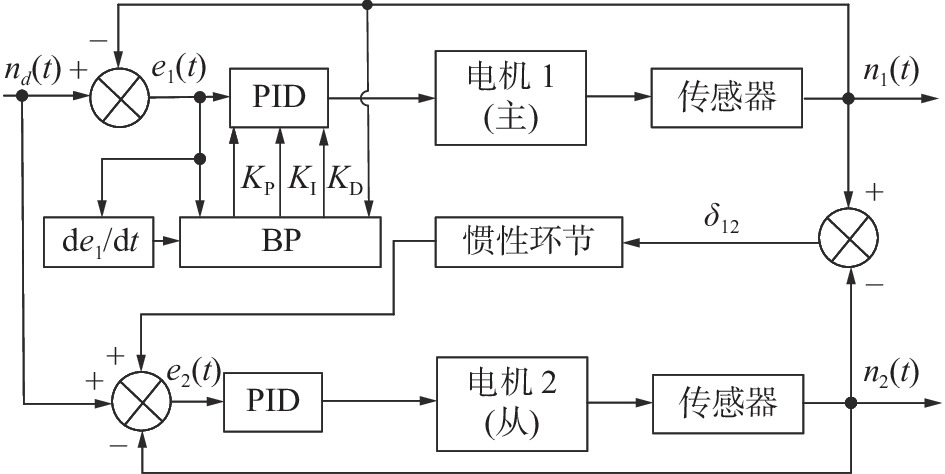
本文设计的主从融合偏差耦合同步控制结构如图7所示，主电机PID控制器参数通过BP神经网络调节，以提高系统抗扰性能；从属电机给定PID控制器参数，将同步误差（偏差）进行前馈补偿，跟随主电机运动实现同步。图7中，
${n_1}(t)$ 与${n_2}(t)$ 为主、从电机输出转速；${n_d}(t)$ 为期望转速；${e_1}(t)$ 与${e_2}(t)$ 为主、从电机转速跟踪误差；${\delta _{12}}$ 为主、从电机同步误差（偏差）。双行走轮同步控制过程为：首先给定期望转速；其次将主电机转速跟踪误差${e_1}(t)$ 、转速跟踪误差导数$ {\text{d}}{e_1}/{\text{d}}t $ 及输出转速${n_1}(t)$ 作为BP神经网络输入信号，调节参数后输出控制信号给主电机（电机1）；最后将从属电机控制器以跟踪误差${e_2}(t)$ 作为信号输入，双电机同步误差${\delta _{12}}$ 经惯性环节作前馈补偿，实现转速同步。
图 7 双行走轮同步控制结构下载:
全尺寸图片
2.3 BP神经网络PID控制
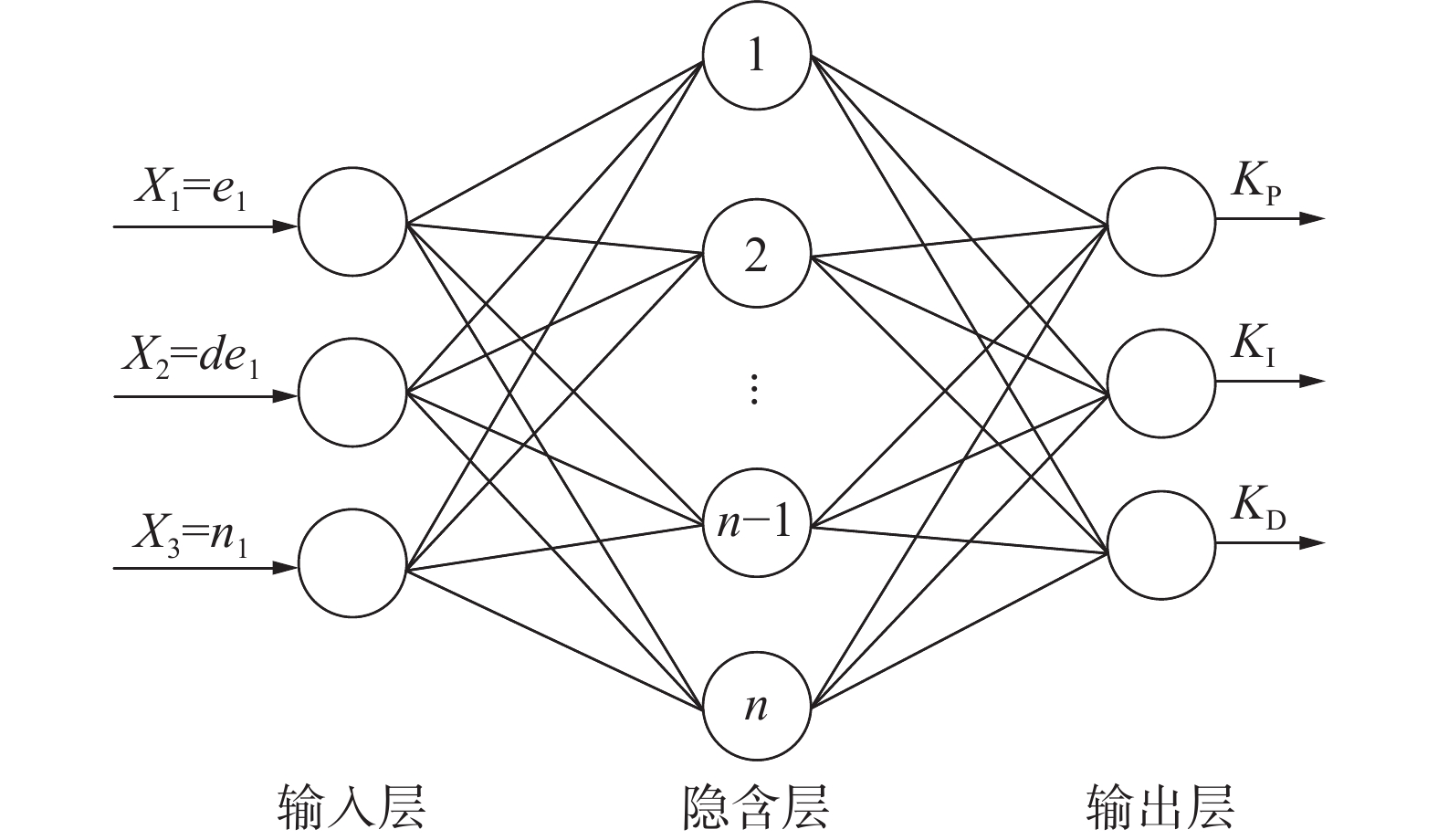
传统PID多电机同步控制易受系统内外扰动影响，很难达到快速、稳定同步控制。本文针对双行走轮同步控制，采用BP神经网络调节PID控制器参数，以提高系统的动态与稳态同步性能。BP神经网络通过误差逆向传播训练形成前馈网络，基于梯度下降使网络输入与输出误差均方差最小，有极强的非线性映射能力与自学习能力。针对双行走轮同步控制系统，本文采用3层BP神经网络，包括输入层、隐含层与输出层，其中隐含层神经元共128个（
$n = 128$ ），如图8所示。
图 8 3层BP神经网络结构下载:
全尺寸图片
BP神经网络输入层表达式为
$$ M_j^1(k) = X(j)(k),\quad j = 1,2,3 $$ 式中：
$M_j^1(k)$ 为BP神经网络的输入集；$X(1)(k)、 X(2)(k)、X(3)(k)$ 为BP神经网络的3个输入项，$k$ 代表第$k$ 时刻。隐含层输入表达式为
$$ \left\{ \begin{gathered} n_1^2(k) = \sum\limits_{j = 1}^4 {w_{ij}^2(k) \cdot Q_j^1(k)} \\ M_i^2(k) = f(n_i^2(k)) \\ \end{gathered} \right. $$ 式中：
$ n_1^2(k) $ 为隐含层的输入中间项，$w_{ij}^2(k)$ 与$Q_j^1(k)$ 为输出和权重，$M_i^2(k)$ 为隐含层的输入，$ f(n_i^2(k)) $ 为激活函数。隐含层神经元激活函数为
$$ f(x) = \tanh (x) = \frac{{{{\text{e}}^x} - {{\text{e}}^{ - x}}}}{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}} $$ BP神经网络输出为
$$ \left\{ \begin{gathered} n_m^3(k) = \sum\limits_{i = 1}^Q {w_{mi}^3(k) \cdot M_i^2(k)} \\ M_m^3(k) = g(n_m^3(k)),\qquad m = 1,2,3 \\ M_m^3(k) = {K_{\text{P}}}O_2^3(k) = {K_{\text{I}}}O_3^3(k) = {K_{\text{D}}} \\ \end{gathered} \right. $$ 式中：
$ n_m^3(k) $ 为激活值；$w_{mi}^3(k)$ 为权重；$M_i^2(k)$ 为隐含层的输入；$ g(n_m^3(k)),m = 1,2,3 $ 为激活函数；$O_2^3(k)$ 与$O_3^3(k)$ 为BP神经网络的输出；${K_{\text{P}}}$ 、${K_{\text{I}}}$ 、${K_{\text{D}}}$ 为BP神经网络的输出，给到主电机PID控制器。实际情况下，因
${K_{\text{P}}}$ 、${K_{\text{I}}}$ 与${K_{\text{D}}}$ 为非负值，故激活函数应取非负：$$ h(x) = \frac{1}{2}[1 + \tanh (x)] = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}} $$ 性能指标函数设置为
$$ E(k) = \frac{1}{2}{[{r_{\text{i}} }(k) + {y_{\text{o}}}]^2} $$ 式中：
$ E(k) $ 为性能指标函数，${r_{\text{i}} }(k)$ 与${y_{\text{o}}}$ 分别为系统的输入输出。通过梯度下降调整BP神经网络权值，对
$E(k)$ 向负梯度方向搜索，为达到快速收敛，设置惯性项为$$ \Delta W_{mj}^3(k) = \gamma \Delta W_{mj}^3(k - 1) - \eta \frac{{\partial E(k)}}{{\partial W_{mj}^3}} $$ 式中
$\gamma $ 、$\eta $ 分别为惯性项惯性系数与学习效率。3. 仿真与实物验证
3.1 仿真实验结果
双行走轮同步控制以MATLAB/Simulink为仿真环境，搭建系统仿真模型，主电机通过BP神经网络调节PID参数，从属电机给定PID参数，
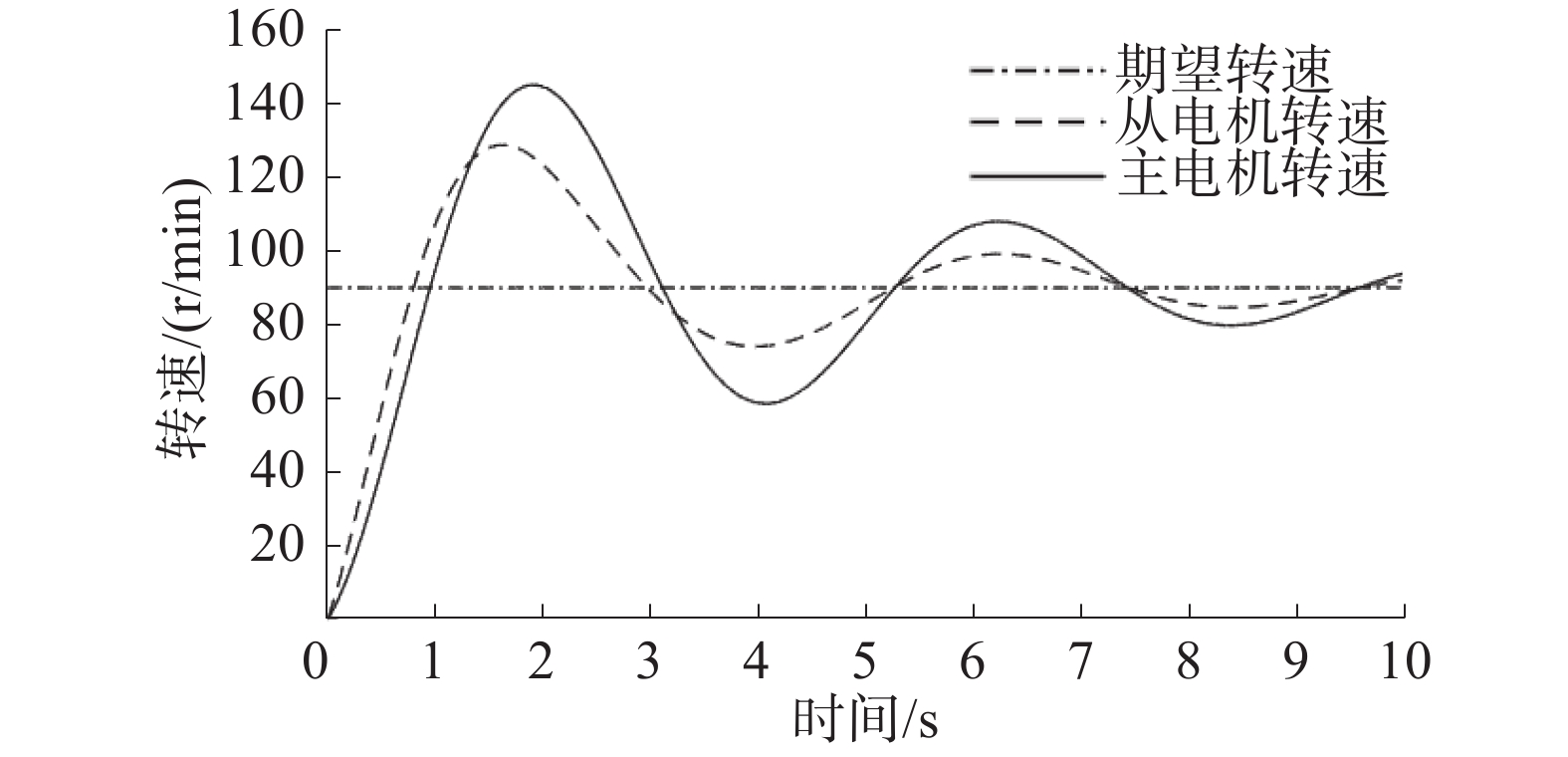
${K_{\text{P}}}$ 、${K_{\text{I}}}$ 、${K_{\text{D}}}$ 分别为0.58、1.61、0.35，完成对控制算法验证。行走轮及驱动电机相关参数如表1所示。表 1 行走轮及驱动电机相关参数参数 符号 值 电机电枢绕组/Ω R 0.2 电机电枢电感/H L 0.0003 电机电气时间常数 T1 0.61 电机转动惯量/(kg·m2) J 0.08 电磁转矩系数/(Nm/A) Cm 0.0678 电机反电势系数(Vs/rad) Ce 0.0071 电机最大转速/(r/min) Nma 90 行走轮相半径/m r 0.21 当期望转速给定为90 r/min、行走轮系统受扰动时，双行走轮同步控制系统的传统PID转速同步控制曲线如图9所示。
图 9 传统PID转速同步控制曲线下载:
全尺寸图片
由图9可看出，传统PID同步控制易受扰动影响，调节时间较长，达到同步运动较为困难，从属电机无法很好地跟随主电机运动，双行走轮无法快速实现转速同步。
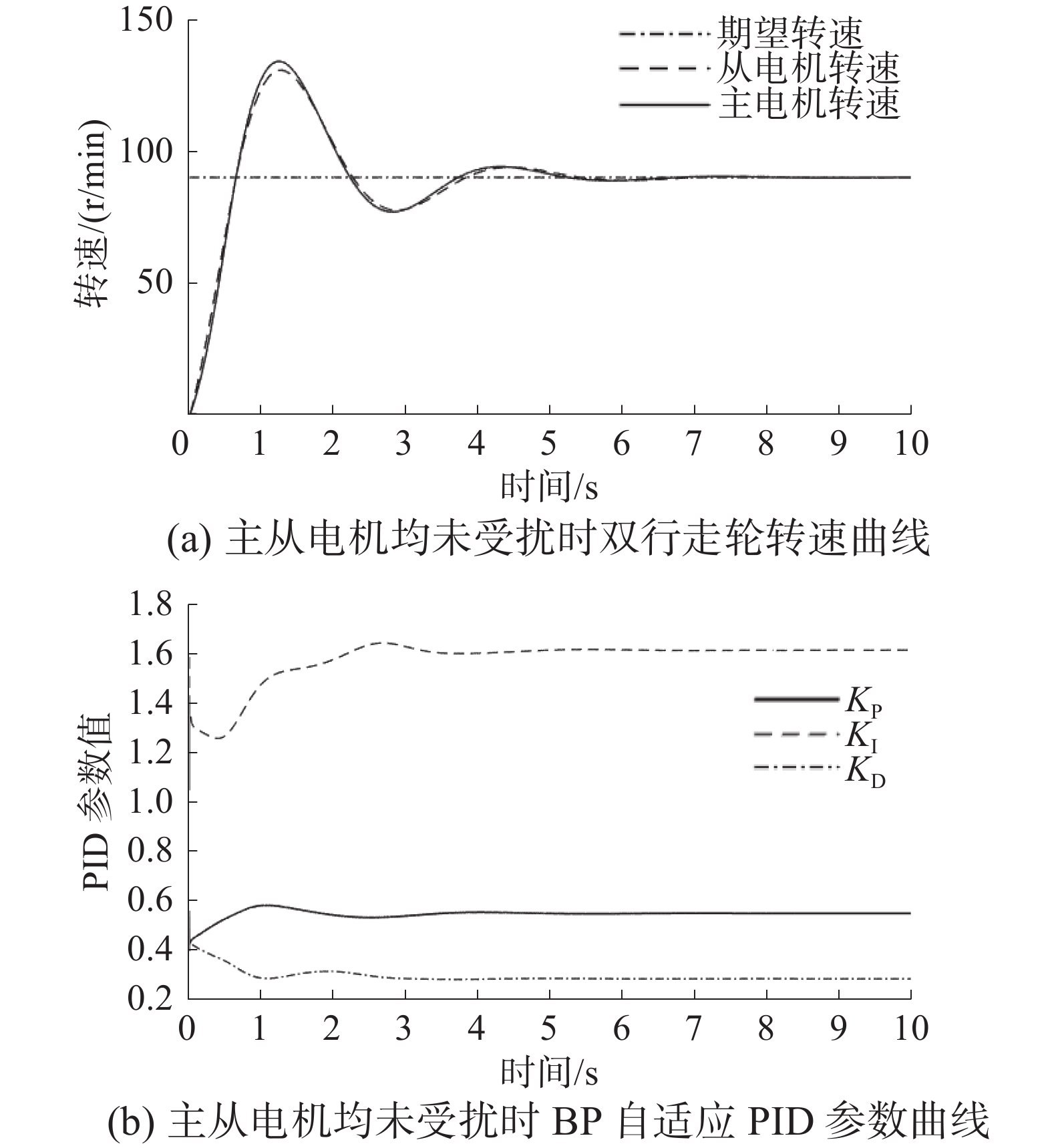
当期望转速给定为90 r/min、行走轮主从电机均未受扰动时，双行走轮同步控制系统的转速曲线与BP调节PID参数曲线如图10所示。
图 10 转速同步与PID参数曲线（无扰动）下载:
全尺寸图片
由图10可看出，从属电机可很好地跟随主电机运动，双行走轮系统可快速实现转速同步。
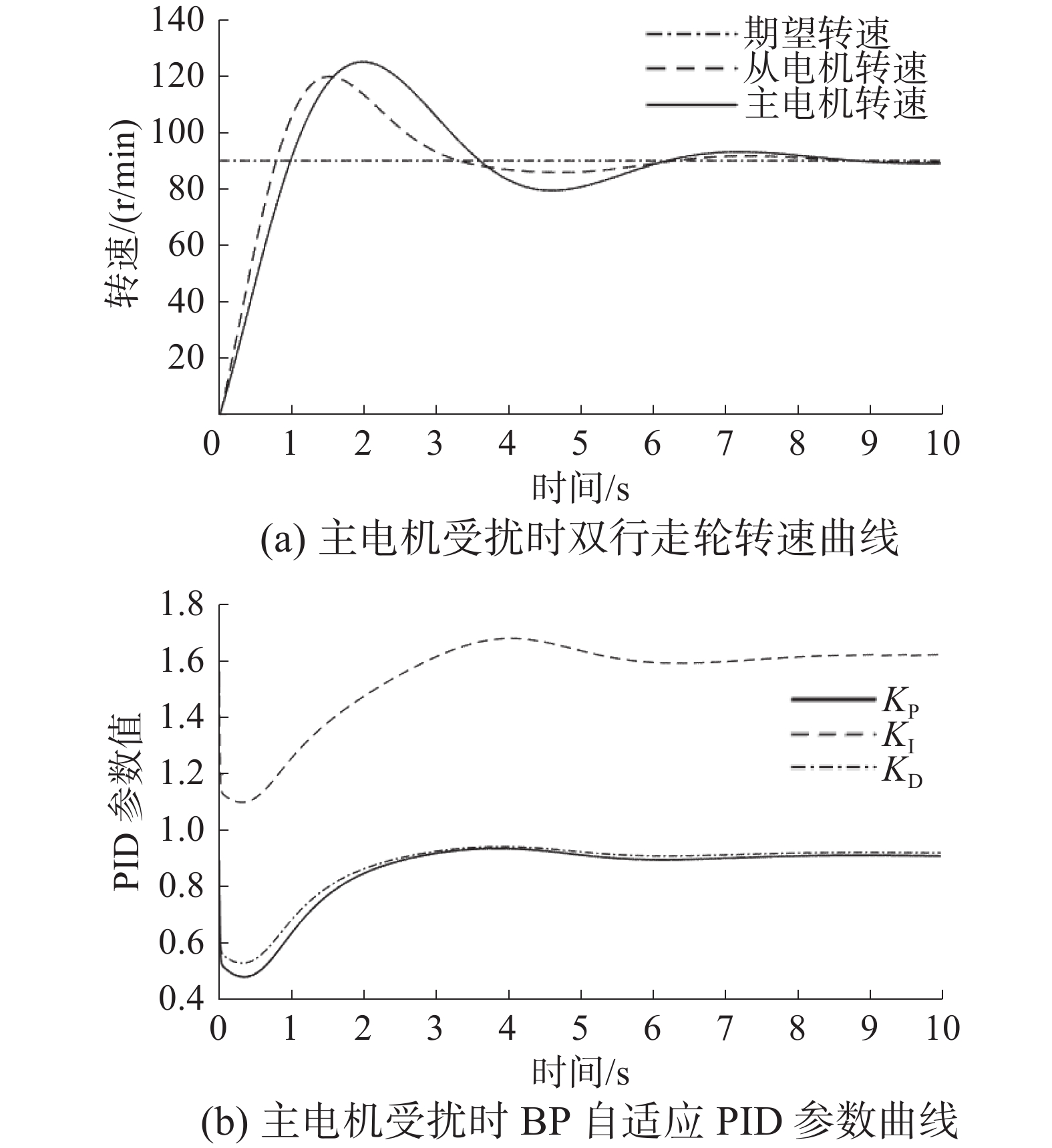
为验证控制器在实际行走过程中的抗扰与同步能力，将期望转速设置成90 r/min，在主电机上加入随机正弦扰动，仿真得到的转速同步控制与BP调节PID参数曲线如图11所示。由图11可以看出，在主电机受扰动情况下，双行走轮依然有较好的同步性能，在6.5 s时进入同步稳态，均达到期望转速。
图 11 转速同步与PID参数曲线（主电机加入扰动）下载:
全尺寸图片
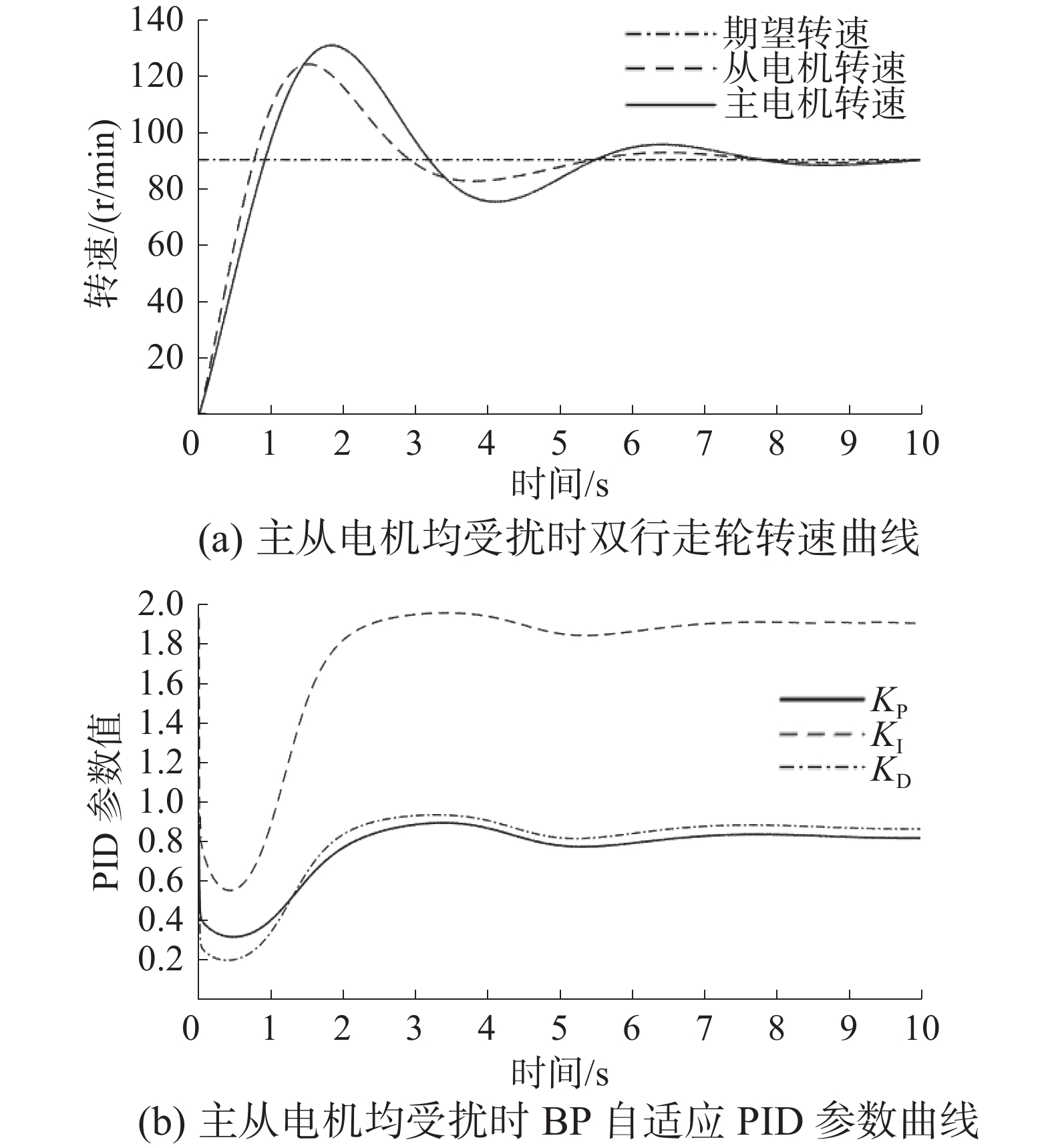
将期望转速设置成90 r/min，在主从电机上均加入随机正弦扰动，仿真得到的转速同步控制曲线如图12所示。
图 12 转速同步与PID参数曲线（主从电机加入扰动）下载:
全尺寸图片
由图12可看出，在主从电机均受扰动情况下，从属电机依然可以很好地跟随主电机运动，在7.5 s时进入同步稳态，达到期望转速。
3.2 实物试验结果
将机器人行走结构按设计加工组装，得到双行走轮系统，如图13所示。
图 13 双行走轮结构实物下载:
全尺寸图片
行走轮轮毂由高强度轻质复合材料所制（直径为21 cm），行走接触面为带有防滑纹的橡胶材料，两驱动电机为135 W的行星减速电机。控制器采用ARM公司的STM32F103芯片，双行走轮同步控制系统结构如图14所示。
图 14 双行走轮同步控制系统结构下载:
全尺寸图片
搭建220 kV级架空线路实验环境，输电线路清障飞行机器人飞行挂载到输电线路上开始行走作业，如图15所示。
图 15 清障机器人挂线行走下载:
全尺寸图片
传感器获得的双行走轮实物试验转速如表2所示，期望转速为90 r/min。
表 2 双行走轮实物试验转速表时间t/s 期望转速/
（r/min）主电机转速/
（r/min）从属电机转速/
（r/min）1 90 130.0 126.0 2 90 101.7 101.0 3 90 78.3 78.0 4 90 92.9 91.0 5 90 91.9 91.2 6 90 90.0 89.2 7 90 90.0 90.0 8 90 90.2 90.0 9 90 90.0 90.2 10 90 91.0 90.8 11 90 92.0 91.4 12 90 91.0 90.9 13 90 90.0 90.0 从表2可看出，本文设计的主从融合偏差耦合控制算法具有良好的同步性能，且对扰动具有良好的抑制能力，具有较高的行走效率，可以满足工程实际需求。
4. 结论
本文针对输电线路异物清除作业困难问题，设计了一种具有飞行挂线、行走作业功能的清障飞行机器人。主要对机器人的挂线行走机构进行机械结构设计，并对双行走轮的不同步问题进行了研究，提出了一种基于BP-PID的双行走轮同步控制器，具体结论如下：
1）根据无人机高空作业环境与无人机构型，设计一种新型行走机构，解决高空无人机作业时受外界环境扰动较大的问题。
2）针对高空作业机器人双行走轮控制误差较大导致的行走轮打滑磨损以及行走效率低等问题，设计了一种基于BP-PID主从融合偏差耦合控制的电机同步控制策略，仿真结果表明在受扰状态下，BP神经网络可以根据实际状态自适应PID参数，使机器人的双行走轮达到良好的同步性能。
3）搭建了机器人双轮行走远程控制系统实物，通过机器人爬线行走试验，证明了机器人挂线行走机构的可行性与双行走轮控制系统的同步性。
通过仿真与物理验证表明，本文设计的机器人挂线行走机构有效，提出的BP-PID双轮行走同步控制算法有效解决了驱动电机转速不完全同步导致的行走轮打滑、磨损及行走效率降低等问题。
-
图 1 V型行走轮力学分析
下载:
全尺寸图片
图 2 机器人V型行走轮
下载:
全尺寸图片
图 3 机器人挂线行走机构
下载:
全尺寸图片
图 4 直流电机等效电路
下载:
全尺寸图片
图 5 双电机主从控制
下载:
全尺寸图片
图 6 偏差耦合控制
下载:
全尺寸图片
图 7 双行走轮同步控制结构
下载:
全尺寸图片
图 8 3层BP神经网络结构
下载:
全尺寸图片
图 9 传统PID转速同步控制曲线
下载:
全尺寸图片
图 10 转速同步与PID参数曲线（无扰动）
下载:
全尺寸图片
图 11 转速同步与PID参数曲线（主电机加入扰动）
下载:
全尺寸图片
图 12 转速同步与PID参数曲线（主从电机加入扰动）
下载:
全尺寸图片
图 13 双行走轮结构实物
下载:
全尺寸图片
图 14 双行走轮同步控制系统结构
下载:
全尺寸图片
图 15 清障机器人挂线行走
下载:
全尺寸图片
表 1 行走轮及驱动电机相关参数
参数 符号 值 电机电枢绕组/Ω R 0.2 电机电枢电感/H L 0.0003 电机电气时间常数 T1 0.61 电机转动惯量/(kg·m2) J 0.08 电磁转矩系数/(Nm/A) Cm 0.0678 电机反电势系数(Vs/rad) Ce 0.0071 电机最大转速/(r/min) Nma 90 行走轮相半径/m r 0.21 表 2 双行走轮实物试验转速表
时间t/s 期望转速/
（r/min）主电机转速/
（r/min）从属电机转速/
（r/min）1 90 130.0 126.0 2 90 101.7 101.0 3 90 78.3 78.0 4 90 92.9 91.0 5 90 91.9 91.2 6 90 90.0 89.2 7 90 90.0 90.0 8 90 90.2 90.0 9 90 90.0 90.2 10 90 91.0 90.8 11 90 92.0 91.4 12 90 91.0 90.9 13 90 90.0 90.0 -
[1] ZHANG Xinghua, JIANG Cheng, HUANG Heyan, et al. Automatic classification of transmission lines based on edge detection filtering algorithm and laser point cloud data processing[J]. Electrica, 2022, 23(2): 231−239. [2] 孙夕彬, 李勇, 唐伟刚. 主网输变电设备漂浮物故障分析与隐患管控[J]. 湖北电力, 2022, 46(3): 106−112. [3] 金勋俊, 李端玲. 输电线路树木修枝机械的研究现状与发展趋势[J]. 林业机械与木工设备, 2022, 50(11): 11−17. doi: 10.3969/j.issn.2095-2953.2022.11.002 [4] 许昌亮, 杨忠, 姜遇红, 等. 新型多旋翼作业型空中机器人自抗扰控制[J]. 控制理论与应用, 2022, 39(4): 581−592. [5] 廖禄伟, 杨忠, 王灿等. 悬挂伸缩刀具的树障清理空中机器人飞行控制方法[J]. 控制理论与应用, 2023, 40(2): 343−352. [6] 张秋雁, 廖禄伟, 肖书舟, 等. 输电线路异物清除空中机器人飞行控制技术研究[J]. 应用科技, 2023, 50(3): 57−63. [7] SHEN L B, TIAN L P. A static load position identify-cation method for optical fiber-composite structures b-ased on particle swarm optimization- back Propagation neural network algorithm[J]. Measurement and control, 2023, 56(3/4): 820−831. [8] LIU Jiayi, CUI Yongmei, SONG Huihui, et al. Stabilit-y analysis of T-S fuzzy-model-based coupled control systems with nonlinear T-S fuzzy control and its appli-cation[J]. Neural computing and applications, 2021, 33(22): 15481−15493. doi: 10.1007/s00521-021-06170-9 [9] 李捷文, 杨忠, 张秋雁, 等. 树障清理机器人刀具系统自抗扰控制器设计[J]. 应用科技, 2020, 47(1): 68−73. [10] 留若宸. 多电机伺服系统同步控制研究[D]. 杭州: 浙江大学, 2020. [11] 吴鑫煜. 多电机同步驱动伺服系统控制器设计[D]. 南京: 南京理工大学, 2021. [12] LI Miaoyu, JIANG Zhuohan, LIU Yutong, et al. Sitse-n: passive sitting posture sensing based on wireless d-evices[J]. International journal of distributed sensor networks, 2021, 17(7): 155014772110248. [13] 马龙, 马昊, 桑锦明, 等. V型轮在输电线路机器人的应用研究[J]. 现代机械, 2022(2): 10−13. [14] HAQ Z U, JIANG Yang, ZIA-UL-HAQ M, et al. Surface modified alpha zirconium phosphate (α-ZrP) reinforced natural rubber composites for tire tread applicat-ion[J]. Journal of polymer research, 2023, 30(3): 121. doi: 10.1007/s10965-023-03502-2 [15] WANG He, DU Hualong, CUI Qiuyu, et al. A multi-motor speed synchronization control enhanced by artificial bee colony algorithm[J]. Measurement and control, 2023, 56(1/2): 133−146.
