Obstacle avoidance strategy of multi-USV based on improved artificial potential field
-
摘要: 针对多无人艇编队避障问题，对静态避障的路径消耗问题进行建模分析，在动态避障时提出一种偏置人工势场法使策略符合艇群国际海上避碰规则（swarm International Regulations for Preventing Collisions at Sea，sCOLREGS）。本方法首先对传统人工势场法进行改进，定义符合艇群会遇态势判断需求的sCOLREGS，通过速度障碍法实时判断碰撞风险，然后利用偏置斥力区域的改进人工势场法实现对规则的遵守。仿真实验表明，本文方法在障碍物与编队大小相当时可显著减少避障路程，在确保避障实时性的同时，较好地遵守了国际海上避碰规则相关条例。研究结论可为海面无人艇集群安全航行提供参考。Abstract: For the multiple unmanned surface vehicles formation obstacle avoidance problem, the path consumption problem of static obstacle avoidance was modeled and analyzed, and a biased artificial potential field method was proposed for dynamic obstacle avoidance to make the strategy conform to the swarm International Regulations for Preventing Collisions at Sea(sCOLREGS). This method firstly improved the traditional artificial potential field method, defined the rules that meet the needs of the swarm situation, judged the collision risk by the velocity obstacle method, and then used the improved artificial potential field with biased repulsive region to achieve compliance with the rules. Simulation experiments show that the method in this paper can significantly reduce the obstacle avoidance distance when the obstacle is comparable to the formation size, and better comply with the regulations of International Regulations for Preventing Collisions at Sea (COLREGS) while ensuring real-time obstacle avoidance. The conclusion can provide a reference for the safe navigation of unmanned boat clusters on the sea surface.
-
水面无人艇（unmaned surface vehicle，USV）是一种通过遥控或自主方式在水面作业的智能化小型平台，广泛用于情报搜集、海上救援、反潜等任务，对于维护我国海上安全与海洋权益具有重大意义。无人艇实时路径规划是水面无人艇研究的重要内容之一。路径规划算法可以分为全局规划和局部规划两部分，其中经典的全局路径规划方法包括A*算法、Dijkstra算法、快速探索随机树（rapidly-exploring random trees，RRT）、栅格法等；局部规划包括人工势场法（artificial potential field，APF）、动态窗口法（dynamic window approach，DWA）等[1]。全局规划根据已知的全局环境信息，使用各种寻优算法获取全局最优路径，其能够在任意不规则障碍物环境中计算出全局最优解，但是存在计算量大、搜索效率低的缺陷，且对突发情况应对能力不足，所以单纯的全局规划算法难以应用于探索环境未知的海域。局部规划根据智能体传感器采集的实时障碍物与位置信息，获取到目标点的局部最优路径，优点是实时性强、计算量小，能够实现对于突发事件的快速响应，但是局部规划容易陷入局部最优解，降低USV执行任务的效率。
APF由Khabit于1986年首次提出，其基本思想是仿照静电场中电势和电势场的概念，在目标点与障碍物位置处分别构造引力场
$ {U_{{\text{att}}}} $ 与斥力场$ {U_{{\text{rep}}}} $ ，其中，引力势场将吸引USV向目标点移动而斥力势场帮助USV实现障碍物规避。在势场中，USV视为一个质点，其在当前位置的合力作用下移动一个指定单位步长，到达下一位置后实时更新势场，进行下一步路径规划。APF的显著优点之一是实时性强，能较好地应对目标的变化与环境中的动态障碍物。但是在复杂地形多障碍物环境下若不同障碍物对USV施加的斥力与目标点引力的合力为0时，USV将陷入局部最优解无法脱离导致路径规划失败或目标点不可达等问题。同时APF生成的规划路径曲率变化较大，路径不平滑，对USV机动性提出挑战[2]。针对传统APF中存在的目标点不可达、无效碰撞等问题，通过对势场函数进行修正[3]，基于碰撞锥的分层人工势场[4]等方法可以加以改进。同时近年来许多工作在进行USV路径规划时考虑了国际海上避碰规则（International Regulations for Preventing Collisions at Sea，COLREGS）的要求[5-9]，但大多数是根据规则对斥力场函数分类讨论，且对保持USV编队的规则情形较少关注。COLREGS规定了存在碰撞风险时应采取的机动类型，当USV在其他船只附近航行时必须遵守COLREGS，以便USV安全避开其他海上智能体，同时给其他运动船只的决策提供可靠参考。
本文首先对经典人工势场法的障碍物形状和斥力函数进行改进以平滑规划路径，以避障过程路径消耗为指标研究了基于改进人工势场法的多无人艇群静态避障策略，提出一种进行艇群会遇态势判断的艇群国际海上避碰规则（swarm-COLREGS，sCOLREGS），并结合改进人工势场法提出符合sCOLREGS的偏置障碍物区域多USV动态避障策略。最后通过仿真验证改进APF能有效平滑规划路径，同时证明了在特定环境下分散编队避障将显著降低路程消耗，所提出的偏置障碍区域算法能够在保证实时性与安全性的情况下遵守国际海上避碰规则。
1. 改进人工势场法
在经典斥力场中，场函数是距离倒数的平方，这使得经典APF算法中的斥力场函数曲线升降过快，斥力大小在短距离内显著变化，导致规划路径曲率变化过大，对USV转向机动性提出挑战，同时造成额外的路径消耗。
为平滑避障路径，提高避障效率，本节通过增加缓冲区域使避障区域沿无人艇速度方向扩展改进斥力场形状，同时设计平滑修正系数改进斥力场函数。
1.1 障碍物区域建模
无人艇使用质点模型建模，其运动状态仅受虚拟势场力及艇间通信影响，并将执行任务环境抽象为二维平面，不考虑海浪、海流等因素的干扰。记障碍物在平面中占据的空间为点集
$ {V_{{\text{obs}}}} $ 。将环境平面划分为一系列适当精度的正方形栅格
$ {\alpha _i} $ ，若栅格属于某一障碍物（岛屿、船只等），将其赋值为1，否则为0。当划分的栅格足够小时，可近似将小栅格视为平面中的一点$ (x,y) $ ，二值障碍物地图如图1所示。
图 1 二值障碍物栅格地图
下载:
全尺寸图片
1.2 改进人工势场构建
考虑二维平面n艘无人艇集合
$ S(n) = \{ {S_i} = $ $({x_i},{y_i})|i = 1,2,\cdots,n\}$ ，记第$ i $ 艘无人艇$ {S_i} $ 到目标（goal）点${g}({x_{{\text{goal}}}},{y_{{\text{goal}}}}) $ 的距离为$\rho (i,{\text{goal}}) = \left\| ({x_i},{y_i}) - \right.$ $\left.({x_{{\text{goal}}}},{y_{{\text{goal}}}}) \right\|_2 $ ，则目标点对$ {S_i} $ 产生的引力场$ {U_{{\text{att}}}} $ 为$$ {U_{{\text{att}}}} = \frac{1}{2}\varepsilon {\rho ^2}(i,{\text{goal}}) $$ 式中
$ \varepsilon $ 为对应的引力相关正比例系数。则引力为$$ {F_{{\text{att}}}} = - \nabla {U_{{\text{att}}}} = \varepsilon \rho (i,{\text{goal}}){} {\boldsymbol{n}}_{i, g}$$ 式中
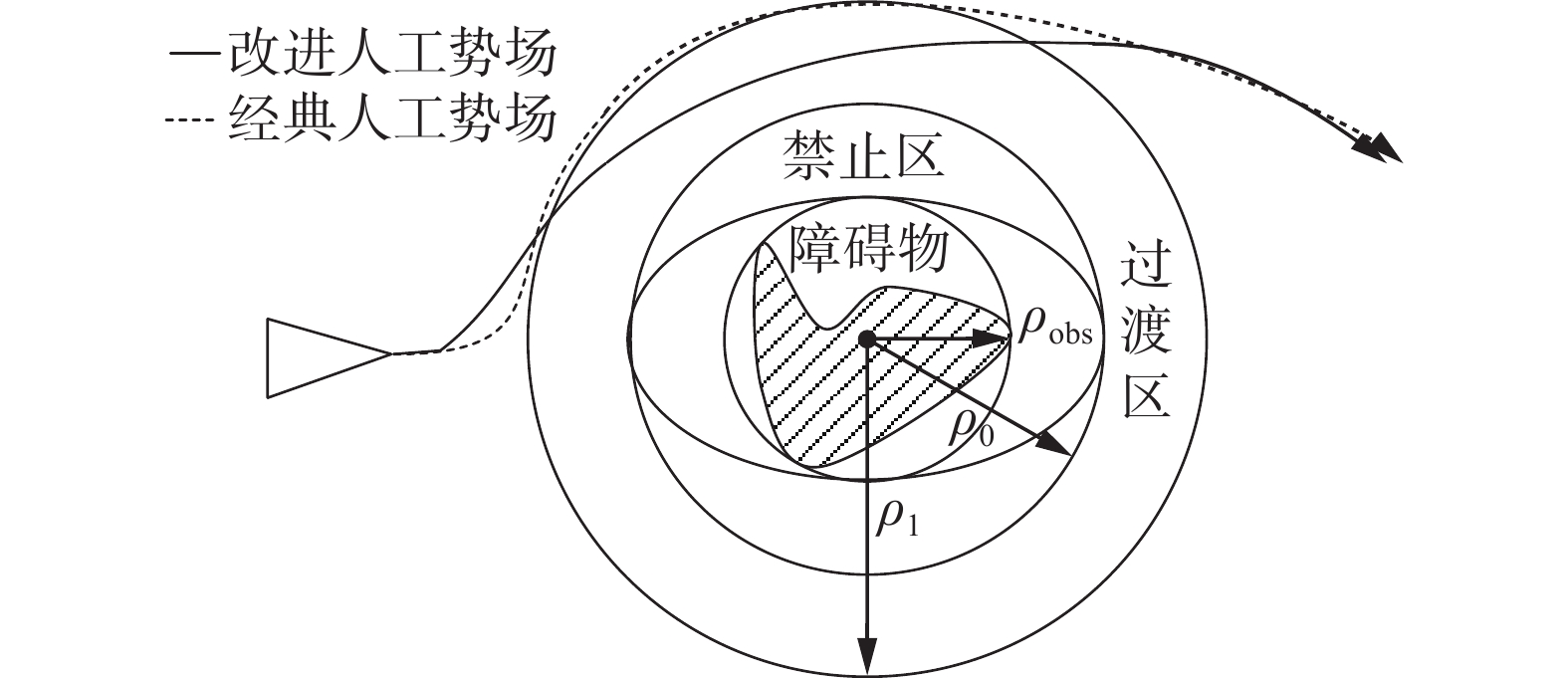
${\boldsymbol{n}}_{i, g}$ 为$ {S_i} $ 指向目标点的单位矢量。记$ {S_i} $ 到平面上一障碍物（obs）点$ {\alpha _i}({x_{{\text{obs}}}},{y_{{\text{obs}}}}) $ 距离为$$ \rho(i, \text { obs })=\left\|\left(x_i, y_i\right)-\left(x_{\text {obs }}, y_{\text {obs }}\right)\right\|_2 $$ 改进后的斥力场由障碍物椭圆、禁止区、过渡区3部分组成，如图2所示。其中
$ {\rho _{{\text{obs}}}} $ 为不规则障碍物最小圆覆盖半径，表征障碍物大小；$ {\rho _0} $ 为预设禁止距离，若USV进入此区域将无法成功避碰；$ {\rho _1} $ 为过渡区半径，当USV距障碍物为$ {\mathrm{\rho }}_{1} $ 时开始避碰，且从$ {\mathrm{\rho }}_{1} $ 降至$ {\mathrm{\rho }}_{0} $ ，斥力由0以指数速度增至最大值。
图 2 改进人工势场法斥力分区下载:
全尺寸图片
本文以
$ {\mathrm{\rho }}_{\mathrm{o}\mathrm{b}\mathrm{s}} $ 为短轴长度、$ {\mathrm{\rho }}_{0} $ 为长轴长度、USV与障碍物中心连线为长轴方向构造改进的椭圆形斥力场，通过对斥力场形状进行改进，可以使无人艇较经典方法提前进行避障，提高航行安全性，同时也使路径更为平滑，减小转向角。改进后斥力场函数的数学表达式为
$$ {U_{{\text{rep}}i}} = \lambda {\left(\frac{1}{{\rho (i,{\text{obs}})}} - \frac{1}{{{\rho _0}}}\right)^2} $$ 式中
$ \lambda $ 为斥力场改进系数，定义如下$$ \lambda=\left\{\begin{array}{l} \eta_s,\quad \rho(i, \mathrm{obs}) \leqslant \rho_0 \\ \eta_s \exp \left[\gamma\left(\frac{1}{\rho_{i 1}^m}-\frac{1}{\rho_{01}^m}\right)\right],\quad \rho_0<\rho(i, \mathrm{obs})<\rho_1 \\ 0,\quad \rho(i, \mathrm{obs}) \geqslant \rho_1 \end{array}\right. $$ 式中：
$ {\eta _s} $ 为比例系数，$ \gamma $ 为负实数，$ m $ 为大于1的实数，$ {\rho _{i1}} = \left| {{\rho _1} - \rho (i,{\text{obs}})} \right| $ ，$ {\mathrm{\rho }}_{01}=\left|{\mathrm{\rho }}_{1}-{\mathrm{\rho }}_{0}\right| $ ，由于$\mathrm{\rho }\left({i},\mathrm{o}\mathrm{b}\mathrm{s}\right) > {\mathrm{\rho }}_{0}$ ，故在过渡区${\rho _{i1}} < \left| {{\rho _1} - {\rho_0}} \right| = {\rho _{01}}$ ，指数系数$ \gamma (1/\rho _{i1}^m - 1/\rho _{01}^m) < 0 $ ，由指数函数的特点知在$ \left( { - \infty ,0} \right] $ 上$ \lambda $ 由0随$ \rho (i,{\text{obs}}) $ 增速变化至$ {\eta _s} $ ，且变化较为缓慢，更容易控制。通过求解斥力场的梯度可以得到USV所受斥力为$$ {F_{{\text{rep}}i}} = - \nabla {U_{{\text{rep}}i}} $$ 故无人艇在
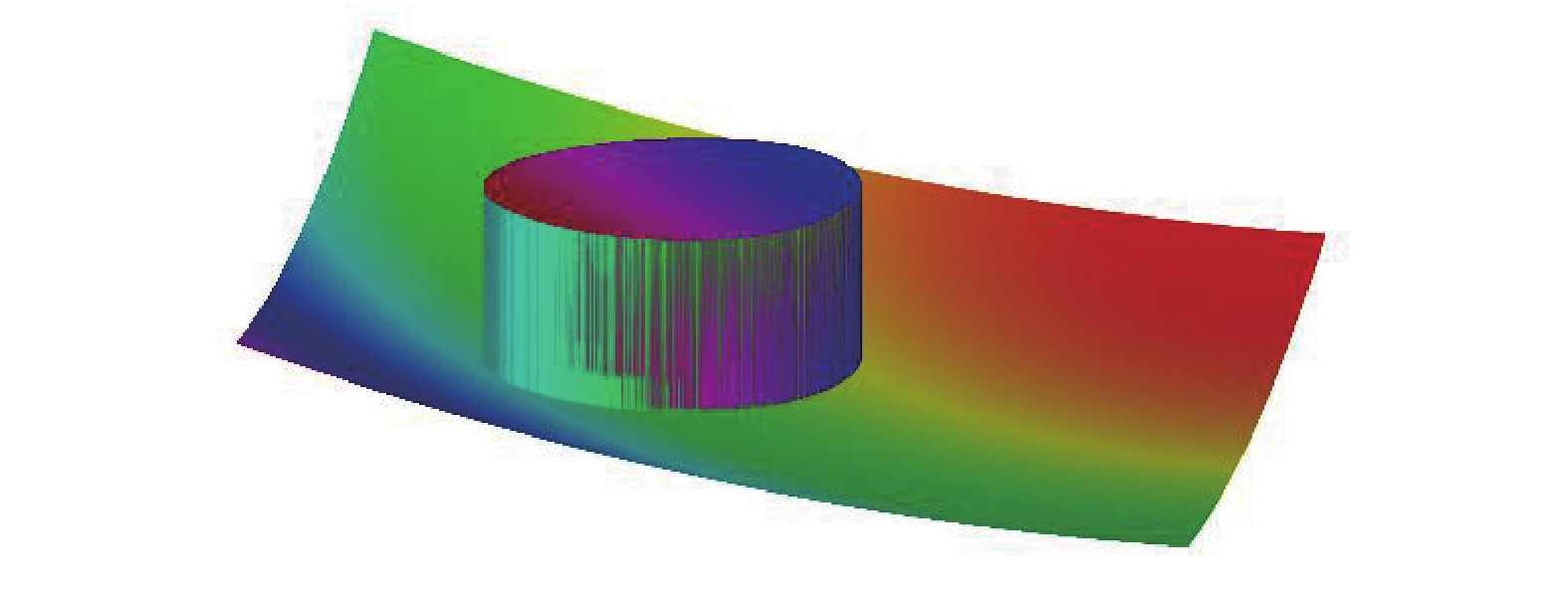
$ ({x_i},{y_i}) $ 处所受的虚拟势场合力为$$ {F_{{\text{total}}}} = {F_{{\text{att}}}} + \iint\limits_{{V_{{\text{obs}}}}} {{F_{{\text{rep}}i}}{\text{d}}S} $$ 合势力场形状如图3所示。
图 3 改进人工势场法合势力场形状下载:
全尺寸图片
2. 路程评价的艇群分散避障策略
USV在执行任务过程中，可能会遇到大小尺寸不同的障碍物。USV编队在复杂地形环境中作业时，障碍物规避问题成为USV编队需要面对的一大挑战。由于复杂环境下障碍物数量与分布随机，为保证安全性USV编队需要低速通过，故此时对于航线长度的要求高于规划路径平稳性，以降低避障过程能量消耗，提高USV编队续航能力[10]。本节首先介绍编队控制方法，在此基础上研究当障碍物与编队大小相当时以编队避障总路程为评价指标的一种编队变换避障策略。
2.1 基于一致性的一阶分布式编队控制
多无人艇编队采用leader-follower编队形式[11]，以一虚拟领航者为中心，编队成员均匀对称分布于半径为
$ r $ 的圆周。设编队成员数为$ N $ 的艇群为$S(N) = \{ {S_i}|i = 0,1,\cdots,N\}$ ，其中$ {S_0} $ 为编队虚拟领航者（Leader）。定义加权有向图$ G = (V,E) $ 表示编队通信拓扑结构，其中节点集$ V = S(N) $ 表示编队成员，边集$ E = \{ {e_{ij}} = ({S_i},{S_j})\} $ 表示编队成员$ i、j $ 间是否存在通信关系，对应的eij取值为1、0。定义邻接矩阵$$ {\boldsymbol{A}} = {[{a_{ij}}]_{N \times N}} = \{ 0,1\} $$ 式中：当
$ {e_{ij}} = 1 $ 时，$ {a_{ij}} = 1 $ ；否则$ {a_{ij}} = 0 $ 。本文编队拓扑图如图4所示。
图 4 编队通信拓扑结构有向图下载:
全尺寸图片
定义入度矩阵
$$ {\boldsymbol{D}} = {\rm{diag}}\{ {d_i}\} $$ 式中
$ {d_i} = \sum\nolimits_j {{a_{ij}}} $ 为加权入度。出度为$ d_i^o = \sum\nolimits_j {{a_{ji}}} $ ，可体现此成员对其他编队成员的控制作用，$ d_i^o $ 越大其对编队一致性的影响也越大，由$ {\boldsymbol{A}} $ 及图4可知S0出度最大，为领导节点。定义有向图
$ G $ 的拉普拉斯矩阵为$$ {\boldsymbol{L}} = {\boldsymbol{D}} - {\boldsymbol{A}} $$ 式中
$ {\boldsymbol{L}} $ 是半正定阵。编队一阶线性连续控制方程为
$$ {\dot {\boldsymbol{x}}_i} = {u_i} $$ 式中：
$ {{\boldsymbol{x}}_i} $ 为状态量，$ {u_i} $ 为如下线性输入量。$$ {u_i} = \sum\limits_{j \in N(i)} {{a_{ij}}({{\boldsymbol{x}}_j} - {{\boldsymbol{x}}_i}) = {\boldsymbol{Ax}} - {\boldsymbol{Dx}} = - {\boldsymbol{Lx}}} $$ 使用Lyapunov函数
$V = {{\boldsymbol{x}}^{\text{T}}}{\boldsymbol{x}}/2$ 研究此系统稳定性。对状态量求导，并利用$ L $ 的半正定性可得$$ \dot V = {{\boldsymbol{x}}^{\text{T}}}\dot{\boldsymbol{x}} = - {{\boldsymbol{x}}^{\text{T}}}{\boldsymbol{Lx}} \leqslant 0 $$ 考虑
$ \dot V = 0 $ 的情形。注意到图$ G $ 联通，即存在生成树，故$ {\boldsymbol{L }}$ 有且仅有一个0特征值，且其特征向量为1向量[12]，即$$ {\boldsymbol{L}} {\mathbf{1}}_{{n}} ={\mathbf{0}}_{{n}} $$ 由
$ {\boldsymbol{L}} $ 的半正定性知${{\boldsymbol{x}}^{\text{T}}}{\boldsymbol{Lx}} = 0$ 与${\boldsymbol{Lx}} ={\mathbf{0}}_{{n}}$ 同解，所以${\boldsymbol{x}} = {{\boldsymbol{x}}_0}{{{ {1} }}_{{n}}}({{\boldsymbol{x}}_0} \in R)$ ，此时诸状态量达到一致，且仅与$ L $ 及初状态有关。故当状态量不一致时由$ \dot V < 0 $ 状态量将逐步收敛至${{\boldsymbol{x}}_0}(\dot V = 0)$ ，系统稳定性得到证明。离散时间情形下编队一阶控制方程为
$$ {{\boldsymbol{x}}_i}(k + 1) = {{\boldsymbol{x}}_i}(k) + {u_i}(k) $$ 编队中跟随者（follower）控制算法为
$$ {u_i} = \varepsilon \sum\limits_{j \in N(i)} {{a_{ij}}({{\boldsymbol{x}}_j}(k) - {{\boldsymbol{x}}_i}(k) - {d_{ij}}(k))} $$ 式中：
$ \varepsilon > 0 $ 为常数，$ N(i) $ 为节点$ i $ 的邻居节点集合，$ {d_{ij}} $ 为节点$ i $ 、$ j $ 间距离。Leader控制算法为第1节所导的APF合力，即
$$ {u_N}(k) = {F_{{\text{total}}}} + \varepsilon \sum\limits_{j \in N(i)} {{a_{Nj}}{d_{Nj}}(k)} $$ 2.2 避障开始与结束规定
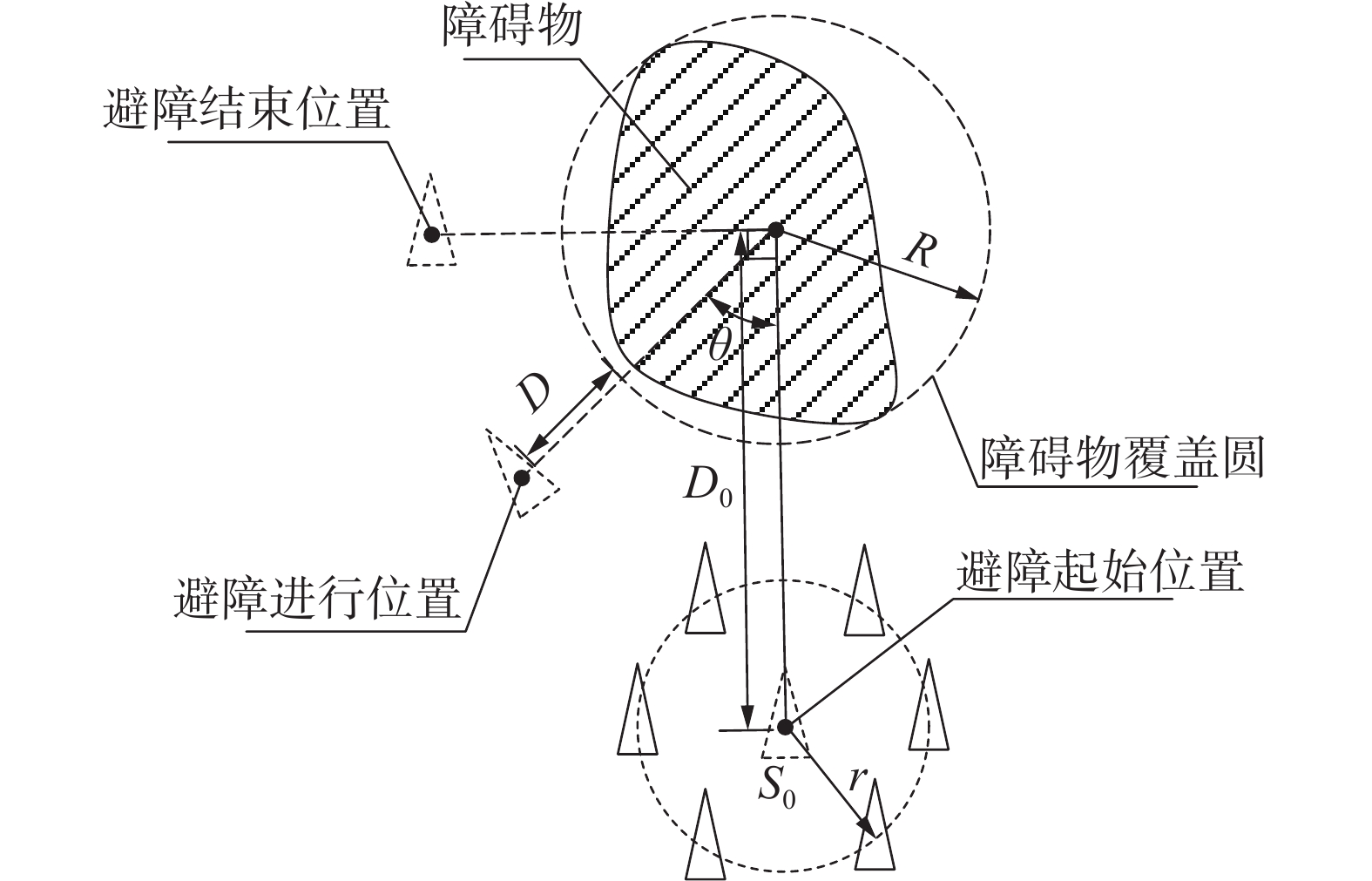
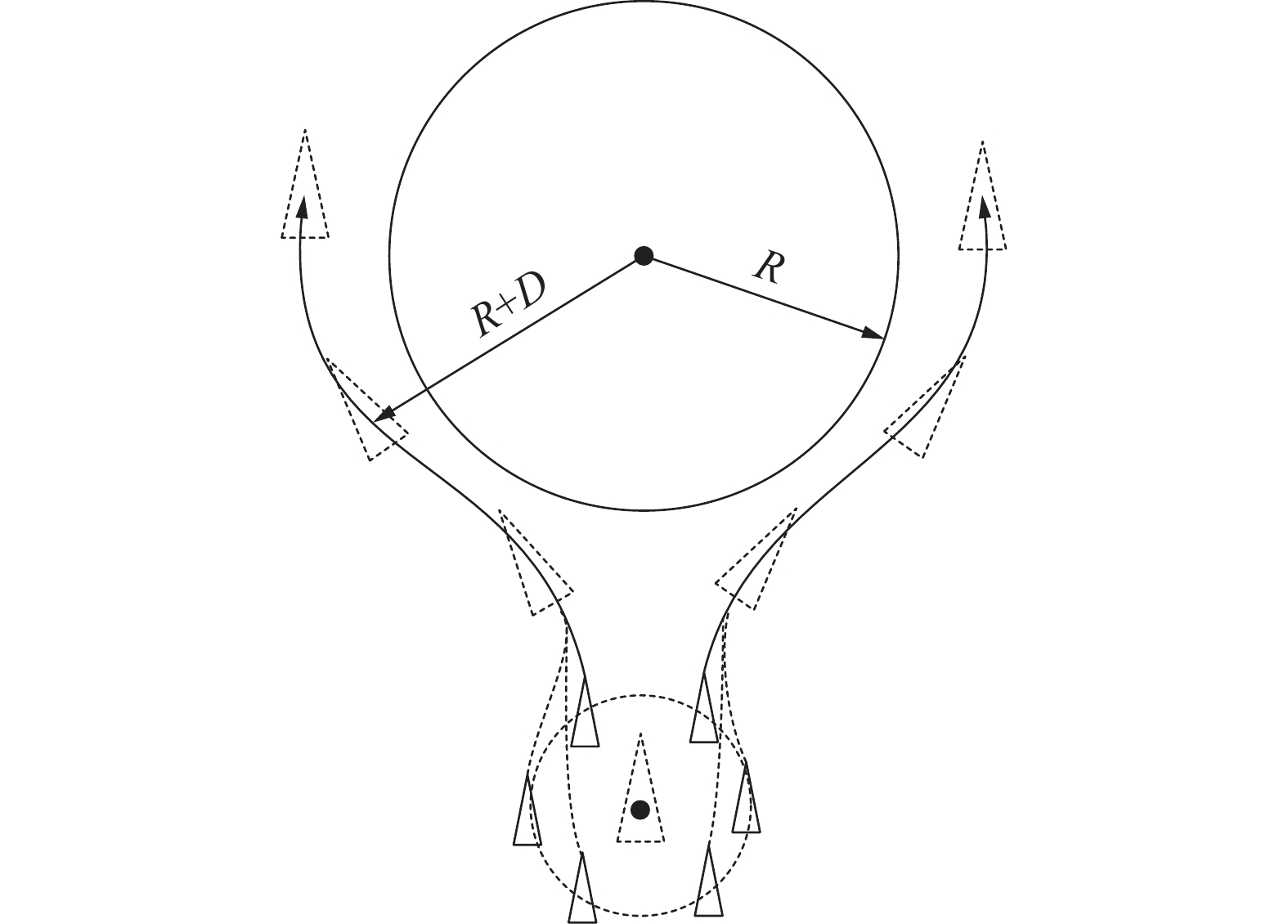
如图5所示，设障碍物最小覆盖圆大小为
$ R $ ，单艇避碰过程中到障碍物圆的最小许可距离为$ D $ ，当虚拟领航者S0距离障碍物中心小于$ {D_0}( > R + D + r) $ 时，开始避障程序。
图 5 避障开始与结束位置示意下载:
全尺寸图片
记
$ {S_i} $ 从开始避障位置相对障碍物中心驶过的角度为$ \theta $ ，当$ {0^\circ } < \theta < {90^\circ } $ 时，USV处于避障阶段。当$ \theta = {90^\circ } $ 时，结束避障。2.3 避障策略建模对比
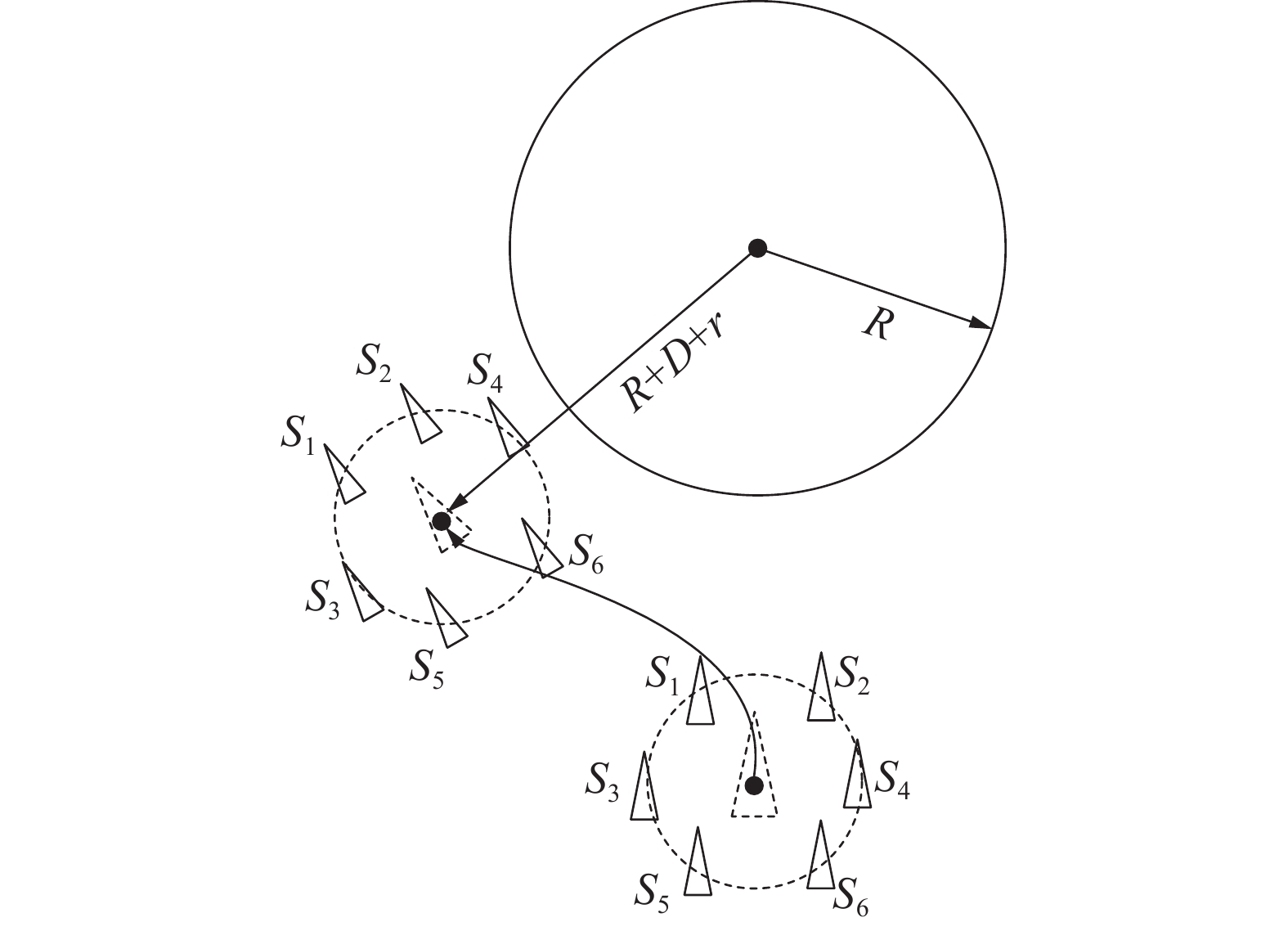
若避障时USV编队保持结构刚性，不进行编队变换，按照虚拟领航者所受人工势场力进行路径规划，整体从障碍物一侧绕过，这一策略的示意如图6所示。
图 6 策略1示意下载:
全尺寸图片
避障总路程与最小许可距离
$ D $ 有关，设此函数关系为$ f(D) $ 。在上述策略中，由编队队形的对称性，当艇群成员数
$ j $ 为偶数时，在虚拟领航者两侧的一对无人艇行驶的总路程可以等效为虚拟领航者行驶总路程的2倍，故所有编队成员避障总路程为虚拟领航者的$ 2 \times j/2 = j $ 倍；当$ j $ 为奇数时，设第1艘无人艇在虚拟领航者正前方，则此艘艇行驶总路程与虚拟领航者相等，对其余$ j - 1 $ （偶数）艘无人艇，化归为上述偶数情形，故所有编队成员避障总路程为虚拟领航者的$ 1 + (j - 1) = j $ 倍。编队成员数量为奇数和偶数时的队形对称等效示意如图7所示。
图 7 USV编队对称性分析下载:
全尺寸图片
综合2种情形，无人艇编队避障总路程消耗为
$$ {d_1} = j \cdot f(D + r) + \sum\limits_i {{r_{1i}}} $$ 式中
$ \sum\nolimits_i {{r_{1i}}} $ 为避碰标准误差距离，其描述艇群在避碰时行驶的总路程与等效虚拟领航者避碰路程的差值。USV编队靠近障碍物侧成员（如图6中的$ {S_2} $ 、$ {S_4} $ 、$ {S_6} $ ）对应的$ {r_{1i,{\text{in}}}} < 0 $ ，远离障碍物一侧成员（如图6中的$ {S_1} $ 、$ {S_3} $ 、$ {S_5} $ ）对应的$ {r_{1i,{\text{out}}}} > 0 $ ，由编队对称性得$$ {r_{1i,{\text{in}}}} + {r_{1i,{\text{out}}}} \approx 0 $$ 故
$ \sum\nolimits_i {{r_{1i}}} = \sum\nolimits_i ({{r_{1i,{\text{in}}}} + {r_{1i,{\text{out}}}})} \approx 0 $ 。在不考虑编队变换的情况下，USV编队将保持当前结构从障碍物短侧绕行，这种策略不仅导致USV编队的总体能量消耗提升，不利于USV编队进行长时间作业，而且会增大与紧邻障碍物碰撞的风险，降低USV航行的安全性。
下面考虑编队分散的避障策略。当虚拟领航者
$ {S_0} $ 距离障碍物中心小于$ {D_0} $ 时，开始避障程序。此时编队队形不再保持，各艇按照距离障碍物最近距离，由小到大开始进入避障程序，目标点为引力点，障碍物及其他艇为斥力点形成的人工势场中进行路径规划，如图8所示。
图 8 编队分散避障策略示意下载:
全尺寸图片
上述策略中无人艇编队避障总路程消耗为
$$ {d_2} = j \cdot f(D) + \sum\limits_i {{r_{2i}}} $$ 式中
$ \sum\nolimits_i {{r_{2i}}} $ 类似$ \sum\nolimits_i {{r_{1i}}} $ 定义，描述每一艘艇在编队避碰时行驶的路程与虚拟领航者避碰时行驶路程的差值。这一差值主要由进入避障的先后顺序造成的时间差产生。由编队对称性知此项几乎为0，对于USV编队的总规划路程长度几乎没有影响。故2种策略的路程比为$$ \frac{{{d_1}}}{{{d_2}}} = \frac{{j \cdot f(D + r) + \sum\nolimits_i {{r_{1i}}} }}{{j \cdot f(D) + \sum\nolimits_i {{r_{2i}}} }} \approx \frac{{f(D + r)}}{{f(D)}} $$ 将
$ f(D + r) $ 在$ D $ 处进行泰勒展开，得$$ f(D + r) = f(D) + rf'(D) + \frac{{{r^2}}}{2}f''(D) + \sum\limits_{i = 3}^n {\frac{{{r^i}}}{{i!}}{f^{(i)}}(D)} $$ 当
$ R $ 足够大时，避碰段曲线$ f $ 近似为二次曲线，可认为$ {f^{(i)}}(D) = 0，i \geqslant 3 $ 。$$ \frac{{{d_1}}}{{{d_2}}} \approx 1 + r\frac{{f'(D)}}{{f(D)}} + \frac{{{r^2}}}{2}\frac{{f''(D)}}{{f(D)}} = 1 + {f_1} + {f_2} $$ (1) 式中：
$ {f_1} = rf'(D)/f(D) = r(\ln f(D))' $ 为主导项,$ {f_2} = {r^2}f''(D)/(2f(D)) $ 为高阶余项。由式(1)可知2种策略的路程比仅与编队半径
$ r $ 、障碍物覆盖圆半径$ R $ ($ f $ 与$ R $ 有关)以及安全距离$ D $ 相关。对改进APF椭圆形斥力场，记安全距离为$ {\rho _0} $ ，对1/4椭圆弧长，有如下Ramanujan近似公式[13]：$$ f(D) = \frac{{\text{π }}}{4}({\rho _0} + R + 2D)\left(1 + \frac{{3{\lambda ^2}}}{{10 + \sqrt {4 - 3{\lambda ^2}} }}\right) $$ 式中
$ \lambda = ({\rho _0} - R)/({\rho _0} + R + 2D) $ 。对变量$ D $ 求偏导，有$ \lambda ' = - 2{\lambda ^2}/({\rho _0} - R) $ ，$ \lambda '' = 8{\lambda ^3}/{({\rho _0} - R)^2} $ 。由于
$ ({\rho _0} - R) \ll ({\rho _0} + R + 2D) $ ，所以$ \lambda \approx 0 $ ，故$$ \begin{gathered} f^{\prime \prime}(D)=\left\{\frac{{\text{π}}}{4} \frac{\rho_0-R}{\lambda}\left(1+\frac{3 \lambda^2}{10+\sqrt{4-3 \lambda^2}}\right)\right\}^{\prime \prime} \approx \\ \frac{{\text{π}}\left(\rho_0-{R}\right)}{4}\left(\frac{1}{\lambda}+\frac{\lambda}{4}\right)^{\prime \prime}=\frac{{\text{π}} \lambda^3}{2\left(\rho_0-{R}\right)} \end{gathered} $$ $$\therefore f_2=\frac{{\text{π}}^2 r^2 \lambda^3}{4\left(\rho_0-{R}\right)} \left/\left\{\frac{{\text{π}}}{4} \frac{\rho_0-R}{\lambda}\left(1+\frac{\lambda^2}{4}\right)\right\}=\frac{r^2 \lambda^4}{\left(\rho_0-{R}\right)^2}\right. $$ 由于
$ \ln (1 + 3{\lambda ^2}/(10 + \sqrt {4 - 3{\lambda ^2}} )) \approx \ln (1 + {\lambda ^2}/4)\approx $ $ {\lambda ^2}/4 $ ，有$$ \begin{aligned} {f_1} = r(\ln f(D))' & = r\left(\ln \left(\frac{{\text{π}}}{4}\right) + \ln ({\rho _0} + R + 2D) + \frac{{{\lambda ^2}}}{4}\right)' = \\ & \frac{{2r}}{{{\rho _0} - R}}\left(\lambda - \frac{1}{2}{\lambda ^3}\right) \\ \end{aligned} $$ 所以
$$ \frac{{{d_1}}}{{{d_2}}} = 1 + \frac{{2r}}{{{\rho _0} - R}}\left(\lambda - \frac{1}{2}{\lambda ^3}\right) + \frac{{{r^2}{\lambda ^4}}}{{{{{\text{(}}{\rho _0}-{\text{ R)}}}^2}}} $$ 略去
$ \lambda $ 的高阶无穷小项，得$$ \frac{{{d_1}}}{{{d_2}}} \approx 1 + \frac{{2r}}{{{\rho _0} - R}}\lambda = 1 + \frac{{2r}}{{{\rho _0} + R + 2D}} $$ 综上所述，在改进椭圆形人工势场情形下，当编队大小
$ r $ 与障碍物大小$ R $ 在同一数量级时，避障总路程之比$ {d_1}/{d_2} $ 将会显著大于1，$ r $ 与$ R $ 的比值越大，2种策略的路程比也越大，此时采用第2种策略将大大降低USV编队的能量消耗，提升编队的续航能力。3. 符合COLREGS的偏置人工势场法
本节考虑艇群与动态障碍物(如船只)会遇的局面。通过速度障碍法判断碰撞风险，按照艇群避碰需求对COLREGS对遇、右交叉、左交叉3种会遇态势进行修正，提出艇群国际海上避碰规则，提出一种基于改进APF的偏置障碍区域避碰方法。
3.1 速度障碍法避碰判断
速度障碍法(velocity obstacle，VO)常用于无人艇紧急避碰中[14]。假设无人艇当前的位置为
$ {P_{{S_i}}} $ ，速度为${{\boldsymbol{v}}} _{{S_i}}$ 。将障碍物抽象为一圆形区域，障碍物中心位置为$ {P_{{\text{obs}}}} $ ，速度为${ {{\boldsymbol{v}}} _{{\text{obs}}}}$ ，无人艇与障碍物圆的2条切线分别为${\boldsymbol {T} _1}$ 、${\boldsymbol {T} _2}$ 。如图9所示，两者的相对速度为${\boldsymbol {v} _{{\text{uo}}}} = {\boldsymbol {v} _{{S_i}}} - {\boldsymbol {v} _{{\text{obs}}}}$ ，若$\max \left\{\left\langle\boldsymbol{v}_{\text {uo } }, \boldsymbol{T}_1\right\rangle,\left\langle\boldsymbol{v}_{\text {uo } }, \boldsymbol{T}_2\right\rangle\right\} \leqslant \left\langle\boldsymbol{T}_1, \boldsymbol{T}_2\right\rangle$ 成立，则认为可能碰撞，此时无人艇速度${\boldsymbol {v} _{{S_i}}}$ 称为一个速度障碍。所有速度障碍组成的集合可以表示为
图 9 速度障碍法示意下载:
全尺寸图片
$$ \begin{aligned} & \;\;V_{\mathrm{vo}}=\left\{\boldsymbol{v}_{S_i} \mid \boldsymbol{v}_{S_i}=\left(\boldsymbol{v}_{\boldsymbol{i}} \cos \theta, \boldsymbol{v}_{\boldsymbol{i}} \sin \theta\right),\right. \\ & \left.\max \left\{\left\langle\boldsymbol{v}_{\mathrm{uo} }, \boldsymbol{T}_1\right\rangle,\left\langle\boldsymbol{v}_{\text {uo }}, \boldsymbol{T}_2\right\rangle\right\} \leqslant\left\langle\boldsymbol{T}_1, \boldsymbol{T}_2\right\rangle\right\} \end{aligned}$$ 当速度
$ {\boldsymbol{v}_{{S_i}}} \in {V_{{\text{VO}}}} $ 时，为保证航行的安全性USV优先执行避障任务；当$ {\boldsymbol{v}_{{S_i}}} \notin {V_{{\text{VO}}}} $ 时认为此时刻无碰撞风险，USV保持原方向与速度继续航行。3.2 国际海上避碰规则(COLREGS)
自1972年提出以来，国际海上避碰规则一直是航海实践中会遇态势判断与避碰策略选择的重要依据。对于两艇会遇局面下的COLREGS遵守，已有较多的工作[15-16]。然而当USV通信距离受限，需要在保持编队的情况下进行动态避障时，上述方法将难以在保证安全性的前提下严格遵守COLREGS。本节根据艇群避碰特点，提出适用于艇群与动态障碍物会遇的sCOLREGS。
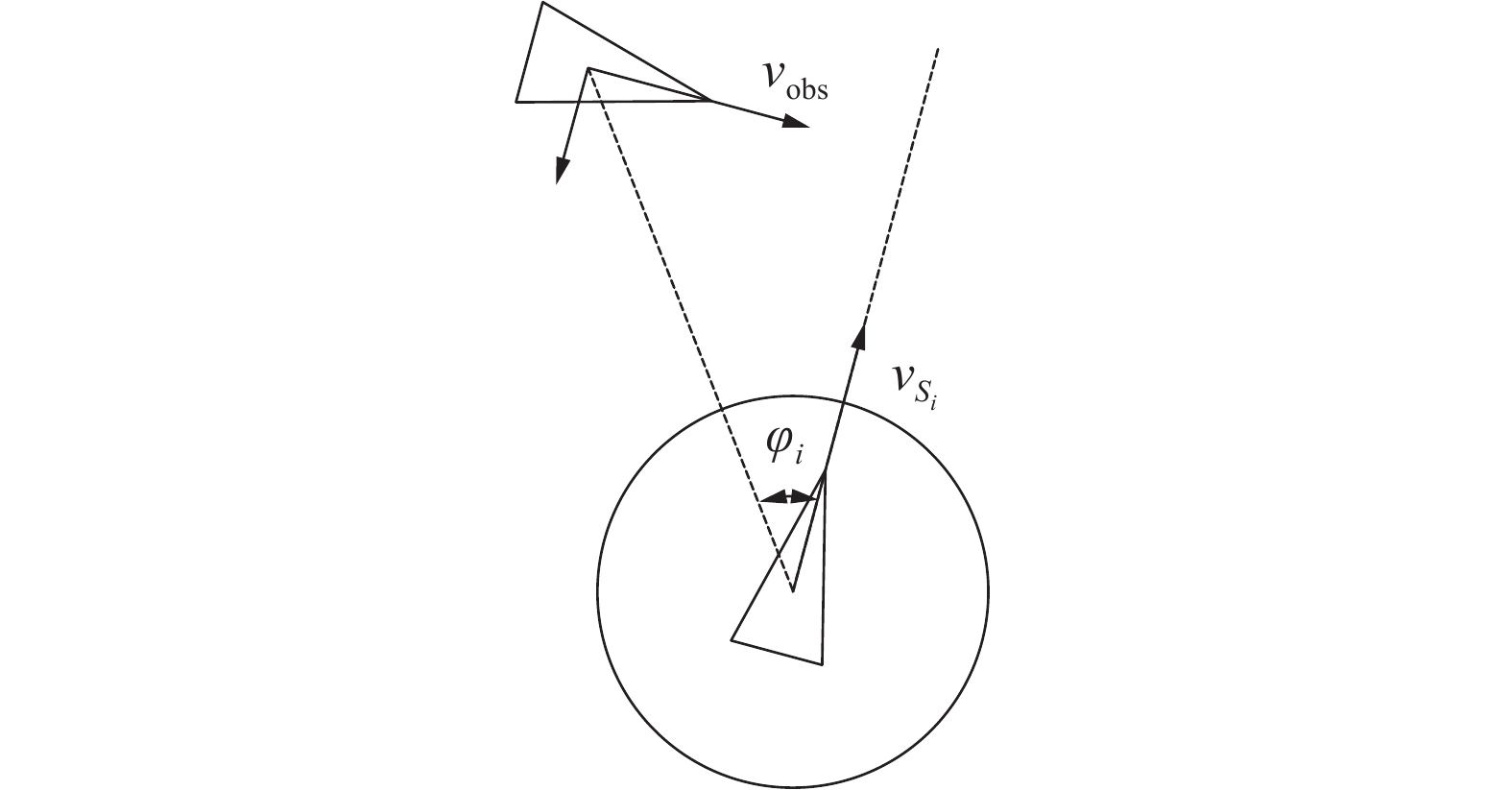
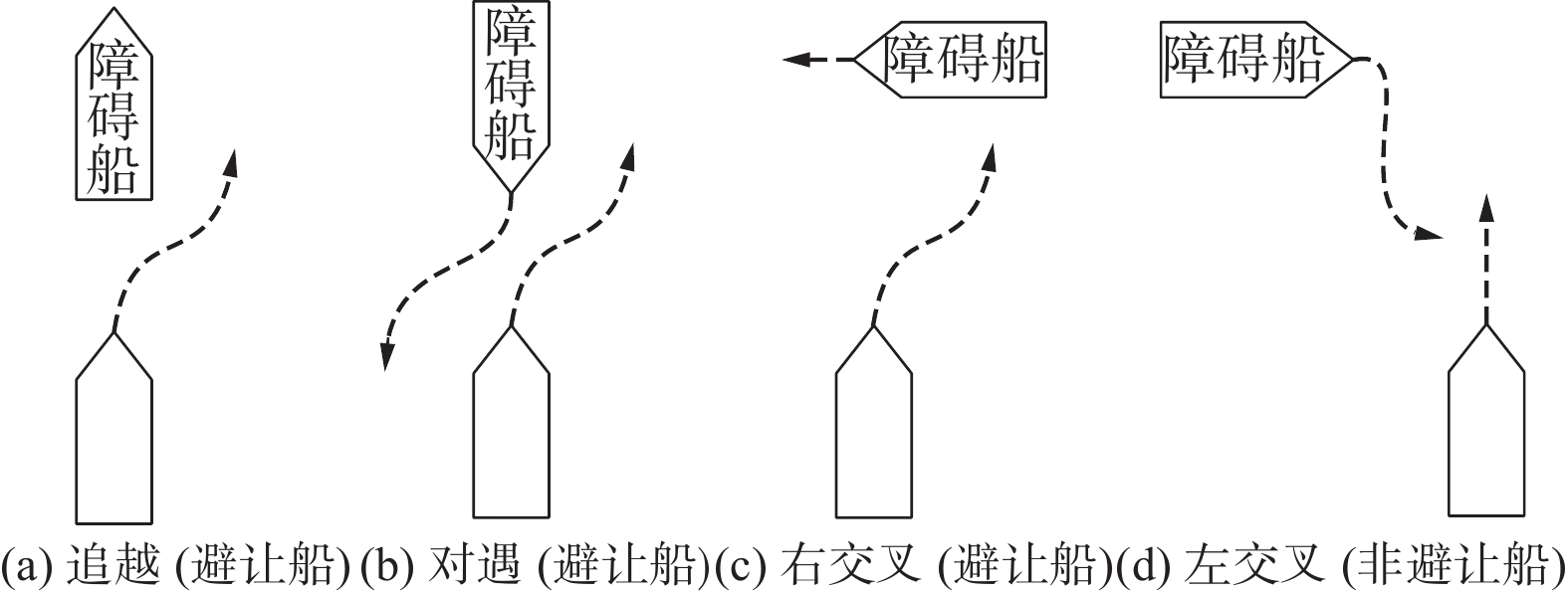
首先介绍COLREGS对两单艇会遇态势与避碰责任的规定。如图10所示，定义会遇角
$ {\varphi _i} \in ({0^{\circ} },{360^{\circ} }) $ 为本船与障碍船质心连线与本船速度$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} _{{S_i}}} $ 方向所成角[17]。在有碰撞风险的情况下，依照国际海上避碰规则指导，以$ {\alpha _1} = {5^{\circ} } $ 、${\alpha _1} = {112.5^{\circ} }$ 为阈值，按$ {\varphi _i} $ 的大小及船速比将本船采取的避障策略分为表1中的5种情况，对应的策略示意如图11所示。
图 10 COLREGS会遇态势判断下载:
全尺寸图片
表 1 会遇态势判断表$ {\varphi _i} $ ${v_{ {S_i} } }/{v_{{\rm{obs}}} }$ 态势 ${v_{{S_i}}} \in {V_{{\text{VO}}}}$ 本船策略 $ ( - {5^{\circ} },{5^{\circ} }) $ — 对遇 是 右转避让 $ \begin{gathered} ({5^{\circ} },{112.5^{\circ} }) \end{gathered} $ <0.95 右交叉 是 右转避让 $ \begin{gathered} ({5^{\circ} },{112.5^{\circ} }) \end{gathered} $ >0.95 右交叉 是 保速直行 $ ({112.5^{\circ} },{360^{\circ} }) $ — 左交叉 是 保速直行 — — — 否 保速直行 
图 11 COLREGS避碰策略示意下载:
全尺寸图片
对于艇群与动态障碍物会遇态势判断，由于一方从单艇膨胀为艇群，上述规则不能直接应用。为此，分别以USV编队虚拟leader
$ {S_0} $ （编队方）与动态障碍船$ {S_{{\text{obs}}}} $ （单艇方）为参考，定义如下判断准则sCOLREGS。对于编队方，定义
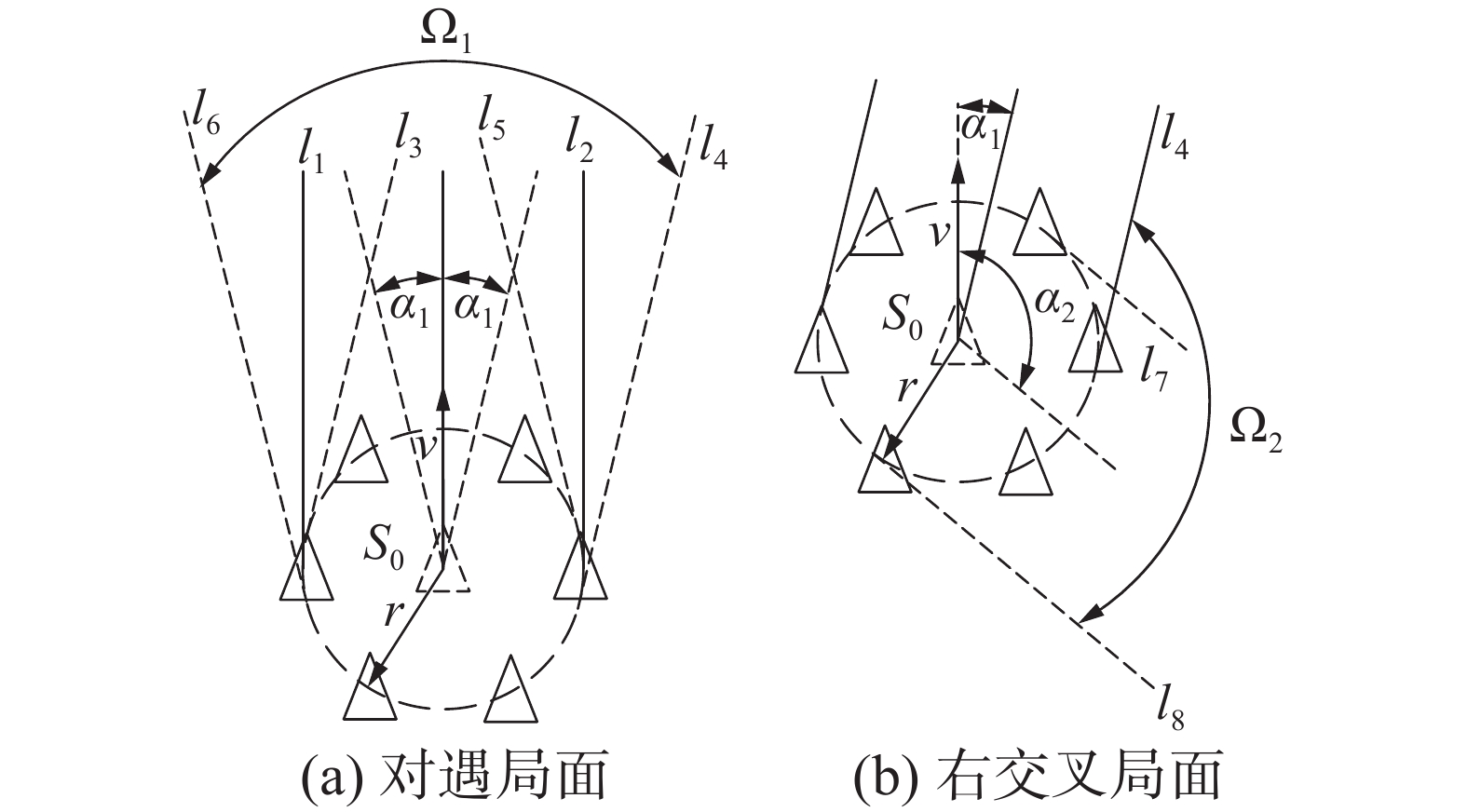
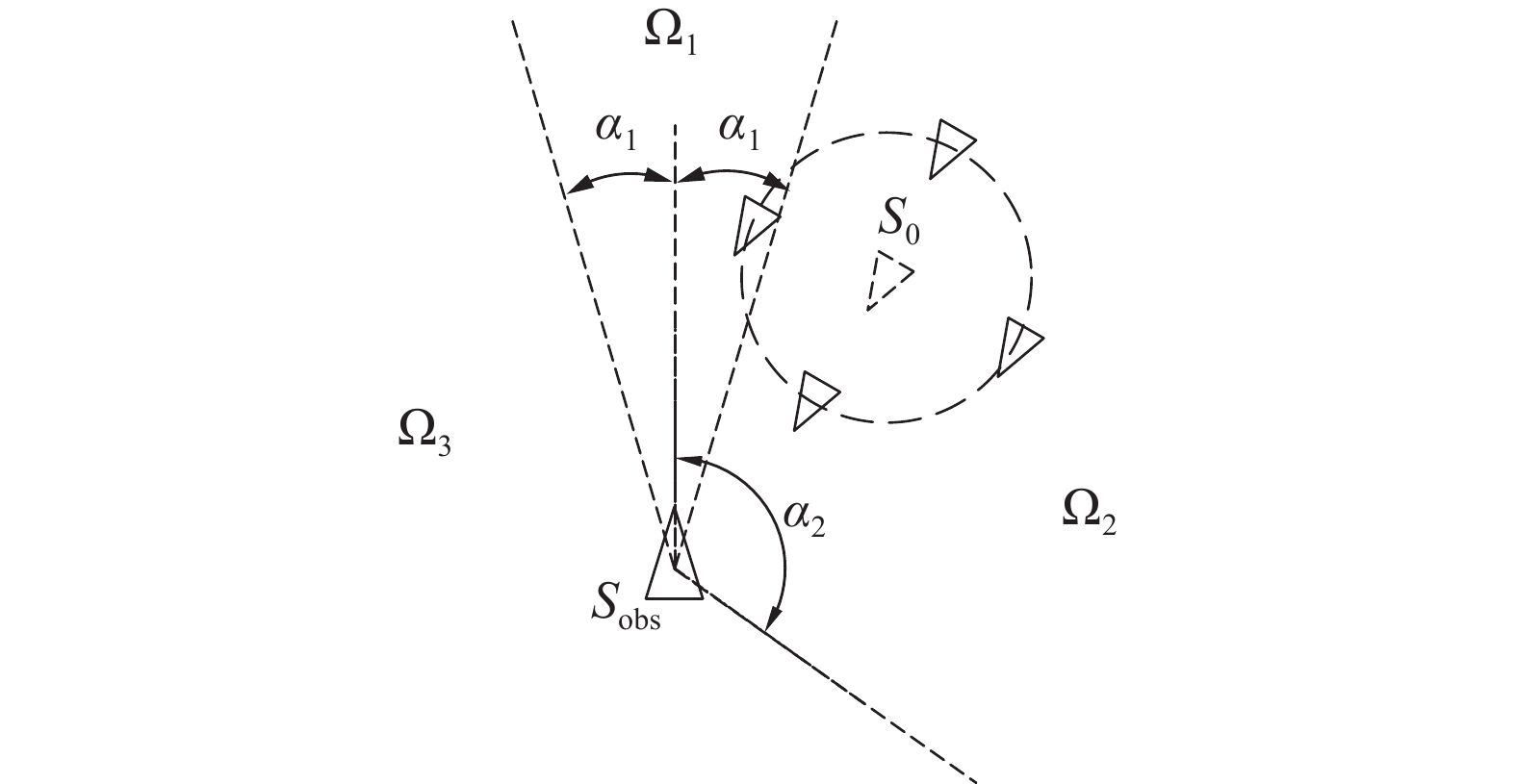
$ \alpha - $ 前向区域为编队沿速度方向前进时覆盖的区域，其中$ \alpha $ 为区域与速度方向顺时针夹角。图12中射线$ {l_1} $ 、$ {l_2} $ 形成的区域即为此时编队的$ {0^{\circ} } - $ 前向区域。
图 12 sCOLREGS编队方会遇态势判断下载:
全尺寸图片
记编队的
$ {\alpha _1} - $ 前向区域与$ ( - {\alpha _1}) - $ 前向区域的边界$ {l_4} $ 、$ {l_6} $ 所夹区域为$ {\Omega _1} $ ，如图12(a)所示。编队的$ {\alpha _1} - $ 前向区域与$ {\mathrm{\alpha }}_{2} $ 前向区域的边界$ {l_4} $ 、$ {l_8} $ 所夹区域为$ {\Omega _2} $ ，如图12(b)所示。当$ {S_{{\text{obs}}}} \in {\Omega _1} $ 时，认为此时相当于COLREGS中的对遇局面；当$ {S_{{\text{obs}}}} \in {\Omega _2} $ 时，认为此时相当于COLREGS中的右交叉局面；当$ {S_{{\text{obs}}}} \in {\bar \Omega _1} \cap {\bar \Omega _2} $ 时，认为此时相当于COLREGS中的左交叉局面。对于单艇方，以区域编队成员最大累计数为指标进行会遇态势划分。以
$ {S_{{\text{obs}}}} $ 为中心将平面按与速度夹角为$ ({360^{\circ} } - {\alpha _1},{360^{\circ} }) \cup ({0^{\circ} },{\alpha _1}),({\alpha _1},{\alpha _2}), ({\alpha _2},{360^{\circ} } - {\alpha _1}) $ 分为$ {\Omega _1} $ 、$ {\Omega _2} $ 、$ {\Omega _3} $ 共3部分，如图13所示。
图 13 sCOLREGS单艇方会遇态势判断下载:
全尺寸图片
设编队成员为
$ {S_j}(j = 1,2,\cdots,n) $ ，定义区域$ {\Omega _i} $ 编队成员累计数为$ {\sigma _i}(i = 1,2,3) $ 。$$ {\sigma _i} = \mathop {{\text{card}}}\limits_{{S_j} \in {\Omega _i}} {\text{ }}S $$ 区域编队成员最大累计数为
$ \sigma = \max \{ {\sigma _1},{\sigma _2},{\sigma _3}\} $ 。若$ \sigma = {\sigma _1} $ ，认为此时相当于COLREGS中的对遇局面；若$ \sigma = {\sigma _2} $ ，认为此时相当于COLREGS中的右交叉局面；若$ \sigma = {\sigma _3} $ ，认为此时相当于COLREGS中的左交叉局面；以图13为例说明，此时$ {\sigma _1} = 1,{\sigma _2} = 3,{\sigma _3} = 0,\sigma = \max \{ 1,3,0\} $ $ = 3 = {\sigma _2} $ ，认为此时为右交叉会遇态势，本船采取右转避让策略。3.3 满足sCOLREGS的偏置APF动态避碰策略
高速航行的无人艇进行避碰，对避碰路径的生成速率及实时性有较高要求。考虑到APF具有实时性且运算量较小的特点，本节提出一种满足sCOLREGS的偏置障碍区域改进APF实时动态避碰方法。
设艇群在宽阔海域执行任务，艇载雷达感知范围为
$ {\rho _{\max }} $ ，当有动态障碍物与艇群成员最近距离小于$ {\rho _{\max }} $ 时，USV编队将执行避障程序。设动态障碍物速度为
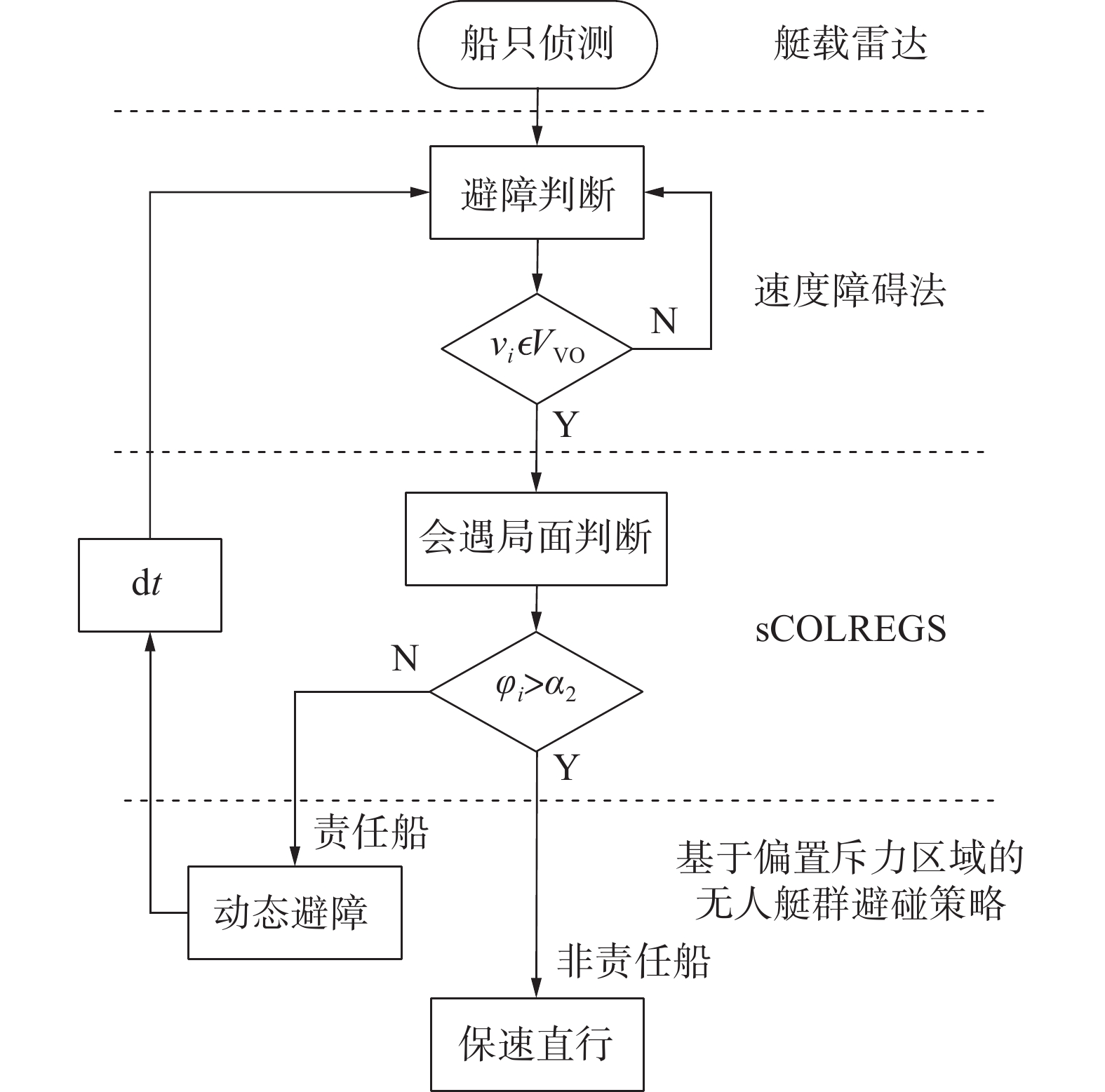
$ {\boldsymbol{v}_{{\text{obs}}}} $ ，此时通过速度障碍法进行避碰判断。若$ {\boldsymbol{v}_{{\text{obs}}}} \in {V_{{\text{VO}}}} $ ，则认为有碰撞风险，进行下一步程序，否则认为无碰撞风险，保速直行，同时重复速度障碍法避碰判断直至动态障碍物与所有艇群成员最近距离大于$ {\rho _{\max }} $ 。当碰撞风险存在时，USV根据sCOLREGS判断会遇态势，若我方为非避让船，则保速直行，同时重复速度障碍法避碰判断直至动态障碍物与艇群成员最近距离大于
$ {\rho _{\max }} $ 。若我方为责任船，则按照本节接下来提出的实时人工势场策略进行动态避障，同时进行速度障碍法判断碰撞风险，直至动态障碍物与艇群成员最近距离大于$ {\rho _{\max }} $ 。避障策略框架如图14所示。
图 14 动态避障策略流程下载:
全尺寸图片
图15以右交叉会遇局面为例展示了基于改进人工势场法的无人艇动态避碰策略。图15中无人艇
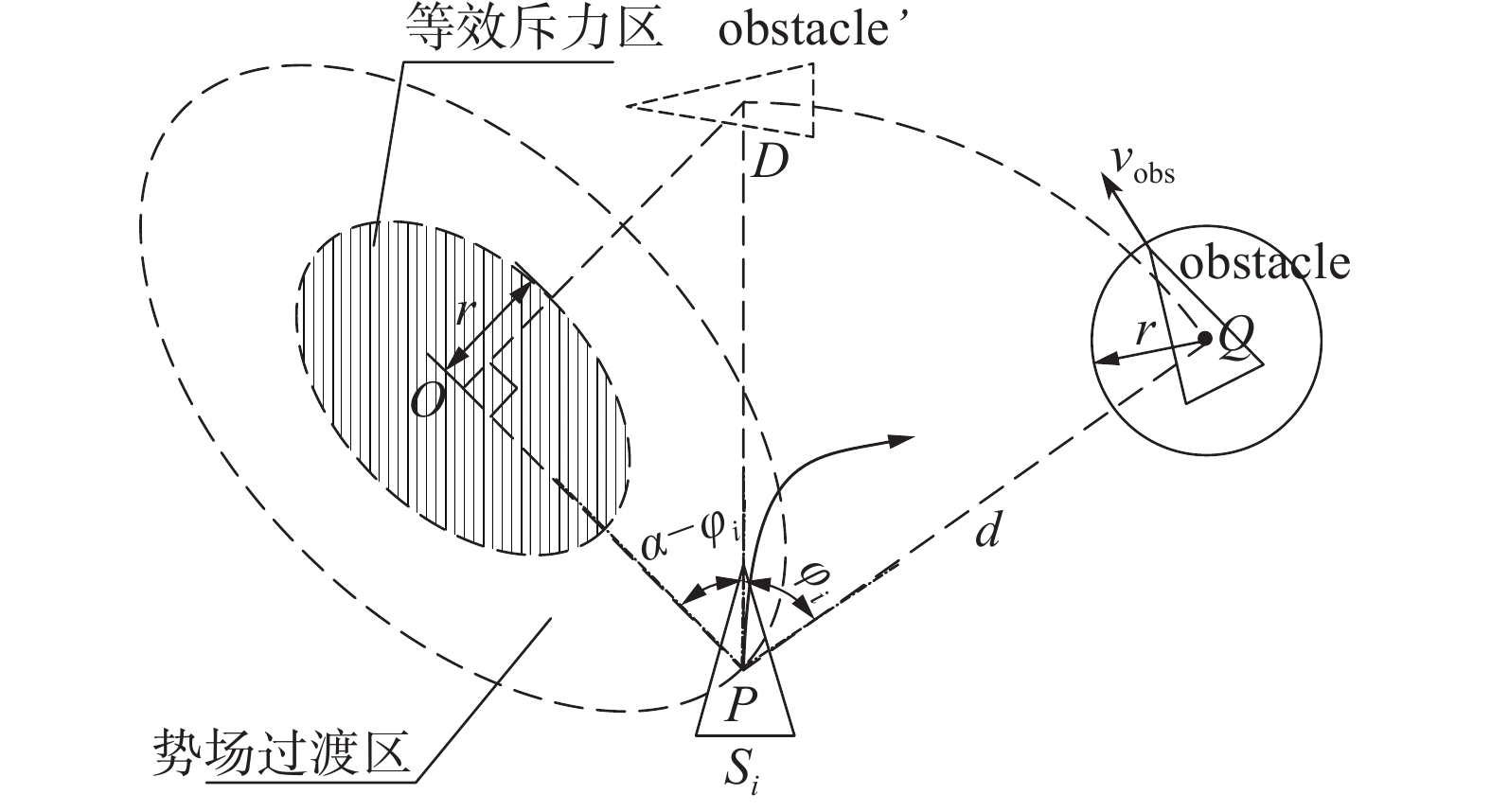
$ {S_i} $ 位置为$ P({x_i},{y_i}) $ ，速度为$ {v_{{S_i}}} $ 。障碍船位置为$ Q({x_{{\text{obs}}}},{y_{{\text{obs}}}}) $ , 速度为$ {v_{{\text{obs}}}} $ ，两船间距$ d $ 为$ \left\| {({x_i},{y_i}) - } \right. $ $ {\left. {({x_{{\text{obs}}}},{y_{{\text{obs}}}})} \right\|_2} $ ，会遇角$ {\varphi _i} \in ( - {5^{\circ} }, {112.5^{\circ} }) $ ，$ {v_{{S_i}}} \in {V_{{\text{VO}}}} $ ，$ {v_{{S_i}}}/{v_{{\text{obs}}}} < 0.95 $ ，故属于右交叉情形，且本船为避让船。
图 15 偏置障碍物区域示意下载:
全尺寸图片
为实现国际海上避碰规则规定的右转避让，USV执行动态避碰策略构造左偏置斥力区域。以
$ P $ 为圆心、$ d $ 为半径将障碍物所在点$ Q $ 旋转至速度方向上的$ D $ 点，以$ PD $ 为斜边作直角三角形$ OPD $ ，其中$ \angle OPD = \alpha - {\varphi _i} $ ，$ \alpha $ 为临界角度$ {112.5^{\circ} } $ 。设障碍船半径为
$ r = {v_{{\text{obs}}}} \cdot {\rm{d}}t $ ，代表单位时间后动态障碍物的可能位置范围。以$ O $ 为中心、$m \cdot I_{\text{OP}} \cdot {\boldsymbol {n} _{{\text{OP}}}}$ 为长轴、$n \cdot r \cdot {\boldsymbol {n} _{{\text{OD}}}}$ 为短轴建立前文所提及改进椭圆人工斥力场，其中$ m $ 、$ n $ 为长短轴系数，${\boldsymbol n _{{\text{OP}}}}$ 、${\boldsymbol {n} _{{\text{OD}}}}$ 为$ {\text{OP}} $ 、$ {\text{OD}} $ 方向单位向量。$ {\varphi _i} $ 越小，即动态障碍物位置越接近本船正前方时，椭圆斥力区域越偏离运动方向，右转幅度越小。反之，障碍物越偏离本船正前方时（此时碰撞概率较大），椭圆区域越接近运动方向，本船右转幅度较大，符合实际避碰需求。为使APF符合COLREGS的约束，常见的工作是对斥力场形状、函数根据不同会遇态势进行分类讨论，得出的结果较为复杂，本节通过将斥力场位置进行变换实现对COLREGS遵守的方法较为简便。同时，多数工作并没有考虑基于编队保持的COLREGS遵守[18]，本节提出的sCOLREGS考虑了艇群的编队尺寸，较传统COLREGS更符合海上USV编队动态避障的安全需求。本节依据改进APF，在满足动态避障的实时性的同时，考虑了对国际海上避碰规则的遵守，具有较高的安全性与求解规划路径速度。
4. 仿真实验与分析
使用科学计算平台对本文所提出的改进型人工势场路径规划、编队分散避碰策略、遵守国际海上避碰规则的多艇动态避碰策略进行仿真分析，证明提出算法的可行性。
4.1 编队分散避碰策略仿真验证
本小节对1.2节提出的分散编队避障策略进行软件仿真验证，仿真程序参数如下设置：地图大小
$20{\text{ n mile}} \times 20{\text{ n mile, }}r= 2\text{ n mile}, {\rho _{{\text{obs}}}} = 1.5 {\text{ n mile, }} {\rho _0} $ =$ 2{\text{ n mile, }}{\rho _1} = 3{\text{ n mile, }}\varepsilon {\text{ = 100, }}{\eta _s} = 300, \gamma = 10 $ ，无人艇速度上限$ {v_{\max }} = 2{\text{ n mile/h}} $ ，加速度上限$ {a_{\max }} = 0.5{\text{ n }} $ mile/h，角速度上限$ {\omega _{\max }} = {5^{\circ} }/{\rm{s}} $ ，出发点坐标$ (0{\text{ n mile}},0{\text{ n mile}}) $ ，目标点坐标$ (16{\text{ nmile}} $ ，$ 17{\text{ n mile}}) $ ，障碍物中心坐标$ (9{\text{ n mile}},9{\text{ n mile}}) $ 。2种策略的仿真航迹如图16所示，避障过程中的路径消耗、最大转向角、距障碍物最近距离如表2所示，关键理论参数的实验结果如表3所示。
图 16 改进APF静态避障策略航迹图下载:
全尺寸图片
表 2 策略参数对比参数 $ {r}/{R} $ 路程/n mile 最大转向角/$ (^\circ ) $ 最近距离$ D $ /n mile 策略1
策略21.33
1.33117.23
74.3182.5
85.41.42
1.43表 3 关键理论参数实验结果参数 $ 1 + 2r/({\rho _0} + R + 2D) $ $ {d_1}/{d_2} $ r/D 数值 1.631 1.578 1.408 由仿真设置，编队半径
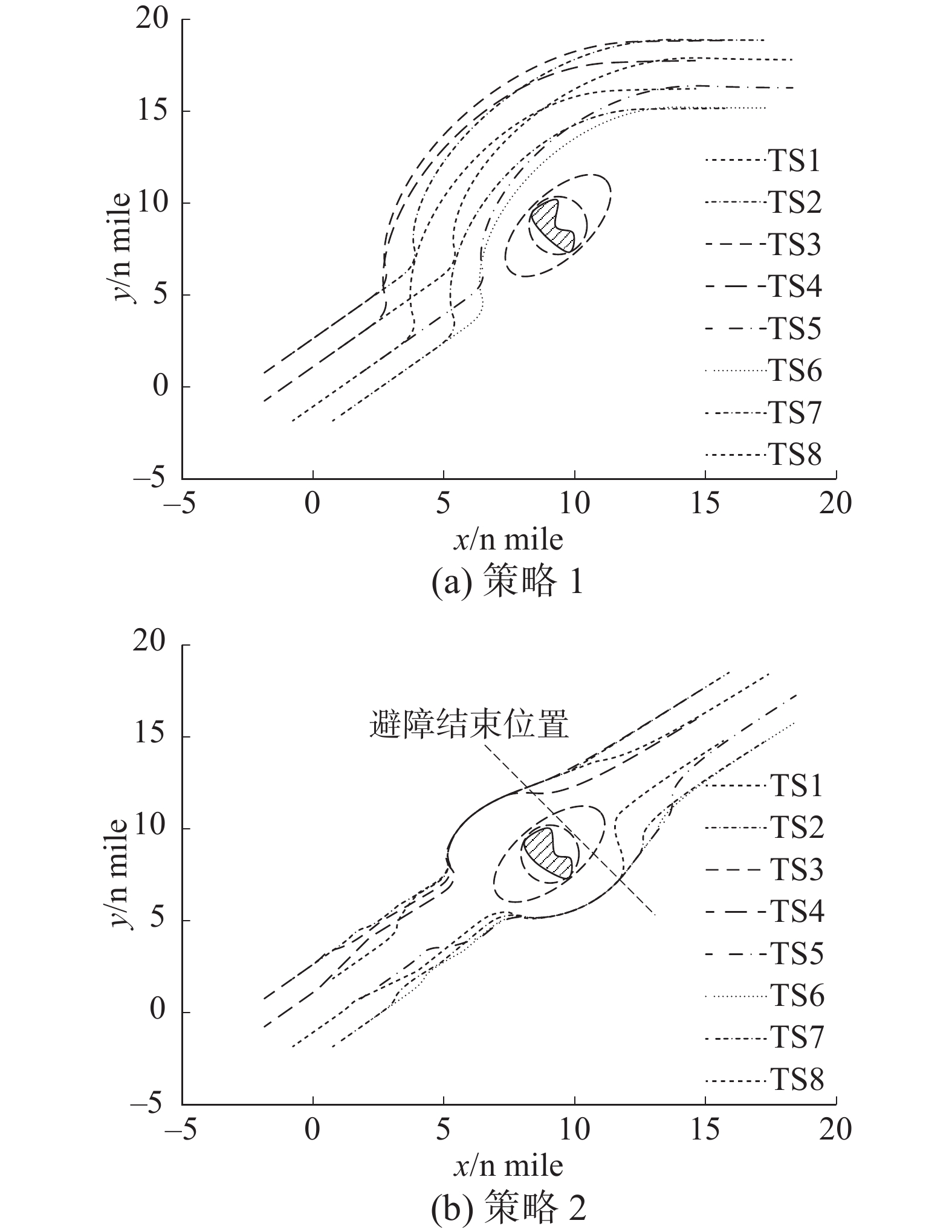
$ r $ 与实际最近距离$ D $ 的比值为1.408，具有较大的距离裕度，能保证无人艇群的避障安全。图16显示本文改进的人工势场法可以安全地实现避障，且路径较为平滑。由表2知策略2分散避障的最大转向角略大于策略1，在复杂环境下USV编队速度较低，对航迹长度的要求大于对转向角的要求。
本仿真情景中
$ r/R = 1.33 $ 接近1，可以认为无人艇编队大小与障碍物大小相当。此时策略1（保持编队）的路程消耗明显大于策略2（分散编队），由图16仿真航迹及2.2节分析，所减少的路径消耗主要来自编队外侧无人艇。表3显示$ {d_1}/{d_2} $ 与$ 1 + 2r/({\rho _0} + R + 2D) $ 较为接近，符合2.2节推导的理论式，艇群分散避障策略的建模分析得到仿真验证。4.2 符合COLREGS的多艇动态避碰
本小节对第3节提出的基于偏置APF的sCOLREGS遵守策略进行仿真验证。在一次航行任务中依次设置对遇、右交叉、左交叉3种海上会遇态势，并在对遇、左交叉局面中设置动态干扰艇以检验算法对多移动障碍物的有效性。仿真参数设置为：
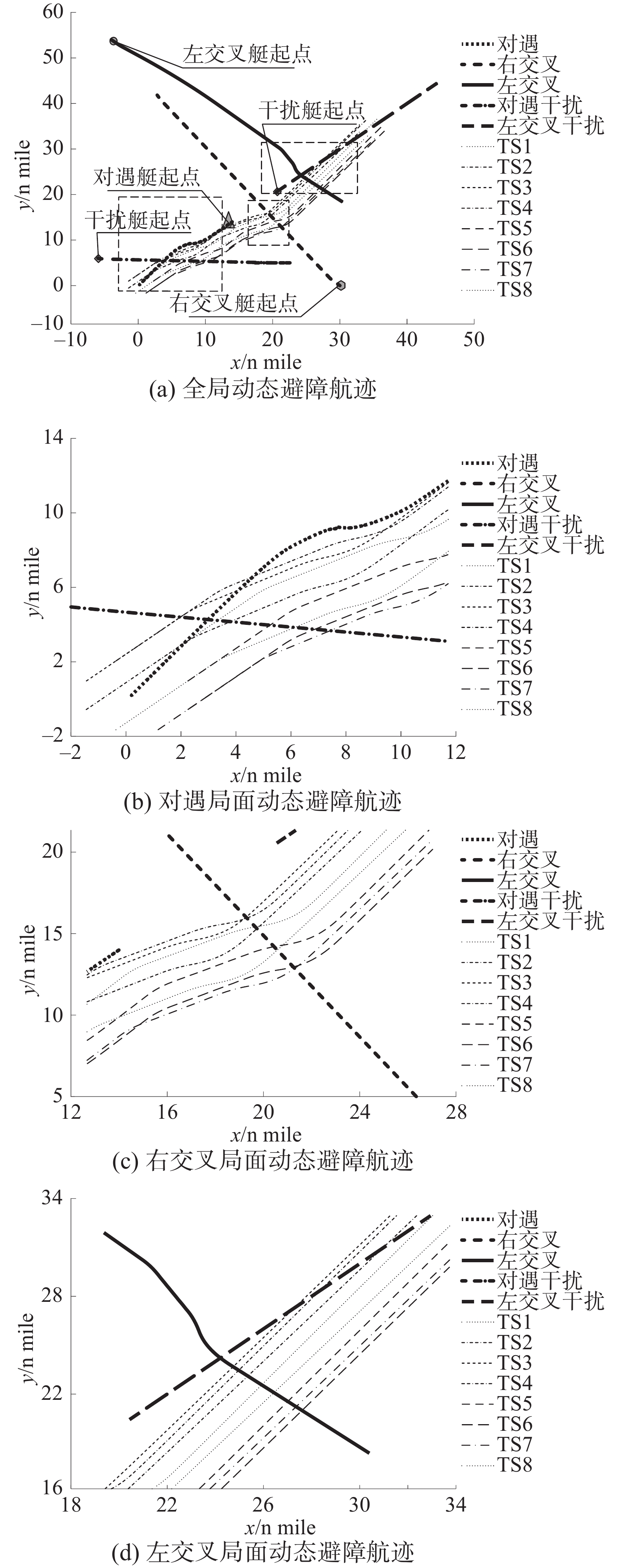
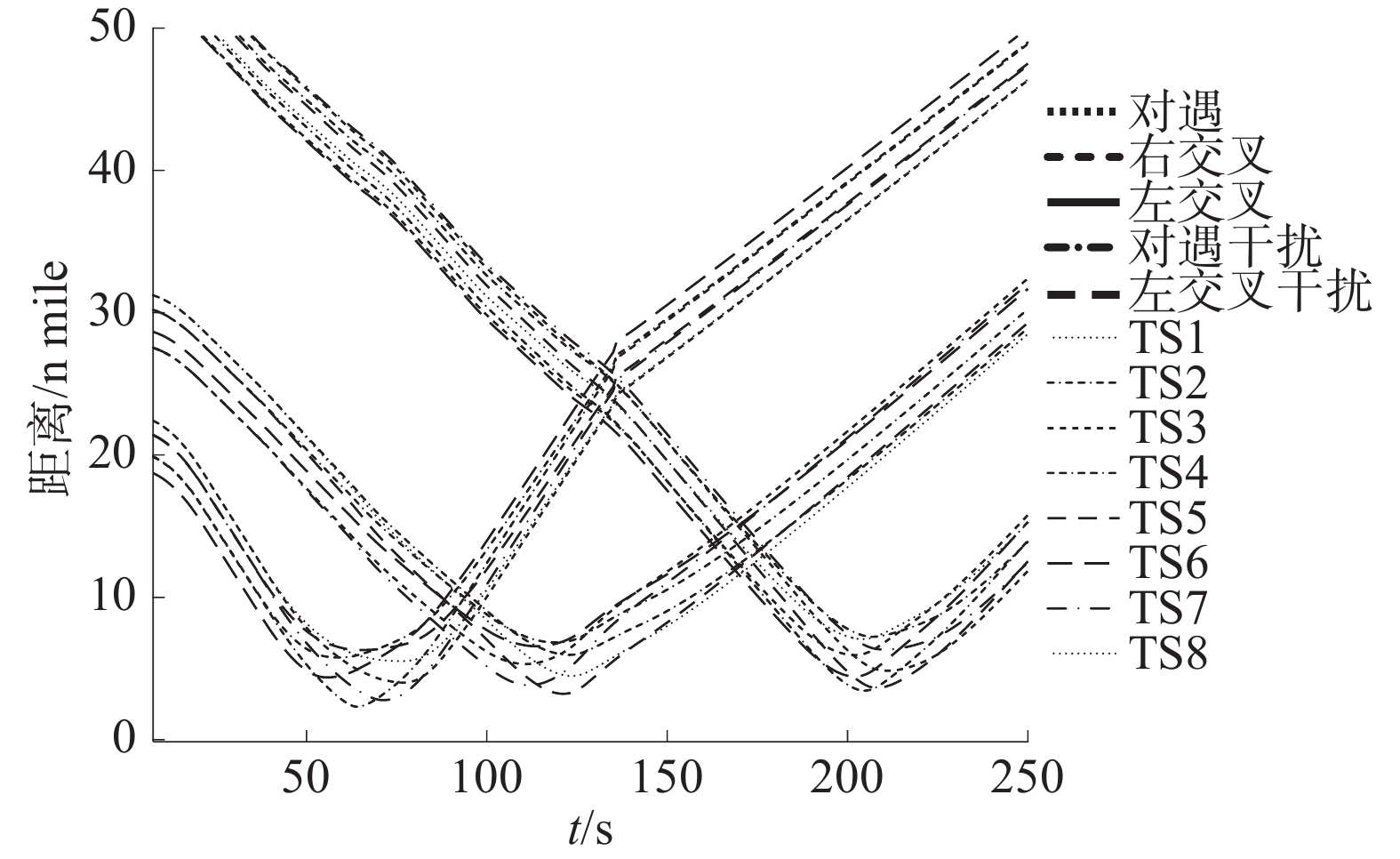
$r = 2{\text{ n mile, }}m{\text{ = 2}}{\text{.5, }}n{\text{ = 1}}{\text{.5}}$ ，无人艇速度上限$ {v_{\max }} $ 、加速度上限$ {a_{\max }} $ 、角速度上限$ {\omega _{\max }} $ 与4.1节一致。艇群初始中心$(0{\text{ n mile}},0{\text{ n mile}})$ ，地图大小$50{\text{ n mile}} \times 50{\text{ n mile}}$ ，地标位置参数设置如表4所示。表 4 地标位置参数设置地标 对应地图坐标 对遇障碍艇起点 $(14{\text{ n mile} },14{\text{ n mile} })$ 对遇障碍艇目标点 $(0{\text{ n mile} },0{\text{ n mile} })$ 对遇干扰艇起点 $(6{\text{ n mile} },6{\text{ n mile} })$ 对遇干扰艇目标点 $(25{\text{ n mile} },5{\text{ n mile} })$ 右交叉障碍艇起点 $(30{\text{ n mile} },0{\text{ n mile} })$ 右交叉障碍艇目标点 $(0{\text{ n mile} },46{\text{ n mile} })$ 左交叉障碍艇起点 $( - 4{\text{ n mile} },54{\text{ n mile} })$ 左交叉障碍艇目标点 $(50{\text{ n mile} },0{\text{ n mile} })$ 左交叉干扰艇起点 $(20{\text{ n mile} },20{\text{ n mile} })$ 左交叉干扰艇目标点 $(50{\text{ n mile} },50{\text{ n mile} })$ 规划生成的全局航迹如图17（a）所示，对遇、右交叉、左交叉会遇态势的放大局部航迹分别如图17（b）、图17（c）、图17（d）所示。全程USV编队成员与障碍艇距离如图18所示。
图 17 偏置APF-sCOLREGS仿真航迹下载:
全尺寸图片
图 18 (sCOLREGS)USV编队与障碍艇距离曲线下载:
全尺寸图片
在仿真结果图17中，处于对遇局面时，USV编队与动态障碍船均为责任船，均采取右转避让措施，如图17（b）所示；处于右交叉局面时，USV编队为责任船，采取右转避让措施，动态障碍船非责任船，保速直行，如图17（c）所示；处于左交叉局面时，动态障碍船为责任船，采取右转避让措施，USV编队非责任船，保速直行，如图17（d）所示。故第3节提出的基于改进APF的偏置障碍区域sCOLREGS遵守方法能完全符合国际海上避碰规则条例，可以实现USV集群海面保持编队进行动态避障。此外，在对遇、左交叉局面中设置的动态干扰艇并没有改变无人艇群根据sCOLREGS选择的避障策略，说明所提出的方法具有一定的抗干扰能力，可以处理多移动障碍物局面。
图18中从左至右分别为全程航行过程中USV编队与对遇障碍艇、右交叉障碍艇、左交叉障碍艇的距离曲线。由图18可知障碍物与USV编队具有较充足的距离裕度，可以保证USV编队动态避碰的安全性，同时为突发情况提供了缓冲区域。此距离裕度主要是因为sCOLREGS对单艇会遇的COLREGS进行了物理范围的扩充，考虑了编队的几何尺寸。若不考虑sCOLREGS规则，在对遇情形下由于原COLERGS的阈值角度为
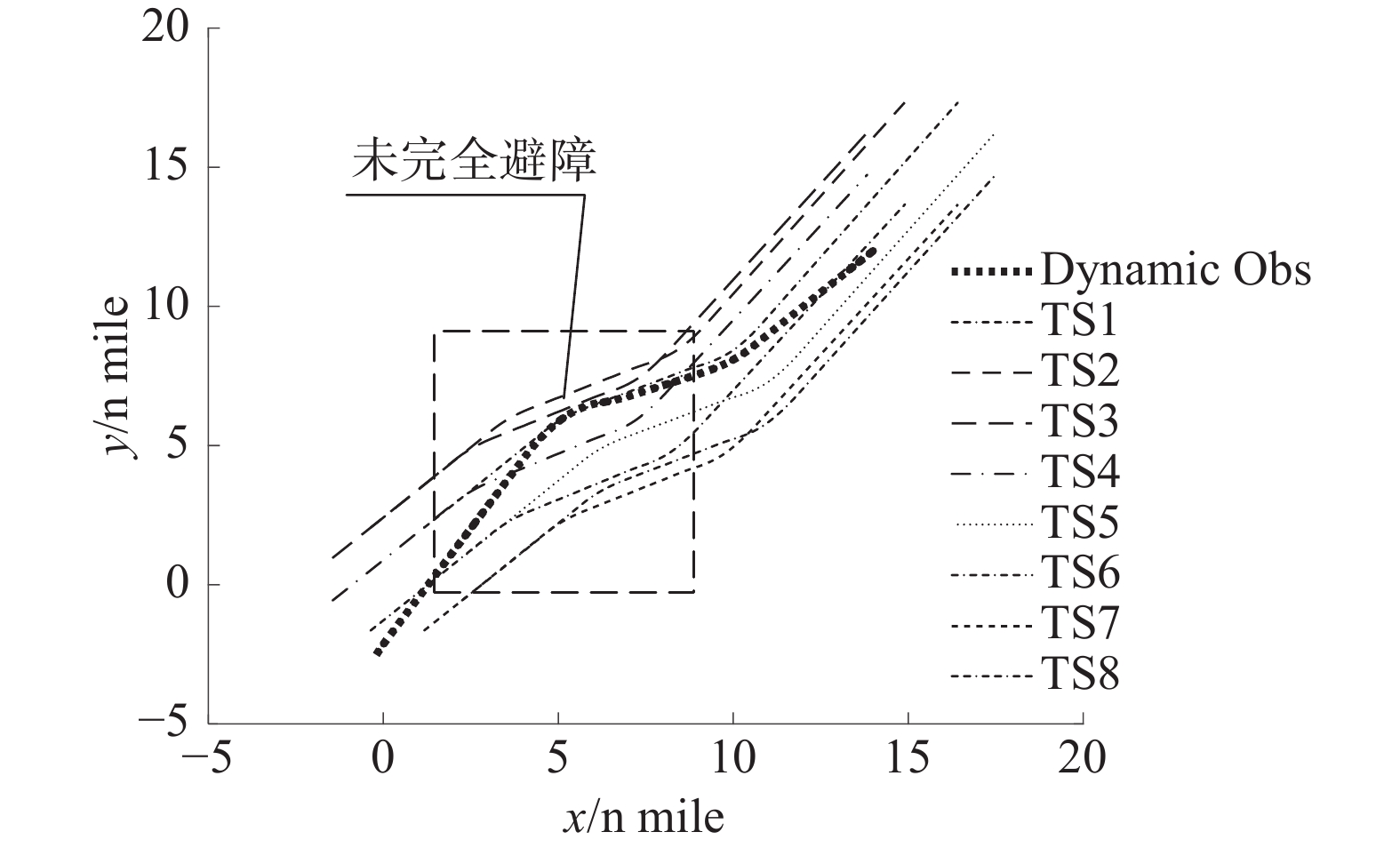
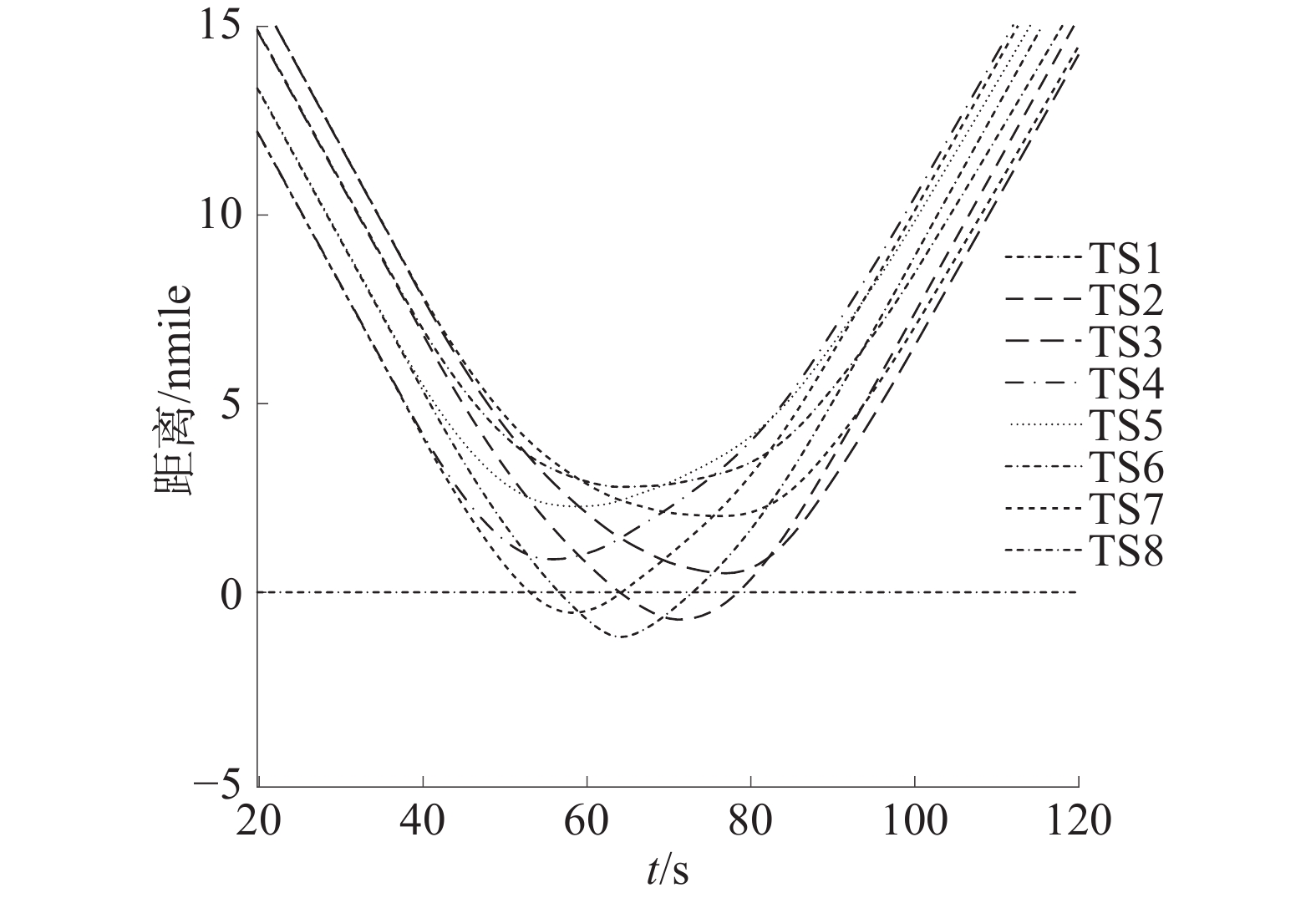
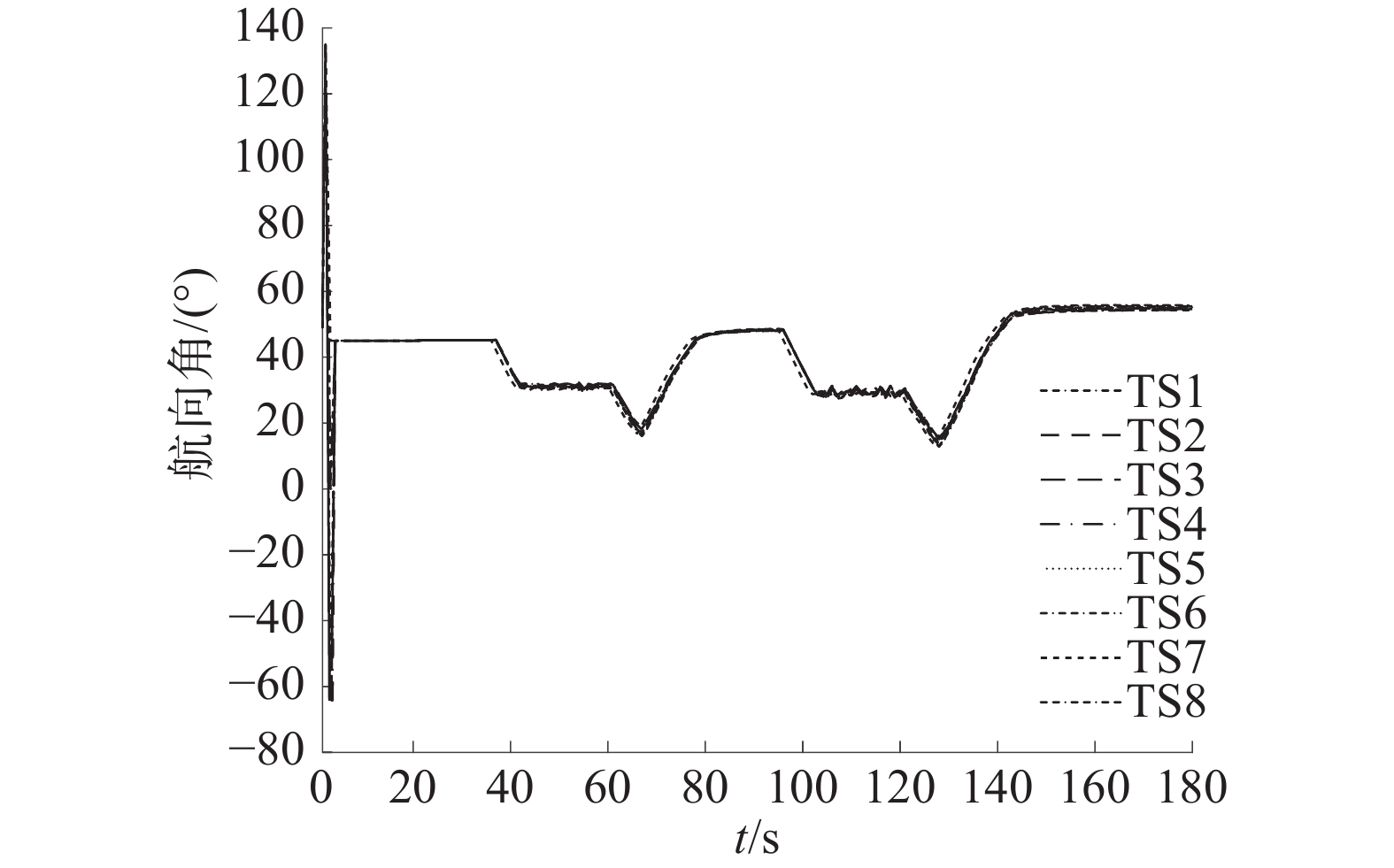
$ {5^{\circ} } $ ，难以完全避开艇群，往往会导致碰撞的发生，如图19、图20所示。
图 19 COLREGS航迹下载:
全尺寸图片
图 20 (COLREGS)USV编队与障碍艇距离曲线下载:
全尺寸图片
图21为避障过程中USV编队航向角变化曲线。本文所提出的算法航向角极差约为
$ {37^{\circ} } $ ，对USV的转向机动性能要求较低。由于航向角变化较小，生成的航迹曲线较为平滑，既避免了尖锐的转向，也节省了额外的路径消耗，提高了USV编队执行任务的续航能力。图21中可观察到航向角在刚开始变化时有一段维持过程，这是因为对遇与右交叉态势中偏置APF障碍区域的转向夹角$ (\alpha - {\varphi _i}) $ 较大，障碍物椭圆区域接近USV编队正左方，对USV编队右转偏向斥力场较小，从而转向不明显。这一过程为平滑航迹做出了贡献。
图 21 USV编队航向角曲线下载:
全尺寸图片
5. 结束语
本文针对传统人工势场法路径不平滑的问题，首先对斥力场形状与函数进行修正，针对复杂环境下多无人艇群避障时的额外路径消耗，提出一种分散避碰策略，同时结合艇群会遇态势判断特点，提出艇群国际海上避碰规则，结合改进人工势场法偏置斥力场区域实现动态避障。实验结果表明，本文提出的分散策略在设定情境中避障总路程显著小于维持编队策略，提高了编队的续航能力。
本文提出的动态避障策略，在对遇、右交叉、左交叉3种常见海上会遇态势中以较大的距离裕度进行符合规则的动态避障，编队转向角度范围较小，规划航迹平滑，能在确保实时性的同时较好地遵守国际海上避碰规则的相关条例。
-
图 1 二值障碍物栅格地图
下载:
全尺寸图片
图 2 改进人工势场法斥力分区
下载:
全尺寸图片
图 3 改进人工势场法合势力场形状
下载:
全尺寸图片
图 4 编队通信拓扑结构有向图
下载:
全尺寸图片
图 5 避障开始与结束位置示意
下载:
全尺寸图片
图 6 策略1示意
下载:
全尺寸图片
图 7 USV编队对称性分析
下载:
全尺寸图片
图 8 编队分散避障策略示意
下载:
全尺寸图片
图 9 速度障碍法示意
下载:
全尺寸图片
图 10 COLREGS会遇态势判断
下载:
全尺寸图片
图 11 COLREGS避碰策略示意
下载:
全尺寸图片
图 12 sCOLREGS编队方会遇态势判断
下载:
全尺寸图片
图 13 sCOLREGS单艇方会遇态势判断
下载:
全尺寸图片
图 14 动态避障策略流程
下载:
全尺寸图片
图 15 偏置障碍物区域示意
下载:
全尺寸图片
图 16 改进APF静态避障策略航迹图
下载:
全尺寸图片
图 17 偏置APF-sCOLREGS仿真航迹
下载:
全尺寸图片
图 18 (sCOLREGS)USV编队与障碍艇距离曲线
下载:
全尺寸图片
图 19 COLREGS航迹
下载:
全尺寸图片
图 20 (COLREGS)USV编队与障碍艇距离曲线
下载:
全尺寸图片
图 21 USV编队航向角曲线
下载:
全尺寸图片
表 1 会遇态势判断表
$ {\varphi _i} $ ${v_{ {S_i} } }/{v_{{\rm{obs}}} }$ 态势 ${v_{{S_i}}} \in {V_{{\text{VO}}}}$ 本船策略 $ ( - {5^{\circ} },{5^{\circ} }) $ — 对遇 是 右转避让 $ \begin{gathered} ({5^{\circ} },{112.5^{\circ} }) \end{gathered} $ <0.95 右交叉 是 右转避让 $ \begin{gathered} ({5^{\circ} },{112.5^{\circ} }) \end{gathered} $ >0.95 右交叉 是 保速直行 $ ({112.5^{\circ} },{360^{\circ} }) $ — 左交叉 是 保速直行 — — — 否 保速直行 表 2 策略参数对比
参数 $ {r}/{R} $ 路程/n mile 最大转向角/$ (^\circ ) $ 最近距离$ D $ /n mile 策略1
策略21.33
1.33117.23
74.3182.5
85.41.42
1.43表 3 关键理论参数实验结果
参数 $ 1 + 2r/({\rho _0} + R + 2D) $ $ {d_1}/{d_2} $ r/D 数值 1.631 1.578 1.408 表 4 地标位置参数设置
地标 对应地图坐标 对遇障碍艇起点 $(14{\text{ n mile} },14{\text{ n mile} })$ 对遇障碍艇目标点 $(0{\text{ n mile} },0{\text{ n mile} })$ 对遇干扰艇起点 $(6{\text{ n mile} },6{\text{ n mile} })$ 对遇干扰艇目标点 $(25{\text{ n mile} },5{\text{ n mile} })$ 右交叉障碍艇起点 $(30{\text{ n mile} },0{\text{ n mile} })$ 右交叉障碍艇目标点 $(0{\text{ n mile} },46{\text{ n mile} })$ 左交叉障碍艇起点 $( - 4{\text{ n mile} },54{\text{ n mile} })$ 左交叉障碍艇目标点 $(50{\text{ n mile} },0{\text{ n mile} })$ 左交叉干扰艇起点 $(20{\text{ n mile} },20{\text{ n mile} })$ 左交叉干扰艇目标点 $(50{\text{ n mile} },50{\text{ n mile} })$ -
[1] 刘祥, 叶晓明, 王泉斌, 等. 无人水面艇局部路径规划算法研究综述[J]. 中国舰船研究, 2021, 16(S1): 1−10. [2] 陈超, 耿沛文, 张新慈. 基于改进人工势场法的水面无人艇路径规划研究[J]. 船舶工程, 2015, 37(9): 72−75. [3] GE S S, CUI Y J. Dynamic motion planning for mobile robots using potential field method[J]. Autonomous robots, 2002, 13: 207−222. doi: 10.1023/A:1020564024509 [4] LYU Hongguang, YIN Yong. COLREGS-constrained real-time path planning for autonomous ships using modified artificial potential fields[J]. The journal of navigation, 2019, 72(3): 588−608. doi: 10.1017/S0373463318000796 [5] 宁君, 李学健, 李伟, 等. 基于改进人工势场法的船舶自动避碰研究[J]. 舰船科学技术, 2021, 43(23): 59−64, 154. [6] 马杰, 苏钰栋, 熊勇, 等. 基于速度障碍和人工势场的受限水域船舶避碰决策方法[J]. 中国安全科学学报, 2020, 30(11): 60−66. [7] LI Lingyu, WU Defeng, HUANG Youqiang, et al. A path planning strategy unified with a COLREGS collision avoidance function based on deep reinforcement learning and artificial potential field[J]. Applied ocean research, 2021, 113: 102759. doi: 10.1016/j.apor.2021.102759 [8] ZHANG Liang, MOU Junmin, CHEN Pengfei, et al. Path planning for autonomous ships: a hybrid approach based on improved apf and modified vo methods[J]. Journal of marine science and engineering, 2021, 9(7): 761. doi: 10.3390/jmse9070761 [9] CHEN Wenyu, XIN Bo, ZHU Zhangqing. Real-time collision avoidance for unmanned ships under constraints of rules[C]//2019 IEEE 16th International Conference on Networking, Sensing and Control. Banff: IEEE, 2019: 80-85. [10] 毛晨悦, 吴鹏勇. 基于人工势场法的无人机路径规划避障算法[J]. 电子科技, 2019, 32(7): 65−70. [11] 周伟江, 陈涛, 任牧青. 基于虚拟领航者的UUV空间编队方法[J]. 应用科技, 2011, 38(11): 9−12. [12] WEI Ren, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE transactions on automatic control, 2005, 50(5): 655−661. doi: 10.1109/TAC.2005.846556 [13] IGLESIAS PASTRANA C, NAVAS GONZÁLEZ F J, CIANI E, et al. Bayesian linear regression and natural logarithmic correction for digital image-based extraction of linear and tridimensional zoometrics in dromedary camels[J]. Mathematics, 2022, 10(19): 3453. doi: 10.3390/math10193453 [14] 吉大海, 杨溢, 戴捷, 等. 高速水面无人艇动态障碍物危险规避算法[J]. 应用科技, 2014, 41(3): 40−45. [15] KIM H G, YUN S J, CHOI Y H, et al. Collision avoidance algorithm based on COLREGs for unmanned surface vehicle[J]. Journal of marine science and engineering, 2021, 9(8): 863. doi: 10.3390/jmse9080863 [16] GUO Xinghai, JI Mingjun, ZHAO Ziwei, et al. Global path planning and multi-objective path control for unmanned surface vehicle based on modified particle swarm optimization (PSO) algorithm[J]. Ocean engineering, 2020, 216: 107693. doi: 10.1016/j.oceaneng.2020.107693 [17] YANG Shun, LI Tieshan, SHI Quan, et al. Artificial potential-based formation control with collision and obstacle avoidance for second-order multi-agent systems[C]//2020 7th International Conference on Information, Cybernetics, and Computational Social Systems. Guangzhou: IEEE, 2020: 58-63. [18] TAN Guoge, ZOU Jin, ZHUANG Jiayuan, et al. Fast marching square method based intelligent navigation of the unmanned surface vehicle swarm in restricted waters[J]. Applied ocean research, 2020, 95: 10201.
