Resistance calculation and structure design of underwater vehicles
-
摘要: 随着海洋探索的不断发展，水下作业对水下航行器提出了更高的要求。为了提高某水下航行器的减阻性能，本文基于计算流体力学（computational fluid dynamics，CFD）方法对预选的多种艏部型线以及舵板进行数值模拟，对比了它们的减阻性能，最终为航行器选择效果最佳的艏部型线以及舵板，并计算配备有最佳减阻效果的艇艏和舵板的航行器总阻力，对比分析其周围压力和流场特性。结果显示，所选的零部件相较于其他选择拥有更好的减阻性能，更适用于本文的水下航行器。本文研究结果可为航行器的结构设计和选择提供一定的参考。Abstract: With the continuous development of ocean exploration, underwater operations put forward higher requirements for underwater vehicles. In order to improve the resistance reduction performance of an underwater vehicle, based on the computational fluid dynamics (CFD) method, this paper carries out numerical simulation for a variety of pre-selected bow profiles and rudder plates, compares their resistance reduction performances, finally selects the best bow profile and rudder plate for the vehicle. In addition, the total resistance of the vehicle equipped with the bow and rudder plates with the optimum resistance reduction effect is calculated, the surrounding pressure and flow-field characteristics are compared and analyzed. The results show that, the selected components have better resistance reduction performance than other options and are more suitable for the underwater vehicle proposed in this paper. The results of this research can provide a certain reference for the structural design and selection of underwater vehicles.
-
21世纪，海洋划界争端、海底油气资源争端、渔业资源争端、深海矿产资源争端层出不穷[1]。随着人们对海洋探索的愈加深入，海洋装备也在不断地改进升级。自主水下机器人（autonomous under-water vehicle，AUV）是一种能够自主在水下进行海洋科学研究、水下搜索和救援等任务的无人机器人[2]。智能水下机器人的出现，加快了人类探索海洋的速度，由于其经济费用低、作业效率高、可在复杂的水域环境中持续作业等优点，针对水下机器人各项技术的研究己经成为目前船舶方向的科研工作者们的重点研究内容之一[3]。
其中，AUV的型线优化一直是海洋工程领域的重要研究方向之一，它很大程度上影响着航行器的性能以及能耗和生产等问题[4]。AUV型线设计的手段在于通过减小水流的阻力来提高作业性能，从而使AUV能够快速准确地完成各种水下任务。除此之外，舵板是一个不可忽视的部件，AUV的稳定性和快速性可以凭借对舵板的操控达到预期的运动，对于指导AUV的型线优化、提高其操控性能具有重要意义。对于结构的优化效果可以通过阻力分析来确定，优化的目的之一便是减小水阻。当前，对AUV的阻力性能进行研究的方法主要包括试验和计算模拟。通过试验可以获得较为准确的AUV阻力数据，但对试验设备的要求较高，存在财力与人力上的限制。相比之下，计算流体力学（computational fluid dynamics，CFD）方法具有成本低、可重复性强等优点，是目前应用最广泛的AUV阻力计算方法之一[5]。通过建立AUV的几何和流场模型，可以模拟AUV在水中的运动状态，计算AUV受到的阻力及其分布情况。在过去的几十年里，许多学者针对AUV结构设计优化及数值算法开展了大量的研究。Alvarez等[6]对水下航行器的最佳船体形状进行优化研究，采用模拟退火算法来搜索定义航行器形状的参数设置，以最小化波浪阻力。金碧霞等[7]对某流线型AUV进行改进，建立了阻力系数计算模型，优化AUV艏部结构为分体式，增强结构整流作用的同时又能减小水流阻力。胡克等[8] 对几种不同型线回转体进行了CFD 数值仿真模拟，给出了一些壳体型线优化的建议。戴鹏[9]针对水下航行器的总体设计进行研究，主要研究对象是螺旋桨效率及阻力等性能参数，并用参数优化法优化了航行器的外形。Gao等[10]提出了一种通过计算流体动力学方法估算流体动力系数的省时方法。Hong等[11]通过CFD方法对便携式AUV的水动力特性进行研究，建立了AUV动力学模型，对水动力系数进行估计。
本文采用数值模拟方法，基于计算流体力学知识原理，使用STAR-CCM+软件对水下航行器模型的整体阻力进行计算，分析航行器表面压力和周围流场特性，并对艏部型线以及舵板截面进行减阻优化，确保所选择的部件为减阻性能更好的一种。
1. 数值计算方法
1.1 控制方程与湍流模型
流体运动需要遵循物理守恒定律，这些守恒定律可通过控制方程来进行数学表达。由于本文涉及的流体为绝热不可压缩的牛顿流体，没有能量的交换，所以本文的控制方程为质量守恒方程与能量守恒方程。
质量守恒方程的表达式为
$$ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho u} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w} \right)}}{{\partial {\textit{z}}}} = 0 $$ 式中：
$ \rho $ 为密度，$ t $ 为时间，u、v、w分别为速度矢量U在x、y、z等3个方向上的分量。对于牛顿流体在x、y、z共3个方向上的动量守恒方程（也称Navier-Stokes方程）为
$$ \left\{ \begin{gathered} \frac{{\partial \left( {\rho u} \right)}}{{\partial t}} + {\text{div}}\left( {\rho u {\boldsymbol{U}} } \right) = {\rm{div}}\left( {\mu {\text{grad}}u} \right) - \frac{{\partial p}}{{\partial x}} + {S_u} \\ \frac{{\partial \left( {\rho v} \right)}}{{\partial t}} + {\text{div}}\left( {\rho v{\boldsymbol{U}} } \right) = {\rm{div}}\left( {\mu {\text{grad}}v} \right) - \frac{{\partial p}}{{\partial y}} + {S_v} \\ \frac{{\partial \left( {\rho w} \right)}}{{\partial t}} + {\text{div}}\left( {\rho w{\boldsymbol{U}} } \right) = {\rm{div}}\left( {\mu {\text{grad}}w} \right) - \frac{{\partial p}}{{\partial {\textit{z}}}} + {S_w} \\ \end{gathered} \right. $$ 式中：
$ \mathrm{\mu } $ 为动力黏度，$ S_{u} $ 、$ S_{v} $ 和$ S_{w} $ 为动量守恒方程的广义源项，p为流体微元上的压力。本文中涉及的流体流动属于湍流的范畴。一般来说，本领域内认为，无论湍流的运动有多么复杂，非稳态的连续方程以及Navier-Stokes方程对于湍流的瞬时运动仍然是适用的。
本文选择采用目前工程研究上应用最广泛的雷诺平均（reynolds average navier-stokes，RANS）方程方法解决湍流问题，RANS方法首先将满足动力学方程的湍流瞬时运动分解成平均运动与湍流运动2部分，然后将脉动运动部分对平均运动的贡献通过雷诺应力项加以模拟，也就是通过湍流模型来封闭N-S方程，使之可以被求解得到结果。RANS方法忽略了密度脉动带来的影响，但它同时考虑了平均密度的变化。雷诺时均Navier-Stokes方程如下：
$$ \frac{\partial\left(\rho u_i\right)}{\partial t}+\frac{\partial}{x_j}\left(\rho u_i u_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial}{x_j}\left(\mu \frac{\partial u_i}{\partial x_j}-\rho \overline{u_i^{\prime} u_j^{\prime}}\right)+S_i $$ 式中i和j取值为1、2、3。
方程中有关湍流脉动值的Reynolds应力项
$-\rho {{\overline {u_i^{'}u_j^{'}} }}$ [12]属于全新的未知量，因此导致方程不封闭。本文采用目前使用最广泛的$ k-\varepsilon $ 模型来封闭方程，此模型针对的是充分发展的、高雷诺数的湍流模型，目前己被应用于各种不同流动的模拟。湍动能k和湍动耗散率ε定义为
$$ \begin{gathered} k = \frac{{\overline {u_i^{'}u_j^{'}} }}{2} = \frac{1}{2}\left( {\overline {{u^{'2}}} + \overline {{v^{'2}}} + \overline {{w^{'2}}} } \right) \\ \varepsilon = \frac{\mu }{\rho }\overline {\left( {\frac{{\partial u_i^{'}}}{{\partial {x_k}}}} \right)\left( {\frac{{\partial u_i^{'}}}{{\partial {x_k}}}} \right)} \\ \end{gathered} $$ 在标准k-ε模型中，与之相对应的输运方程为
$$ \begin{gathered} \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k} \\ \\ \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ {G_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_k} + {G_{3\varepsilon }}{G_b}} \right) - {G_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_k} \\ \end{gathered} $$ 式中：
$ G_{k} $ 为湍动能k的第1产生项，它是由平均速度梯度引起的；$ G_{b} $ 为湍动能k的第2产生项，它是由浮力引起的；$ Y_{M} $ 为在可压湍流中脉动扩张的贡献项；$G_{1 \varepsilon}$ 、$G_{2 \varepsilon}$ 、$G_{3 \varepsilon}$ 为一般经验常数；$ \sigma_{k} $ 和$\sigma_{\varepsilon}$ 均为Prandtl数，它们分别与湍动能k和耗散率$ \varepsilon $ 对应；$ S_{k} $ 和$ S_{\varepsilon} $ 为源项，由用户定义。1.2 数值离散方法
本文采用有限体积法对上述控制方程进行离散，离散过程如下：
用
$ \phi $ 表示各物理量，对微分方程在控制体积V 内进行积分，即$$\begin{array}{c}{\displaystyle \underset{V}{\int }\frac{\partial \left(\rho \phi \right)}{\partial \text{t}}}{\rm{d}}V+{\displaystyle \underset{V}{\int }{\rm{div}}\left(\rho \varphi \boldsymbol{U}\right)}{\rm{d}}V=\\{\displaystyle \underset{V}{\int }{\rm{div}}\left(\Gamma ·{\rm{grad}}\left(\varphi \right)\right)}{\rm{d}}V+ {\displaystyle \underset{V}{\int }{S}_{\varphi }}{\rm{d}}V\end{array} $$ 然后通过高斯公式：
${\displaystyle \underset{V}{\int }{\rm{div}}\left(\boldsymbol{a}\right)}{\rm{d}}V={\displaystyle \underset{A}{\int }\boldsymbol{n}·\boldsymbol{a}}{\rm{d}}A$ 将其化为$$ \begin{gathered} \frac{\partial }{{\partial t}}\left( {\int\limits_V {\rho \phi {\rm{d}}V} } \right) + \int\limits_A { {\boldsymbol{n}} \cdot \left( {\rho \phi {\boldsymbol{u}}} \right)} {\rm{d}}A = \\ \int\limits_A { {\boldsymbol{n}} \cdot \left( {\Gamma \cdot {\rm{grad}}\left( \phi \right)} \right)} {\rm{d}}A + \int\limits_V {{S_\phi }} {\rm{d}}V \\ \end{gathered} $$ 离散之后可以得到
$$ \begin{gathered} \frac{\partial }{{\partial t}}\left( {\int\limits_V {\rho \phi {\rm{d}}V} } \right) + \sum\limits_f^{N_{\rm{face}}} {{\rho _f}{u_f}{\phi _f}} \cdot {{ {\boldsymbol{A}}}_f} =\\ \sum\limits_f^{N_{\rm{face}}} {{\Gamma _\phi }\left( {{\rm{div}}\phi } \right)} n \cdot {{ {\boldsymbol{A}}}_f} + {S_\phi }V \\ \end{gathered} $$ 式中：
$ \phi_{f} $ 为$ \phi $ 在$ f $ 面上的对流值，${\left( {{\rm{div}}\phi } \right)_n}$ 为$ ({\rm{div}}\phi) $ 在$ f $ 面上的法线方向数值，$\rho_{f} u_{f} \phi_{f} \cdot {{\boldsymbol{A}}_{f}}$ 为通过$ f $ 面的质量通量，${{\boldsymbol{A}}}_{f}$ 为$ f $ 面的面积向量，$N_{\rm{face}}$ 为控制体周围的单元面数量，$ \Gamma_{\phi} $ 为$ \phi $ 的扩散系数，$ S_{\phi} $ 为源项。离散之后，使用求解压力耦合方程组的半隐式压力修正方法，即压力耦合方程组的半隐式方法（semi-implicit method for pressure linked equations，SIMPLE）对离散后的方程进行求解。
2. 阻力性能计算
2.1 计算模型
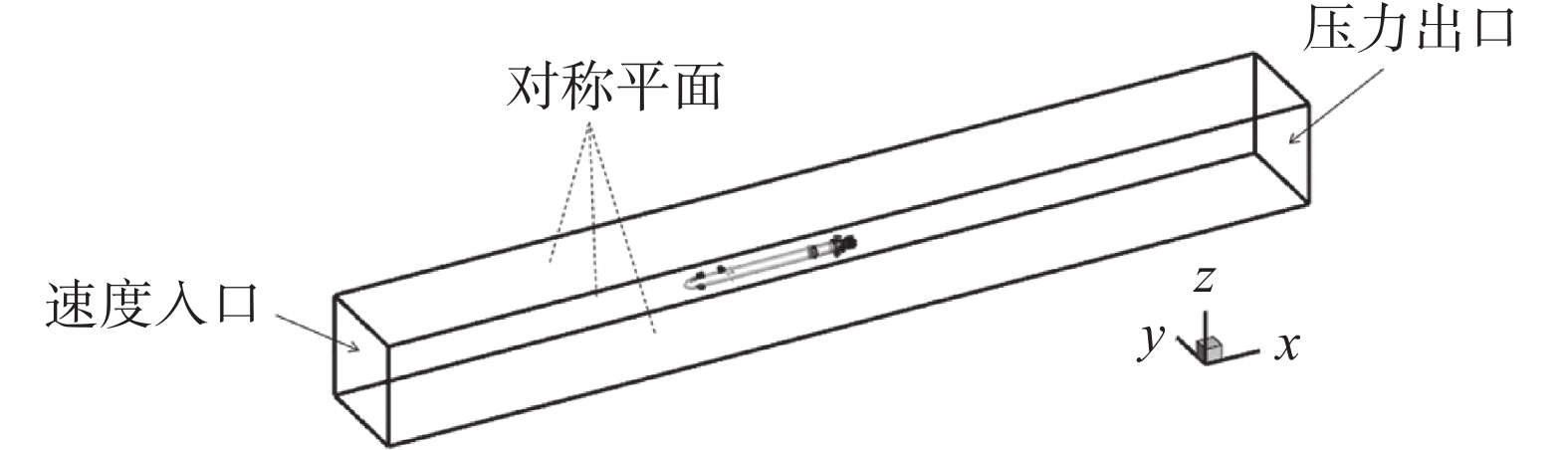
本文数值模拟所用的水下航行器计算模型如图1所示，模型全艇体长8.3 m，艇体最大半径0.5 m，坐标系采用直角坐标系，坐标原点选为模型头部顶端，x轴与艇体的中心对称轴重合，方向与无攻角时来流方向一致，z轴选为竖直向上。
图 1 水下航行器计算模型
下载:
全尺寸图片
根据计算模型确定计算域范围，AUV的运动往往决定了计算域的选择，把重要的流体区域计算进去。数值计算中，计算域的范围选择为前端从AUV艏部向前延伸1.5倍艇长，后端从AUV尾部向后延伸2.5倍艇长，左右两侧沿宽度方向左右各延伸2倍艇宽，上下两侧深度方向各延伸2倍艇高，形成一个长方体计算区域，如图2所示，并通过体积控制进行了网格加密，确保计算精度。
图 2 航行器模型计算域下载:
全尺寸图片
2.2 边界条件
计算域划分之后进行边界条件的设置，计算区域的入口处设置为速度入口条件（velocity inlet），在区域–边界中设置相应的速度值，方向沿x轴的负方向；计算区域的出口处设置为压力出口条件（pressure outlet），此处是完全发展的流动，通过区域内部外推可以得到出流面的流动情况，且应用此方法不会对上游流动产生影响；其他的控制域边界条件均设置为速度入口条件，但速度大小设置为0，可以模拟AUV在水下的真实情况。AUV的表面设置为无滑移的壁面条件（wall），因为计算域设置的足够大，因此其四周不受AUV艇身的影响；另外，整个计算域设置为流体。
2.3 网格设置
进行流场求解计算前，要将计算区域离散化，即划分网格。高质量的网格对于进行可靠且准确的计算流体动力学分析是至关重要的，因为网格质量的好坏不仅决定了工况的计算速度，还会对计算结果的准确可靠性产生很大的影响。
在划分网格的过程中注意到虽然多面体网格可以最大限度保留计算区域的几何特征，但是其网格质量不高、尺寸太大，在计算中容易带来误差。除此之外，切割体网格的收敛速度要快于多面体网格，所以选用切割体网格进行计算。为更好地捕捉航行器附近的流场细节，在航行器围壳附近生成体控制，以加密此处的网格，网格划分结果如图3所示。
图 3 航行器模型切割体网格下载:
全尺寸图片
2.4 网格无关性验证
为确保阻力计算结果的准确性，在航速选择为7 kn的情况下，设置了4组网格数量逐渐增加的工况进行，在除网格数以外的条件均相同的情况下完成各工况阻力计算对网格的无关性进行验证，验证结果如表1所示。
表 1 网格无关性网格数量 基础网格尺寸/m 阻力/N 1076359 0.04 566.42 1823651 0.03 551.38 2416471 0.02 545.91 4300075 0.01 544.52 通过计算结果可以得知，随着网格数量的加密，阻力值逐渐下降，当网格数量为430万和242万时，网格增加几乎一倍，但阻力值变化很小，仅减少了0.25%，可以认为结果已经收敛，验证了网格的无关性。而由于网格的加密，后者的计算时间远大于前者，因此综合考虑计算效率与结果的准确性，本文最终选择的网格数量为2416471。
2.5 计算结果及分析
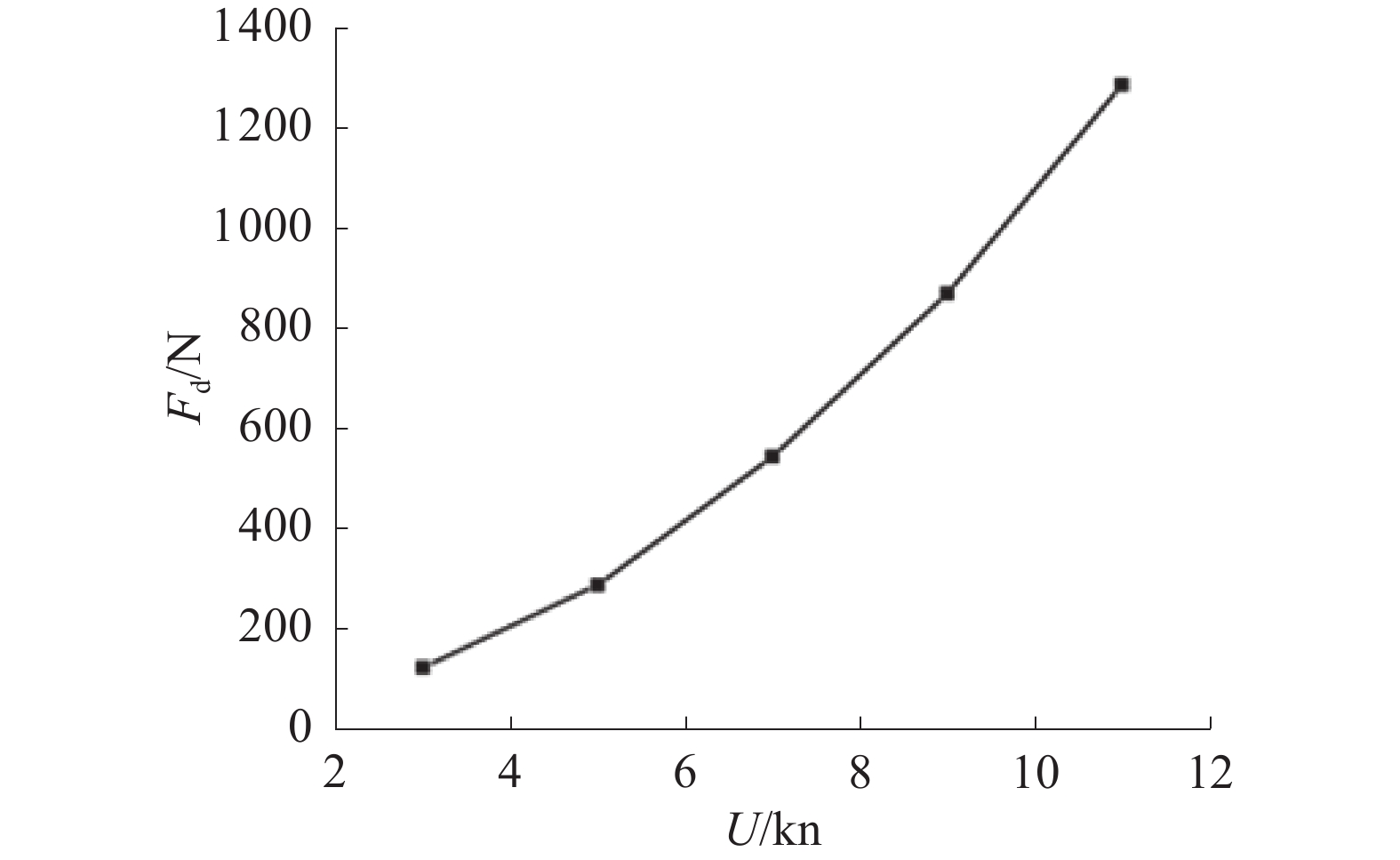
根据上述设置，通过改变边界的流入速度，分别计算航速为3、5、7、5、9和11 kn时，AUV所受到的航行阻力，计算结果如表2所示。为清楚地观察阻力变化趋势，绘制受力曲线如图4所示。其中Fd为阻力，U为航速。
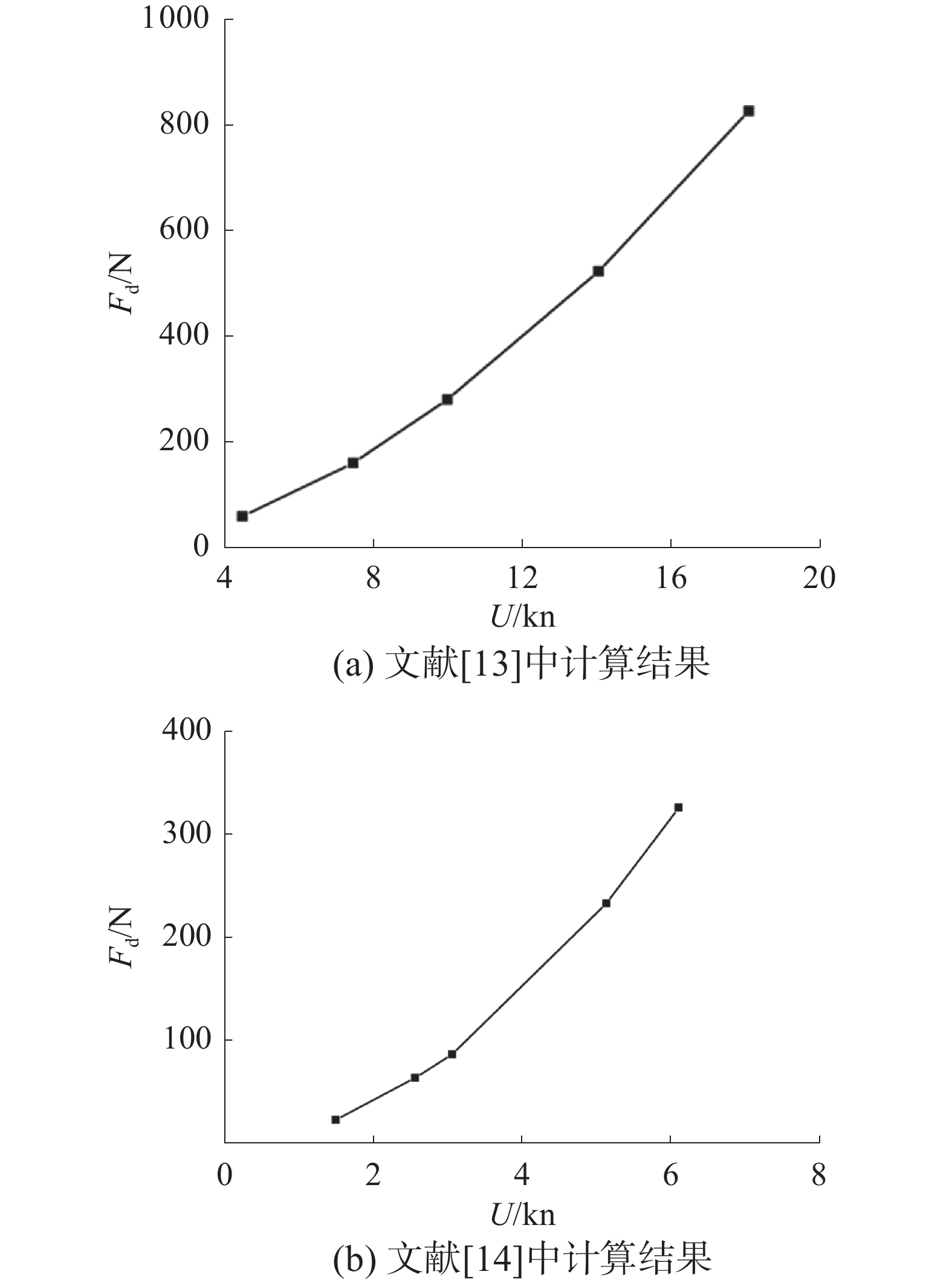
表 2 阻力预报数值航速/kn 3 5 7 9 11 阻力/N 125.72 290.38 545.91 871.33 1287.36 
图 4 阻力曲线下载:
全尺寸图片
根据计算结果可知，AUV的阻力随着航速的增加逐渐增大，增大趋势大致呈二次曲线形式，这与文献[13-14]中计算水下航行器阻力所得到的结果（列于图5（a）和图5（b）中）呈现相同的趋势，验证了结果的准确性。
图 5 阻力结果趋势参考下载:
全尺寸图片
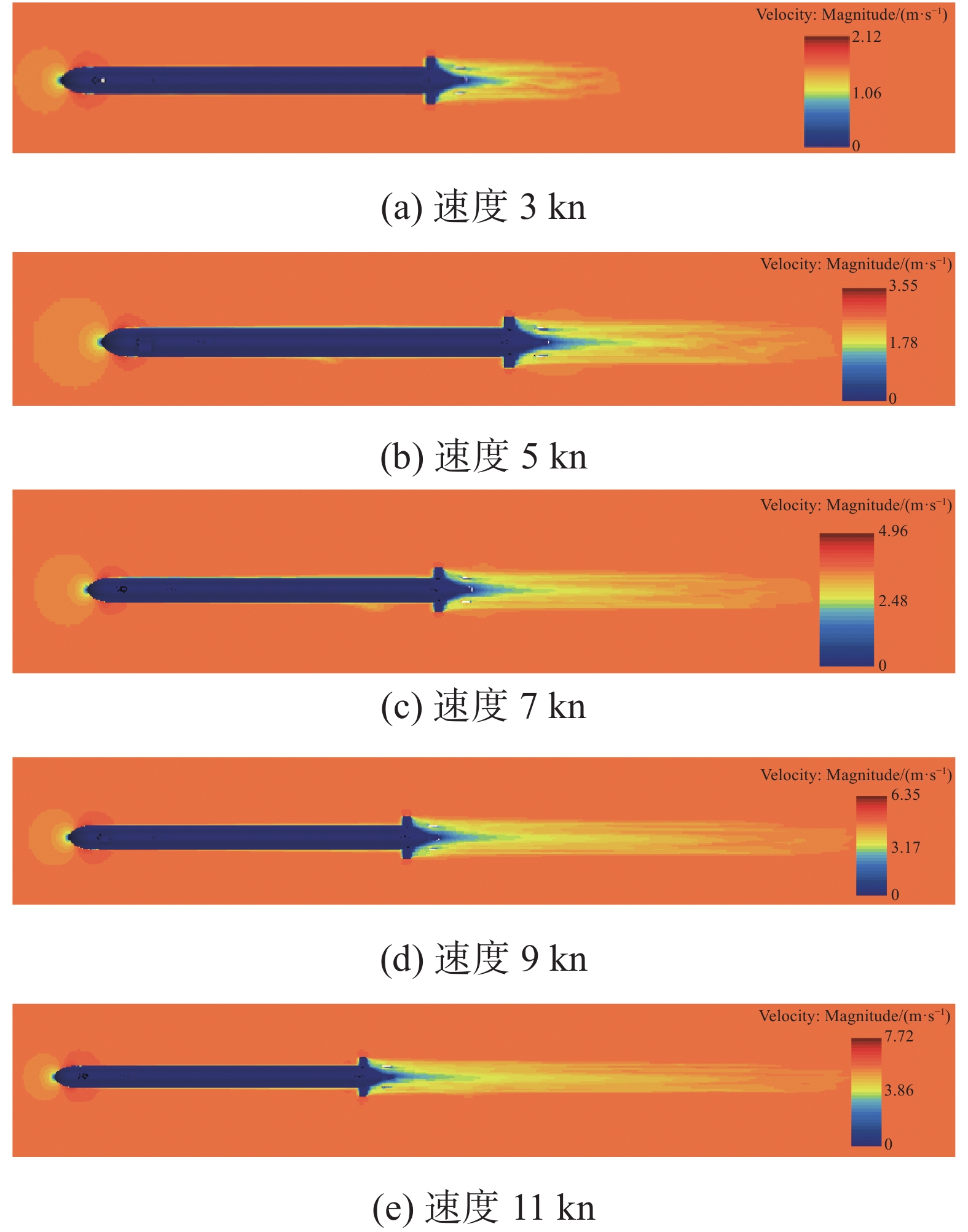
不同航速下水下航行器的流场速度如图6所示。由图6可知，随着航行器速度的增大，周围流场的速度随之增大，由于物体的存在，航行器首端和尾端的流场速度均有不同程度的减小，并且随着航速的增大，尾流场速度受影响的区域范围逐渐增大。在尾流场速度受影响的区域内，从靠近航行器尾端到远离航行器的方向流场速度从0逐渐增大，直至与航速一致。
图 6 航行器周围流场速度下载:
全尺寸图片
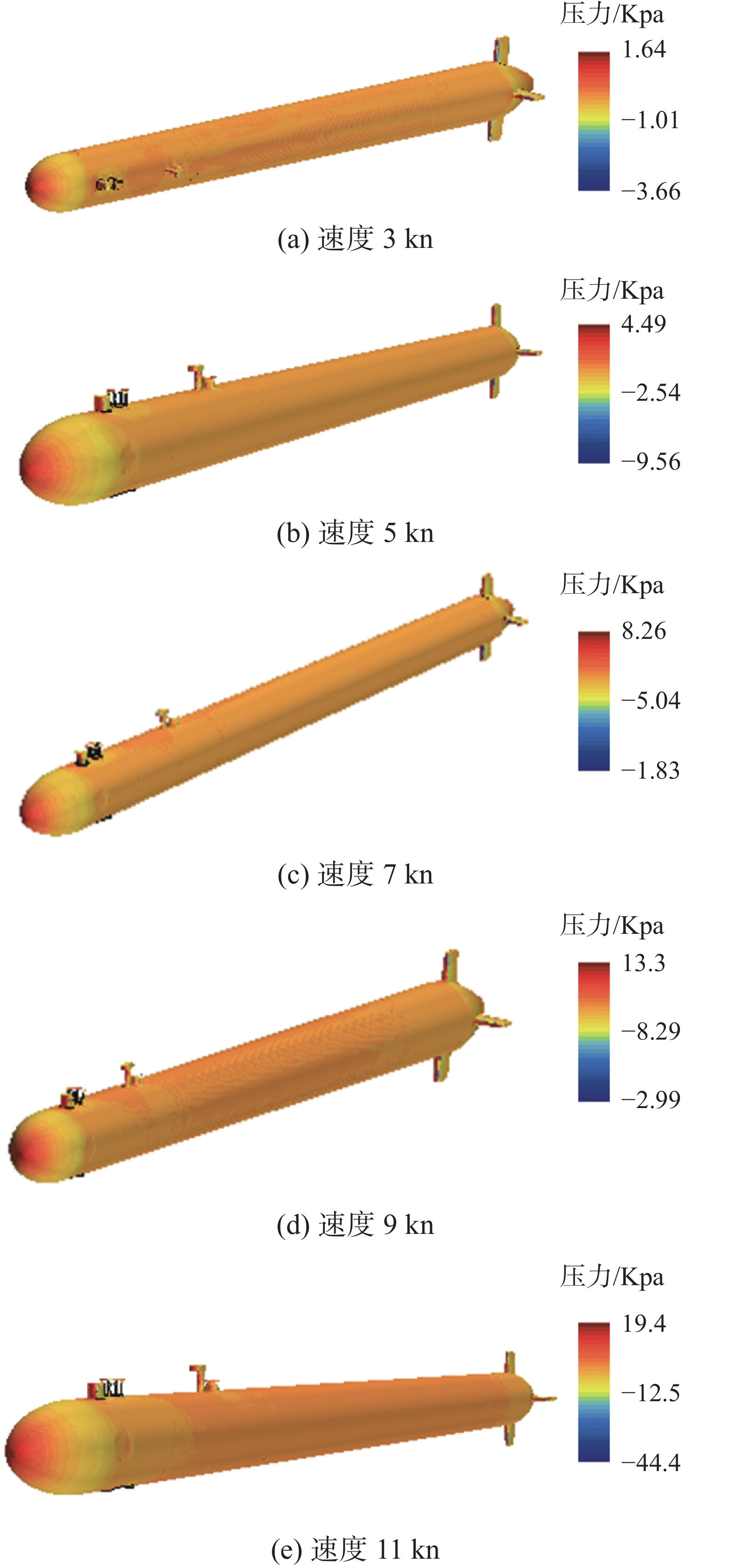
不同航速下水下航行器的表面压力如图7所示。由图7可知，航行器的表面压力随着航速的增大逐渐增大，并且在航行器艏部出现压力最大值的情况。在艏部结构设计中应加强强度，以提高航行器艏部的耐压性。
图 7 航行器表面压力下载:
全尺寸图片
3. 艏尾部结构设计
文中的水下航行器模型是经过多重结构设计最终确定下来的阻力最小的最优模型，在结构设计过程中进行了艏部型线设计以及舵板剖面确定等内容。
3.1 艏部型线设计
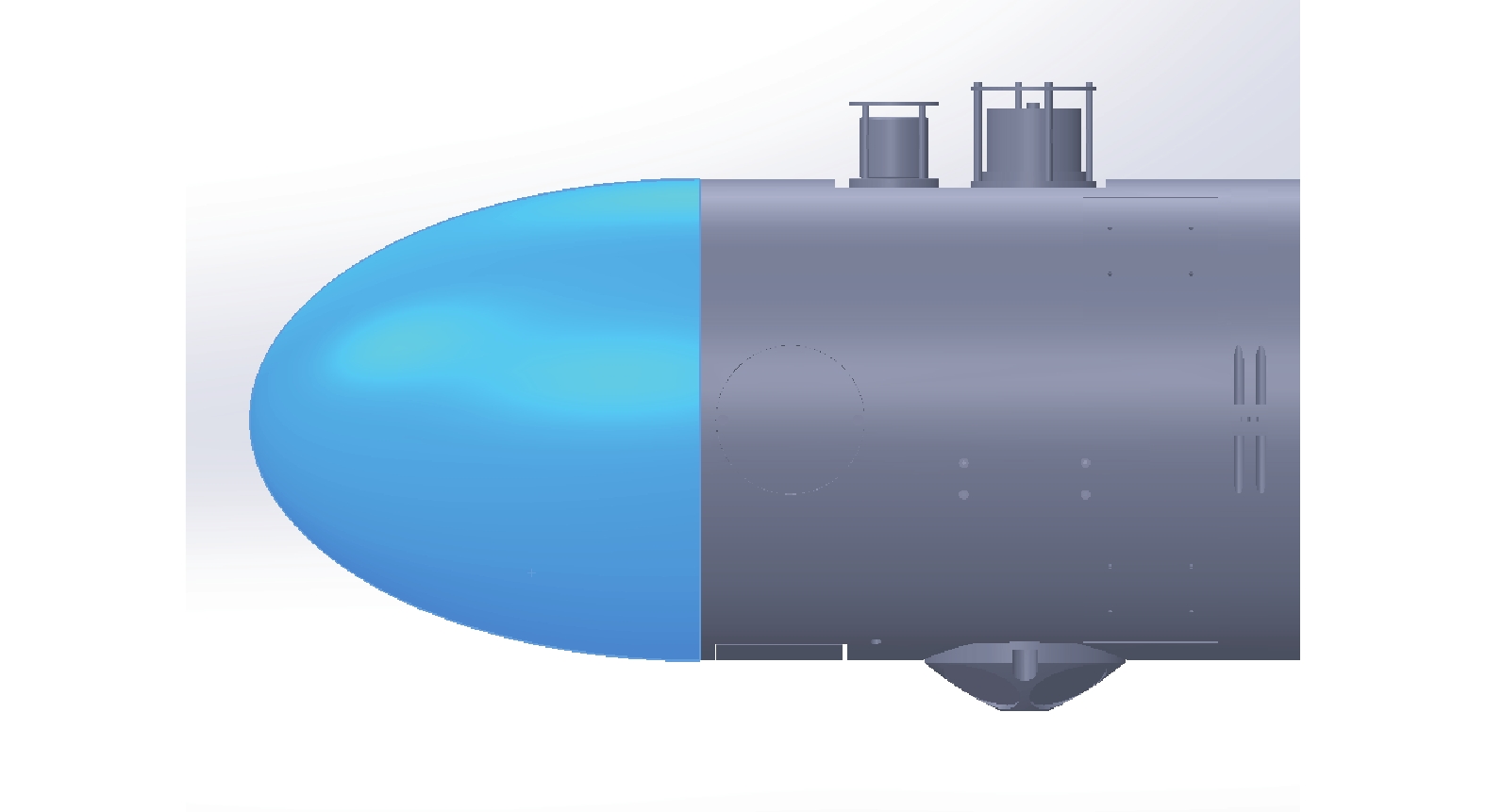
经大量研究，学者们发现了减阻性能较好的水滴型、MYing型、半椭型以及鱼雷型等型线，可用于水下航行器的艏部型线[15]。本文在艏部型线的选择上共有4种方案，除了最终选择的上述改进型艏部型线以外，还提供了水滴型、半椭型、MYing型3种艏部型线供选择，3种型线的示意如图8~10所示。
图 8 水滴型艇艏下载:
全尺寸图片
图 9 半椭型艇艏下载:
全尺寸图片
图 10 MYing型艇艏下载:
全尺寸图片
水滴型艏部数学表达式为
$$ {{y}}_{{s}}=\frac{{D}}{2}\left[1-\left(\frac{{{x}}_{{s}}}{{{L}}_{{s}}}\right)^{{{n}}_{{s}}}\right]^{1/{{n}}_{{s}}} $$ 式中：
$ y_{x} $ 为曲线各点处的半径；$ x_{s} $ 为轴向位置；D为最大剖面直径，即平行中段直径；Ls为艏部的长度；ns为艏部形状指数，其值的大小表示艏部曲线的丰满程度，本设计中选择ns=2.4。半椭型艏部数学表达式为
$$ y_{1}= \pm \frac{D}{L_{3}} \sqrt{L_{3}^{2}-x_{4}^{2}} $$ MYing型艏部数学表达式为
$$y_s=\frac{1}{2} D\left[1-\left(\frac{x_s-L_s}{L_s}\right)^2\right]^{\tfrac{1}{n}}$$ 式中n为头部形状指数，本设计中选择n=2。
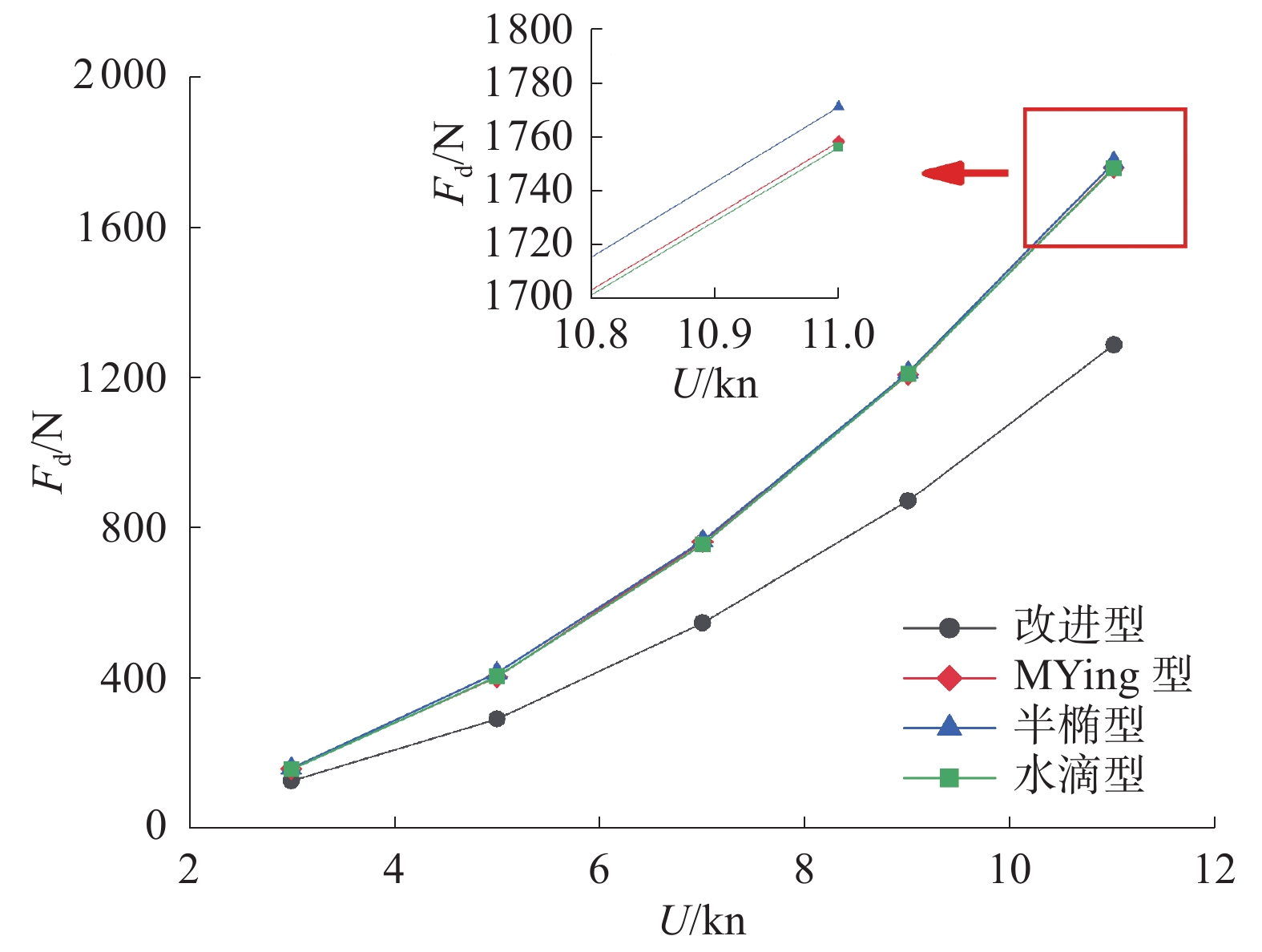
将4种方案分别计算5组速度–阻力值并进行对比，确定艏部型线最优结果，计算以及对比结果如表3所示。为清晰对比4种艏部型线的阻力结果，将计算结果绘制曲线图，如图11所示。
表 3 不同艇艏阻力计算值航速/
Kn速度/
（m/s）改进型
阻力/N水滴型
阻力/N半椭型
阻力/NMYing
阻力/N3 1.542 125.72 157.23 159.73 156.37 5 2.570 290.38 402.10 413.13 403.29 7 3.598 545.91 761.65 764.16 753.95 9 4.626 871.33 1208.37 1213.97 1209.38 11 5.654 1287.36 1758.50 1771.38 1756.35 
图 11 不同艇首阻力曲线对比图下载:
全尺寸图片
由计算结果可以发现，当航速很低时，4种型线的阻力结果相近，但随着航速的增加，半椭型艏部型线的AUV阻力值上升是最快的，水滴型和MYing型艏部型线与其相差很小，只略小于半椭型，整体来看，3种常规艏部型线的阻力结果几乎一致。而经过特殊优化的艏部型线的阻力结果上升趋势明显小于其他3种，有较好的减阻性能，是更合理的艏部型线选择，也就是文中第2节中计算AUV阻力是选择的艏部型线。
3.2 舵板设计
除了艏部型线外，舵的选择也会对AUV阻力造成影响，由于作业需要以及结构要求，文中水下航行器的舵的结构以及形式已经确定，现在对舵的截面进行确定，使得提高AUV升力的同时尽可能减少阻力。本节选择了2种不同截面的舵板进行升力和阻力性能比较，选择结果相对较好的一种供航行器使用。2种舵板分别是按照NACA0012和NACA0020共2种翼型作为横剖面形状设计的，它们的计算模型如图12~13所示。其中，后掠角均选择20°，舵高选择0.3 m，舵宽选择0.45 m。
图 12 NACA0012型舵板下载:
全尺寸图片
图 13 NACA0020型舵板下载:
全尺寸图片
NACA0012几何表达式为
$$\begin{split} & \frac{y}{2} = \pm t \left[1.484\;5\sqrt {\frac{x}{b}} - 0.630\;0\frac{x}{b} - 1.758{\left(\frac{x}{b}\right)^2} +\right.\\& \left. \qquad 1.421\;5{\left(\frac{x}{b}\right)^3} - 0.507\;5\left( \frac{x}{b}\right)^4 \right] \end{split} $$ 式中：t=0.12，b为舵宽（取0.45），
$ x、y $ 为横纵坐标。NACA0020几何表达式为
$$ \begin{split} & \frac{y}{2} = \pm t \left[1.484\;5\sqrt {\frac{x}{b}} - 0.630\;0\frac{x}{b} - 1.758{\left(\frac{x}{b}\right)^2} +\right.\\& \left. \qquad 1.421\;5{\left(\frac{x}{b}\right)^3} - 0.507\;5\left( \frac{x}{b}\right)^4 \right] \end{split}$$ 式中：t=0.20，b为舵宽（取0.45），
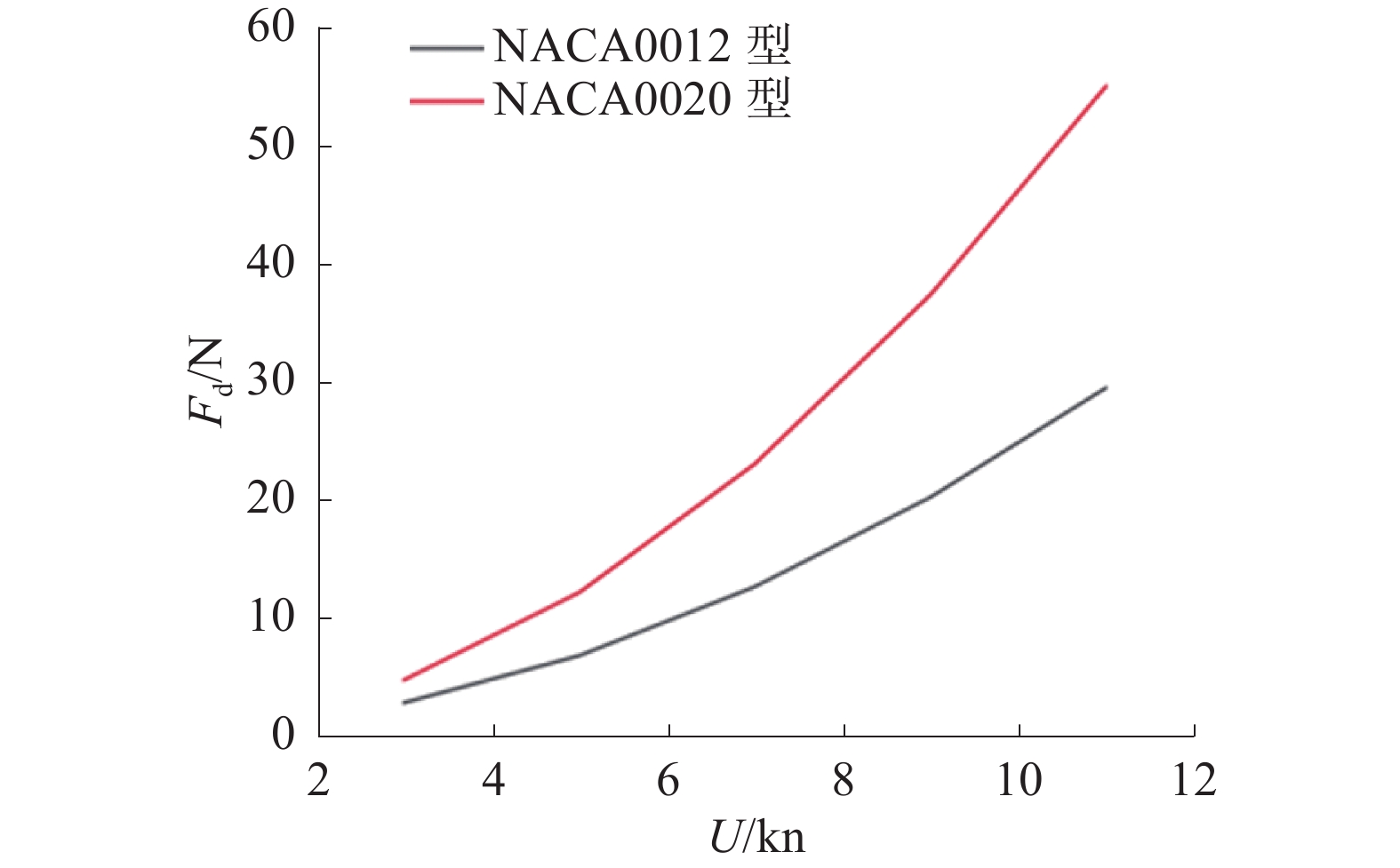
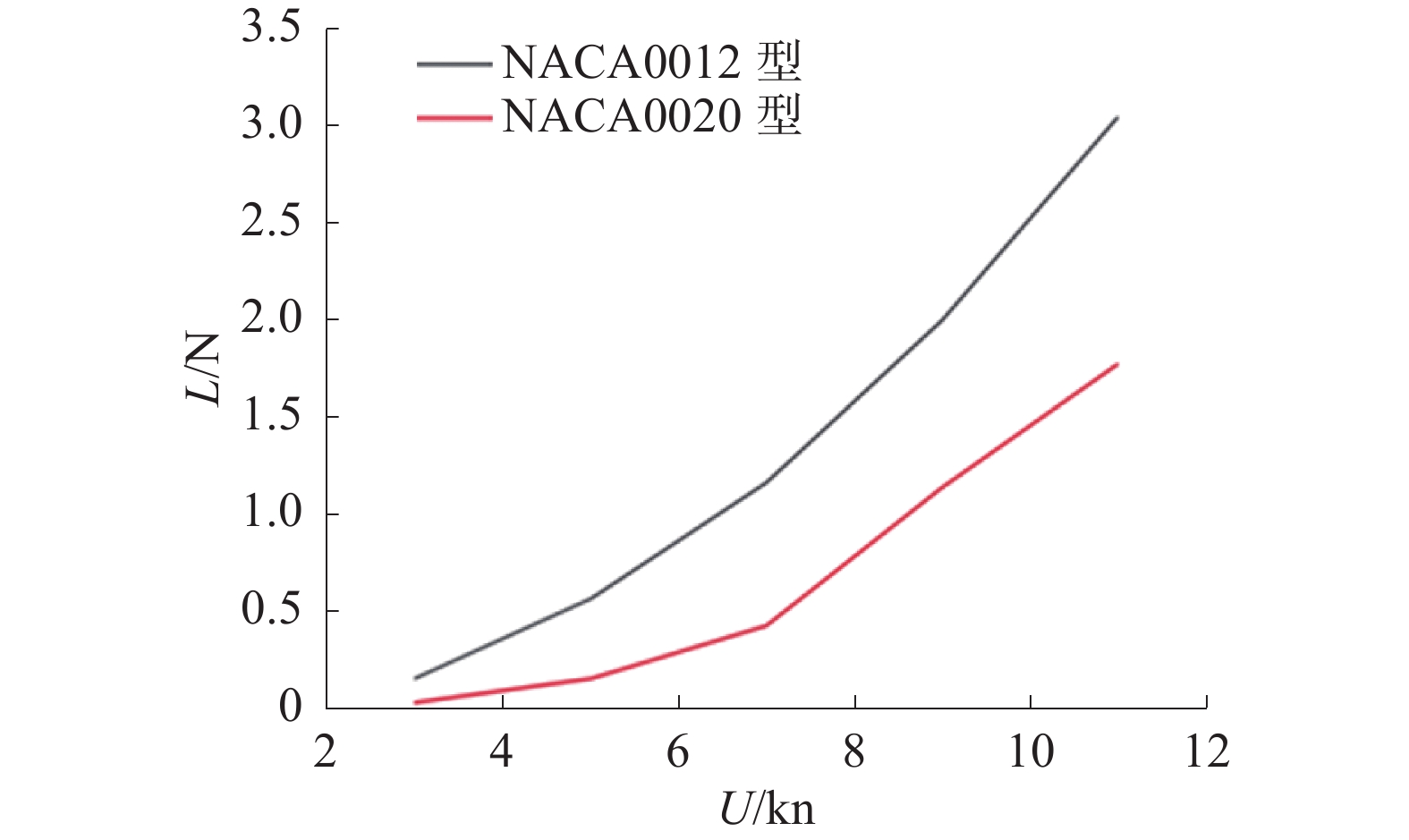
$ x、y $ 为横纵坐标。2种舵板的阻力和升力的计算结果如表4所示。为更清晰化比较，将结果作图对比，如图14和图15所示，其中，U表示航行速度，Fd表示阻力，L表示升力。
表 4 2种舵板不同航速下计算结果航速/
kn速度/
(m/s)舵板NACA0012 舵板NACA0020 阻力/N 升力/N 阻力/N 升力/N 3 1.542 2.52 0.15 4.46 0.03 5 2.57 6.54 0.56 11.90 0.15 7 3.598 12.37 1.16 22.80 0.42 9 4.626 19.96 1.99 37.15 1.13 11 5.654 29.26 3.04 54.86 1.77 
图 14 2种舵板阻力对比下载:
全尺寸图片
图 15 2种舵板升力对比下载:
全尺寸图片
由计算结果可知，随着航速的提高，2种舵板的阻力和升力都随之增加，但NACA0012型舵板的阻力增加更缓慢，并且升力增加更迅速，是更好的舵板截面选择。因此最终本水下航行器选择安装的是NACA0012型舵板。
4. 结论
通过STAR-CCM+软件对本文水下航行器进行结构优化设计以及阻力计算，结果显示：
1）航行器整体阻力值整体随着航速的增大而增大，大致呈二次曲线形式。不同的艏部型线对航行器的阻力有较大的影响，使用优化型艏部型线可以较其他型线使阻力增涨的更缓慢。因此本文选择的优化型艏部型线较其他常规性艏部型线有更好的减阻效果。
2）航行器周围流场速度随着航速的增大而增大。航行器使其首尾端的流场速度有不同程度的减小，且随着航速的增大，尾流场速度受影响的区域范围逐渐增大。
3）航行器表面压力同样随着航速的增大而增大，并且在航行器艏部达到最大值，也就是说航行器的最艏部是整体结构中受力最大的，在结构设计时应着重考虑。
4）对于舵板的选择，NACA0012型舵板不仅比NACA0020型舵板可提供更大的升力，并且阻力值也更小，是水下航行器更优的舵板选择。
-
图 1 水下航行器计算模型
下载:
全尺寸图片
图 2 航行器模型计算域
下载:
全尺寸图片
图 3 航行器模型切割体网格
下载:
全尺寸图片
图 4 阻力曲线
下载:
全尺寸图片
图 5 阻力结果趋势参考
下载:
全尺寸图片
图 6 航行器周围流场速度
下载:
全尺寸图片
图 7 航行器表面压力
下载:
全尺寸图片
图 8 水滴型艇艏
下载:
全尺寸图片
图 9 半椭型艇艏
下载:
全尺寸图片
图 10 MYing型艇艏
下载:
全尺寸图片
图 11 不同艇首阻力曲线对比图
下载:
全尺寸图片
图 12 NACA0012型舵板
下载:
全尺寸图片
图 13 NACA0020型舵板
下载:
全尺寸图片
图 14 2种舵板阻力对比
下载:
全尺寸图片
图 15 2种舵板升力对比
下载:
全尺寸图片
表 1 网格无关性
网格数量 基础网格尺寸/m 阻力/N 1076359 0.04 566.42 1823651 0.03 551.38 2416471 0.02 545.91 4300075 0.01 544.52 表 2 阻力预报数值
航速/kn 3 5 7 9 11 阻力/N 125.72 290.38 545.91 871.33 1287.36 表 3 不同艇艏阻力计算值
航速/
Kn速度/
（m/s）改进型
阻力/N水滴型
阻力/N半椭型
阻力/NMYing
阻力/N3 1.542 125.72 157.23 159.73 156.37 5 2.570 290.38 402.10 413.13 403.29 7 3.598 545.91 761.65 764.16 753.95 9 4.626 871.33 1208.37 1213.97 1209.38 11 5.654 1287.36 1758.50 1771.38 1756.35 表 4 2种舵板不同航速下计算结果
航速/
kn速度/
(m/s)舵板NACA0012 舵板NACA0020 阻力/N 升力/N 阻力/N 升力/N 3 1.542 2.52 0.15 4.46 0.03 5 2.57 6.54 0.56 11.90 0.15 7 3.598 12.37 1.16 22.80 0.42 9 4.626 19.96 1.99 37.15 1.13 11 5.654 29.26 3.04 54.86 1.77 -
[1] 修志强. 水下滑翔机控制系统与控制算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2009. [2] 宋保维, 潘光, 张立川,等. 自主水下航行器发展趋势及关键技术[J]. 中国舰船研究, 2022, 17(5): 27−44. [3] 潘光, 宋保维, 黄桥高,等. 水下无人系统发展现状及其关键技术[J]. 水下无人系统学报, 2017, 25(2): 44−51. [4] 饶太春. 基于多学科设计优化的水下航行器型线设计优化[D]. 福州: 福州大学, 2019. [5] 胡志强, 林扬, 谷海涛. 水下机器人粘性类水动力数值计算方法研究[J]. 机器人, 2007(2): 145−150. [6] ALVAREZ A, BERTRAM V, GUALDESI L. Hull hydrodynamic optimization of autonomous underwater vehicles operating at snorkeling depth[J]. Ocean engineering, 2009, 36(1): 105−112. doi: 10.1016/j.oceaneng.2008.08.006 [7] 金碧霞, 熊传志. 某流线型观测用水下机器人艏部的改进设计[J]. 机械制造, 2014, 52(6): 10−12. [8] 胡克, 俞建成, 张奇峰. 水下滑翔机器人载体外形设计与优化[J]. 机器人, 2005(2): 108−112. [9] 戴鹏. 基于参数化的三体组合式自主水下航行器多目标优化设计研究[D]. 广东: 华南理工大学, 2020. [10] GAO Ting, WANG Yaxing, PANG Yongjie, et al. A time-efficient CFD approach for hydrodynamic coefficient determination and model simplification of submarine[J]. Ocean engineering, 2018, 154: 16−26. doi: 10.1016/j.oceaneng.2018.02.003 [11] HONG Lin, FANG Renjie, CAI Xiaotian, et al. Numerical investigation on hydrodynamic performance of a portable AUV[J]. Journal of marine science and engineering, 2021, 9(8): 812. doi: 10.3390/jmse9080812 [12] VERSTEEG H K, MALALASEKERA W. An introduc-tion to computational fluid dynamics: finite volume method[M]. 北京: 世界图书出版公司, 2010. [13] 谭浩. 援潜救生艇与失事潜艇对接过程中的水动力干扰研究[D]. 哈尔滨: 哈尔滨工程大学, 2019. [14] 王亚兴. AUV 的水动力优化及近水面运动性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2015. [15] 杜月中, 闵健, 郭字洲. 流线型回转体外形设计综述与线型拟合[J]. 声学技术, 2004(2): 93−97.
