Radar distortion correction algorithm based on IMU and wheel odometer fusion
-
摘要: 为了校正低帧率2D激光雷达在机器人快速移动时产生的运动畸变，提出一种惯性测量单元(inertial measurement unit, IMU)和轮式里程计联合的激光雷达运动畸变较正方法。在传统轮式里程计辅助法的基础上，针对轮式里程计高速时容易打滑造成角度测量误差较大的缺点，利用局部角速度精度较高的IMU数据来完成激光雷达角度误差的较正。算法采用麦克纳姆全向轮式机器人进行验证。实验结果表明：IMU和轮式里程计联合较正运动畸变的方法能够克服轮式里程计打滑的机械性缺陷，有效减小雷达的位移误差和角度误差，大大提高低帧率2D激光雷达地图构建的质量。Abstract: In order to correct distortion of 2D laser radar data with low data frame rate when robots move rapidly, we propose a new method of laser radar motion distortion correction based on inertial measurement unit (IMU) and wheel odometer. Based on traditional auxiliary method of wheel odometer, in order to overcome the disadvantage that the wheel odometer is easy to slip at high speed, which causes large angle measurement error, the IMU data with high accuracy of partial angular velocity is used to correct the angle error of laser radar. The algorithm is verified by Mecanum omnidirectional wheeled robots. Experimental results show that the method of combining IMU and wheel odometer to correct motion distortion can overcome mechanical defect of wheel odometer slipping, and effectively reduce the displacement error and angle error of radar, which greatly improves the quality of low frame rate 2D laser radar map construction.
-
诸多商用机器人为了控制硬件成本，采用数据帧率较低的2D激光雷达，导致机器人在快速移动时雷达数据将产生较大运动畸变[1]。迭代最近点(iterative closest point, ICP)算法[2]为经典的畸变校正算法，在两帧数据之间进行扫描匹配，但未考虑机器人的运动因素，虽然通过不断迭代能够收敛，但仍存在误差[3]；融合主成分分析算法(principal component analysis, PCA)的ICP算法作为ICP算法的改进，利用有效点对中欧式距离较大的点对完成精配准，但在点云较稠密时配准误差较大[4]；轮式里程计辅助法[5]在理想状态下精度较高，但在速度过快时驱动轮打滑的概率增加，所导致的角度误差难以处理[6]，致使高速状态下激光雷达角度误差不能够被准确校正；有学者提出轮式里程计与ICP融合算法[7-8]，改进了轮式里程计位置线性假设的缺陷，将其转为位置误差的线性假设[9]，算法能够达到更高的畸变校正上限但无法处理轮式里程计打滑的问题。为解决轮式里程计辅助法缺陷，本文利用惯性测量单元(inertial measurement unit, IMU)传感器[10]在快速移动时仍然能够提供高频率准确航向角信息的特点，弥补轮式里程计的机械缺陷，提出了IMU和轮式里程计融合的激光雷达运动畸变校正的方法。
1. 激光雷达运动畸变产生原理
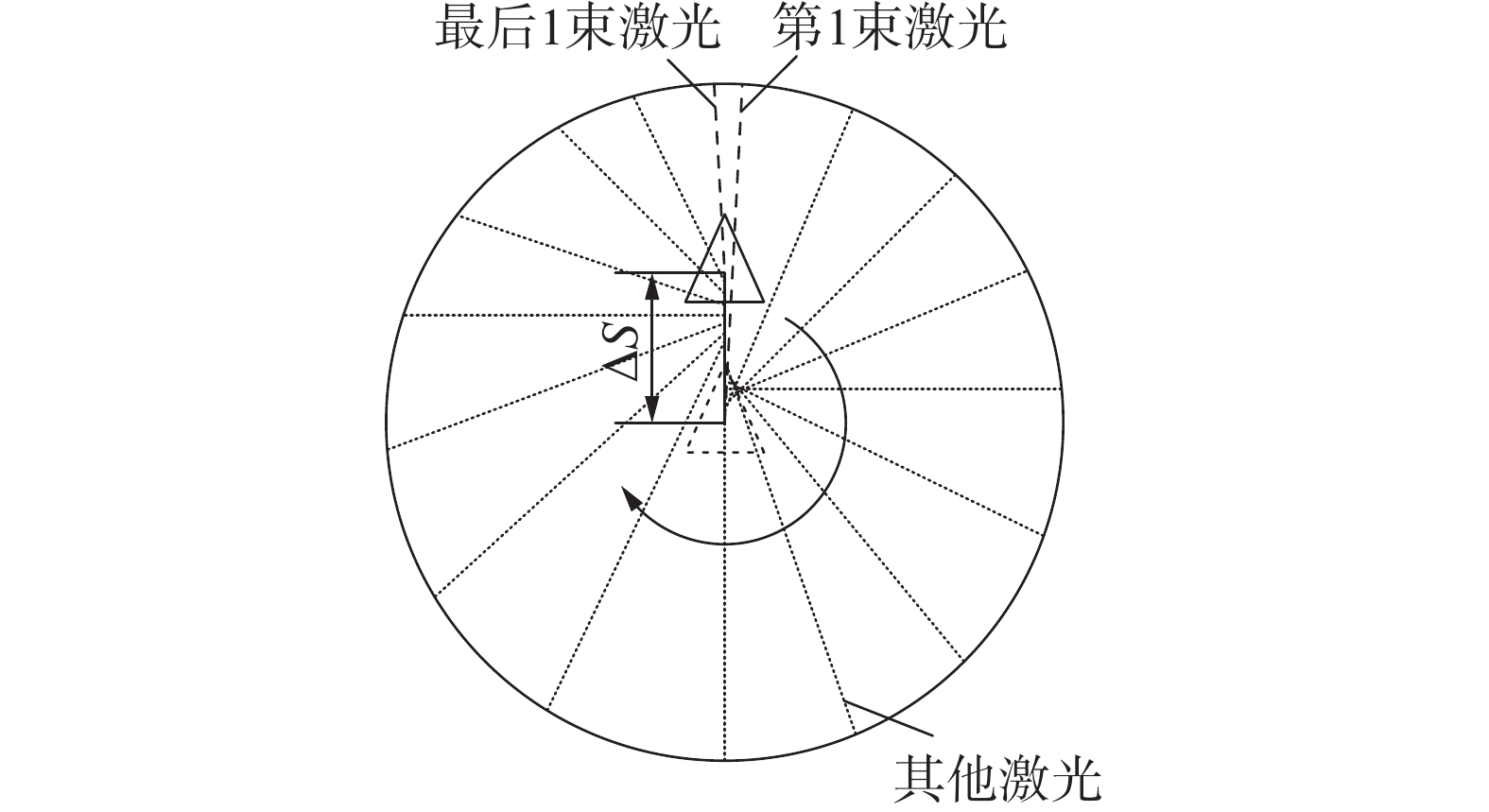
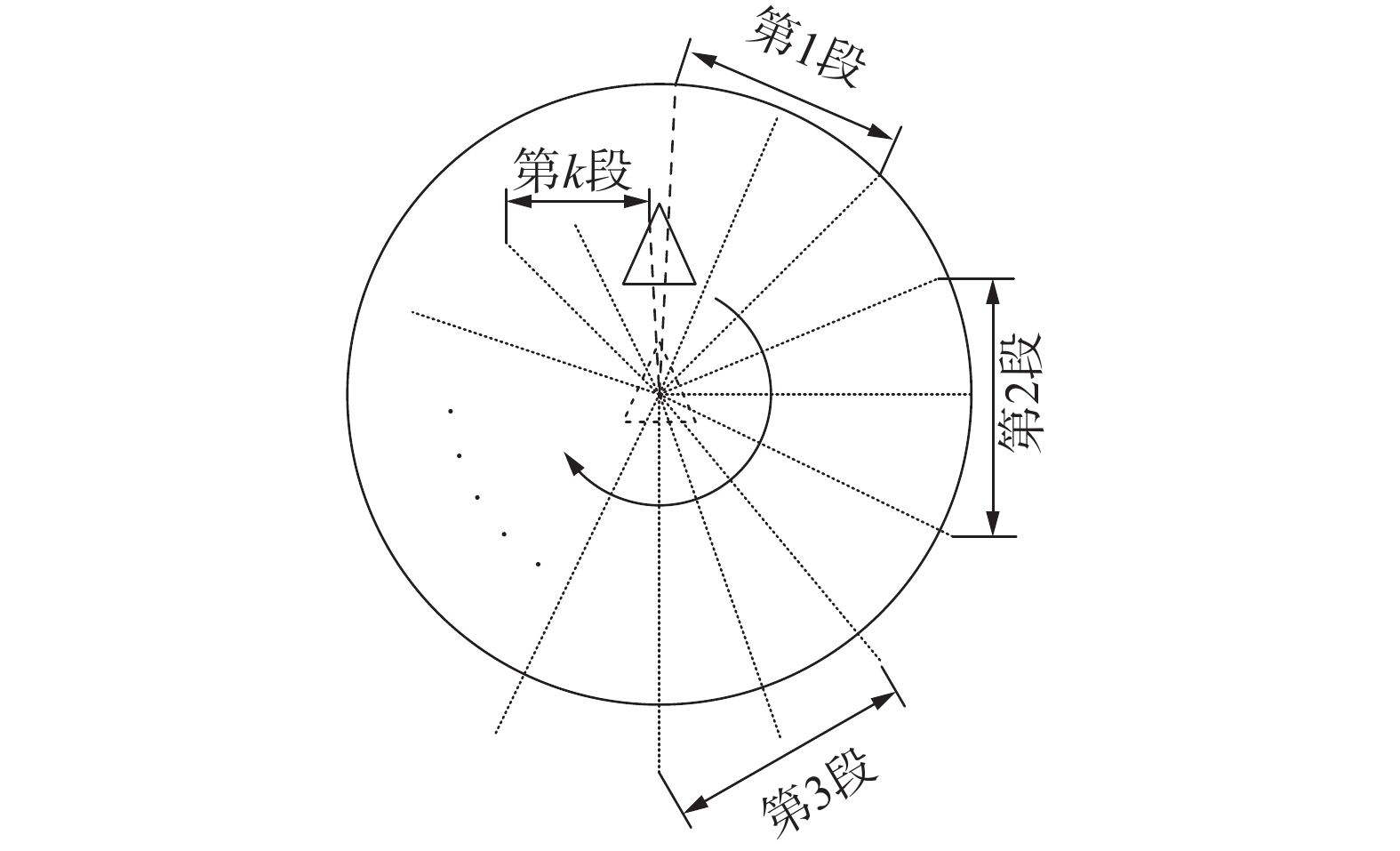
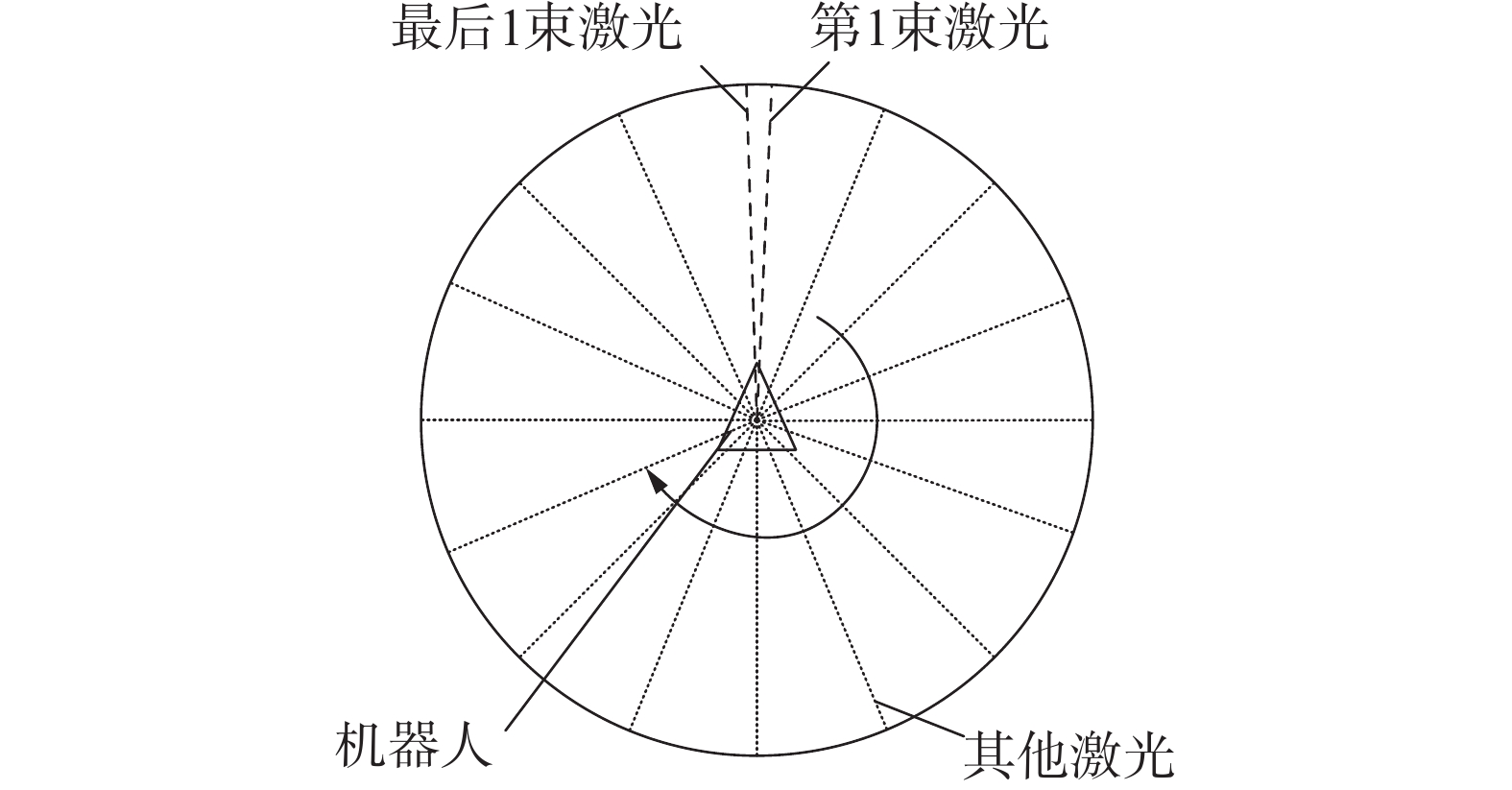
雷达运动畸变产生的主要原因是：激光雷达扫描数据并非瞬间完成却将其理想化为瞬间完成进行数据封装，忽略了激光雷达在单个数据周期内的运动[11]。设机器人处于封闭圆形区域，机器人向前做速度为v的匀速运动，雷达数据帧率f，其理想化数据应为图1所示。
图 1 理想的激光雷达数据
下载:
全尺寸图片
实际上，激光雷达在第1束与最后1束激光的时间间隔内随机器人运动，激光的发射点不断向前平移，实际的激光数据扫描情况为图2所示，一帧中越靠后的激光束发射点位移越大，误差越大。
图 2 实际的激光扫描情况下载:
全尺寸图片
最后数据封装时，雷达被理想化为静止，所有激光发射点被统一到第1束激光发射点处，最终得到畸变的雷达数据，如图3所示。误差顺着扫描方向逐渐增加。当前帧数据最大畸变量ΔLmax约为一帧数据周期内机器人所移动的距离，在v=0.5 m/s、f=5 Hz条件下有：
图 3 畸变的激光雷达数据下载:
全尺寸图片
$$ {{\Delta }}{L_{\max }} \approx v \times \frac{1}{f} = 10{\text{ }}{\text{cm}} $$ 可见数据畸变较大，不可忽略。上述论述的是机器人平移过程的位移畸变产生原理，具有一帧中越靠后的激光束发射点位移越大误差越大的特点。旋转产生的角度畸变原理与之类似，并且同样具有一帧中激光束越靠后角度误差越大的特点。
2. 算法主要思想
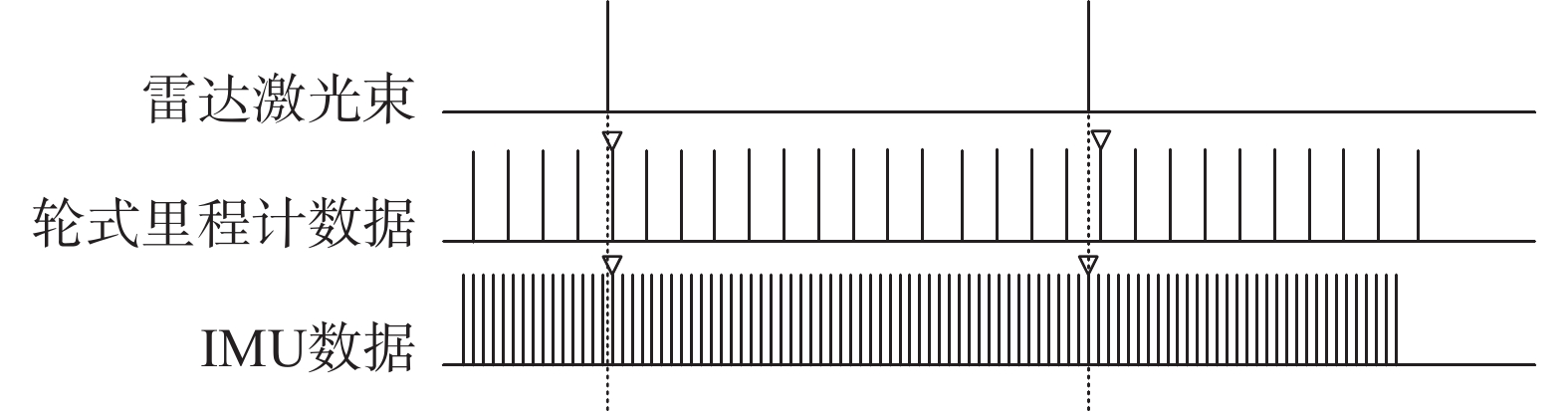
低成本2D激光雷达数据帧率低至5 Hz，轮式里程计数据帧率一般在100 Hz以上，而IMU数据帧率最高，可达200~1000 Hz。雷达、轮式里程计、IMU数据帧率对比如图4所示。通过多传感器融合补全雷达在单数据周期内的运动信息[12]，从而校正由于运动带来的点云畸变。
图 4 雷达、轮式里程计、IMU数据帧率对比下载:
全尺寸图片
激光雷达在一个数据周期内的移动使得每一束激光对应的雷达坐标系位置均不相同。算法通过轮式里程计数据获取激光雷达坐标系在一个数据周期内的运动情况，据此来初步修正每束激光数据。针对轮式里程计在机器人快速移动时容易打滑造成角度测量误差较大的问题，通过读取IMU数据来获取一个数据周期内机器人准确的旋转运动情况，对角度误差实现更加精准的校准[13]。
校正过程涉及到多次坐标系转换，以下对相关坐标系进行说明：
1）里程计坐标系Odom[14]：{O}(OOXOYOZO)，全局唯一，数据来源于电机编码器。
2）一帧雷达数据中第i束激光对应的激光雷达坐标系Radari：{Ri}(ORXRYRZR)，每一束激光都拥有自己对应的{Ri}，该坐标系原点即为激光雷达发射点，激光雷达运动时对于不同i，{Ri}并不相同，即如果一帧雷达数据包含360个激光点，则该数据周期内有360个不同{Ri}。
3）基准坐标系Base：{B}(OBXBYBZB)，一帧雷达数据中第0束激光对应雷达坐标系，{B}={R0}，所有激光点都需要校正到该坐标系进行数据封装。
首先借助里程计坐标系{O}为中间媒介，将所有激光各自对应的激光雷达坐标系{Ri}转换到该帧雷达数据的基准坐标系{B}下，完成轮式里程计辅助的初步校正；然后再通过IMU数据获取激光雷达坐标系{Ri}与基准坐标系{B}之间精确的旋转变换关系，对初步校正后的各激光束再次进行精度更高的角度校正；最后以基准坐标系{B}来封装数据。
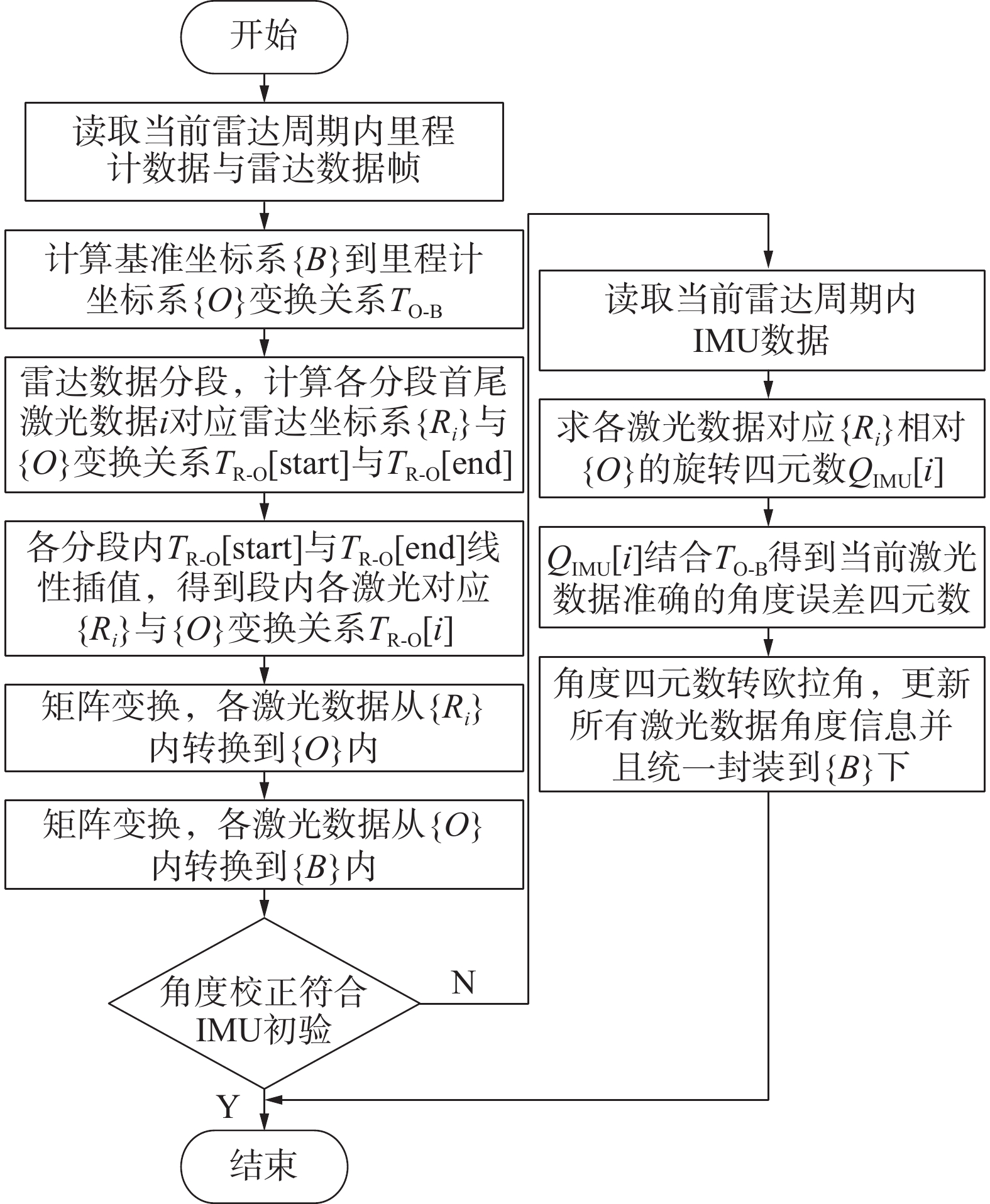
通常不带有磁力校准的IMU在测量航向角时会存在逐渐增大的累计误差[15-16]，但算法中计算的是IMU雷达扫描周期内的旋转增量，误差不会累积。算法的主要流程如图5所示。
图 5 算法流程下载:
全尺寸图片
3. 轮式里程计初步校正
3.1 激光束i对应{Ri}与{O}的变换关系
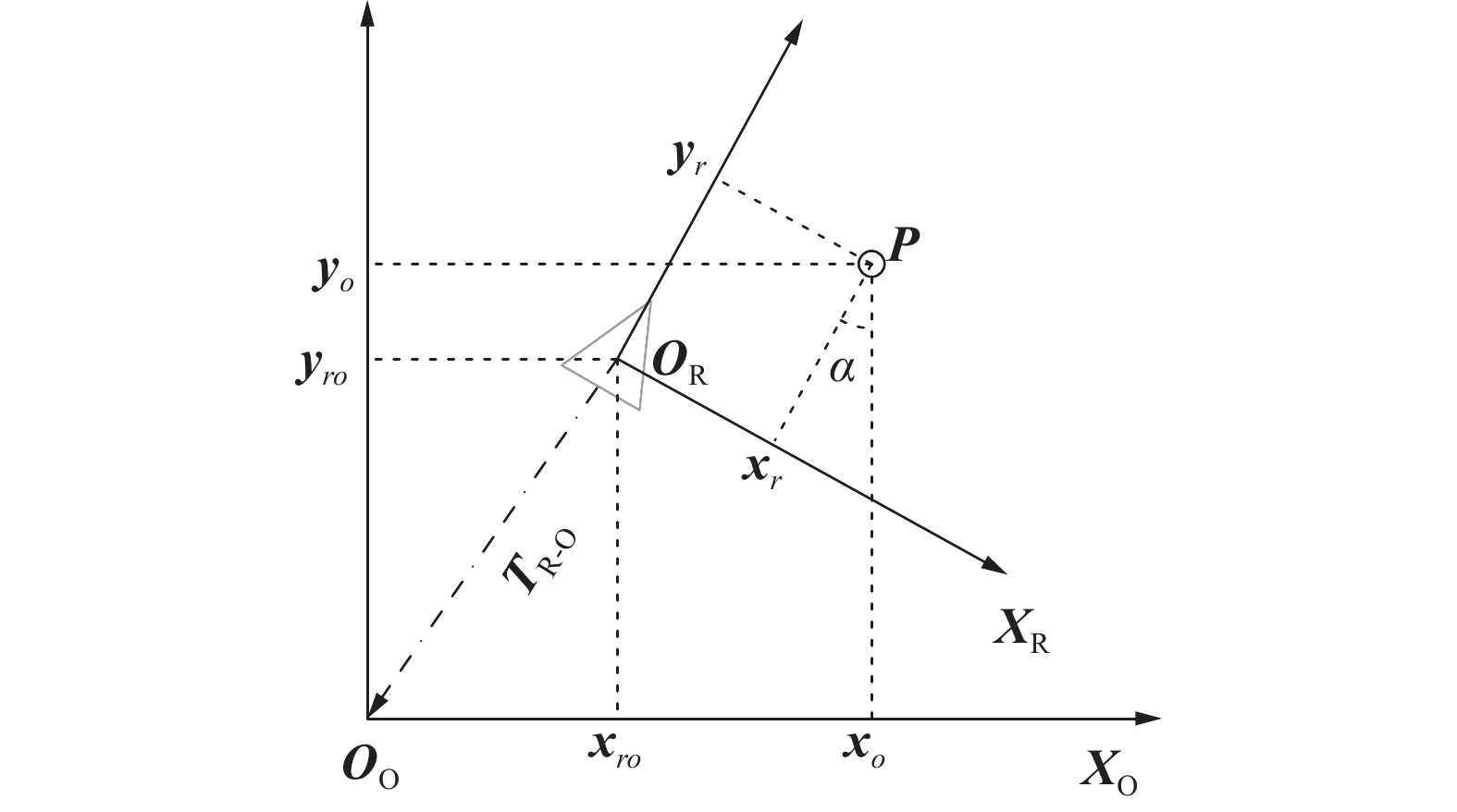
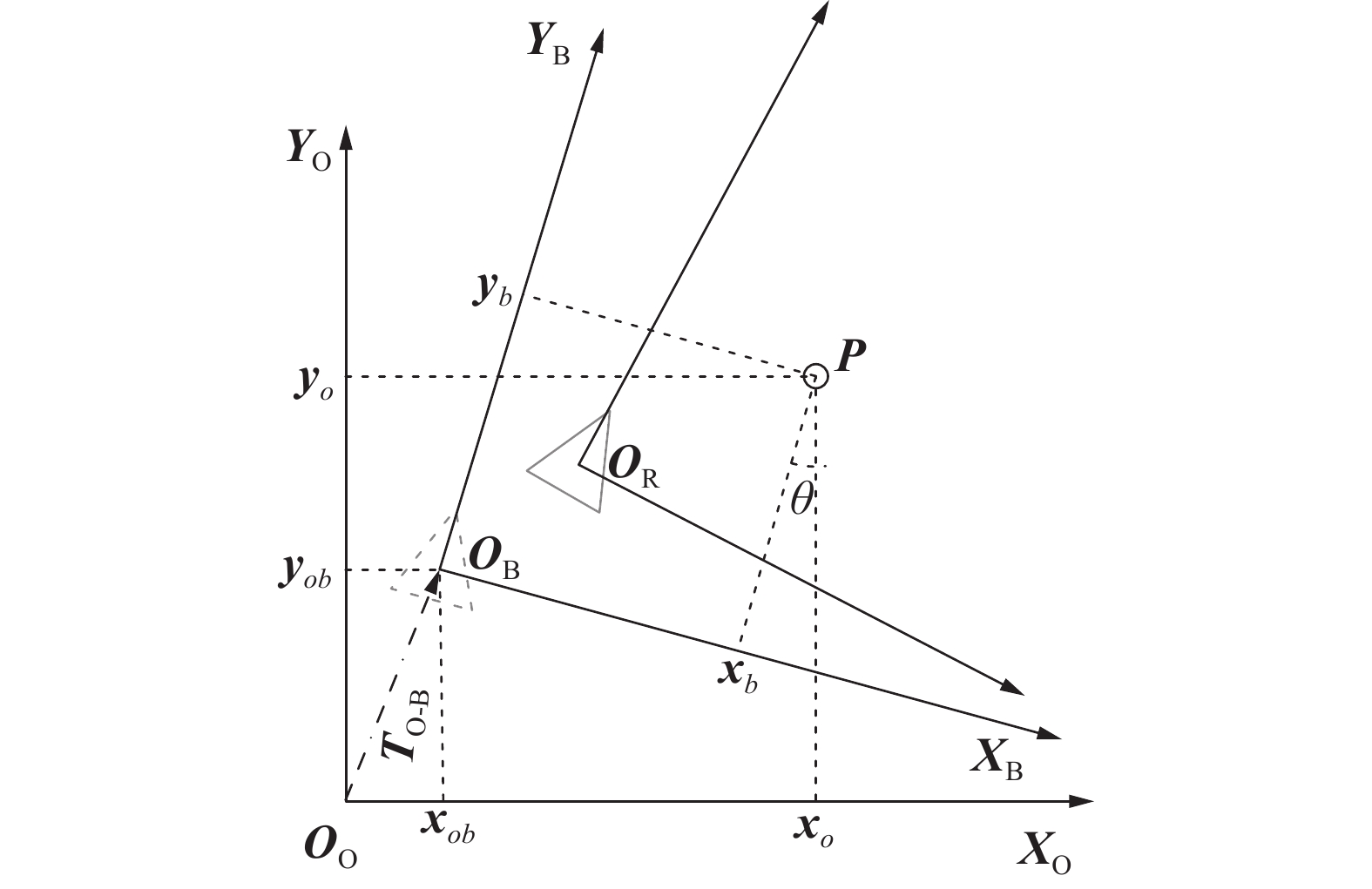
如图6所示，设激光点P在{Ri}中的坐标为(xr,yr)，在{O}中的坐标为(xo,yo)，则存在该激光点对应的{Ri}到{O}变换关系，该变换关系由旋转矩阵RR-O和平移向量TR-O组成。
图 6 {Ri}和{O}变换关系下载:
全尺寸图片
旋转矩阵RR-O变换为四元数QR-O便于插值：
$$ {{\boldsymbol{R}}_{{\text{R-} {\rm{O}}}}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}} \\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}} \\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha }&0 \\ { - \sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right] $$ $$ {{\boldsymbol{T}}_{{\text{R-} {\rm{O}}}}} = \left[ {\begin{array}{*{20}{c}} { - {x_{{{ro}}}}} \\ { - {y_{{{ro}}}}} \\ 0 \end{array}} \right] $$ (1) $$ {{\boldsymbol{Q}}_{{\text{R-} {\rm{O}}}}} = \left[ {\begin{array}{*{20}{c}} {{q_0}} \\ {{q_1}} \\ {{q_2}} \\ {{q_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{2} \times \sqrt {1 + {r_{11}} + {r_{22}} + {r_{33}}} } \\ {\dfrac{{{r_{32}} - {r_{23}}}}{{2 \times \sqrt {1 + {r_{11}} + {r_{22}} + {r_{33}}} }}} \\ {\dfrac{{{r_{13}} - {r_{31}}}}{{2 \times \sqrt {1 + {r_{11}} + {r_{22}} + {r_{33}}} }}} \\ {\dfrac{{{r_{21}} - {r_{12}}}}{{2 \times \sqrt {1 + {r_{11}} + {r_{22}} + {r_{33}}} }}} \end{array}} \right] $$ (2) 设激光雷达当前数据帧的激光总数为N，激光束之间的间隔时间为Δt。由于不一定能够找到与激光束发出时刻完全对应的轮式里程计数据，为了实现第i束激光对应的激光雷达坐标系{Ri}在轮式里程计坐标系{O}当中的准确匹配，如图7所示，需要对雷达数据帧进行分段，针对分段始末对应的{Ri}与{O}变换关系进行线性插值。
图 7 激光雷达点云分段下载:
全尺寸图片
每个分段中激光束个数为k，则第j段中的第1束激光在雷达数据帧中编号为j×k ，发出时刻为tstart，对应{Ri}在{O}中的变换关系由旋转矩阵RR-O[j×k]和平移向量TR-O[j×k]共2部分组成，二者可通过轮式里程计数据获取。同理，最后1束激光在数据帧中编号为(j+1)×k−1，发出时刻为tend，旋转矩阵RR-O[(j+1)×k−1]和平移向量TR-O[(j+1)×k−1]。
第i个点P的发出时间为ti，分段号为j，则有：
$$ j = i/k $$ $$ {t_i} = {t_{{\text{start}}}}[j] + \left( {i\% k} \right) \times \Delta t $$ 根据式(2)，将RR-O[j×k]转换为四元数QR-O[j×k]，RR-O[(j+1)×k−1]转换为四元数QR-O[(j+1)×k−1]进行插值，插值原理见式(3)、(4)以及图8、9。
图 8 插值原理下载:
全尺寸图片
图 9 四元数与向量插值下载:
全尺寸图片
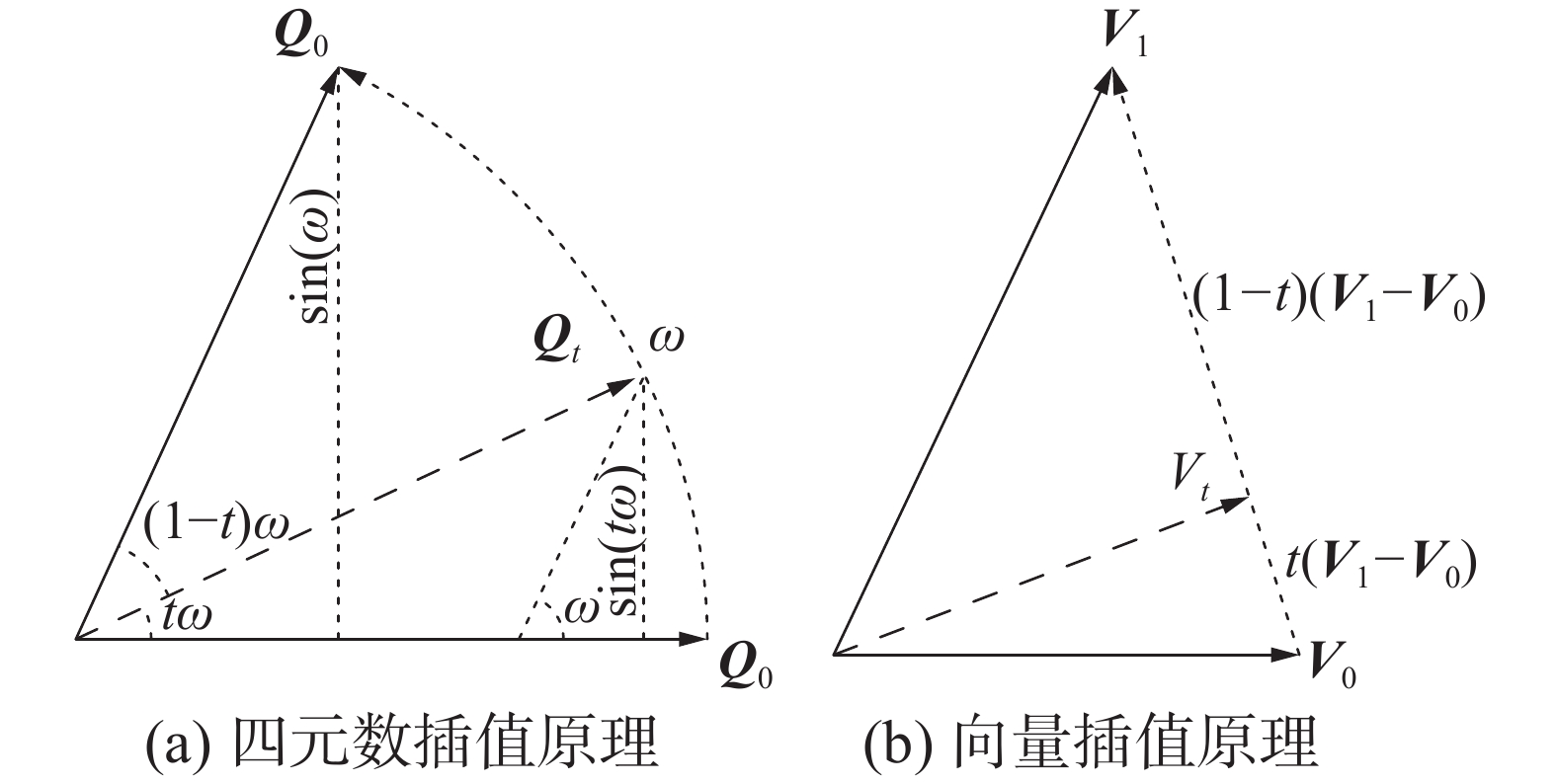
$$ \begin{split} & {{\boldsymbol{Q}}_{{\text{R-} {\rm{O}}}}}\left[ i \right] = {\text{slerp}}\left( {{\boldsymbol{Q}}_{{\text{R-} {\rm{O}}}}}\left[ {j \times k} \right],{{\boldsymbol{Q}}_{{\text{R-} {\rm{O}}}}}\left[ {\left( {j + 1} \right) \times k} \right],\right.\\& \left.\qquad\qquad\qquad \frac{{\left( {i\% k} \right) \times {{\Delta }}t}}{{{t_{{\text{start}}}}\left[ j \right] - {t_{{\text{end}}}}\left[ j \right]}} \right) \end{split} $$ (3) $$ \begin{split} & {{\boldsymbol{T}}_{{\text{R-} {\rm{O}}}}}\left[ i \right] = {\text{lerp}}\left( {{\boldsymbol{T}}_{{\text{R-} {\rm{O}}}}}\left[ {j \times k} \right],{{\boldsymbol{T}}_{{\text{R-} {\rm{O}}}}}\left[ {\left( {j + 1} \right) \times k} \right],\right.\\& \left.\qquad\qquad\qquad\frac{{\left( {i\% k} \right) \times \Delta t}}{{{t_{{\text{start}}}}\left[ j \right] - {t_{{\text{end}}}}\left[ j \right]}} \right) \end{split}$$ (4) 四元数球面线性插值为
$$ {{\boldsymbol{Q}}_{\boldsymbol{t}}} = {\text{slerp}}\left( {{{\boldsymbol{Q}}_{\text{0}}},{{\boldsymbol{Q}}_{\text{1}}},t} \right) = \frac{{\sin \left( {1 - t} \right)\omega }}{{\sin \omega }}{{\boldsymbol{Q}}_{\text{0}}} + \frac{{\sin \omega t}}{{\sin \omega }}{{\boldsymbol{Q}}_{\text{1}}} $$ 向量线性插值为
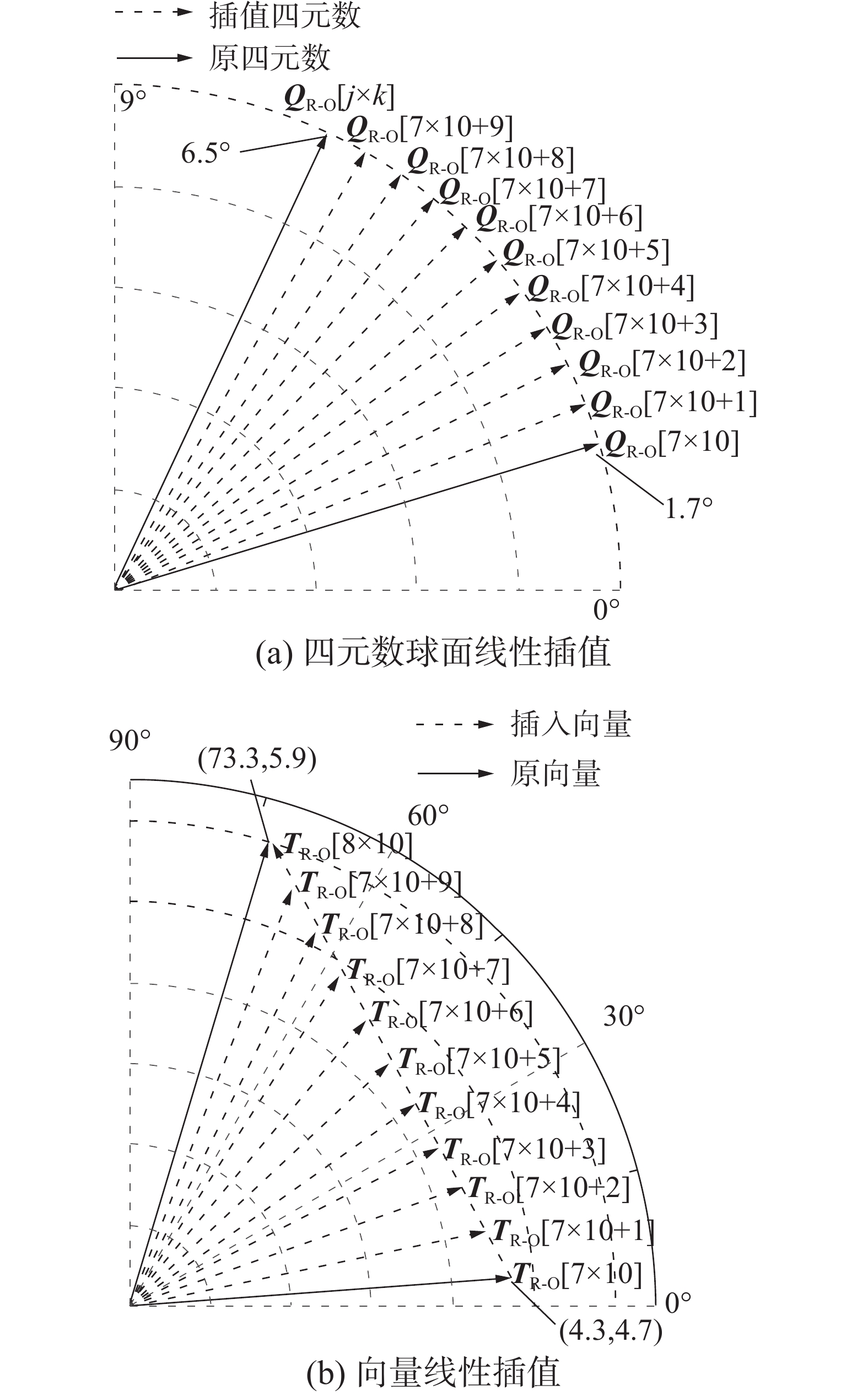
$$ {{\boldsymbol{V}}_{\boldsymbol{t}}} = {\text{lerp}}\left( {{{\boldsymbol{V}}_{\text{0}}},{{\boldsymbol{V}}_{\text{1}}},t} \right) = {{\boldsymbol{V}}_{\text{0}}} + t\left( {{{\boldsymbol{V}}_{\text{1}}} - {{\boldsymbol{V}}_{\text{0}}}} \right) $$ 机器人在Vx=0.4 m/s、Az=0.45 rad/s条件下，2D激光雷达数据帧按每10束激光进行分段处理，其中第7段激光四元数QR-O [7×10]到QR-O [8×10]球面线性插值与向量TR-O [7×10]到TR-O [8×10]线性插值情况如图9所示。
3.2 激光坐标系{Ri}转{O}
激光点需要由对应激光雷达坐标系{Ri}变换到轮式里程计坐标系{O}。假设第i个激光点P在雷达极坐标系中角度为angles[i]，距离为ranges[i]；转换为{R}中的坐标(xr,yr)，此时{Ri}与{O}变换关系由四元数QR-O[i]和平移向量TR-O[i]表示，有：
$$ {x_{{r}}} = {\text{ranges}}\left[ i \right] \times \cos \left( {{\text{angles}}\left[ i \right]} \right) $$ $$ {y_{{r}}} = {\text{ranges}}\left[ i \right] \times \sin \left( {{\text{angles}}\left[ i \right]} \right) $$ 结合式(2)得到图6中{Ri}与{O}夹角α：
$$ \alpha = {\text{atan2}}\left( {2 \times \left( {{q_0}{q_3} - {q_1}{q_2}} \right),1 - 2 \times \left( {{q_2}^2 + {q_3}^2} \right)} \right) $$ 结合式(1)将该激光点在{Ri}的坐标(xr,yr)转换为在轮式里程计坐标系{O}中的坐标(xo,yo)：
$$ \left[ {\begin{array}{*{20}{c}} {{x_{{o}}}} \\ {{y_{{o}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha } \\ {\sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{{r}}}} \\ {{y_{{r}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - {x_{{{ro}}}}} \\ { - {y_{{{ro}}}}} \end{array}} \right] $$ 3.3 激光坐标系{O}转{B}
如图10所示，设激光点P在{B}中的坐标为(xb,yb)，则存在该激光点对应的轮式里程计坐标系{O}与基准坐标系{B}变换关系。
图 10 {O}和{B}变换关系下载:
全尺寸图片
该变换关系由旋转矩阵RO-B和平移向量TO-B表示，设:
$$ {{\boldsymbol{T}}_{{\rm{O}}{\text{-} {{{\rm{B}}}}}}} = \left[ {\begin{array}{*{20}{c}} {{x_{{{ob}}}}} \\ {{y_{{{ob}}}}} \\ 0 \end{array}} \right] $$ $$ {{\boldsymbol{R}}_{{\rm{O}}{\text{-} {{{\rm{B}}}}}}} = \left[ {\begin{array}{*{20}{c}} {{o_{11}}}&{{o_{12}}}&{{o_{13}}} \\ {{o_{21}}}&{{o_{22}}}&{{o_{23}}} \\ {{o_{31}}}&{{o_{32}}}&{{o_{33}}} \end{array}} \right] $$ 将RO-B转换为四元数QO-B：
$$ {{\boldsymbol{Q}}_{{\rm{O}}{\text{-} {{{\rm{B}}}}}}} = \left[ {\begin{array}{*{20}{c}} {{s_0}} \\ {{s_1}} \\ {{s_2}} \\ {{s_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{2} \times \sqrt {1 + {o_{11}} + {o_{22}} + {o_{33}}} } \\ {\dfrac{{{o_{32}} - {o_{23}}}}{{2 \times \sqrt {1 + {o_{11}} + {o_{22}} + {o_{33}}} }}} \\ {\dfrac{{{o_{13}} - {o_{31}}}}{{2 \times \sqrt {1 + {o_{11}} + {o_{22}} + {o_{33}}} }}} \\ {\dfrac{{{o_{21}} - {o_{12}}}}{{2 \times \sqrt {1 + {o_{11}} + {o_{22}} + {o_{33}}} }}} \end{array}} \right] $$ QO-B转欧拉角得到图10中{O}与{B}的夹角θ：
$$ \theta = {\text{atan2}}\left( {2 \times \left( {{s_0}{s_3} - {s_1}{s_2}} \right),1 - 2 \times \left( {{s_2}^2 + {s_3}^2} \right)} \right) $$ 该激光点在{O}中的坐标(xo, yo)转换为在{B}中坐标(xb, yb)完成激光束数据的里程计初步校正：
$$ \left[ {\begin{array}{*{20}{c}} {{x_{{b}}}} \\ {{y_{{b}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta } \\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{{o}}}} \\ {{y_{{o}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{x_{{{ob}}}}} \\ {{y_{{{ob}}}}} \end{array}} \right] $$ 4. IMU激光雷达角度误差校正
通过读取IMU数据可以得到激光束i对应激光雷达坐标系{Ri}与轮式里程计坐标系{O}之间的旋转变换关系，该关系通过四元数QIMU[i]给出：
$$ {{\boldsymbol{Q}}_{{\text{IMU}}}}\left[ i \right] = \left[ {\begin{array}{*{20}{c}} {{u_0}} \\ {{u_1}} \\ {{u_2}} \\ {{u_3}} \end{array}} \right] $$ 四元数转欧拉角得到从IMU获取到的激光雷达坐标系{Ri}与轮式里程计坐标系{O}夹角γ：
$$ \gamma = {\text{atan2}}\left( {2 \times \left( {{u_0}{u_3} - {u_1}{u_2}} \right),1 - 2 \times \left( {{u_2}^2 + {u_3}^2} \right)} \right) $$ 初步校正中通过轮式里程计数据已知轮式里程计坐标系{O}与基准坐标系{B}之间的夹角θ，则由式(5)可得{R}与{B}基准坐标系之间的夹角φ，即当前激光束从第1束激光发出到当前激光束时刻发生的角度偏移量，angles[i]- φ即为激光束i经过IMU修正后的最终角度。至此激光数据校正完毕。
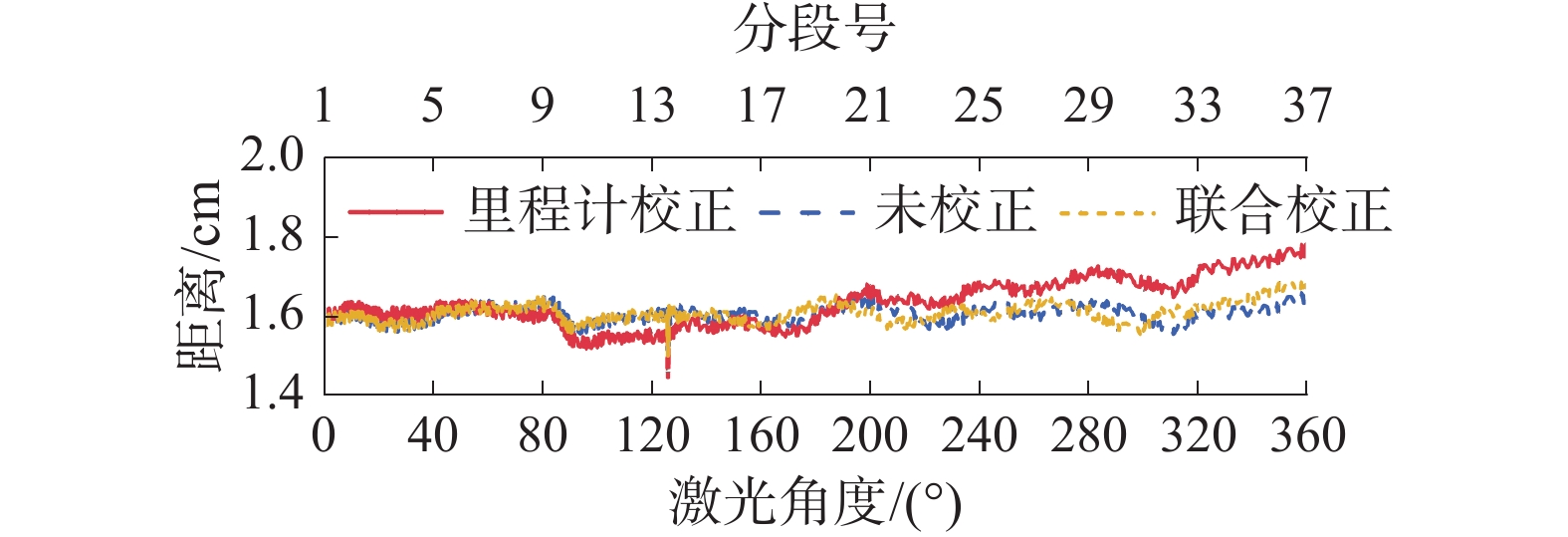
$$ \varphi = \left\{ {\begin{array}{*{20}{l}} {\theta - \gamma } \\ {\theta - \gamma + \pi } \\ {\theta - \gamma - \pi } \end{array}\begin{array}{*{20}{c}} { - \pi < \theta - \gamma \leqslant \pi } \\ {\theta - \gamma \leqslant - \pi } \\ {\theta - \gamma > \pi } \end{array}} \right. $$ (5) 为了体现各个校正变换的效果，将机器人置于一半径1.6 m规则圆形场地内进行实验，机器人在Vx=0.4 m/s、Az=0.45 rad/s条件下，激光雷达帧按每10束激光进行分段处理，数据如图11所示。
图 11 校正前后激光雷达数据曲线下载:
全尺寸图片
未校正的雷达数据曲线在220°之后（尾部）有明显的上升趋势，这是因为一帧中越靠后的激光束发射点位移越大，激光雷达距离测量误差越大。
完成轮式里程计初步校正后的雷达数据无明显上升趋势，其距离数值在场地的半径（1.6 m）附近正常波动，但是其角度校正精度较差，雷达数据存在角度误差。
对比分析完成IMU激光雷达角度误差校正后的雷达数据，算法利用IMU数据完成了角度滞后误差的校正，所以数据曲线相对于完成轮式里程计初步校正后的雷达数据有一定的角度超前，且一帧中越靠后的数据角度超前量越大，符合前述的角度误差特点。
5. 实验验证与结果分析
实验采用机器人操作系统(robot operating system, ROS)麦克纳姆轮全向机器人为平台，采用Rviz插件作为雷达数据可视化工具，相关误差数据利用ros_bag工具导出由origin软件绘图。激光雷达采用思岚RPLIDAR A1单线激光雷达，IMU采用MPU6050，直流电机自带霍尔编码器。机器人、激光雷达、IMU霍尔编码器实物及相关参数分别如图12、表1~表3所示。
表 2 MPU6050参数项目 典型值 量程加速度/g ±16 量程角速度/（°/s） ±2000 量程角度/(°) X/Z轴±180，Y轴±90 加速度分辨率/g 0.0005 角速度分辨率/(°/s) 0.61 角度测量精度/(°) 静态0.05，动态0.1 数据输出频率/Hz 200 扫描频率/Hz 5 
图 12 全向机器人与实验场地下载:
全尺寸图片
表 1 思岚RPLIDAR A1参数项目 典型值 测量范围/m 12 扫描角度/(°) 0.15~12.00 测距方向 逆时针 测距分辨率/mm 实际距离×0.01 角度分辨率/(°） ≤1 扫描频率/Hz 5 表 3 直流电机参数项目 典型值 减速比 1∶30 额定电压/V 12 减速后额定转速/(r/min) 293±21 额定扭矩/（kg·cm） 1 编码器线数/ppr 13 5.1 位移误差
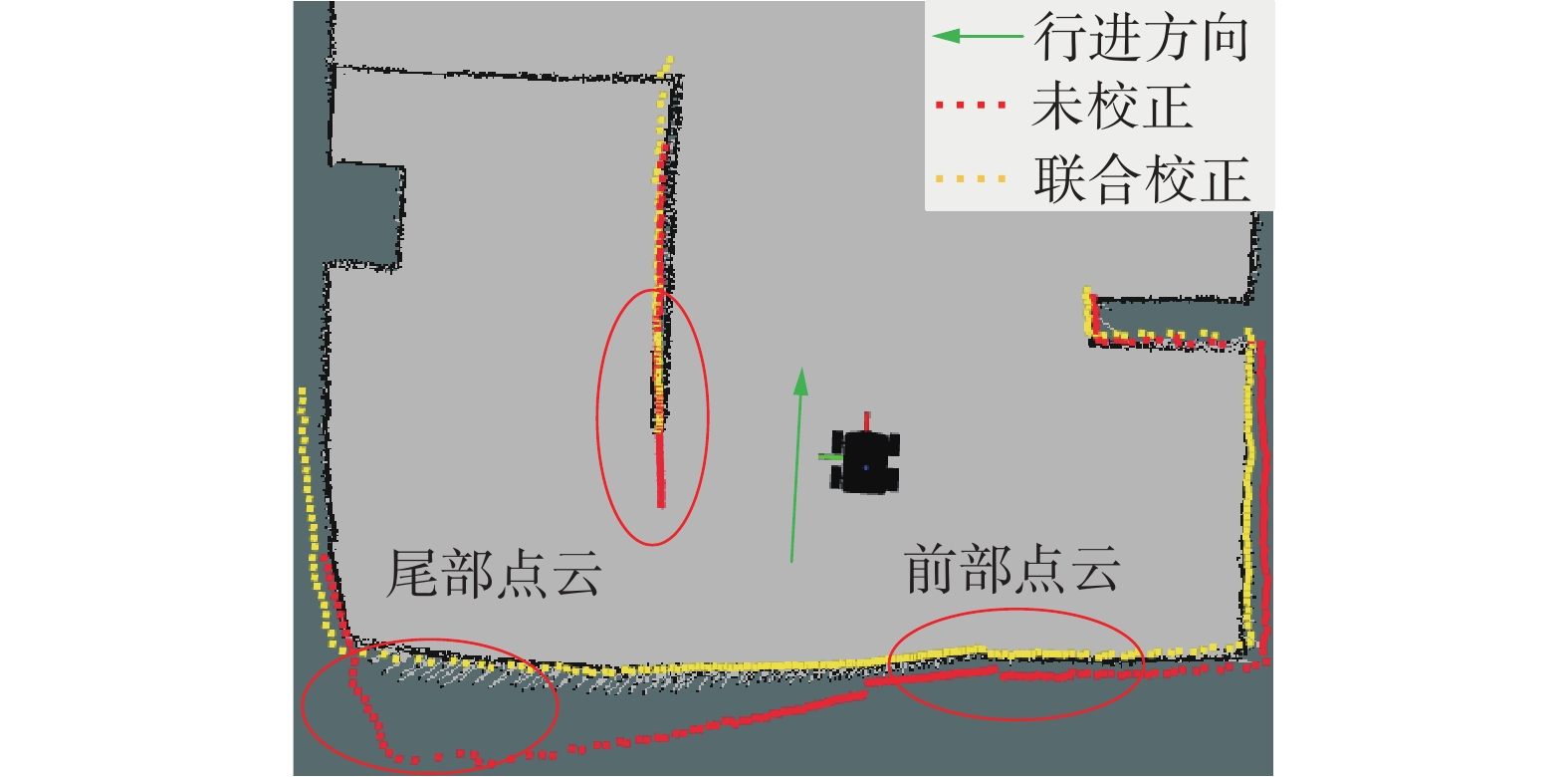
机器人前向速度Vx=1.15 m/s，所得激光雷达点云数据如图13所示。
图 13 激光雷达位移校正点云下载:
全尺寸图片
未校正雷达一帧点云数据中的前部数据误差不大，但由于RPLIDAR A1是逆时针扫描，误差按照逆时针方向逐渐增大，在当前帧的尾部达到最大，地图左下方边缘与实际地图存在较大错位。
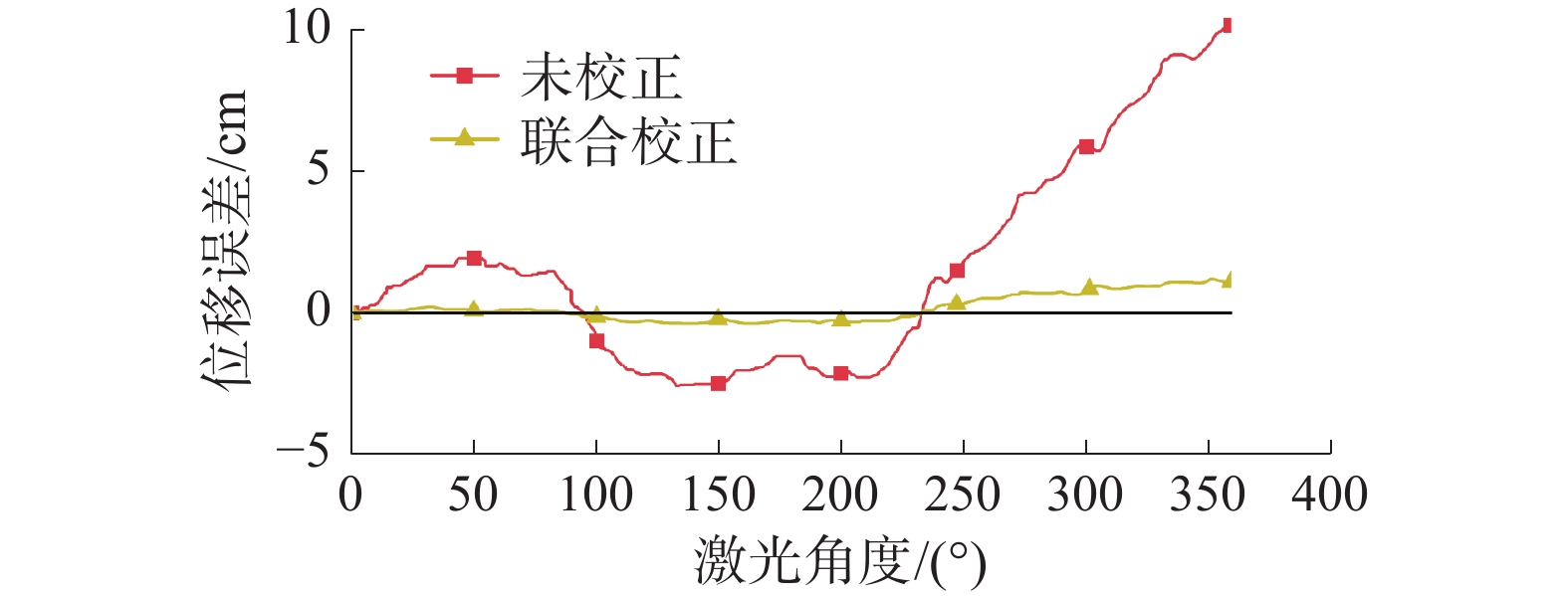
对比分析联合校正后的点云数据，各部分均与实际静态地图贴合。校正前后位移误差曲线如图14所示。
图 14 激光雷达位移误差曲线下载:
全尺寸图片
联合校正后位移误差相比校正前大大减小，误差最大值由10.5 cm减小为0.85 cm，由此可见联合校正下位移误差得到有效矫正。
5.2 角度误差
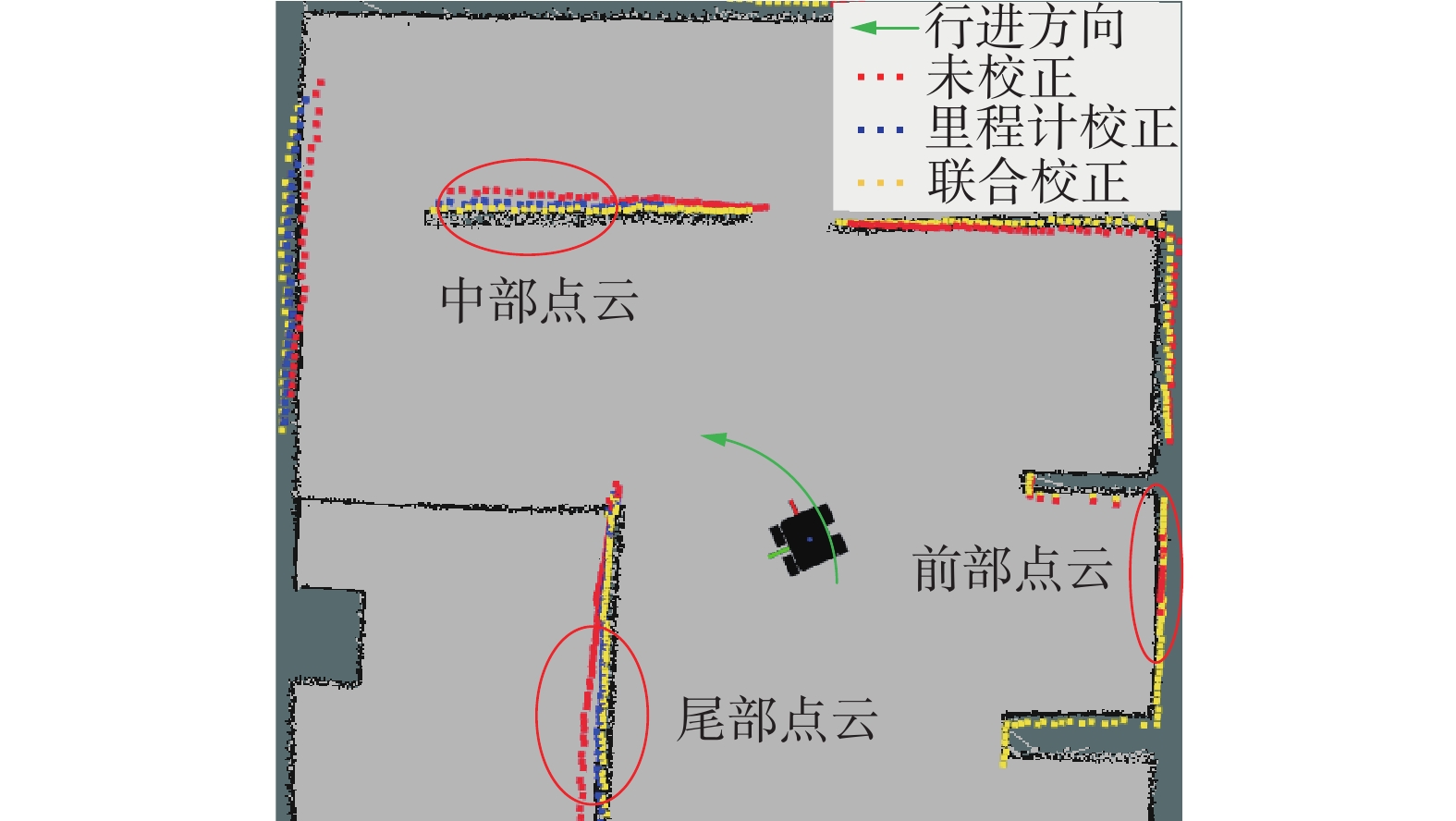
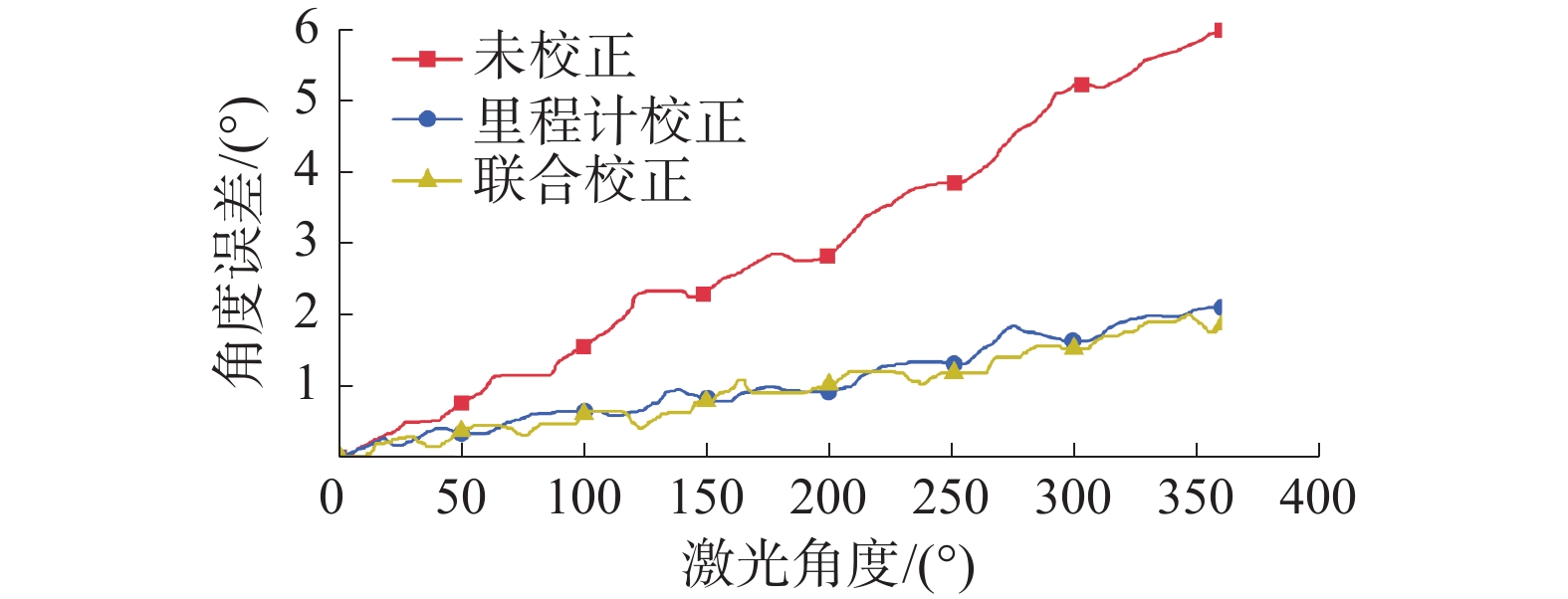
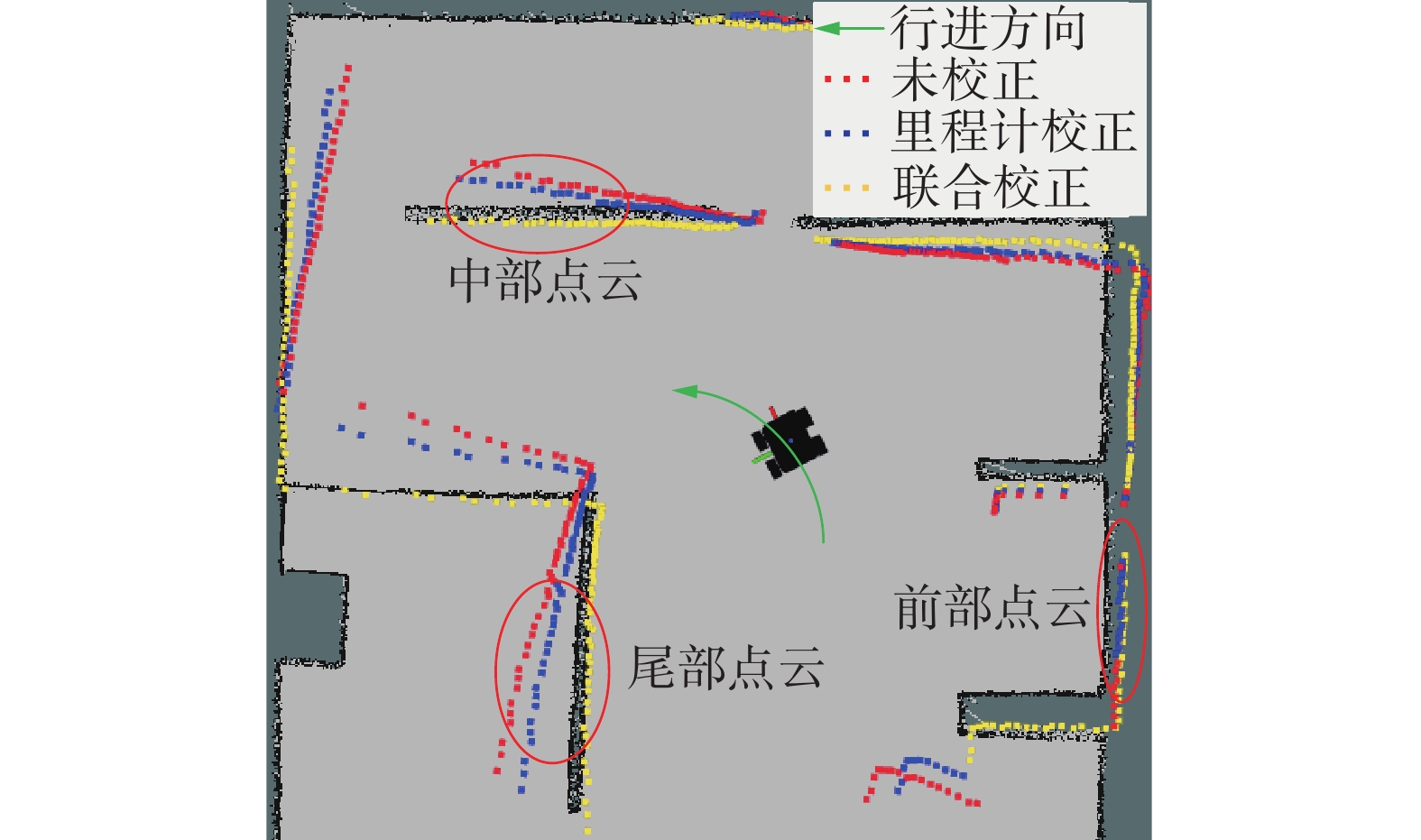
在慢速（Vx=0.4 m/s，Az=0.45 rad/s）情况下，如图15、16所示，未校正的数据帧前部角度误差较小，中部误差略大，尾部误差最大约为5°，雷达数据与静态地图存在较明显错位。
图 15 低速角度校正点云下载:
全尺寸图片
图 16 低速角度误差曲线下载:
全尺寸图片
对比分析里程计初步校正与联合校正后的数据，两者点云均与静态地图基本重合，因为在低速情况下驱动轮不易打滑，里程计数据尚且较为准确。但是里程计校正误差曲线整体略高于联合校正误差曲线，可知相对于未校正的雷达数据，两者角度误差均得到有效校正，但联合校正精度相比里程计校正更高。
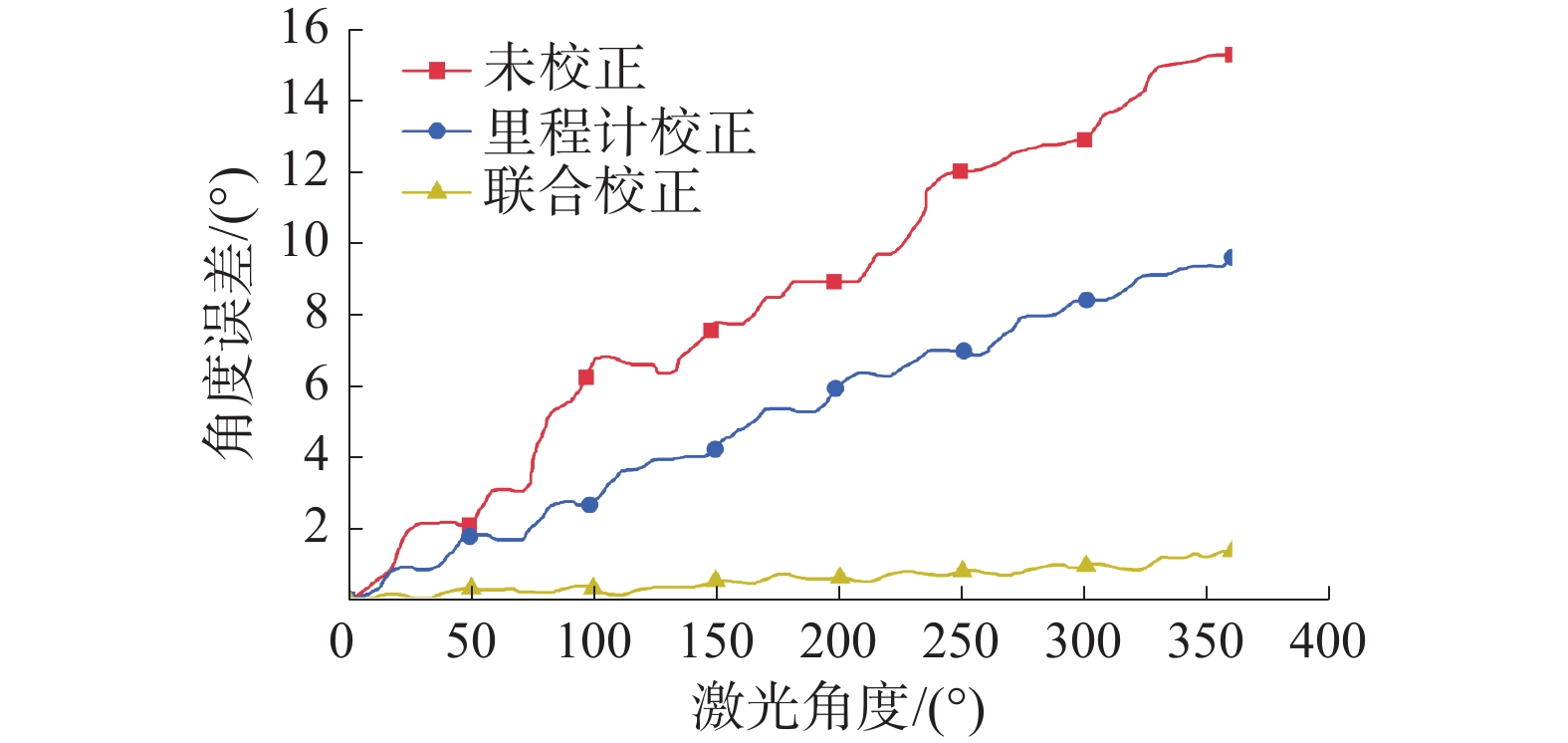
在高速（Vx=0.85 m/s，Az=1.2 rad/s）情况下，如图17、18所示，未校正的雷达数据存在最大为15°的角度误差，而轮式里程计校正的数据结果其数据帧尾部也存在10°的角度误差，因为高速状态下驱动轮多次不可避免地细微滑动，轮式里程计并不能够提供准确的机器人旋转数据，且该误差将持续累积，导致雷达数据与地图错位。
图 17 高速角度校正点云下载:
全尺寸图片
图 18 高速角度误差曲线下载:
全尺寸图片
对比分析IMU里程计联合校正的数据，其点云始终与静态地图吻合，角度误差曲线不超过2°。由于IMU不存在轮式里程计驱动轮打滑的问题，机器人角速度较大时依然能够准确提供姿态信息，将角度误差进行良好校正。所以在高速状态下，角度误差校正实际表现远优于轮式里程计校正。
综上所述，低速状态下轮式里程计校正和联合校正均具备较好的角度校正效果，但是高速状态下联合校正克服了轮式里程计的机械性缺陷，具备更好的角度校正性能。
5.3 地图构建质量
低速（Vx=0.4 m/s，Az=0.45 rad/s）情况下的机器人地图构建结果如图19所示。轮式里程计辅助法与IMU轮式里程计联合校正下的地图构建结果均较为理想，没有发生明显的地图错位，说明在机器人速度较低的条件下，驱动轮不容易发生打滑现象，2种方法均能够很好地校正激光雷达运动畸变。
图 19 低速建图对比下载:
全尺寸图片
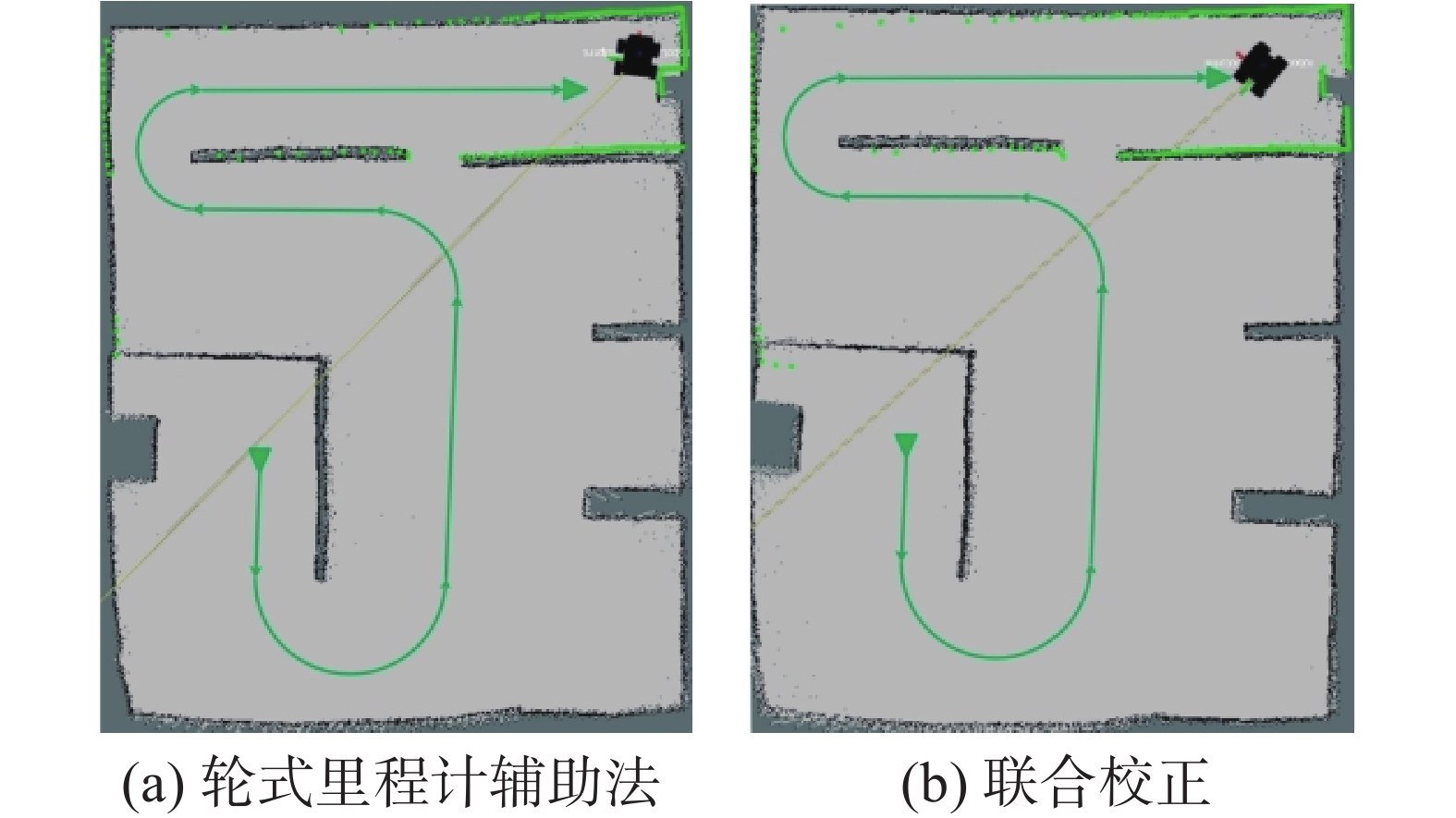
高速（Vx=0.85 m/s，Az=1.2 rad/s）情况下的机器人地图构建结果如图20所示。地图可大致分为A、B、C共3大区域，其中C为地图主体区域。机器人由A经过咽喉要道1后进入C区域，再经过咽喉要道2进入B区域完成探索。
图 20 高速建图对比下载:
全尺寸图片
轮式里程计辅助法中，机器人从A进入C时在1处急转弯时，由于高速行驶下驱动轮打滑，根据轮式里程计数据进行矫正的激光雷达数据发生较大角度误差，使刚进入C区域时获取到的C区域地形信息随之附带相应的角度错误，导致A区域构图结果相对于地图的主体区域C区域存在明显的顺时针角度错位。同样，从C区域经由咽喉要道2进入B区域时也发生了类似情况，导致B区域地图相对于C区域也存在逆时针方向的角度错位。
IMU轮式里程计联合校正算法中，由于激光雷达数据的角度信息最终是由IMU进行校正，雷达数据的角度误差校正不受轮式里程计打滑的影响，所以即使是在高速状态下依然能够实现较好的建图质量，不会产生地图不同区域之间的角度错位。少数墙体因为机器人速度太快、采集激光束过少，造成墙体构建较薄、障碍物点稀疏，该问题可通过反复探索来解决。
综上所述，机器人在构建地图时通过狭窄咽喉通道进入新区域，由于进入新区域后难以再扫描到旧区域的环境，新区域与旧区域之间的连接区域的信息大部分在该通道中获得（如图20中的1、2处），如果此时机器人驱动轮打滑会使得里程计数据错误从而使得激光雷达运动畸变反而加剧，2个区域的连接处产生角度错位，得到错误的地图。
而IMU不存在该机械性缺陷，即使在高速情况下依然能够准确反映激光雷达在自身一个数据周期内的旋转情况，从而消除在此间隔内由于激光雷达本身的运动造成的激光雷达运动畸变。
6. 结论
针对低帧率2D激光雷达的运动畸变问题，本文分析了雷达运动畸变的产生原因，阐述了轮式里程计辅助校正的不足，针对其在快速移动时容易打滑的问题，提出了IMU和轮式里程计融合激光雷达运动畸变校正方法。
算法通过轮式里程计获取校正位移误差的运动信息，通过IMU获取校正角度误差的运动信息，利用线性插值完成2个传感器与雷达数据的时间戳匹配。轮式机器人实机验证表明，该算法相比于传统里程计辅助法具备更高的角度误差校正精度，能够有效克服轮式里程计在机器人快速移动时打滑的机械缺陷，消除此问题所带来的角度误差，大大提升机器人地图构建的质量，极大改善了低帧率2D激光雷达的动态性能。
-
图 1 理想的激光雷达数据
下载:
全尺寸图片
图 2 实际的激光扫描情况
下载:
全尺寸图片
图 3 畸变的激光雷达数据
下载:
全尺寸图片
图 4 雷达、轮式里程计、IMU数据帧率对比
下载:
全尺寸图片
图 5 算法流程
下载:
全尺寸图片
图 6 {Ri}和{O}变换关系
下载:
全尺寸图片
图 7 激光雷达点云分段
下载:
全尺寸图片
图 8 插值原理
下载:
全尺寸图片
图 9 四元数与向量插值
下载:
全尺寸图片
图 10 {O}和{B}变换关系
下载:
全尺寸图片
图 11 校正前后激光雷达数据曲线
下载:
全尺寸图片
图 12 全向机器人与实验场地
下载:
全尺寸图片
图 13 激光雷达位移校正点云
下载:
全尺寸图片
图 14 激光雷达位移误差曲线
下载:
全尺寸图片
图 15 低速角度校正点云
下载:
全尺寸图片
图 16 低速角度误差曲线
下载:
全尺寸图片
图 17 高速角度校正点云
下载:
全尺寸图片
图 18 高速角度误差曲线
下载:
全尺寸图片
图 19 低速建图对比
下载:
全尺寸图片
图 20 高速建图对比
下载:
全尺寸图片
表 2 MPU6050参数
项目 典型值 量程加速度/g ±16 量程角速度/（°/s） ±2000 量程角度/(°) X/Z轴±180，Y轴±90 加速度分辨率/g 0.0005 角速度分辨率/(°/s) 0.61 角度测量精度/(°) 静态0.05，动态0.1 数据输出频率/Hz 200 扫描频率/Hz 5 表 1 思岚RPLIDAR A1参数
项目 典型值 测量范围/m 12 扫描角度/(°) 0.15~12.00 测距方向 逆时针 测距分辨率/mm 实际距离×0.01 角度分辨率/(°） ≤1 扫描频率/Hz 5 表 3 直流电机参数
项目 典型值 减速比 1∶30 额定电压/V 12 减速后额定转速/(r/min) 293±21 额定扭矩/（kg·cm） 1 编码器线数/ppr 13 -
[1] 张釜恺, 芮挺, 何雷, 等. 一种低成本的机器人室内可通行区域建模方法[J]. 北京航空航天大学学报, 2019, 45(12): 2470−2478. doi: 10.13700/j.bh.1001-5965.2019.0393 [2] ELIZEU Martins Oliveira Junior, DANIEL Rodrigues Santos, GIOVANA Angélica Ross Miola. A new variant of the ICP algorithm for pairwise 3D point cloud registration[J]. American academic scientific research journal for engineering, technology, and sciences, 2022, 85(1): 71−88. [3] ZENG Qingxi, KAN Yuchao, TAO Xiaodong, et al. LiDAR positioning algorithm based on ICP and artificial landmarks assistance[J]. Sensors, 2021, 21(21): 7141. doi: 10.3390/s21217141 [4] 王太学, 江智, 江德港, 等. 融合PCA的改进ICP激光点云配准算法[J]. 遥感信息, 2022, 37(2): 70−76. doi: 10.3969/j.issn.1000-3177.2022.02.009 [5] 陈强, 陈海波, 张沥化. 一种基于NDT配准与轮式里程计的激光雷达运动畸变补偿方法: CN115047485A[P]. 2022-09-13. [6] 贝旭颖, 平雪良, 高文研. 轮式移动机器人里程计系统误差校核[J]. 计算机应用研究, 2018, 35(9): 2696−2699, 2703. doi: 10.3969/j.issn.1001-3695.2018.09.031 [7] 杨超, 李天剑, 胡欢, 等. 融合速度估计与里程计位姿的扫描匹配改进算法[J]. 科学技术与工程, 2020, 20(28): 11632−11638. doi: 10.3969/j.issn.1671-1815.2020.28.034 [8] WU Hongwei, ZHU Liucun, CHENG Jingdi, et al. Research on motion distortion optimization algorithm of laser SLAM[J]. Journal of physics:conference series, 2022, 2330(1): 51−56. [9] 王雪, 李登峰, 黄杉杉, 等. 激光雷达运动畸变去除的算法设计[J]. 自动化仪表, 2021, 42(5): 89−91. [10] FENG Daquan, WANG Chunqi, HE Chunlong, et al. Kalman filter based integration of IMU and UWB for high-accuracy indoor positioning and navigation[J]. IEEE internet of things journal, 2020, 7(4): 3133−3146. doi: 10.1109/JIOT.2020.2980606 [11] 李晨阳, 彭程, 张振乾, 等. 融合里程计信息的农业机器人定位与地图构建方法[J]. 农业工程学报, 2021, 37(21): 16−23. doi: 10.11975/j.issn.1002-6819.2021.21.003 [12] KACZMAREK Adrian, ROHM Witold, KLINGBEIL Lasse, et al. Experimental 2D extended Kalman filter sensor fusion for low-cost GNSS/IMU/Odometers precise positioning system[J]. Measurement, 2022(S2): 40−42. [13] ZHANG Xiqiao, JENKINS Gregory J, HAKIM Chady H, et al. Four-limb wireless IMU sensor system for automatic gait detection in canines.[J]. Scientific reports, 2022, 12(1): 4788. doi: 10.1038/s41598-022-08676-1 [14] YAN Yaxuan, ZHANG Baohua, ZHOU Jun, et al. Real-time localization and mapping Uuilizing multi-sensor fusion and visual-IMU-wheel odometry for agricultural robots in unstructured, dynamic and GPS-denied greenhouse environments[J]. Agronomy, 2022, 12(8): 1740. doi: 10.3390/agronomy12081740 [15] 上官伟, 陈晶晶, 谢朝曦, 等. 基于IMU误差补偿的磁力计增强型组合定位方法[J]. 铁道学报, 2022, 44(7): 80−90. doi: 10.3969/j.issn.1001-8360.2022.07.010 [16] ZhANG Quan, NIU Xiaoji, ShI Chuang. Impact assessment of various IMU error sources on the relative accuracy of the GNSS/INS systems[J]. IEEE sensors journal, 2020, 20(9): 5026−5038. doi: 10.1109/JSEN.2020.2966379
