Auxiliary power grid frequency regulation control strategy of power electronic transformer
-
摘要: 为减小当前低惯性电力系统受到扰动时的频率偏差,提高系统惯性,本文基于控制负荷消耗理念提出了一种基于电力电子变压器的频率控制策略。根据有功/频率下垂特性,电力电子变压器通过在线负荷灵敏度识别准确地控制电压敏感负载的电压来改变负载有功消耗,可作为功率储备用以支持配电系统的一次调频,在频率暂态期间为系统提供有功支撑。最后设计了应用场景,通过仿真验证了其有效性。结果表明,在相同扰动情况下,使用电力电子变压器进行辅助调频能够有效减小频率偏差,提高系统的抗干扰能力。Abstract: In order to reduce frequency deviation when the current low inertia power system is disturbed, and improve inertia of the system, this paper presents a frequency control strategy based on power electronic transformer in terms of the concept of controlling load consumption. According to the characteristics of active power/frequency droop, the power electronic transformer accurately controls the voltage sensitive load’s voltage through on-line load sensitivity recognition to change the active power consumption of the load. This can be used as a power reserve to support the primary frequency regulation of the power system, providing active power support for the system during the frequency transient. Finally, the application scenario is designed, and its effectiveness is verified by simulation. The results show that using power electronic transformer for auxiliary frequency regulation can effectively reduce frequency deviation and improve the anti-interference ability of the system under the same disturbance condition.
-
近年来,大规模电动汽车接入电网给电网的安全运行带来了挑战[1],特别是在负荷高峰时期会造成区域重过载等问题。同时,风能、太阳能等作为清洁的可再生能源的发电比例正不断升高[2]。而风能、太阳能等清洁能源发电需要使用电力电子变流器来接入电网或用户,电力电子变流器的显著特点是响应迅速、惯性低,因此新能源发电并网会一定程度上降低电网的惯性,增加了电网受到扰动后的频率偏差。在严重的情况下,电网惯性的减小会影响电网的稳定性。电网发生扰动(故障、线路断开等)或电动汽车负荷大量接入后,会导致频率偏离标称值。如果系统惯性较大,在短暂瞬态后,频率恢复到接近标称值。然而,如果在弱电网系统中发生干扰,由于系统惯性低,增加了受到扰动后的频率偏差,频率可能会崩溃,在严重的情况下影响电网的稳定性和电能质量[3-4]。
对于维持频率稳定的措施有低频减载[5]、风力涡轮机的惯性控制和频率下垂特性[6-7]、电池储能系统[8-9]等,以上方法都是从网侧控制起到对频率的支撑作用。另一种方式是从负荷侧来进行管理,与电力系统相互作用。控制负荷消耗的优势在于电网中分布式控制点的可用性以及响应的快速性[10]。节能降压(conservation voltage reduction,CVR)是一种已提出并验证的负荷管理理念[11],也是最具成本效益的节能方法之一。其通过以可控的方式降低配电系统的电压,可以减少用电峰值的需求并实现节约能源的目的。在1973年,美国电力系统进行了CVR操作测试[12],这是较早进行的负荷管理方法,也验证了CVR实施的效果。但CVR仅仅是降低负荷的有功消耗,不为电网提供电压和频率的稳定性调节,但这种理念为以后的负荷管理提供了借鉴。在此基础上有学者提出了电压主导负荷管理[13],其理念是利用变压器分接头在允许范围内调节负荷电压以达到控制负荷消耗的目的,相比于CVR,电压主导负荷管理既可以降低负荷消耗也可以提高负荷消耗。除此之外国内外许多学者还提出了新的负荷管理方法,如电力弹簧[14-17],电力弹簧与实际负载串联组合成智能负载,电力弹簧的电压和功率消耗都可以改变,甚至可以充当一个电源(其内部包含有储能装置),因此电力弹簧与实际负载组合而成的智能负载在外部来看其电压与功率都没有波动,因此可以实现电网的稳定。但电力弹簧主要用于负载侧,不便于实现负载的集中管理,不适合用于为网侧做频率支撑。
以上几种方法都是通过电压来控制负荷消耗,因此控制负荷消耗的关键在于负载是否对电压敏感,如果负载对电压的敏感度较低,则需要很大的电压变化才能改变相应的负载消耗水平,负载控制效果就比较差,当负载对电压较为敏感时采用电压控制效果较好,因此,负荷的电压敏感度成为一个关键问题。近年来,由于电力电子变流器的发展,电器更多地朝着恒功率类型负载方向发展。然而,配电网中仍然存在大量对电压依赖的负荷。如文献[18]所述,这些负载:如空调、感应灯、微波炉、冰箱以及各种加热设备等,在功率吸收中具有一定的恒阻抗贡献。如果将这些负荷与其他恒功率负荷一起考虑在住宅电网中,则总负荷仍然对电压变化敏感,仍可实现电压控制负荷消耗效果。
电力电子变压器[19] (power electronic transformer,PET)为负荷管理提供了更为方便的控制方式,PET可以根据负载对电压的敏感性,通过控制负载的电压来降低负载消耗有功功率,从而实现更软的负载降低。这种方法的准确性取决于对负载有功功率与电压关系的准确识别。这种方法与电压主导负荷消耗理念类似,把传统变压器替换成了电力电子变压器,相比于传统变压器的分接头来控制电压,电力电子变压器在控制方式上更为灵活,且其拓展性更好,且能够实现无极调压。
本文以电网频率稳定为目标,提出了基于电力电子变压器的实时频率控制器,当配电网电动汽车充电负荷突增时电网频率f发生变化,通过PET将负荷电压在允许的范围内进行调整,负荷有功相应地变化,以调节电网频率[20]。并详细分析了实时频率控制器的实现方式,在仿真中验证其有效性,最后给出了结论。
1. 实时频率控制方法
1.1 工作原理
在电力系统中,频率与有功功率呈现强相关性,当网侧频率出现偏差时,一般是由于有功不平衡所导致,电动汽车负荷大量接入配电网将会导致配电网负荷突增,影响配电网的频率稳定,且这一情况在夜间更为严重[21]。因此,通过有功功率的供需平衡来实现频率的稳定。本文提出的实时频率控制器从负荷入手,让负荷主动适应系统频率变化做出相应的功率相应,参与到系统的一次调频过程。
当系统频率变化时,为了实现系统所需的功率变化必须提前计算有功功率负载对电压的灵敏度。通过PET进行负载灵敏度识别[22],根据有功与电压的关系,定义了如下有功功率电压灵敏度系数表达式:
$$ {K_p} = \frac{{[P\left( {{t_n}} \right) - P\left( {{t_{n - 1}}} \right)]/P\left( {{t_{n - 1}}} \right)}}{{[V\left( {{t_n}} \right) - V\left( {{t_{n - 1}}} \right)]/V\left( {{t_{n - 1}}} \right)}} $$ (1) 式中:
$ K_p $ 为有功功率电压灵敏度;$P\left(t_n\right) $ 与$ V\left(t_n\right) $ 为当前时刻的有功值与电压有效值;$P\left(t_{n-1}\right) $ 与$V\left(t_{n-1} \right) $ 为前一时刻有功值与电压有效值。当网侧频率变化时,通过频率偏差得到系统的有功偏差
$ \Delta P $ ,此时需要被控负载响应来抵抗扰动,则三相负载有功变化量的总额应该与扰动量相等:$$ \Delta P = \Delta {P_{\text{A}}} + \Delta {P_{\text{B}}} + \Delta {P_{\text{C}}} $$ (2) 式中:
$\Delta P_{\mathrm{A}}、 \Delta P_{\mathrm{B}}、 \Delta P_{\mathrm{C}} $ 分别为A、B、C三相的有功偏差。而每相负载的有功变化量可通过式(1)定义的负载灵敏度系数得出。
$$ \left\{ \begin{gathered} \Delta {P_{\text{A}}} = {K_{{P_{\text{A}}}}}\frac{{{P_{\text{A}}}}}{{{V_{\text{A}}}}}\left( {V - {V_{\text{A}}}} \right) \\ \Delta {P_{\text{B}}} = {K_{{P_{\text{B}}}}}\frac{{{P_{\text{B}}}}}{{{V_{\text{B}}}}}\left( {V - {V_{\text{B}}}} \right) \\ \Delta {P_{\text{C}}} = {K_{{P_{\text{C}}}}}\frac{{{P_{\text{C}}}}}{{{V_{\text{C}}}}}\left( {V - {V_{\text{C}}}} \right) \\ \end{gathered} \right. $$ (3) 式中:
$V_{\mathrm{A}}、 V_{\mathrm{B}}、 V_{\mathrm{C}} $ 分别为三相初始电压,$K_{P_{\mathrm{A}}}、 K_{P_{\mathrm{B}}}、 K_{P_{\mathrm{C}}} $ 分别为三相有功功率电压灵敏度, V为所需有功功率变化的实际电压有效值。将式(3)带入式(2)中,且假设三相初始电压相等都为
$ {V_0} $ ,则可以得到抵抗网侧扰动所需施加在负载上的实际电压,如式(4)所示:$$ V = \frac{{\Delta P + {P_{\text{A}}}{K_{{P_{\text{A}}}}} + {P_{\text{B}}}{K_{{P_{\text{B}}}}} + {P_{\text{C}}}{K_{{P_{\text{C}}}}}}}{{{{\left( {{P_{\text{A}}}{K_{{P_{\text{A}}}}} + {P_{\text{B}}}{K_{{P_{\text{B}}}}} + {P_{\text{C}}}{K_{{P_{\text{C}}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{P_{\text{A}}}{K_{{P_{\text{A}}}}} + {P_{\text{B}}}{K_{{P_{\text{B}}}}} + {P_{\text{C}}}{K_{{P_{\text{C}}}}}} \right)} {{V_0}}}} \right. } {{V_0}}}}} $$ (4) 电力电子变压器检测网侧系统频率,当系统频率发生偏差时,通过P-f下垂特性得到有功偏差指令值
$ \Delta {P^{\text{*}}} $ ,通过式(4)计算实际要施加在负载上的电压,以弥补有功功率偏差,进而达到频率稳定的目的。1.2 实时频率控制器的实现方法
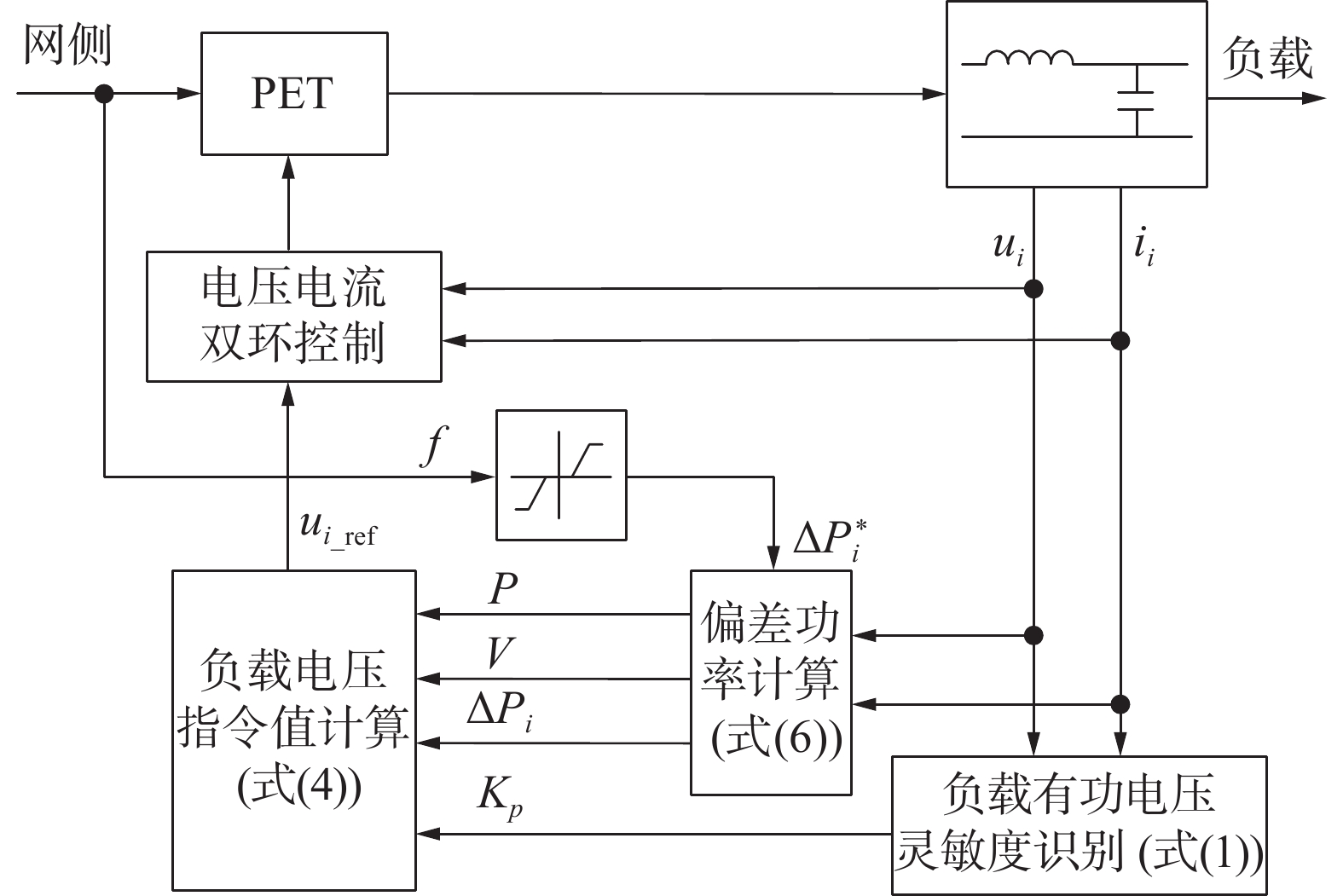
实时频率控制器的系统控制框图如图1所示。
整个控制过程可分为3个部分:
1)负载灵敏度识别:PET进行负载灵敏度识别,在负载端施加1个很小的梯形波电压扰动,根据式(4),在电压斜坡期间计算负载有功电压灵敏度,当负载灵敏度计算结束后电压恢复至标称值,负载灵敏度数值保存至下一次计算结束后更新这个数值。
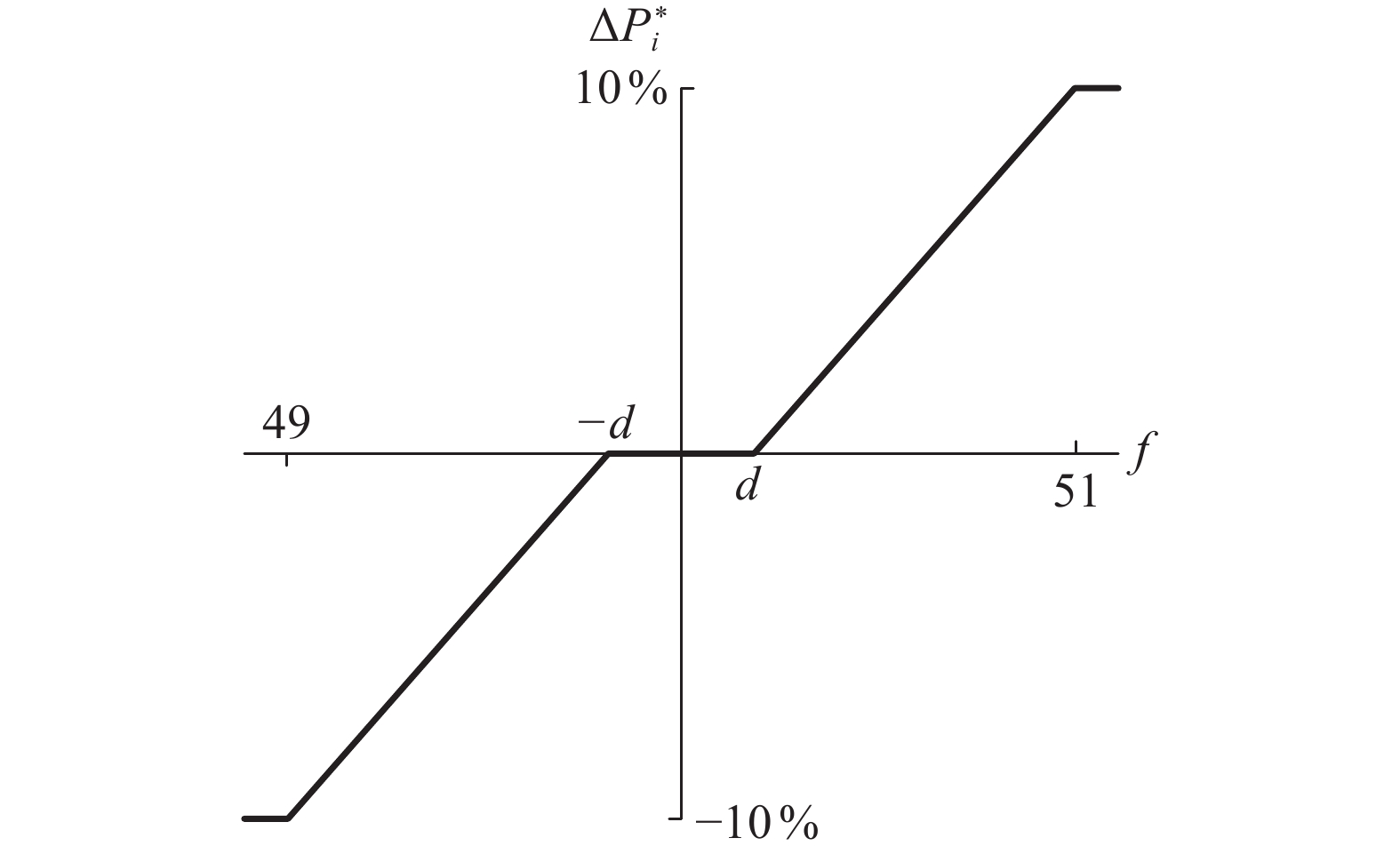
2)频率检测与功率偏差计算:PET检测网侧频率,为避免因临时负载/发电不平衡引起的小频率变化情况下的电力电子变压器干预,频率检测环节需要设定死区(±0.2 Hz),如图2所示。为避免频率误差过大时超出可调节范围,因此设置饱和(±1 Hz)。
当频率误差已知时,通过图2所示关系计算每个PET有功指令值
$ \Delta {P_i}^{\text{*}} $ 。$$ \Delta {P_i}^* = - {K_{{\text{dr}}}}\Delta \omega $$ (5) 式中:
$ {K_{{\text{dr}}}} $ 为图2曲线描述的下垂系数,$ \Delta \omega $ 为频率变化,$ \Delta {P^{\text{*}}} $ 为有功偏差指令值。假设所有电力电子变压器具有相同的下垂系数,则所有的电力电子变压器为系统频率变化所提供支撑的有功功率值由式(6)表示:
$$ \Delta {P_{{\text{PET}}}} = - {K_{{\text{PET}}}}{K_{{\text{dr}}}}\Delta \omega $$ (6) 式中:
$ {K_{{\text{PET}}}} $ 为电力电子变压器所带负载占系统总负荷的比例,也是电力电子变压器在系统中的占比;$ \Delta {P_{{\text{PET}}}} $ 为电力电子变压器下的负载有功变化量。3)负载电压值计算:当需要负载作出响应的有功指令值已知时,将式(6)代入式(4)就可以得到用于弥补网侧频率偏差的电力电子变压器负载端的电压,而负载电压应该满足国标GB/T 12325–2008《电能质量供电电压偏差》规定:220 V单向供电电压偏差为标称电压的 −10%~7%,即198~235.4 V。
负载电压施加后,相应有功功率作出响应,同时,网侧也启用一次调频,在频率跌落过程中实时频率控制器为网侧的一次调频提供一定支撑,防止频率偏差过大导致系统失稳,在一定程度上增加了系统的惯性和抗扰动能力。
从以上分析可知,实时频率控制器对频率的调节功能依赖于负荷对电压是否敏感(当总负荷的电压灵敏度大于1时,认为负荷对电压敏感)。而电动汽车充电负荷可近似看做一种恒功率负荷[23],对电压变化不敏感,且由于其随机性强,相对不可控,对电网的具有一定的冲击性,会降低电能质量,主要体现在电压、频率和谐波[24],因此不将其考虑在PET控制的可调负荷内,而是作为电网的有功扰动。
本文提出的辅助调频方法的调节范围不局限于频率跌落时的调节,当频率超出额定频率时(如电动汽车充电负荷切除),也可以通过增加负荷消耗来稳定网侧频率。
2. 三级式电力电子变压器控制策略
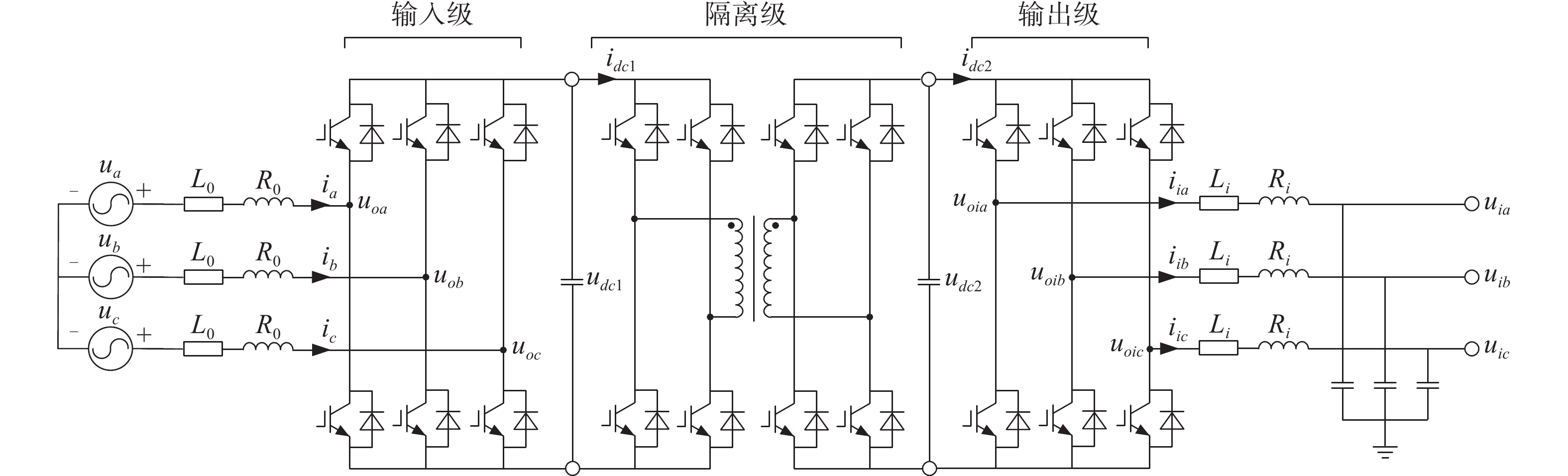
本文第1节介绍了实时频率控制器的控制原理及方法,而实时频率控制器的实现依赖于电力电子变压器,在目前PET的三大类拓扑结构(单级AC-AC拓扑、两级AC-DC-AC拓扑和三级AC-DC-DC-AC拓扑)中选择应用最为广泛的三级式AC-DC-DC-AC电力电子变压器。相较于其余2种拓扑结构,三级式PET可实现变压器输入输出电压、电流和功率的灵活控制,从拓扑角度来看,控制的灵活性和可拓展性等优点也使得三级PET拓扑成为使用最为广泛的拓扑[25-29]。为了清晰说明基于实时频率控制器的三级式电力电子变压器的原理及控制策略,根据其工作原理和拓扑结构将三级式电力电子变压器分为输入级和隔离级以及输出级,其电路简化图如图3所示。
2.1 输入级控制策略
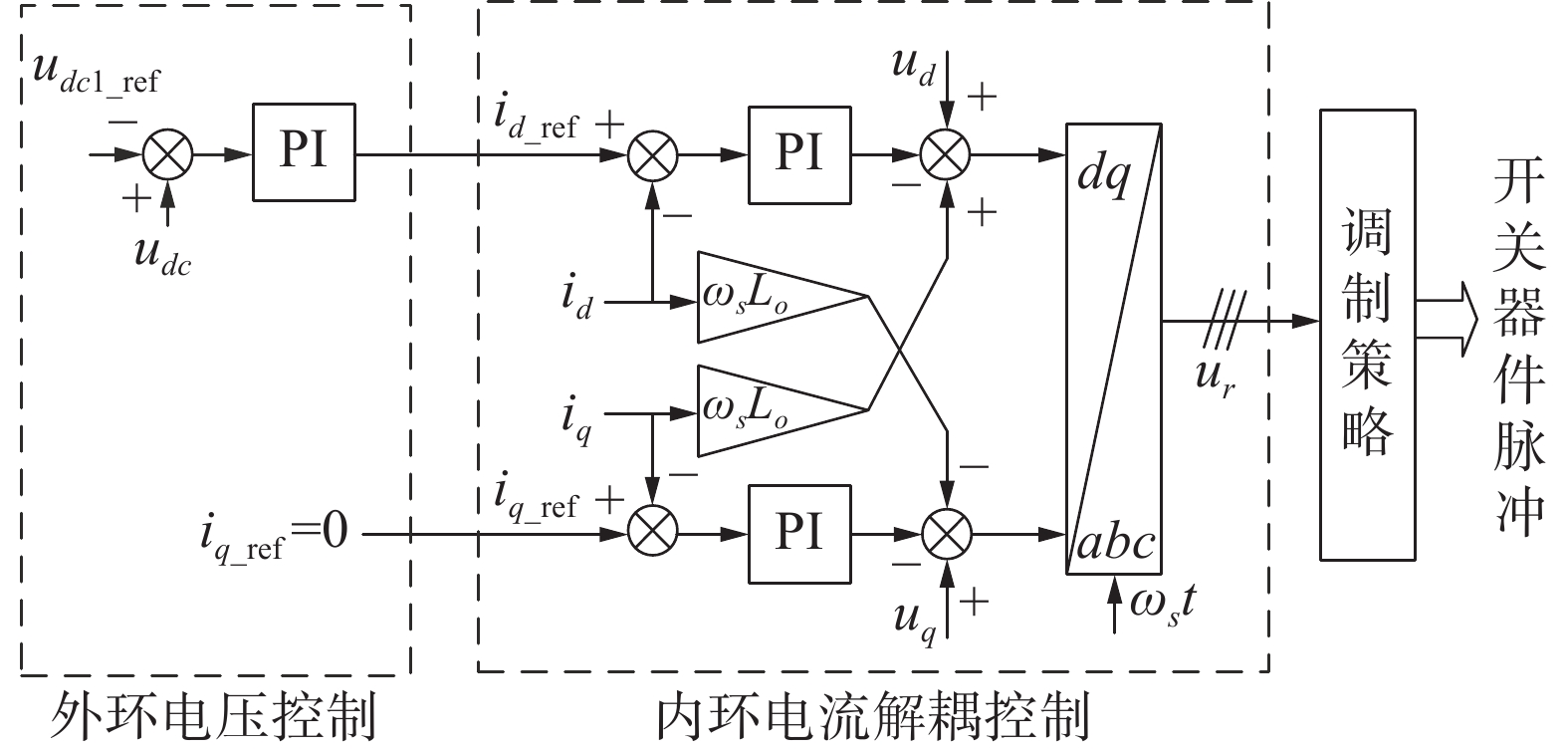
如图3所示,三级式PET的输入级为电压型三相全控桥式整流电路,其最常用的控制方式为电压电流双闭环解耦控制,即电压外环、电流内环前馈解耦控制。PET的输入级控制策略如图4所示。
电压控制器和电压反馈构成外环,电压外环的输出作为d轴电流(有功电流id_ref)指令值,电流控制和电流反馈构成内环。内环电流控制是将dq轴上的参考电流与实际电流比较得到的误差值作为PI控制器的输入,经过前馈解耦得到调制波,经过SPWM调制策略控制开关管最终得到目标输出电压,输出电压反馈至电压外环控制器,由此实现定电压控制。
除此之外,还可以通过控制无功电流参考值iq_ref来达到控制功率因数的目的,一般采用iq_ref为0来得到单位功率因数。
2.2 隔离级控制策略
DC/DC隔离级为双有源桥(dual active bridge,DAB)变流器,中间通过高频变压器隔离,中间隔离级需要将来自输入级的直流电压调制成高频方波信号,并经过高频变压器耦合到副方,再还原成直流信号。DAB 控制旨在调节DAB副边直流电压以跟踪电压基准值。在DAB的多种控制方法中,单移相控制为最经典的控制方式。图5为DAB的移相控制回路。PI控制器根据输出级直流母线电压与电压基准之间的电压误差调整相移角,通过控制移相角来达到控制输出电压的目的。
2.3 输出级控制策略
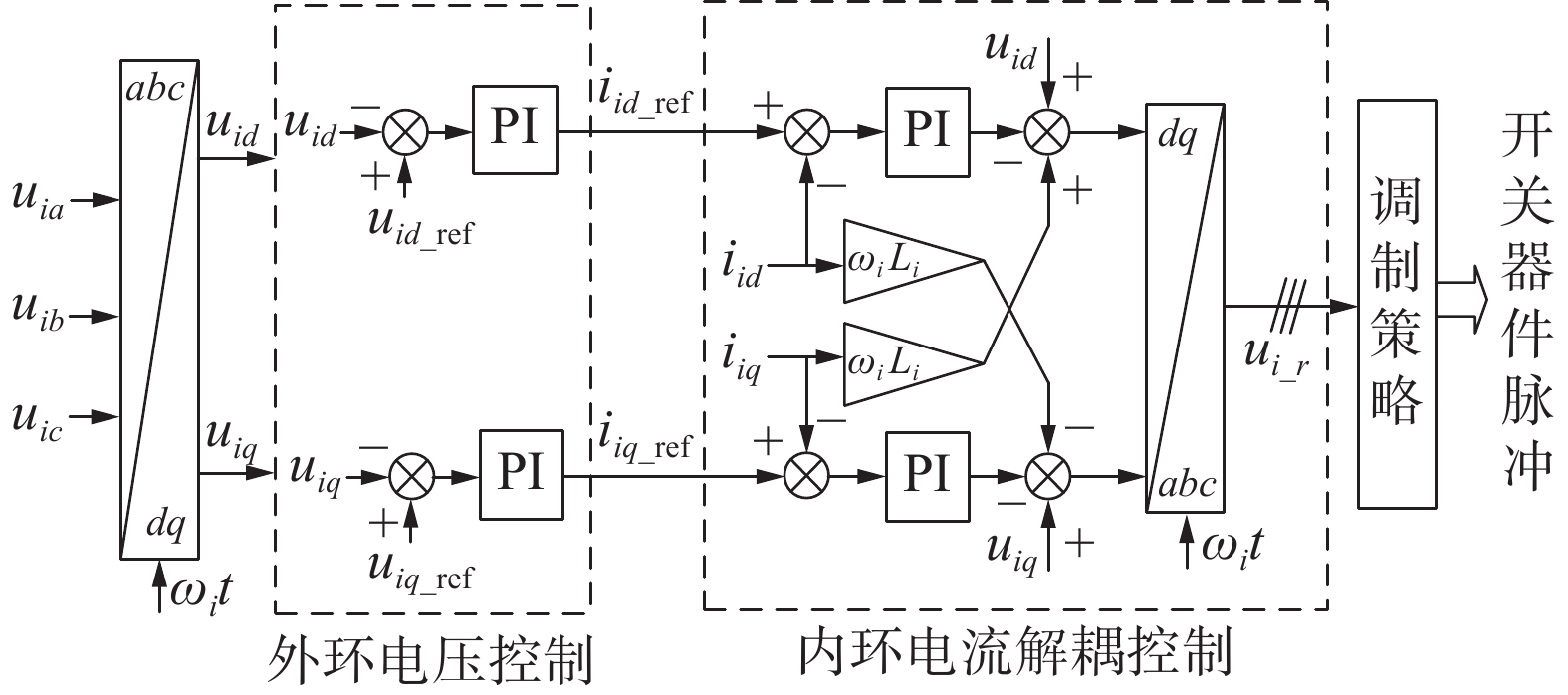
输出级控制负责三相输出电压的调节,同时实时频率控制器也在输出级实现。与输入级相反,输出级是电压型三相桥式逆变器,其整体控制方式与输入级整流电路控制方式类似,都采用外环电压、内环电流解耦控制。当频率发生波动时由实时频率控制器得到对应频率扰动需要负载响应有功功率变化的负载电压(由式(4)得出),式(4)得出的电压为有效值数值,将其进行三相化后得到三相电压参考值,对应图1中的ui_ref,经abc/dq变换得到d轴电压指令值,q轴电压指令值取0。
以上得到了外环电压的d轴与q轴电压指令值,同时采样输出电压电流,经过abc/dq变换后得到输出电压电流的d轴与q轴分量,经电压外环电流内环解耦控制得到调制波,对应图1中的电压电流双环控制。详细控制图如图6所示,再通过SPWM调制方式得到开关管脉冲,滤波后得到输出电压。
3. 仿真验证
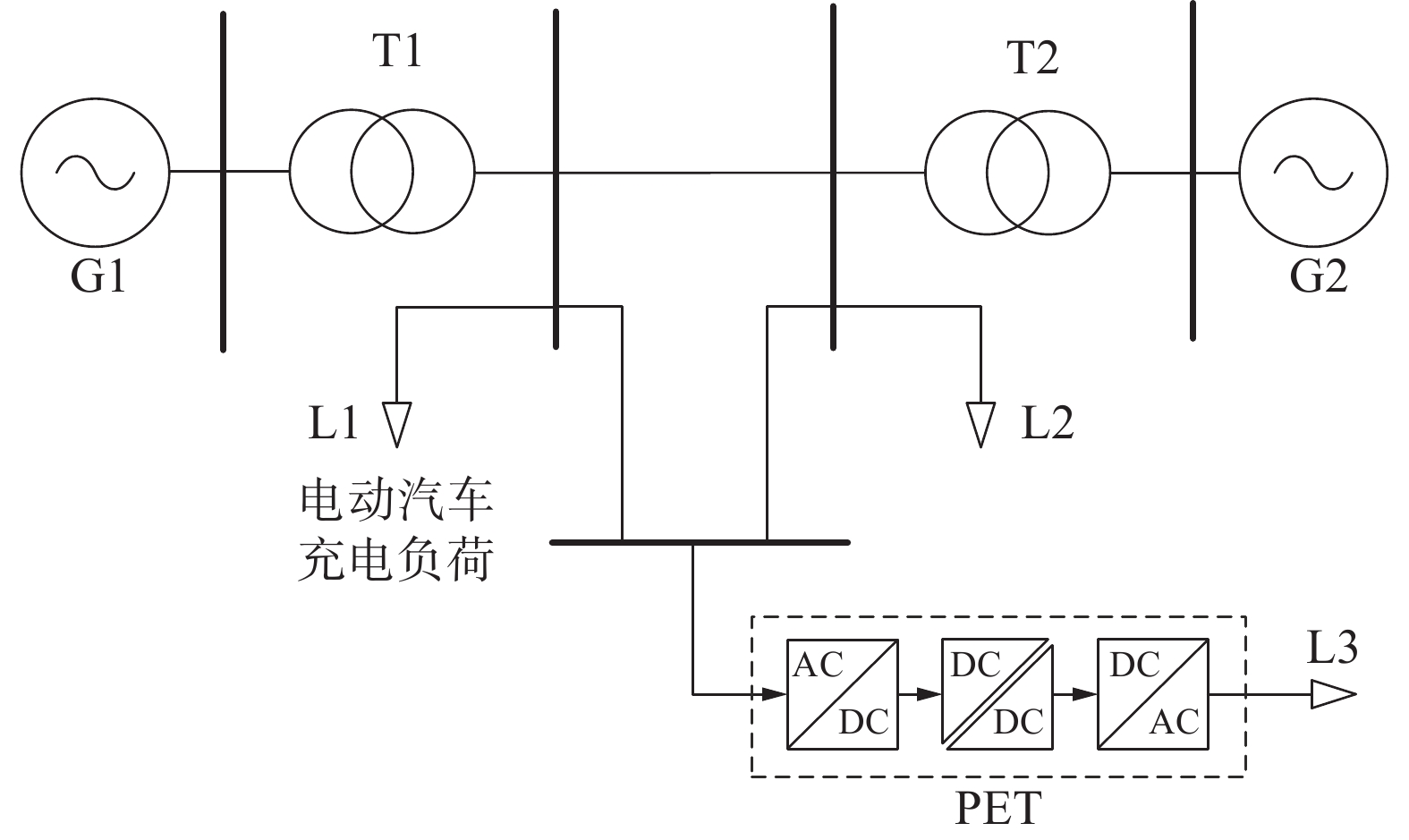
为了验证实时频率控制器对频率的支撑效果,在MATLAB/Simulink中搭建了简化的系统模型进行仿真验证,仿真验证系统采用两机五节点系统,仿真系统如图7所示,其中L3为PET控制的可调负载,L1为电动汽车充电负荷,通过突增L1的功率来模拟电动汽车的接入,系统参数如表1所示。
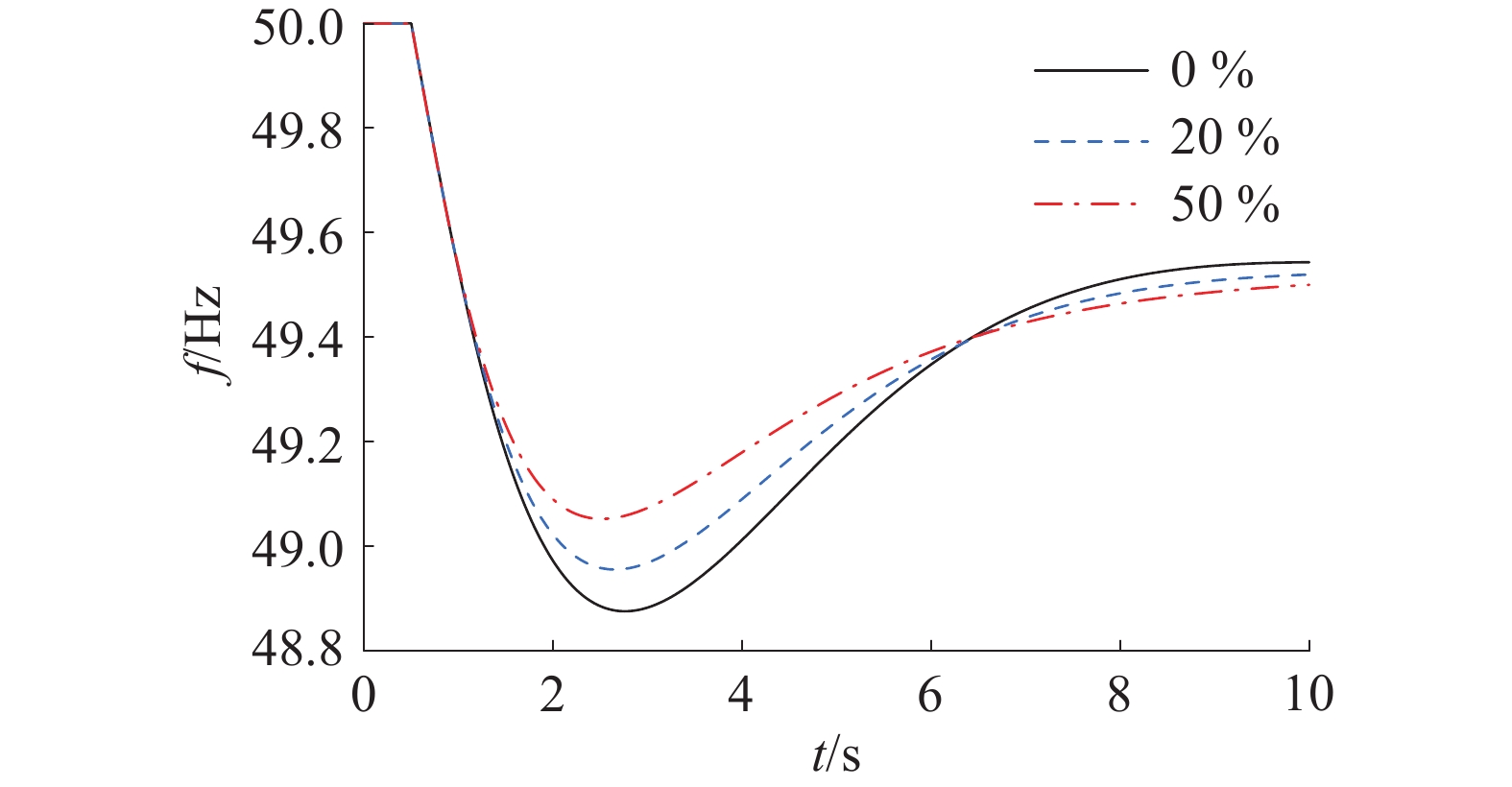
表 1 系统参数设置表名称 取值 G1、G2输出电压/kV 10 T1、T2二次侧输出电压/V 380 G1容量/kVA 200 G2容量/kVA 300 系统总有功容量/kW 400 PET网侧输入电压/V 380 隔离级原边电压/V 700 隔离级副边电压/V 700 PET输出电压/V 380 系统容量/kW 400 系统额定频率/Hz 50 PET控制负载的功率因数 1 PET采用的下垂系数 −6.25 图8描述了在0.5 s时在L1上增加占系统有功20%的电动汽车充电有功负荷情况下PET控制负载在系统中所占不同比例时系统的频率响应。从图8可以看出,在没有PET干预的情况下,频率会降低到49 Hz以下;当增加电网中PET的比例(
$ {K_{{\text{PET}}}} $ ),电网的瞬态频率下降减小。当电网中$ {K_{{\text{PET}}}} = 20\% $ 时,频率跌落将减少0.1 Hz左右;在$ {K_{{\text{PET}}}} = 50\% $ 情况下,频率跌落将减少0.2 Hz左右。由此可以得出初步结论,基于PET的实时频率控制器可以在一定程度上增加系统的惯性,减小受到扰动后的瞬态频率偏差。下面以
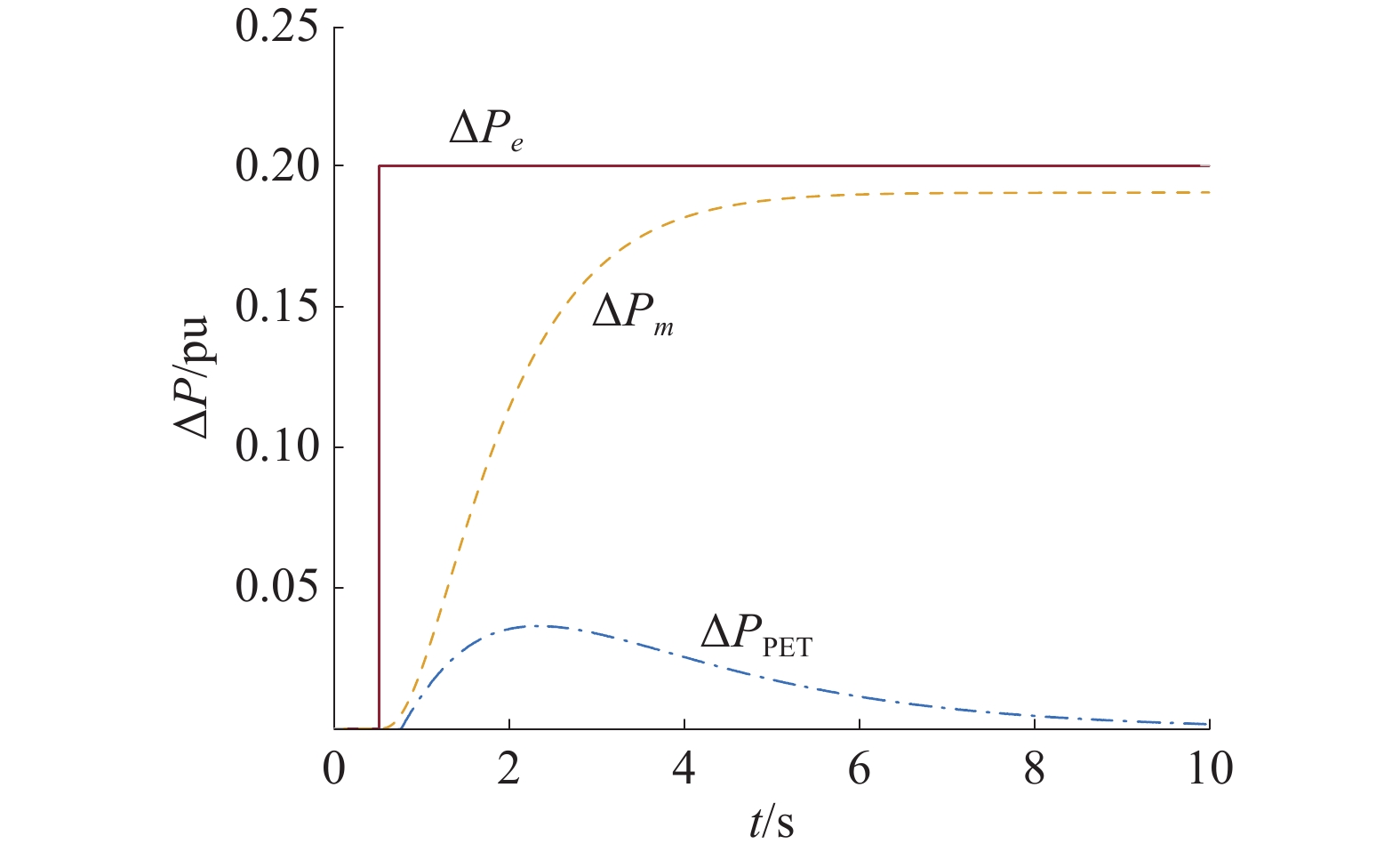
${K_{{\text{PET}}}} = 50 \%$ 为例,分析系统在调节过程中各个环节电压电流及功率的变化。图9为L1上增加占系统有功20%的电动汽车充电有功负荷时整个调节过程中扰动量
$ \Delta {P_e} $ 、PET贡献量$ \Delta {P_{{\text{PET}}}} $ 以及系统调节量$ \Delta {P_m} $ 的有功功率在标幺值下的波形图。其中,以系统总有功容量标幺值为1 pu。从图9中可以看出,PET只在暂态过程中支撑一定的功率变化,起到对频率的支撑作用,在系统稳定后退出,以防止长时间的干预对用户造成影响,最终的有功差额由网侧弥补,使频率最终达到稳定。
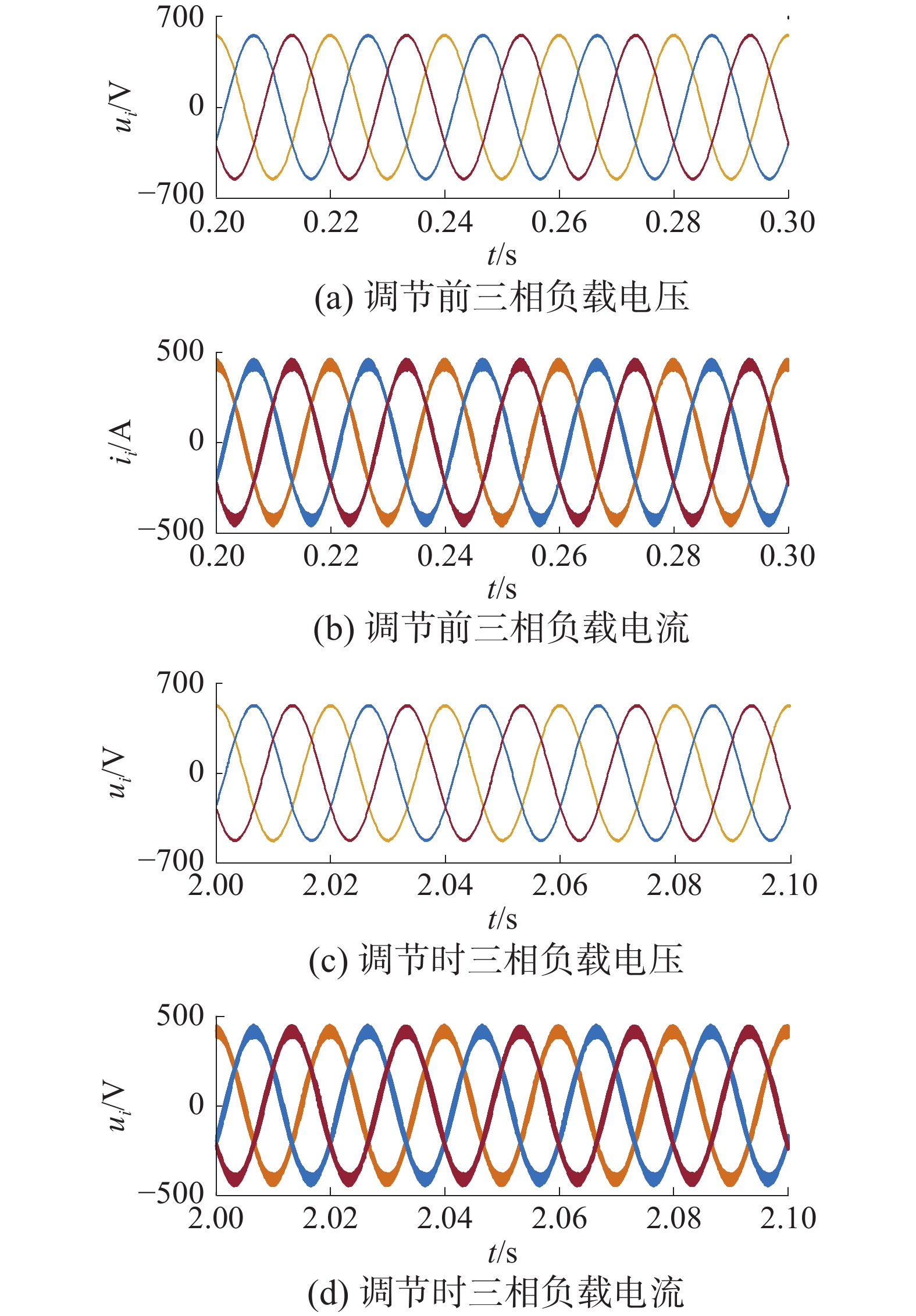
PET控制负载瞬时有功功率功率波形图如图10所示。从图10可以看出,在调节过程中,PET控制负载的有功功率经过短暂的下降后恢复至初始值,即PET在频率瞬态下降期间减小被控负载的有功消耗,用以弥补系统的有功偏差,在频率瞬态结束后恢复负载功率,整个调节过程时间很短,且功率下降幅度较小,短时间内不会对用户造成不良影响。
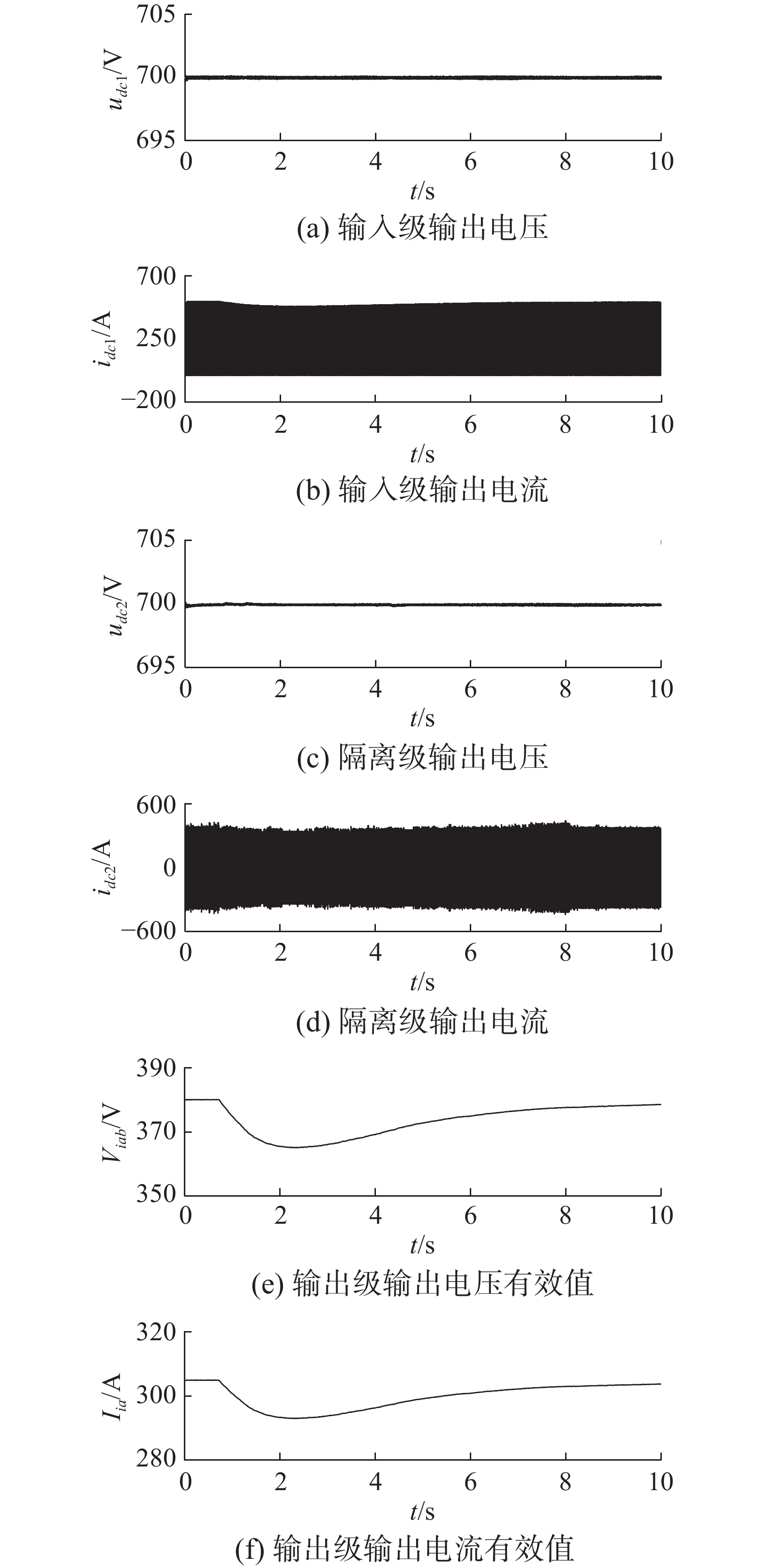
PET各级输出电压电流波形如图11所示。其中,为清楚地表现输出电压的变化,输出级的输出电压电流为有效值波形。从图11中可以看出,在系统频率变化时,PET输入级与隔离级电路输出电压均不变,输入级与隔离级的输出电流有小幅度变化,对应负载的功率变化。输出级电路输出电压与电流均有一定程度上减小而又恢复,对应图10中负载功率的先减小后恢复。在频率稳定后,负载电压与负载电流均恢复至初始值,整个调节过程大约持续8 s,且负载电压不是突变式的下跌,而是缓慢的下降,而后缓慢恢复,对被控负载而言在电压允许范围内短暂而缓慢的电压下降不会对被控负载造成不良影响。
图12给出了PET在启动频率调节前后的电压电流瞬时波形图。从图12中可以看出,在PET启动频率调节前后,PET输出电压电流正常,且由图12调节中的电压电流瞬时波形对应图11中输出级输出电压电流有效值跌落最低的时间段,此时PET输出电压电流均无畸变,PET工作正常。
4. 结论
本文通过电力电子变压器控制负荷的有功消耗,为电网提供频率支撑。通过识别负载对电压变化的敏感性,可以在频率瞬态期间准确地控制负荷的有功功率,在配电网中电动汽车充电负荷突增时为电网一次调频提供支撑。并通过仿真验证了系统的调节能力,在扰动期间PET工作正常,且负载电压最终恢复至标称值,对被控负载影响较小,减小了频率偏差,在一定程度上增加了系统惯性。
-
表 1 系统参数设置表
名称 取值 G1、G2输出电压/kV 10 T1、T2二次侧输出电压/V 380 G1容量/kVA 200 G2容量/kVA 300 系统总有功容量/kW 400 PET网侧输入电压/V 380 隔离级原边电压/V 700 隔离级副边电压/V 700 PET输出电压/V 380 系统容量/kW 400 系统额定频率/Hz 50 PET控制负载的功率因数 1 PET采用的下垂系数 −6.25 -
[1] 郭磊, 王克文, 文福拴, 等. 电动汽车充电设施规划研究综述与展望[J]. 电力科学与技术学报, 2019, 34(3): 56−70. doi: 10.3969/j.issn.1673-9140.2019.03.006 [2] 刘永奇, 陈龙翔, 韩小琪. 能源转型下我国新能源替代的关键问题分析[J]. 中国电机工程学报, 2022, 42(2): 515−524. [3] KROPOSKI B, JOHNSON B, ZHANG Yingchen, et al. Achieving a 100% renewable grid: Operating electric power systems with extremely high levels of variable renewable energy[J]. IEEE power energy mag, 2017, 15(2): 61−73. doi: 10.1109/MPE.2016.2637122 [4] 董伟杰, 白晓民, 朱宁辉, 等. 间歇式电源并网环境下电能质量问题研究[J]. 电网技术, 2013, 37(5): 1265−1271. [5] YOU Haibao, Vittal V, YANG Zhong. Self-healing in power systems: an approach using islanding and rate of frequency decline-based load shedding[J]. IEEE transactions on power systems, 2003, 18(1): 174−181. doi: 10.1109/TPWRS.2002.807111 [6] MARGARIS I D, PAPATHANASSIOU S A, HATZIARGYRIOU N D, et al. Frequency control in autonomous power systems with high wind power penetration[J]. IEEE transactions on sustainable energy, 2012, 3(2): 189−199. doi: 10.1109/TSTE.2011.2174660 [7] RAMTHARAN G, EKANAYAKE J B, JENKINS N. Frequency support from doubly fed induction generator wind turbines[J]. IET renewable power generation, 2007, 3(2): 3−9. [8] PULENDRAN S, TATE J E. Energy storage system control for prevention of transient under-frequency load shedding[J]. IEEE transactions on smart grid, 2017, 8(2): 927−936. [9] OUDALOV A, CHARTOUNI D, OHLER C. Optimizing a battery energy storage system for primary frequency control[J]. IEEE transactions on power systems, 2007, 22(3): 1259−1266. doi: 10.1109/TPWRS.2007.901459 [10] CALLAWAY D S, HISKENS I A. Achieving controllability of electric loads[J]. Proceedings of the IEEE, 2011, 99(1): 184−199. doi: 10.1109/JPROC.2010.2081652 [11] WANG Zhaoyu, WANG Jianhui. Review on implementation and assessment of conservation voltage reduction[J]. IEEE transactions on power systems, 2014, 29(3): 1306−1315. doi: 10.1109/TPWRS.2013.2288518 [12] PREISS R F, WARNOCK V J. Impact of voltage reduction on energy and demand[J]. IEEE transactions on power apparatus and systems, 1978, PAS-97(5): 1665−1671. doi: 10.1109/TPAS.1978.354658 [13] BALLANTI A, OCHOA L F. Voltage-led load management in whole distribution networks[J]. IEEE transactions on power systems, 2018, 33(2): 1544−1554. doi: 10.1109/TPWRS.2017.2716945 [14] HUI S Y, LEE C K, WU F F. Electric springs—a new smart grid technology[J]. IEEE transactions on smart grid, 2012, 3(3): 1552−1561. doi: 10.1109/TSG.2012.2200701 [15] LEE C K, CHAUDHURI N R, CHAUDHURI B, et al. Droop control of distributed electric springs for stabilizing future power grid[J]. IEEE transactions on smart grid, 2013, 4(3): 1558−1566. doi: 10.1109/TSG.2013.2258949 [16] TAN S C, LEE C K, HUI S Y. General steady-state analysis and control principle of electric springs with active and reactive power compensations[J]. IEEE transactions on power electronics, 2013, 28(8): 3958−3969. doi: 10.1109/TPEL.2012.2227823 [17] 王青松. 电力弹簧若干关键技术研究[D]. 南京: 东南大学, 2016. [18] BOKHARI A, ALKAN A, DOGAN R, et al. Experimental determination of the zip coefficients for modern residential, commercial, and industrial loads[J]. IEEE transactions on power delivery, 2014, 29(3): 1372−1381. doi: 10.1109/TPWRD.2013.2285096 [19] 毛承雄, 范澍, 王丹, 等. 电力电子变压器的理论及其应用(Ⅰ)[J]. 高电压技术, 2003(10): 4−6. doi: 10.3969/j.issn.1003-6520.2003.10.002 [20] CARNE G De, BUTICCHI G, LISERRE M, et al. Real-time primary frequency regulation using load power control by smart transformers[J]. IEEE transactions on smart grid, 2019, 10(5): 5630−5639. doi: 10.1109/TSG.2018.2888687 [21] 孙铨杰. 大规模电动汽车接入电网的负荷需求及其影响研究[D]. 上海: 上海电力大学, 2021. [22] CARNE G De, LISERRE M, VOURNAS C. On-line load sensitivity identification in LV distribution grids[J]. IEEE transactions on power systems, 2017, 32(2): 1570−1571. doi: 10.1109/TPWRS.2016.2581979 [23] 周念成, 蒲松林, 王强钢, 等. 电动汽车快速充电站的储能缓冲系统控制策略[J]. 电力系统保护与控制, 2013, 41(17): 127−134. doi: 10.7667/j.issn.1674-3415.2013.17.020 [24] 胡宜平. 规模化电动汽车充电对电网的影响及其调频应用研究[D]. 武汉: 华中科技大学, 2015. [25] WANG Xinyu, LIU Jinjun, OUYANG Shaodi, et al. Control and experiment of an H-bridge-based three-phase three-stage modular power electronic transformer[J]. IEEE transactions on power electronics, 2016, 31(3): 2002−2011. doi: 10.1109/TPEL.2015.2434420 [26] 毛承雄, 范澍, 黄贻煜, 等. 电力电子变压器的理论及其应用(Ⅱ)[J]. 高电压技术, 2003(12): 1−3. doi: 10.3969/j.issn.1003-6520.2003.12.001 [27] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274−1289. [28] 季振东. 级联型电力电子变压器关键技术研究[D]. 南京: 东南大学, 2015. [29] 邓卫华, 张波, 胡宗波. 电力电子变压器电路拓扑与控制策略研究[J]. 电力系统自动化, 2003(20): 40−44,48. doi: 10.3321/j.issn:1000-1026.2003.20.009
















 下载:
下载: