Prediction of gas permeability of containment concrete under severe accident conditions
-
摘要: 核电站发生严重事故时安全壳内部形成的高温、高湿、高压条件对安全壳混凝土的抗气体渗透能力有着极大的考验。本文基于理论分析模型建立数据样本,环境温度、水蒸气分压、升温速率和混凝土的水扩散系数作为为输入变量,安全壳混凝土气体渗透深度作为输出变量,利用BP算法设计了包含4个输入层节点、12个隐含层节点、1个输出层节点的人工神经网络结构,对严重事故工况下安全壳混凝土的抗气体渗透性能进行分析预测。模型测试结果的相对误差在5%以内,相关系数达到了0.9997,研究结果表明反向传播神经网络(BPNN)有着有效可靠的预测能力,能对安全壳混凝土的气体渗透深度进行高精度预测。Abstract: The high temperature, high humidity and high pressure conditions formed inside the containment of a nuclear power plant during a serious accident have a great impact on the gas permeation resistance of the containment concrete. In this paper, data samples are established based on the theoretical analysis model, with ambient temperature, partial pressure of water vapor, heating rate and water diffusion coefficient of concrete materials as input variables and gas permeation depth of containment concrete as output variables. Using back propagation (BP) algorithm to design an artificial neural network, containing 4 input layer nodes, 12 implicit layer nodes and 1 output layer node structure, so as to predict the gas permeation resistance of containment concrete under severe accident conditions. The relative error of the model test result is within 5%, and the correlation coefficient reaches 0.999 7. The research results show that the BP artificial neural network has effective and reliable prediction ability, and it can predict the gas penetration depth of containment concrete with high accuracy.
-
Keywords:
- severe accident /
- containment /
- concrete /
- environment condition /
- coupling effect /
- gas permeation depth /
- BP algorithm /
- prediction model
-
安全壳作为核反应堆的第3道屏障,在机组正常运行时可以限制放射性物质从反应堆扩散出去;在发生严重事故时又承受着压力和温度负载作用,控制放射性物质释放量,保护公众免遭放射性物质的伤害[1-2]。混凝土作为安全壳结构最重要的组成材料之一,其气体渗透性是保障安全壳正常运行状态下的耐久性以及事故条件下安全性的关键,有着至关重要的作用[3]。在核反应堆发生失去冷却水的严重事故时,大量的高温高压流体将以蒸汽形式释放到安全壳内[4],在安全壳内部形成高温、高湿、高压的环境。在这种情况下,安全壳混凝土会发生物理转化和化学分解[5],导致其性能显著退化,严重影响安全壳混凝土的气体渗透性能,从而影响安全壳结构整体密封性。
目前,对于严重事故条件下安全壳混凝土的气体渗透性缺乏有效的测试与预测评估方法,亟需建立有效可靠的预测模型。伴随着人工智能的发展,人工神经网络理论逐渐趋于成熟,其模型也得到了飞速的发展,在混凝土工程领域中得到了广泛使用,为混凝土气体渗透性方面的研究提供了有力的支持[6-7]。目前人工神经网络领域主要应用反向传播神经网络(back propagation neural network,BPNN)、多层感知器(multilayer perceptron,MLP)、卷积神经网络(convolutional neural network,CNN)和递归神经网络(recursive neural network,RNN)等模型[8]。其中BPNN具有较强的非线性映射能力、灵活的网络结构和较高的预测精度,无需构建复杂的理论模型,可以直接体现输入指标和输出指标的数量关系[9],从而揭示客观规律,可以很大程度上避免分析复杂问题的成因及条件,减少试验成本,适用于分析严重事故条件下安全壳混凝土渗透性问题。为此本文采用有限元分析方法计算安全壳混凝土在严重事故工况下的气体渗透深度,通过BPNN对安全壳严重事故工况下的气体渗透性进行预测分析。
1. 严重事故条件下安全壳混凝土气体渗透性分析模型
1.1 安全壳混凝土气体渗透性分析理论
在严重事故工况下,安全壳内存在复杂的环境条件,安全壳腔内温度可达到150 ℃以上,压力可达到0.5 MPa以上,相对湿度可达到100%[10],安全壳混凝土受到单侧高温高压高湿作用,由于传热传质及材料的热胀,混凝土内部的温湿度场会发生变化,且二者的变化不是相对独立的。上述耦合关系还应与混凝土单侧受高温高压高湿作用形成的温度、孔隙压力和湿度梯度叠加[11]。可见,本文中混凝土内部的变化可以抽象为多孔多相介质中温、湿度场的耦合分析问题。相关的多场耦合分析模型主要包括外国学者提出的Bazant模型[12]、Gawin模型[13]、Ahmed模型[14]等,以及国内学者李荣涛[15]提出的模型。上述模型中,Bazant模型受到了最为广泛的应用,本文将该模型作为有限元分析理论基础,将混凝土在高温下的温湿度场作为分析重点,通过修正公式考虑孔隙压力对混凝土孔隙率的影响,在降低模型非线性的同时保证计算精度。
在Bazant模型中,高温下混凝土的水分质量守恒方程和能量守恒方程为
$$ \frac{{{\partial} w}}{{\partial t}} - \frac{{\partial {w_d}}}{{\partial t}} = - {\text{div}}J $$ $$ \rho C\frac{{\partial T}}{{\partial t}} - {C_a}\frac{{\partial w}}{{\partial t}} - {C_w}J{\text{grad}}T = - {\text{div}}q $$ 式中:w是含水量,即在固定温度下的单位体积混凝土中自由水(即除去化学结合水)的总质量;wd是化学结合水的质量(由于高温引起的混凝土固相中的脱水过程释放到混凝土孔隙中的水的质量);J为质量流;ρ和C分别为混凝土(包括化学结合水,不含自由水)的密度和比热;T为温度;Ca和Cw分别是自由水吸附热和液态水的等压热容量;q为热流。
除控制方程外,温湿度场耦合模型分析还需明确高温下混凝土中渗流行为的本构关系。渗流本构由达西定律定义,Hagen-Poiseuille方程是描述气体在多孔介质中渗透过程的基础理论模型,其形式为[16]
$$ {k_A} = {\text{2}}\mu L\frac{{{P_2}}}{{(P_1^{\text{2}} - P_2^{\text{2}})}}\frac{Q}{A} $$ (1) 式中:kA为表观渗透系数,μ为黏度系数,L为渗流路径长度,P1、P2为渗流长度两端的气体压力,Q为气体流量,A为材料渗流面积。
式(1)中并未考虑边界滑流的影响,故计算出的kA会受到加载气压大小的干扰,不能体现混凝土材料真实的气体渗透性。Klinkenberg[17]考虑了气体流动的边界滑移效应,给出了本征渗透系数k0和表观渗透系数kA之间的关系式:
$$ {k_A} = {k_0}({\text{1}} + \frac{{b^{\prime} }}{{{P_m}}}) $$ 式中:b'为Klinkenberg修正系数,Pm为P1和P2的平均值。
采用VGM模型[18]和Gawin模型对安全壳混凝土初始表观气体渗透系数k0进行修正。VGM模型可以用于描述孔隙水饱和度与混凝土气体渗透性之间的关系:
$$ {k_{0S}}({S_{\text{w}}}) = {k_0}{({\text{1}} - {S_W})^P}{({\text{1}} - {({S_W})^{\frac{{\text{1}}}{m}}})^{{\text{2}}m}} $$ 式中:k0S为含水状态下混凝土的气体本征渗透系数,Sw为孔隙水饱和度,p、m分别为模型系数。
Gawin给出了气体渗透性与温度之间的关系式:
$$ {k_{0T}} = {k_0}\exp [{C_T}(T - {T_0})] $$ 式中:k0T为混凝土在高温下的气体本征渗透系数,k0为在参考温度T0下混凝土的气体本征渗透系数,CT为模型系数。
1.2 有限元模型建立
Shekarchi等[19]曾对严重事故下核电站高性能混凝土的气体渗透性进行了研究,当环境温度条件以7.5 ℃/h的速率上升到200 ℃、蒸汽压力增加到1.3 MPa、相对湿度在85%左右,混凝土在该环境条件下暴露48 h,其试验和数值结果对比如图1和图2。其结果表明了基于Bazant理论所建立的模型,为严重事故条件下混凝土的气体渗透性研究提供了一种方便的工具,对于模拟混凝土在高温和蒸气压力梯度作用下气体渗透行为有着令人满意的结果。本文基于Bazant模型作为理论基础所建立的安全壳混凝土有限元仿真模型可以有效地重现高温、高湿、高压条件下混凝土的多场耦合行为,模拟出混凝土内部温湿度场分布,得到安全壳混凝土的气体渗透深度。
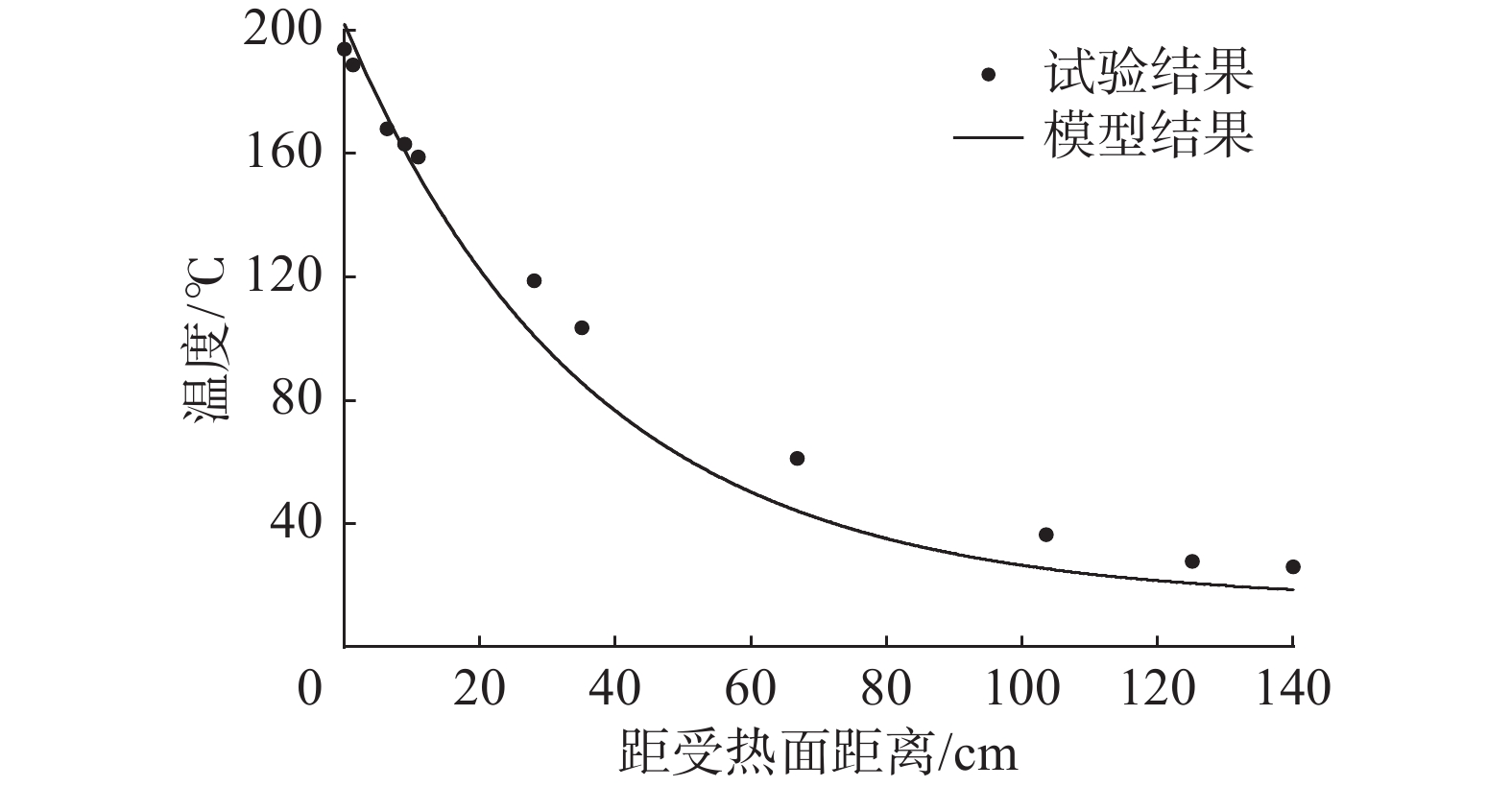 图 1 混凝土内部温度试验和数值计算结果[19]
图 1 混凝土内部温度试验和数值计算结果[19]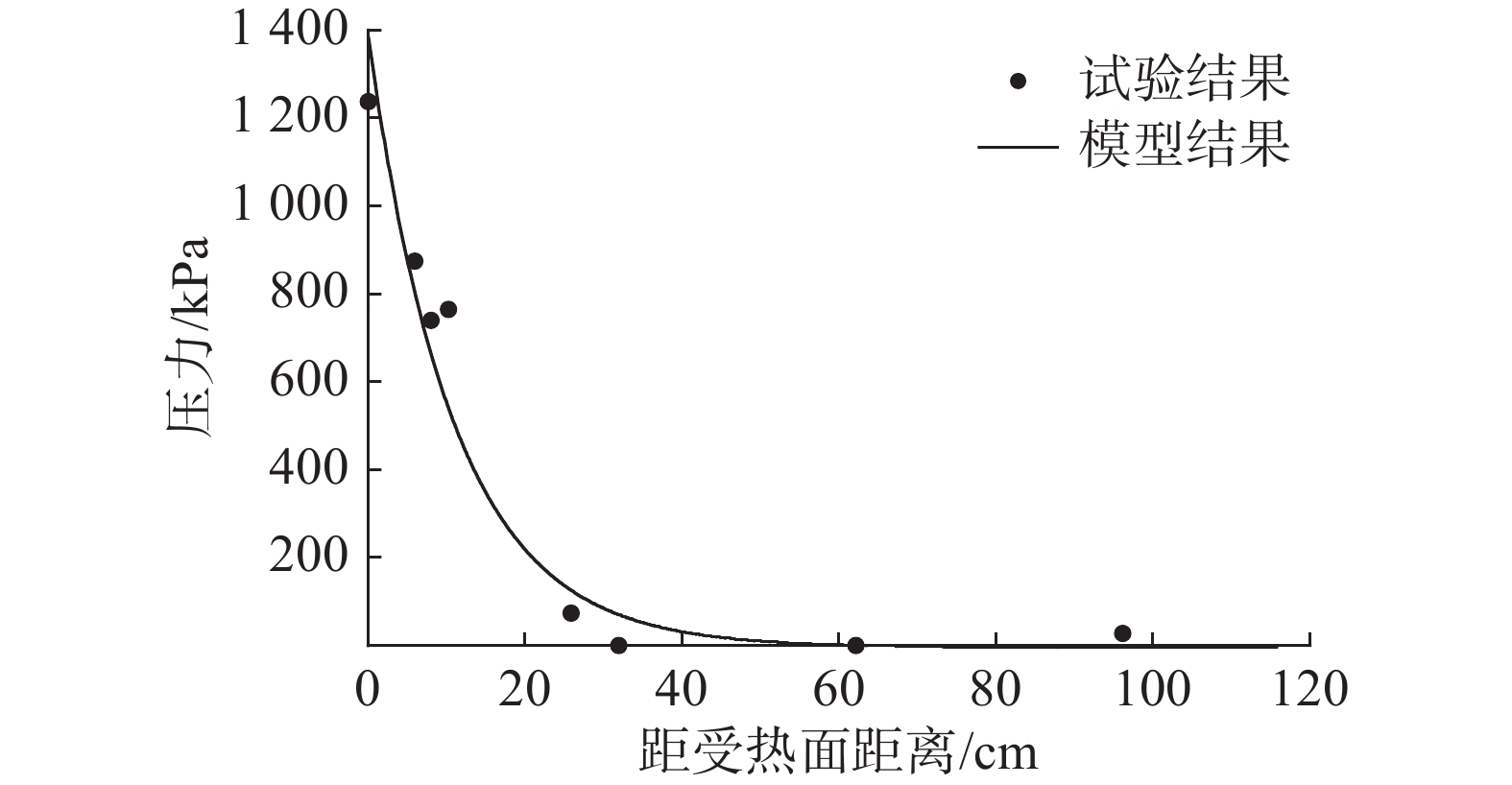 图 2 混凝土内部蒸汽压试验和数值计算结果[19]
图 2 混凝土内部蒸汽压试验和数值计算结果[19]本文在COMSOL Multiphysics 5.5软件平台上进行高温、高湿、高压耦合作用下安全壳混凝土气体渗透性的数值模拟分析。COMSOL软件中内置了多种基础的物理场分析,但其内置物理场不能直接满足Bazant模型的分析要求,因此需要根据本文1.1节中的理论模型对其内置模块进行调整,使得软件能够求解与Bazant模型一致的偏微分方程组。本文以C60混凝土作为计算对象,模型参数则来源于所做C60混凝土材料性能实验和文献[20-22],将安全壳腔内的环境温度和水蒸气分压作为模型中控制温度、湿度和压力的变量,本模型将水蒸气分压作为环境温度的饱和蒸汽压,即认为作用在安全壳混凝土上的相对湿度为100%。在模拟环境温度作用时,环境温度由初始温度升温至目标温度并保持。根据实际条件设定模型的边界条件和初始条件,计算得出在承受72 h的高温高湿高压作用后安全壳混凝土厚度方向上的温湿度场分布,包括温度分布、孔隙水压力分布和孔隙水饱和度分布。当混凝土内部孔隙水饱和度升高达到某一临界值(临界饱水度)时,连通孔隙全部被阻塞,混凝土中的气体将停止流动[23],根据模型中孔隙水饱和度分布从而输出安全壳混凝土气体渗透深度。
2. BPNN预测模型构建
2.1 BPNN
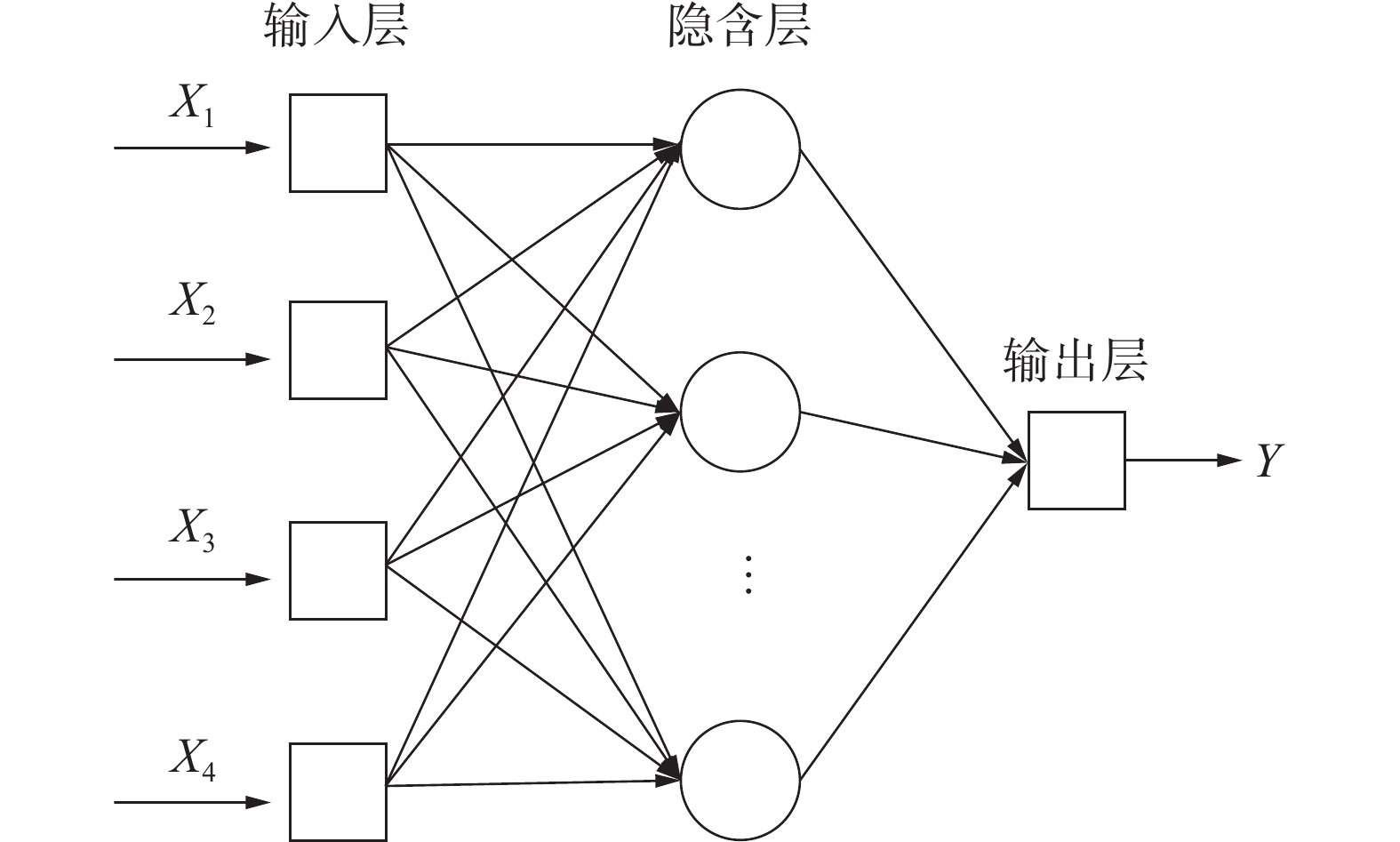
BPNN通常都含有3层神经元,各层连接状态如图3所示。在该网络中,输入值通过权重矩阵连接到每个神经元的输入[24]。BP算法的目的就是通过误差的反向传播来求得各神经元之间的连接权值,通过调整输入节点和隐含层节点之间的连接强度、隐含层节点和输出节点之间的连接强度和阈值,使误差沿梯度方向减小[25]。
2.2 样本集构建与处理
将环境温度、水蒸气分压、升温速率和水扩散系数作为输入变量,安全壳混凝土气体渗透深度作为输出变量,结合上述混凝土本构关系和控制方程,进行温湿度场耦合模拟计算,输出得到不同工况下的安全壳混凝土气体渗透深度值,由此构成63组样本数据集,其范围分布见表1。
表 1 样本数据集的范围分布变量 输入 输出 温度/℃ 水蒸气分压/
MPa升温速率/
(℃·h-1)水扩散
系数/s气体渗透
深度/cm最小值 130 0.2705 28 5.00×10−16 2.780 最大值 190 1.2564 56 5.00×10−14 27.786 均值 160 0.6830 40 1.85×10−14 15.6953 标准差 20.1606 0.3330 11.8703 2.2529×10−14 7.6662 样本集还需进行归一化预处理,当所有样本的输入信号都为正值时,与第1隐含层神经元相连的权值只能同时增加或减小,从而导致学习速度很慢。对输入信号进行归一化,不但加快网络学习速度,同时也能防止因输入值的绝对值过大而导致神经元输出饱和。归一化函数其原理如式(2)所示:
$$ y = 2 \times \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} - 1 $$ (2) 输出的预测值通过反归一化函数再进行还原,如式(3):
$$ x = \frac{{(y + 1)({x_{\max }} - {x_{\min }})}}{2} + {x_{\min }} $$ (3) 式中:x、xmin、xmax分别为原始的输入量、输入量最小值和输入量最大值,y为归一化后的输入量[26]。
2.3 预测模型建立
本文将归一化后的63组工况的数据作为样本,抽取其中8组工况作为测试集样本,其余为训练集样本。环境温度、水蒸气分压、升温速率和水扩散系数作为输入变量,因此该网络输入层有4个神经元节点,安全壳混凝土气体渗透深度作为输出变量,即输出层有1个神经元节点。隐含层节点数对网络模型性能有着极大的影响,其神经元节点数根据经验公式确定[27]:
$$ {n_1} = \sqrt {n + m} + c $$ $$ {n_1} \geqslant \log {{\text{2}}^n} $$ 式中:n1为隐含层节点数,n为输入层节点数,m为输出层节点数,c为1~10的1个常数。
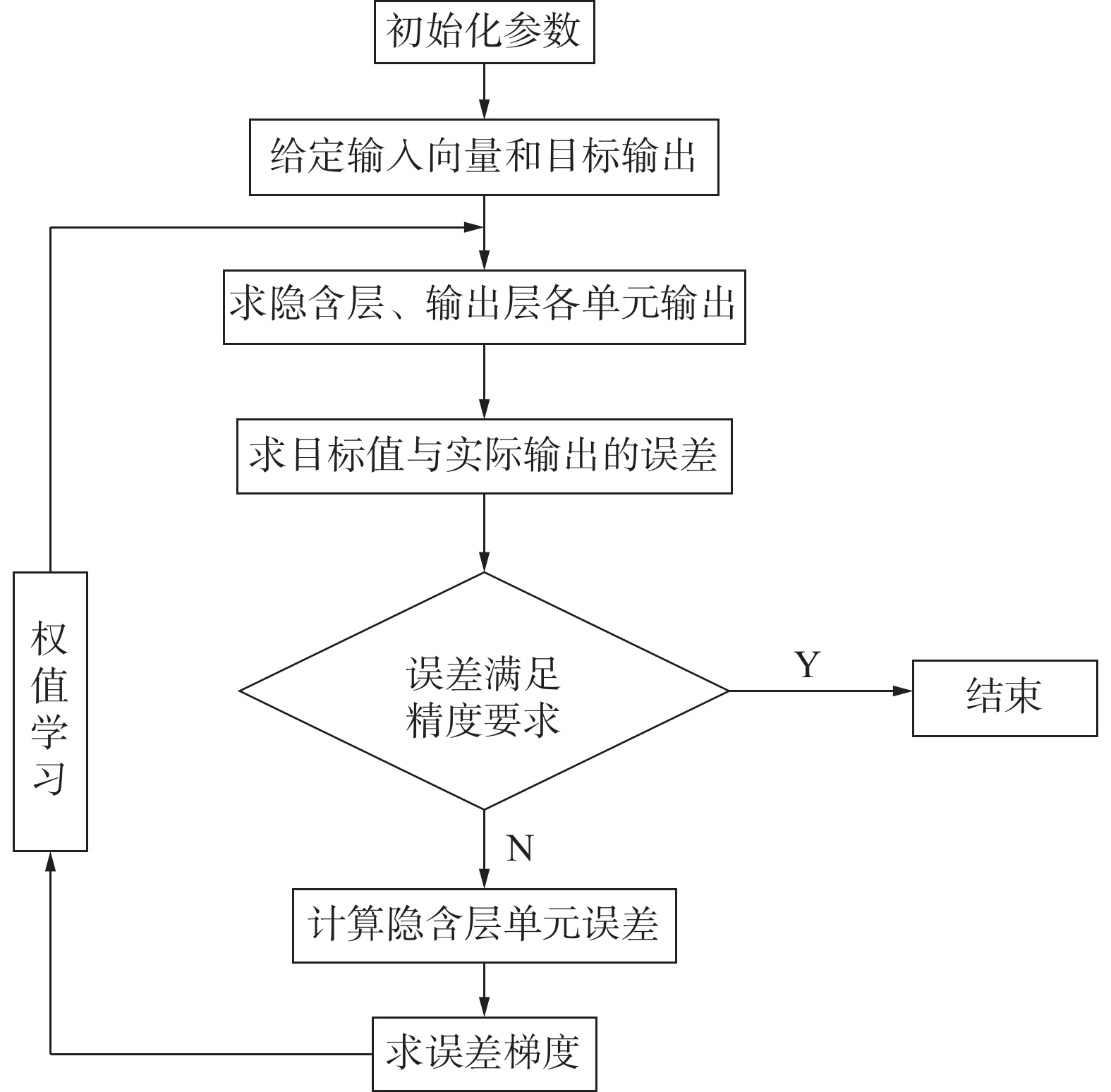
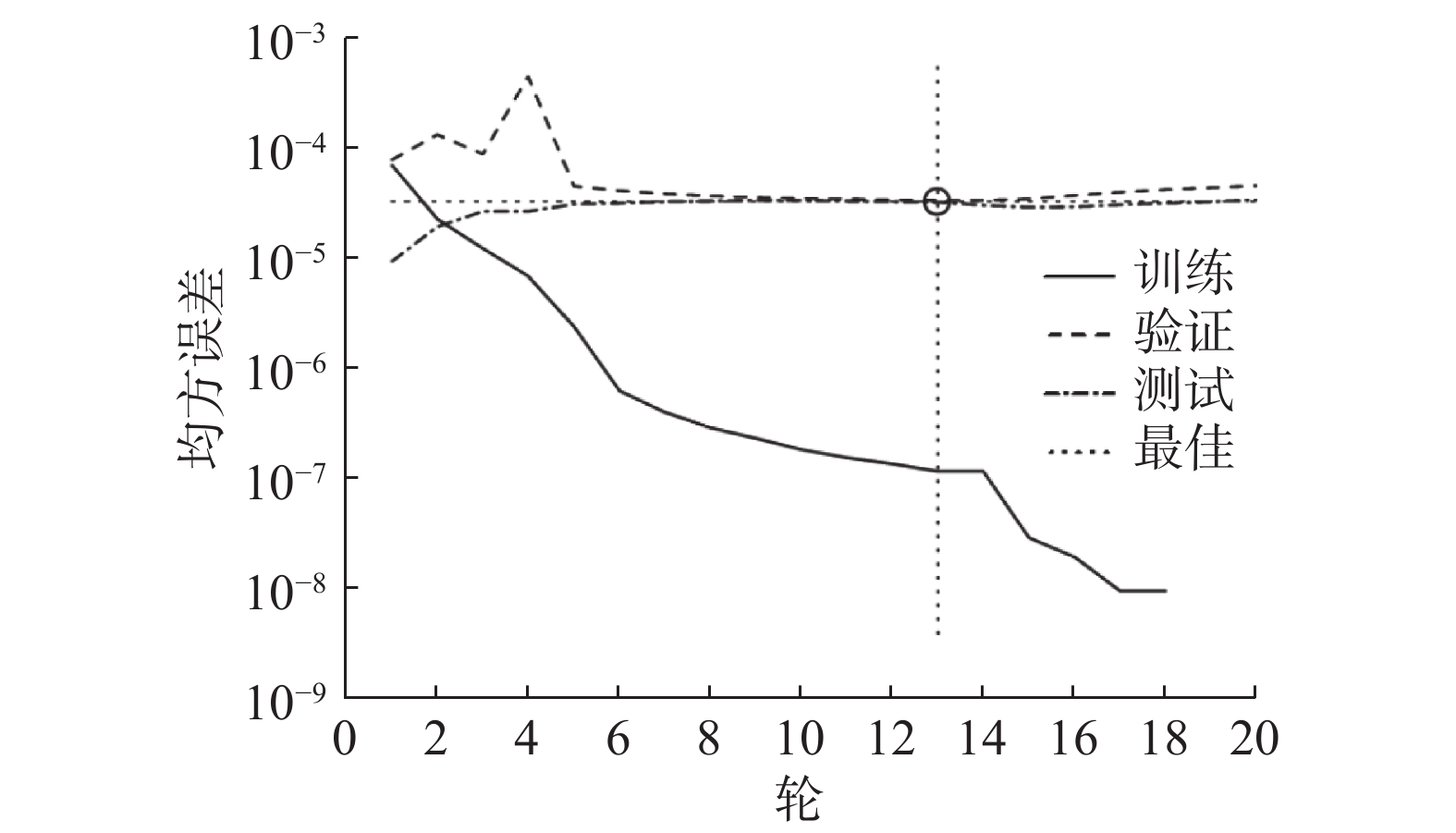
基于以上经验试算式对隐含层节点数进行试凑,经比较分析,当预测模型隐含层神经元节点数设置为12时,该网络模型结构最优。图4为本文所建立的BPNN的计算流程,导入训练集的数据,设定网络参数,并选择Levenberg-Marquardt算法作为训练算法做最小二乘迭代,再进行BPNN的训练。在训练集中将其随机分为3组,分别为训练集、验证集和测试集,将均方误差(mean-square error,MSE)作为评判模型训练性能的标准,当MSE达到目标MSE时,停止训练,其均方误差如图5所示。从图5可以看出在13轮时,达到最小MSE,其值为3.3793×10−5,此后网络训练继续进行,在指定的训练数据上对神经网络进行迭代训练,并间接地采用训练后的验证步骤来监控神经网络的过拟合,当验证步骤的误差逐渐收敛时,BPNN训练停止,输出网络结构[28]。在训练好的网络中对测试集的输入进行BPNN预测,得到测试集对应的预测输出值。将预测结果反归一化处理,还原成原来的数量级,见表2。
表 2 反归一化后的网络测试集cm 工况 归一化后的
预测值归一化后的
实际值反归一化后的
预测值/cm反归一化后的
实际值/cm1 0.3247 0.3083 10.8998 10.490 2 0.5842 0.5752 17.3885 17.164 3 0.7652 0.7883 21.9146 22.492 4 0.4392 0.4381 13.7626 13.736 5 0.7288 0.7286 21.0044 21.000 6 0.9527 0.9609 26.6032 26.808 7 0.4527 0.4576 14.1002 14.223 8 0.7628 0.7617 21.8546 21.826 3. 预测结果分析
3.1 预测结果分析
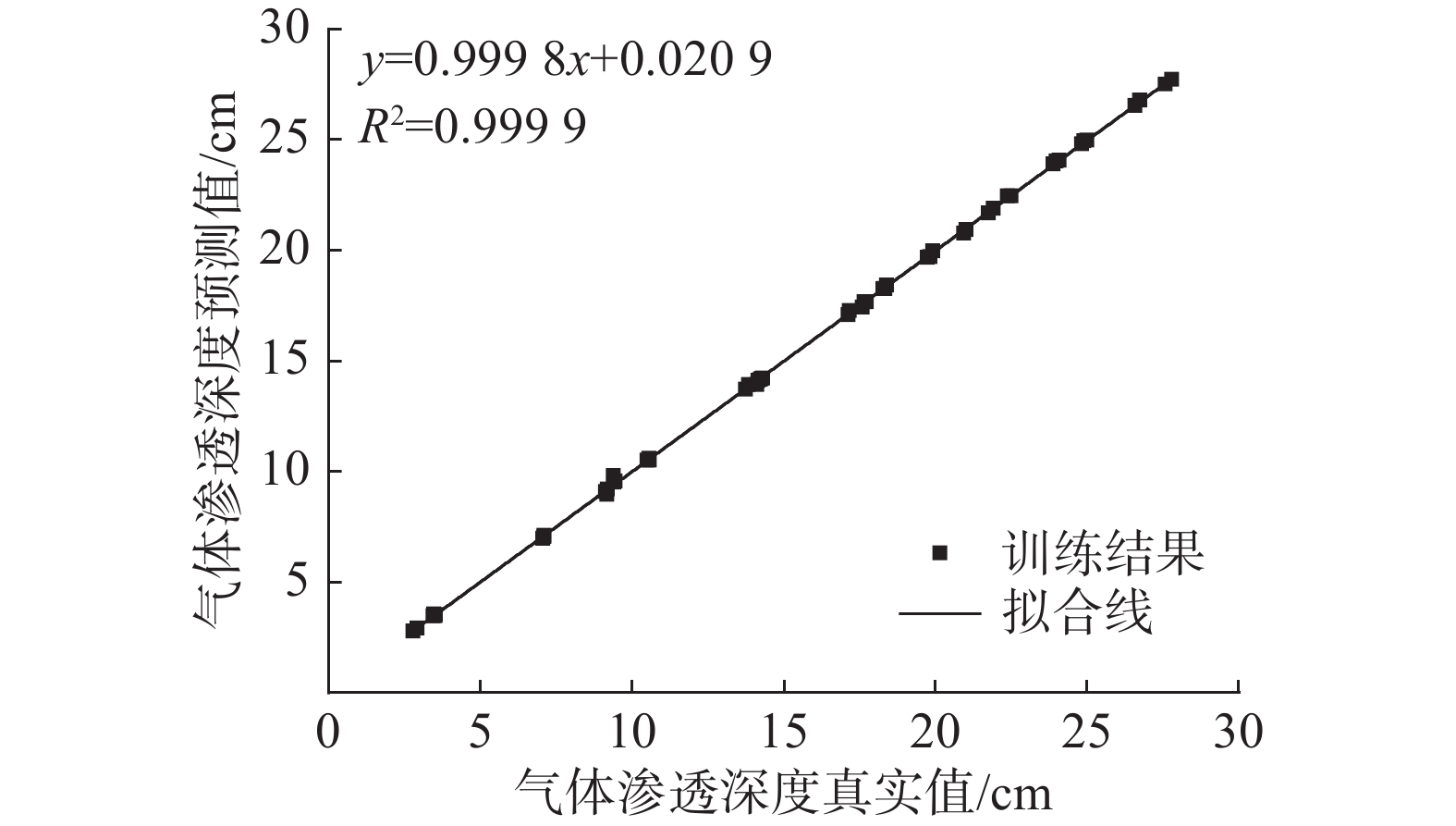
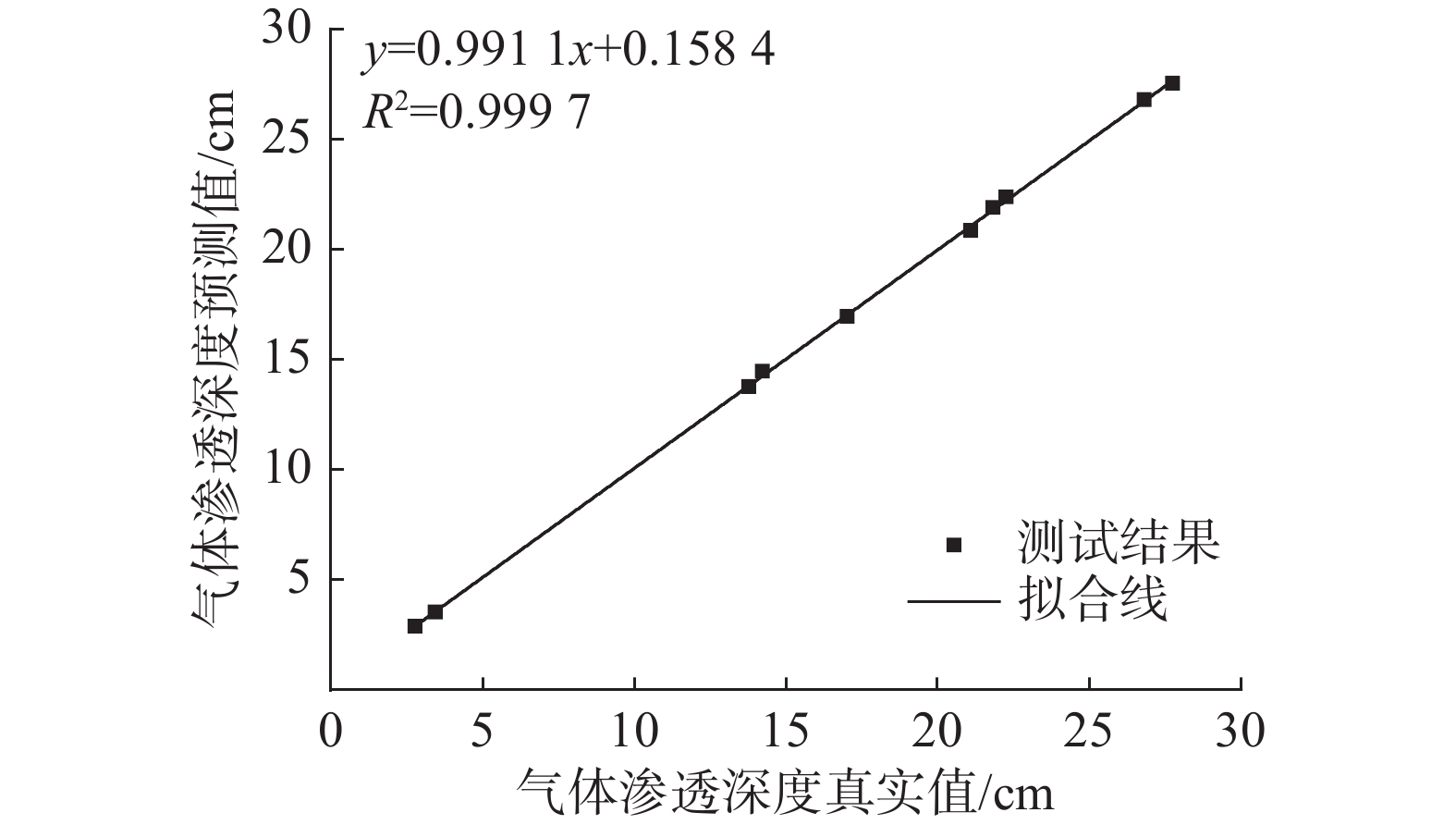
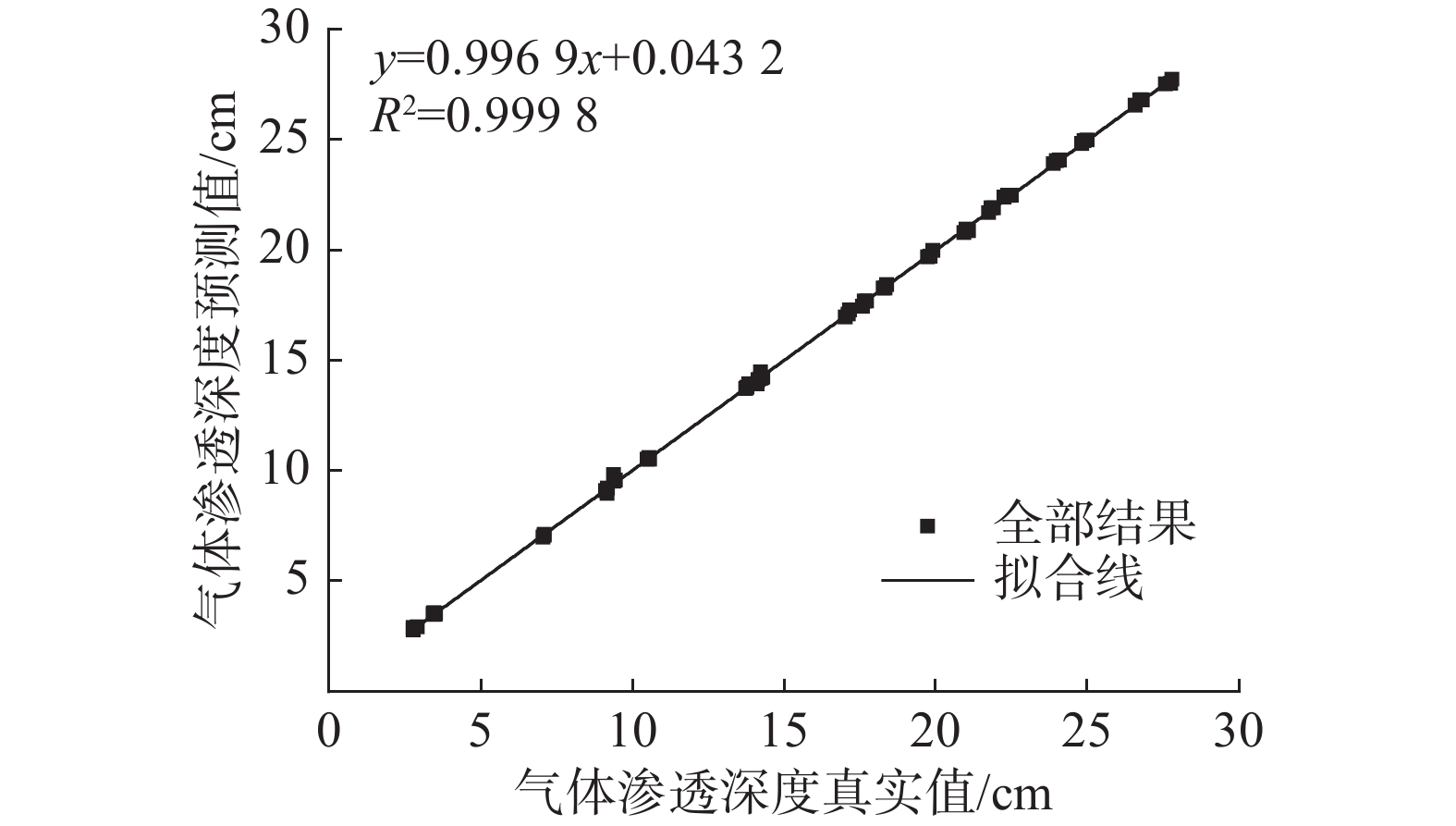
预测模型的建立能直观地得到在不同环境条件下安全壳混凝土内部的气体渗透深度,且结果具有高精度性。模型训练和测试的结果如图6~图8所示。模型训练和测试结果的相关系数R2分别为0.9999和0.9997,整体数据集的相关系数R2为0.9998,表明数据高度线性相关,基于BPNN所建立的模型对安全壳混凝土气体渗透深度能够做出较好的预测。
3.2 误差对比分析
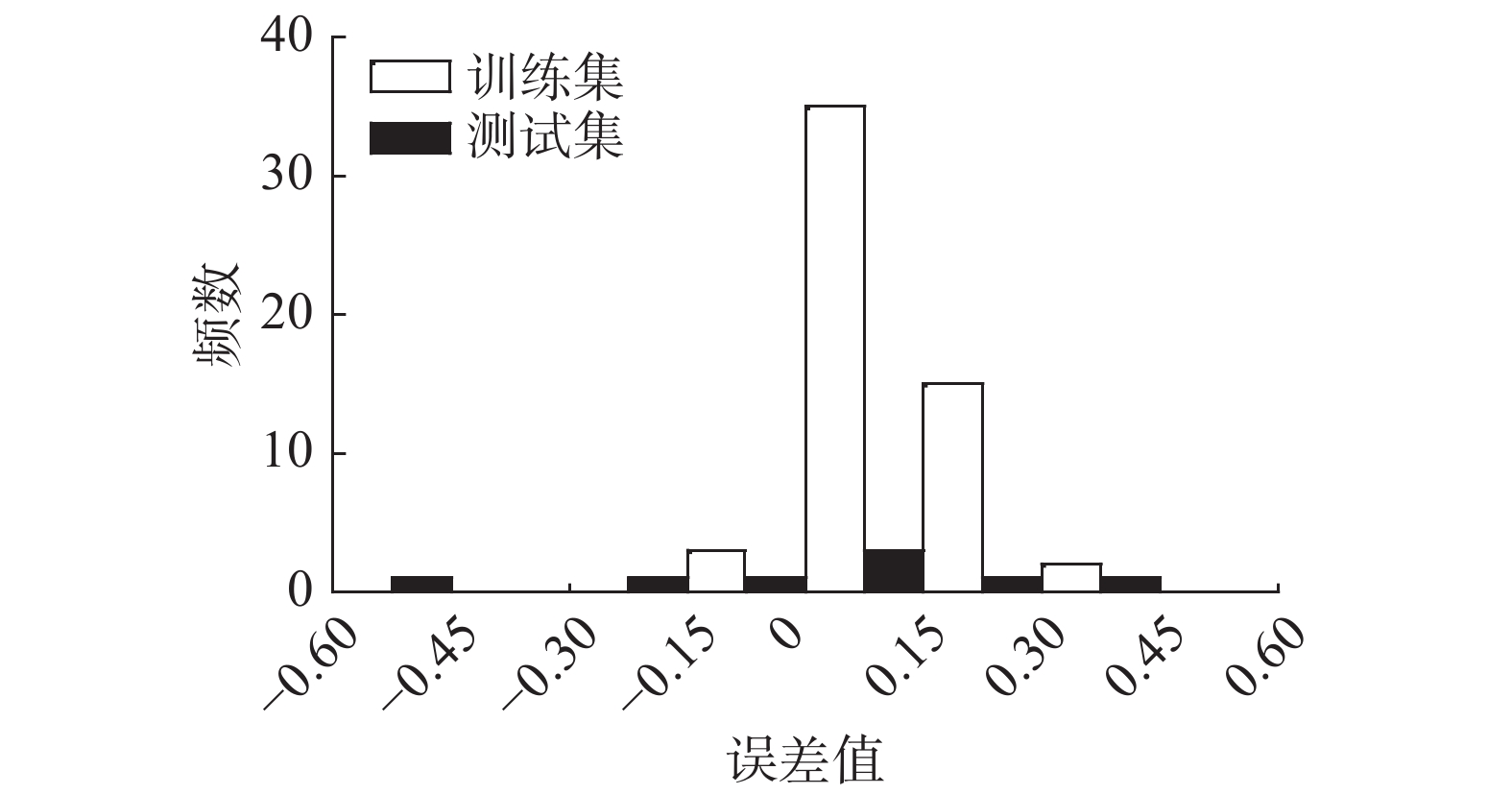
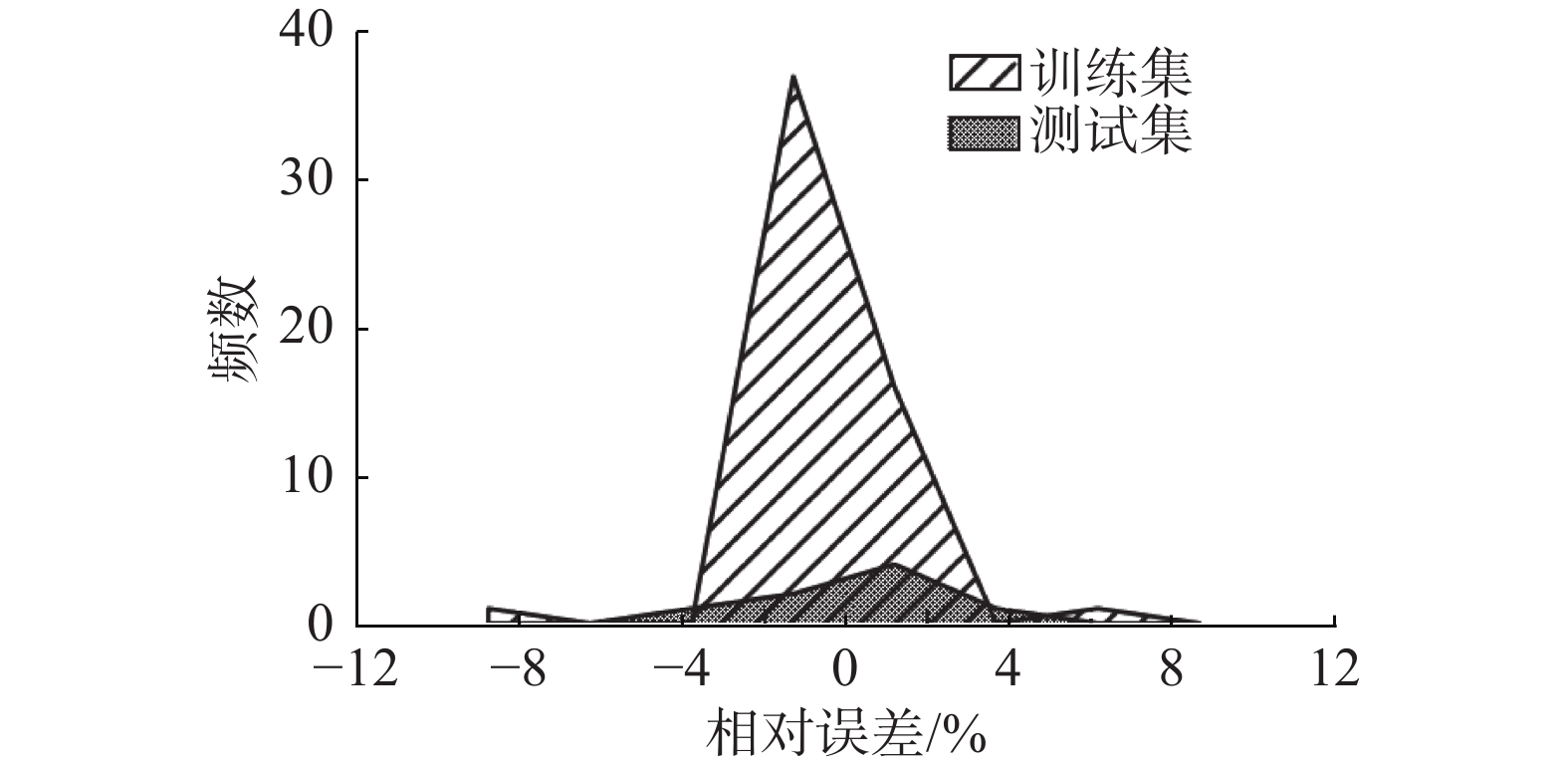
将预测模型中的训练集和测试集结果与工况结果进行误差分析,得到误差分布如图9所示。由图9可知训练集误差值在[0,0.075]时,所占频数最大,为35组,其所占比例超过训练集样本数的60%;测试集误差分布范围与训练集误差分布范围相比较分散,在[0.075,0.15]时所占频数最大,为3组,占测试集样本数量的37.5%。图10给出了训练集和测试集结果的相对误差分布,不难发现训练集相对误差和测试集相对误差基本分布在[−5%,5%]以内,整体误差较小,表明模型预测精度高。
4. 结论
1)本文建立高温高湿高压作用下安全壳混凝土气体渗透性仿真模型以获取神经网络训练样本,在给定相应的环境温度、水蒸气分压、升温速率和水扩散系数后,能够利用该仿真模型进行计算,得到相应的混凝土气体渗透深度。
2)通过仿真模型建立了63组数据,其中55组作为训练集样本,8组作为测试集样本,所建立的BPNN模型能够高精度地预测安全壳混凝土气体渗透深度。
3)预测模型训练结果与样本训练集数据相比,其相对误差在±10%以内,相关系数R2为0.9999,表明数据相关性好、模型精度高。模型所预测的结果与测试集数据相比,其相对误差大小在±5%以内,相关系数R2为0.9997,该结果表明BPNN具有良好的预测性。
4)本文所建立的BPNN模型能预测给定训练样本以外更极限环境条件下安全壳混凝土的气体渗透深度,与实验相比,提高了工作效率并节约资源,同时无需构建复杂的理论模型,可代替计算耗时的有限元仿真建模。
-
图 1 混凝土内部温度试验和数值计算结果[19]
图 2 混凝土内部蒸汽压试验和数值计算结果[19]
表 1 样本数据集的范围分布
变量 输入 输出 温度/℃ 水蒸气分压/
MPa升温速率/
(℃·h-1)水扩散
系数/s气体渗透
深度/cm最小值 130 0.2705 28 5.00×10−16 2.780 最大值 190 1.2564 56 5.00×10−14 27.786 均值 160 0.6830 40 1.85×10−14 15.6953 标准差 20.1606 0.3330 11.8703 2.2529×10−14 7.6662 表 2 反归一化后的网络测试集
cm 工况 归一化后的
预测值归一化后的
实际值反归一化后的
预测值/cm反归一化后的
实际值/cm1 0.3247 0.3083 10.8998 10.490 2 0.5842 0.5752 17.3885 17.164 3 0.7652 0.7883 21.9146 22.492 4 0.4392 0.4381 13.7626 13.736 5 0.7288 0.7286 21.0044 21.000 6 0.9527 0.9609 26.6032 26.808 7 0.4527 0.4576 14.1002 14.223 8 0.7628 0.7617 21.8546 21.826 -
[1] 王龙. EPR核电安全壳高强高性能混凝土配合比设计与性能研究[M]. 中国核科学技术进展报告(第五卷)——中国核学会2017年学术年会论文集第3册(核能动力分卷). 北京: 中国原子能出版社, 2018: 278-284. [2] 高凡. 核电站安全壳密封性试验系统搭建[J]. 中国核电, 2020, 13(3): 307−313. [3] 石亮, 刘建忠, 刘加平, 等. 核电安全壳混凝土气密性研究[J]. 混凝土, 2018(8): 144−148. doi: 10.3969/j.issn.1002-3550.2018.08.035 [4] 崔旭阳, 卢向晖, 杨江, 等. 华龙一号安全壳热工响应确定论现实方法研究[J]. 原子能科学技术, 2021, 55(9): 1721−1728. [5] CHEN Xiaoting, Davy C A, SHAO Jianfu, et al. Experimental and micro-mechanical analysis of the mecha-nical and transport properties of mortar containing heatinduced microcracks[J]. Cement and concrete comp-o-sites, 2010, 32(9): 678−685. doi: 10.1016/j.cemconcomp.2010.07.016 [6] 冯昭君, 李春丽, 任振中. 人工神经网络模型在混凝土领域应用综述[J]. 南方农机, 2019, 50(9): 206−207. doi: 10.3969/j.issn.1672-3872.2019.09.166 [7] XUE Jing, SHAO Jianfu, BURLION N. Estimation of constituent properties of concrete materials with an artificial neural network based method[J]. Cement and concrete research, 2021, 150: 106614. doi: 10.1016/j.cemconres.2021.106614 [8] 张驰, 郭媛, 黎明. 人工神经网络模型发展及应用综述[J]. 计算机工程与应用, 2021, 57(11): 57−69. [9] CHEN Shoukai, ZHAO Yunpeng, BIE Yajing. The prediction analysis of properties of recycled aggregate permeable concrete based on back-propagation neural network[J]. Journal of cleaner production, 2020, 276: 69−74. [10] 孙婧, 马秀歌, 陈巧艳. 事故后安全壳内环境条件计算分析[J]. 南方能源建设, 2015, 2(4): 53−56. [11] SAKLANI N, BANWAT G, SPNCER B, et al. Damage development in neutron-irradiated concrete in a test reactor: hygro-thermal and mechanical simulations[J]. Cement and concrete research, 2021, 142: 106349. doi: 10.1016/j.cemconres.2020.106349 [12] BAZANT Z P. Thermodynamics of interacting continua with surfaces and creep analysis of concrete structures[J]. Nuclear engineering and design, 1972, 20(2): 477−505. doi: 10.1016/0029-5493(72)90124-0 [13] GAWIN D, PESAVENTO F, SCHREFLER B A. Modelling of hygro-thermal behaviour and damage of concrete at temperature above the critical point of water[J]. International journal for numerical and analytical methods in geomechanics, 2010, 26(6): 537−562. [14] AHMED G N, HURST J P. Modeling pore pressure moisture, and temperature in high-strength concrete columns exposed to Fire[J]. Fire technology, 1999, 35(3): 232−262. doi: 10.1023/A:1015436510431 [15] 李荣涛. 高温下混凝土中化学–热–湿–力学耦合过程的数值模拟及破坏分析[D]. 大连: 大连理工大学, 2007. [16] SOGBOSSI H, VERDIER J, MULTON S. Permeability and damage of partially saturated concrete exposed to elevated temperature[J]. Cement and concrete com-posites, 2020, 109: 103563. doi: 10.1016/j.cemconcomp.2020.103563 [17] KLINKENBERG L J. The permeability of porous media to liquids and gases[J]. Drilling and production practice, 1941, 2(2): 200−213. [18] TH VGM. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils1[J]. Soil science society of america journal, 1980, 44(5): 892−898. doi: 10.2136/sssaj1980.03615995004400050002x [19] SHEKARCHI M, DEBICKI G, BILLARD Y. Heat and mass transfer of high performance concrete for reactor containment under severe accident conditions[J]. Fire technology, 2003, 39(1): 63−71. doi: 10.1023/A:1021779210983 [20] 李荣涛. 混凝土火灾高温中传热传质的数值模拟分析[J]. 混凝土, 2010(4): 10−13. doi: 10.3969/j.issn.1002-3550.2010.04.004 [21] BAZANT Z P, THONGUTHAI W. Pore pressure in heated concrete walls: theoretical prediction[J]. Magazine of concrete research, 2015, 31(107): 67−76. [22] 刘桂宏. 城市深层热储热水力多场耦合模拟方法与应用[D]. 徐州: 中国矿业大学, 2019. [23] 桂强, 秦敏峰, 李克非. 水泥基材料气体渗透性研究进展[J]. 硅酸盐学报, 2015, 43(10): 1500−1510. doi: 10.14062/j.issn.0454-5648.2015.10.21 [24] HODHOD O A, AHMED H I. Developing an artificial neural network model to evaluate chloride diffusivity in high performance concrete[J]. HBRC journal, 2013, 9(1): 15−21. doi: 10.1016/j.hbrcj.2013.04.001 [25] HUANG Lihua, CHEN Jian, TAN Xinyi. BP-ANN based bond strength prediction for FRP reinforced concrete at high temperature[J]. Engineering structures, 2022, 257(Apr.15): 114026.1−11. [26] 焦楚杰, 谭思琪, 崔力仕, 等. 基于神经网络的植生型多孔混凝土抗压强度预测模型[J]. 混凝土, 2022(1): 7−10. doi: 10.3969/j.issn.1002-3550.2022.01.002 [27] 龙旭, 毛明晖, 卢昶衡, 等. 基于人工神经网络的混凝土类材料SHPB动态压缩性能预测[J]. 南京航空航天大学学报, 2021, 53(5): 789−800. doi: 10.16356/j.1005-2615.2021.05.017 [28] 赵明亮, 水中和, 周华新, 等. 中低强度等级混凝土抗压强度的BP神经网络模型预测研究[J]. 混凝土, 2021(3): 35−38. doi: 10.3969/j.issn.1002-3550.2021.03.009







 下载:
下载: