A permittivity measurement device for oblique aperture ridge waveguide
-
摘要: 为准确测量腐蚀性液体的复介电常数并扩展微波能的工业应用，本文提出了一种基于传输/反射法的非接触式斜孔脊波导介电常数测量装置。在2.45 GHz频率和室温条件下测量了甲醇和乙醇及其混合溶液的散射参数，采用人工神经网络算法，以散射参数为输入，反演得到相应溶液的介电常数。测量结果与文献一致，验证了测量的准确性。待测物以试管为容器，避免了液体对测量装置的腐蚀。该系统还可测量固体及固体粉末的常温和高温介电特性，在微波能的工业应用中具有良好的前景。Abstract: In order to accurately measure the complex permittivity of corrosive liquids and expand the industrial application of microwave energy, a non-contact permittivity measurement device for oblique aperture ridge waveguide based on transmission/reflection method is proposed in this paper. The scattering parameters of methanol, ethanol and their mixed solutions were measured at 2.45 GHz frequency and room temperature. The permittivity of corresponding solutions were obtained by inversion using artificial neural network algorithm, taking the scattering parameter as input. The measurement results are consistent with the references, which verifies accuracy of the measurement. The test tube is used as the container for the object to be tested, which avoids corrosion of the liquid to the measuring device. The system can also measure the dielectric properties of solids and solid powders at room and high temperature, having a good prospect in the industrial application of microwave energy.
-
随着人类社会的不断发展，微波技术越来越受到人们的重视。它在环境科学、医学、化学、生物学和日常生活中有着广泛的应用[1-7]。这些应用涉及微波在介质中的传输、反射和吸收3个主要特性[8-10]。这3个特性与介质的复介电常数密切相关。复介电常数能反映电磁波与介质相互作用过程中，介质对电磁波的吸收、反射及透射能力。准确获得材料的介电常数对于微波工程中合理地使用材料是非常必要的。液体的介电常数是微波能应用中的重要参数，对液体介电常数测量方法及系统开展的研究较多[11-13]。实际中，许多工业用溶剂具有腐蚀性，准确获知腐蚀性液体的介电特性，可以为微波能处理腐蚀性液体提供依据。然而，目前许多测量方法及系统中，待测物与测量装置会直接接触，腐蚀性液体在测量过程中容易使测量装置受损，影响测量的精度，导致腐蚀性液体的介电常数难以准确测量。因此，研究如何准确测量腐蚀性液体的介电常数具有重要意义。基于此，本文提出一种非接触式介电常数测量装置，可用于腐蚀性液体的介电常数测量。装置测量了频率为2.45 GHz、室温条件下甲醇和乙醇以及其混合溶液的散射参数，结合人工神经网络反演得到不同配比条件下混合溶液的复介电常数。
1. 测量系统设计
1.1 系统整体设计
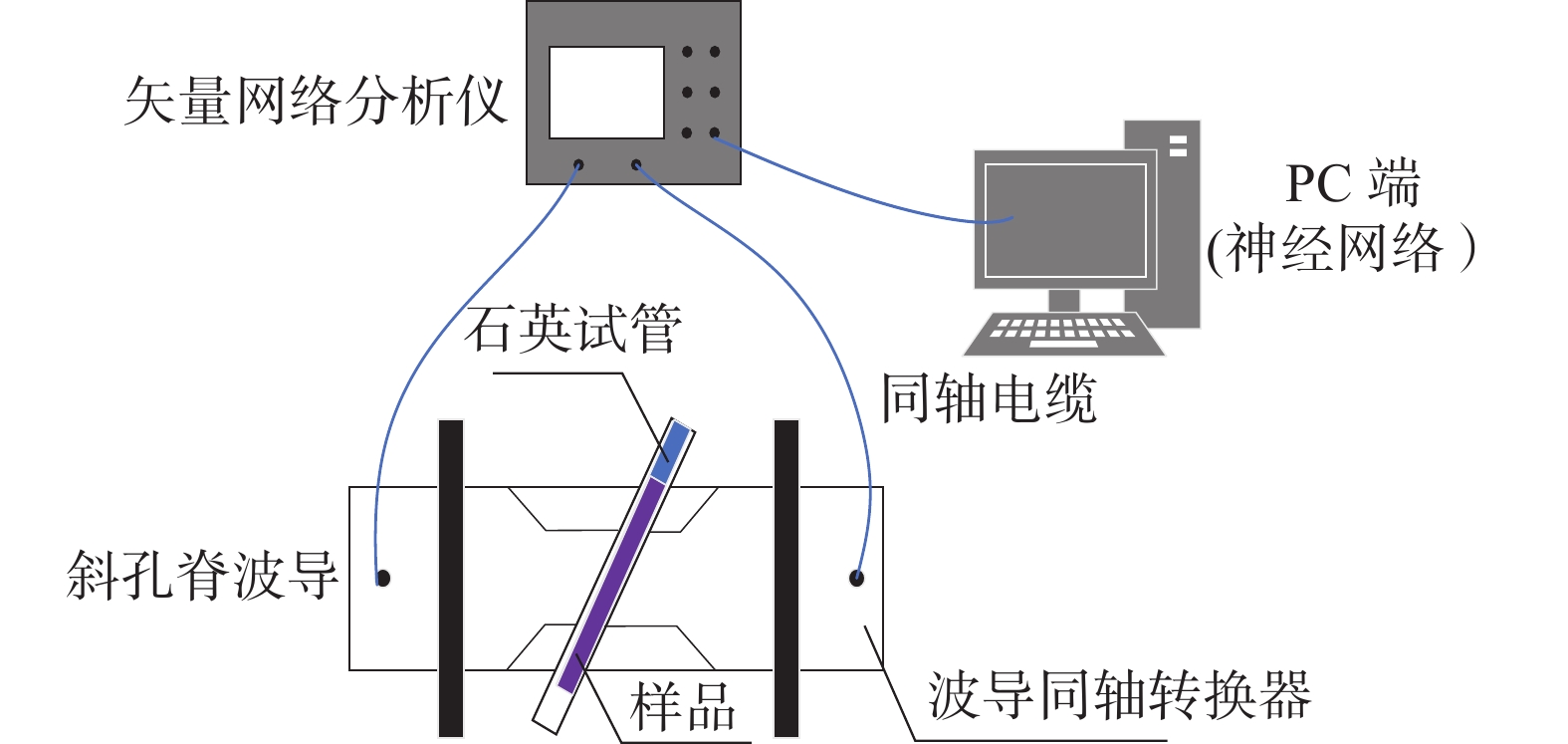
本文所提出的基于斜孔脊波导的介电常数测量系统如图1所示。该系统由斜孔脊波导装置、波导同轴转换器、矢量网络分析仪、同轴电缆、石英试管以及PC端组成。斜孔脊波导用于放置待测样品，让待测物处于电磁场中；矢量网络分析仪测量得到的散射参数，送入PC端利用人工神经网络算法反演得到样品的介电常数。该系统具有操作方便、样品准备简单和所需样品少等优点。
图 1 介电测量系统
下载:
全尺寸图片
1.2 核心装置设计
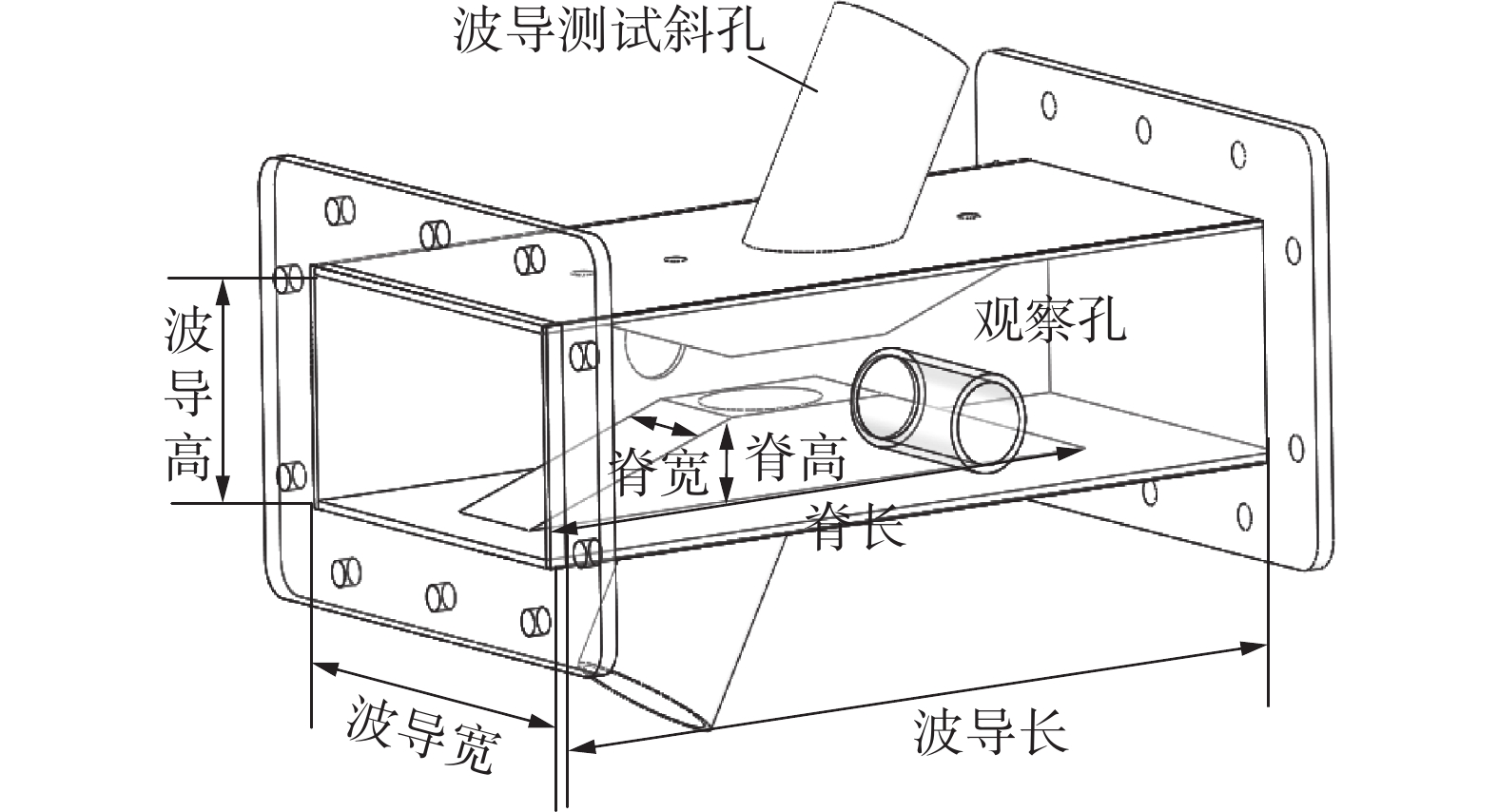
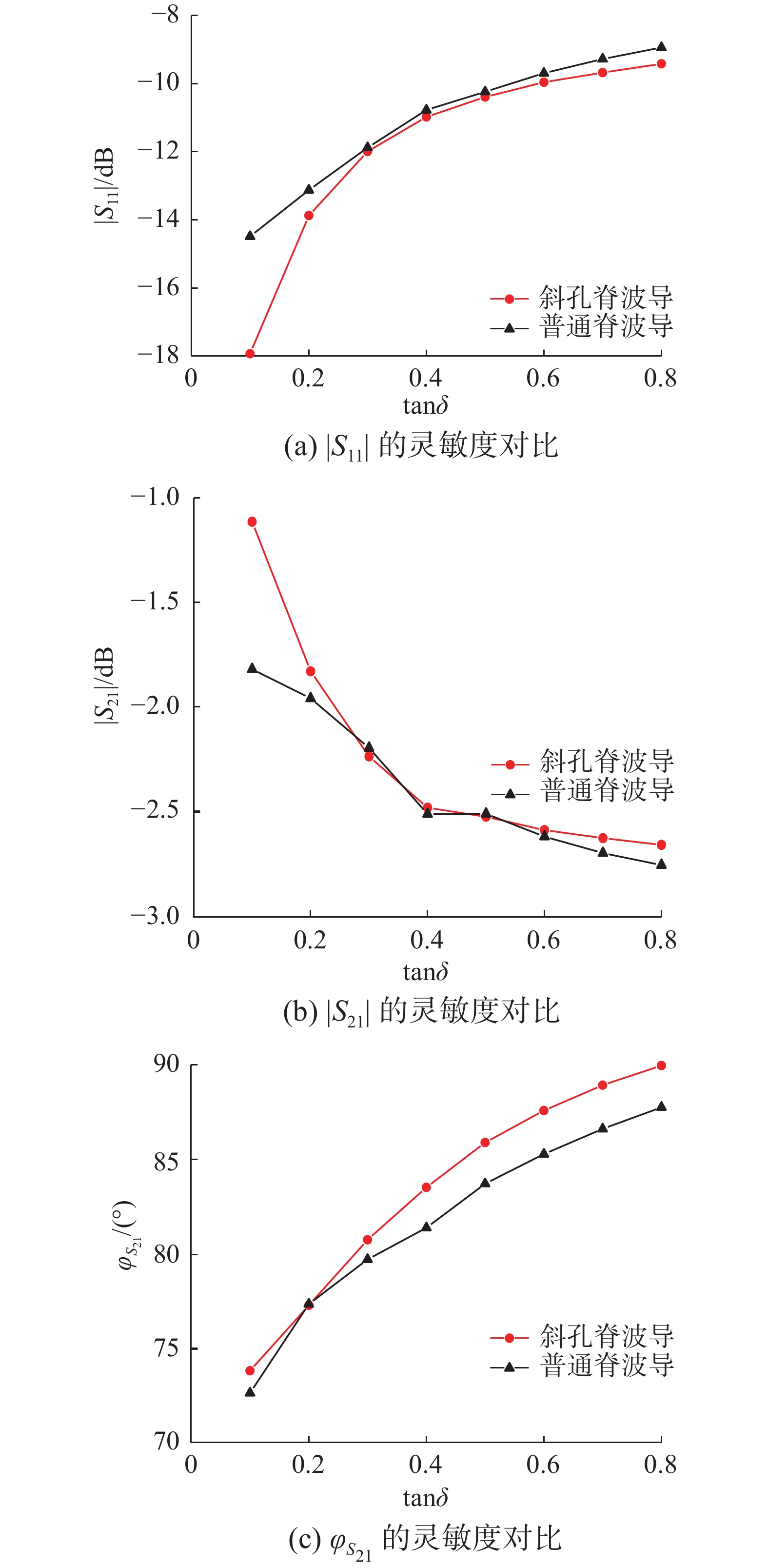
2.45 GHz为微波能工业应用的常用频率，系统基于该频率设计测量装置。该介电常数测量系统的核心装置是斜孔脊波导，包括矩形波导、上下2个脊、波导测试斜孔以及观察孔4个部分，如图2所示。脊波导是在标准矩形波导BJ22的基础上，将宽壁弯折而形成脊，能够将电磁场聚焦在两脊之间。在脊波导的窄壁中心位置开了2个相互垂直的孔，用于观察待测样品状态，为避免电磁能量外泄，观察孔向外延伸形成圆波导，该圆波导工作在截止状态。脊上开测量孔，用于放置待测物，测量孔相连的圆波导也设计成截止状态，测量孔与波导腔体成一定的夹角，该结构使待测物位于电场较强的区域，便于提高测量灵敏度。利用电磁仿真软件CST模拟仿真了待测物质介电常数实部1~40、损耗角正切0.1~0.8变化时散射参数的计算结果。反演时采用
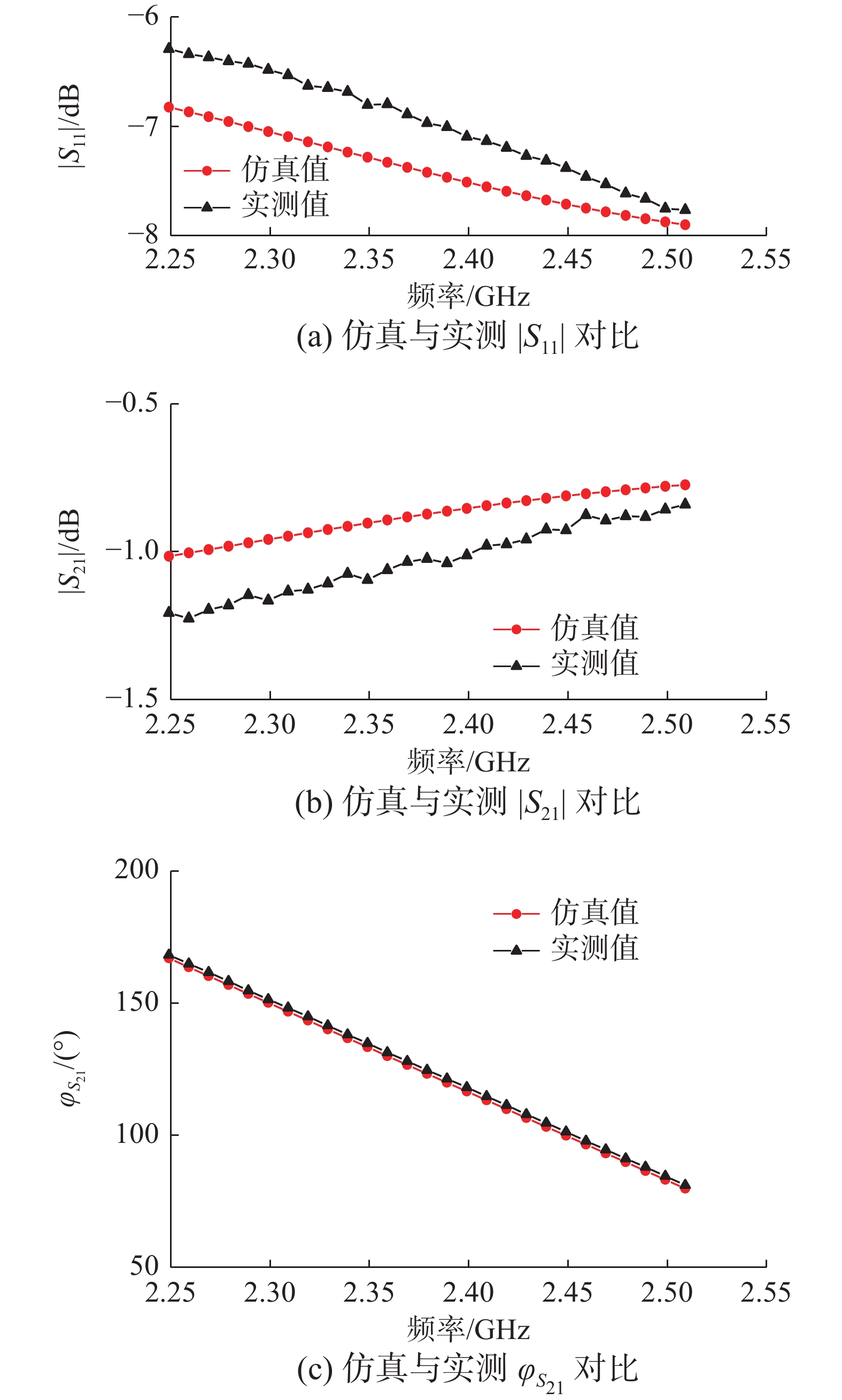
$ |{S_{11}}| $ 、$ |{S_{21}}| $ 和$ {\varphi _{{S_{21}}}} $ 共3种参数，对这3个参数进行仿真计算。仿真计算结果表明实部在1~40、损耗角正切在0.1~0.8，3种散射参数能反映物质介电常数的变化。斜孔脊波导与普通脊波导[14]实部为25、损耗角正切在0.1~0.8的仿真结果如图3所示。对斜孔和普通脊波导的散射参数进行对比，在同一损耗角正切变化区间内，斜孔脊波导散射参数的变化范围更大，具有更高的测量灵敏度。通过对比测量灵敏度，优化脊波导各种参数值，所得脊波导的长度为237 mm，宽度为109.22 mm，高度为54.61 mm；脊的长度为180 mm，宽度为34 mm，高度为20 mm。
图 2 脊波导结构下载:
全尺寸图片
图 3 斜孔脊波导与普通脊波导的灵敏度对比下载:
全尺寸图片
为了实现介电常数的准确计算，快速得到介质的复介电常数，还需要将实测与仿真数据进行对比，测量空试管的散射参数并与仿真结果对比，如图4所示。仿真与实测结果表明，该系统实际测量结果与仿真计算数据接近，且变化趋势一致，为后续介电常数准确测量提供了依据。
图 4 仿真与实测对比下载:
全尺寸图片
2. 神经网络设计
近年来，机器学习得到了快速发展，人工神经网络也变得无处不在，推动着各种应用的发展。机器学习以大数据为基础，发现数据背后的规律，从而实现预测或判断的功能，例如探地雷达数据反演、地震数据的速度反演、电阻率数据反演以及图像识别[15-18]等。借助人工神经网络通过系统测量散射参数来得到待测物质的介电常数。
物质的复介电系数（
$ \varepsilon $ ）表示为$$ \varepsilon = {\varepsilon '} - j{\varepsilon {''}} $$ 式中：
$ {\varepsilon '} $ 为复介电系数的实部，决定着材料储存能量的能力；$ {\varepsilon {''}} $ 为复介电系数的虚部，代表材料对电磁波的介电损耗能力[19]。损耗角正切（$ \tan \delta $ ）是计算复介电系数虚部与实部比值的参数，表示介质的损耗程度，其定义为$$ \tan \delta = \frac{{{\varepsilon {''}}}}{{{\varepsilon '}}} $$ 一般情况下，物质的介电常数难以用仪器直接测量得到。通过矢量网络分析仪可以测量系统的散射参数，而待测物的介电常数和系统的散射参数之间存在较为复杂的数学函数关系。深度学习允许由多个处理层组成的计算模型来学习具有多个抽象层次的数据表示，可以学习非常复杂的函数[20]，能用于物质介电常数的反演。
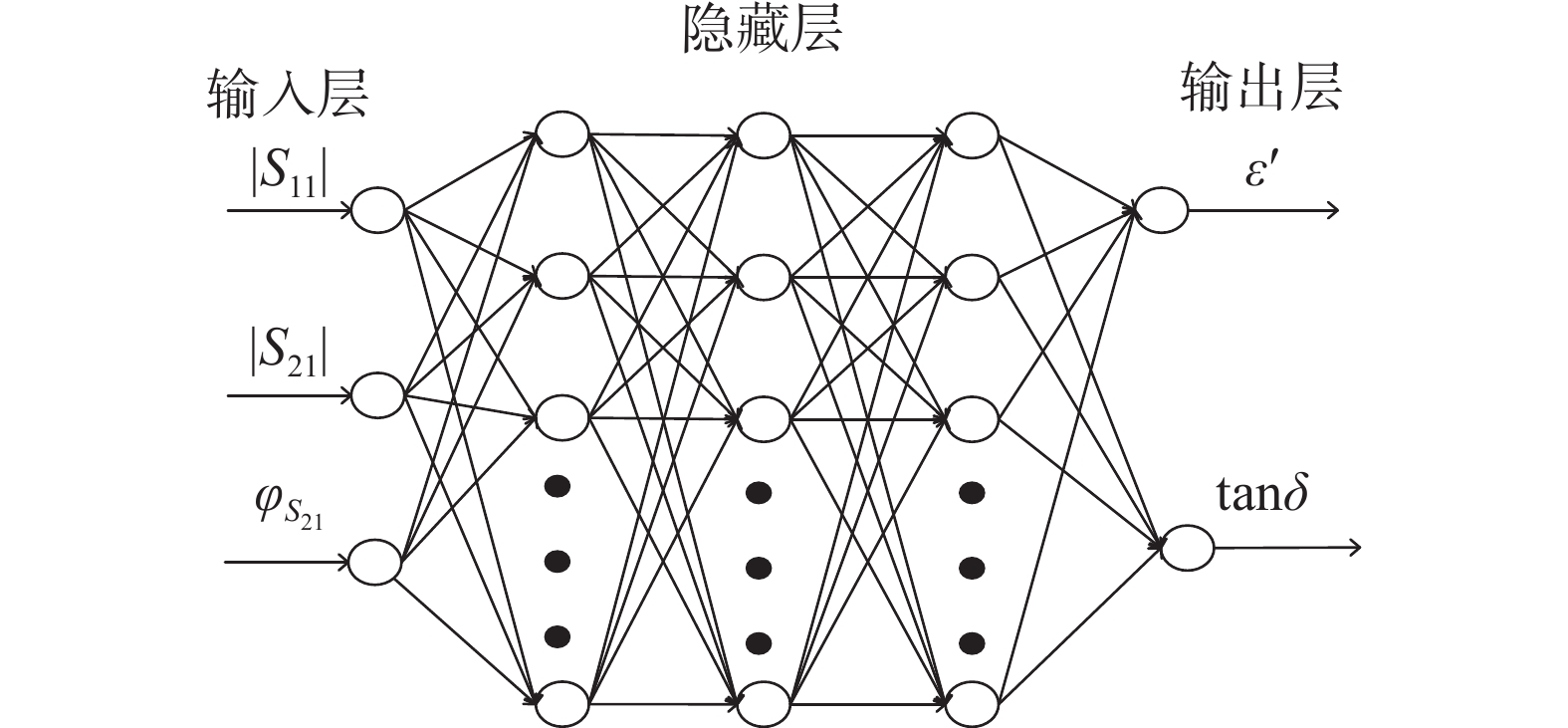
在人工神经网络中，第1层为输入层，最后1层为输出层，其余层都是隐藏层。每一层都是由节点和神经元组成的。层与层之间是全连接的，即每一个神经元与之相邻层的所有神经元连接。隐藏层神经元从上1层接收输入数据，再利用激活函数进行非线性变换，然后继续输出到下1层。本文采用人工神经网络算法对复介电系数进行反演时，网络主要由1个输入层、3个隐藏层和1个输出层3部分组成。输入层的输入向量为散射参数（
$ |{S_{11}}| $ 、$ |{S_{21}}| $ 、$ {\varphi _{{S_{21}}}} $ ），输出层输出2个介电特性向量（${\varepsilon '}$ 、$ \tan \delta $ ），如图5所示。
图 5 神经网络预测模型下载:
全尺寸图片
第
$ i $ 层的输出值${{{a}}^{{i}}}({{i}} = 1,2,3,4)$ 为$$ {{{a}}}^{{{i}}}={{f}}\left({\displaystyle {\sum }_{{{j}}-1}^{{{m}}}{\omega }^{{{i}}-1}{{{a}}}^{{{i}}-1}+{{{b}}}^{{{i}}-1}}\right) $$ 式中：
$ m $ 为第$ i - 1 $ 层的神经元的数量，$ {\omega ^{i - 1}} $ 为第$ i - 1 $ 层的权重系数矩阵，${{a}}_{{j}}^{{{i}} - 1}$ 为第$ i - 1 $ 层的第$ j $ 个神经元的输出值，${{{b}}^{{{i}} - 1}}$ 为第$ i - 1 $ 层的偏置，$ f(x) $ 为激活函数，输入层${{\boldsymbol{a}}^0}$ 为散射参数。$$ {{\boldsymbol{a}}}^{0}={[|{{{S}}}_{11}|,|{{{S}}}_{21}|，{\varphi }_{{{{S}}}_{21}}]}^{{\rm{T}}} $$ 输出层
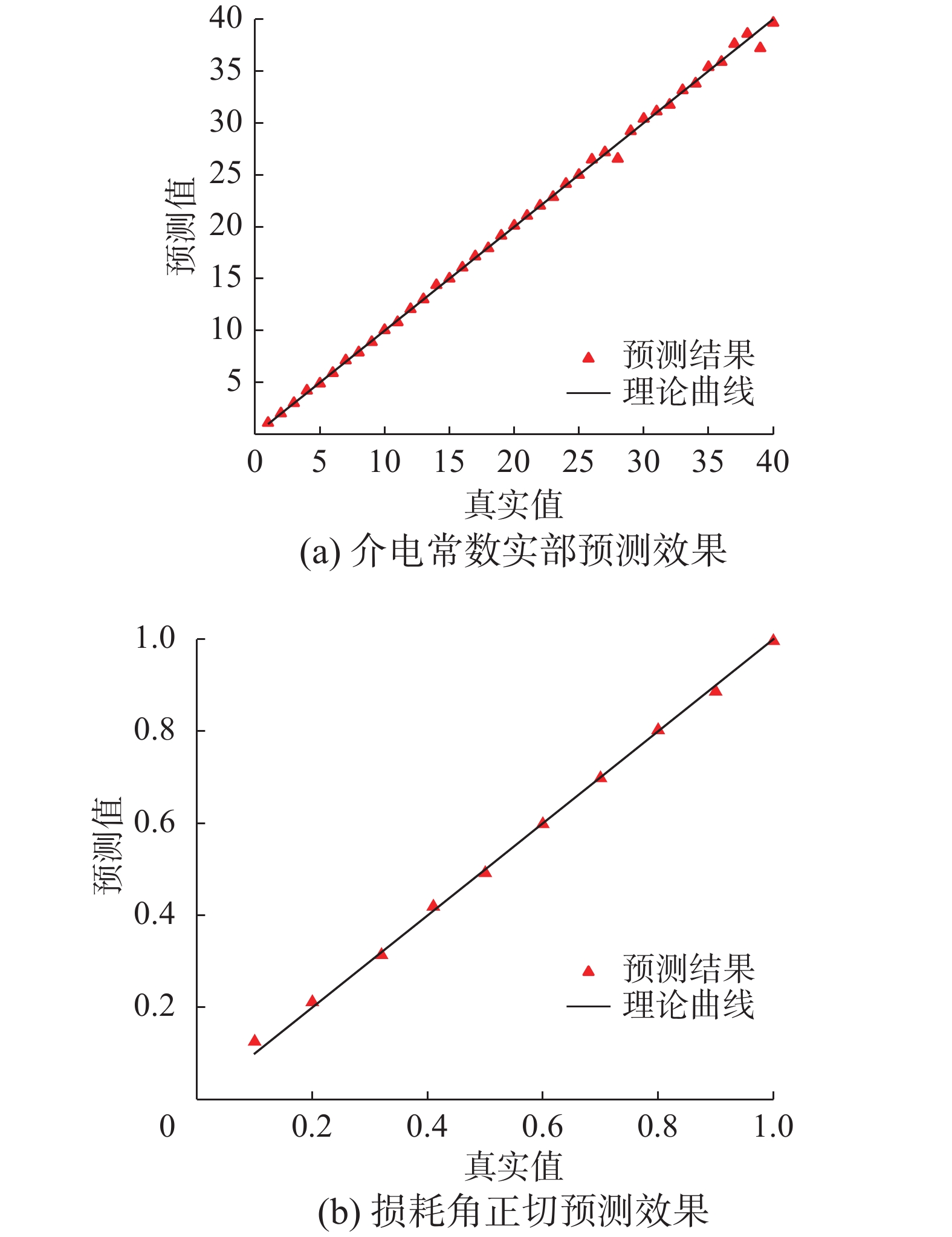
${{\boldsymbol{a}}^4}$ 为介电特性：$$ {{\boldsymbol{a}}^4} = {[{\varepsilon '},\tan \delta ]^{\rm{T}}} $$ 基于仿真与实测结果一致，选取部分仿真数据作为训练样本，完成神经网络的训练。为验证神经网络的预测效果，选择仿真数据中未用于训练的40组样本数据输入训练好的神经网络中，其预测结果如图6所示。当预测值和真实介电常数值的关系越接近
$ y = x $ 理论曲线，说明神经网络的预测结果准确度越高。图6中介电常数实部和损耗角正切的预测平均绝对误差分别为1.45 %和1.02 %，表明该神经网络模型可信度高。
图 6 介电常数预测效果下载:
全尺寸图片
3. 实验结果与分析
为了验证系统的可行性和准确性，本文在室温下对液体进行测量。甲醇和乙醇是常用的有机溶剂，且甲醇和乙醇及其混合溶液的介电常数有理论计算值，因此选择甲醇和乙醇为待测溶剂。甲醇、乙醇的介电常数实部参考值[21]分别为24.97和8.94。常规情况下，混合溶液的介电常数实部将依据甲醇、乙醇混合的比例在8.94~24.97变化，可用于验证测量的准确性。在室温下对甲醇和乙醇及其混合溶液进行了复介电常数测量。搭建测量系统，如图7所示。
图 7 测量系统实物下载:
全尺寸图片
将待测液体注入石英试管中，再将石英试管置于脊波导的测试孔内，通过矢量网络分析仪测量散射参数，最后将测得的散射参数输入神经网络模型，得到不同体积比的甲醇、乙醇混合溶液的介电常数。
同时，混合溶液的复介电常数可通过Bruggeman公式[22]计算得到：
$$ \begin{split}{\varepsilon _{{\rm{eff}}}} = \dfrac{1}{4}[(3\alpha -& 1){\varepsilon _i} + (2 - 3\alpha ){\varepsilon _e}] + \frac{1}{4}\{ [(1 - 3\alpha ){\varepsilon _i} + \\ &(3\alpha - 2){\varepsilon _e}{]^2} + 8{\varepsilon _i}{\varepsilon _e}{\} ^{\frac{1}{2}}} \end{split}$$ 式中：εeff为混合溶液的介电常数，εi为混入溶液的介电常数, εe为基底溶液的介电常数，α为混入溶液与混合溶液的体积比。依据Bruggeman公式计算混合溶液介电常数参考值，体积比α采用每组变化20%的方式。
选取待测溶液总体积为100 mL，配制6组溶液。第1组只取乙醇溶液100 mL；后续每组乙醇溶液比上一组减20 mL，甲醇溶液增加20 mL，直至得到第6组全部为甲醇溶液100 mL，实现1~6组混合溶液介电常数按配比8.94~24.97变化。在室温下，分别对6组溶液的复介电常数进行测量，取3次实验测试的平均值为物质的测量值。实验的测量结果如表1和表2所示。
从表1和表2可知，本文所提出的测量装置及系统在常温下对测量甲醇、乙醇溶剂及其混合溶液的复介电常数的准确度较高，与参考文献的理论值一致，其中复介电常数的实部测量相对误差在9%以内，损耗角正切的测量相对误差在5%以内。实验中测量误差最大的试剂为甲醇和乙醇按照1∶4混合的溶液，误差产生的原因可能由于该比例条件下甲醇与乙醇混合互溶后，溶液性质发生一些细微变化或者互溶度不高导致溶液的介电特性随之有微小的改变。Polonskii等[23]曾对此进行了研究，研究表明对于混合溶液的复介电常数值用公式来进行表征可能存在一定的误差。此外，测量仪器误差、腔体加工尺寸偏差及反演误差等多种因素都可能影响测量结果的准确度。
4. 结论
1）本文设计的斜孔脊波导测量了甲醇和乙醇混合溶液的散射参数，并通过人工神经网络反演，得到了溶液的介电常数。
2）混合溶液复介电常数与理论公式计算结果吻合良好。
3）设计的非接触式测量系统为腐蚀性液体的介电常数测量提供了方法，将有助于微波能工业应用范围的扩展。
本文采用传输/反射法设计了基于斜孔脊波导的测量装置，并构成了非接触式介电常数测量系统，结合神经网络，利用散射参数反演待测物质的介电常数，验证了测量系统的可靠性。在室温下测量了甲醇和乙醇及其混合溶液的介电常数，结果较准确，证明该系统可以用于液体、固体及固体粉末的介电常数测量。同时，该系统具有待测物与测量装置非接触的结构，还可用于腐蚀性液体及高温条件下物质介电常数的测量。
-
图 1 介电测量系统
下载:
全尺寸图片
图 2 脊波导结构
下载:
全尺寸图片
图 3 斜孔脊波导与普通脊波导的灵敏度对比
下载:
全尺寸图片
图 4 仿真与实测对比
下载:
全尺寸图片
图 5 神经网络预测模型
下载:
全尺寸图片
图 6 介电常数预测效果
下载:
全尺寸图片
图 7 测量系统实物
下载:
全尺寸图片
表 1 溶液介电常数实部测量结果
-
[1] 林芳, 吕明, 岳林霞, 等. 微波辅助羟胺降解全氟辛酸[J]. 北京大学学报(自然科学版), 2022, 58(3): 546−552. [2] 刘铁芳, 藏晓, 李萌, 等. 磁共振扩散加权成像在肝癌微波消融预后评估中的应用研究[J]. 磁共振成像, 2022, 13(6): 112−116. [3] HAN Zhong, LI Ying, LUO Donghui, et al. Structural variations of rice starch affected by constant power microwave treatment[J]. Food chemistry, 2021, 359: 129887. doi: 10.1016/j.foodchem.2021.129887 [4] 李之钦, 李商略, 庄绪宁, 等. 微波焙烧强化废锂离子电池中的金属回收研究[J]. 中国环境科学, 2021, 41(10): 4712−4719. [5] CHEN Jianan, ZHU Jun, XU Wentao, et al. Highly efficient H2 and S production from H2S decomposition via microwave catalysis over a family of TiO2 modified MoxC microwave catalysts[J]. Fuel processing technology, 2022, 226: 107069. doi: 10.1016/j.fuproc.2021.107069 [6] 罗光宏, 王海蓉, 崔晶, 等. 微波辅助低共熔溶剂提取、部分纯化螺旋藻多糖及其体外生物学活性研究[J]. 食品与发酵工业, 2022, 48(11): 107−113. [7] GUZIK P, KULAWIK P, ZAJAC M, et al. Microwave applications in the food industry: an overview of recent developments[J]. Critical reviews in food science and nutrition, 2021, 62(29): 7989−8008. [8] 高海燕, 杨欣达, 周波, 等. 耦合诱导的四分之一波长超导谐振器微波传输透明[J]. 物理学报, 2022, 71(6): 337−345. [9] OCHI H, SHIMAMOTO S, LIU J, et al. Non-contact blood pressure estimation with pulse wave employing microwave reflection[C]//2021 IEEE International Conference on Communications Workshops. New York: IEEE, 2021: 1-6. [10] CHOE H S, LEE J S, KWEON J H, et al. High-performance microwave absorption heating honeycomb sandwich composite with electroless nickel-plated glass fiber[J]. Composite structures, 2022, 283: 115138. doi: 10.1016/j.compstruct.2021.115138 [11] STERZL G, HESSELBARTH J. Characterization of permittivity of liquids-in-flow with spherical dielectric resonators[C]//European Microwave Association, 2020 50th European Microwave Conference. New York: IEEE, 2021: 901-904. [12] 苗润, 高冲, 彭亦童, 等. 基于同轴谐振器的液体材料复介电常数测试研究[C]//2021年全国微波毫米波会议论文集. 南京: 中国电子学会, 2021: 345-347. [13] 龙卓, 刘长军. 一种双频基片集成波导介电常数测试系统[J]. 应用科技, 2019, 46(3): 21−24. [14] 晏晗, 陈倩, 黄卡玛, 等. 一种基于脊波导的高温煤粉介电系数测量[J]. 应用科技, 2021, 48(4): 38−42. [15] WANG Jing, LIU Hanchi, JIANG Peng, et al. GPRI2Net: a deep-neural-network-based ground penetrating radar data inversion and object identification framework for consecutive and long survey lines[J]. IEEE transactions on geoscience and remote sensing, 2021, 60: 1−20. [16] LI Shucai, LIU Bin, REN Yuxiao, et al. Deep-learning inversion of seismic data[EB/OL]. (2020-06-26) [2022-11-01]. https://arxiv.org/abs/1901.07733v2. [17] LIU Bin, GUO Qian, Li Shucai, et al. Deep learning inversion of electrical resistivity data[J]. IEEE transactions on geoscience and remote sensing, 2020, 58(8): 5715−5728. doi: 10.1109/TGRS.2020.2969040 [18] ELOGRI O, KARMOUNI H, SAYYOURI M, et al. 3D image recognition using new set of fractional-order Legendre moments and deep neural networks[J]. Signal processing:image communication, 2021, 98: 116410. doi: 10.1016/j.image.2021.116410 [19] 黄庭远. 硫化钴基复合纳米材料的制备及微波吸收性能研究[D]. 南京: 东南大学, 2017. [20] LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436−444. doi: 10.1038/nature14539 [21] 华伟, 杨晓庆, 夏祖学, 等. 2.45 GHz 下常用有机试剂复介电常数的测量与研究[J]. 化学研究与应用, 2006, 18(10): 1232−1234. doi: 10.3969/j.issn.1004-1656.2006.10.023 [22] NELSON S. Dielectric properties of agricultural products and applications[J]. IEEE trans on instrumentation & measurement, 1991, 41(1): 116−122. [23] POLONSKII Y A, PAVLOVA G A, SAVEL'EV V N, et al. Dielectric properties of optical quartz glass in the ultra-high frequency range and at temperatures of up to 1 500 °C[J]. Glass and ceramics, 1971, 28(3): 182−184. doi: 10.1007/BF00674891
