Comprehensive evaluation of cruise cabin design based on entropy weight analytic hierarchy process
-
摘要: 针对邮轮居住舱室设计方案评价存在主观性过强和模糊性的问题,提出一种基于熵权层次分析的综合评价方法。本研究根据邮轮居住环境设计的评价约束条件,考虑舱室布局、室内环境和安全性的影响,构建融合乘客、舱室家具和舱室环境三者形成典型居住舱室“人−机−环境”系统的评价指标体系及综合评价模型,形成一套适用于邮轮居住舱室科学设计评估的理论与方法体系;最后应用舱室不同空间分布的数据,采用此方法进行综合评价,从而对设计方案进行排序,以确定最优的设计方案。本文研究结果可为邮轮居住舱室的设计方案的确定提供参考。Abstract: Aiming at the problems of subjectivity and fuzziness in the evaluation of cruise cabin design, we propose a comprehensive evaluation method based on entropy weight analytic hierarchy process. According to the evaluation constraint conditions for cruise living environment design, and taking the influence of the cabin layout, indoor environment and safety into account, the evaluation index system and comprehensive evaluation model of "man-machine-environment" system of typical accommodation are constructed by integrating passengers, cabin furniture and cabin environment, forming a set of theory and method system suitable for scientific design and evaluation of cruise accommodation. Finally, comprehensive evaluation is carried out by this method, using the data of different spatial distribution of the cabin, so as to sort out the design schemes and determine the optimal design scheme. The research results of this paper can provide reference for the design of cruise accommodation.
-
邮轮居住舱室的设计须遵守相关规范且在布局设计方面自由度较大,一般情况下依赖于设计者的经验,导致居住舱室设计方案评价指标模糊性较强且彼此之间相互关联,再加上传统的评价方法存在一定的主观随意性,难以对居住舱室设计方案的好坏做出科学客观的判断[1-2]。因而科学高效的邮轮居住舱室评价方法十分重要。
目前应用较多的综合评价方法主要有专家经验法和客观评价法,其中专家经验法主要包括层次分析法 (analytic hierarchy process,AHP)和模糊综合评价方法,客观评价方法主要有逼近理想解排序方法(technique for order preference by similarity to an ideal solution,TOPSIS)和熵权法。姚竞争等[3]利用层次分析法完成邮轮生活舱室评价,该方法可以把定性指标转化为定量指标,但对指标赋权时仍会受到人为因素的干扰。陈思旭等[4]利用模糊综合评价方法进行邮轮客舱设计综合评价研究,该方法计算步骤较为复杂且计算量过大,指标权重向量确定主要靠专家经验,主观性较强。主成分分析法要求各指标之间须有较强的相关性且结果解释性较差。马青等[5]利用TOPSIS评价法进行邮轮居住舱室舒适性评价,但该方法只能应用于方案优劣排序,不可以进行归类解释。熵权法由克劳德·香农在1948年最早提出,应当属于热力学的范围,他将熵权法整理到信息体系构建进程中[6]。根据信息熵的定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其熵值越小,指标的离散程度越大,该指标对综合评价的影响(即权重)就越大。熵权法在评价领域是利用熵概念确定评价指标权重的客观评价方法,能够定量计算评价指标的权重值,不依赖于专家评价,结果更加准确合理且具有较强的客观性[7]。马相鹏等[8]利用AHP–熵权法对极地探险娱乐设备选型的各个指标进行了综合评价,提高了方案选择的可靠性、客观性和有效性。
综上,考虑到居住舱室设计评价是一个复杂的多属性评价问题且存在一系列相互关联的模糊性指标,本文选择熵权法和层次分析法相结合的方法来确定居住舱室设计评价指标权重,通过熵权层次分析法确定的指标权重既包含了一定倾向的主观意愿,又能客观反映指标数据的真实有效性,该方法可为邮轮居住舱室提供一个科学高效的评价方法,具有一定的应用价值。
1. 邮轮居住舱室熵权层次分析综合评价
1.1 确定评价的因素集
设定首层指标中评价对象有
$ m $ 个评价指标,则评价因素集可以表示为$$ A = \{ {b_1},{b_2},\cdot \cdot \cdot ,{b_i}, \cdot \cdot \cdot ,{b_m}\} $$ 评价因素集A的任意评价指标包含若干子因素集,设定第
$ i $ 个评价指标对应的二级指标个数为$ n $ ,那么第2层中第$ i $ 个评价指标的因素集合可以表示为$$ {A}_{i}=\{{b}_{i1},{b}_{i2},\cdot \cdot \cdot,{b}_{ij},\cdot \cdot \cdot ,{b}_{in}\}, (j=1,2,\cdot \cdot \cdot ,n) $$ 1.2 评价指标权重确定
1.2.1 建立层次结构模型
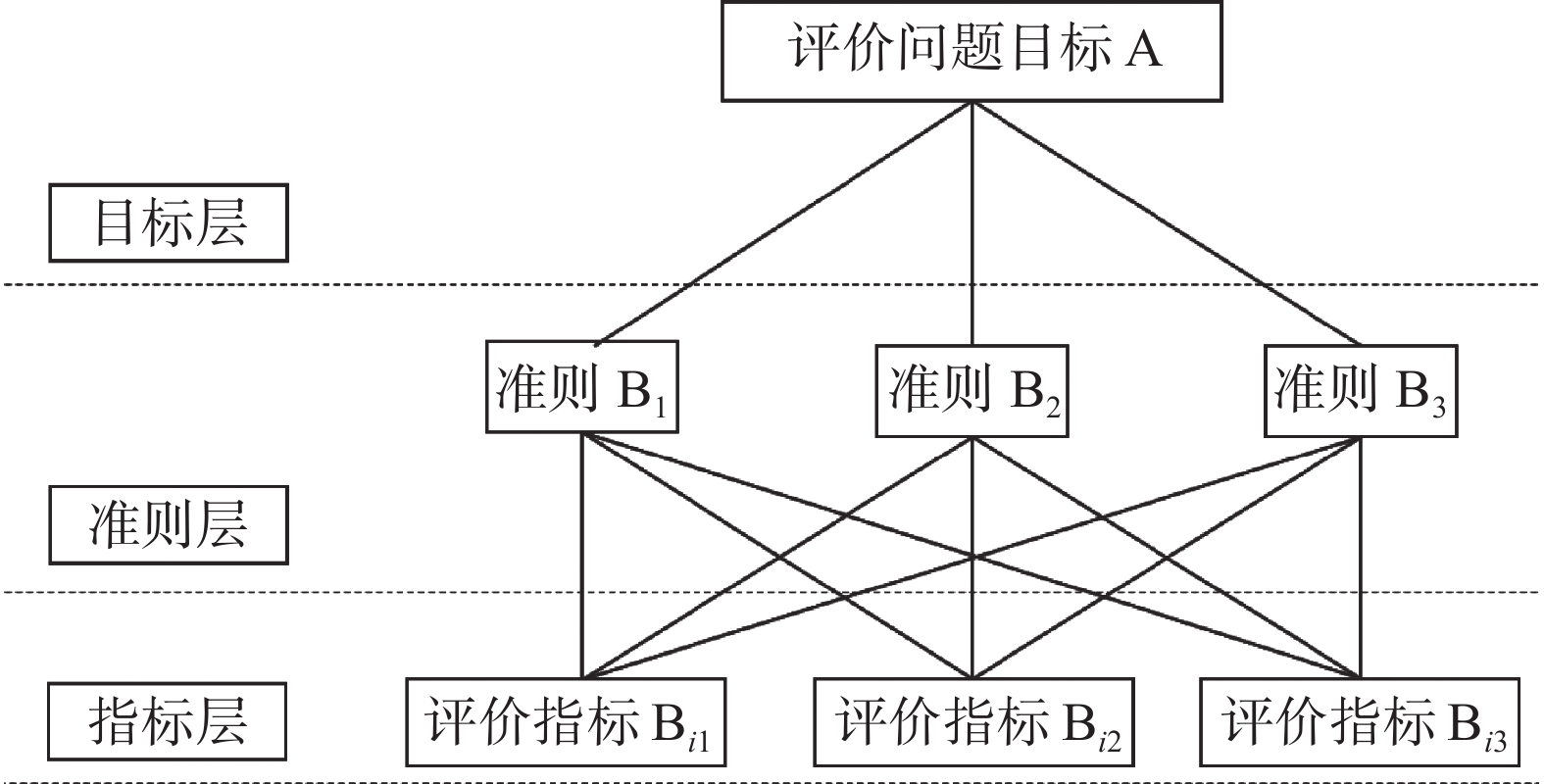
在深入分析实际问题的基础上,将相关因素自上而下分解成层次,结构模型如图1所示。
1.2.2 构造判断矩阵
按照层次结构对同一层次的评价指标进行两两重要性比较,依据相对重要程度分成若干等级,从而量化,对不同性质指标加权,弱化判断的主观性[9-10]。
构造出准则层对目标层的判断矩阵
$ {\boldsymbol{B}} = {({b_{ij}})_{n \times n}} $ ,以$ {b_{ij}} $ 表示$ {b_i} $ 对$ {b_j} $ 相对重要性数值。$$\boldsymbol{B}=\left[\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1 n} \\ b_{21} & b_{22} & \cdots & b_{2 n} \\ \vdots & \vdots & & \vdots \\ b_{n 1} & b_{n 2} & \cdots & b_{n n} \end{array}\right] $$ 指标层对准则层的判断矩阵与判断矩阵B类似。使用1−9比列标度法来对每层评价指标的重要度大小进行评判[11],其含义如表1所示。
表 1 判断矩阵标度及其含义标度wmn 含义 1 2元素比较,前者和后者同样重要 3 2元素比较,前者对后者稍微重要 5 2元素比较,前者对后者较强重要 7 2元素比较,前者对后者非常重要 9 2元素比较,前者对后者绝对重要 2,4,6,8 两者的重要度在相邻等级之间 倒数 bij和bji互为倒数 1.2.3 计算各层次指标权重
计算指标权重的方法有很多种,例如方根法、最小二乘法、特征根法和和积法[12],由于本研究的精度要求不是很高,采用方根法即可满足需求。
1)利用乘积运算方法对构建好的判断矩阵B各行向量连乘得到判断矩阵B各行指标的乘积
$ {T_i} $ 。$$ {T_i} = \prod\limits_{n - 1}^r {{{\boldsymbol{B}}_{ij}}} $$ 式中r 为判断矩阵B的阶数。
2)计算计算判断矩阵B各行指标乘积
$ {T_i} $ 的几何平均值$ \overline {{{\boldsymbol{V}}_{\mathbf{i}}}} $ 。$$ \overline {{{\boldsymbol{V}}_{\boldsymbol{i}}}} = \sqrt[n]{{{T_i}}}{\mathbf{ }} $$ 3)向量
$ \bar {\boldsymbol{V}} $ 进行归一化处理后得到各指标的权重值$ {V_i} $ 。$$ {V_i} = \frac{{\overline {{V_i}} }}{{ \displaystyle\sum\limits_{n = 1}^r {\overline {{V_i}} } }} $$ 1.2.4 进行一致性检验
为确定判断矩阵的不一致性范围,需检验各判断矩阵是否满足一致性检验要求,当判断矩阵出现初始权值互斥或阶数太高时,必须一致性检验[13]。
判断矩阵检验一致性步骤如下:
1)首先计算矩阵的最大特征值
$ {\lambda _{\max }} $ 。$$ {\lambda _{\max }} = \frac{1}{r}\sum\limits_{n = 1}^r {\frac{{{{({\boldsymbol{WX}})}_m}}}{{{{\boldsymbol{X}}_m}}}} {\text{ (}}m = 1,2,\cdots,r{\text{)}} $$ 式中:
$ {({\boldsymbol{WX}})_m} $ 为向量WX的第$ m $ 个指标,$ {{\boldsymbol{X}}_{{m}}} $ 为矩阵W的特征向量。2)对衡量判断矩阵一致性的指标CI 进行计算。CI的大小与判断矩阵符合一致性的程度成反比,CI的值越趋近于0,表示该判断矩阵符合一致性标准;CI的值越大,表示判断矩阵不一致的现象越严重。
$$ {\rm{CI}}{\text{ = }}\frac{{{\lambda _{\max }} - r}}{r} $$ 3)考虑到CI作为验证判断矩阵一致性的最终评判标准可能会存在一致性的偏离,故引入随机一致性指标CR。随机一致性指标RI与判断矩阵的阶数有关,根据判断矩阵B结束的阶数,查表得随机一致性指标RI,表2列出了1−9阶的RI取值。
表 2 随机一致性指标RI阶数 1 2 3 4 5 6 7 8 9 取值 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 把CI和CR的比值作为衡量判断矩阵一致性的最终判断依据,即检验系数CR为
$$ {\rm{CR}} = \frac{{{\rm{CI}}}}{{{\rm{RI}}}} $$ 当
${\rm{ CR}}<\text{0}\text{.1} $ 时,表示该判断矩阵满足一致性检验的要求,反之则重新构造判断矩阵,直到其符合一致性检验的要求。1.3 熵权法确定指标权重
1.3.1 建立评价指标原始矩阵
假设有
$ i $ 个评价对象和$ j $ 个评价指标所产生的原始评价矩阵为$$ {\boldsymbol{X}}=\left({x}_{m n}\right)_{i \times j}: {\boldsymbol{X}}=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 j} \\ x_{21} & x_{22} & \cdots & x_{2 j} \\ \vdots & \vdots & \ddots & \vdots \\ x_{i 1} & x_{i 2} & \cdots & x_{i j} \end{array}\right] $$ 式中为第
$ m $ 个对象对第$ n $ 个评价指标的初始评价值。1.3.2 标准化处理及指标评估值计算
由于评价体系中各指标之间存在差异,需对指标进行标准化处理,即将绝对值转化为相对值,解决各因素同质化问题[14]评价体系中,按照评价指标对评价对象的作用将其分为正指标、适度指标和逆指标3类,对于正指标来说,评价指标的数值越大越好,适度指标是数值在某一区间内最好的评价指标,逆指标是数值越小越好的评价指标,本研究借助模糊数学中的隶属函数对3类评价指标进行标准化处理[15]。
正指标标准化处理:
$$ Y_m(s)=\left\{\begin{split} & \dfrac{1}{2}+\dfrac{1}{2} \sin \left[\dfrac{{\text{π}}}{s_{m_{\max }}-s_{m_{\min }}}\left(s_m-\dfrac{s_{m_{\max }}+s_{m_{\min }}}{2}\right)\right], \\ &\qquad\qquad \;\; s_{m_{\min }}<s_m<s_{m_{\max }} \\&0,\;\; \text { 其他 } \end{split} \right.$$ 式中:
$ {Y_m}(s) $ 为第m项正指标标准化处理后的评价值,$ {s_m} $ 为第m项正指标的初始值,$ {s_{{m_{\max }}}} $ 为第m项正指标的最大值,$ {s_{{m_{\min }}}} $ 为第m项正指标的最小值。适度指标标准化处理:
$$ Y_m(s)=\left\{\begin{array}{l} \dfrac{1}{2}+\dfrac{1}{2} \sin \left[\dfrac{{\text{π}}}{s_{m_{\mathrm{mod}}}-s_{m_{\mathrm{min}}}}\left(s_m-\dfrac{s_{m_{\mathrm{mod}}}+s_{m_{\mathrm{min}}}}{2}\right)\right], \\\qquad\qquad\;\; s_{m_{\mathrm{min}}}<s_{{ }_m}<s_{m_{\mathrm{mod}}} \\ \dfrac{1}{2}-\dfrac{1}{2} \sin \left[\dfrac{{\text{π}}}{s_{m_{\mathrm{max} }}-s_{m_{\mathrm{mod}}}}\left(s_m-\dfrac{s_{m_{\mathrm{max}}}+s_{m_{\mathrm{mod}}}}{2}\right)\right] ,\\\qquad\qquad\;\; s_{m_{\mathrm{mod}}}<s_m <s_{m_{\mathrm{max}}} \\ 0, \;\; \text { 其 他 } \end{array}\right. $$ 式中
$ {s_{{m_{\bmod }}}} $ 为第m项适度指标的最佳值。逆指标标准化处理:
$$Y_m(s)=\left\{\begin{array}{l} \dfrac{1}{2}-\dfrac{1}{2} \sin \left[\dfrac{{\text{π}}}{s_{\max }-s_{\min }}\left(s_m-\dfrac{s_{\max }+s_{\min }}{2}\right)\right], \\\qquad\qquad\;\; s_{\min }<s_m<s_{\max } \\ 0, \;\; \text { 其他 } \end{array}\right. $$ 在设计评价体系中客观指标直接标准化处理,主观指标采用集值统计法转化为客观指标,进行标准化处理。假设有k个专家对设计评价体系中的n个主观指标进行打分,其中第m个专家对第j个主观指标的评价区间为
$ G(U) $ ,可以得到k个评价区间形成的集值分值u落在k个评价区间的概率用样本落影函数$ \bar X(U) $ ,表示如下:$$ \bar X(U) = \frac{1}{k}\sum\limits_{m = 1}^k {x[u_1^m,u_2^m](u),{\text{ 0}} \leqslant } \bar X(U) \leqslant 1 $$ $$ x[{u}_{1}^{m},{u}_{2}^{m}](u)=\left\{\begin{array}{l} 1,\;\;{u}_{1}^{m}\le u\le {u}_{2}^{m}\text{ }\\ 0,\text{ }其他\end{array} \right.$$ 计算其集值统计序列U的重心,得到该指标的评估值,集值统计序列的U重心
$ G(U) $ 为$$ G(U) = \frac{{ \displaystyle\sum\limits_{m = 1}^k {[{{(u_2^m)}^2} - {{(u_1^m)}^2}]} }}{{2 \displaystyle\sum\limits_{m = 1}^k {(u_2^m - u_1^m)} }} $$ 1.3.3 计算各个评价指标的熵权值
1)计算第n个评价指标的指标特征值比重
$ {p_{mn}} $ 。$$ {p_{mn}} = \frac{{x_{_{mn}}^\prime}}{{ \displaystyle\sum\nolimits_{m = 1}^i {x_{_{mn}}^\prime} }} $$ 2)计算第n个评价指标的熵值
$ {e_n} $ 。$$ {e_n} = - k\sum\nolimits_{m = 1}^i {{p_{mn}} \times \ln {p_{mn}}} $$ 式中
$ k = \dfrac{1}{{\ln i}} $ ;当$ {p_{mn}} $ =0时,通常令$ {p_{mn}} \times \ln {p_{mn}} $ =0。3)计算第n个评价指标的熵权值
$ {w_n} $ 。$$ {w_n} = \frac{{1 - {e_n}}}{{ \displaystyle\sum\nolimits_{n = 1}^j {(1 - {e_n})} }} $$ 1.3.4 熵权层次分析法确定指标最终权重
熵权层次分析法确定的指标组合权重记为y,数学公式为
$$ y = \rho W + (1 - \rho )w $$ (1) 式中
$ \rho $ 为分辨系数,本文取0.5。1.4 居住舱室设计方案综合评价
根据准则层各指标标准化后的数值,结合熵权层次分析法确定的指标权重,最后计算得出居住舱室设计方案的评价值,并对各个方案进行排序,从而得出最优设计方案。
2. 邮轮居住舱室综合评价案例分析
邮轮居住舱室设计的综合评价是多态、模糊性问题,在建立评价指标体系的时候需要考虑“人−机−环境”综合影响因素,为了检验本文熵权层次分析法的可行性,本文对邮轮居住舱室的不同布局及综合环境等多指标数据进行具体分析。
2.1 邮轮居住舱室设计评价指标体系建立
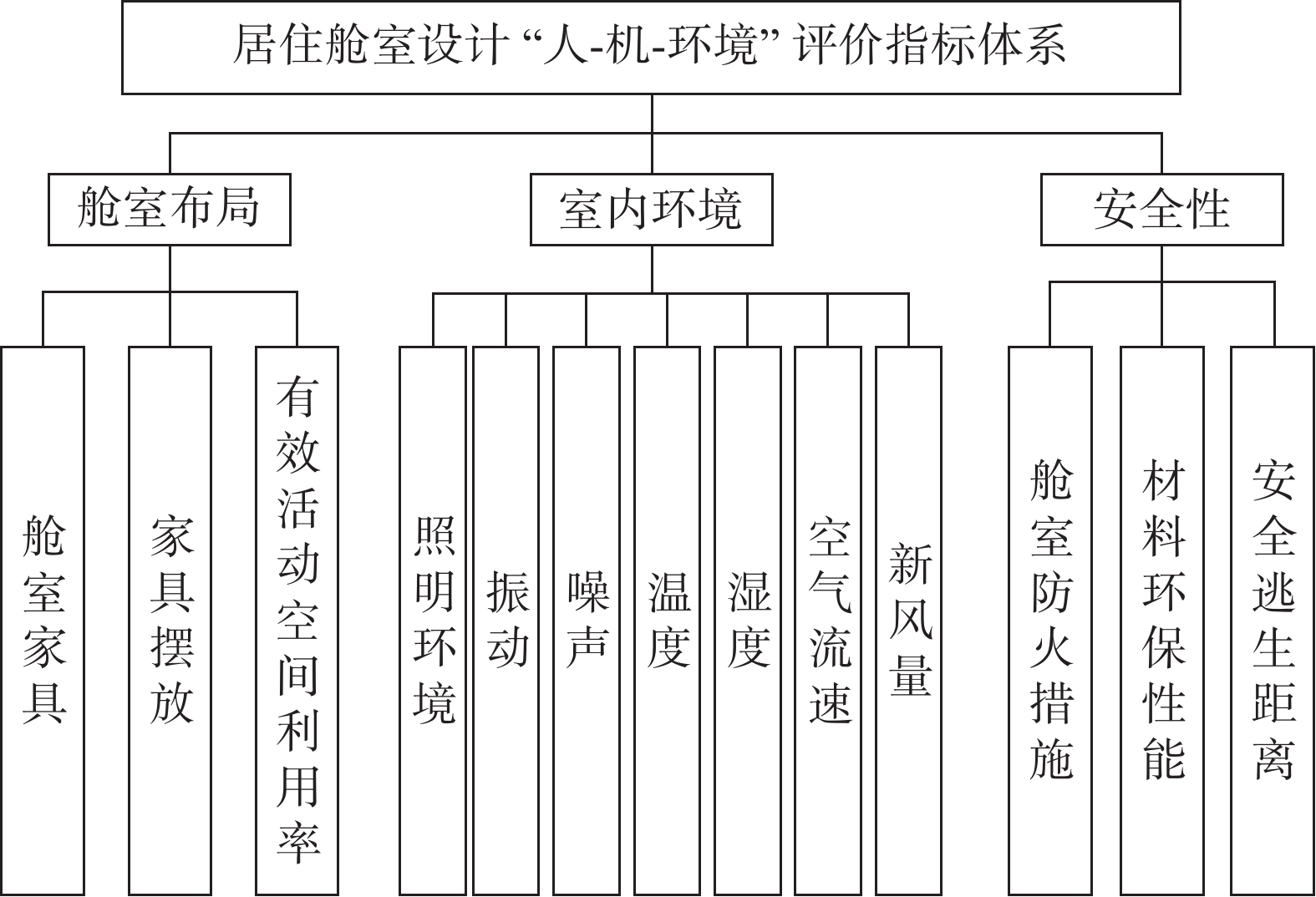
居住舱室设计“人−机−环境”评价指标体系是对乘客体验、舱室家具和舱室环境这些评价对象进行详细分析从而确立的。由于居住舱室中的“人−机−环境”系统存在一些难以定量化且互相关联的指标,需要从多角度多目标构建居住舱室设计的评价指标体系。因此,运用人因工程学理论分析了邮轮居住舱室中的“人−机−环境”系统,从舱室布局、室内环境和安全性3个方面挑选影响居住舱室设计的评价指标,其中,舱室家具、家具摆放、舱室防火措施、材料环保性能属于客观指标,不易量化,采用集值统计法转化为客观指标,再同余下的二级指标使用熵权层次分析法进行评价。最终建立居住舱室设计“人−机−环境”评价指标体系。
2.2 构建综合评价的评价集
根据居住舱室设计“人−机−环境”评价指标体系,确定评价因素集。
首层评价指标:
$$ U=\left\{{u}_{1},{u}_{2},{u}_{3}\right\}=\left\{舱室布局,室内环境,安全性\right\}$$ 第2层评价指标:
$$ {u}_{1}=\left\{{u}_{11},{u}_{12},{u}_{13}\right\}=\left\{\begin{array}{l}舱室家具,家具摆放,\\有效活 动空间利率\end{array}\right\} $$ $$ {u}_{2} = \left\{\begin{array}{l}{u}_{21},{u}_{22},{u}_{23},{u}_{24},\\ {u}_{25},{u}_{26},{u}_{27}\end{array}\right\} = \left\{\begin{array}{l}照明环境,振动,噪\\声, 温度,湿度,空气\\ 流速,新风量\end{array}\right\} $$ $$u_3=\left\{u_{31}, u_{32}, u_{33}\right\}=\left\{\begin{array}{l} \text { 舱室防火措施,材料环保性 } \\ \text { 能, 安全逃生距离 } \end{array}\right\} $$ 2.3 评价指标权重确定
采用层次分析法建立的居住舱室设计评价指标体系按照目标层、准则层以及指标层等3个层次进行分解结构如图2所示。
2.3.1 各层指标权重确定
对同一指标层的各个因素根据1-9标度法两两比较,构造判断矩阵。首先邀请业内专家按照比列标度法对3个居住舱室设计评价体系层次结构指标进行合理性评估,所构造的判断矩阵如表3所示。
表 3 准则层判断矩阵指标名称 舱室布局 室内环境 安全性 舱室布局 1 1/2 1/3 室内环境 2 1 1/2 安全性 3 2 1 根据层次分析法计算,准则层
$ {b_i} $ 、$ {\lambda _{\max }} $ 、CI、CR分别为:$ {b_{\text{i}}} $ =[0.1634 0.2970 0.5396],$ {\lambda _{\max }} = 3.009\;2 $ ,$ {\rm{CI}} = 0.004\;6 $ ,${\rm{ CR}} = 0.007\;9 $ 。以准则层中舱室布局为例,业内专家按照比列标度法对其指标层的3个评价指标构造判断矩阵。
$$ {{\boldsymbol{M}}_{B1}} = \left[ {\begin{array}{*{20}{c}} 1&{1/5}&{1/3} \\ 5&1&2 \\ 3&{1/2}&1 \end{array}} \right]$$ 根据上述的方法对判断矩阵
$ {{\boldsymbol{M}}_{B1}} $ 进行计算得$ {\rm{CI}} = 0.001\;9 $ ,$ {\rm{CR }}= 0.003\;3 < 0.1 $ ,室内环境最大特征值$ {\lambda _{\max }} = 7.788\;7 $ ,${\rm{ CI}} = 0.131\;5 $ ,${\rm{ CR}} = 0.099\;6 < 0.1 $ ,安全性最大特征值为$ {\lambda _{\max }} = 3.081\;3 $ ,$ {\rm{CI}} = 0.040\;7 $ ,$ {\rm{CR}} = 0.070\;2 < 0.1 $ ,均满足一致性检验要求。综上所述,邮轮居住舱室设计评价体系层次结构模型所构造的判断矩阵均符合一致性检验要求,上文只列出了部分指标评判结果,但在研究时对各层次指标权值进行了详细计算,且各层次指标权重值如表4所示。
表 4 各层次指标权重值准则层 权重W 指标层 权重W 整体权重W 舱室布局 0.1634 舱室家具 0.1095 0.0179 家具摆放 0.5815 0.0950 有效活动空间利用率 0.3090 0.0505 室内环境 0.2970 照明环境 0.0460 0.0137 振动 0.0794 0.0236 噪声 0.2835 0.0842 温度 0.1298 0.0386 湿度 0.1785 0.0530 空气流速 0.1296 0.0385 新风量 0.1532 0.0455 安全性 0.5396 舱室防火措施 0.5584 0.3013 材料环保性能 0.0658 安全逃生距离 0.3196 0.1725 2.3.2 熵权法确定指标权重
本文选取10种不同的邮轮居住舱室设计方案构造评价矩阵,其中,准则层1舱室家具和家具摆放指标属于主观指标,利用集值统计法转化为客观指标。以舱室家具指标为例,邀请5位有丰富相关邮轮设计经验专家对10种居住舱室设计方案的舱室家具指标进行打分,并把分数划分在5个分数区间,计算出综合得分,舱室家具指标的专家打分值和综合得分见表5。家具摆放指标同舱室家具指标类似,有效活动空间利用率指标见表6。
表 5 舱室家具指标专家打分值和综合得分方案 专家1 专家2 专家3 专家4 专家5 综合得分 方案1 [0.70,0.75] [0.65,0.72] [0.61,0.67] [0.70,0.75] [0.60,0.70] 0.6783 方案2 [0.62,0.70] [0.65,0.75] [0.58,0.63] [0.63,0.68] [0.56,0.64] 0.6494 方案3 [0.42,0.48] [0.45,0.50] [0.52,0.58] [0.41,0.50] [0.46,0.54] 0.4844 方案4 [0.21,0.26] [0.24,0.32] [0.30,0.35] [0.26,0.32] [0.25,0.32] 0.2831 方案5 [0.64,0.70] [0.62,0.68] [0.70,0.75] [0.68,0.76] [0.65,0.73] 0.6917 方案6 [0.45,0.55] [0.51,0.57] [0.48,0.55] [0.50,0.57] [0.54,0.62] 0.5324 方案7 [0.42,0.48] [0.40,0.50] [0.45,0.50] [0.52,0.58] [0.46,0.53] 0.4806 方案8 [0.66,0.75] [0.60,0.65] [0.72,0.78] [0.64,0.70] [0.65,0.75] 0.6942 方案9 [0.40,0.45] [0.46,0.52] [0.51,0.58] [0.42,0.48] [0.45,0.55] 0.4876 方案10 [0.47,0.53] [0.45,0.55] [0.50,0.55] [0.44,0.52] [0.48,0.55] 0.5019 表 6 准则层1各指标的原始数据方案 舱室家具 家具摆放 有效活动空间利用率/% 方案1 0.6783 0.4858 43.37 方案2 0.6494 0.8971 65.61 方案3 0.4844 0.6787 55.21 方案4 0.2831 0.6938 56.42 方案5 0.6917 0.4853 43.14 方案6 0.5324 0.5092 47.25 方案7 0.4806 0.6778 54.80 方案8 0.6942 0.8869 63.16 方案9 0.4876 0.7059 60.22 方案10 0.5019 0.6935 56.28 对准则层1舱室家具中各指标均属于正指标类型,各指标数值进行标准化处理如表7所示。
表 7 准则层1各指标标准化后的数值方案 舱室家具 家具摆放 有效活动空间利用率% 方案1 0.7657 0.4777 0.3966 方案2 0.7262 0.9741 0.7355 方案3 0.4755 0.7662 0.5815 方案4 0.1851 0.7860 0.6002 方案5 0.7832 0.4769 0.3931 方案6 0.5508 0.5144 0.4569 方案7 0.4695 0.7650 0.5751 方案8 0.7865 0.9688 0.7009 方案9 0.4805 0.8013 0.6578 方案10 0.5030 0.7856 0.5980 同理对准则2和准则层3中各指标数值各自标准化处理,结合指标标准化后的数据计算不同设计方案中的准则层各指标评价值,如表8所示。
表 8 准则层指标评价值序号 舱室布局评价 室内环境评价 安全性评价 方案1 0.5053 0.6748 0.4565 方案2 0.8360 0.9514 0.9841 方案3 0.6395 0.5983 0.6767 方案4 0.5968 0.6785 0.4544 方案5 0.5072 0.7660 0.4629 方案6 0.5004 0.7139 0.8530 方案7 0.6354 0.6500 0.6453 方案8 0.8330 0.7115 0.8274 方案9 0.6839 0.7348 0.6477 方案10 0.6595 0.5746 0.6965 根据熵权法确定指标权重的基本步骤确定邮轮居住舱室设计评价指标体系中各指标的权重值如表9所示。
表 9 熵权法确定指标权重准则层 权重w 指标名称 权重w 整体权重w 舱室布局 0.3726 舱室家具 0.2002 0.0746 家具摆放 0.4291 0.1599 有效活动空间利用率 0.3707 0.1381 室内环境 0.2648 照明环境 0.0773 0.0205 振动 0.1693 0.0448 噪声 0.2079 0.0551 温度 0.1314 0.0348 湿度 0.1167 0.0309 空气流速 0.1094 0.0290 新风量 0.1880 0.0498 安全性 0.3626 舱室防火措施 0.4548 0.1649 材料环保性能 0.2809 0.1019 安全逃生距离 0.2643 0.0958 2.3.3 熵权层次分析法确定指标最终权重
把使用层次分析法计算得到的各指标权重W和通过熵权法计算得到的各指标权重w代入式(1),计算得到的各指标组合权重y如表10所示。
表 10 熵权层次分析法确定指标权重值准则层 权重y 指标层 权重y 舱室布局 0.2681 舱室家具 0.0463 家具摆放 0.1275 有效活动空间利用率 0.0943 室内环境 0.278 照明环境 0.0171 振动 0.0342 噪声 0.0697 温度 0.0367 湿度 0.0420 空气流速 0.0338 新风量 0.0447 安全性 0.4521 舱室防火措施 0.2331 材料环保性能 0.0839 安全逃生距离 0.1342 2.3.4 AHP、熵权法、熵权层次分析法确定指标权重对比分析
利用AHP、熵权法、熵权层次分析法对确定的各指标权重值进行对比,见表11。
表 11 AHP、熵权法、熵权层次分析法确定指标权重对比指标名称 AHP
权重W熵权法
权重w熵权层次分析法
权重y舱室家具 0.0179 0.0746 0.0463 家具摆放 0.0950 0.1599 0.1275 有效活动空间利用率 0.0505 0.1381 0.0943 照明环境 0.0137 0.0205 0.0171 振动 0.0236 0.0448 0.0342 噪声 0.0842 0.0551 0.0697 温度 0.0386 0.0348 0.0367 湿度 0.0530 0.0309 0.0420 空气流速 0.0385 0.0290 0.0338 新风量 0.0455 0.0498 0.0477 舱室防火措施 0.3013 0.1649 0.2331 材料环保性能 0.0658 0.1019 0.0839 安全逃生距离 0.1725 0.0958 0.1342 对于上述案例分析,对比表11中3种方法确定的指标权重数值,各方法确定权重数值差异较大,这是因为在指标权重确定过程中,各方法特性以及指标属性不同,例如:准则层1中舱室家具、家具摆放、舱室防火措施指标,准则层3中舱室防火措施、材料环保性能指标属于专家打分项, 利用AHP可以有效减少个人主观因素带来的弊端,但是AHP是一种主观随意性大的赋予权重值的方法,在体现科学性方面有一定的缺陷 。对于邮轮的居住舱室设计的综合评价是一个涉及多指标的任务,单一的使用主观获得的权重可操作性不强,并在权重分配上没有考虑专家评价过程中的不确定性和指标得分的差异程度,然而,熵权法是一种以客观为主的赋权重值的方法,能够使得评价结果具有较强的客观性,但其却未体现出专家实践积累经验知识和意见,有时候获取的权重值可能不符合指标的实际重要性程度。
基于上述的分析,层次分析法的优点在于凭借相关专家对评价对象的认识与分析,为能得到较为客观准确的评价结果打下基础,熵权法不仅可以对指标数据进行计算获得指标的权重,还能有效去除主观因素的干扰。所以,分别选择层次分析法和熵权法来确定邮轮居住舱室设计评价指标权重。此外,考虑到居住舱室设计评价是一个复杂的多属性评价问题且存在一系列相互关联的模糊性指标,单独使用层次分析法和熵权法都会有一定的局限性,选择熵权法和层次分析法相结合的方法来确定指标权重,通过熵权层次分析法确定的指标权重既包含了一定倾向的主观意愿,又客观反应了指标数据真实有效。
2.4 居住舱室设计方案综合评价
根据各指标标准化后的数值并结合上节熵权层次分析法确定的指标权重计算得到居住舱室设计方案的综合评价值如表12所示。
表 12 居住舱室设计方案综合评价值设计方案 综合评价值 设计方案排序 设计方案1 0.5056 10 设计方案2 0.9380 1 设计方案3 0.6516 6 设计方案4 0.5635 8 设计方案5 0.5331 9 设计方案6 0.7142 3 设计方案7 0.6553 5 设计方案8 0.8012 2 设计方案9 0.6634 4 设计方案10 0.6481 7 由各居住舱室设计方案评价结果可以看出,设计方案2远优于其他设计方案,所以选择设计方案2来对居住舱室进行设计。
3. 结论
邮轮居住舱室设计涉及多专业、多学科,因此居住舱室设计方案的评价是一个复杂模糊的评价问题。本文从邮轮居住舱室设计方案评价问题,提出了基于熵权层次分析的综合评价方法。
1)应用人因工程学理论,从舱室家具、室内环境和安全性3个方面选取影响居住舱室设计的指标并建立了居住舱室设计“人−机−环境”评价指标体系。
2)对常用的评价方法进行改进,结合熵权法和层次分析法的优点建立了基于熵权层次分析法的居住舱室设计评价模型,针对10种不同的居住舱室设计方进行了综合评价,结果表明该方法具有一定的可行性。
3)熵权层次分析法不仅考虑了居住舱室设计的主观因素,还把客观因素也予以了考虑,能充分挖掘出设计方案中各指标数据的客观信息,帮助评价者做出较为准确合理的评价决策。
-
表 1 判断矩阵标度及其含义
标度wmn 含义 1 2元素比较,前者和后者同样重要 3 2元素比较,前者对后者稍微重要 5 2元素比较,前者对后者较强重要 7 2元素比较,前者对后者非常重要 9 2元素比较,前者对后者绝对重要 2,4,6,8 两者的重要度在相邻等级之间 倒数 bij和bji互为倒数 表 2 随机一致性指标RI
阶数 1 2 3 4 5 6 7 8 9 取值 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 表 3 准则层判断矩阵
指标名称 舱室布局 室内环境 安全性 舱室布局 1 1/2 1/3 室内环境 2 1 1/2 安全性 3 2 1 表 4 各层次指标权重值
准则层 权重W 指标层 权重W 整体权重W 舱室布局 0.1634 舱室家具 0.1095 0.0179 家具摆放 0.5815 0.0950 有效活动空间利用率 0.3090 0.0505 室内环境 0.2970 照明环境 0.0460 0.0137 振动 0.0794 0.0236 噪声 0.2835 0.0842 温度 0.1298 0.0386 湿度 0.1785 0.0530 空气流速 0.1296 0.0385 新风量 0.1532 0.0455 安全性 0.5396 舱室防火措施 0.5584 0.3013 材料环保性能 0.0658 安全逃生距离 0.3196 0.1725 表 5 舱室家具指标专家打分值和综合得分
方案 专家1 专家2 专家3 专家4 专家5 综合得分 方案1 [0.70,0.75] [0.65,0.72] [0.61,0.67] [0.70,0.75] [0.60,0.70] 0.6783 方案2 [0.62,0.70] [0.65,0.75] [0.58,0.63] [0.63,0.68] [0.56,0.64] 0.6494 方案3 [0.42,0.48] [0.45,0.50] [0.52,0.58] [0.41,0.50] [0.46,0.54] 0.4844 方案4 [0.21,0.26] [0.24,0.32] [0.30,0.35] [0.26,0.32] [0.25,0.32] 0.2831 方案5 [0.64,0.70] [0.62,0.68] [0.70,0.75] [0.68,0.76] [0.65,0.73] 0.6917 方案6 [0.45,0.55] [0.51,0.57] [0.48,0.55] [0.50,0.57] [0.54,0.62] 0.5324 方案7 [0.42,0.48] [0.40,0.50] [0.45,0.50] [0.52,0.58] [0.46,0.53] 0.4806 方案8 [0.66,0.75] [0.60,0.65] [0.72,0.78] [0.64,0.70] [0.65,0.75] 0.6942 方案9 [0.40,0.45] [0.46,0.52] [0.51,0.58] [0.42,0.48] [0.45,0.55] 0.4876 方案10 [0.47,0.53] [0.45,0.55] [0.50,0.55] [0.44,0.52] [0.48,0.55] 0.5019 表 6 准则层1各指标的原始数据
方案 舱室家具 家具摆放 有效活动空间利用率/% 方案1 0.6783 0.4858 43.37 方案2 0.6494 0.8971 65.61 方案3 0.4844 0.6787 55.21 方案4 0.2831 0.6938 56.42 方案5 0.6917 0.4853 43.14 方案6 0.5324 0.5092 47.25 方案7 0.4806 0.6778 54.80 方案8 0.6942 0.8869 63.16 方案9 0.4876 0.7059 60.22 方案10 0.5019 0.6935 56.28 表 7 准则层1各指标标准化后的数值
方案 舱室家具 家具摆放 有效活动空间利用率% 方案1 0.7657 0.4777 0.3966 方案2 0.7262 0.9741 0.7355 方案3 0.4755 0.7662 0.5815 方案4 0.1851 0.7860 0.6002 方案5 0.7832 0.4769 0.3931 方案6 0.5508 0.5144 0.4569 方案7 0.4695 0.7650 0.5751 方案8 0.7865 0.9688 0.7009 方案9 0.4805 0.8013 0.6578 方案10 0.5030 0.7856 0.5980 表 8 准则层指标评价值
序号 舱室布局评价 室内环境评价 安全性评价 方案1 0.5053 0.6748 0.4565 方案2 0.8360 0.9514 0.9841 方案3 0.6395 0.5983 0.6767 方案4 0.5968 0.6785 0.4544 方案5 0.5072 0.7660 0.4629 方案6 0.5004 0.7139 0.8530 方案7 0.6354 0.6500 0.6453 方案8 0.8330 0.7115 0.8274 方案9 0.6839 0.7348 0.6477 方案10 0.6595 0.5746 0.6965 表 9 熵权法确定指标权重
准则层 权重w 指标名称 权重w 整体权重w 舱室布局 0.3726 舱室家具 0.2002 0.0746 家具摆放 0.4291 0.1599 有效活动空间利用率 0.3707 0.1381 室内环境 0.2648 照明环境 0.0773 0.0205 振动 0.1693 0.0448 噪声 0.2079 0.0551 温度 0.1314 0.0348 湿度 0.1167 0.0309 空气流速 0.1094 0.0290 新风量 0.1880 0.0498 安全性 0.3626 舱室防火措施 0.4548 0.1649 材料环保性能 0.2809 0.1019 安全逃生距离 0.2643 0.0958 表 10 熵权层次分析法确定指标权重值
准则层 权重y 指标层 权重y 舱室布局 0.2681 舱室家具 0.0463 家具摆放 0.1275 有效活动空间利用率 0.0943 室内环境 0.278 照明环境 0.0171 振动 0.0342 噪声 0.0697 温度 0.0367 湿度 0.0420 空气流速 0.0338 新风量 0.0447 安全性 0.4521 舱室防火措施 0.2331 材料环保性能 0.0839 安全逃生距离 0.1342 表 11 AHP、熵权法、熵权层次分析法确定指标权重对比
指标名称 AHP
权重W熵权法
权重w熵权层次分析法
权重y舱室家具 0.0179 0.0746 0.0463 家具摆放 0.0950 0.1599 0.1275 有效活动空间利用率 0.0505 0.1381 0.0943 照明环境 0.0137 0.0205 0.0171 振动 0.0236 0.0448 0.0342 噪声 0.0842 0.0551 0.0697 温度 0.0386 0.0348 0.0367 湿度 0.0530 0.0309 0.0420 空气流速 0.0385 0.0290 0.0338 新风量 0.0455 0.0498 0.0477 舱室防火措施 0.3013 0.1649 0.2331 材料环保性能 0.0658 0.1019 0.0839 安全逃生距离 0.1725 0.0958 0.1342 表 12 居住舱室设计方案综合评价值
设计方案 综合评价值 设计方案排序 设计方案1 0.5056 10 设计方案2 0.9380 1 设计方案3 0.6516 6 设计方案4 0.5635 8 设计方案5 0.5331 9 设计方案6 0.7142 3 设计方案7 0.6553 5 设计方案8 0.8012 2 设计方案9 0.6634 4 设计方案10 0.6481 7 -
[1] 龚昌奇. 船舶造型及舱室设计方案的模糊综合评价[J]. 武汉交通科技大学报, 1996(5): 74−78. [2] 李晓文, 朱兆一, 熊云峰, 等. 基于信息集成算子的舰船舱室设计方案评估[J]. 大连理工大学学报, 2018, 58(4): 357−362. doi: 10.7511/dllgxb201804004 [3] 姚竞争, 马青, 孙洪源, 等. AHP法的邮轮生活舱室评价[J]. 船舶工程, 2021, 43(6): 56−60. [4] 陈思旭, 商蕾, 汪敏, 等. 基于模糊层次分析的邮轮客舱设计综合评价研究[J]. 舰船科学技术, 2021, 43(21): 68−73. [5] 马青, 陈哲, 孙洪源, 等. 基于AHP与TOPSIS法的游轮居住舱室舒适性评价[J]. 山东交通学院学报, 2022, 30(1): 44−51. doi: 10.3969/j.issn.1672-0032.2022.01.007 [6] 王清源, 潘旭海. 熵权法在重大危险源应急救援评估中的应用[J]. 南京工业大学学报, 2011, 33(3): 87−92. [7] 马莎, 刘聪聪, 张润华. 基于熵权–层次分析法的地下空间适宜性评价[J]. 科学技术与工程, 2021, 21(23): 10013−10020. doi: 10.3969/j.issn.1671-1815.2021.23.047 [8] 马相鹏, 高海波, 林治国, 等. 基于AHP–熵权法的极地探险娱乐设备选型[J]. 应用科技, 2021, 48(4): 18−22. doi: 10.11991/yykj.202009002 [9] 王明年, 郭晓晗, 于丽, 等. 基于AHP–熵权法的铁路隧道单双洞选型决策研究[J]. 铁道工程学报, 2019, 36(11): 51−56. doi: 10.3969/j.issn.1006-2106.2019.11.009 [10] 李若皙, 文勇, 晓冬. 船舶风险控制方案的层次分析–模糊综合评价[J]. 中国航海, 2019, 42(1): 68−72. doi: 10.3969/j.issn.1000-4653.2019.01.014 [11] 文静, 李方正, 董浩, 等. 层次分析法中两因素间标度值确定方法的探讨[C]//第十二届全国体育科学大会论文摘要汇编——墙报交流(体育统计分会). 日照: 中国体育科学学会, 2022: 29-30. [12] 程仕平, 陈明, 殷悦. AHP层次分析与K-means聚类相结合的博士学位论文评价指标权重确定方法[J]. 创新与创业教育, 2021, 12(5): 72−76. doi: 10.3969/j.issn.1674-893X.2021.05.011 [13] CHENG Qiyue, QIU Wanhua. Relationentropy and transferable entropy think of aggregation on group decision making[J]. Journal of systems science and systems engineering, 2002, 11(1): 13−1. [14] 欧阳, 正江. 基于熵权集对分析的船舶海上应急能力评价[J]. 大连海事大学学报, 2014(4): 2−36. doi: 10.3969/j.issn.1006-7736.2014.04.008 [15] 梁鸿博. 基于AHP-TOPSIS的城市排水管材选用评价方法研究[D]. 重庆: 重庆大学, 2021.







 下载:
下载: