Winding temperature prediction of primary pump motors based on CEEMDAN-GRU
-
摘要: 针对核电站主泵电机绕组温度的预测问题，提出了基于自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)和门控循环单元(gated recurrent unit，GRU)的预测模型。首先使用CEEMDAN对采集到的绕组温度序列进行分解，经过分量重构得到其高、低频分量和趋势项，在此基础上分别构建各分量的GRU预测模型，将各分量的预测结果叠加集成得到绕组温度的整体预测值。仿真结果表明，与传统的循环神经网络(recurrent neural network，RNN)、长短期记忆(long short-term memory，LSTM)模型和GRU模型相比，本文提出的预测模型在多元评价指标方面均优于其他模型，具有更高的预测精度，验证了该模型的可行性。Abstract: A prediction model based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and gated recurrent unit (GRU) is proposed to predict the winding temperature of primary pump motors in the nuclear power plant. Firstly, CEEMDAN is used to decompose the collected winding temperature series, and its high and low frequency components and trend items are obtained through component reconstruction. On this basis, the GRU prediction model of each component is respectively constructed, and the prediction results of each component are superimposed and integrated to obtain the overall predicted value of the winding temperature. The simulation results show that compared with the traditional recurrent neural network (RNN), long short-term memory (LSTM) model and GRU model, the prediction model proposed in this paper is superior to other models in terms of multiple evaluation indicators, and it has higher prediction accuracy. Thereby, the feasibility of the model is verified.
-
核主泵是反应堆一回路压力边界的重要组成部分之一，是反应堆及一回路系统中最关键的旋转设备，其主要功能是将一回路中的冷却剂进行升压，克服冷却剂在设备和管道中的流动阻力，促使其将堆芯中产生的热量传递到蒸汽发生器，保证堆芯的正常冷却，因此保证主泵电机长期、安全、稳定、可靠地运行至关重要。而在夏季时，由于环境温度升高，主泵电机定子绕组运行温度会接近其跳泵限值[1]，对机组构成了潜在威胁，需要对其定子绕组温度进行预测，以便工作人员判断其运行趋势并且采取相应的安全保护措施。
对于设备运行参数，传统的预测方法主要有3类：回归分析法，此方法的计算原理和结构形式都比较简单，预测速度快，但对复杂多变的数据预测精度较低；整合移动平均自回归(autoregressive integrated moving average, ARIMA)模型，利用差分对原始序列进行平稳化，根据序列特性求得相关参数来进行预测，此模型较为简单，只需要原始序列产生的变量而不需要其他外生变量，但其要求原始序列或原始序列差分后的序列是稳定的，并且无法捕捉非线性关系；机器学习模型，此类方法主要以当前时间点的数据特征进行建模预测，未考虑数据的时序性，在对基于时间序列的数据进行预测时误差较大[2]。
近年来，众多的国内外学者开始将深度学习用于时间序列的预测中。王鑫等[3]利用长短期记忆(long short-term memory, LSTM)神经网络对复杂系统的历史故障数据进行时间序列预测，王祥雪等[4]通过对LSTM网络逐层构建和精细化调参来预测短时交通流，并且可以根据预测精度进行参数的自适应更新。牛哲文等[5]在传统门控循环单元(gated recurrent unit, GRU)神经网络的基础上融合了卷积神经网络(convolutional neural networks, CNN)来预测风电场的短期风功率，并引入随机失活(dropout)技术减少模型的过拟合现象。针对时间序列数据固有的不平稳导致预测精度较低的问题，很多研究人员引入模态分解方法，去除一部分噪声，再对不同尺度下的分量分别预测[6-12]。相较于上述应用场景，时间序列预测方法在核电站中的应用较少，武云云等[13]将ARIMA模型应用于环境放射性水平的预测，结果表明预测值与实际值基本一致。张思原等[2]提出了基于LSTM的多特征融合多步状态预测模型，对蒸汽发生器的蒸汽压力进行预测，验证了该方法的有效性。朱少民等[14]结合ARIMA和LSTM的优势，利用组合模型对核电厂主泵的运行状态进行预测，结果表明该方法具有更加稳健的预测性能。
本文采用自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)与门控循环单元结合的模型来对时间序列进行预测。相比于集合经验模态分解(ensemble empirical mode decomposition, EEMD)，该方法在分解过程中添加的是白噪声经过经验模态分解(empirical mode decomposition, EMD)得到的各阶本征模态函数(intrinsic mode functions, IMF)，最后重构信号中的噪声残余更小，降低了筛选次数，同时也避免了各模态分量结果差异造成的集合平均难以对齐的问题。利用GRU神经网络对分解重构得到的各分量分别建立相应的预测模型，对各预测结果进行叠加从而得到最终的预测结果。
1. CEEMDAN的基本原理
EMD是一种基于信号局部特征自适应的信号分解方法，它根据信号的局部特征尺度，按频率由高到低将复杂的非线性、非平稳信号分解为有限个本征模态函数之和。然而大量的实践证明，EMD分解方法存在的模态混叠现象限制了其应用。随后Wu等[15]提出了对此问题的改进措施——EEMD，即给原始信号添加均匀分布的白噪声，使得不同尺度的信号会自动映射到合适的参考尺度上。虽然EEMD抑制了模态混叠，但是对原序列添加的白噪声仍有可能残存于分解后的模态分量中，影响了后续信号的进一步分析。在此基础上，Torres等[16]提出在分解时添加自适应白噪声，有效降低了EEMD重构时的误差。其具体步骤为：
1）对原始序列
$ {f(t)} $ 添加白噪声序列，得到含有噪声的信号序列$ {{f_i}(t)} $ ，对此序列进行N次EMD分解后取算术平均值得到第1个模态分量${ {F_{{\text{IMF}}}}_1(t) }$ ：$$ {f_i}(t) = f(t) + {\varepsilon _0}{\omega _i}(t) $$ $$ {F_{{\text{IMF}}}}_1(t) = \frac{1}{N}\sum\limits_{i = 1}^N {{F_{{\text{IMF}}}}_{1,i}} (t) $$ 式中：
$ {\varepsilon _0} $ 为噪声系数，$ {\omega _i}(t) $ 为第$ i $ 次分解加入的服从标准正态分布的白噪声序列。2）计算第一残余分量：
$$ {r_1}(t) = f(t) - {F_{{\text{IMF}}}}_1(t) $$ 3）定义
$ {E_j}( \cdot ) $ 为对序列进行EMD分解后的第$ j $ 个模态分量，则对$ {r_1}(t) + {\varepsilon _1}{E_1}({\omega _i}(t)) $ 分解得到：$$ {F_{{\text{IMF}}}}_2(t) = \frac{1}{N}\sum\limits_{i = 1}^N {{E_1}({r_1}(t) + {\varepsilon _1}{E_1}({\omega _i}(t)))} $$ 4）重复步骤2)、3)得到其余的模态分量和残余分量，直到所得到的残余分量极值点个数小于等于2，则停止分解，此时得到固有模态分量
$ {F_{{\text{IMF}}}}_K $ 和最终残余分量$ R(t) $ 。最终残余分量可表示为$$ R(t) = f(t) - \sum\limits_{i = 1}^K {{F_{{\text{IMF}}}}_i(t)} $$ CEEMDAN分解通过添加自适应白噪声对序列进行了干扰脉冲的平滑处理，进一步降低了重构时的误差，提高了完整度。
2. GRU的基本原理
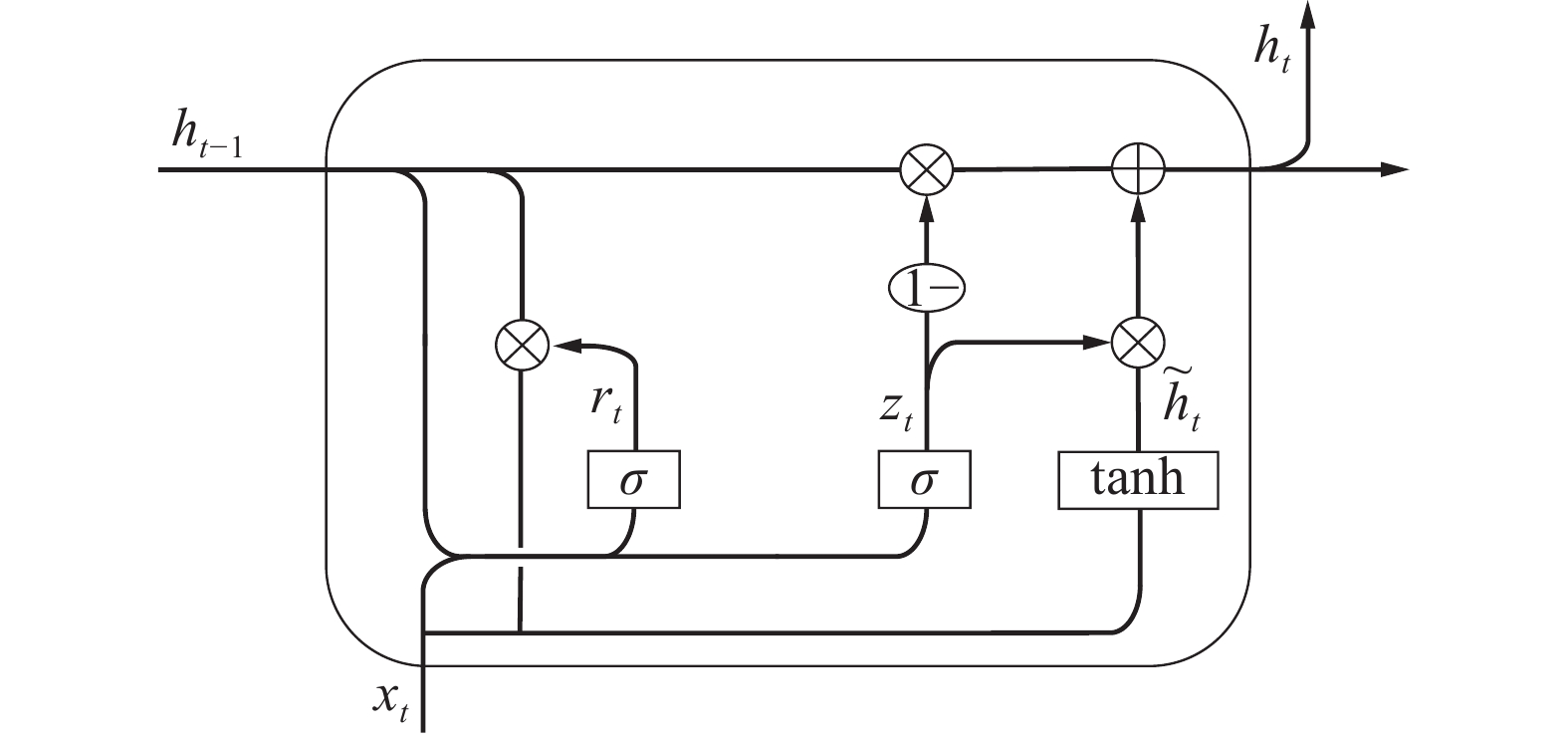
循环神经网络(recurrent neural network，RNN)是深度学习领域中一类特殊的内部存在自连接的神经网络，它通过隐藏层上的回路连接使得前一时刻的网络状态能够传递给当前时刻，当前时刻的状态也可以传递给下个时刻。LSTM神经网络是在RNN中梯度错误累积过多而导致梯度消失或梯度爆炸的基础上所提出的，其将门控的机制引入到循环单元中，可以有选择性地添加和删除数据信息，起到了控制信息数据流通的作用。GRU是一种LSTM的变体，它将LSTM的输入门和遗忘门耦合为更新门，用于控制隐藏状态的更新，减少了矩阵乘法的运算，有效加速了网络的收敛。GRU的结构如图1所示。
图 1 GRU结构
下载:
全尺寸图片
GRU的前向传播计算过程可表示为
$$ {r_t} = \sigma \left( {{{\boldsymbol{W}}_{\text{r}}} \cdot \left[ {{h_{t - 1}},{x_t}} \right]} \right) $$ $$ {z_t} = \sigma \left( {{{\boldsymbol{W}}_{\text{z}}} \cdot \left[ {{h_{t - 1}},{x_t}} \right]} \right) $$ $$ {\tilde h_t} = \tanh \left( {{{\boldsymbol{W}}_{\text{h}}} \cdot \left[ {{r_t} * {h_{t - 1}},{x_t}} \right]} \right) $$ $$ {h_t} = \left( {1 - {z_t}} \right) * {h_{t - 1}} + {z_t} * {\tilde h_t} $$ 式中：
$ {x_t} $ 为神经元的输入，$ {h_{t - 1}} $ 为前一时刻隐藏层的状态，$ {{\boldsymbol{W}}_{\text{r}}} $ 、$ {{\boldsymbol{W}}_{\text{z}}} $ 和$ {{\boldsymbol{W}}_{\text{h}}} $ 分别为重置门$ {r_t} $ 、更新门$ {z_t} $ 和隐藏层的权重矩阵。重置门由该时刻的输入和上一时刻的隐藏状态控制，其决定了是否将隐藏状态的信息遗忘，从而发掘数据间的短期联系；更新门则控制上一时刻的信息在当前时刻的保留量。3. CEEMDAN-GRU预测模型
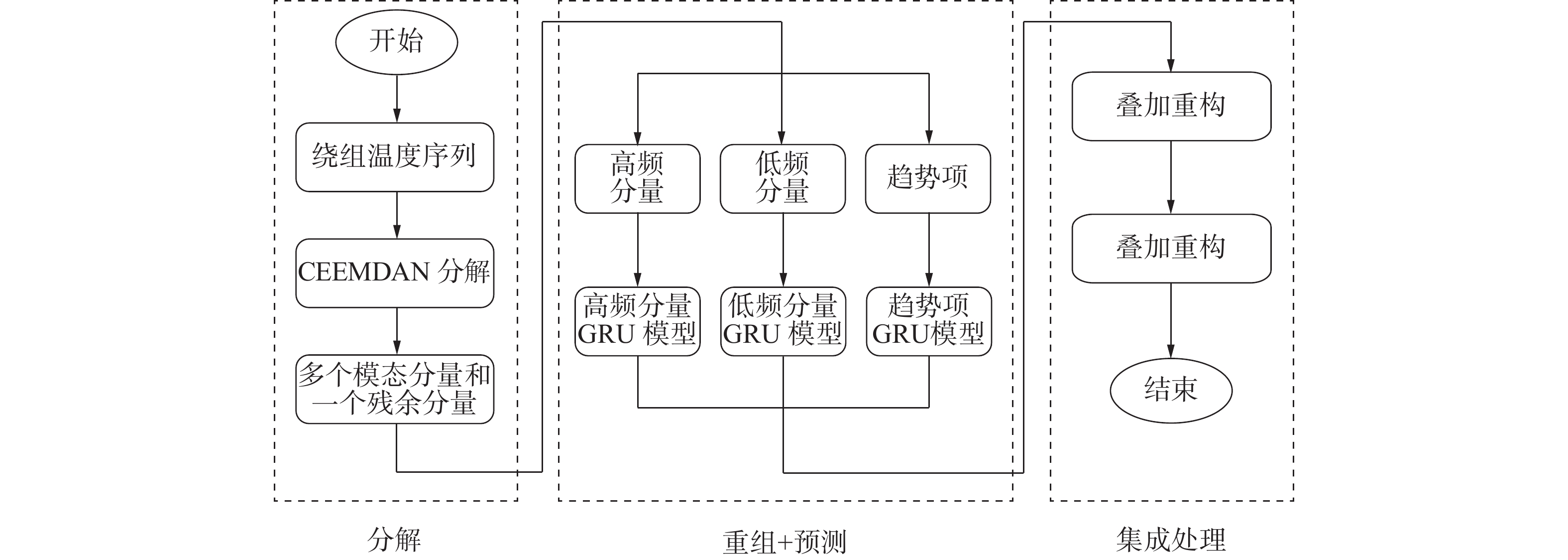
利用CEEMDAN将原始序列分解为若干个频率不同的固定模态分量和1个残余分量，同时为了降低预测建模的复杂度和避免模型过拟合，对各分量进行重新组合得到高频分量、低频分量和趋势项，运用GRU网络分别对重组后的分量进行预测，最后将预测结果叠加集成得到最终的预测结果。图2给出了此方法的预测流程，具体步骤如下：
图 2 CEEMDAN-GRU预测流程下载:
全尺寸图片
1）利用CEEMDAN将绕组温度序列分解为K个模态分量
$ {F_{{\text{IMF}}}}_i(t)(i = 1,2, \cdots ,K) $ 和1个残余分量$ R(t) $ ；2）分别对
${F_{\text{IMF}}}_i(t)$ 做显著性水平$ \alpha = 0.05 $ 下均值为0的单样本t检验；3）若
$ {F_{{\text{IMF}}}}_m(t) $ 为第1个$ {P_{{\text{value}}}} < 0.05 $ 的模态分量，则将$ {F_{{\text{IMF}}}}_1(t) + {F_{{\text{IMF}}}}_2(t) + \cdots + {F_{{\text{IMF}}}}_{m - 1}(t) $ 的结果作为高频分量，将$ {F_{{\text{IMF}}}}_m(t) + {F_{{\text{IMF}}}}_{m + 1}(t) + \cdots + {F_{{\text{IMF}}}}_K(t) $ 的结果作为低频分量，最后将残余分量作为趋势项；4）针对重组得到的3个分量，分别构建相应的GRU预测模型，得到各分量的预测值；
5）通过叠加处理得到最终绕组温度的预测结果。
4. 实验验证及分析
4.1 数据来源
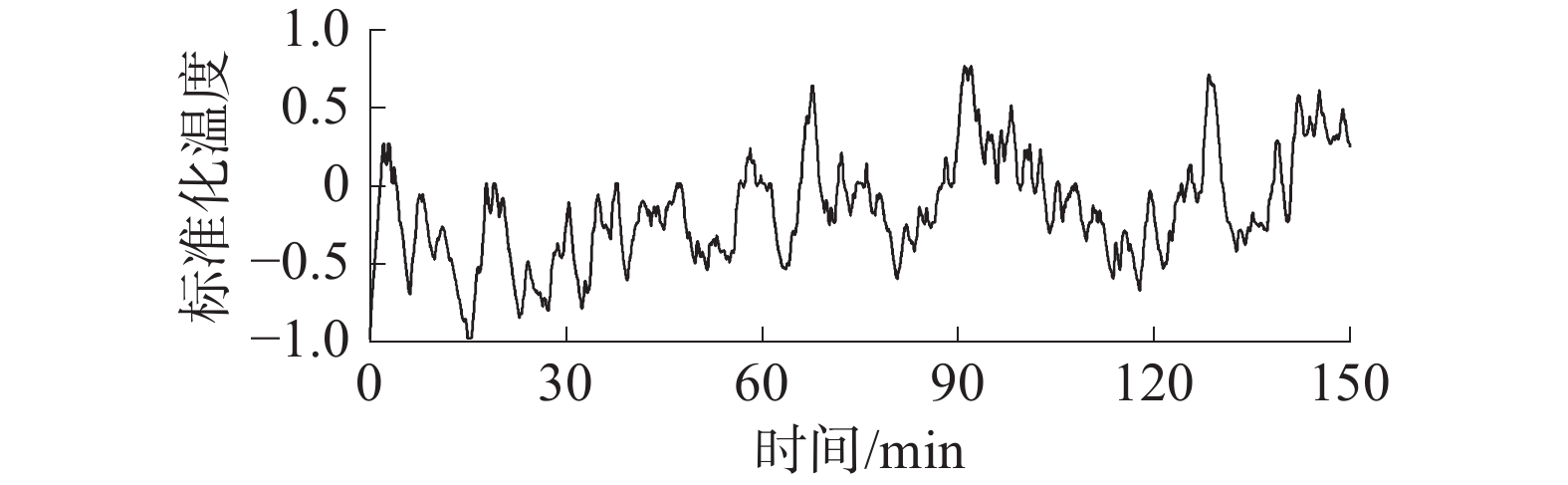
主泵电机是核电站的关键设备，通常采用的是易于安装、使用和维护的异步电动机，而同步电机与异步电机的不同之处在于转子的结构，其定子绕组都是相同的。本文采用来自德国Universität Paderborn永磁同步电机(permanent magnet synchronous motor, PMSM)的实验数据[17]进行预测方法的验证，数据集共有12个特征，包括温度传感器测量的环境温度、冷却液温度、永磁表面温度、定子轭温度、定子齿温度、定子绕组温度以及电压d轴分量、电压q轴分量、电机转速、电流引起的扭矩、电流d轴分量和电流q轴分量。仿真实验的目标特征为定子绕组温度。数据集共包含52个测量阶段，基本涵盖了电机温度变化的全过程，每个测量阶段通过相对应的标签加以区分，所有测量序列均以2 Hz的采样频率在测试台上完成。为降低计算成本，本文选取某个测量阶段中时间间隔为150 min的数据作为原始序列，标准化后的绕组温度如图3所示。在图3所示的时间区间内，绕组温度先后大致经历了振荡、上升、下降以及再振荡的阶段，构成了相对完整的温度变化周期，使得本文建立的预测模型对绕组温度变化的特征提取更加充分，增强了研究结论的说服力。
图 3 原始绕组温度序列下载:
全尺寸图片
4.2 CEEMDAN分解与重组
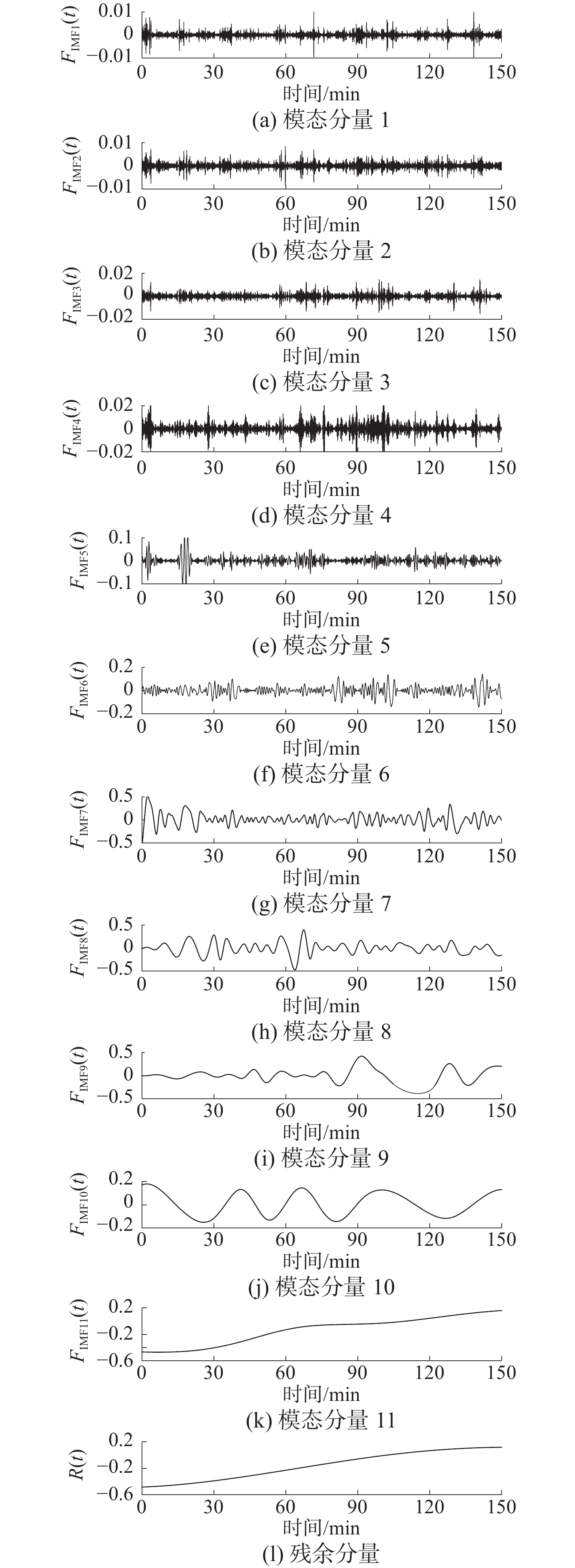
对图3所示的序列进行CEEMDAN分解，得到11个固有模态分量和1个残余分量，分解结果如图4所示。
图 4 CEEMDAN分解结果下载:
全尺寸图片
按顺序依次对各分量进行显著性水平
$ \alpha = 0.05 $ 下均值为0的单样本t检验，各模态分量的t检验结果如表1所示。表 1 各分量的t检验结果模态分量 $ {P_{{\text{value}}}}(\alpha = 0.05) $ ${F_{\text{IMF}} }_1(t)$ 0.8986 ${F_{\text{IMF}} }_2(t)$ 0.6541 ${F_{\text{IMF}} }_3(t)$ 0.7087 ${F_{\text{IMF}} }_4(t)$ 0.3786 ${F_{\text{IMF}} }_5(t)$ 0.0414 ${F_{\text{IMF}} }_6(t)$ $ 0 $ ${F_{\text{IMF}} }_7(t)$ 0.0129 ${F_{\text{IMF}} }_8(t)$ 0.0006 ${F_{\text{IMF}} }_9(t)$ $ 0 $ ${F_{\text{IMF}} }_{10}(t)$ $ 0 $ ${F_{\text{IMF}} }_{11}(t)$ $ 0 $ $ R(t) $ 0 由表1可知，
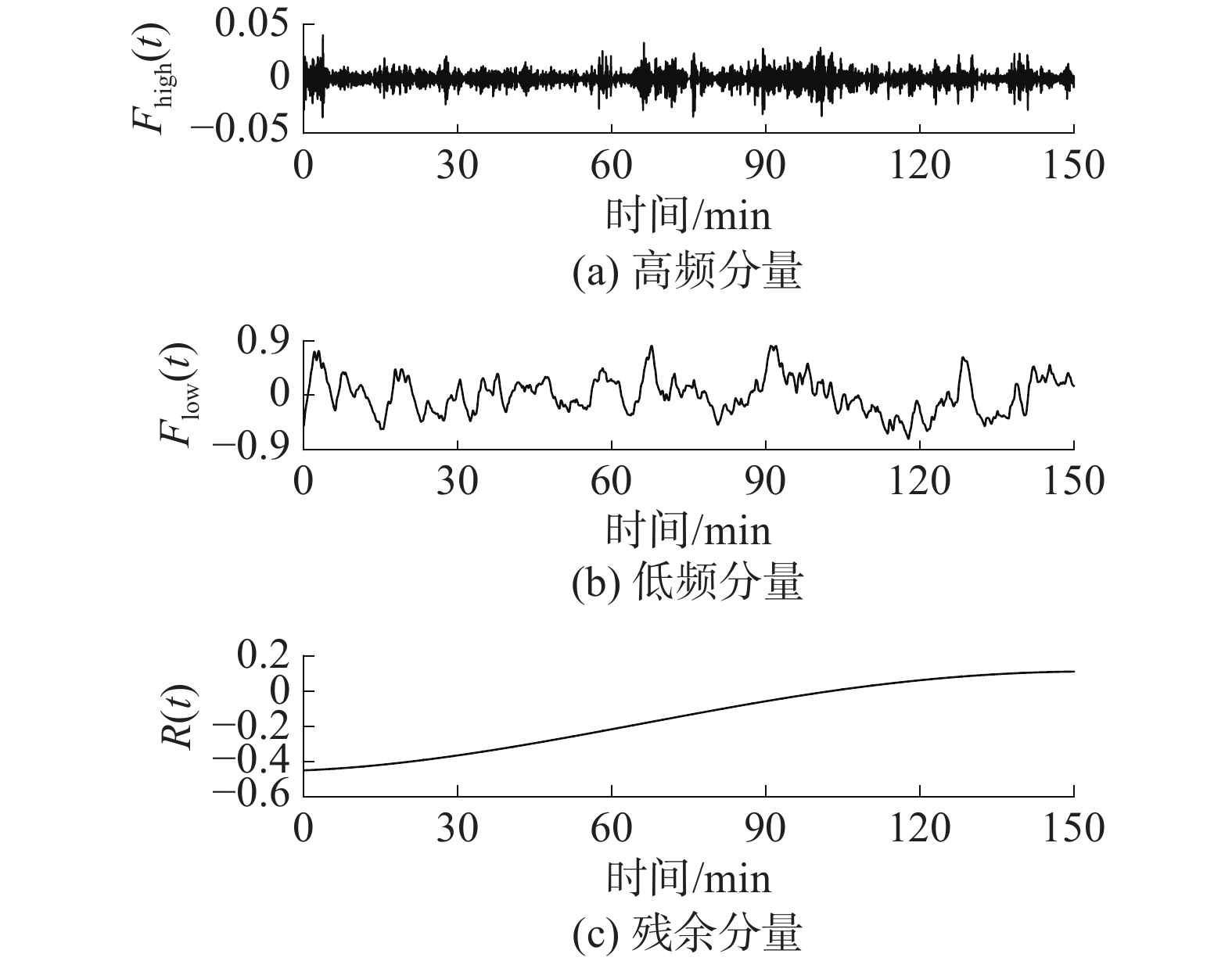
$ {F_{{\text{IMF}}}}_1(t) \sim {F_{{\text{IMF}}}}_4(t) $ 的$ {P_{{\text{value}}}} $ 均大于0.05，而$ {F_{{\text{IMF}}}}_5(t) \sim {F_{{\text{IMF}}}}_{11}(t) $ 的$ {P_{{\text{value}}}} $ 均小于0.05，即在当前显著性水平下第1个均值显著偏离0的模态分量为$ {F_{{\text{IMF}}}}_5(t) $ 。因此可将$ {F_{{\text{IMF}}}}_1(t) \sim {F_{{\text{IMF}}}}_4(t) $ 叠加得到高频分量$ {F_{{\text{high}}}}(t) $ ，表示序列的短期波动项；将$ {F_{{\text{IMF}}}}_5(t) \sim {F_{{\text{IMF}}}}_{11}(t) $ 叠加得到低频分量$ {F_{{\text{low}}}}(t) $ ，表示序列的中期重要因素影响项；残余分量$ R(t) $ 不变，作为序列的长期趋势项。重组后的结果如图5所示。
图 5 分量重组结果下载:
全尺寸图片
4.3 GRU神经网络的建模
对于重组后的分量，采用滚动时间窗的方式对子序列进行预测，选择前80%的数据作为训练集，后20%的数据作为测试集。采用双层GRU神经网络，输入序列长度为30，即选取前30个样本对序列进行预测，输出序列长度为1，同时设置失活率为0.2的Dropout层以抑制网络的过拟合。具体的GRU神经网络超参数如表2所示。为了消除数据间量纲的差异，加速网络的收敛，在将数据输入网络之前采用MinMaxScaler估计器对数据进行归一化，使数据处于[0,1]，其计算公式为
表 2 GRU神经网络的超参数超参数 取值或设置情况 GRU层数 2 输入序列长度 30 输出序列长度 1 隐藏层神经元个数 64 Dropout层失活率 0.2 最大迭代次数 1000 初始学习率 0.001 损失函数 MSE 优化算法 Adam $$ \tilde x = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $$ 4.4 预测评价指标的选择
预测评价指标有很多种，为了对选用的方法进行全面的分析和评价，本文选用平均绝对误差(mean absolute error, MAE)
$ {E_{{\text{MA}}}} $ 、均方根误差(root mean square error, RMSE)$ {E_{{\text{RMS}}}} $ 、对称平均绝对百分比误差(symmetric mean absolute percentage error, SMAPE)$ {E_{{\text{SMAP}}}} $ 以及校正决定系数(adjusted R-square)$ R_{{\text{Adjusted}}}^2 $ 来评估预测模型的优劣，相应的计算公式为$$ {E_{{\text{MA}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{\hat y}_i} - {y_i}} \right|} $$ $$ {E_{{\text{RMS}}}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}} } $$ $$ {E_{{\text{SMAP}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left| {{{\hat y}_i} - {y_i}} \right|}}{{(\left| {{{\hat y}_i}} \right| + \left| {{y_i}} \right|)/2}}} $$ $$ {R^2} =\left( 1 - {{ \displaystyle\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}} }}\right)\Biggr/{{ \displaystyle\sum\limits_{i = 1}^n {{{\left(\frac{1}{n} \displaystyle\sum\limits_{i = 1}^n {{y_i}} - {y_i}\right)}^2}} }} $$ $$ R_{{\text{Adjusted}}}^2 = 1 - \frac{{(1 - {R^2})(n - 1)}}{{n - p - 1}} $$ 式中：
$ {\hat y_i} $ 为预测值；$ {y_i} $ 为真实值；$ n $ 为样本数；$ p $ 为特征数量；$ {E_{{\text{MA}}}} $ 、$ {E_{{\text{RMS}}}} $ 、$ {E_{{\text{SMAP}}}} $ 均用来衡量预测值与真实值之间的偏差，值越小表明模型的预测能力越强；$ R_{{\text{Adjusted}}}^2 $ 是在决定系数$ {R^2} $ 上的基础上所提出的，抵消了样本数量对R2的影响，相比之下更能描述回归模型拟合的效果，其值越接近于1表明拟合的效果越好，预测越精确。4.5 预测结果与对比分析
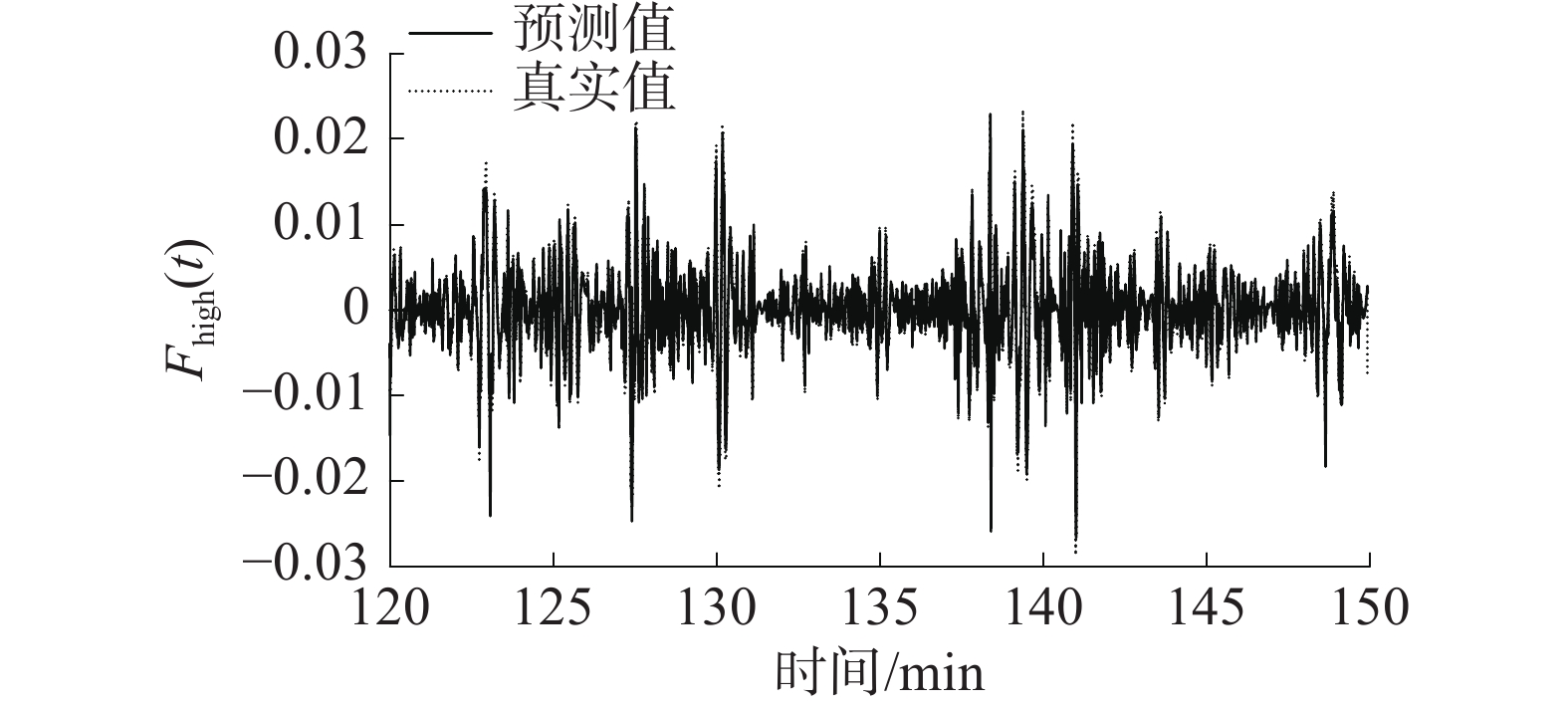
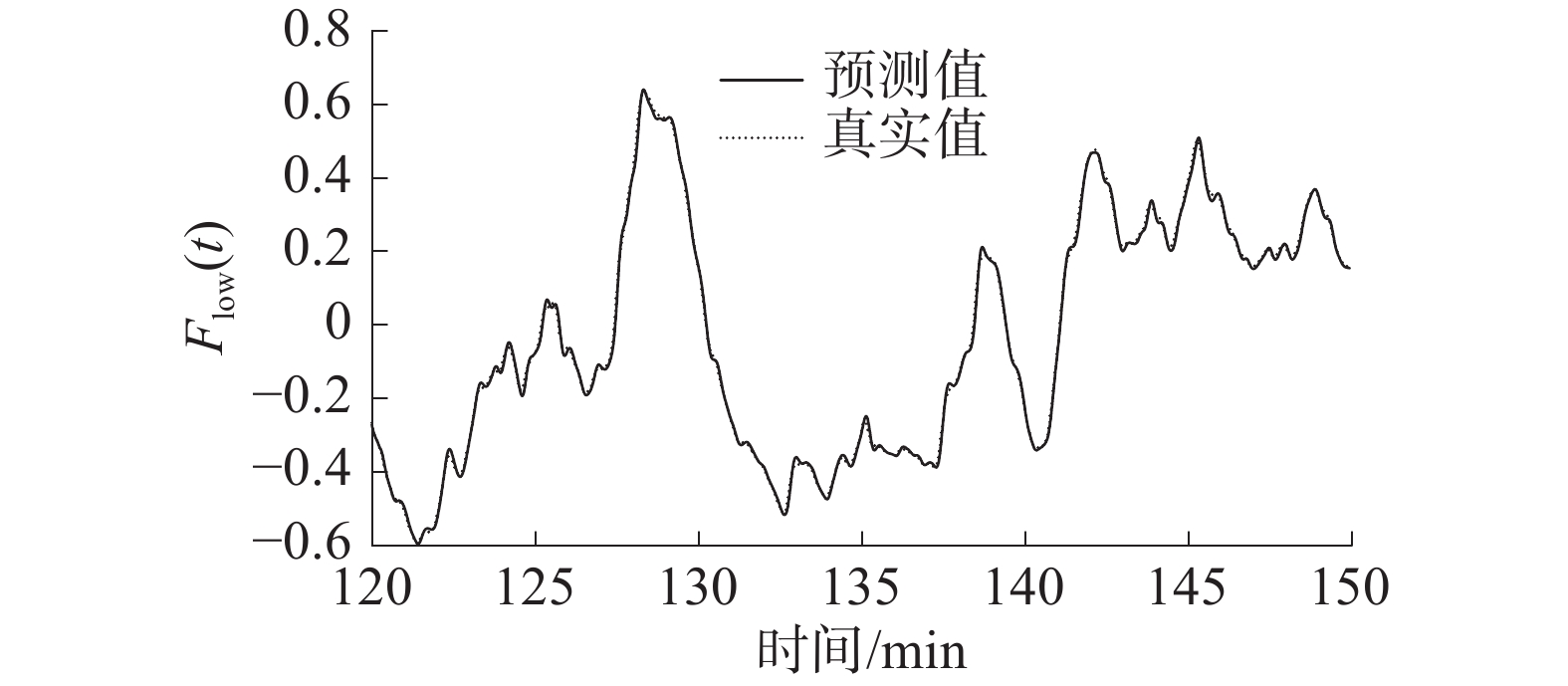
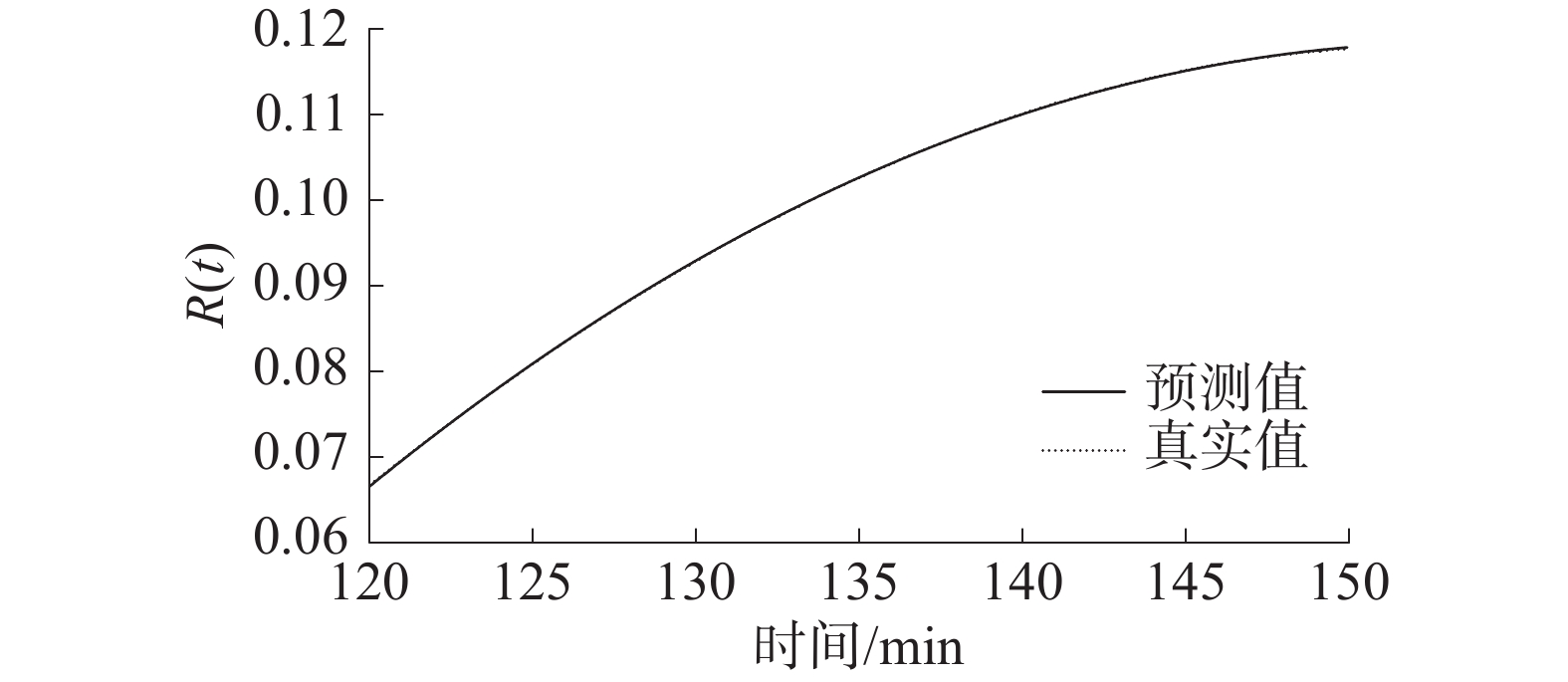
经过网络的训练和测试，高、低频分量和趋势项预测结果如图6~图8所示，对应的预测评价指标如表3所示。
图 6 高频分量预测结果下载:
全尺寸图片
图 7 低频分量预测结果下载:
全尺寸图片
图 8 趋势项预测结果下载:
全尺寸图片
表 3 重组分量的评价指标分量 EMA ERMS ESMAP $ R_{{\text{Adjusted}}}^2 $ 高频分量 0.00860 0.01188 0.66025 0.85742 低频分量 0.00129 0.00193 0.06801 0.99861 趋势项 0.00004 0.00005 0.00045 0.99999 从预测曲线图6~图 8中可以看出，经过分解、重组得到的3个分量在测试集上的预测结果均与原分量序列基本重合，即预测模型对数据具有较强的解释能力。
由表3可知，高频分量的
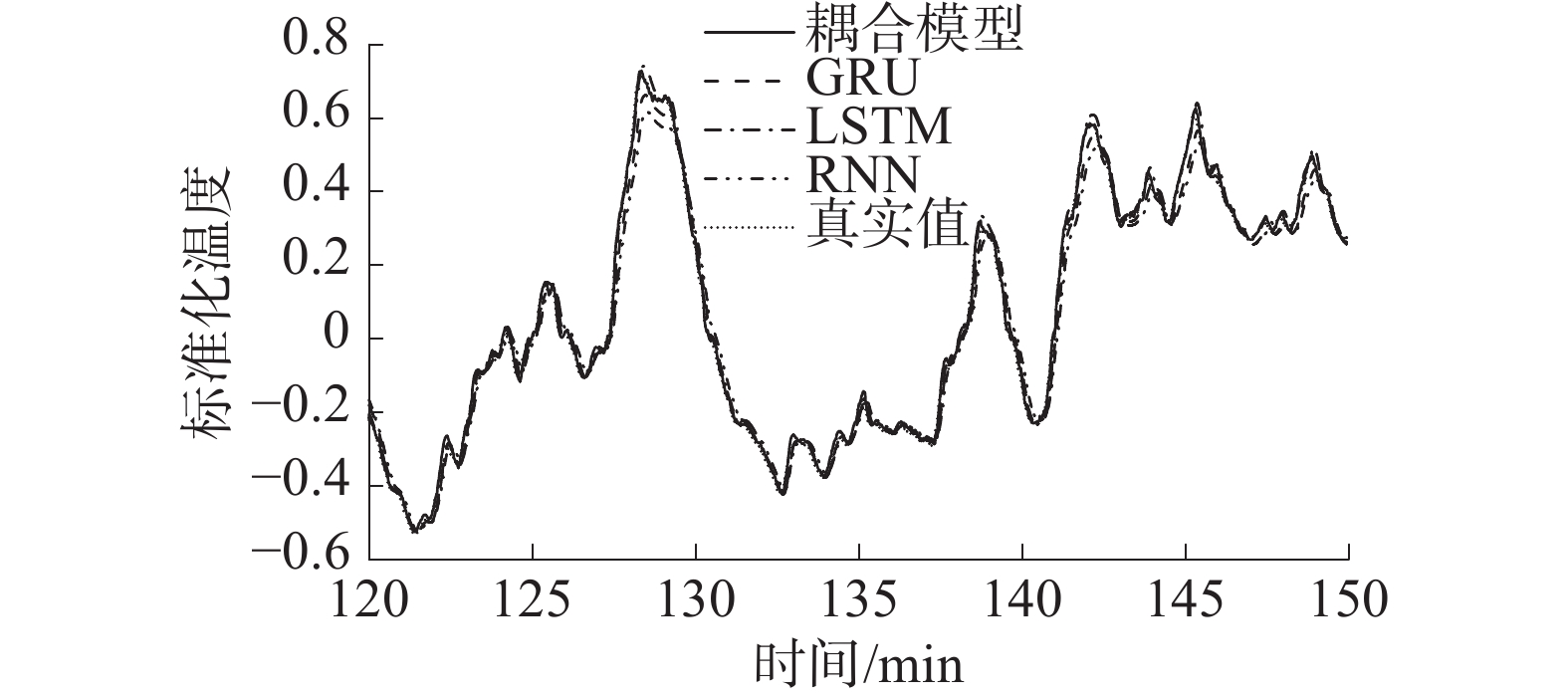
$ R_{{\text{Adjusted}}}^2 $ 小于0.86，而低频分量和趋势项对应的$ R_{{\text{Adjusted}}}^2 $ 均超过了0.99，表明高频分量的模型拟合效果不如其余2分量，这主要是由于原始序列包含着特征信息的同时也夹杂着大量的噪声[18]。随着分量频率的减小，MAE、RMSE、SMAPE值均显著降低，表明模型的预测能力更强，拟合效果更好。将这3个分量的预测结果进行集成重构得到绕组温度在测试集上的预测结果，同时与传统RNN、LSTM和GRU模型进行对照实验，如图9所示。
图 9 不同模型的预测结果下载:
全尺寸图片
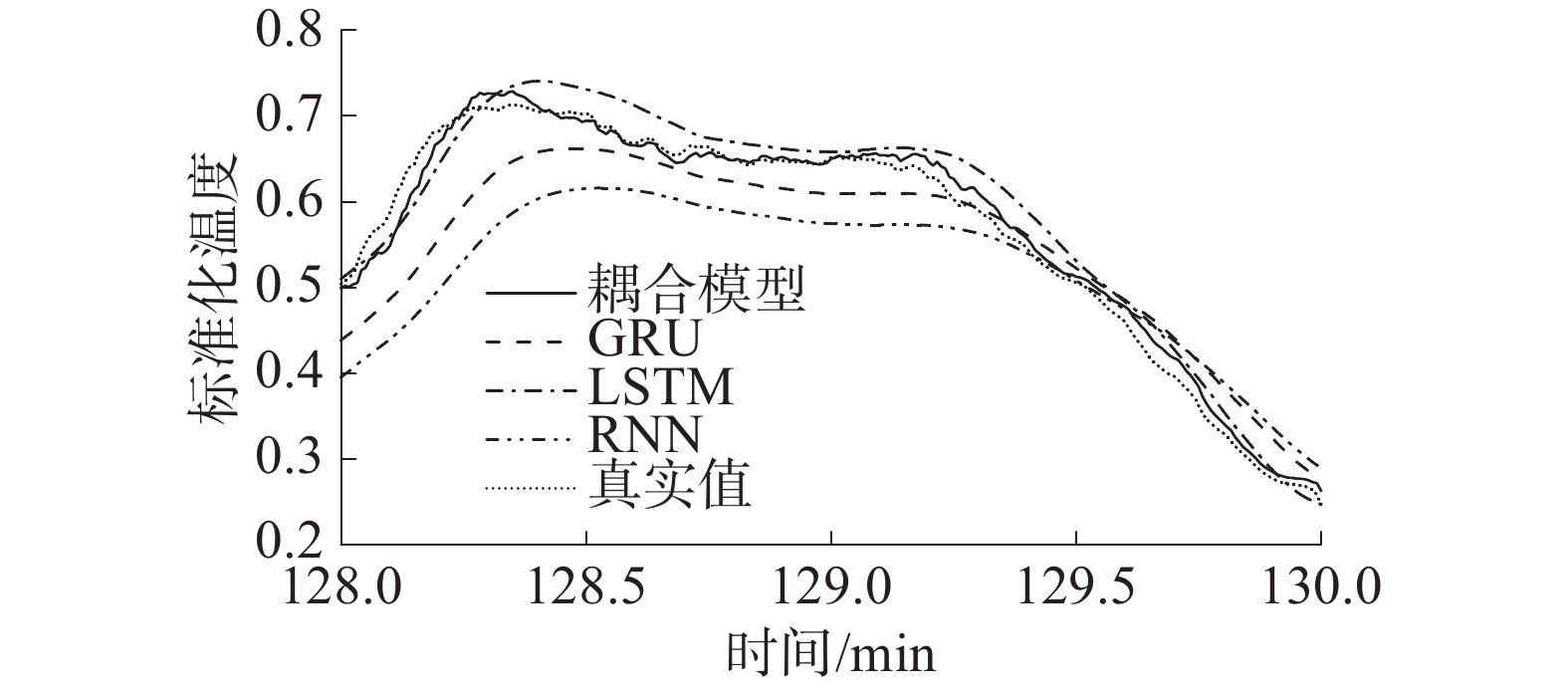
为了便于在具体的部分区域上比较不同模型之间的差异，对测试集中第128~130 min的变化趋势进行局部放大，如图10所示。从图10中可以看出，传统神经网络模型虽然在整体趋势上与实际趋势保持一致，但在某些极值区域的预测输出与实际值有不小的差距；而本文提出的预测模型不仅成功预测出了绕组温度的变化趋势，而且在局部极值处与真实值的误差最小，在波动频繁的区域也能捕捉到原始序列的细节特征，具有更强的预测能力。
图 10 不同模型局部区间的预测结果下载:
全尺寸图片
同时表4也给出了各预测模型的评价指标结果。数据表明，相比于其他模型，本文所提出的CEEMDAN-GRU预测模型的MAE、RMSE、SMAPE值均最小，而Adjusted-R2值最大，即认为在所给出的评价指标上优于其他模型。同时，将本文的模型与使用GRU直接预测相比较，当分解重构的方法融入预测模型后，预测效果均取得了较大改善，验证了CEEMDAN分解可以更好地提取数据的内在特征，提高预测精度。
表 4 不同模型的评价指标对比模型 MAE RMSE SMAPE $ R_{{\text{Adjusted}}}^2 $ RNN 0.03879 0.05256 0.30365 0.97405 LSTM 0.01978 0.02906 0.18465 0.99207 GRU 0.01099 0.01709 0.12934 0.99725 耦合模型 0.00991 0.01300 0.10877 0.99841 5. 结论
为了提高核电站中主泵电机的预警能力，适当优化其维护策略，本文提出了一种基于CEEMDAN-GRU的主泵电机绕组温度预测算法，主要包括：
1) CEEMDAN分解善于提取复杂时间序列的波动模式，GRU神经网络在提取数据间的长期依赖关系方面具有优势，将二者有效结合，建立了新的时间序列预测耦合模型；
2) 通过计算分解后各模态分量的
$ {P_{{\text{value}}}} $ 进行分量的重组，以此作为网络的输入，降低了预测模型的复杂度，避免了模型的过拟合；3) 相较于其他对比模型，CEEMDAN-GRU的耦合模型在多元评价指标中均有明显的优势，具有更好的预测性能。
在后续工作中，将对GRU的参数优化方法等展开进一步的研究。
-
图 1 GRU结构
下载:
全尺寸图片
图 2 CEEMDAN-GRU预测流程
下载:
全尺寸图片
图 3 原始绕组温度序列
下载:
全尺寸图片
图 4 CEEMDAN分解结果
下载:
全尺寸图片
图 5 分量重组结果
下载:
全尺寸图片
图 6 高频分量预测结果
下载:
全尺寸图片
图 7 低频分量预测结果
下载:
全尺寸图片
图 8 趋势项预测结果
下载:
全尺寸图片
图 9 不同模型的预测结果
下载:
全尺寸图片
图 10 不同模型局部区间的预测结果
下载:
全尺寸图片
表 1 各分量的t检验结果
模态分量 $ {P_{{\text{value}}}}(\alpha = 0.05) $ ${F_{\text{IMF}} }_1(t)$ 0.8986 ${F_{\text{IMF}} }_2(t)$ 0.6541 ${F_{\text{IMF}} }_3(t)$ 0.7087 ${F_{\text{IMF}} }_4(t)$ 0.3786 ${F_{\text{IMF}} }_5(t)$ 0.0414 ${F_{\text{IMF}} }_6(t)$ $ 0 $ ${F_{\text{IMF}} }_7(t)$ 0.0129 ${F_{\text{IMF}} }_8(t)$ 0.0006 ${F_{\text{IMF}} }_9(t)$ $ 0 $ ${F_{\text{IMF}} }_{10}(t)$ $ 0 $ ${F_{\text{IMF}} }_{11}(t)$ $ 0 $ $ R(t) $ 0 表 2 GRU神经网络的超参数
超参数 取值或设置情况 GRU层数 2 输入序列长度 30 输出序列长度 1 隐藏层神经元个数 64 Dropout层失活率 0.2 最大迭代次数 1000 初始学习率 0.001 损失函数 MSE 优化算法 Adam 表 3 重组分量的评价指标
分量 EMA ERMS ESMAP $ R_{{\text{Adjusted}}}^2 $ 高频分量 0.00860 0.01188 0.66025 0.85742 低频分量 0.00129 0.00193 0.06801 0.99861 趋势项 0.00004 0.00005 0.00045 0.99999 表 4 不同模型的评价指标对比
模型 MAE RMSE SMAPE $ R_{{\text{Adjusted}}}^2 $ RNN 0.03879 0.05256 0.30365 0.97405 LSTM 0.01978 0.02906 0.18465 0.99207 GRU 0.01099 0.01709 0.12934 0.99725 耦合模型 0.00991 0.01300 0.10877 0.99841 -
[1] 俞学成. 核电站循环冷却水泵电机定子绕组温度高原因分析与处理[J]. 电工技术, 2016(9): 86−87. doi: 10.3969/j.issn.1002-1388.2016.09.039 [2] 张思原, 卢忝余, 曾辉, 等. 基于LSTM的核电传感器多特征融合多步状态预测[J]. 核动力工程, 2021, 42(4): 208−213. doi: 10.13832/j.jnpe.2021.04.0208 [3] 王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测[J]. 北京航空航天大学学报, 2018, 44(4): 772−784. doi: 10.13700/j.bh.1001-5965.2017.0285 [4] 王祥雪, 许伦辉. 基于深度学习的短时交通流预测研究[J]. 交通运输系统工程与信息, 2018, 18(1): 81−88. doi: 10.16097/j.cnki.1009-6744.2018.01.012 [5] 牛哲文, 余泽远, 李波, 等. 基于深度门控循环单元神经网络的短期风功率预测模型[J]. 电力自动化设备, 2018, 38(5): 36−42. doi: 10.16081/j.issn.1006-6047.2018.05.005 [6] 邓带雨, 李坚, 张真源, 等. 基于EEMD-GRU-MLR的短期电力负荷预测[J]. 电网技术, 2020, 44(2): 593−602. doi: 10.13335/j.1000-3673.pst.2019.0113 [7] HUANG Guoyan, LI Xinyi, ZHANG Bing, et al. PM2.5 concentration forecasting at surface monitoring sites using GRU neural network based on empirical mode decomposition[J]. Science of the total environment, 2021, 768: 144516. doi: 10.1016/j.scitotenv.2020.144516 [8] 张晓晗, 冯爱民. 基于经验模态分解和长短期记忆神经网络的短期交通流量预测[J]. 计算机应用, 2021, 41(1): 225−230. [9] CHEN Yaoran, DONG Zhikun, WANG Yan, et al. Short-term wind speed predicting framework based on EEMD-GA-LSTM method under large scaled wind history[J]. Energy conversion and management, 2021, 227: 113559. doi: 10.1016/j.enconman.2020.113559 [10] 黄冬梅, 唐振, 胡安铎, 等. 基于VMD-GRU的电力短期负荷预测方法[J]. 物联网技术, 2021, 11(4): 67−70. doi: 10.16667/j.issn.2095-1302.2021.04.020 [11] DING Shifei, ZHANG Zichen, GUO Lili, et al. An optimized twin support vector regression algorithm enhanced by ensemble empirical mode decomposition and gated recurrent unit[J]. Information sciences, 2022, 598: 101−125. doi: 10.1016/j.ins.2022.03.060 [12] LI Fugang, MA Guangwen, CHEN Shijun, et al. An ensemble modeling approach to forecast daily reservoir inflow using bidirectional long- and short-term memory (Bi-LSTM), variational mode decomposition (VMD), and energy entropy method[J]. Water resources management, 2021, 35(9): 2941−2963. doi: 10.1007/s11269-021-02879-3 [13] 武云云, 刘建香, 崔宏星, 等. 探讨ARIMA模型在核电站外围环境放射性水平预测中的应用[J]. 现代预防医学, 2014, 41(11): 1941−1944. [14] 朱少民, 夏虹, 吕新知, 等. 基于ARIMA和LSTM组合模型的核电厂主泵状态预测[J]. 核动力工程, 2022, 43(2): 246−253. [15] WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in adaptive data analysis, 2009, 1(1): 1−41. doi: 10.1142/S1793536909000047 [16] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decompo-sition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2011: 4144-4147. [17] KIRCHGÄSSNER W, WALLSCHEID O, BÖCKER J. Estimating electric motor temperatures with deep residual machine learning[J]. IEEE transactions on power electronics, 2020, 36(7): 7480−7488. [18] 贺毅岳, 李萍, 韩进博. 基于CEEMDAN-LSTM的股票市场指数预测建模研究[J]. 统计与信息论坛, 2020, 35(6): 34−45. doi: 10.3969/j.issn.1007-3116.2020.06.005
