Numerical simulation and experimental study on the noise generated by scientific research equipment entering water in an inclined slideway
-
摘要: 为了研究科考设备斜滑道入水的噪声预报问题，本文设计了一种斜滑道装置，利用CFD软件对不同入水速度与投放角度进行投放噪声的数值模拟，选用分离涡模型（detached-eddy simulation，DES）和FW-H(Ffowcs Williams-Hawkings，FW-H)声类比模型开展入水物体噪声计算。在计算得到水动力噪声的时域脉动压力结果后，通过傅里叶变换得到频域的噪声分布。本文设计了相关实验对数值结果进行验证，并通过分析典型工况下的流场域以及噪声的时域及频域特性，进一步分析实验与数值系统误差的来源。结果表明，流致噪声占总噪声的主要部分，斜滑道与科考设备之间的相互耦合作用、滑道壁的流固耦合现象、传送过程中不可避免的机械噪声以及声辐射特性数值模拟模型的不完备性是系统性误差的来源。Abstract: In order to study the noise prediction of scientific research equipment entering water in an inclined slideway, a kind of inclined slideway delivery device is designed in this paper. The CFD software is used to carry out the numerical simulation of launching noise at different entry speeds and with different incident angles. The detached-eddy simulation (DES) model and Ffowcs Williams-Hawkings (FW-H) acoustic analogy model are selected to calculate the noise generated by the equipment entering water. After calculation on the time-domain pulsation pressure of hydrodynamic noise, the noise distribution in frequency domain is obtained by Fourier transform. In this paper, relevant experiments are designed to verify the numerical results. The sources of systematic errors of the experimental and numerical methods are further derived by analyzing the flow field under typical working conditions and the characteristics of noise in time domain and frequency domain. The results show that the flow-induced noise is the main part of noises. The coupling between the inclined slideway and scientific research equipment, the fluid-structure coupling phenomenon of the slideway wall, the inevitable mechanical noise during the transmission process and the incomplete numerical simulation model of acoustic radiation characteristics are the sources of systematic errors.
-
科考设备在海洋研究方面发挥着至关重要的作用，从科考船内将科考设备释放入水是一种强烈的砰击问题，自由液面附近发生剧烈变化，其噪声辐射特性具有非线性、非稳态的特点[1]，对于这类问题的研究有助于提高物体入水噪声预报的准确性，有效降低船舶入水作业的噪声级。因此，该研究具有重要的科学价值及实际工程意义。
水下装备的噪声试验需围绕水洞等实验设备开展[2-3]，受到水洞尺寸及背景噪声影响，对于可测试的设备的尺寸及测试精度都有所限制。流激噪声的数值模拟一直是一个重要的问题，国内外对此有很多相关的研究。Yeo等[4]将水动力计算后的数值结果，应用气泡噪声模型和Ffowcs Williams-Hawkings（FW-H）方程的渗透形式，计算了潜艇的流致噪声，通过与韩国船舶与海洋工程研究所大型空化风洞实验结果的对比，验证了流致噪声的数值结果。白俊强等[5]通过采用基于可穿透数据面的FW-H方法模拟声学远场，该方法与传统的半经验方法相比具有计算量小、计算精确、易于工程实现的特点，可以计算非线性噪声。欧阳绍修等[6]研究了三维非定常雷诺平均N-S方程和分离涡模拟（detached eddy simulation，DES）方法在空腔流动及空腔噪音问题的应用，利用2种方法对三维空腔流动及噪音进行了数值计算并与实验数据进行了对比，通过分析比较发现DES方法得到的结果更加准确，特别是通过声压级（sound pressure level，SPL）分析发现DES方法能够较好地捕捉空腔流动中的压强脉动及噪声水平。张群峰等[7]分别利用DES方法和求解非线性脉动方程组的非线性声学方法，对来流马赫数为2.0条件下、长度与深度比为5.88的开式空腔进行了数值模拟，计算结果表明DES方法能较为准确地捕捉噪声源。
结合Lighthill声类比理论的FW-H噪声预报模型是现阶段前景良好的噪声计算手段之一[8]。王春旭等[9]对该方法的基本原理和适用性进行了讨论，确认了这一手段在工程应用中的价值。随着研究的深入，这一模型在噪声预报领域的应用逐渐扩大，已从传统的推进器噪声预报扩展到多种结构体的噪声预报工作中。刘波等[10]结合流体域体积（volume of fraction，VOF）方法与k-ω模型完成了对船舶绕流场发声机理的相关研究。
从国内外研究来看，投送设备的入水方式大多是在水面以上直接抛出经抛物线运动后自由落水。为了考虑结构的安全性以及降低噪声级，本文提出了一种斜滑道装置，能够将设备以一定角度及入水速度释放。针对该投送入水设备，基于CFD软件，结合分离涡DES湍流模型和FW-H声学模型进行建模和数值模拟。根据得到的噪声时域脉动情况，通过傅里叶变换得到频域噪声分布，对声指向性和总声级进行分析，并与实验数据进行对比。分析不同工况下载荷、流场信息，时域和频域特性的数值结果的误差原因。
1. 数值方法
1.1 建立DES湍流模型
滑道投放噪声是基于水动力计算结果开展计算和分析的，在现阶段常用的湍流模型中，雷诺平均方程(Reynolds average Navier-Stokes，RANS)的优势在于可以较好地计算时均载荷，但对湍流特征不能精确展示；大涡模拟（large eddy simulation，LES）的优势在于能够较好地展示螺旋桨周围的湍流脉动，但所需计算量很大。DES综合了这2种方法的优点，因而计算采用DES湍流模型。在DES方法中，湍流动能k的方程可以用修正的耗散项写成：
$$ \rho \frac{{{\text{d}}k}}{{{\text{d}}t}} = P - \frac{{\rho {k^{3/2}}}}{{{l_{{\text{DES}}}}}} + D $$ 式中：ρ为流体密度；t为时间；P为湍流的生成项，表示为雷诺应力和平均运动变形率张量的二重标量积；lDES为长度尺度；D为扩散项。DES的长度尺度被定义为RANS长度尺度和局部分辨率Δ的最小值，RANS长度尺度为
$$ {l_{{\text{RANS}}}} = \sqrt k /{\beta ^*}\omega $$ 式中：ω为耗散率，
$ {\beta ^*}{\text{ = 0}}{\text{.09}} $ 为模型常数，局部分辨率Δ被评估为局部壁面距离的最小值和网格分辨率的最大值（Δxi），其中Δxi为不同折射率方向上网格单元的厚度。这时DES的长度尺度为$$ {l_{{\text{DES}}}} = \min ({C_{{\text{DES}}}}\varDelta ,{l_{{\text{DES}}}}) $$ 式中系数
$ {C_{{\text{DES}}}} $ 的计算公式为$$ {C_{{\text{DES}}}} = \left( {1 - {F_1}} \right)C_{{\text{DES}}}^{k - \varepsilon } + {F_{\text{1}}}C_{{\text{DES}}}^{k - \varepsilon } $$ 其中：常数
$ C_{{\text{DES}}}^{k - \varepsilon }{\text{ = 0}}{\text{.61}} $ ，$ C_{{\text{DES}}}^{k - \varepsilon }{\text{ = 0}}{\text{.78}} $ ，F1是Menter[11]所提到的混合功能。值得一提的是，当使用延迟分离涡模拟(delayed detached eddy simulation, DDES)方法时，长度尺度表示为[12]$$ {l_{{\text{DDES}}}} = {l_{{\text{RANS}}}} - {F_1}\max \left( {0,{l_{{\text{RANS}}}} - {C_{{\text{DES}}}}\varDelta } \right) $$ 式中
$ {F_1} \to {\text{1}} $ ，位于边界层之外，在网格间距允许的情况下，长度尺度变为${l_{{\text{DDES}}}} = {C_{{\text{DES}}}}\varDelta$ 。DES变型DDES的目的在于提高计算的精度，因为在DES的长度尺度计算公式中，在某些情况下已存在网格诱导分离现象。1.2 声学模型FW-H方程
FW-H方程[13]是解决声学预测问题的重要方法，Farassat[14]发展了几个时域公式用来求解FW-H方程[15]。FW-H方程是一个非齐次波动方程，它由广义函数形式的质量和动量守恒定律产生：
$$ \begin{gathered} {{\bar D}^2}\hat p\left( {x,t} \right) = \frac{{\bar \partial }}{{\partial t}}\left\{ {\left[ {{\rho _0}{{\boldsymbol{v}}_{\text{n}}} + \rho \left( {{{\boldsymbol{u}}_{\text{n}}} - {{\boldsymbol{v}}_{\text{n}}}} \right)} \right]\text{δ} \left( f \right)} \right\} - \\ \frac{{\bar \partial }}{{\partial {x_i}}}\left\{ {\left[ {\Delta {P_{ij}}{n_j} + \rho {{\boldsymbol{u}}_i}\left( {{{\boldsymbol{u}}_{\text{n}}} - {{\boldsymbol{v}}_{\text{n}}}} \right)} \right]\text{δ} \left( f \right)} \right\} + \frac{{{{\bar \partial }^2}}}{{\partial {x_i}\partial {x_j}}}\left\{ {{{\boldsymbol{T}}_{ij}}{\text{H}}\left( f \right)} \right\} \\ \end{gathered} $$ 式中：
$ \hat p $ 为声压脉动；ui和vi分别为流体和表面的速度分量；ρ0、ρ分别表示介质恒密度和扰动下的介质密度；下标n表示沿着法向方向的投影；f为描述任意表面的方程；δ(f)为狄拉克函数；H(f)为海维赛德函数；$ {\bar D^2} $ 为达朗贝尔算子，$$ {\bar D^2} = \frac{1}{{c_0^2}}\frac{{{{\bar \partial }^2}}}{{\partial {t_2}}} - {\bar \nabla ^2} $$ Lighthill张量
${{\boldsymbol{T}}_{ij}}$ 为$$ {{\boldsymbol{T}}_{ij}} = \rho {{\boldsymbol{u}}_i}{{\boldsymbol{u}}_j} + {{\boldsymbol{P}}_{ij}} - c_0^2\;\tilde \rho {\text{δ} _{ij}} $$ 式中：
$ {c_0} $ 为在无扰动介质中的声速，${{\boldsymbol{u}}_{ij}}$ 为压应力张量，${\text{δ}_{ij}}$ 为克罗内克符号。1.3 声压级换算方法
声压谱级为单位频率带宽内的声压级，频率分辨率1 Hz，则总声级L1为
$$ {L_1} = 10\lg \left( {\frac{{{p^2}\left( f \right)}}{{p_0^2}}} \right) = 20\lg \left( {\frac{{p\left( f \right)}}{{{p_0}}}} \right) $$ 式中参考声压
${p_0} = 1 \times {10^{ - 6}}{\text{Pa}}$ 。1/3频程谱级是在每1/3个倍频程内噪声的声压谱级，其中心频率
${f_0}$ 按ISO推荐频率为1.0×10m、1.25×10m、1.6×10m、2.0×10m、2.5×10m、3.15×10m、4.0×10m、5.0×10m、6.3×10m、8.0×10m Hz。由声压谱级计算1/3倍频程谱级为$$ {L_{\frac{1}{{{\text{3oct}}}}}} = 10\lg \sum\limits_f {{{10}^{\frac{{{L_1}\left( f \right)}}{{10}}}}} - 10\lg {f_0} + 6.38 $$ 式中
${2^{ - \frac{1}{6}}}{f_0} \leqslant f \leqslant {2^{\frac{1}{6}}}{f_0}$ 。1/3倍频程带级是指一定频带内的声压级，由声压谱级或1/3倍频程谱级可以计算得到1/3倍频程带级，用于表征一定频带内的噪声水平，表达式为
$$ {L_{{\text{band}}}} = 10\lg \sum\limits_{{f_{\text{l}}}}^{{f_{\text{h}}}} {{{10}^{\frac{{{L_1}\left( f \right)}}{{10}}}}} = 10\lg \sum\limits_{{f_{\text{l}}}}^{{f_{\text{h}}}} {{f_i}{{10}^{{L_{\frac{1}{{{\text{3oct}}}}}}\frac{{\left( {{f_i}} \right)}}{{10}}}}} - 6.38 $$ 式中：
${f_i}$ 为指定频率范围内所包含的1/3倍频程中心频率，${f_{\text{l}}}$ 和${f_{\text{h}}}$ 分别为频率范围上、下限频率。总声级是指整个频带范围内的声压级，用来表征整个频带内的噪声水平，其表达式为
$$ {L_{\text{p}}} = 10\lg \sum\limits_{{f_{\text{l}}}}^{{f_{\text{h}}}} {{{10}^{\frac{{{L_{{\text{band}}}}}}{{10}}}}} $$ 2. 计算域及网格划分
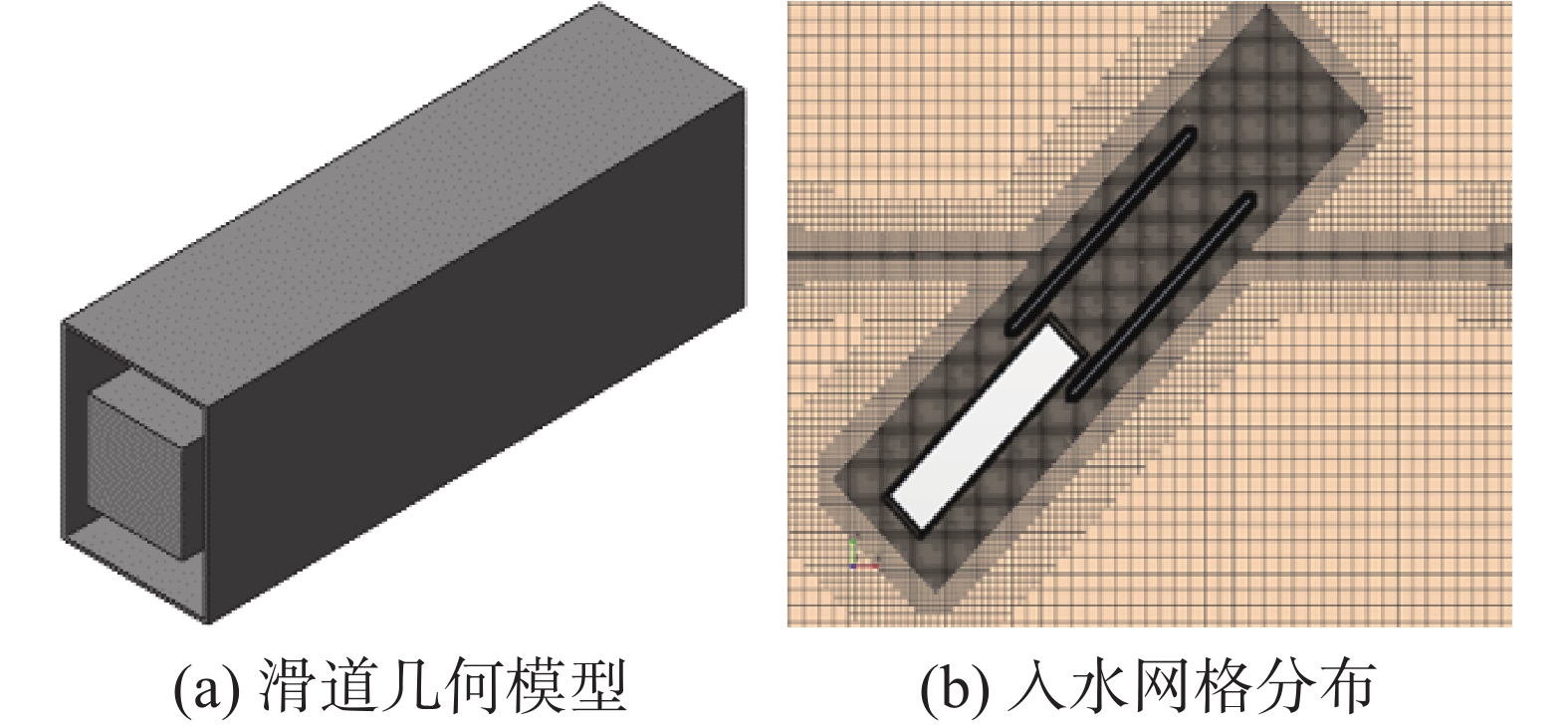
滑道入水几何模型如图1所示，入水模型置于滑道正中央，模型前端与滑道前端对齐。滑道内径宽度440 mm，高度560 mm，模型截面尺寸为300 mm×300 mm。
图 1 滑道及入水模型
下载:
全尺寸图片
物理模型选择SST（Menter）k-ω分离涡、DES，另外结合全y+壁面处理，精确壁面距离模型，确保近壁面流动精度。考虑重力、湍流、VOF波和欧拉多相流，形成水气两相并创建其分界面。后期计算流体域噪声时，需要选择气动声学模型和FW-H非稳态模型。水动力计算过程不添加噪声计算模型，选取时间步长为1.0×10−3 s。
流场充分发展后，在时间步节点位置暂停计算，选取噪声计算物理模型。采用FW-H声类比模型开展后续声学计算，依据水中声学参数设置声学接收器的相关参数，取接收器位置处声速为1482.9 m/s，密度为1025 kg/m3。时间步长通过最大声波求解频率fmax确定：
$$ {\text{ }}{s_{{\text{time}}}} = \frac{1}{{{f_{\max }}}} $$ 当最大求解频率为5000 Hz时，可求得时间步长为1×10−4 s。
为提高噪声预报研究的准确性，选取粗、中、细3个网格策略和2.0×10−4、1.0×10−4、5.0×10−5这3个噪声计算时间步长进行网格与时间步长的无关性分析。进行网格无关性分析时，噪声计算时间步长暂定为1.0×10−4 s，投放速度为2 m/s。由表1可知，综合考虑计算精度及计算成本，中等网格策略与实验的对比误差为2.1%，已满足要求。
表 1 网格收敛性对比网格策略 噪声级/dB 27°误差/% 粗 125.67 9.7 中 117.10 2.1 细 116.73 1.9 实验 114.53 — 在中等网格策略的基础上，调整噪声计算阶段时间步长，具体结果如表2。时间步长为1.0×10−4和5.0×10−5 s时与实验结果进行对比，误差分别为2.1%和2.6%，相差极小，因此噪声计算阶段时间步长取为1.0×10−4 s。
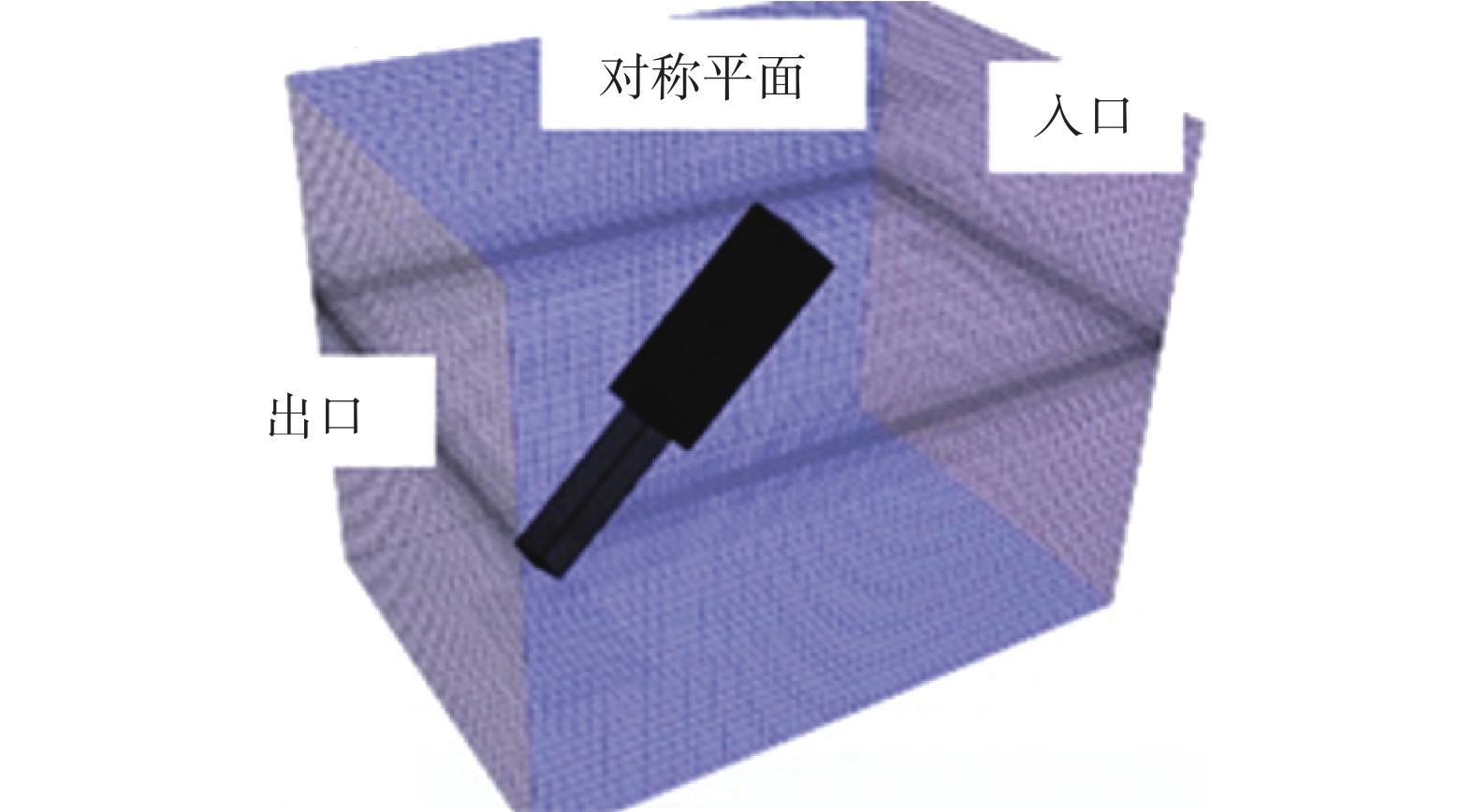
表 2 时间步收敛性对比时间步长/s 噪声级/dB 27°误差/% 2.0×10−4 123.65 8.0 1.0×10−4 117.10 2.1 5.0×10−5 117.54 2.6 实验 114.53 — 中等网格策略生成的网格总数为519万，其中，静止域网格数为475万，运动域网格数为44万。入水模型表面网格数为55万，滑道模型表面网格数为5万。滑道和入水物体表面进行了自定义表面重构，其表面的网格尺寸设置为基础尺寸的6.25%。计算域包括滑道在内的流体域、入水模型在内的运动域以及远场域。流体入口和出口分别设置为速度入口和压力出口，周向4个流场界面均为对称平面，如图2所示。
图 2 计算域及边界条件下载:
全尺寸图片
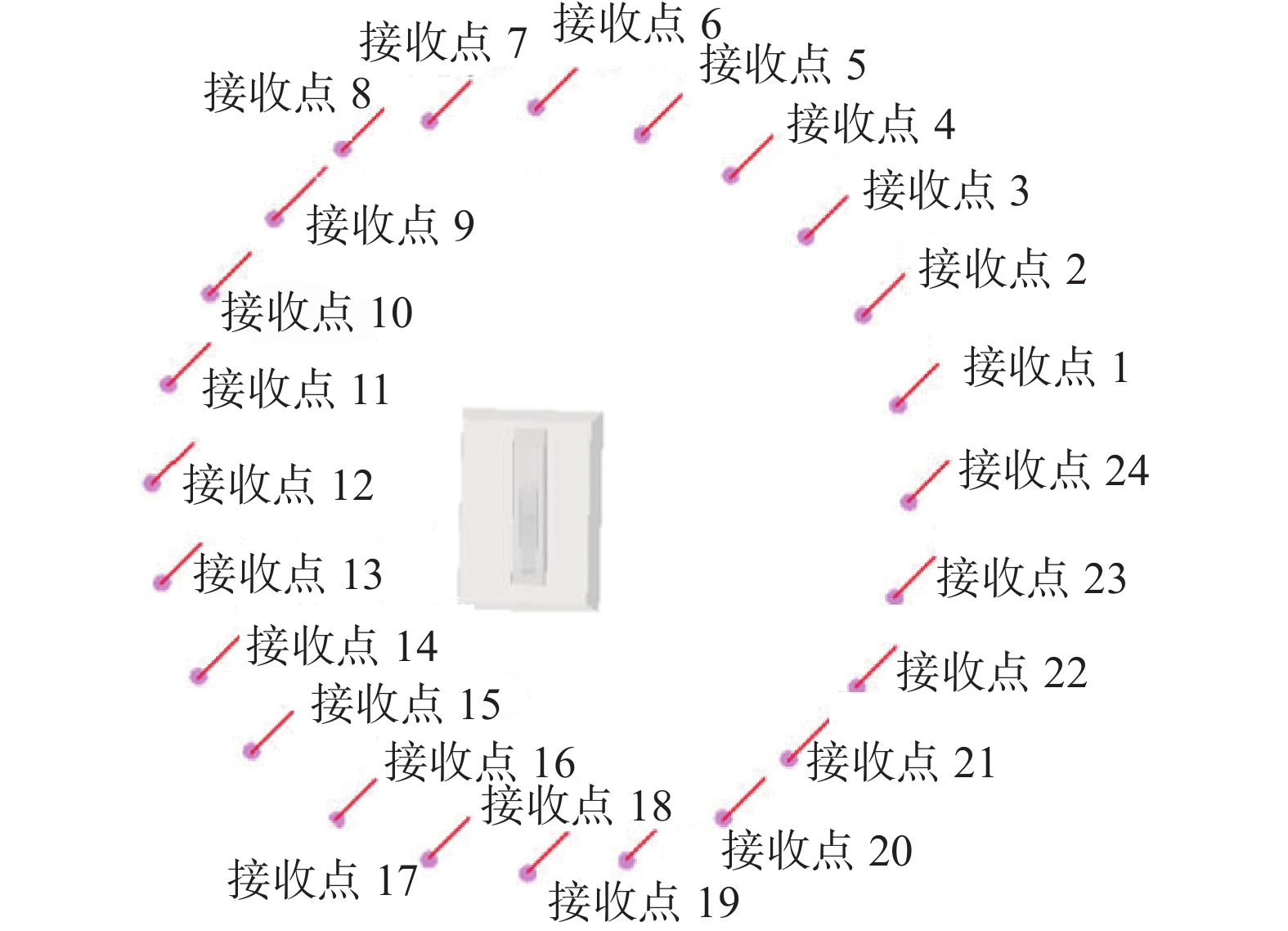
流体域外一共设置有24个接收点，接收点位于平面y=0上，接收点按照1~24逆时针分布于半径为10 m的圆周上，相邻之间的角度为15°，编号顺序如图3所示。接收点6为船尾方向，接收点18为船首方向。
图 3 监测点分布下载:
全尺寸图片
3. 实验设备
本次实验是在哈尔滨工程大学低频消声水池进行的。其基本参数如下：消声频率下限为3 kHz，尺寸为50 m×25 m×15 m。实验水池的背景噪声保持在85 dB以下，与实验结果间的差距远大于10 dB，符合国家噪声测试标准的规定，不会影响实验结果。本次实验中选择的丹麦的BK8104型水听器，如图4所示。
图 4 低频消声水池与BK8104水听器下载:
全尺寸图片
本次实验中制作的台架以及下水滑块模型如图5所示。
图 5 斜滑道台架及下水滑块模型下载:
全尺寸图片
4. 实验结果与仿真对比分析
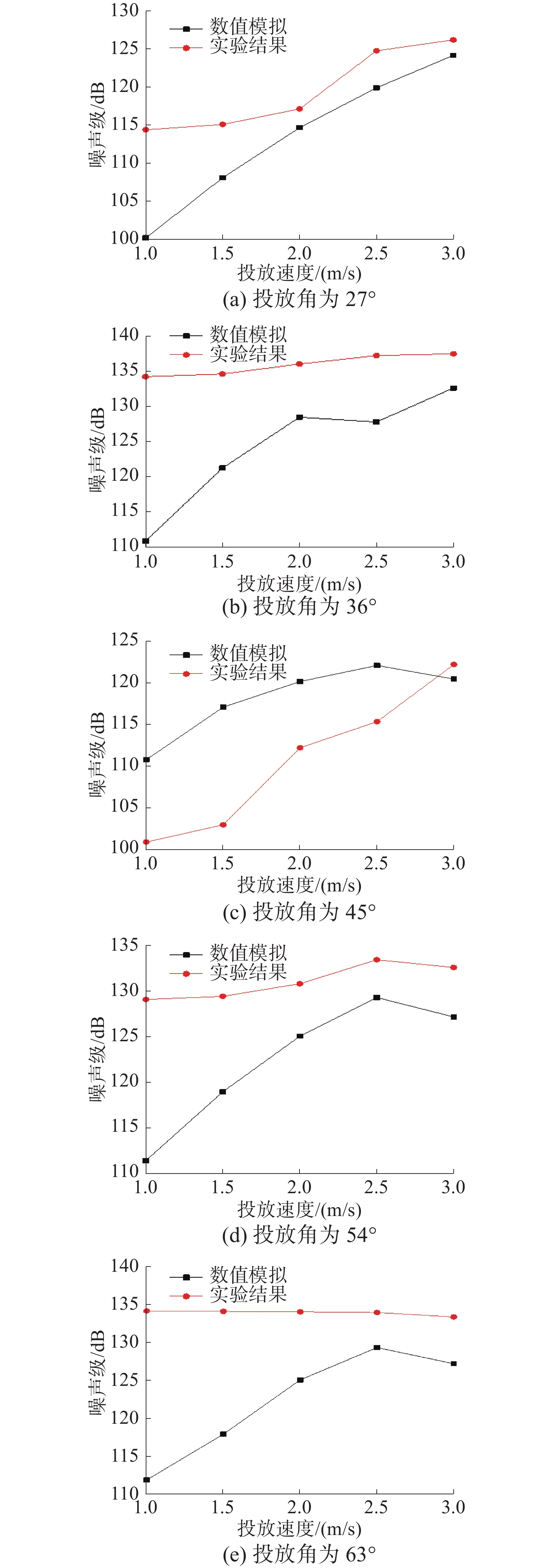
设定流速为零，滑道台架投放角度分别为27°、36°、45°、54°和63°，每个投放角度设有5个投放速度，分别为1、1.5、2、2.5和3 m/s。不同投放角下数值模拟与实验结果对比如图6所示。
图 6 不同投放角下数值模拟与实验结果对比下载:
全尺寸图片
数值与实验结果误差与平均误差结果如表3所示。对比图6（a）~（e）可以看出，随着投放速度的增加，入水速度提高，计算瞬时状态进一步缩短，截取的计算时长减少，分辨率开始降低，因此实验结果中噪声级在逐渐增加，仿真结果噪声级也大致呈增长趋势，而且噪声级平均误差绝大部分在10%以内。从上面的分析可以看出仿真结果与实验结果吻合较好。
表 3 数值模拟与实验结果误差统计投放速度/（m/s） 误差/% 27° 36° 45° 54° 63° 平均值 1.0 12.4 17.5 9.8 13.6 16.5 13.9 1.5 6.1 9.9 13.7 8.1 12.0 9.9 2.0 2.1 5.5 7.1 4.4 6.7 5.1 2.5 3.9 6.8 5.8 3.1 3.4 4.6 3.0 1.6 3.5 1.4 4.1 4.6 3.1 5. 典型工况分析
完成对实验结果与数值模拟的数据对比后，本节针对典型工况下的自由液面处以及噪声的时域与频域特性方面对实验环境与数值仿真的误差来源进行分析。
5.1 自由液面处的变化
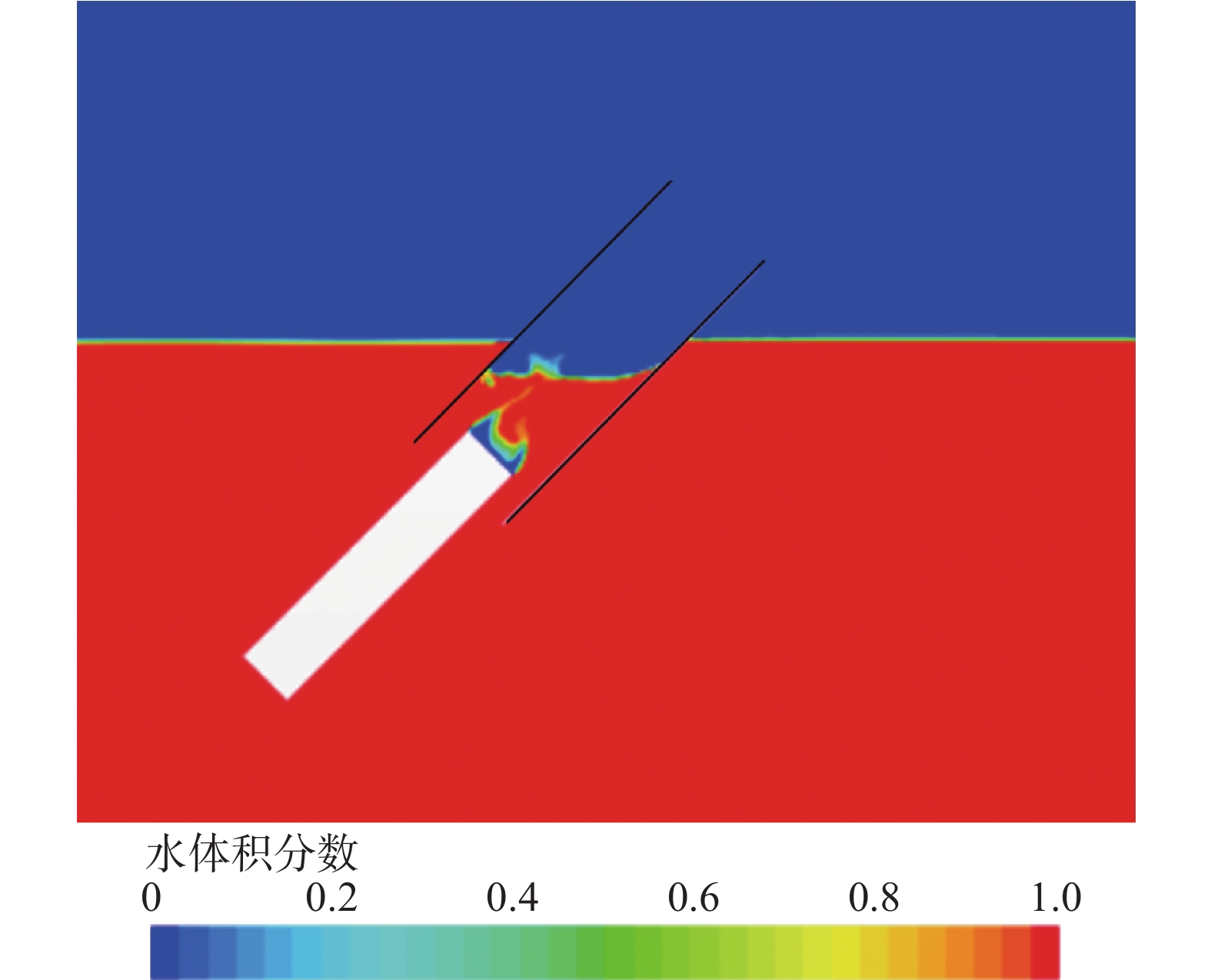
在投放角度54°，投放速度3 m/s工况下，从气液相体积分数图图7中可以看到，模型沿滑道斜向下发生入水砰击运动时，自由面发生剧烈变化，流体受到强烈扰动，从而产生流场速度和压力的瞬时脉动。不同于以往的完全浸没的航行体噪声实验，实验入水物体有一个高速穿越自由液面的过程，由此导致声信号的瞬态特性。另外，实验还需考虑斜滑道与入水物体的共同作用，在没有滑道的情况下，自由液面仅会产生斜射流以及飞溅现象；但当滑道存在时，自由液面的变化会和滑道发生相互作用，从而引发强烈的二次声辐射。
图 7 入水后自由液面附近气液两相分布下载:
全尺寸图片
流固耦合振动噪声是斜滑道入水噪声的另外一部分，滑道的主要骨架结构强度较大，不易产生流固耦合运动。但是，实验的滑道壁比较薄，仅用轻桁材支撑，会导致滑道壁的流固耦合运动，从而诱导声辐射的产生。滑道壁的流固耦合运动所导致的声辐射和其运动的模态有关，高阶模态对辐射噪声贡献比较小，低阶模态虽然被流体噪声所掩盖，但是对实验结果的总声级起到一定作用。
在科考设备入水时，由于机械传动以及电机驱动等原因，不可避免地会产生一些机械噪声，这也是实验结果与数值结果的误差来源之一。
因此，本文所研究的声辐射机理是十分复杂的，涉及到流激噪声、机械噪声和流固耦合噪声以及自由液面效应。另外，本实验缺少相关的经验借鉴，针对性的频谱特性分析方法不够成熟，尤其是针对瞬态声辐射问题，滑道不同噪声成分及频谱特征的提取和识别在短时间内很难完成，这也是未来需要进一步研究的关键技术问题。
5.2 噪声时域特性与频域特性
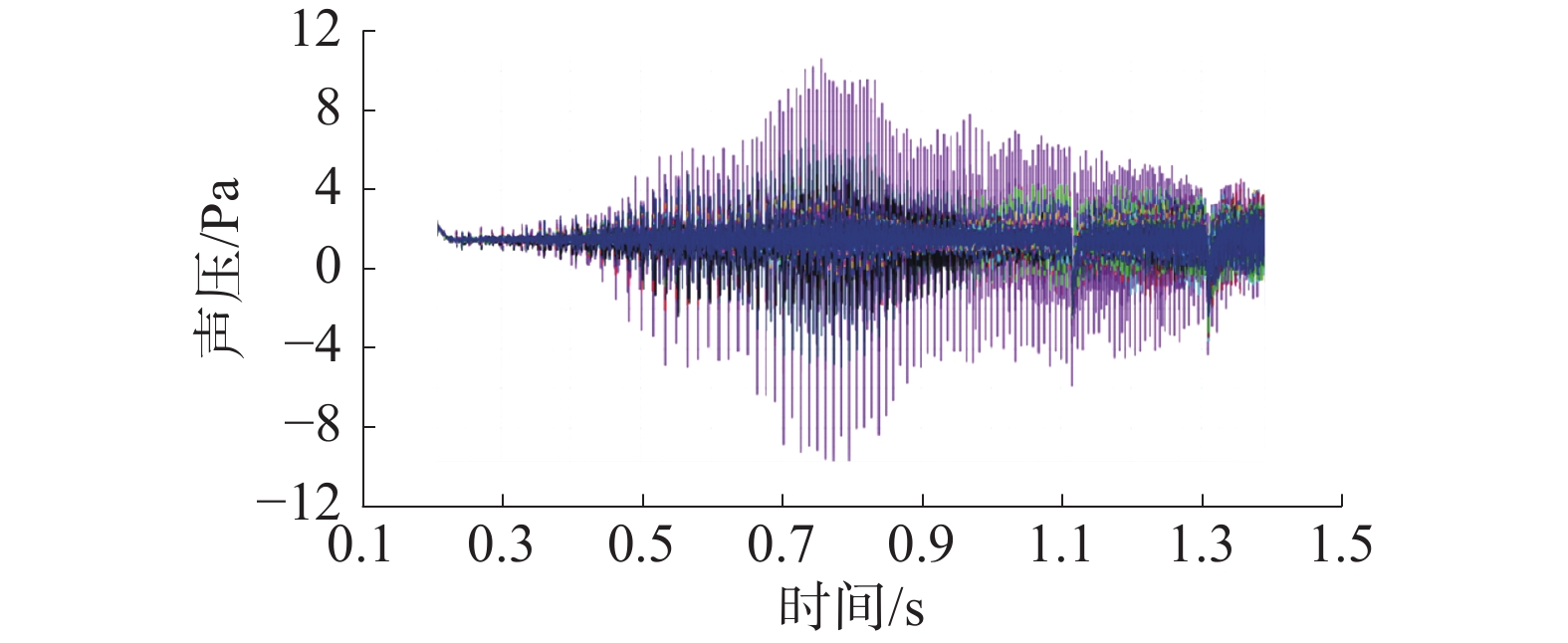
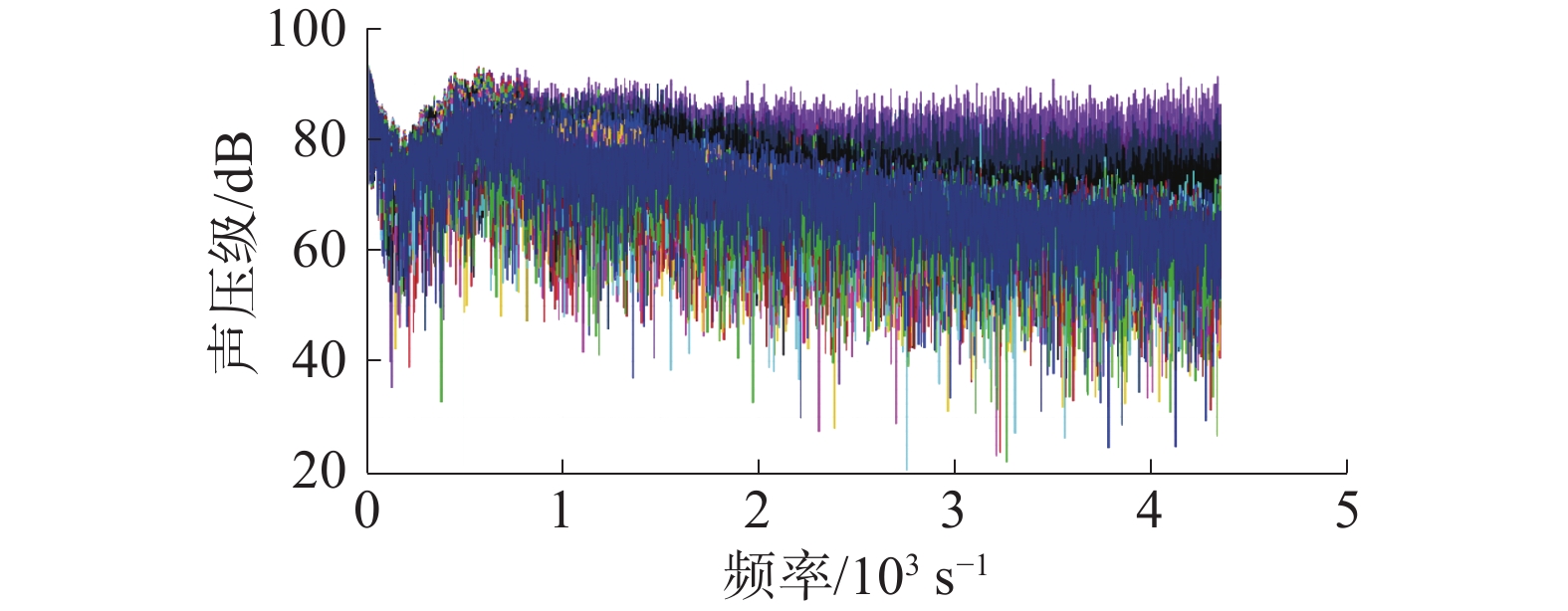
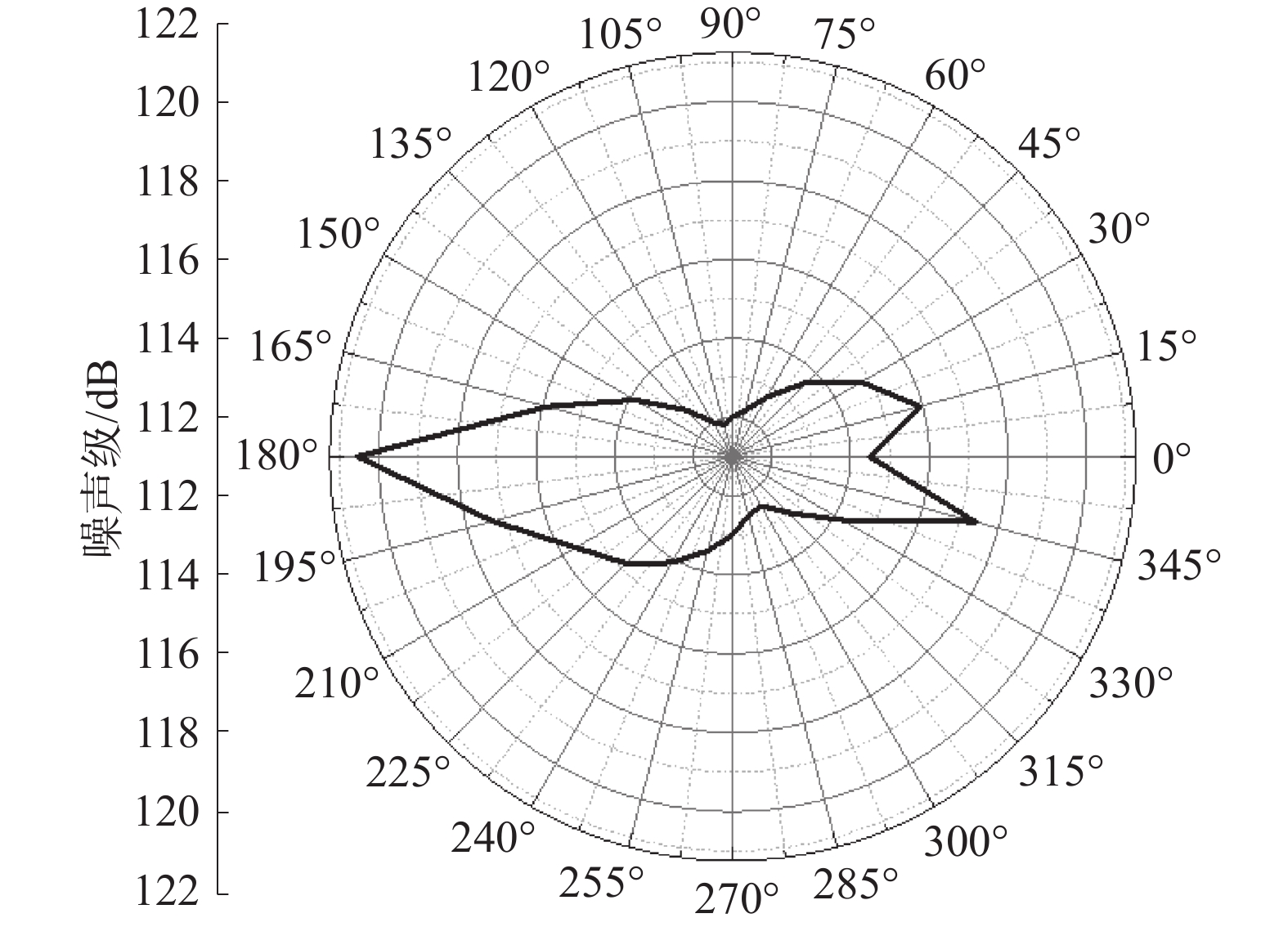
在投放角度45°、投放速度3 m/s工况下，如时域图图8中所示，刚开始声压波动较小，而后波动幅度逐渐增加，最后逐渐减小。模块入水瞬间产生较大压力，而后在阻力的作用下不断减速直至浮出水面。在频域图图9中，投放过程的噪声能量集中于低频段，位于500~1000 Hz，之后随着频率的增加，噪声级逐渐减小。在噪声指向性图图10中，90°是船尾方向，270°是船首方向，可以看出船舶左舷和右舷方向噪声较大，且呈非对称分布。
图 8 45°投放角噪声时域下载:
全尺寸图片
图 9 45°投放角全入水过程辐射噪声频域下载:
全尺寸图片
图 10 45°投放角噪声指向性下载:
全尺寸图片
斜滑道入水科考设备模型从气态介质进入液态介质，自由液面运动和变形较难预测，与此同时，科考设备与滑道之间的流体砰击声传播机理还未完全清楚，使得实验结果与数值计算很难保证完全的一致性。
6. 结论
本文建立了斜滑道科考设备入水噪声预报数值模型，并通过实验进行验证，通过对比数值结果与实验数据，结果表明基于分离涡DES与FW-H方法预报入水噪声问题具有合理性。文章进一步地结合科考设备入水过程时的流场与声场特性，对实验与数值的系统性误差来源作出解释。本文研究结论总结如下：
1）在噪声的总声级方面，流致噪声占总噪声的主要部分。模型头部入水时即入水模型和液面发生接触砰击时噪声达到最大值，模型在与水接触砰击后噪声下降明显，在尾部入水时噪声再次增大，整个过程中模型头部入水和尾部入水时噪声到达2个峰值，这2个峰值对船舶的噪声级影响较大。
2）在声指向性方面，入水时船舶四周的声辐射都有增强，但船首尾方向的声辐射增强更为明显，这意味着模型入水时会沿着船舶的首尾方向产生更大的噪声，进而增强船首尾方向的噪声级。
3）由于斜滑道与科考设备之间的相互耦合作用、滑道壁流固耦合现象的存在、传送过程中不可避免的机械噪声以及声辐射特性数值模拟模型的不完备性，造成了数值模拟与实验之间存在误差的结果。但通过对两者之间的误差分析可以看出，使用分离涡DES以及FW-H模型数值模拟科考设备斜滑道入水问题与真实情况相比误差较小，对其噪声特性的预报具有参考价值，对改善船舶释放科考设备的噪声级具有指导意义。
-
图 1 滑道及入水模型
下载:
全尺寸图片
图 2 计算域及边界条件
下载:
全尺寸图片
图 3 监测点分布
下载:
全尺寸图片
图 4 低频消声水池与BK8104水听器
下载:
全尺寸图片
图 5 斜滑道台架及下水滑块模型
下载:
全尺寸图片
图 6 不同投放角下数值模拟与实验结果对比
下载:
全尺寸图片
图 7 入水后自由液面附近气液两相分布
下载:
全尺寸图片
图 8 45°投放角噪声时域
下载:
全尺寸图片
图 9 45°投放角全入水过程辐射噪声频域
下载:
全尺寸图片
图 10 45°投放角噪声指向性
下载:
全尺寸图片
表 1 网格收敛性对比
网格策略 噪声级/dB 27°误差/% 粗 125.67 9.7 中 117.10 2.1 细 116.73 1.9 实验 114.53 — 表 2 时间步收敛性对比
时间步长/s 噪声级/dB 27°误差/% 2.0×10−4 123.65 8.0 1.0×10−4 117.10 2.1 5.0×10−5 117.54 2.6 实验 114.53 — 表 3 数值模拟与实验结果误差统计
投放速度/（m/s） 误差/% 27° 36° 45° 54° 63° 平均值 1.0 12.4 17.5 9.8 13.6 16.5 13.9 1.5 6.1 9.9 13.7 8.1 12.0 9.9 2.0 2.1 5.5 7.1 4.4 6.7 5.1 2.5 3.9 6.8 5.8 3.1 3.4 4.6 3.0 1.6 3.5 1.4 4.1 4.6 3.1 -
[1] 师长, 陈云赛, 黄礼敏, 等. 失事航天器高速入水砰击数值模拟研究[J]. 华中科技大学学报(自然科学版), 2021, 49(5): 44−49. doi: 10.13245/j.hust.210508 [2] 罗柏华, 刘宇陆. 湍流边界层流场与噪声实验研究[J]. 实验力学, 2001, 16(4): 378−386. doi: 10.3969/j.issn.1001-4888.2001.04.005 [3] 张浩, 冯涛, 刘碧龙, 等. 离心泵流噪声实验研究[J]. 噪声与振动控制, 2013, 33(1): 119−122. [4] YEO S J, HONG S Y, SONG J H, et al. Integrated analysis of flow-induced noise from submarine under snorkel condition[J]. Proceedings of the institution of mechanical engineers, part M:journal of engineering for the maritime environment, 2020, 234(4): 771−784. doi: 10.1177/1475090220916594 [5] 白俊强, 余培汛, 郭博志, 等. 用CFD/FW-H混合方法计算圆柱/翼型的气动噪声[J]. 西北工业大学学报, 2012, 30(6): 847−851. doi: 10.3969/j.issn.1000-2758.2012.06.009 [6] 欧阳绍修, 刘学强, 张宝兵. DES方法模拟空腔流动及噪声分析[J]. 南京航空航天大学学报, 2012, 44(6): 792−796. doi: 10.3969/j.issn.1005-2615.2012.06.005 [7] 张群峰, 闫盼盼, 黎军. 分离涡模拟和非线性声学方法求解腔体气动噪声对比分析[J]. 兵工学报, 2016, 37(6): 1096−1103. doi: 10.3969/j.issn.1000-1093.2016.06.018 [8] 李环, 刘聪尉, 吴方良, 等. 水动力噪声计算方法综述[J]. 中国舰船研究, 2016, 11(2): 72−89. doi: 10.3969/j.issn.1673-3185.2016.02.011 [9] 王春旭, 吴崇建, 陈乐佳, 等. 流致噪声机理及预报方法研究综述[J]. 中国舰船研究, 2016, 11(1): 57−71. doi: 10.3969/j.issn.1673-3185.2016.01.008 [10] 刘波, 武国启. 船体绕流场及流噪声的CFD模拟方法[J]. 舰船科学技术, 2019, 41(19): 63−69. doi: 10.3404/j.issn.1672-7649.2019.10.012 [11] MENTER F R. Influence of freestream values on k-omega turbulence model predictions[J]. AIAA journal, 1992, 30(6): 1657−1659. doi: 10.2514/3.11115 [12] SPALART P R, DECK S, SHUR M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and computational fluid dynamics, 2006, 20(3): 181−195. doi: 10.1007/s00162-006-0015-0 [13] WILLIAMS J E F, HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion[J]. Philosophical transactions of the royal society of London series A, mathematical and physical sciences, 1969, 264(1151): 321−342. doi: 10.1098/rsta.1969.0031 [14] FARASSAT F. Linear acoustic formulas for calculation of rotating blade noise[J]. AIAA journal, 1981, 19(9): 1122−1130. doi: 10.2514/3.60051 [15] SI Qiaorui, SHEN Chunhao, ALI A, et al. Experimental and numerical study on gas-liquid two-phase flow behavior and flow induced noise characteristics of radial blade pumps[J]. Processes, 2019, 7(12): 920–939. doi: 10.3390/pr7120920
