Multi-agent confrontation strategy algorithm based on deep reinforcement learning
-
摘要: 针对在复杂军事化背景下多智能体决策算法探索效率低下、收敛缓慢的问题，提出了基于多头注意力机制和优先经验回放的多智能体深度确定性策略梯度算法（AP-MADDPG）。算法采用基于优先级的经验回放减少算法的训练时间；采用多头注意力机制在复杂的对抗环境中实现智能体之间的稳定、高效的合作竞争。实验结果表明，该算法可以使多智能体更加有效地学习联合策略，拥有更快的收敛速度和更好的稳定性，同时可以获得更高的回合奖励。Abstract: Aiming at the problem of low-efficiency exploration and slow convergence of multi-agent decision-making algorithms in the context of complex militarization, this paper proposes a multi-agent depth deterministic policy gradient algorithm (AP-MADDPG) based on muti-head-attention mechanism and prior experience replay mechanism. Priority experience replay replaces uniform sampling to reduce the training time of the algorithm; the multi-head attention mechanism is used to achieve stable and high-efficiency cooperation and competition between agents in a complex confrontation environment. Experimental results show that the algorithm can make multi-agent learn joint strategies more effectively. The algorithm has a faster convergence speed and better stability, and at the same time, obtains higher round rewards.
-
随着科技的进步和发展，未来战争的规模和复杂度不断增大，作战方式的多样性也逐渐增强。针对如此复杂多变的战争场景，仅仅依靠人来指挥作战决策，难以实现高效且正确的作战方针。深度强化学习广泛应用于处理序贯决策问题，通过将前人的作战经验和决策方式联系在一起，为现代化战争指明了新的发展方向。
随着人工智能的不断发展，强化学习在单智能体竞争中取得了巨大成功，如围棋游戏[1]和雅达利游戏[2]。然而，由于智能体数量的不断增加，智能体动作状态的维度呈指数级增长，传统的强化学习方法如Q-learning和策略梯度[3]已经不适合多智能体环境。在多智能体环境中，所有智能体同时学习，当1个智能体的策略改变时，其他智能体的最优策略可以会受到影响，从而导致算法难以收敛[4]。目前，多智能体场景下的强化学习已广泛应用于机器人控制[5]、通信[6]、无人机[7-8]等领域。
多智能体强化学习在智能体的合作对抗作战任务中更为困难。多智能体强化学习的研究主要集中在合作和竞争2个方面。Tampuu等[9]使用深度Q网络(deep Q network，DQN)代替Q学习算法对每个智能体进行单独训练，并提出了一个深度强化学习(deep reinforcement learning，DRL)模型，该模型通过根据不同的目标动态调整奖励来相互合作和竞争。但是由于其他智能体的策略总是在变化，导致环境变得不平稳。Tesauro等[10]尝试通过将其他智能体的策略参数输入到Q函数，显式地将迭代索引添加到重播缓冲区，但性能并没有得到太大改善。Sukhbataret等[11]设计了一种称为CommNet的神经网络，来实现合作环境中的持续通信。Palmeret等[12]提出了Lenient DQN，引入基于双DQN[13]的Lenient损失函数，以适应多智能体强化学习的合作问题。Foersteret等[14]提出了使用集中式评论家的反事实多智能体策略算法(counterfactual multi-agent policy gradients，COMA)，集中式评论家可以获得全局信息来指导每个智能体，从而进一步提高每个智能体的信息建模能力。然而，由于只有1个集中的评论家家，智能体不允许有不同的奖励函数。Rashid等[15]提出了QMIX算法，该方法通过在混合网络结构中添加全局状态信息来提高算法性能。
在传统的连续控制领域中，智能体动作空间大且动作值连续，如果智能体直接从像素级信息中学习，任务将变得十分困难。近来，一种多智能体深度确定性策略梯度(multi-agent deep deterministic policy gradient, MADDPG)[16]算法，通过将确定性策略梯度算法与游戏技巧相结合，在许多模拟的连续控制问题中取得了良好的性能。本文采用DRL方法，基于MADDPG算法来解决多智能体竞争环境下的决策问题，通过引入多头注意力机制和基于优先级的经验回放机制，提出了一种改进的AP-MADDPG算法，有效地提高了训练效率，缩短了收敛时间。本文以多智能体粒子环境(multi-agent particle envs, MPE)为测试环境，在4种多智能体对抗环境中验证算法的性能。
1. 多智能体策略模型
1.1 多智能体协同对抗决策流程设计
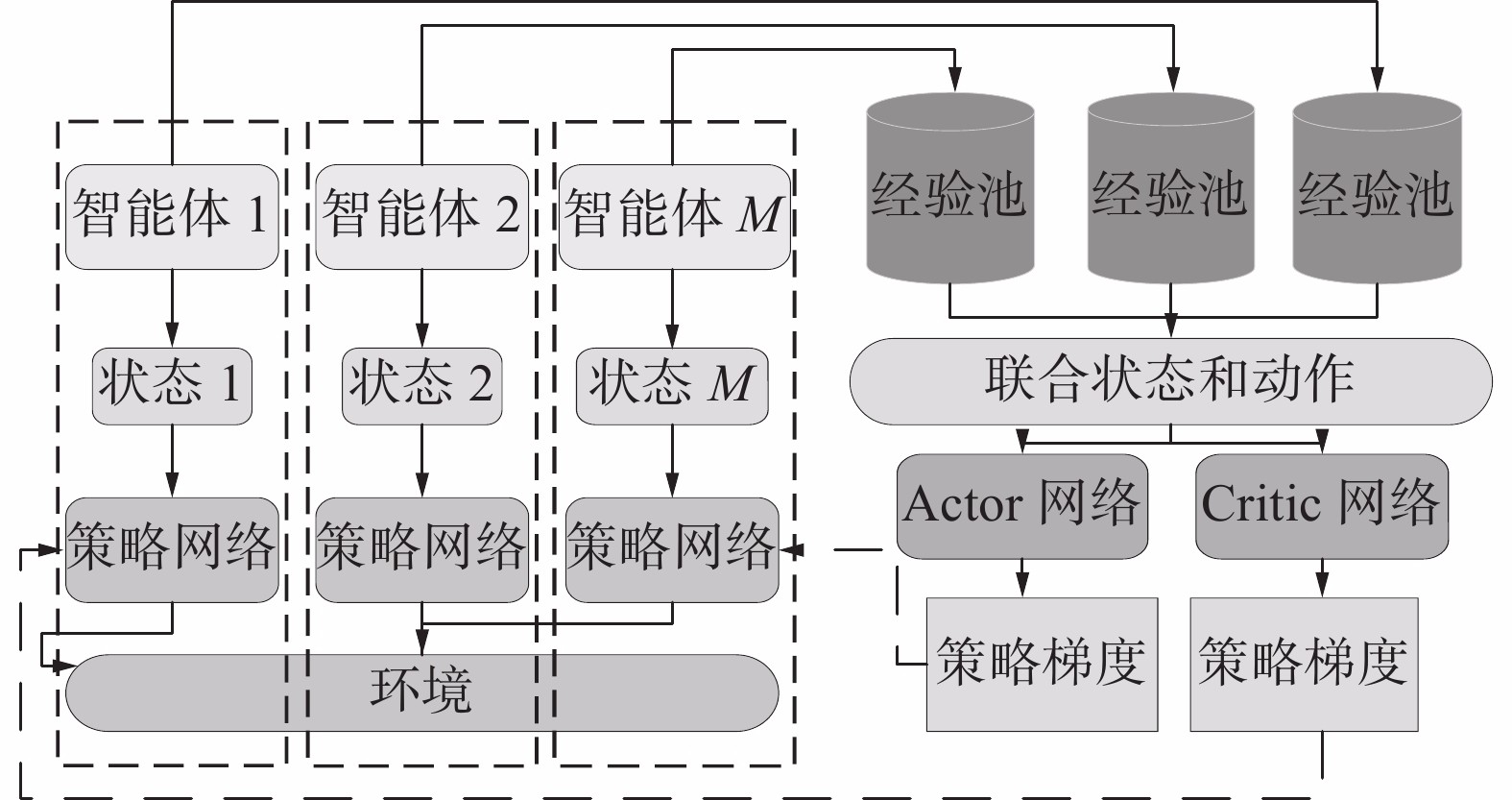
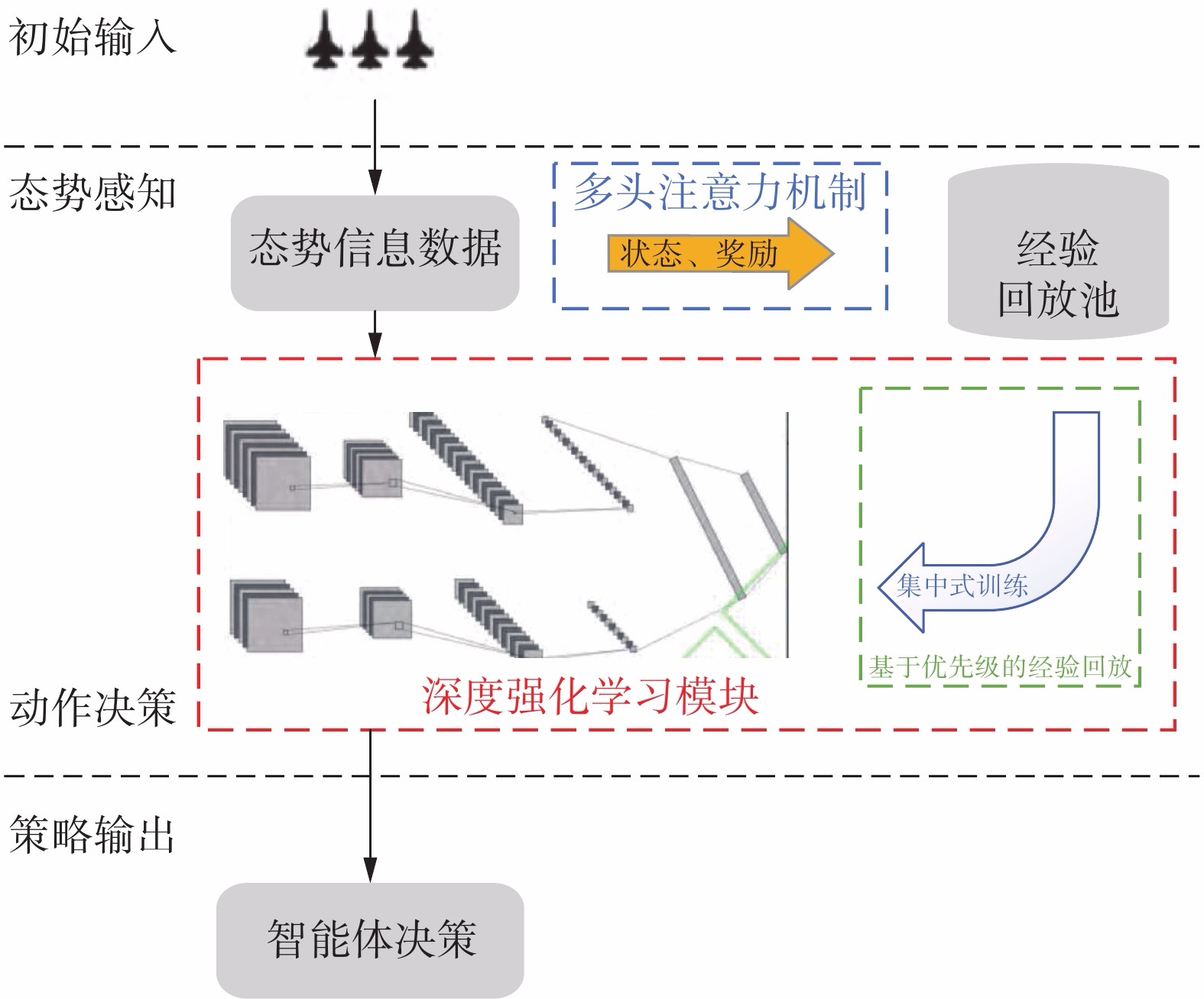
多智能体协同对抗决策框架由3个部分组成，分别为态势信息数据处理、深度强化学习训练、智能体策略输出。决策模型如图1所示。态势感知处理模块将智能体所处的环境信息进行融合处理，这些环境信息是智能体做出决策的重要依据。深度强化学习模块接受态势信息数据，输出动作决策。输出的动作作用于环境得到新的状态信息和此状态动作下环境给予的奖励值。将这些经验数据存储放入经验回放池，训练神经网络时，从经验回放池抽取经验样本进行网络的训练。
图 1 多智能体协同对抗决策模型
下载:
全尺寸图片
1.2 MADDPG算法
MADDPG算法是深度确定性策略梯度算法 (deep deterministic policy gradient, DDPG)在多智能体环境下的改进算法，它采用Actor-Critic结构。Actor网络和Critic网络都包含2个网络、1个online策略网络和target策略网络。Actor网络根据智能体观测状态计算执行动作，Critic网络通过评估Actor的动作来改进Actor网络的性能。Critic网络采用中心化训练和非中心化执行的训练方式，在训练过程中，引入全局观测的Critic训练Actor网络，测试过程中，使用局部观测的Actor来输出动作。
相对于传统Actor-Critic算法，MADDPG算法环境中共有M个智能体，第i个智能体的策略用
$ \pi_{\mathrm{i}} $ 表示，且其策略参数为$ \theta_{i} $ ，则可以得到M个智能体的策略集为$\pi=\{\pi_{1}, \pi_{2}, \cdots, \pi_{i}\}$ ，策略参数集合为$\theta= \{\theta_{1}, \theta_{2}, \cdots, \theta_{M}\}$ 。第i个智能体的期望收益梯度为$$ \nabla_{\theta_{i}} J\left(\theta_{i}\right)={{\rm{E}}}_{s \sim p^{\pi}, a_{i} \sim \pi_{i}}\left[\nabla_{\theta_{i}} \log \pi_{i}\left(a_{i} \mid o_{i}\right) Q_i^{\pi} (s, a)\right] $$ 式中：
$p^{\pi}$ 为状态分布，s=(o1,o2,···,oN)表示联合状态，a=(a1,a2,···,aN)表示联合动作，$Q_i^{\pi}$ (s, a)为联合动作值函数。本文提出的算法框架如图2所示。对于单个智能体，其首先将观测到的环境状态信息输入到策略网络中，策略网络输出动作信息，环境状态发生改变，智能体会得到新的环境状态和奖励值，将这些信息存储到经验池中。由于环境中存储在多个智能体，每个智能体都会和环境不断继续进行交互，这些信息会存储到他们各自的经验池中。
图 2 MADDPG算法框架下载:
全尺寸图片
在神经网络的训练过程中，随机从各个智能体的经验池中抽取相同时刻的数据，将其组成一组经验样本
$ \left\langle S, A, S^{\prime}, R\right\rangle $ 。其中S是所有智能体智能体的状态信息集合，S'是智能体做出动作后环境的状态信息集合，A是智能体的动作集合，R是智能体获得的奖励值。将所有智能体的状态动作信息组成联合状态和动作，输入第i个智能体的Critic网络中，得到智能体i下一时刻的目标Q值，目标Q值的计算公式如下：$$ y_{i}=r_{i}+\gamma Q^{\prime}\left(s_{i+1}, \mu^{\prime}\left(s_{i+1} \mid Q^{\mu^{\prime}}\right) \mid \theta^{Q^{\prime}}\right) $$ 实际Q值通过评价网络得到，利用TD误差(temporal-difference, TD-error)来更新评价网络。算法使用策略梯度来更新策略网络。每个智能体的更新方法除了在输入方面有所差别，其余更新方法相同。
2. MADDPG算法改进
2.1 面向多智能体竞争的注意力机制
MADDPG算法采用联合状态解决了智能体之间的不可观测性，但是随着智能体数量增加而带来的维度爆炸弊端依然没有解决。本文为了解决多智能体数量不断增加而导致的强化学习算法难以收敛的问题，引入多头注意力机制。
在多智能体环境中，注意力机制就是帮助各智能体能够观测到到其他智能体的观，并将此信息根据注意力权重的大小整合到自身动作值函数估计中。2017年，Vaswani等[17]提出多头注意力机制(multi-head attention)，将模型分为多个头，形成多个子空间，将Scaled Dot-Product运算进行h次，再把输出合并起来，有助于模型接收各个方面的信息。本文将多头注意力机制引入多智能体学习，相比其他的注意力机制，它没用对输入的空间或时间局部性做出假设，多头注意力机制结构如图3所示。
图 3 多头注意力机制结构下载:
全尺寸图片
如图3所示，在计算智能体的Q函数时，不仅将智能自身的观测和其他智能体的观测一起作为Q函数的输入，而且增加了1个两层的多层感知机(multi-layer perception, MLP)网络，智能体i的Q值函数计算方式如下：
$$ Q_{i}(o, a)=f_{i}\left(g_{i}\left(o_{i}, a_{i}\right), x_{i}\right) $$ 式中：
$ f_{i} $ 为1个两层的多层感知机（multilayer perceptron，MLP）网络，$ \mathrm{g}_{i} $ 为1个单层的 MLP 网络，$ \boldsymbol{x}_{i} $ 为其他智能体对第i个智能体价值的加权和。计算方式如下：$$ x_{i}= \displaystyle \sum_{j \neq i} \alpha_{j} v_{j}= \displaystyle \sum_{j \neq l} \alpha_{j} h\left({\boldsymbol{V}}g_{j}\left(o_{j}, a_{j}\right)\right) $$ 式中：
$ h $ 为ReLU激活函数；$ v_{j} $ 由共享矩阵${\boldsymbol{V}}$ 和编码器$ g_{j} $ 计算得到；$ \alpha_{j} $ 为注意力权重，表示agenti和agentj的相似性权重，计算方式如下：$$ \alpha_{j}=\exp \left(e_{j}^{{\rm{T}}} {\boldsymbol{W}}_{k}^{{\rm{T}}} {\boldsymbol{W}}_{q} e_{i}\right) $$ 式中：Wk和Wq分别为2个线性映射的矩阵；
$ e_{i} $ 和$ e_{j} $ 分别为智能体i和j的状态编码；Wq将$e_{i}$ 转化为查询值；Wk将$ e_{j} $ 转化为键值，然后将矩阵进行维度计算，防止梯度消失。在多头注意力机制中，每个头的参数(Wq, Wk, V)独立，从而区分每个智能体对不同状态位置的智能体的关注度。2.2 基于优先级的经验回放机制
经验回放方法通过存储智能体的经验并且进行随机采样，削弱了数据之间的相关性。MADDPG算法中，采用经验重放机制打破输入训练经验与目标网络之间的相关性，并利用目标网络方法赋予训练过程一个一致的目标。同时，采用批处理归一化约束网络参数的变化。这些方法稳定了训练过程，并使大型非线性神经网络的训练成为可能。但是MADDPG算法中的经验回放采用随机抽样方法，由于经验质量参差不齐，导致算法学习效率低、收敛速度慢。
为了解决上述问题，优先经验回放方法 (prioritized experience replay，PER)已广泛应用于DQN、DDPG等算法中，在单智能体强化学习问题中表现良好。但是，在多智能体任务中，由于每个智能体都有单独的经验回放池来存储自己的经验，根据各自的评价进行存储和回放会破坏集中式经验训练的相关性。
针对MADDPG算法集中训练的特点，本文使用集中式经验缓冲区，该缓冲区存储了智能体的联合信息
$ \left(s, a, r, s^{\prime}\right) $ 。所以本文采用基于优先级的经验回放对MADDPG算法进行改进。优先经验回放的核心理念是更频繁地回放非常成功或非常糟糕的经验。因此，界定经验的价值是核心问题。在大多数强化学习的算法中，使用TD-error来更新动作值函数Q(s,a)的估计。TD-error的值作为对估计的修正，可以隐含地反映智能体从经验中学习的程度。如果 TD-error 的绝对值越大，就表示对动作值函数的修正的作用越大。因此，TD-error 越大的经验就具有越高的价值，并且可以帮助智能体找到更好的动作。此外，具有较大负TD-error的经验是智能体表现不佳的动作和状态，更频繁地重复这些经验，可以帮助智能体逐渐意识到相应状态下错误行为的真实后果，避免在这些条件下再次做出错误行为，从而提高整体性能。因此，这些糟糕的学习经验也是高价值的。
本文选取TD-error的绝对值作为评价经验价值的标准。对经验j计算TD-error的公式为
$$ \delta_{j}=r\left(s_{t}, a_{t}\right)+\gamma Q^{\prime}\left(s_{t+1}, a_{t+1}, w\right)-Q\left(s_{t}, a_{t}, w\right) $$ 在TD-error值较大的情况下，目标网络的评估值与该经验的实际值存在较大差异。因此，需要增加采样频率，尽快将目标网络和评估网络的值进行耦合，以达到最佳的训练效果，因此，我们引入抽样经验概率，将经验j的抽样概率定义为
$$ P({j})=\dfrac{D_{j}^{\alpha}}{ \displaystyle \sum_{k} D_{k}^{\alpha}} $$ 式中：
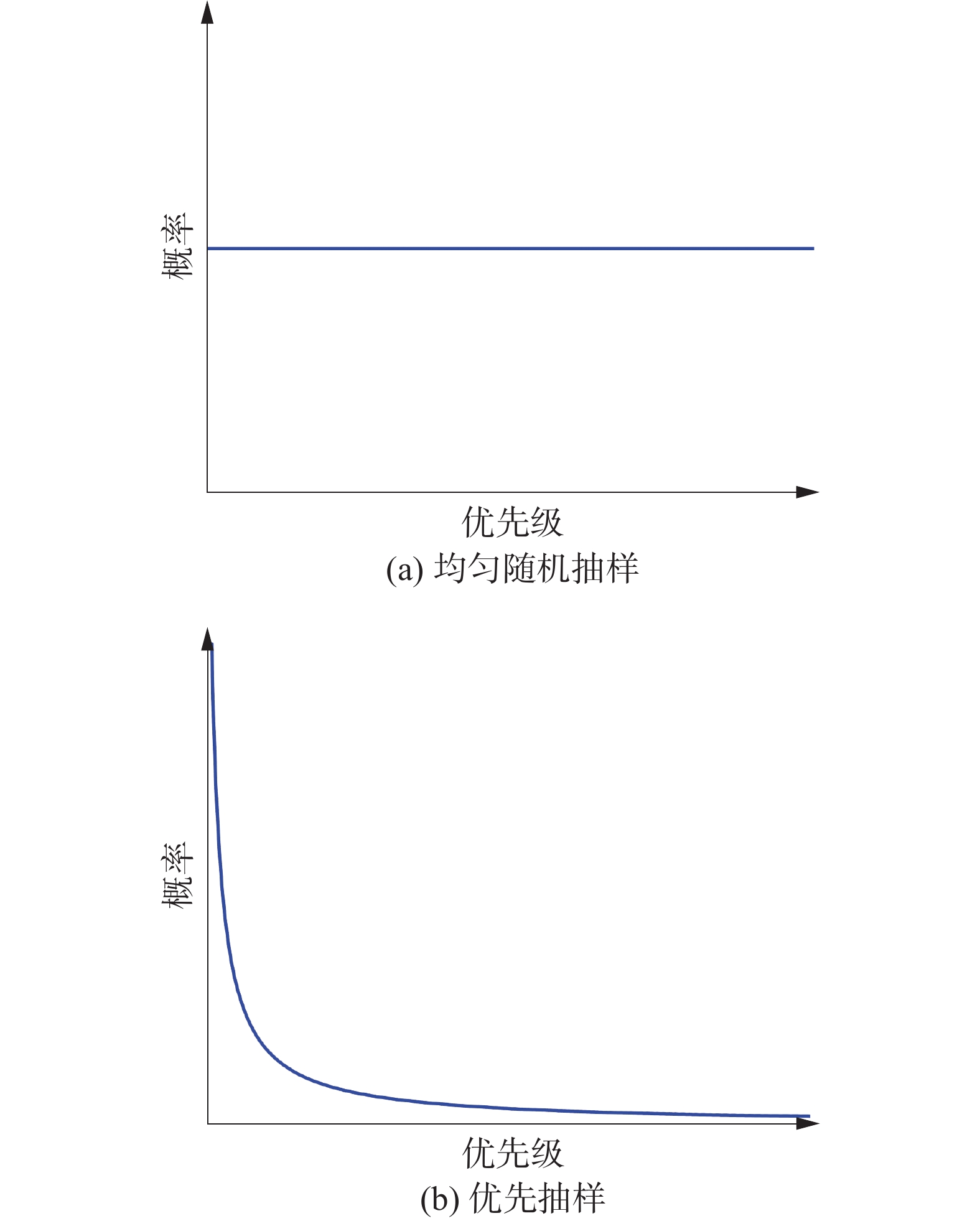
$D_j=\dfrac{1} {{\rm{rank}}(j)}$ ，rank(j)为基于TD-error绝对值的第j个经验在经验缓冲池中的位置等级；参数a决定优先级，当a=0时，就是均匀采样。经验抽样概率与经验等级的关系如图4所示，由图4可以看出，当TD-error较低时，经验也可能被抽样，保证了抽样经验的多样性，有助于防止神经网络过拟合。
图 4 经验概率与经验等级关系下载:
全尺寸图片
但是由于对高TD-error经验的频繁重放，会改变状态的访问频率，可能会导致神经网络的训练过程容易出现震荡甚至放散，为了解决这个问题，引入重要性采样权重：
$$ \omega_{{j}}=\frac{1}{S^{\beta}P(j)^{\beta}} $$ 式中：S为经验缓冲池的大小；P(j)是经验j的采样概率；参数β用来控制重要性采样权重在学习过程中的影响，当β增加为1，代表完全抵消优先级经验缓冲池对收敛结果的影响。
当训练过程趋于收敛时，无偏的更新对于误差收敛至关重要。为了提高算法模型的稳定性，我们使用
$ 1 / \max _{j} \omega_{j} $ 对权重进行归一化处理，使其只向下缩放更新。我们将中损失函数的定义改为$$ \mathcal{L}\left(\theta_{i}\right)=\frac{1}{j} \sum_{j} \omega_{j} \delta_{j}^{2} $$ 算法 AP-MADDPG算法整体流程
输入 优先采样参数α、β、最小批次K、经验回放池D
输出 智能体策略集合
$ \pi=\pi_{1}, \pi_{2}, \cdots, \pi_{i} $ 1）for episode = 1 to M do:
2）初始化随机变量N作为探索因子
3）接收初始状态
$s=\left(o_{1}, o_{2},\cdots, o_{N}\right)$ 4）for t = 1 to max-episode-length do:
5）对于每个智能体i，选择动作
$a_{i}= \mu_{i}\left(o_{i}\right)+ N_{t}$ 执行动作$a=\left(a_1,a_2, \cdots, a_{N}\right)$ 接受奖励r并转移到新的状态s’6）将
$\left(s, a, r, s^{\prime}\right)$ 放入经验回放池D7）for 智能体i = 1 to N do:
8）for j = 1 to K do:
9）从经验回放池采样样本经验k的概率P(k)
10）计算重要性采样权重ωk和TD-error δk
11）根据绝对经验误差|δk|更新经验k的优先级
12）end for
13）从经验池D中按照优先级抽取最小批次K个经验样本
$\left(s^{j}, a^{j}, r^{j}, s^{\prime j}\right)$ 14）计算
$s_{i}= \displaystyle\sum_{j\neq i} a_{j} h\left({Vg}_{j}\left(o_{j},a_{j}\right)\right)$ 15）令
$y^{j}=r_{i}^{j}+\left.\gamma Q_{i}^{\mu ́^{\prime}}\left(o^{\prime j}, {a}^{\prime}_{1}, \ldots, {a}^{\prime}_{N}, s_{i}\right)\right|_{a^{\prime}_k=\mu^{\prime}_k(o_k^j) }$ 16）通过最小化损失函数更新Critic网络:
$$ \mathcal{L}\left(\theta_{i}\right)=\frac{1}{K} \sum_{k} \omega_{k} \delta_{k}^{2} $$ 17）采用策略梯度函数更新Actor网络:
$$ \nabla_{\theta_{i}} j=\left.\frac{1}{K} \sum_{k} \nabla_{\theta i} \mu_{i}\left(o_{i}^{k}\right) \nabla_{a_i} Q_i\left(s^{k}, a^{k}\right)\right|_{a_i=\mu_i(o_i^k) } $$ 18）end for
19）软更新Actor目标网络和Critic目标网络参数：
$$ \text { soft update }\left\{\begin{array}{l} \theta^{Q^{\prime}} \leftarrow \tau \theta^{Q}+(1-\tau) \theta^{Q^{\prime}} \\ \theta^{\mu ^{\prime}} \leftarrow \tau \theta^{\mu}+(1-\tau) \theta^{\mu ^{\prime}} \end{array}\right. $$ 20）end for
21）end for
3. 实验与结果分析
3.1 实验场景设置
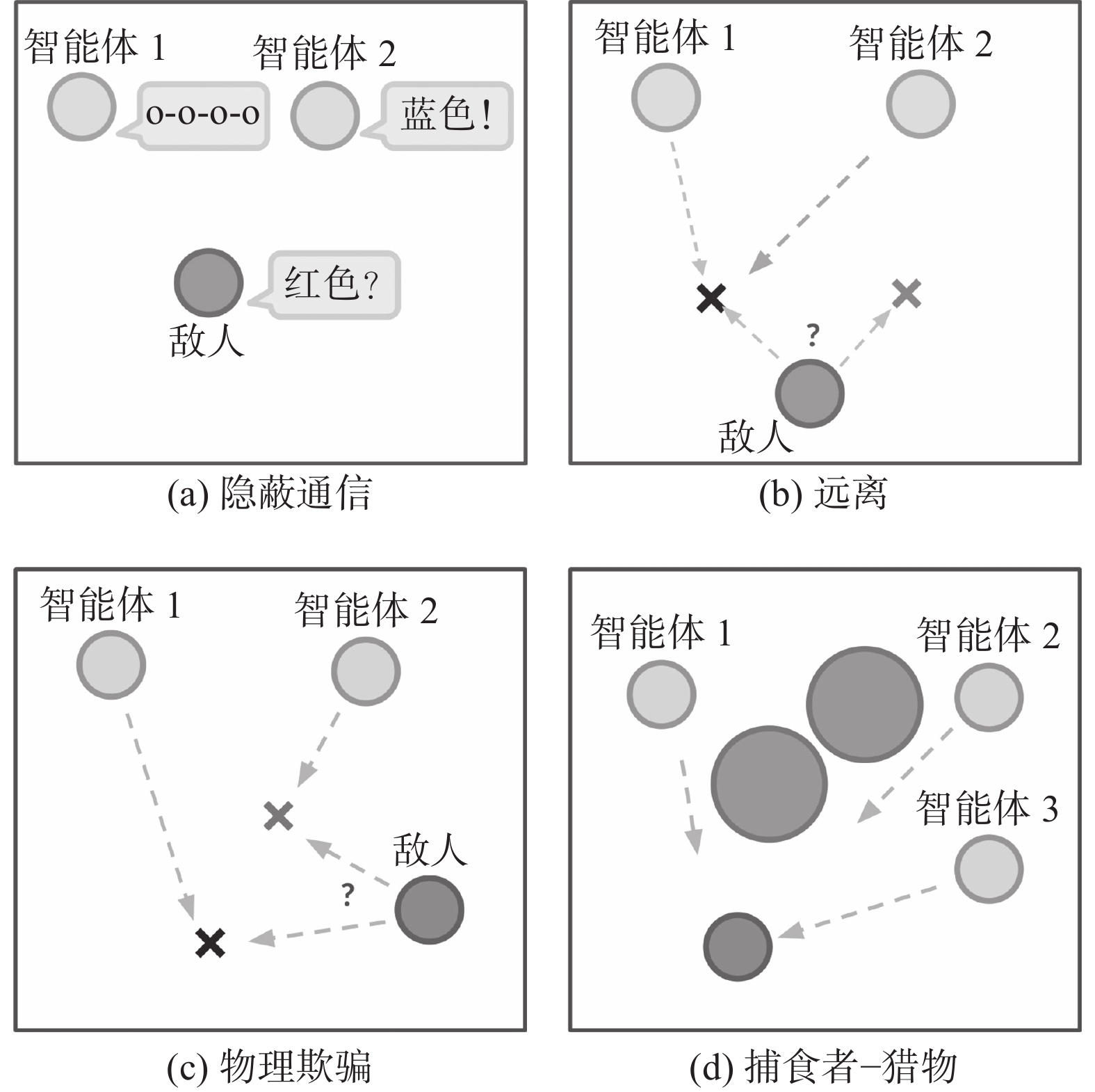
本文采用了MPE多智能体粒子环境，该环境由具有连续空间和离散时间的智能体和地标组成。我们选取环境中具有对抗性的4种场景验证算法的性能。实验场景如图5所示。
图 5 多智能体竞争环境下载:
全尺寸图片
图5(a)为隐蔽通信，该场景由2个智能体和1名敌对智能体构成。合作的智能体通过重构信息进行通信，对手通过解密信息获得奖励。图5(b)为远离，该场景由1个目标地标、n个合作智能体以及敌对智能体组成。合作智能体要到达目标地标，而对手要做的就是把智能体从目标地标推开。图5(c)为物理欺骗，该场景由1个敌对智能体、n个智能体和n个地标（其中1个为目标地标）组成。合作智能体要通过尽可能的覆盖所有地标来阻止对手到达目标地标。图5(d)为捕食者−猎物，该场景由n个合作智能体和1个敌对智能体组成。每次合作智能体与对手发生碰撞时，智能体得到奖励。
3.2 实验参数设置
本文中网络结构为两层全连接神经网络，隐藏层神经元个数为64，激活函数为Relu函数。网络采用Adam Optimizer优化器和Gumbel-Softmax estimator。算法超参数设置如表1所示。
表 1 算法超参数设置参数名称 数值 描述 Batch_size 1024 批尺寸 Gamma 0.95 折损因子 Episode 60000 训练回合数 Max_episode 106 最大回合步数 Learning rate 0.01 学习率 Num_units 64 隐藏层神经元 Buffer_size 106 经验缓冲池大小 Policy_update_rate 2 策略网络更新率 α 0.6 优先级重复程度 β 0.4 重要性采样权重 3.3 实验结果及分析
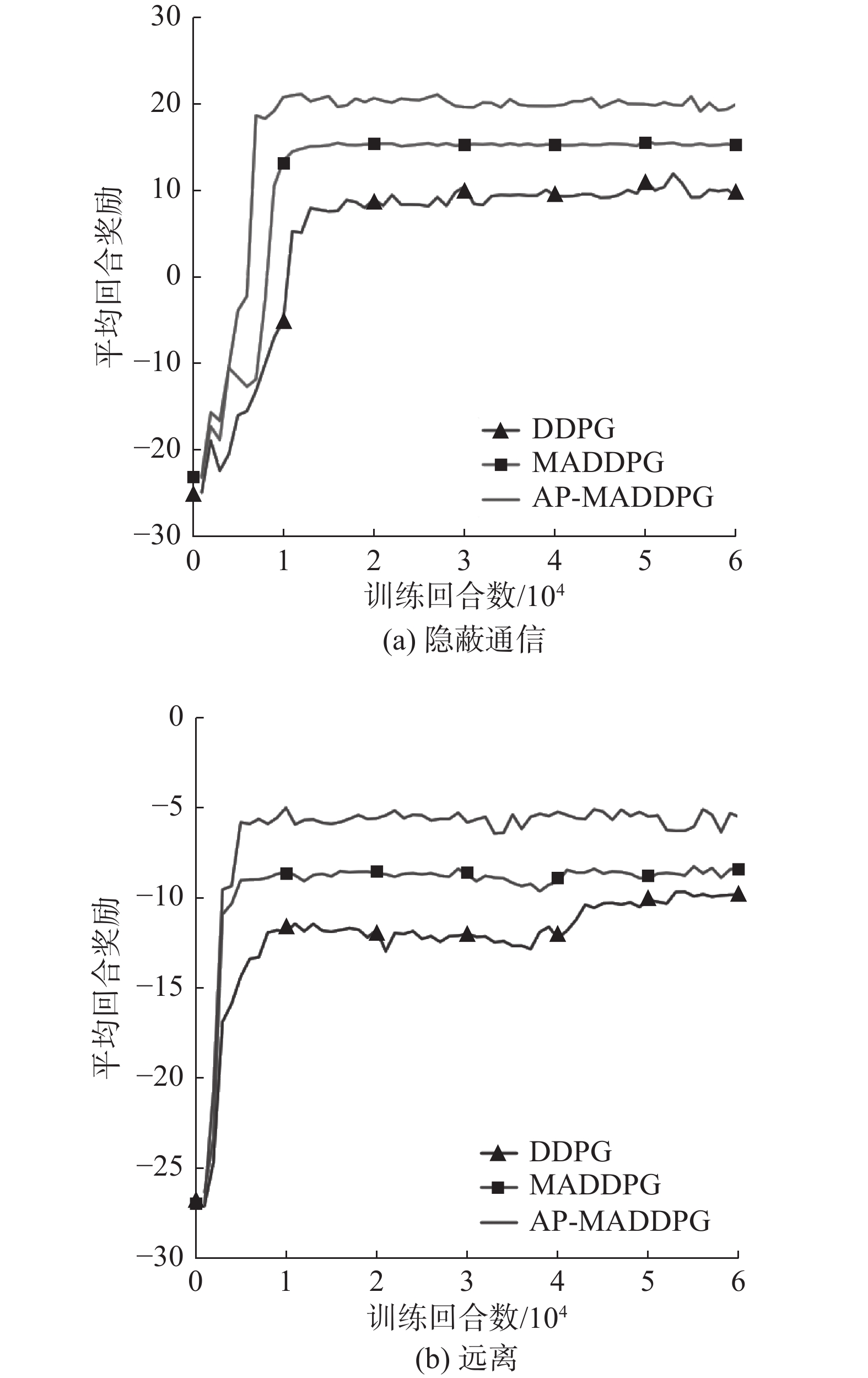
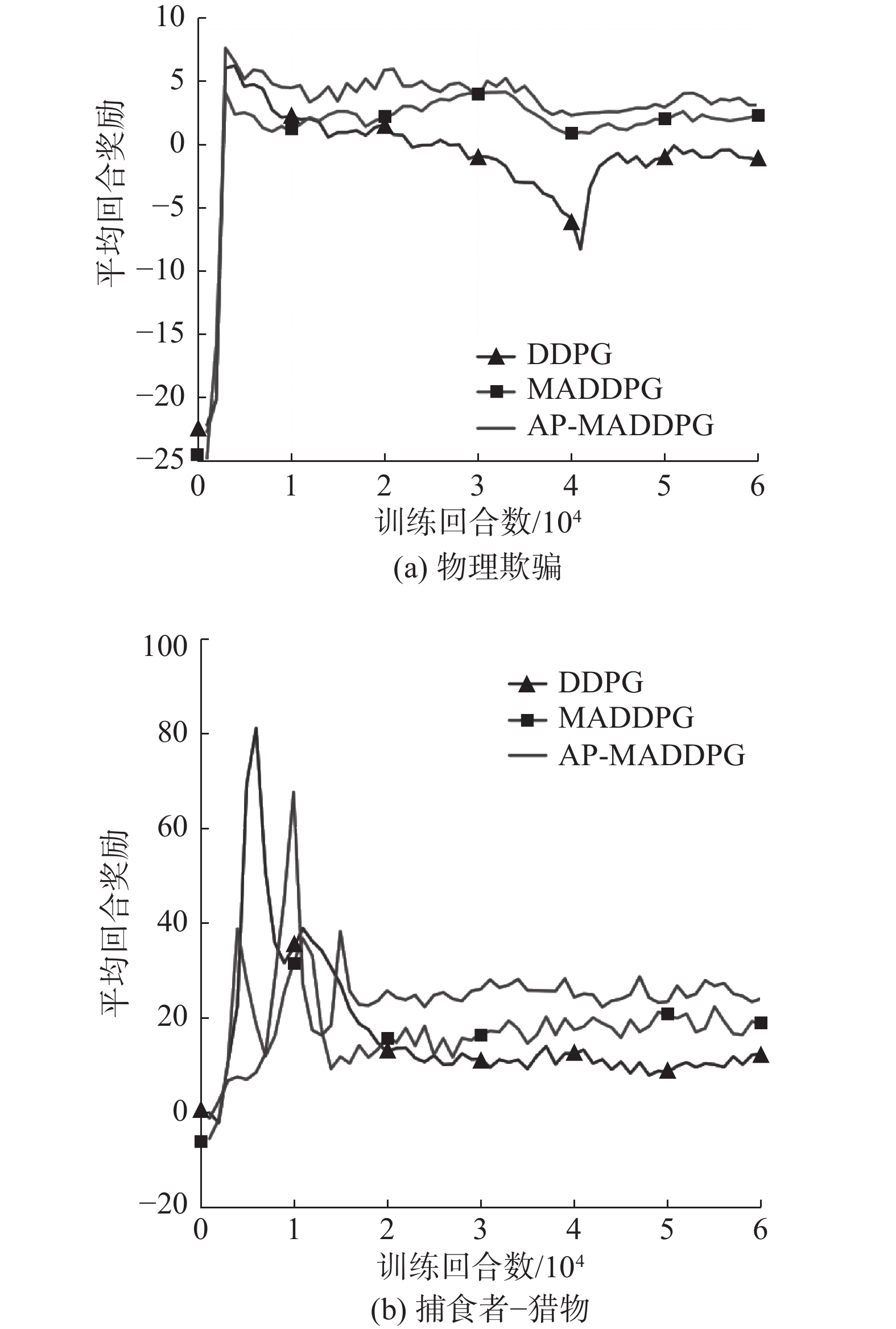
本文在上述4种环境下与DDPG算法、MADDPG算法进行对比实验，训练模型直到收敛，平均奖励曲线如图6所示。
图 6 合作通信场景下智能体平均奖励下载:
全尺寸图片
在图6场景中，合作智能体分别采用AP-MADDPG算法、MADDPG算法和DDPG算法，对手智能体采用单智能体DDPG算法。
由图6中可以看出传统的DDPG算法在多智能体中表现不佳，MADDPG算法通过集中式训练−分布式执行的方法，引入联合动作值函数、联合状态值函数，智能体做出决策时还考虑到对环境中其他智能体的影响，让环境对智能体奖励达到一个整体最优解，从而提高平均回合奖励。本文提出的AP-MADDPG算法通过引入基于优先级的经验回放和多头注意力机制能够准确地从经验中学习最优策略，让智能体之间的交流更加高效。图6中对比结果表明，本文采取的AP-MADDPG算法比其他连续算法回合奖励更高，收敛速度更快。
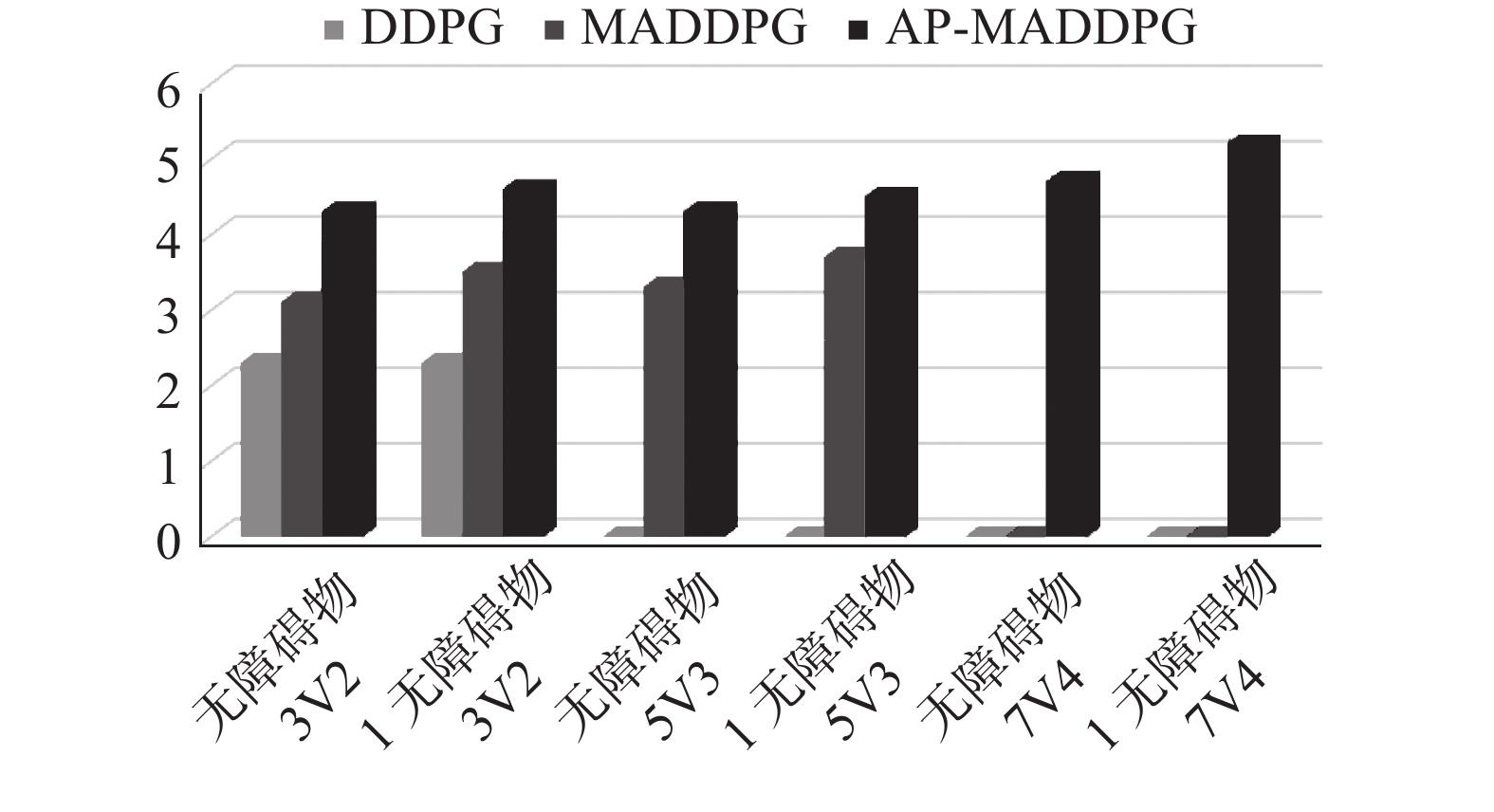
在图6(a)和图6(b)合作任务场景中，由于MADDPG算法和DDPG算法没有通信机制，需要迭代较长时间才能找到其最优策略，且收敛后选择的策略依然不太稳定。而AP-MADDPG算法通过引入了注意力机制，智能体之间允许在集中式训练下对分散策略进行端到端学习，整合不同方面的状态信息，使智能体之间能够进行全面的通信，从而学习到了更好的策略并取得了最高的回合奖励。在图7(a)物理欺骗场景中，随着场景的难度系数增加，AP-MADDPG的收敛速度虽然没有明显变快，但还是能找到最佳的策略趋于平稳并且具有较高的回合奖励。在图7(b)中，3种算法的波动都比较大，但AP-MADDPG 算法在混合环境依然能保存较高的回合奖励。为了验证基于多头注意力机制的MADDPG算法多智能体对抗场景下的有效性，我们对比了各个算法在捕食者-猎物场景下的平均碰撞次数，实验结果如图8所示。
图 7 合作对抗场景下智能体平均奖励下载:
全尺寸图片
图 8 不同场景设置下平均碰撞次数下载:
全尺寸图片
图8中对比了2种场景无障碍 (no landmark)和有障碍 (lanmark)，分别设置不同对抗数量的智能体3v2、5v3、7v4。由图8可以看出，AP-MADDPG算法通过引入注意力机制，多智能体之间的合作变得更加高效，算法通过注意力权重的大小整合状态信息，在围捕猎物时与猎物的平均碰撞次数在场景逐渐复杂的状态下仍然持续增加，而DDPG算法在5v3场景下已无法处理这种复杂规模的场景，MADDPG算法在7v4的场景也无法适用。从图中可以看出，AP-MADDPG算法使智能体变得更加智能化，可以处理较大规模的群体对抗问题。
4. 结论
本文提出了一种基于深度强化学习的多智能体对抗策略算法AP-MADDPG。1）通过多头注意力机制，将注意力权重的大小整合到自身动作值函数，有选择性的关注可以获得更大回报的状态信息，从而获得更高的回合奖励。2）采用基于优先级的经验回放，大大缩短了训练总时间，提高了算法的稳定性。3）AP-MADDPG算法受超参数变化的影响较小，与原MADDPG算法相比具有更强的鲁棒性。4）通过多智能体粒子仿真平台(MPE)的四种对抗场景进行实验，实验结果表明本文所提出的算法可以在多智能体对抗环境中使智能体获得更高的回合奖励，并且具有更快的收敛速度，验证了算法的有效性和稳定性。
-
图 1 多智能体协同对抗决策模型
下载:
全尺寸图片
图 2 MADDPG算法框架
下载:
全尺寸图片
图 3 多头注意力机制结构
下载:
全尺寸图片
图 4 经验概率与经验等级关系
下载:
全尺寸图片
图 5 多智能体竞争环境
下载:
全尺寸图片
图 6 合作通信场景下智能体平均奖励
下载:
全尺寸图片
图 7 合作对抗场景下智能体平均奖励
下载:
全尺寸图片
图 8 不同场景设置下平均碰撞次数
下载:
全尺寸图片
表 1 算法超参数设置
参数名称 数值 描述 Batch_size 1024 批尺寸 Gamma 0.95 折损因子 Episode 60000 训练回合数 Max_episode 106 最大回合步数 Learning rate 0.01 学习率 Num_units 64 隐藏层神经元 Buffer_size 106 经验缓冲池大小 Policy_update_rate 2 策略网络更新率 α 0.6 优先级重复程度 β 0.4 重要性采样权重 -
[1] SILVER D, SCHRITTWIESER J, SIMONYAN K, et al. Mastering the game of Go without human knowledge[J]. Nature, 2017, 550(7676): 354−359. doi: 10.1038/nature24270 [2] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529−533. doi: 10.1038/nature14236 [3] CHEN Liang, GUO Ting, LIU Yunting, et al. Survey of multi-agent strategy based on reinforcement learning[C]//2020 Chinese Control and Decision Conference. IEEE, 2020: 604-609. [4] BUŞONIU L, BABUŠKA R, DE SCHUTTER B. Multi-agent reinforcement learning: An overview[J]. Innovations in multi-agent systems and applications-1, 2010: 183−221. [5] DAI Wei, LU Huimin, XIAO Junhao, et al. Multi-robot dynamic task allocation for exploration and destruction[J]. Journal of intelligent & robotic systems, 2020, 98(2): 455−479. [6] PENG Peng, WEN Ying, YANG Yaodong, et al. Multiagent bidirectionally-coordinated nets: emergence of human-level coordination in learning to play starcraft combat games. [EB/OL]. (2015-11-27)[2021-11-07]. https://arxiv.org/abs/1511.08779. [7] ZHANG Yu, ZHUANG Zirui, GAO Feifei, et al. Multi-agent deep reinforcement learning for secure UAV communications[C]//2020 IEEE Wireless Communications and Networking Conference. Seoul: IEEE, 2020: 1-5. [8] XU Xiaowei, ZHANG Xinyi, YU Bei, et al. Dac-sdc low power object detection challenge for uav applications[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 43(2): 392−403. [9] TAMPUU A, MATIISEN T, KODELJA D, et al. Multiagent cooperation and competition with deep reinforcement learning[J]. PloS one, 2017, 12(4): e0172395. doi: 10.1371/journal.pone.0172395 [10] TESAURO G. Extending Q-learning to general adaptive multi-agent systems[J]. Advances in neural information processing systems, 2003(6): 871−878. [11] SUKHBAATAR S, FERGUS R. Learning multiagent communication with backpropagation[J]. Advances in neural information processing systems, 2016, 29: 2244−2252. [12] PALMER G, TUYLS K, BLOEMBERGEN D, et al. Lenient multi-agent deep reinforcement learning[EB/OL]. (2017-07-14)[2021-11-07]. https://arxiv.org/abs/1707.04402. [13] VAN HASSELT H, GUEZ A, SILVER D. Deep reinforcement learning with double q-learning[C]// Proceedings of the AAAI conference on artificial intelligence. Phoenix: AAAI, 2016, 30(1): 2094-2100. [14] FOERSTER J, FARQUHAR G, AFOURAS T, et al. Counterfactual multi-agent policy gradients[C]// Proceedings of the AAAI Conference on Artificial Intelligence. New Orleans: AAAI, 2018, 32(1): 2974-2982. [15] RASHID T, SAMVELYAN M, De Witt C S, et al. Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning[J]. Journal of machine learning research, 2020, 21(1): 7234−7284. [16] LOWE R, WU Y, TAMAR A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments[J]. Advances in neural information processing systems, 2017: 30. [17] VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[J]. Advances in neural information processing systems, 2017, 30: 5998−6008.
