作为典型的航空机电系统，电液伺服系统是集机、电、液于一身的复杂控制系统，具有控制精度高、响应速度快、信号处理灵活以及各种参数的反馈系统等优点^[1]。电液伺服系统在航空航天工程中应用越来越广泛，特别是在大型飞机舵面控制以及飞行模拟器控制等^[2]。然而电液伺服系统结构复杂，不可避免地存在组件故障隐患。一旦其某个部件发生故障，很容易引发连锁反应，甚至造成更严重的后果，系统的可靠性和安全性会因此大大降低。故障发生后如何保证系统稳定性以及令人满意的跟踪性能，使得电液伺服系统控制器设计成为一个有趣且具有挑战性的课题。

在设计电液伺服系统时，有几个需要着重考虑的问题。电液伺服系统容易受到参数不确定性和外部干扰影响，例如外负载力、供油压力变化、液压油中混入空气以及内泄漏等。国内外针对电液伺服系统控制器的研究，主要是提出利用各种先进控制算法来克服其非线性和不确定性问题，例如模糊PI控制^[3]、动态滑模控制^[4]、自适应最优补偿控制^[5]、基于反步法的非线性鲁棒控制^[6]以及混合模型预测控制^[7]等。尽管控制效果和抗干扰能力有所提高，但传感器故障和执行器退化等部件故障并未得到重视，电液伺服系统的可靠性和安全性没有被真正加强。因此，有必要为其设计一个能够自动容忍潜在故障的控制系统，即容错控制系统。文献[8]为了解决比例阀失效的问题，采用了由标准直驱比例阀组成的双阀系统。若1个阀门发生故障，将会被检测到，内部的控制结构将会转移到另一个阀门上。文献[9]针对电液伺服系统内泄露故障，在定量反馈理论的基础上设计了1个固定增益的线性定常控制律，在系统发生的故障的情况下，对故障进行补偿同时拥有良好的跟踪性能。文献[10]设计了基于免疫原理的电液伺服系统故障自愈策略，针对液压内泄漏故障和传感器故障实现了故障自修复。显然，上述研究所针对故障类型单一且方法不具有普适性。

重构控制技术是确保一些系统安全运行的关键技术之一，在保证控制系统经济性的基础上，提高系统可靠性，多应用于航空航天领域^[11-12]。自适应控制具有对系统参数和环境不确定性的适应性，使得其成为主流的重构控制方法^[13-14]。然而，单一模型的控制器瞬态性能差，在面对比较严重的故障时，响应时间长，系统参数与无故障时相差甚远，从而导致较大的瞬态误差产生^[15]。基于单一模型的自适应控制器需要更长的时间才能使故障系统接近新的运行状态，电液伺服系统的性能可能严重受损，甚至不可控。这使得相关的重构问题变得十分棘手。

基于上述分析，本文采用基于多模型的自适应控制对电液伺服系统进行重构控制设计，建立多模型集来逼近系统故障模型。研究者们已经将多模型自适应控制广泛应用于重构问题上并取得不错的效果。针对飞控系统的执行器故障问题，文献[16]提出利用基于多模型自适应控制对其进行重构；文献[17]将多模型自适应控制应用于近空间飞行器以补偿执行器故障；文献[18]基于自适应控制和多模型组合，为具有电机动力部分失效故障的四旋翼直升机设计了最优重构控制方案。多模型自适应控制在其他领域的应用研究也取得了良好的成果^[19-21]。

针对电液伺服系统潜在的执行器、传感器等组件故障问题，本文提出了自适应控制与组合多模型相结合的重构控制策略。首先建立电液伺服系统数学模型，然后设计了基于模型跟随自适应控制的重构控制器并给出其稳定性证明；紧接着设计1个由多个固定模型和1个自适应模型构成的组合多模型集，用以改善系统故障重构后的瞬态性能，并根据合适的切换机制完成相应控制器切换；最后通过仿真验证了所提出方法的优秀控制重构能力以及良好的鲁棒性和抗扰性。

1.   系统数学模型

1.1   系统组成

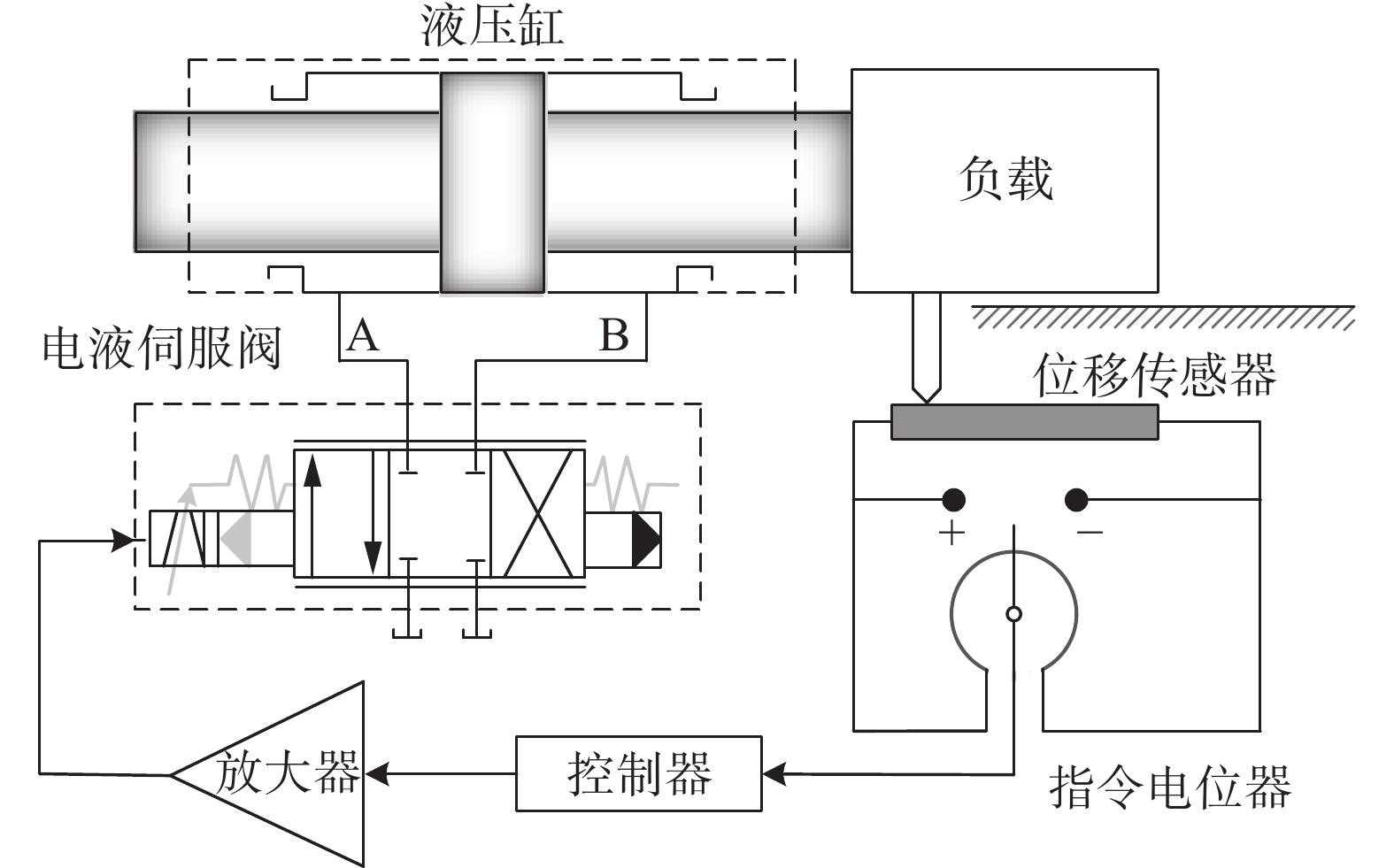
本文选择负载位移作为电液伺服系统输出。电液伺服系统的结构框图如图1所示，其中包括控制器、比例放大器、电液伺服阀、液压缸、位移传感器以及负载^[22]。图1中两电位器组成桥式电路，用以测量输入信号和输出信号之间的位置偏差。位置偏差信号经过控制器得到控制电压，经过放大器放大得到输出电流，用以控制电液伺服阀的阀芯运动。伺服阀的输出压力油推动液压缸活塞杆移动，从而带动工作台移动。

图  1  电液伺服系统原理

下载: 全尺寸图片

1.2   数学模型

1.2.1   液压缸数学模型

液压缸的物理特性由以下方程描述。

1)伺服阀的压力流量方程为

式中： $ q_{L} $ 为负载流量， $ C_d $ 为流量系数，A为电液伺服阀的阀口面积函数， $ x_{v} $ 为伺服阀阀芯位移， $ p_{s} $ 为系统供油压力， $ p_{L} $ 为电液伺服阀的负载压力， $ \rho $ 为液压油密度。

式(1)可以线性化为^[23]

式中： $ K_{q} $ 为流量增益， $K_{c}$ 为流量–压力系数。

2)液压缸的连续性方程可表示为

式中： $ x $ 为活塞杆的位移， $A_t$ 为液压缸的有效作用面积， $C_{tp}$ 为液压缸的等效泄露系数， $ \beta_{e} $ 为油液的等效体积弹性模量， $ V_{t} $ 为液压缸的总压缩容积。

3)液压缸与负载的动力学方程可表示为

式中： $ m $ 为负载作用在活塞杆上的等效质量， $ B_{v} $ 为负载和活塞的粘性阻尼系数， $ k $ 为负载作用在活塞上的弹簧刚度， $ F_{L} $ 为外负载力。

实际应用中，由于系统的弹性负载和粘性阻尼系数都很小，可以忽略不计^[24]，即 $ k=0 $ ， $ B_{v}=0 $ 。令干扰作用 $ F_{L}=0 $ ，可得液压缸状态空间方程：

式中： $ \omega_{h} $ 为液压固有频率， $\omega_{h}=\sqrt{\dfrac{4 \beta_{e} A_{e}^{2}}{m V_{t}}}$ ； $ \zeta_{ {h }} $ 为液压阻尼比， $\zeta_{h}=\dfrac{K_{ce}}{A_{e}} \sqrt{\dfrac{\beta_{e} m}{V_{t}}}$ 。

此外，作为液压缸的一种典型故障，内泄漏是指液压缸的2个压力之间的液压油的相互渗透，主要是由活塞的磨损或液压缸内壁的磨损导致密封性减弱造成的。在仿真中，可以通过改变内泄漏系数 $C_{tp}$ 的值来进行故障的仿真分析^[1]。

1.2.2   电液伺服阀的数学模型

电液伺服阀可视为工作频率接近 $ \omega_{k} $ 的二阶震荡环节，其状态空间方程可表示为

式中： $I_r$ 为输入电流， $K_{ {sv }}$ 为伺服阀增益， $\omega_{sv}$ 为电液伺服阀的固有频率， $\zeta_{sv}$ 为电液伺服阀的阻尼比。

电液伺服阀作为电液伺服系统的执行器，不可避免地受到潜在故障影响，液压油混入空气、内泄漏以及振动等问题严重影响电液伺服阀的工作效率。因此，本文引入了效率损失（loss of efficiency, LOE）来代表电液伺服系统典型的执行器故障。LOE故障的特点是执行器的增益从其额定值下降。在执行器LOE故障的情况下，伺服阀阀芯位移偏离了控制器所期望的指令输出，即

式中： $ x_{v}^{\prime} $ 为伺服阀阀芯的实际位移； ${k_{{\text{LOE}}}}$ 为LOE故障增益， ${k_{{\text{LOE}}}} \in \left( {0,1} \right]$ 。 $ n \% $ LOE等同于LOE故障增益 ${k_{{\text{LOE}}}} = 1 - \dfrac{n}{{100}}$ ， ${k_{{\text{LOE}}}} = 1$ 表示执行器无故障。

因此，液压缸的数学模型可以改写为

需要注意的是，如果组件并不总是具有与无故障相同的特性，就有必要建立故障模型。它不仅清楚地说明了如何将组件故障注入系统，而且为接下来设计多模型集提供了一些准确的故障模型。

1.2.3   位移传感器数学模型

位移传感器视为比例环节：

式中： $ x_{s} $ 为传感器测量位移， $ K_{f} $ 为传感器反馈增益。

与执行器故障类似，传感器增益漂移、失效等典型故障也会严重影响系统性能，甚至导致系统不可控。传感器故障可以表示为

式中： $ x_{s}^{\prime} $ 为传感器的实际输出； ${k_{{\text{DFT}}}}$ 为传感器漂移系数， ${k_{{\text{DFT}}}} \in \left[ {0,2} \right]$ 。 ${k_{{\text{DFT}}}} = 1$ 表示传感器无故障， ${k_{{\text{DFT}}}} = 0$ 表示传感器失效。

1.2.4   控制器数学模型

本文采用PI控制器来保证电液伺服系统的基本跟踪性能，其传递函数如下：

式中： ${u_{s e}}$ 为控制器输出电压， $ K $ 和 $ K_{i} $ 分别为比例增益和积分增益， $ x_{e}=x_{d}-x_{s} $ 是期望位移与测量位移之差。

1.2.5   伺服放大器数学模型

伺服放大器方程为

式中 $ K_{a} $ 是伺服放大器增益。

2.   控制重构设计

2.1   问题描述

无故障的电液伺服系统状态空间表示形式为

式中： ${\boldsymbol{x}}\left({{t}} \right) \in {{\boldsymbol{R}}^n}$ 为状态向量， ${\boldsymbol{u}}\left({{t}} \right) \in {{\boldsymbol{R}}^m}$ 为控制输入向量， ${\boldsymbol{y}}\left({{t}} \right) \in {{\boldsymbol{R}}^q}$ 为输出向量， ${\boldsymbol{A}} \in {{\boldsymbol{R}}^{n \times n}}$ ， ${\boldsymbol{B}} \in {{\boldsymbol{R}}^{n \times m}}$ ， ${\boldsymbol{C}} \in {{\boldsymbol{R}}^{q \times n}}$ 。

本文主要针对位移传感器、执行器（电液伺服阀）以及液压缸等组件故障。故障系统需要进行统一表示来设计重构控制器，可以将其描述为

式中： ${{\boldsymbol{x}}_{{p}}}\left({{t}} \right) \in {{\boldsymbol{R}}^{{n_p}}}$ ， ${{\boldsymbol{u}}_{{p}}}\left({{t}} \right) \in {{\boldsymbol{R}}^{{m_p}}}$ ， ${{\boldsymbol{y}}_{{p}}}\left({{t}} \right) \in {{\boldsymbol{R}}^{{q_p}}}$ ， ${{\boldsymbol{A}}_{{p}}} \in {{\boldsymbol{R}}^{{n_p} \times {n_p}}}$ ， ${{\boldsymbol{B}}_{{p}}} \in {{\boldsymbol{R}}^{{n_p} \times {m_p}}}$ ， ${{\boldsymbol{C}}_{{p}}} \in {{\boldsymbol{R}}^{{q_p} \times {n_p}}}$ ， $\left\{ {\sigma {\boldsymbol{A}},\sigma {\boldsymbol{B}},\sigma {\boldsymbol{C}}} \right\}$ 是由故障引起的具有适当维数的有界参数摄动矩阵。

2.2   模型跟随自适应重构控制器设计

模型跟随自适应控制针对可以用参数未知确定性线性模型描述的被控对象，所采用的控制器是基于参考模型输出与被控对象输出之间的广义误差和稳定性理论进行设计的^[25]。

结合模型跟随自适应控制思想，为故障系统设计重构控制器。取参考模型状态方程为

式中： ${{\boldsymbol{x}}_{{m}}}\left({{t}} \right) \in {{\boldsymbol{R}}^{{n_m}}}$ ， ${\boldsymbol{r}}\left({{t}} \right) \in {{\boldsymbol{R}}^{{m_m}}}$ ， ${{\boldsymbol{y}}_{{m}}}\left({{t}} \right) \in {{\boldsymbol{R}}^{{q_m}}}$ ， ${{\boldsymbol{A}}_{{p}}} \in {{\boldsymbol{R}}^{{n_m} \times {n_m}}}$ ， ${{\boldsymbol{B}}_{{m}}} \in {{\boldsymbol{R}}^{{n_m} \times {m_{{m}}}}}$ ， ${{\boldsymbol{C}}_{{m}}} \in {{\boldsymbol{R}}^{{q_m} \times {n_{{m}}}}}$ 。

最终的控制目标是保持闭环系统里的所有信号均有界的同时，使电液伺服系统的输出 ${{\boldsymbol{y}}_{{p}}}\left({{t}} \right)$ 渐进跟踪参考模型输出 ${{\boldsymbol{y}}_{{m}}}\left({{t}} \right)$ 。

因此，设计的重构控制器如下：

式中 ${\boldsymbol{K}} \in {{\boldsymbol{R}}^{{m_p} \times {m_{{p}}}}}$ 和 ${\boldsymbol{F}} \in {{\boldsymbol{R}}^{{m_p} \times {m_{{p}}}}}$ 为自适应控制增益矩阵。

将式(3)代入式(2)中，得：

定义状态误差为 ${\boldsymbol{e}} = {{\boldsymbol{x}}_{{p}}} - {{\boldsymbol{x}}_{{m}}}$ ，则：

为了保证 ${\boldsymbol{e}} = {{\boldsymbol{x}}_{{p}}} - {{\boldsymbol{x}}_{{m}}}$ 渐进收敛，需满足下列匹配条件：

将式(5)代入式(4)得到：

式中： ${{\tilde {\boldsymbol{F}}}} = {{\boldsymbol{F}}_{{0}}} - {\boldsymbol{F}}$ ， ${{\tilde {\boldsymbol{K}}}} = {{\boldsymbol{K}}_{{0}}} - {\boldsymbol{K}}$ 。

为保证 $\mathop {\lim }\limits_{x \to \infty } {\boldsymbol{e}}=0$ ，设计如下自适应律：

式中 ${{\boldsymbol{\gamma }}_{{F}}} \in {{\boldsymbol{R}}^{{m_p} \times {m_p}}}$ 、 ${{\boldsymbol{\gamma }}_{{K}}} \in {{\boldsymbol{R}}^{{m_p} \times {m_p}}}$ 均为对称的正定矩阵。

定理 　将所设计的自适应控制器(3)和自适应律(7)应用于故障后的电液伺服系统(2)，能够保证闭环系统的所有信号均有界，同时满足： $\mathop {\lim }\limits_{t \to \infty } {\boldsymbol{e}}\left({{t}} \right) = 0$ 和 $\mathop {\lim }\limits_{t \to \infty } {{\boldsymbol{e}}_{{y}}}\left({{t}} \right) = \mathop {\lim }\limits_{t \to \infty } {{\boldsymbol{C}}_{{p}}}{{\boldsymbol{e}}_{{x}}}\left({{t}} \right) = 0$ 。

证明 　构造如下Lyapunov函数：

式中： ${\boldsymbol{P = }}{{\boldsymbol{P}}^{\text{T}}} \in {{\boldsymbol{R}}^{{n_p} \times {n_p}}} > 0$ 满足对于任意的常数矩阵 ${\boldsymbol{Q = }}{{\boldsymbol{Q}}^{\text{T}}} \in {{\boldsymbol{R}}^{{n_p} \times {n_p}}} > 0$ ，都有：

结合式(8)和式(9)，对式(8)求导可得

由此可得： ${\text{0}} \leqslant {\boldsymbol{V}}\left({{t}} \right) \leqslant {\boldsymbol{V}}\left( {\boldsymbol{0}} \right)$ ，则 ${\boldsymbol{V}}\left({{t}} \right) \in {{\boldsymbol{L}}_\infty }$ 。

对式(10)进行积分，得到：

因此 ${\boldsymbol{e}} \in {{\boldsymbol{L}}_{\text{2}}},{{\boldsymbol{L}}_\infty }$ ， ${\boldsymbol{\dot e}} \in {{\boldsymbol{L}}_\infty }$ ，证毕。

3.   组合多模型切换

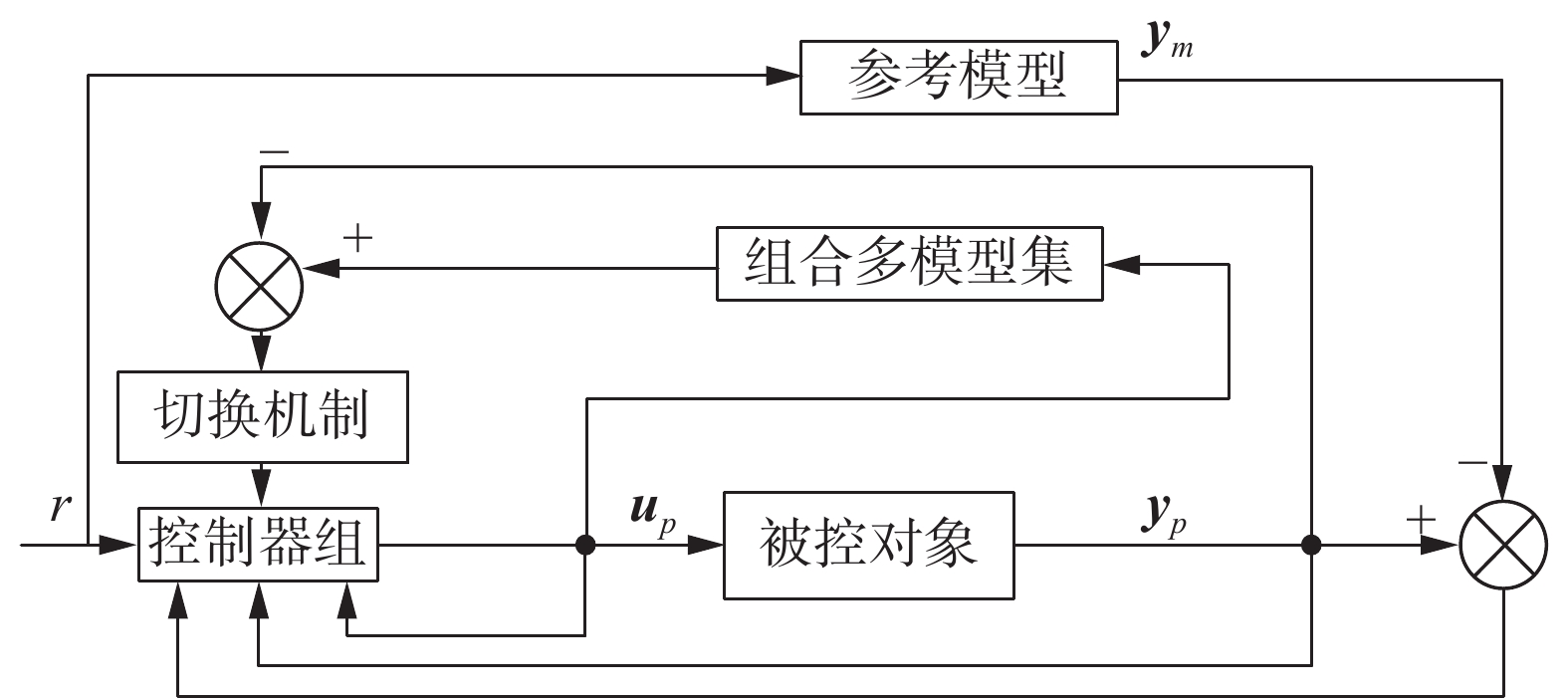
组件故障会引起较大范围的参数跳变，基于单模型的自适应控制器可能需要较长时间来适应新的工作状况。在这段时间间隔内，被控系统可能会产生在实际情况中不能接受的大的瞬态误差。因此，使用单模型自适应控制器可能无法达到预期的控制目标。在这种情况下，设计了如图2所示的基于组合多模型的自适应控制器，来更好地补偿故障产生的不利影响。该方法主要是通过建立多模型集来逼近被控系统当前状态，模型集中的每个模型都有与之相对应的控制器，且每个控制器间相互独立，依据一定的切换性能指标完成对系统的稳定控制。多模型的建立、控制器的设计和切换策略的选择是设计的核心内容。

图  2  基于组合多模型的自适应重构系统原理

下载: 全尺寸图片

3.1   固定模型设计

定义参数向量 ${{\boldsymbol{\theta }}_{{i}}} = \left[ {{{\boldsymbol{A}}_{{{pi}}}},{{\boldsymbol{B}}_{{{pi}}}}} \right]$ ， ${\boldsymbol{W}}\left({{t}} \right){\boldsymbol{ = }}\Big[ {\boldsymbol{x}}_{{p}}^{\text{T}}\left({{t}} \right), {\boldsymbol{u}}_{{p}}^{\text{T}} \left({{t}} \right) \Big]^{\text{T}}$ ，则第 $ f $ 个固定模型可表示为

式中 $i = 1,2, \cdots ,n$ 。

要使被控对象的输出跟踪参考模型的输出，即 ${{\boldsymbol{y}}_{{p}}}\left({{t}} \right) = {{\boldsymbol{y}}_{{m}}}\left({{t}} \right)$ ，则有：

由式(11)即可求得各种固定模型所对应的控制器。

3.2   自适应模型设计

针对故障系统，可以构建如下的自适应辨识模型集：

定义状态误差 ${{\boldsymbol{\hat e}}_{{k}}} = {{\boldsymbol{\hat x}}_{{{pk}}}} - {{\boldsymbol{x}}_{{p}}}$ ，求导可得

式中 ${{\boldsymbol{\psi }}_{{{{u}}_{{k}}}}} = {{\boldsymbol{\hat u}}_{{k}}} - {{\boldsymbol{u}}_{{p}}}$ ，且有：

式中： $-\gamma_{u_k}>0$ 是权值系数； $ \text { Proj } $ 为投影算子，保证参数有界性； ${{\boldsymbol{P}}_{{0}}}$ 是如下Lyapunov方程的1个对称正定解。

且 ${{\boldsymbol{Q}}_{{0}}} = {\boldsymbol{Q}}_{{0}}^{\text{T}} > 0$ 。

故障引起系统参数产生大跳变，虽然固定模型具有不错的快速性，但需要固定模型的数量足够多，才能覆盖故障系统的全参数域；自适应模型可以在被控对象发生故障后动态调整自身参数，用以提高控制精度，但由于计算量较大导致时间滞后的缺点也显而易见。由此可见，多模型集中元素种类和数量的选择直接影响着重构控制的性能。

3.3   切换性能指标

为在多模型中切换以获取“最佳”模型，选择如下的切换性能指标^[26]：

式中： $\varepsilon_{k}=\hat{y}_{pk}-y_{p}$ 为残差， $ c_{1}, c_{2}>0 $ 分别为瞬时误差和累积误差的加权系数， $ \lambda \geq 0 $ 为遗忘因子。在每个时刻对 $ J_{k}(t) $ 进行比较以搜索最小值，以搜索与当前系统最匹配的模型，这时 $\mathop {\lim }\limits_{t \to \infty } \varepsilon_{k}(t)=0$ ， $\mathop {\lim }\limits_{t \to \infty } J_{k}(t)=0$ 。

定理 　切换逻辑式(14)保证系统式(12)和调节律式(13)是稳定的，并且有 $\mathop {\lim }\limits_{t \to \infty } J_{k}(t)=0$ 。

证明 　为了证明，给出下面的Lyapunov函数^[27]:

对式(15)进行微分可得：

考虑到自适应映射算法的特性 ${{\boldsymbol{\psi }}_{{{{u}}_{{k}}}}}{{\boldsymbol{\dot \psi }}_{{{{u}}_{{k}}}}} \leqslant - {\gamma _k}{{\boldsymbol{\psi }}_{{{{u}}_{{k}}}}} \left( {{{{\boldsymbol{\hat e}}}_{{k}}}{{\boldsymbol{P}}_{{0}}}{{\boldsymbol{B}}_{{p}}} + {{{\boldsymbol{\dot u}}}_{{k}}}} \right)$ ，则上述结果意味着 ${{\boldsymbol{\hat e}}_{{k}}} \in {{\boldsymbol{L}}^\infty } \cap {{\boldsymbol{L}}^2}$ , $ e_kL \in {{\boldsymbol{L}}^\infty } $ ， $\mathop {\lim }\limits_{t \to \infty } {{\boldsymbol{J}}_{{k}}}\left({{t}} \right) = 0$ 。当系统发生故障后，切换函数将切换到相应模型，因此 ${{\boldsymbol{\hat e}}_{{k}}}$ 是有界的（在映射算法下 ${{\boldsymbol{\psi }}_{{{{u}}_{{k}}}}}$ 是有界的），进而 ${{\boldsymbol{\hat x}}_{{{pk}}}}$ 和 ${{\boldsymbol{x}}_{{{pk}}}}$ 是有界的。所以 ${{\boldsymbol{u}}_{{k}}}$ 是有界的，这意味着所有信号是有界的，所以 $\mathop {\lim }\limits_{t \to \infty } {{\boldsymbol{\hat e}}_{{k}}}\left({{t}} \right) = 0$ ，进而 $\mathop {\lim }\limits_{t \to \infty } {\boldsymbol{\hat e}}\left({{t}} \right) = 0$ 。

4.   控制重构设计仿真分析

4.1   仿真参数

电液伺服系统主要参数值见表1。

根据本文第2节建模部分，系统可以表示为

式中： ${\boldsymbol{x}}\left( {{t}} \right) = \left[ {\ddot x,\dot x,x,{{\dot x}_v},{x_v},{u_{se}}} \right]$ ， ${\boldsymbol{y}}\left( {{t}} \right) = \left[ x \right]$ ， ${\boldsymbol{u}}\left( {{t}} \right) = \left[ {{x_d}} \right]$ 。

为了使跟踪性能更符合实际情况，本文将无故障电液伺服系统模型作为参考模型，即 ${{\boldsymbol{A}}_{{m}}} = {\boldsymbol{A}}$ ， ${{\boldsymbol{B}}_{{m}}} = {\boldsymbol{B}}$ ， ${{\boldsymbol{C}}_{{m}}} = {\boldsymbol{C}}$ 。相关控制器参数取值为： $ K=1 $ ， $ F=3 $ ， $ y=1 \times 10^{3} $ ， $ c_{1}=0.9 $ ， $ c_{2}=0.1 $ ， $ \lambda=0 $ ， $ \eta=1 $ 。

4.2   仿真结果与分析

本文提出的重构方案主要是针对电液伺服系统的传感器故障、执行器故障和内泄漏故障。执行器故障为执行器效率损失，传感器故障为传感器恒增益漂移。所建立的模型集包括4个固定模型、1个自适应模型。

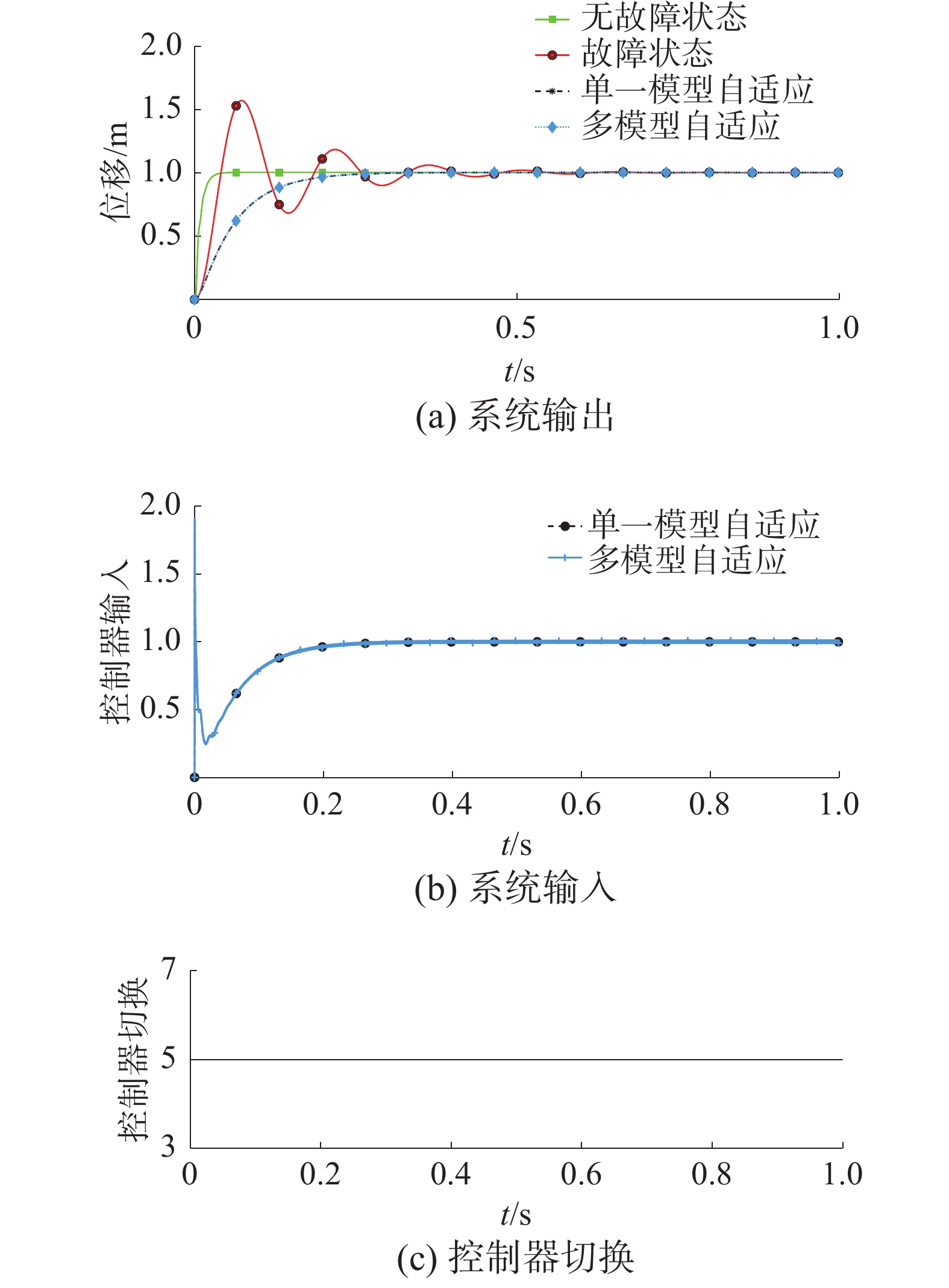
首先，仅考虑液压缸内泄漏故障，系统参考输入为幅值为1的阶跃函数，系统响应如图3所示。

图  3  内泄漏仿真曲线

下载: 全尺寸图片

由图3可以看出，在存在内泄漏的情况下，电液伺服系统输出动态性能差，超调严重并伴有剧烈振荡。自适应控制器仍然能够稳定地保持系统输出渐近跟踪参考输入，瞬态误差较小，控制效果与无干扰时基本一致，有效地消除了不良因素的影响，具有较强的鲁棒性和抗扰性。

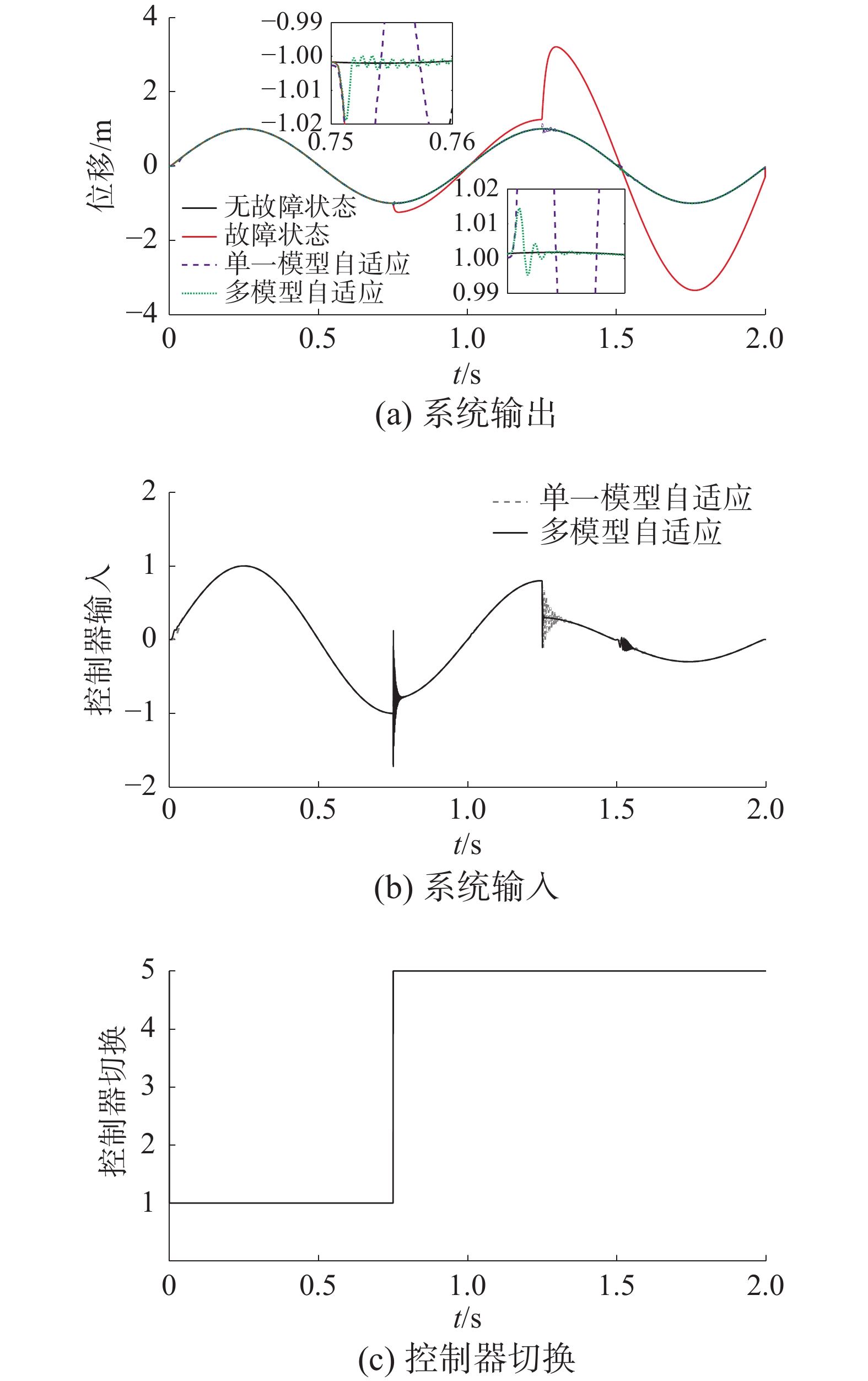
其次，讨论所设计的自适应控制器在单一组件故障情况下的重构效果。系统参考输入设置为 $\sin (2 \text{π} t)$ ，分以下2种情况仿真验证：

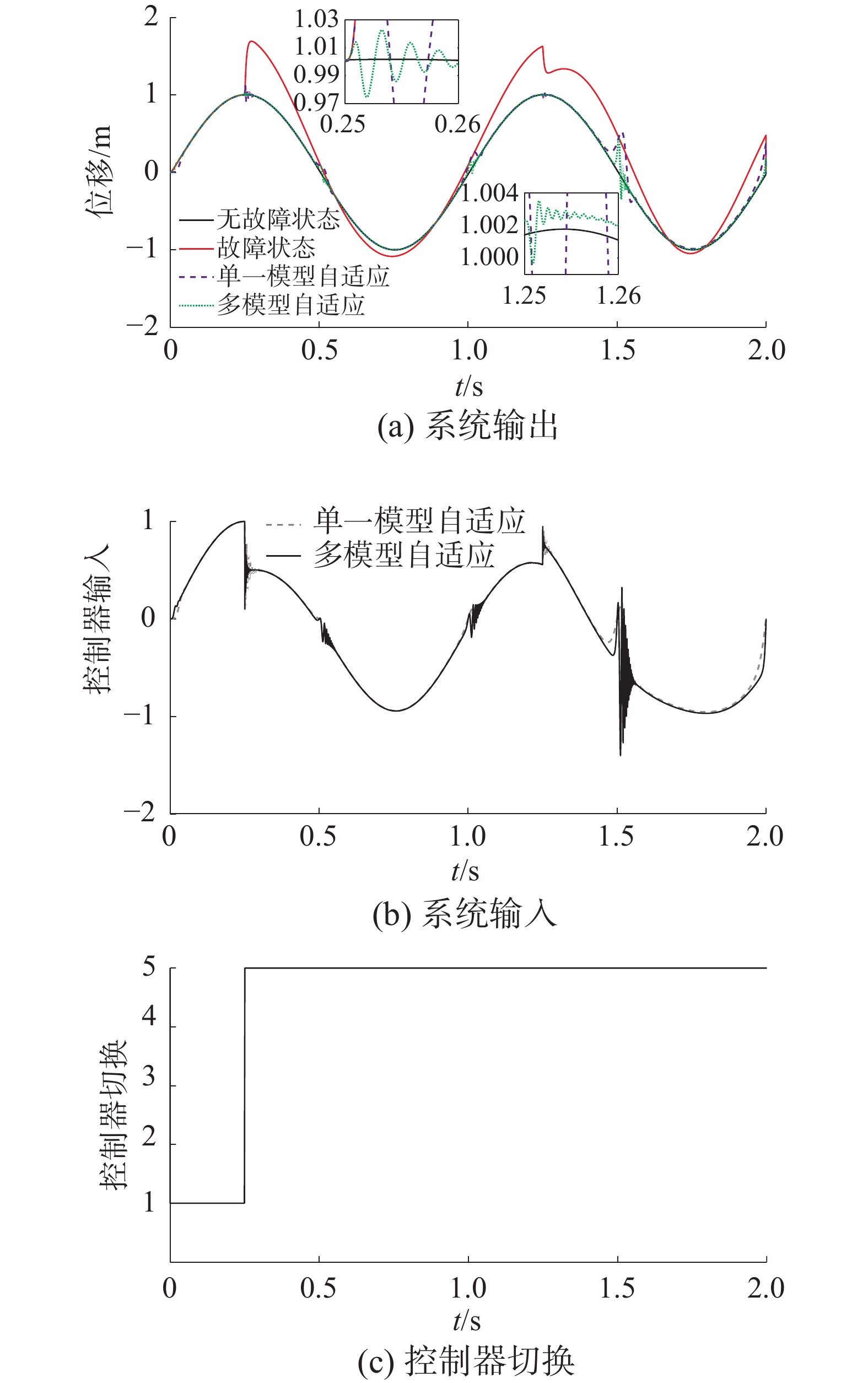
故障1情况 　0 s≤t＜0.75 s，无故障；0.75 s≤t＜1.25 s，传感器恒增益漂移 $ {k_{{\text{DFT}}}}{\text{ = 0}}{\text{.8}} $ ；1.25 s≤t＜2 s，传感器恒增益漂移 $ {k_{{\text{DFT}}}}{\text{ = 0}}{\text{.3}} $ 。仿真结果如图4所示。

图  4  故障1系统仿真曲线

下载: 全尺寸图片

由图4可以看出，传感器故障使系统的输出严重偏离参考输入，可能会造成更严重的后果，仅仅依靠系统基本控制器的鲁棒性无法实现渐进跟踪。加入单一模型自适应控制器后，系统性能得到了改善，输出在一段时间后可以渐进跟踪参考输入。但是，在故障出现瞬间，系统输出产生了明显的瞬态误差，这在一些安全需求较高的应用中是不被接受的。而多模型自适应控制器使得该现象得到了明显的改善，收敛速度更快，保证系统在传感器故障情况下仍能保持良好的跟踪性能与稳定性。

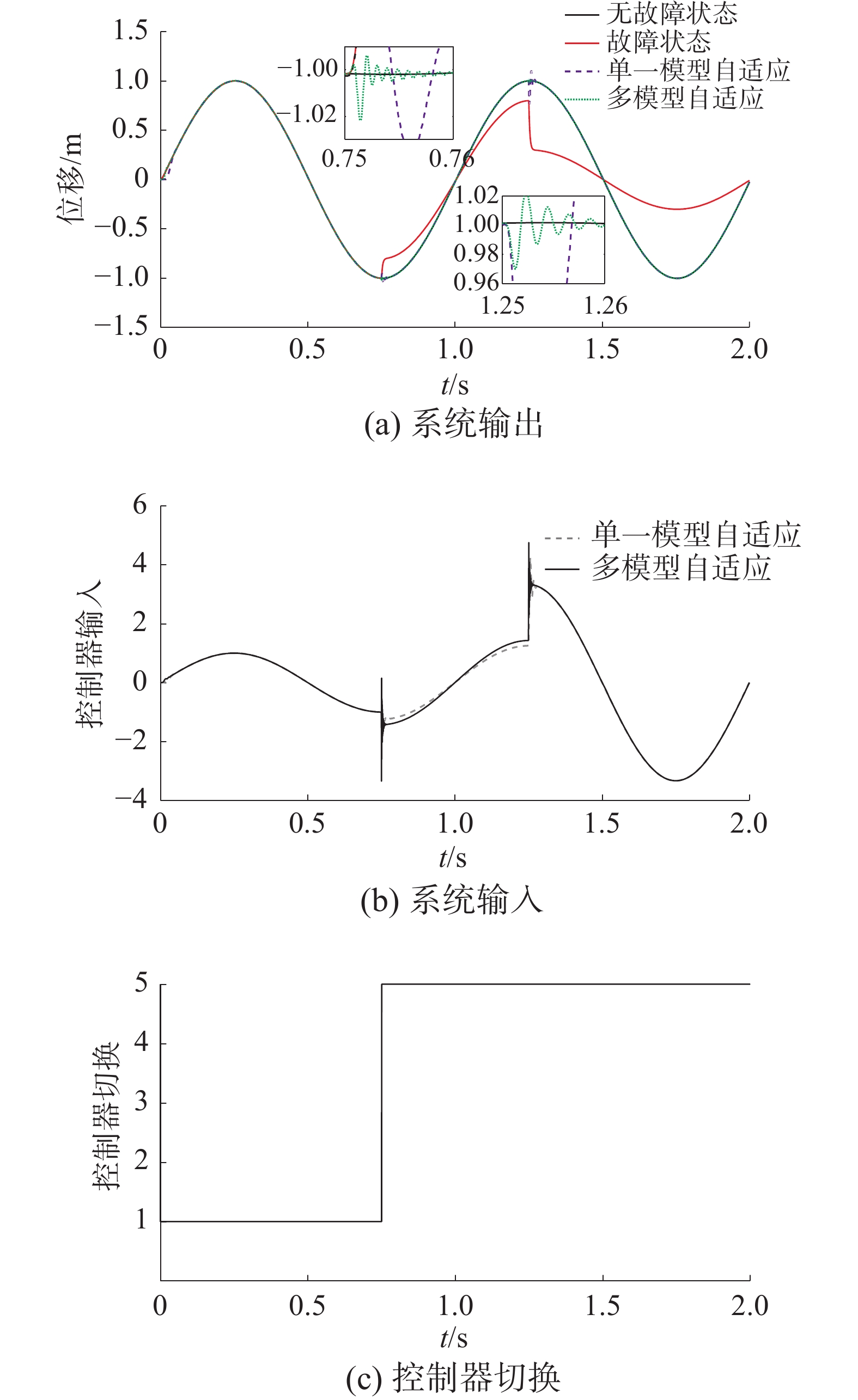
故障2情况 　0 s≤t＜0.75 s，无故障；0.75 s≤t＜1.25 s，执行器LOE ${k_{{\text{LOE}}}} = 0.7$ ；1.25 s≤t＜2 s，执行器LOE ${k_{{\text{LOE}}}} = 0.{\text{3}}$ 。仿真结果如图5所示。

图  5  故障2系统仿真曲线

下载: 全尺寸图片

从图5可以看出，和传感器故障类似，执行器故障也会使系统的输出受到严重影响。相比于单一模型自适应控制，多模自适应控制能够更好地补偿故障带来的不利影响，从而提高系统的鲁棒性。

最后，考虑伴有外部扰动的混合故障的情况。系统参考输入设置为 $ \sin (2{\text{π}} t) $ 。

混合故障如下：0 s≤t＜0.25 s，无故障；0.25 s≤t＜1.25 s，传感器恒增益漂移 $ {k_{{\text{DFT}}}}{\text{ = 0}}{\text{.7}} $ ，同时伴有外部扰动 $ \omega=0.1 \sin (10\; t)+0.15 $ ；1.25 s≤t＜2 s，在传感器恒增益漂移的基础上，执行器LOE ${k_{{\text{LOE}}}} = 0.7$ ，同时扰动增为 $ \omega=0.3 \sin (10\; t)+0.2 $ 。

仿真结果如图6所示。由图6可知，在混合故障情况下，多模型自适应控制器仍然能够保持系统输出渐进跟踪参考输入，瞬态误差较小，有效地消除了不良因素的影响，具有较强的鲁棒性和抗扰性，重构控制效果令人满意。

图  6  混合故障系统仿真曲线

下载: 全尺寸图片

综上，本方法满足了系统在故障条件下增加的性能需求以及安全性和可靠性的要求，能够保持系统的整体稳定性和可接受性能。

5.   结论

针对电液伺服系统潜在的组件故障问题，本文提出了一种自适应控制与组合多模型相结合的重构控制方案，根据电液伺服系统的组成结构和工作原理，建立其数学模型，并对典型组件故障进行建模，设计了基于模型跟随自适应控制的重构控制器，并证明其稳定性，提出了一个覆盖故障范围的组合多模型集，通过合适的切换机制，保证输出渐进跟踪并且改善了系统的瞬态性能。对多种故障情况进行了仿真，其结果验证了该方法较强的鲁棒性、抗扰性以及良好的重构能力。未来工作将重点放在具有非线性项的电液伺服系统重构控制研究上。