Space-time-frequency non-stationary millimeter wave massive MIMO channel model
-
摘要: 为准确描述毫米波大规模多输入多输出（MIMO）信道中功率时延可解析性，本文对基于散射簇的3GPP信道建模方法进行扩展，提出了适用于毫米波大规模MIMO信道的一种基于散射簇的空时频非平稳信道模型。针对毫米波大规模MIMO信道中空时频非平稳特性，在基于生灭过程的散射簇演进算法之上，提出空时频散射簇演进算法，从而建模散射簇在空间、时间和频率改变下的变化过程。仿真结果验证了毫米波大规模MIMO信道特性，并与3GPP实测信道数据进行对比，对比结果说明了所构建信道模型的准确性。Abstract: In order to accurately characterize the power delay resolvability in the millimeter-wave massive multiple input multiple output (MIMO) channel, in this paper the 3GPP scatter cluster-based channel modeling method is extended, and a space-time-frequency non-stationary channel model based on scattering clusters for millimeter-wave massive MIMO channels is proposed. Aiming at the non-stationary characteristics of millimeter-wave massive MIMO channel in space-time-frequency domain, on the basis of the scattering cluster evolution algorithm based on the birth and death process, a space-time-frequency scattering cluster evolution algorithm is proposed, so as to model the changing process of scattering clusters under the changes of space, time and frequency. Simulation results verify the characteristics of the millimeter-wave massive MIMO channel, and the comparison with the measured channel data of 3GPP shows accuracy of the constructed channel model.
-
目前，世界各国正在对5G关键技术进行广泛的研究。毫米波和大规模MIMO的结合将扩展新频谱资源的使用，加深无线资源的空间维度，并大大提高无线传输速率[1-4]，是未来无线通信系统最有潜力的研究方向之一。
信道建模是通信系统设计的基础。信道建模通过数学分析模型来表征传播环境的地理特征，进而准确刻画无线信号的传播机制，是评估无线技术最有效手段之一。基于散射簇的信道建模方法是一种基于统计模型的信道建模方法，已被广泛认可和使用，如COST 259/273/2100、SCM、SCME、WINNER I/II/+、IMT-Advanced、IEEE 802.16m、3GPP 3D MIMO、3GPP D2D、3GPP HF、扩展的SV、5GCM以及METIS等项目和标准组织建议的信道模型[5]。近年来，分别针对毫米波和大规模MIMO而采用的基于散射簇的信道模型的测量和建立工作已经开展。文献[6-7]指出大规模MIMO散射簇的统计特性与传统天线阵列出现显著不同，可以观察到散射簇在空间上沿着天线阵列轴新生和消失，这导致每对收发天线间可以观察到不同的散射簇集合。随着时间变化，可以观察到散射簇的新生和消失，散射簇集合随着时间轴演进，信道呈现空间和时间非平稳特性。文献[8-9]指出毫米波由于波长较短，与传统低频段有着显著不同，毫米波信道具有很高时延分辨率即散射簇，其内子径的功率和时延均可被解析。功率和时延随频率的改变满足了不同的参数分布，呈现出频率的非平稳特性。因此，毫米波大规模MIMO信道具有功率时延可解析性和空时频非平稳特性。
尽管当前毫米波大规模MIMO信道已经引起学术界和工业界的广泛关注，但相关的理论和实际建模研究工作还较少，尚未有广泛认可的信道模型出现[10]。很多新的信道模型都是在基于散射簇的信道模型的基础上进行扩展，并加入散射簇的演进算法，典型算法有基于生灭过程的散射簇演进算法[11]和基于有效散射簇的散射簇演进算法[12]等。但这些针对大规模MIMO信道建模的研究大都在低频段下进行。对毫米波信道建模研究中，更多涉及的是单天线情况。因而无论是从技术发展还是实际需求情况来讲，都应当充分考虑毫米波和大规模MIMO结合后带来的信道新的传播特性，并根据这些特性构建毫米波大规模MIMO信道模型。
本文在基于散射簇的3GPP信道建模方法上进行扩展[13]，提出了基于散射簇的空时频非平稳构建毫米波大规模MIMO的信道模型。首先，重新定义了三维传播环境下信道系数，其中涉及了与空间、时间和频率高度相关的参数，以反映毫米波大规模MIMO信道特性，并对散射簇及子径的功率时延重新定义，以符合可解析性；其次，在基于生灭过程的散射簇演进算法之上提出了空时频散射簇演进算法，充分描述了散射簇在空间、时间和频率上的演进过程，以反映毫米波大规模MIMO信道在空时频上的非平稳特性；最后，仿真了所构建信道的统计特性，并与3GPP实测信道数据对比，以证明所构建信道的准确性。
1. 基于散射簇的空时频非平稳信道模型
假定在发射端（transmitter, TX）和接收端（receiver, RX）分别具有
$ P $ 根发射天线和$ Q $ 根接收天线、系统频率中心频率为$ f $ 的毫米波大规模MIMO系统，三维散射簇模型结构如图1所示。为清楚起见，仅示出了发射天线$ p\left( {p = 1,2, \cdots ,P} \right) $ 和接收天线$ q\left( {r = 1,2, \cdots ,Q} \right) $ 间第$ n $ 个散射簇及散射簇$ n $ 内子径$ m $ 。发射端和接收端天线间隔分别由$ \Delta {x_{{\text{tx}}}} $ 和$ \Delta {x_{{\text{rx}}}} $ 表示；接收端处于运动之中，移动速度为$ {v_{{\text{rx}}}} $ ；所有参数都是时间$ t $ 与频率$ f $ 的参数。
图 1 基于散射簇的空时频非平稳信道模型结构
下载:
全尺寸图片
1.1 信道系数
发射天线
$ p $ 和接收天线$ q $ 间的信道系数可以表示为$$ {h_{pq}}\left( {t,f;\tau } \right) = \sum\limits_{n=1}^N {{h_{pq,n}}\left( {t,f;\tau } \right)} \delta \left( {\tau - {\tau _{pq,n}}} \right) $$ 式中：n为散射簇，
$ n = 1,2, \cdots ,N $ ，其中$ N $ 是散射簇的总数量；m为散射簇内的子径，$ m = 1,2, \cdots ,M $ ，其中$ M $ 为子径总数量；$ {\tau _{pq,n}} $ 表示散射簇$ n $ 的相对时延；散射簇n对应的信道系数${h_{pq,n}}\left( {t,f;\tau } \right)$ 为$$ \begin{array}{c}{h}_{pq,n}\left(t,f;\tau \right)={\displaystyle \sum _{m=1}^{M}\sqrt{{P}_{pq,n,m}}}{\left[\begin{array}{l}{F}_{p,\text{V}}^{\text{tx}}\left({\alpha }_{pq,n,m}^{\text{tx}},{\beta }_{pq,n,m}^{\text{tx}}\right)\\ {F}_{p,\text{H}}^{\text{tx}}\left({\alpha }_{pq,n,m}^{\text{tx}},{\beta }_{pq,n,m}^{\text{tx}}\right)\end{array}\right]}^{\text{T}}\cdot \\ \left[\begin{array}{cc}\sqrt{{\kappa }_{n,m}^{-1}}\mathrm{exp}\left(\text{j}{\theta }_{n,m}^{\text{VV}}\right)& \mathrm{exp}\left(\text{j}{\theta }_{n,m}^{\text{VH}}\right)\\ \mathrm{exp}\left(\text{j}{\theta }_{n,m}^{\text{HV}}\right)& \sqrt{{\kappa }_{n,m}^{-1}}\mathrm{exp}\left(\text{j}{\theta }_{n,m}^{\text{HH}}\right)\end{array}\right]\cdot \\ \left[\begin{array}{l}{F}_{q,\text{V}}^{\text{rx}}\left({\alpha }_{pq,n,m}^{\text{rx}},{\beta }_{pq,n,m}^{\text{rx}}\right)\\ {F}_{q,\text{H}}^{\text{rx}}\left({\alpha }_{pq,n,m}^{\text{rx}},{\beta }_{pq,n,m}^{\text{rx}}\right)\end{array}\right]\cdot \mathrm{exp}\left(\text{j}2\text{π}\frac{{D}_{pq,n,m}^{\text{tr}}}{\lambda }\right)\cdot \\ \mathrm{exp}\left(\text{j}2\text{π}{f}_{pq,n,m}\cdot t\right)\cdot \delta \left(\tau -{\tau }_{pq,n,m}\right)\end{array} $$ 式中：
$ {\text{V}} $ 和$ {\text{H}} $ 分别表示在全局坐标系下，原点位于天线阵列中心时天线的垂直极化和水平极化；$ {P_{pq,n,m}} $ 为散射簇$ n $ 内子径$ m $ 功率；$ {F}_{p,\text{V}}^{\text{tx}}(·) $ 为发射天线$ p $ 三维垂直极化方向图；$ {F}_{p,\text{H}}^{\text{tx}}(·) $ 为发射天线$ p $ 三维水平极化方向图；$ {F}_{q,\text{V}}^{\text{rx}}(·) $ 为接收天线$ q $ 的三维垂直极化方向图；$ {F}_{q,\text{H}}^{\text{rx}}(·) $ 为接收天线$ q $ 的三维水平极化方向图；$ \alpha _{pq,n,m}^{{\text{tx}}} $ 和$ \beta _{pq,n,m}^{{\text{tx}}} $ 分别为发射天线$ p $ 对应散射簇$ n $ 内子径$ m $ 的方位和俯仰离开角；$ \alpha _{pq,n,m}^{{\text{rx}}} $ 和$ \beta _{pq,n,m}^{{\text{rx}}} $ 分别为接收天线$ q $ 对应散射簇$ n $ 内子径$ m $ 的方位和俯仰到达角；$ {\kappa _{n,m}} $ 是交叉极化功率；$\theta _{n,m}^{{\text{VV}}}、 \theta _{n,m}^{{\text{VH}}}、 \theta _{n,m}^{{\text{HV}}}和\theta _{n,m}^{{\text{HH}}}$ 是第四象限第$ n $ 个散射簇内子径$ m $ 的初始随机相位，遵循$ \left( {0,2{\text{π }}} \right) $ 上的均匀分布；$ {\tau _{pq,n,m}} $ 为散射簇$ n $ 内子径$ m $ 的相对时延；${\boldsymbol{D}}_{pq,n,m}^{{\text{tr}}}$ 为发射天线$ p $ 和接收天线$ q $ 之间的位置矢量：$$ {\boldsymbol{D}}_{pq,n,m}^{{\text{tr}}} = {\boldsymbol{D}}_{pq,n,m}^{{\text{tx}}} + {\boldsymbol{D}}_{pq,n,m}^{{\text{rx}}} $$ 式中
${\boldsymbol{D}}_{pq,n,m}^{{\text{tx}}}$ 和${\boldsymbol{D}}_{pq,n,m}^{{\text{rx}}}$ 分别为发射天线$ p $ 与接收天线$ q $ 与散射簇$ n $ 内子径$ m $ 之间的位置矢量：$$ {\boldsymbol{D}}_{pq,n,m}^{{\text{tx}}} = D_n^{{\text{tx}}}{\left[ \begin{gathered} \cos \beta _{pq,n,m}^{{\text{tx}}}\cos \alpha _{pq,n,m}^{{\text{tx}}} \\ \cos \beta _{pq,n,m}^{{\text{tx}}}\sin \alpha _{pq,n,m}^{{\text{tx}}} \\ \sin \beta _{pq,n,m}^{{\text{tx}}} \\ \end{gathered} \right]^{\text{T}}} $$ $$ {\boldsymbol{D}}_{pq,n,m}^{{\text{rx}}} = D_n^{{\text{rx}}}{\left[ \begin{gathered} \cos \beta _{pq,n,m}^{{\text{rx}}}\cos \alpha _{pq,n,m}^{{\text{rx}}} \\ \cos \beta _{pq,n,m}^{{\text{rx}}}\sin \alpha _{pq,n,m}^{{\text{rx}}} \\ \sin \beta _{pq,n,m}^{{\text{rx}}} \\ \end{gathered} \right]^{\text{T}}} $$ 其中，
$ D_n^{{\text{tx}}} $ 和$ D_n^{{\text{rx}}} $ 分别为发射天线阵列中心与接收天线阵列中心与散射簇$ n $ 之间的初始直线距离；$ {f_{pq,n,m}} $ 为多普勒频率：$$ {f_{pq,n,m}} = \frac{{{v_{{\text{rx}}}}{{\left[ \begin{gathered} \cos \beta _{pq,n,m}^{{\text{rx}}}\cos \alpha _{pq,n,m}^{{\text{rx}}} \\ \cos \beta _{pq,n,m}^{{\text{rx}}}\sin \alpha _{pq,n,m}^{{\text{rx}}} \\ \sin \beta _{pq,n,m}^{{\text{rx}}} \\ \end{gathered} \right]}^{\text{T}}}}}{\lambda } $$ 可以看出，多普勒频率
$ {f_{pq,n,m}} $ 是由接收端天线阵列移动引起的，波长$ \lambda = c/f $ 。1.2 功率时延可解析性
毫米波由于波长较短因而与低频段相比具有较大路径损耗、较强大气吸收与雨衰以及较小的穿透性。毫米波段特性使得其不具有低频段下的富散射特性，信号传播主要依赖反射和绕射，大部分的接收信号功率集中在视距和低阶反射路径上，因而拥有很高的时延分辨率。每个散射簇及其内子径的功率和时延都不相同，可被解析[14]。
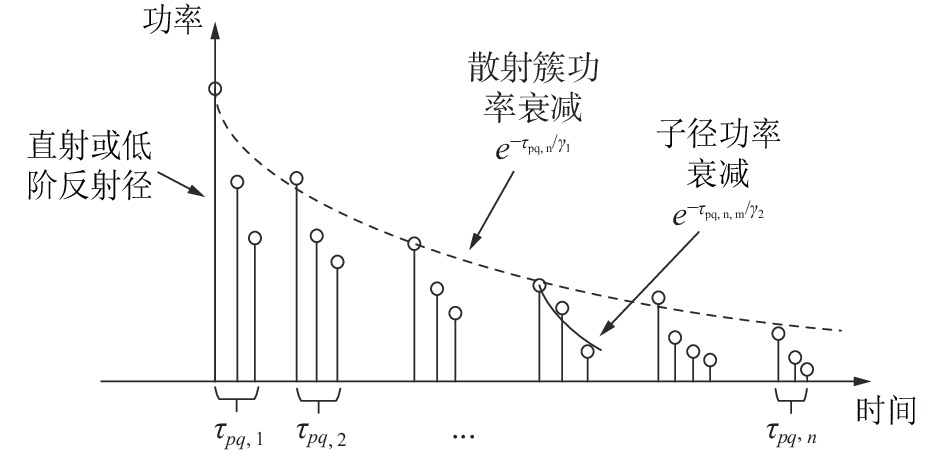
传统的基于散射簇的信道建模中每条子径的功率平均分配，每个散射簇与其内子径时延相同，功率与时延不可被解析[15]，因此不能直接用于表征毫米波大规模MIMO信道。参考MiWEBA项目组[14]对60 GHz毫米波信道实际测量数据，本文所提模型充分考虑了毫米波大规模MIMO信道中功率时延可解析性。在1.1节所提模型中，建立散射簇和子径均具不同的功率与时延模型。信道功率时延示意如图2所示。
图 2 信道功率时延示意下载:
全尺寸图片
每个散射簇的时延相对于前一个散射簇的时延是一个服从指数分布的随机变量，每条子径时延相对于前一条子径的时延也是一个服从指数分布的随机变量，即信道系数中时延分布可表示为
$$ \begin{gathered} \quad \;\; p({\tau _{pq,n}}\left| {{\tau _{pq,n - 1}}} \right.) = {\lambda _1}\exp ( - {\lambda _1}({\tau _{pq,n}} - {\tau _{pq,n - 1}})) \\ p({\tau _{pq,n,m}}\left| {{\tau _{pq,n,m - 1}}} \right.) = {\lambda _2}\exp ( - {\lambda _2}({\tau _{pq,n,m}} - {\tau _{pq,n,m - 1}})) \\ \end{gathered} $$ 式中
$ {\lambda _1} $ 和$ {\lambda _2} $ 分别为散射簇和子径的时延参数，大小与具体的频率大小有关。${\overline P_{pq,n}}$ 和${\overline P_{pq,n,m}}$ 分别为散射簇$ n $ 和子径$ m $ 的平均功率，不同子径功率也不再平均分配。建模每个散射簇的平均功率相对于前一个散射簇的平均功率呈指数衰减，每条子径的平均功率相对于前一条子径也呈指数衰减：$$ \begin{gathered} \quad{\overline P _{pq,n}} = {\overline P _{1,1}}\exp ( - {\tau _{pq,n}}/{\gamma _1}) \\ {\overline P _{pq,n,m}} = {\overline P _{pq,n}}\exp ( - {\tau _{pq,n,m}}/{\gamma _2}) \\ \end{gathered} $$ 式中：
$ {\overline P _{1,1}} $ 为第一个散射簇内第一条子径的平均功率；$ {\gamma _1} $ 和$ {\gamma _2} $ 分别为散射簇和子径的功率衰减参数，大小与具体的频率大小有关。1.3 空时频散射簇演进算法
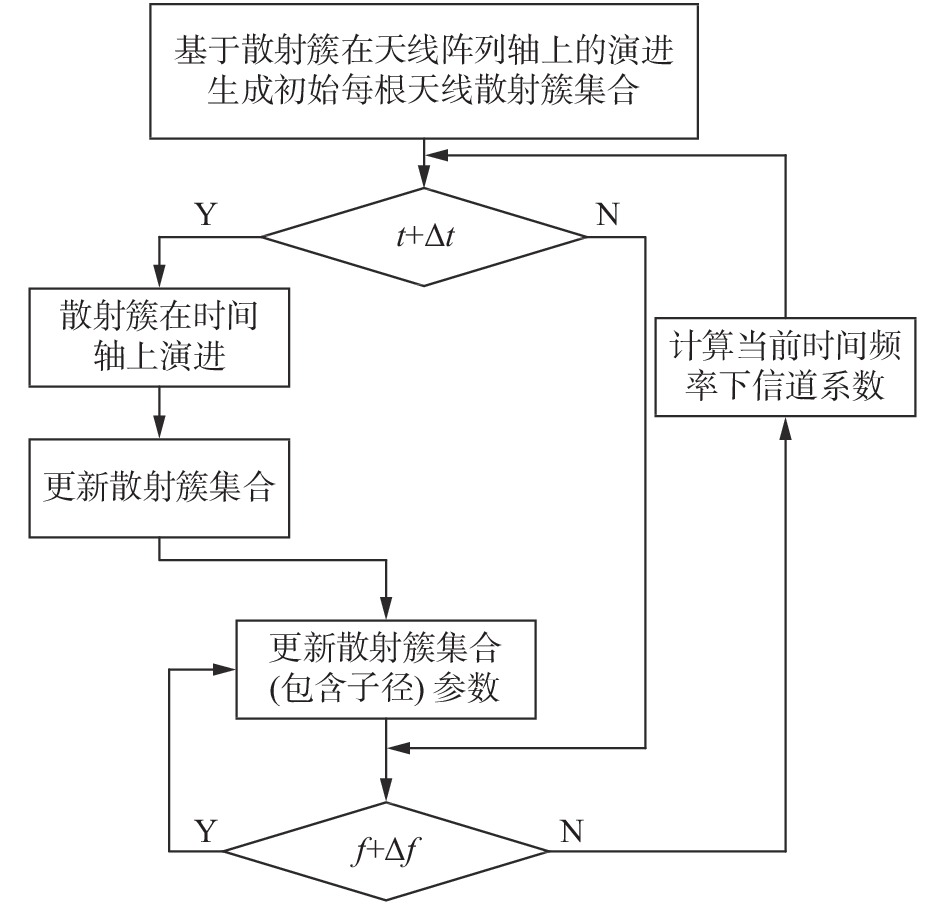
考虑之前提到毫米波大规模MIMO信道所具有的空间、时间和频率上的非平稳特性，需要对散射簇的变化进行充分的描述。因此，在基于生灭过程的散射簇演进算法基础上[16]提出了空时频散射簇演进算法，分别表示了散射簇在天线阵列轴、时间轴和频率上的演进，体现了毫米波大规模MIMO信道在空间、时间和频率上的非平稳特性。算法流程如图3所示。
图 3 空时频散射簇演进算法流程下载:
全尺寸图片
定义散射簇的生成和消亡速率分别为
$ {\lambda _{\text{G}}} $ （个/m）和$ {\lambda _{\text{R}}} $ （个/m），符号$ \xrightarrow{E} $ 表示在天线阵列轴和时间轴上的演进。首先，假设初始
$ t $ 时刻中心频率为$ f $ 时散射簇的初始数量为$ N $ ，第1根发射天线的初始散射簇集合为$$ {C_1}(t,f) = \left\{ {{c_n}(t,f):n = 1,2, \cdots ,N} \right\} $$ 相邻天线间散射簇的存活概率建模为
$$ P_{{\text{survival}}}^{}(t,f) = \exp ( - {\lambda _{\text{R}}}\frac{{\Delta {x_{{\text{tx}}}}}}{{{D_{\text{s}}}}}) $$ 式中
$ {D_{\text{s}}} $ 为空间相关因子，与实际场景复杂程度有关。假设发射天线总数为$ P $ ，散射簇集合$ {C_1}(t,f) $ 中的散射簇通过演进过程生成其他天线在时刻$ t $ 的散射簇集合，具体表示如下：$$ {C_{p - 1}}(t,f)\xrightarrow{{\rm{E}}}{C_p}(t,f),\left( {p = 2,3, \cdots ,P} \right) $$ 此时基于散射簇在天线阵列轴上的演进生成初始每根天线散射簇集合。
接下来，当时间由
$ t $ 到$ t + \Delta t $ 时，天线$ p $ 对应散射簇集合的演进可表示为$$ C_p^{}(t,f)\xrightarrow{{\rm{E}}}C_p^{}(t + \Delta t,f) $$ 信道的时变性可由接收端和传输场景中散射簇的运动造成。此处，引入变量
$ \delta (t + \Delta t,f) $ 来描述在$ t $ 到$ t + \Delta t $ 时刻传输环境的变化，$ \delta (t + \Delta t,f) $ 可用作在$ t $ 到$ t + \Delta t $ 时刻信道变化的度量，表示为$$ \delta (t + \Delta t,f) = {\delta _{{\text{cha}}}}(t + \Delta t,f) + {\delta _{{\text{rx}}}}(t + \Delta t,f) $$ 式中
$ {\delta _{{\text{cha}}}}\left( {t + \Delta t,f} \right) $ 为散射簇运动造成的信道变化量，定义为$$ {\delta _{{\text{cha}}}}(t + \Delta t,f) = \int_t^{t + \Delta t} {{P_{\text{c}}}} \left( {\left| {{v_{p,n}}(\tau )} \right| + \left| {{v_{q,n}}(\tau )} \right|} \right){\text{d}}\tau $$ 其中：
$ {P_{\text{c}}} $ 为环境中运动散射簇的百分比，$ {v_{p,n}}(t) $ 和$ {v_{q,n}}(t) $ 分别为散射簇$ n $ 相对于发收天线的速度。$ {\delta _{{\text{rx}}}} (t + \Delta t,f) $ 为接收端运动造成的信道变化量$$ {\delta _{{\text{rx}}}}(t + \Delta t,f) = \int_t^{t + \Delta t} {\left( {\left| {{v_{{\text{rx}}}}(\tau )} \right|} \right)} {\text{d}}\tau $$ 其中
$ {v_{{\text{rx}}}}\left( t \right) $ 为接收端运动速度。考虑到时间间隔较短，认为散射簇和接收端在信道采样间隔内运动恒定，散射簇的速度由其均值表示：$$ {v_p} = {\text{E}}\left[ {{v_{p,n}}(t)} \right],{v_q} = {\text{E}}\left[ {{v_{q,n}}(t)} \right],{v_{{\text{rx}}}} = {\text{E}}\left[ {{v_{{\text{rx}}}}(t)} \right] $$ 因此，由散射簇和接收端运动造成的信道变化量可简化为
$$ \delta (t + \Delta t,f) = {P_{\text{c}}}\left( {{v_p} + {v_q}} \right)\Delta t + {v_{{\text{rx}}}}\Delta t $$ 此时，
$ t + \Delta t $ 时刻新生成的散射簇数量的均值为$$ \begin{split} {\text{E}}\left[ {{N_{{\text{new}}}}(t + \Delta t,f)} \right] = \qquad \\ \frac{{{\lambda _{\text{G}}}}}{{{\lambda _{\text{R}}}}}(1 - \exp ( - \frac{{{\lambda _{\text{R}}}\delta (t + \Delta t,f)}}{{{D_{\text{s}}}}})) \end{split} $$ (1) 相邻天线间散射簇的存活概率为
$$ {P_{{\text{survival}}}}(t + \Delta t,f) = \exp ( - \frac{{{\lambda _{\text{R}}}\delta (t + \Delta t,f)}}{{{D_{\text{s}}}}}) $$ (2) 当信道受到收发端相对运动影响时，通过式(1)确定新时刻新生散射簇数量，并根据式(2)给出的散射簇存活概率将新生散射簇加入不同的散射簇集合，更新每根天线散射簇集合。
最后，当频率由
$ f $ 到$ f + \Delta f $ 改变时，天线$ p $ 对应散射簇集合的演进可表示如下：$$ C_p^{}(t,f)\xrightarrow{{\rm{E}}}C_p^{}(t,f + \Delta f) $$ 当频率发生改变，需要对功率和时延中参数进行修改：
$$ \begin{gathered} p({\tau _{pq,n}}\left| {{\tau _{pq,n - 1}}} \right.) = {\lambda _1}(f)\exp ( - {\lambda _1}(f)({\tau _{pq,n}} - {\tau _{pq,n - 1}})) \\ p({\tau _{pq,n,m}}\left| {{\tau _{pq,n,m - 1}}} \right.) = {\lambda _2}(f)\exp ( - {\lambda _2}(f)({\tau _{pq,n,m}} - {\tau _{pq,n,m - 1}})) \\ \end{gathered} $$ 式中
$ {\lambda _1}(f) $ 和$ {\lambda _2}(f) $ 分别为散射簇和子径的时延参数，均为频率的函数。当频率发生改变，其值也发生改变，具体数值由当前频段决定。$$ \begin{gathered} \quad {\overline P _{pq,n}} = {\overline P _{1,1}}\exp ( - {\tau _{pq,n}}/{\gamma _1}(f)) \\ {\overline P _{pq,n,m}} = {\overline P _{pq,n}}\exp ( - {\tau _{pq,n,m}}/{\gamma _2}(f)) \\ \end{gathered} $$ 式中
$ {\gamma _1}(f) $ 和$ {\gamma _2}(f) $ 分别为散射簇和子径的功率衰减参数，均为频率的函数。当频率发生改变，其值也发生改变，具体数值由当前频段决定。2. 毫米波大规模MIMO信道模型统计特性
2.1 信道功率时延谱
发射天线
$ p $ 和接收天线$ q $ 之间信道的功率时延谱（power delay spectrum，PDS)可以表示为$$ \begin{gathered} {P_{pq}}\left( {t,f;\tau } \right) = \\ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {{{\left| {{h^{-1}_{pq,n,m}}\left( {t,f;\tau } \right)} \right|}^2}} } \delta \left( {\tau - {\tau _{pq,n}} - {\tau _{pq,n,m}}} \right) \\ \end{gathered} $$ 式中：PDS受到散射簇
$ n $ 相对时延$ {\tau _{pq,n}} $ 及散射簇$ n $ 内子径$ m $ 相对时延$ {\tau _{pq,n,m}} $ 的影响，${h^{-1}_{pq,n,m}}\left( {t,f;\tau } \right)$ 为信道系数${h_{pq,n,m}}(t,f;\tau )$ 的傅里叶反变换，${\left| {{h^{-1}_{pq,n,m}}(t,f;\tau )} \right|^2}$ 为子径$ m $ 的功率。PDS描述了功率与时延之间的关系，所有这些参数都与不断更新的时间和频率有关。2.2 信道空时频相关函数
假定2个任意的信道系数如
${h_{pq}} (t, f;\tau )$ 和${h_{p'q'}} (t,f;\tau )$ 的相关函数可以被定义为没有关联的所有散射簇的总和。为了研究相关性，空时频相关函数${R_h}\left( {\Delta t,\Delta f,\Delta {x_{{\text{tx}}}},\Delta {x_{{\text{rx}}}}} \right)$ 可定义为$$ \begin{split} {R_h}(\Delta t,\Delta f,\Delta {x_{{\text{tx}}}},\Delta {x_{{\text{rx}}}}) = \qquad \qquad\\ {\rm{E}}[{h_{pq}}(t,f;\tau )h_{p'q'}^*(t + \Delta t,f + \Delta f;\tau )] = \quad\;\;\\ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {h_{pq,n,m}^{}(t,f;\tau )h_{p'q',n,m}^*(t + \Delta t,f + \Delta f;\tau )} } \end{split} $$ (3) 2.3 空间互相关函数
空间互相关函数（cross-correlation function，CCF）描述了同一时间和频率下，2根不同天线间的相关性。通过在式(3)中设置
$ \Delta t = 0 $ 和$ \Delta f = 0 $ 来获得空间互相关函数，表示为$$ \begin{gathered} {C_h}(\Delta {x_{{\text{tx}}}},\Delta {x_{{\text{rx}}}}) = {R_h}(0,0,\Delta {x_{{\text{tx}}}},\Delta {x_{{\text{rx}}}}) = \\ {\rm{E}}[{h_{pq}}(t,f;\tau )h_{p'q'}^*(t,f;\tau )] = \\ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {h_{pq,n,m}^{}(t,f;\tau )h_{p'q',n,m}^*(t,f;\tau )} } \\ \end{gathered} $$ 2.4 时间自相关函数
时间自相关函数（auto-correlation function，ACF)描述了同一天线和频率下，不同时间的相关性。通过在式(3)中设置
$ \Delta {x_{{\text{tx}}}} = 0 $ 、$ \Delta {x_{{\text{rx}}}} = 0 $ 和$ \Delta f = 0 $ 来获得时间自相关函数，表示为$$ \begin{gathered} {A_h}(\Delta t) = {R_h}(\Delta t,0,0,0) = \\ {\rm{E}}[{h_{pq}}(t,f;\tau )h_{pq}^*(t + \Delta t,f;\tau )] = \\ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {h_{pq,n,m}^{}(t,f;\tau )h_{pq,n,m}^*(t + \Delta t,f;\tau )} } \\ \end{gathered} $$ 2.5 频率自相关函数
频率自相关函数（frequency auto-correlation function，FCF)描述了同一天线和时间下，不同频率的相关性。通过在式(3)中设置
$ \Delta {x_{{\text{tx}}}} = 0 $ 、$ \Delta {x_{{\text{rx}}}} = 0 $ 和$ \Delta t = 0 $ 来获得频率自相关函数，表示为$$ \begin{gathered} {F_h}(\Delta f) = {R_h}(0,\Delta f,0,0){\text{ = }} \\ {\rm{E}}[{h_{pq}}(t,f;\tau )h_{pq}^*(t,f + \Delta f;\tau )] = \\ \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {h_{pq,n,m}^{}(t,f;\tau )h_{pq,n,m}^*(t,f + \Delta f;\tau )} } \\ \end{gathered} $$ 3. 仿真分析
本节对散射簇的演进过程与所构建的信道模型的统计特性进行仿真分析，并与基于散射簇的理论的3GPP信道模型实测数据[13]进行对比，进一步说明所构建模型的合理与准确性。同时利用仿真结果说明了毫米波大规模MIMO信道功率时延可解析性以及在时间、空间和频率上的非平稳特性，所构建信道模型能够充分建模这些新的传播特性。
3.1 仿真条件
设置仿真参数，发射天线和接收天线数量
$ P = Q = 32 $ ，天线间隔，毫米波段中心频率$f = 60\; {\text{GHz}}$ ，$\Delta {x_{{\text{tx}}}} = \Delta {x_{{\text{rx}}}} = 0.1\; {\text{m}}$ ，接收端移动速度${v_{{\text{rx}}}} = 1 \;{\text{m/s}}$ ；散射簇初始数量$ N = 50 $ ，散射簇时延参数${\lambda _1} = 0.05\; {\text{n}}{{\text{s}}^{ - {\text{1}}}}$ ，子径时延参数${\lambda _2} = 0.31\; {\text{n}}{{\text{s}}^{ - {\text{1}}}}$ ，散射簇功率衰减参数${\gamma _1} = 15 \;{\text{ns}}$ ，子径功率衰减参数${\gamma _2} = 4.5 \;{\text{ns}}$ ；散射簇生成率${\lambda _{\text{G}}} = 80\;个/{\text{m}}$ ，消亡率${\lambda _{\text{R}}} = 4\;个/{\text{m}}$ ，运动散射簇的比例$ {P_C} = 0.3 $ ；发射天线阵列中心与散射簇$ n $ 的初始距离$D_n^{{\text{tx}}} = 50\; {\text{m}}$ ，接收天线阵列中心与散射簇$ n $ 初始距离$D_n^{{\text{rx}}} = 100\; {\text{m}}$ 。其余参数的生成，参考基于散射簇的3GPP信道模型中给出的实测数据[13]。3.2 仿真结果与分析
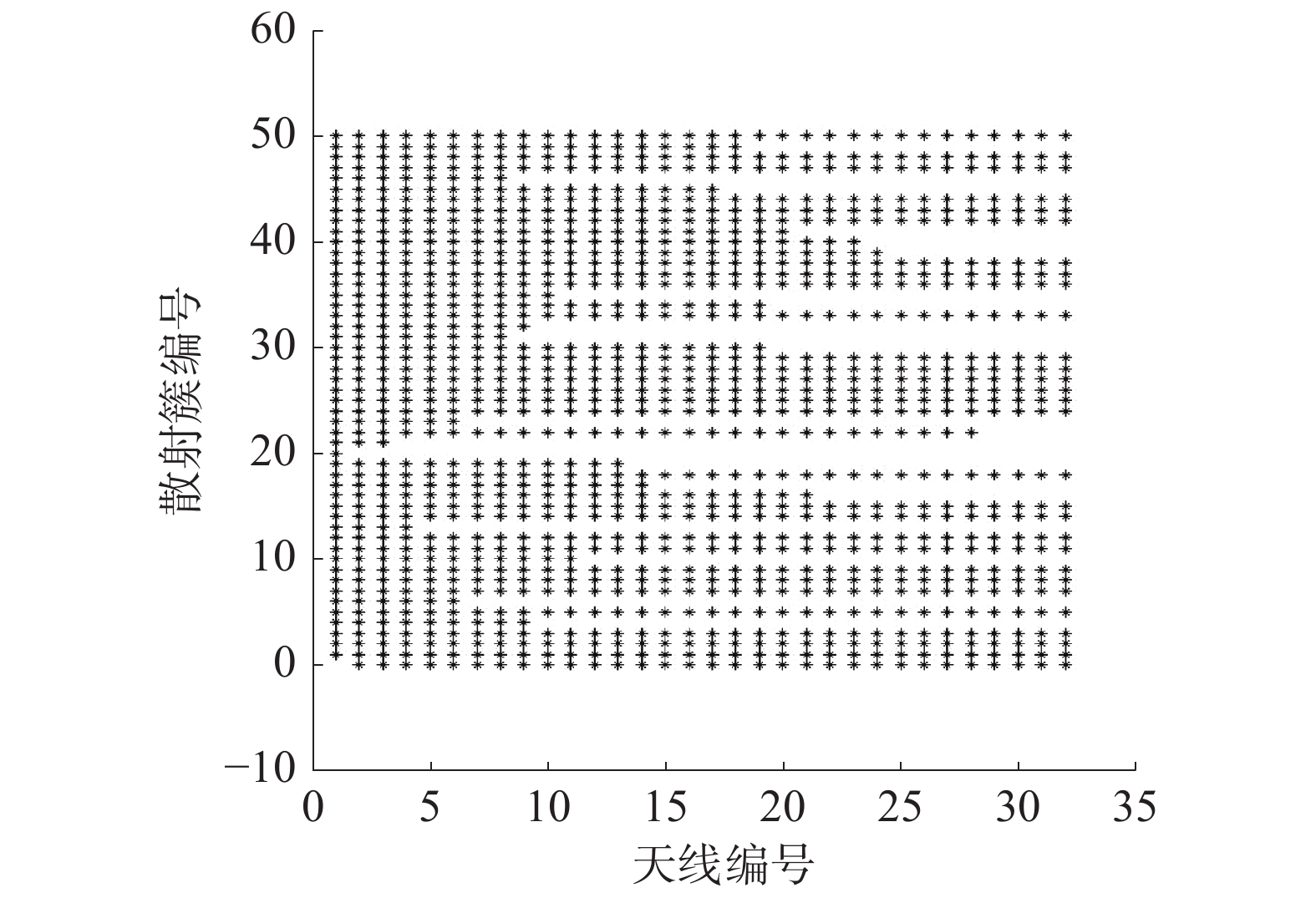
图4仿真了空时频散射簇演进算法中散射簇在天线阵列轴上的演进。
图 4 散射簇在天线阵列轴上演进下载:
全尺寸图片
仿真设置初始散射簇数为50，天线数为32。在所提信道模型中，随着散射簇在天线阵列轴上的演进，每一根天线拥有不同的散射簇集合。其中有相同的部分，2根天线的距离越远，它们观察到相同散射簇概率越小，也有不同即新生散射簇。散射簇在天线阵列轴上的演进，主要体现散射簇的新生消亡过程，仿真结果验证了所提毫米波大规模MIMO信道在空间上的非平稳特性。
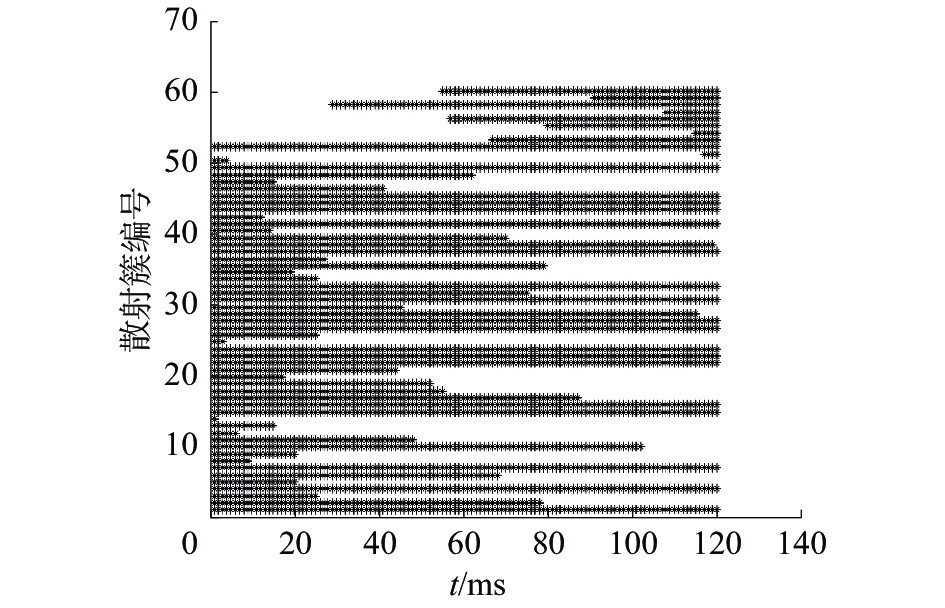
图5仿真了空时频散射簇演进算法中散射簇在时间轴上的演进。
图 5 散射簇在时间轴上演进下载:
全尺寸图片
仿真设置初始散射簇数为20，选取第一根天线。所提信道模型中，随着散射簇在时间轴上的演进，每个时刻天线对应的散射簇集合是不相同的。其中有上个时刻存活下来的散射簇，也有此时刻新生的散射簇。仿真结果验证了所提毫米波大规模MIMO信道在时间上的非平稳特性。
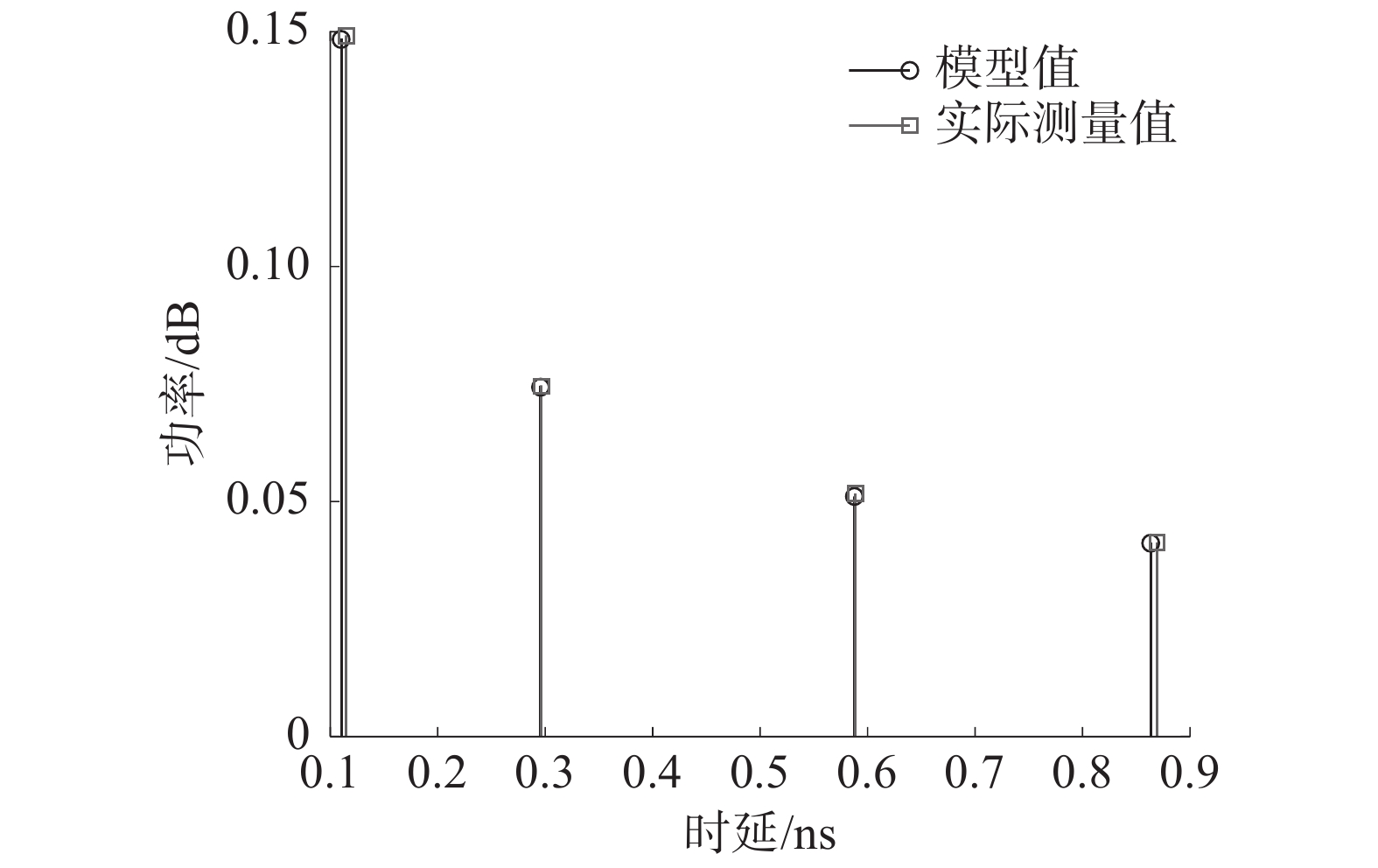
图6仿真了考虑一个散射簇和其内子径功率时延与3GPP信道模型实际信道散射簇及子径功率时延测量值对比。设置仿真环境为城市微蜂窝下同一散射簇，可以看出建模的散射簇和子径时延功率与实际测量的时延功率值表现出较好的一致性。
图 6 模型与实际测量功率时延对比下载:
全尺寸图片
仿真结果验证了毫米波大规模MIMO信道的功率时延可解析性。传统基于散射簇的3GPP信道建模中，散射簇与其内子径时延相同，子径功率平均分配，1.2节对功率时延的重新定义可准确模拟功率时延可解析特性。
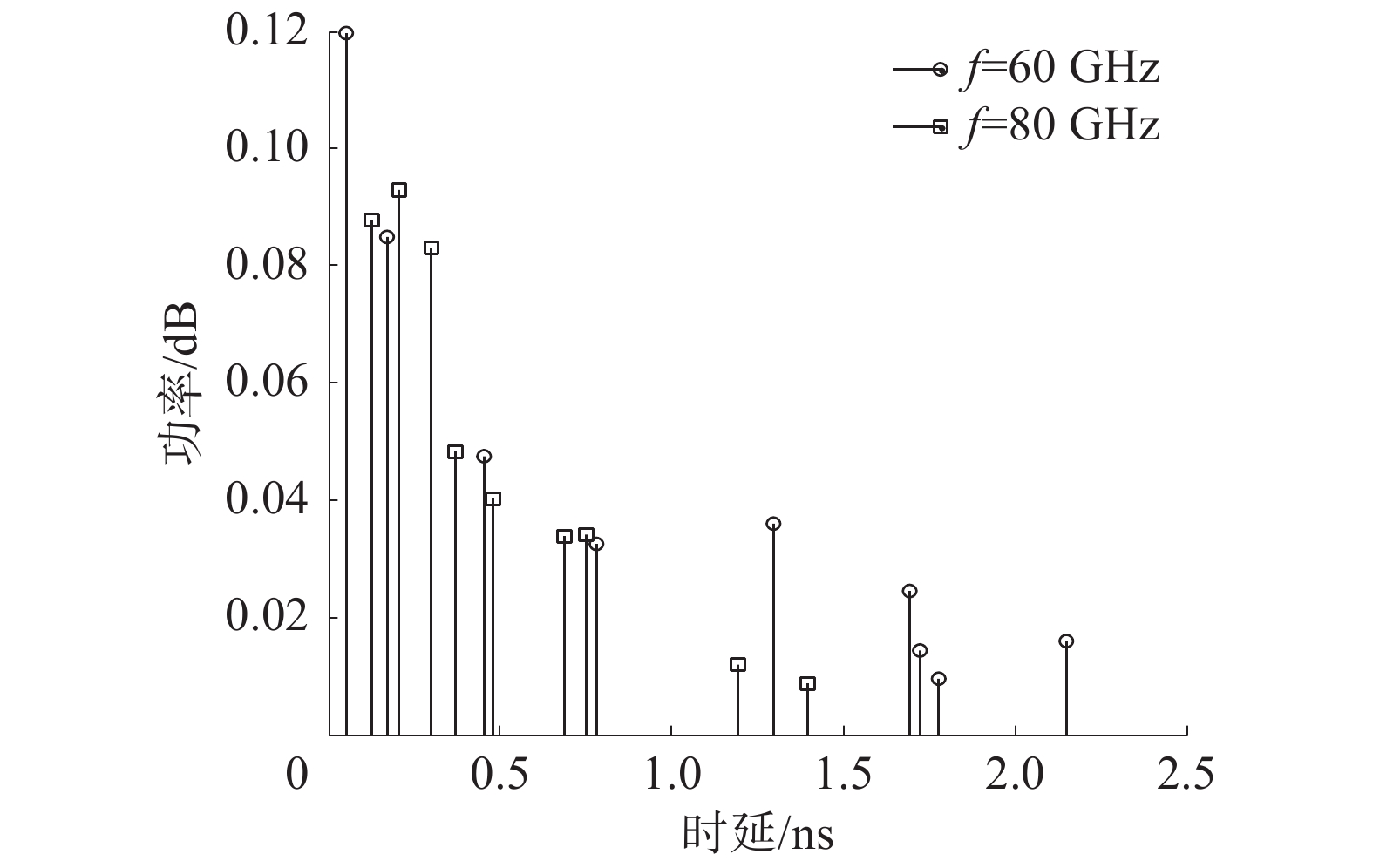
图7仿真了不同频率下信道功率时延谱。仿真设置散射簇数量为3，每个散射簇内有3条子径。所提信道模型中，每个散射簇和子径具有不同的时延和功率，符合毫米波大规模MIMO信道的时延功率可解析性。并且不同的频率下，时延与功率满足不同的参数分布，仿真结果验证了所提毫米波大规模MIMO信道在频率上的非平稳特性。
图 7 不同频率下信道功率时延下载:
全尺寸图片
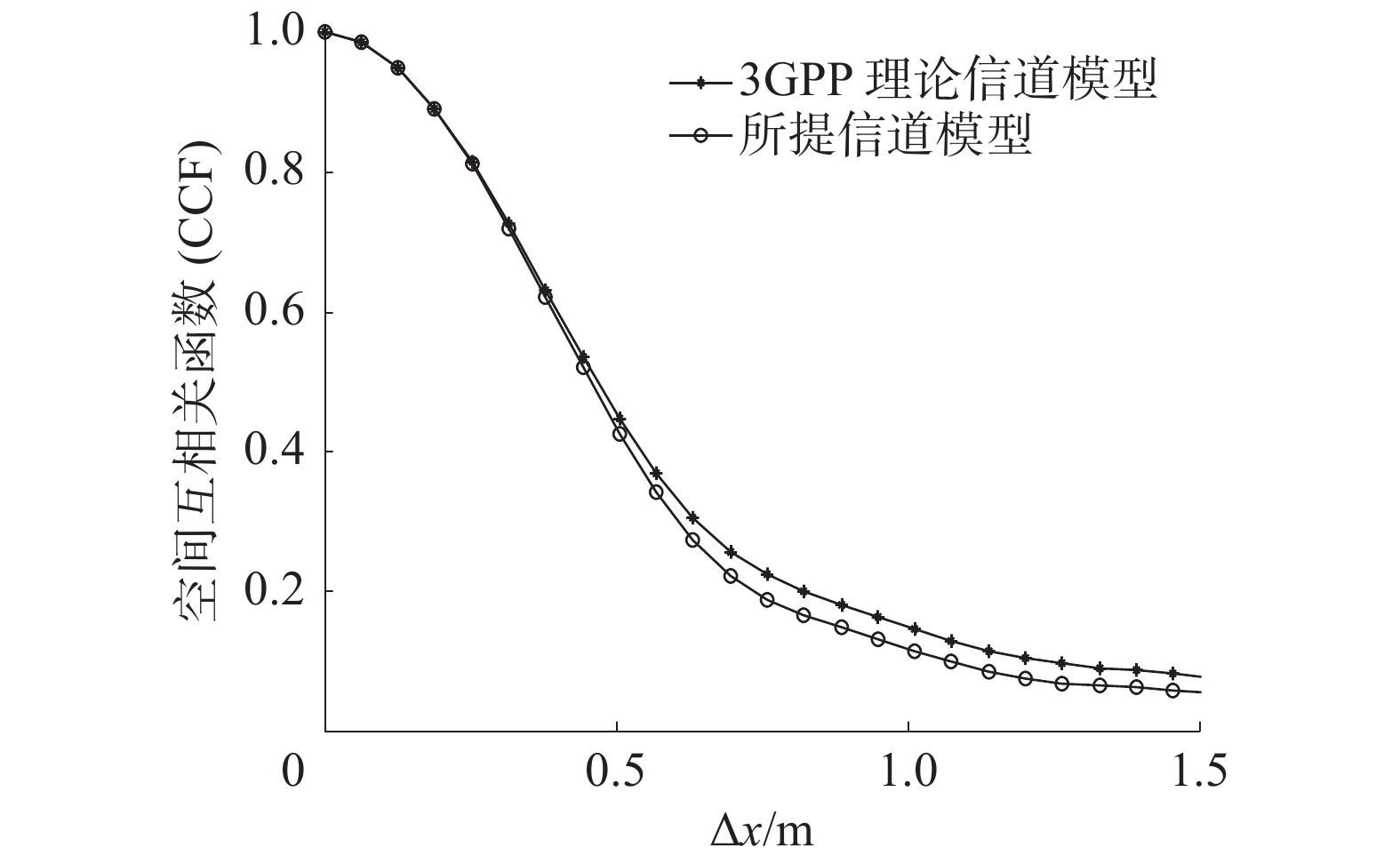
图8仿真了不同天线间距下信道空间互相关函数。仿真设置
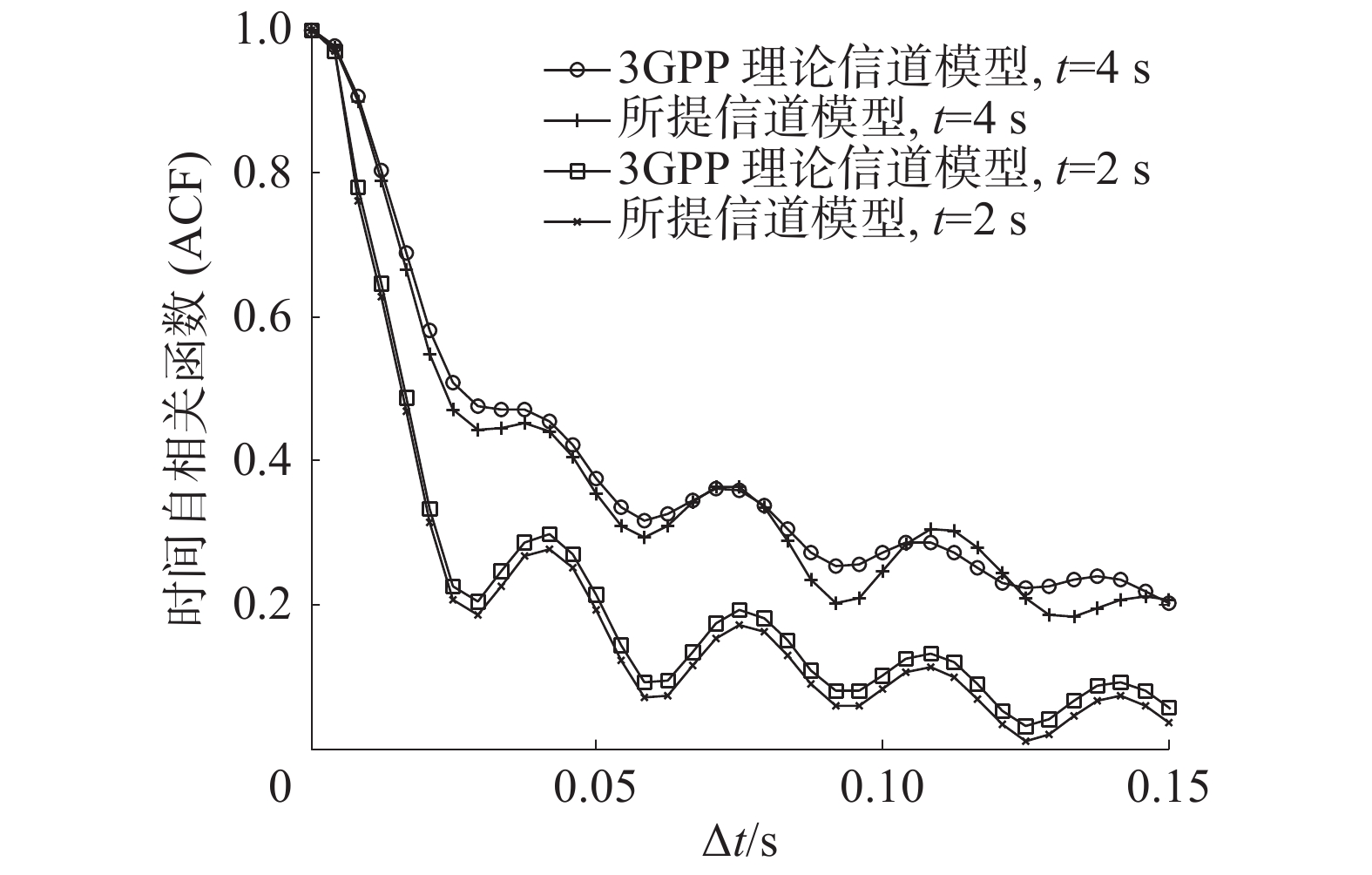
$f = 60\; {\text{GHz}}$ 、$t = 2 \;{\text{s}}$ 。所提信道模型中，随着天线间距增长，2根不同天线所观察到的相同散射簇减少，因此空间CCF呈现下降趋势。不同间距下，所提信道模型具有不同的空间CCF，仿真结果验证了所提毫米波大规模MIMO信道在空间上的非平稳特性。所提信道模型空间CCF与3GPP信道实测数据基本吻合，验证了所提信道模型对信道空间CCF刻画的准确性。
图 8 信道空间互相关函数下载:
全尺寸图片
图9仿真了不同时刻下信道时间自相关函数。仿真设置
$f = 60\;{\text{GHz}}$ ，选取第一根天线。所提信道模型中，在$t = 2 \;{\text{s}}$ 和$t = 4 \;{\text{s}}$ ，随着时间增长，空间中同一根天线所观察到的相同散射簇减少，因此时间ACF呈现下降趋势。不同时刻，信道模型具有不同的时间ACF，仿真结果验证了所提毫米波大规模MIMO信道在时间上的非平稳特性。所提信道模型时间ACF与3GPP信道实测数据基本吻合，验证了所提信道模型对信道时间ACF刻画的准确性。
图 9 信道时间自相关函数下载:
全尺寸图片
图10仿真了不同频率下信道频率自相关函数。仿真设置
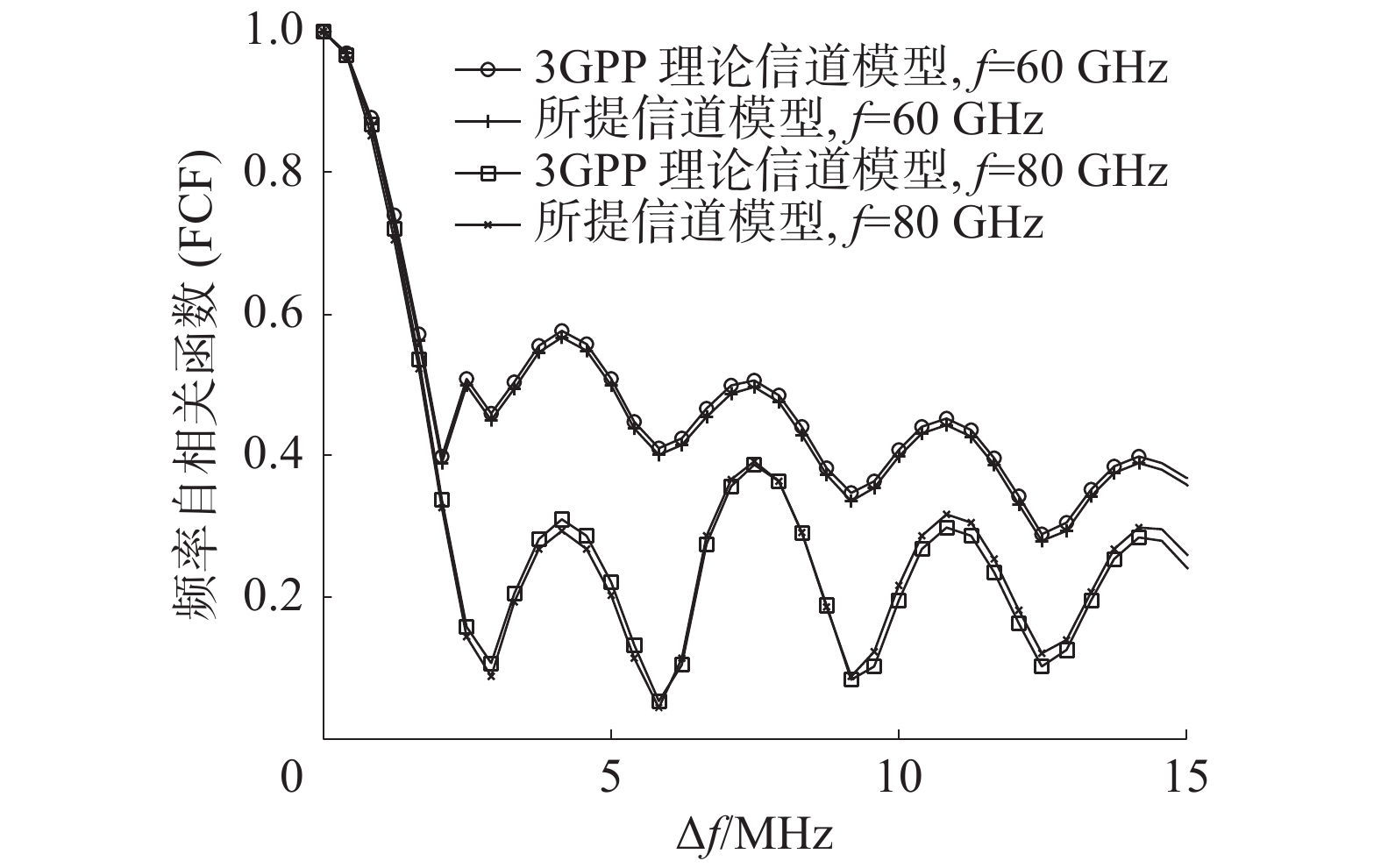
$t = 2\;{\text{s}}$ ，选取第一根天线。所提信道模型中，在$f = 60\;{\text{GHz}}$ 和$f = 80\;{\text{GHz}}$ ，随着频率增长，散射簇功率与时延会发生显著变化，同一根天线所观察到的相同散射簇减少，因此FCF呈现下降趋势。不同频率，信道模型具有不同的FCF，仿真结果验证了所提毫米波大规模MIMO信道在频率上的非平稳特性。所提信道模型FCF与3GPP信道实测数据基本吻合，验证了所提信道模型对信道FCF刻画的准确性。
图 10 信道频率自相关函数下载:
全尺寸图片
4. 结论
本文提出了一种适用于毫米波大规模MIMO的基于散射簇的空时频非平稳信道模型。论文的主要贡献包括：
1）在基于散射簇的3GPP信道模型基础上，重新定义了三维传播场景中的信道系数，并对散射簇及子径的功率和时延重新定义，以反映毫米波大规模MIMO信道在功率和时延上的可解析性。
2）在基于生灭过程的散射簇演进算法基础上，提出了空时频散射簇演进算法，充分描述了散射簇在空间、时间和频率上的演进过程，以反映毫米波大规模MIMO信道在空时频上的非平稳特性。
3）对所构建信道模型统计特性进行仿真，并通过与3GPP实测信道数据的对比，验证了所提模型的合理性与准确性。
-
图 1 基于散射簇的空时频非平稳信道模型结构
下载:
全尺寸图片
图 2 信道功率时延示意
下载:
全尺寸图片
图 3 空时频散射簇演进算法流程
下载:
全尺寸图片
图 4 散射簇在天线阵列轴上演进
下载:
全尺寸图片
图 5 散射簇在时间轴上演进
下载:
全尺寸图片
图 6 模型与实际测量功率时延对比
下载:
全尺寸图片
图 7 不同频率下信道功率时延
下载:
全尺寸图片
图 8 信道空间互相关函数
下载:
全尺寸图片
图 9 信道时间自相关函数
下载:
全尺寸图片
图 10 信道频率自相关函数
下载:
全尺寸图片
-
[1] HE Ruisi, AI Bo, STÜBER G L, et al. Geometrical-based modeling for millimeter-wave MIMO mobile-to-mobile channels[J]. IEEE transactions on vehicular technology, 2018, 67(4): 2848−2863. doi: 10.1109/TVT.2017.2774808 [2] HUANG Jie, LIU Yu, WANG Chengxiang, et al. 5G millimeter wave channel sounders, measurements, and models: recent developments and future challenges[J]. IEEE communications magazine, 2019, 57(1): 138−145. doi: 10.1109/MCOM.2018.1701263 [3] BUSARI S A, HUQ K M S, MUMTAZ S, et al. Millimeter-wave massive MIMO communication for future wireless systems: a survey[J]. IEEE communications surveys & tutorials, 2018, 20(2): 836−869. [4] 卫斯赜. 毫米波大规模多天线室外场景信道特性与建模研究[D]. 北京: 北京交通大学, 2018: 28-50. [5] WANG Chengxiang, BIAN Ji, SUN Jian, et al. A survey of 5G channel measurements and models[J]. IEEE communications surveys & tutorials, 2018, 20(4): 3142−3168. [6] CHEN Jiajing, YIN Xuefeng, CAI Xuesong, et al. Measurement-based massive MIMO channel modeling for outdoor LoS and NLoS environments[J]. IEEE access, 2017, 5: 2126−2140. doi: 10.1109/ACCESS.2017.2652983 [7] CHEN Jianqiao, ZHANG Zhi, TANG Tian, et al. A non-stationary channel model for 5G massive MIMO systems[J]. Frontiers of information technology & electronic engineering, 2017, 18(12): 2101−2110. [8] RAPPAPORT T S, XING Yunchou, MACCARTNEY G R, et al. Overview of millimeter wave communications for fifth-generation (5G) wireless networks—with a focus on propagation models[J]. IEEE transactions on antennas and propagation, 2017, 65(12): 6213−6230. doi: 10.1109/TAP.2017.2734243 [9] ALI S, ASLAM M I, AHMED I. MIMO channel modeling and capacity analysis using 3-D spatial statistical channel model for millimeter wave outdoor communication[C]// 2017 14th International Bhurban Conference on Applied Sciences and Technology (IBCAST). Piscataway: IEEE, 2017: 735-740. [10] 尤力, 高西奇. 毫米波大规模MIMO无线传输关键技术[J]. 中兴通讯技术, 2017, 23(3): 11−13. doi: 10.3969/j.issn.1009-6868.2017.03.003 [11] LIU Yu, WANG Chengxiang, HUANG Jie, et al. Novel 3-D nonstationary MmWave massive MIMO channel models for 5G high-speed train wireless communications[J]. IEEE transactions on vehicular technology, 2019, 68(3): 2077−2086. doi: 10.1109/TVT.2018.2866414 [12] 张薇, 段京京, 王岩松. 一种基于随机散射簇的非平稳3D空间信道模型[J]. 电子与信息学报, 2018, 40(10): 2301−2308. [13] 3GPP. Study on channel model for frequencies from 0.5 to 100 GHz[EB/OL]. [2021–05–09]. https://www.3gpp.org/ftp/Specs/archive/38_series/38.901/. [14] WEILER R J, PETER M, KEUSGEN W, et al. Quasi-deterministic millimeter-wave channel models in MiWEBA[J]. EURASIP journal on wireless communications and networking, 2016, 2016(1): 1−16. doi: 10.1186/s13638-015-0498-8 [15] 贾伟. 大规模MIMO非平稳信道建模及特性研究[D]. 南京: 东南大学, 2017: 41-55. [16] GHAZAL A, YUAN Yi, WANG Chengxiang, et al. A non-stationary IMT-advanced MIMO channel model for high-mobility wireless communication systems[J]. IEEE transactions on wireless communications, 2017, 16(4): 2057−2068. doi: 10.1109/TWC.2016.2628795
