结构在裂纹发生与发展过程中始终处于一个较大范围的屈服状态。在这种状态下,大面积的塑性变形在结构断裂失效之前就已经存在,结构断裂后,可以看出明显的颈缩变形。夏比冲击试验的加载速率为1000~100000 MPa·m/s,是典型的动态试验,锤头惯性力会直接影响到试件断裂。冲击试验设备可获得性强,同时其成本较低、测量时间短、样品处理方便。这一系列优势使得这种试验方法在确定材料脆韧转变温度和判断材料失效特性上具有重要地位,在美国标准中,对不大于16 mm的钢板需要采用夏比冲击试验进行冲击韧性进行验收[1-3],而且因冲击试验便于实现,越来越多的学者纷纷采用这种试验方法来得到断裂相关参数。杨承东等[4]利用三点弯试样的载荷位移曲线计算了A508钢材的断裂韧性,不少学者提出了一系列改进方法,比如修正其加载方式验证与数据,提高钢材断裂韧性的表征准确性,并基于冲击特征曲线形式与断口形貌来描述材料的动态断裂过程。李一磊等[5]对金属材料夏比冲击功与裂纹冲击韧脆关系进行了研究,提出了金属材料裂纹冲击韧性评定方法的基本思路。刘志伟等[6]对对铁素体钢材Q345B进行了夏比冲击试验,确认了冲击吸收功的分布规律。李荣德等[7]对铁素体球墨铸铁进行了示波冲击试验,确定了温度对冲击过程中裂纹形成和裂纹扩展能力的影响。顾浩洋[8]使用示波冲击试验测定了Q235B钢材的的动态断裂韧性值JId。何沐阳等[9]利用仪器化夏比V型缺口冲击试验获得了11MnNiMo钢材的冲击断裂性能,并确定了起裂时间。本研究通过夏比冲击试验得到核用Q390D钢的载荷位移曲线,确定了其准确度的起裂点,分别利用准静态方法、Schindler法和归一化方法计算试件的裂纹扩展阻力曲线,并将3种方法得到的结果进行了对比,分析各自方法的优缺点,为工程实践提供参考。
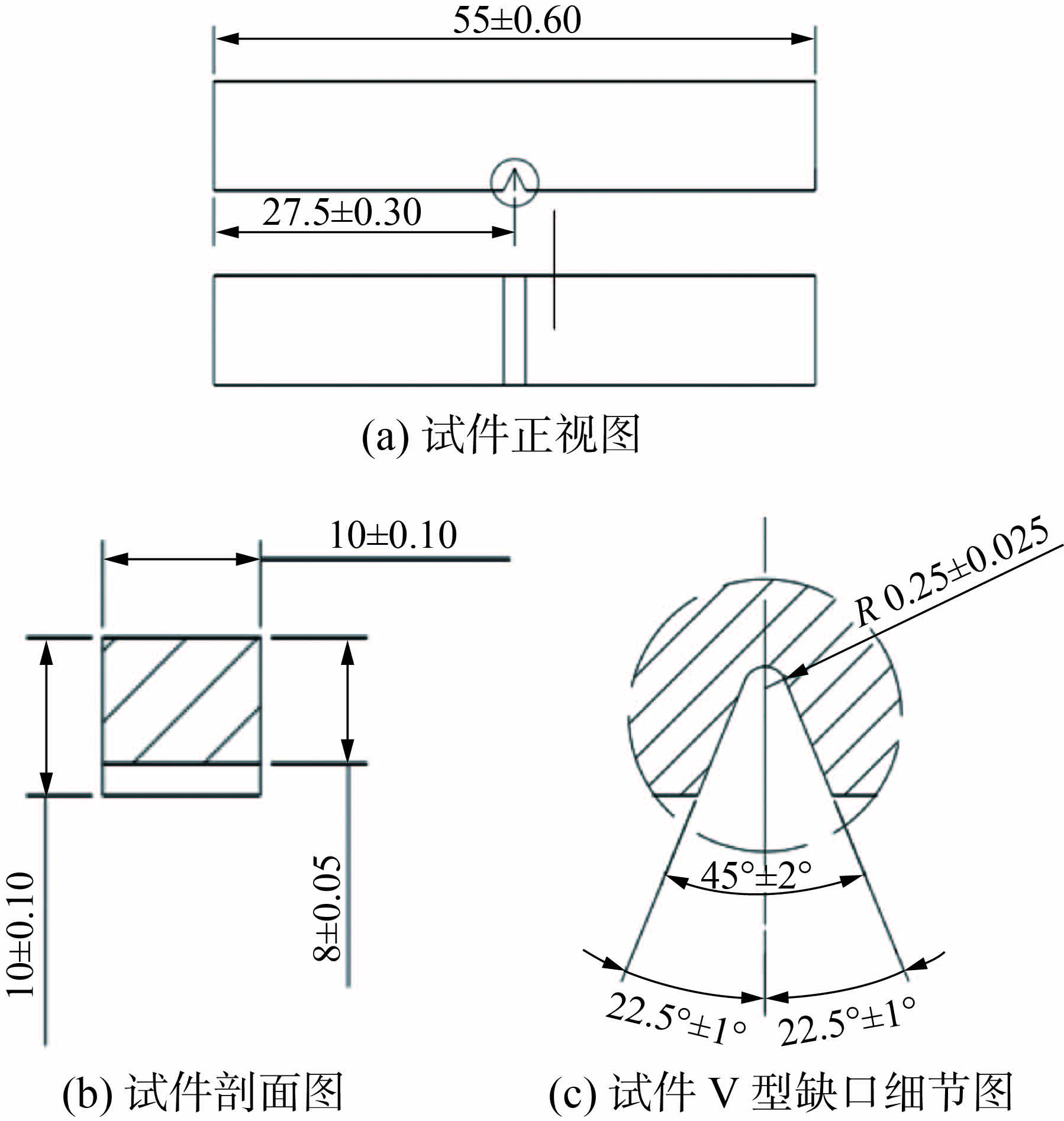
1 试验方法和结果核用钢Q390D是反应堆支承结构的常用钢材,对其进行加工,得到一个长(L)55 mm、宽(W)10 mm、跨距(S)40 mm、厚(B)10 mm、切口角45°、切口长度2 mm的夏比冲击试样,试样尺寸示意见图1,尺寸单位为mm。然后使用INSTRON8801万能试验机预制一定长度的疲劳裂纹见图2,相关参数见表1。
|
Download:
|
| 图 1 试样尺寸示意 | |

|
Download:
|
| 图 2 疲劳裂纹试样加载及裂纹形状 | |
|
|
表 1 夏比冲击试样预制疲劳裂纹参数 |
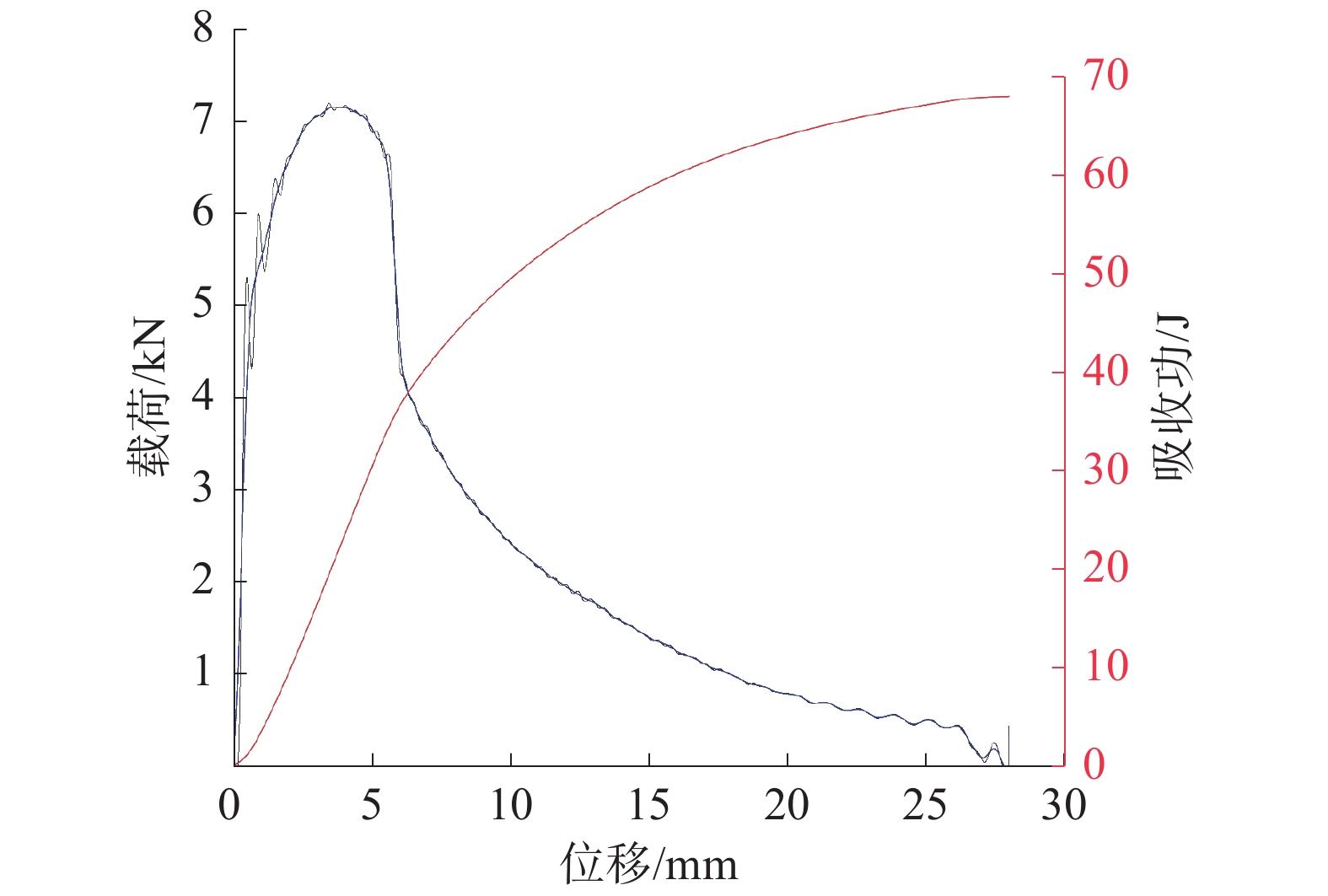
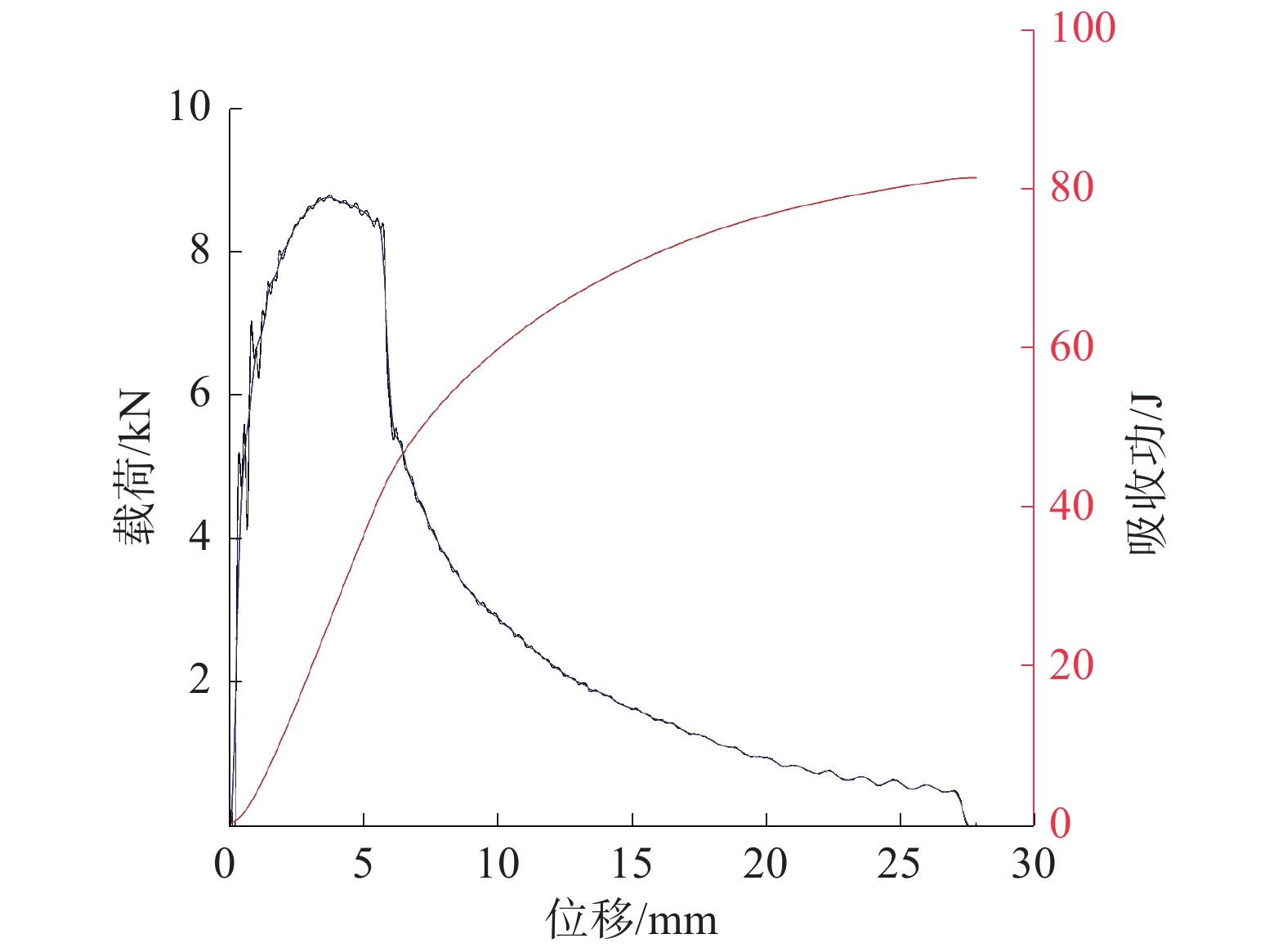
使用德国Zwick公司生产的ZWICK/ROLL摆锤冲击试验机对含预制裂纹Q390D试样进行夏比冲击试验,最大的冲击能量为475 J。具体操作过程参考《GBT229—2007金属材料夏比摆锤冲击试验方法》[10]。试验机可以通过安装在锤头的传感器自动记录冲击过程中的冲击载荷,通过软件可以将数据自动处理为冲击过程中的载荷–时间曲线,如图3和图4所示。
|
Download:
|
| 图 3 试样1载荷位移曲线 | |
|
Download:
|
| 图 4 试样2载荷位移曲线 | |
由图3和图4可以看出,初始阶段载荷和位移成线性增加的关系,这一阶段,试件处于弹性变形阶段;随后第2阶段载荷的增加趋势放缓,此时试件处于净截面屈服状态;第3阶段载荷和位移呈指数关系提高,此时缺口根部的塑性变形持续提高,最终缺口区域失效,产生细小裂纹;若持续增加载荷到最大载荷,则裂纹会进入到扩展阶段,可以看出曲线在缓慢下降一段后出现了载荷陡然下滑的现象,这是由于出现了不稳定裂纹扩展现象;之后曲线又开始了缓慢的下滑直到冲击试验结束,这是由于试样的断面产生了剪切唇,表明材料的韧性较好。
图5为含裂纹Q390D材料的试样断口。通过观察其断面样貌判定为韧性断裂断口,整个断口表面有显著凹凸,而且在其中间有凹陷情况。在对其断面形貌进行观察发现,纤维区主要存在于中间区域,在试样两侧有明显的剪切唇产生。

|
Download:
|
| 图 5 含预制裂纹Q390D夏比冲击试样的断口形貌 | |
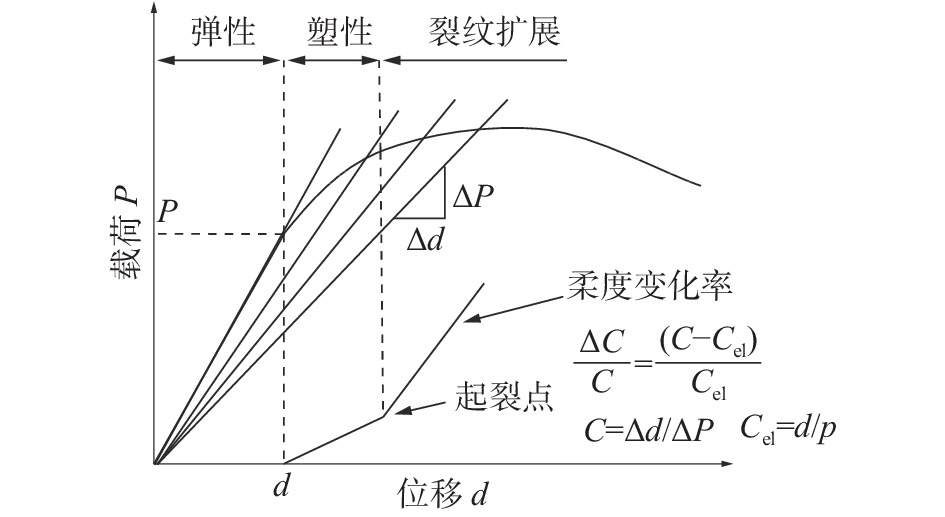
裂纹的起裂点是作为材料动态断裂韧性的重要评估依据。虽然基于准静态加载条件下对于裂纹起裂点的确定方法有很多,但不少方法并不适用动态加载条件,比如电位法是准静态加载条件下裂纹起裂点的常见测定方法。这种方法是基于裂纹起裂后电位骤变来判断具体的起裂点位置,但基于动态加载条件下,因测试系统反应时间存在延迟,导致测量数据有滞后性,这大大影响到最终结果的准确性。现阶段Kobayashi等[11]已经引入柔度变化率法作为测定动态加载条件下的裂纹起裂点方法,并且得到学者们的一致认可,尤其是对于拥有良好延性的材料,这种方法往往能够得出准确度较高的结果。再加上这种方法只用一次试验即可得出起裂点,因此得到广泛应用,其数学表达式为
| $ \frac{{\Delta C}}{C} = \frac{{\left( {C - {C_{{\text{el}}}}} \right)}}{{{C_{{\text{el}}}}}} $ |
式中:
图6为柔度变化率方法原理图。对于弹性变形区而言,试样的柔度始终为一定值,有C=Cel,
|
Download:
|
| 图 6 柔度变化率方法原理 | |
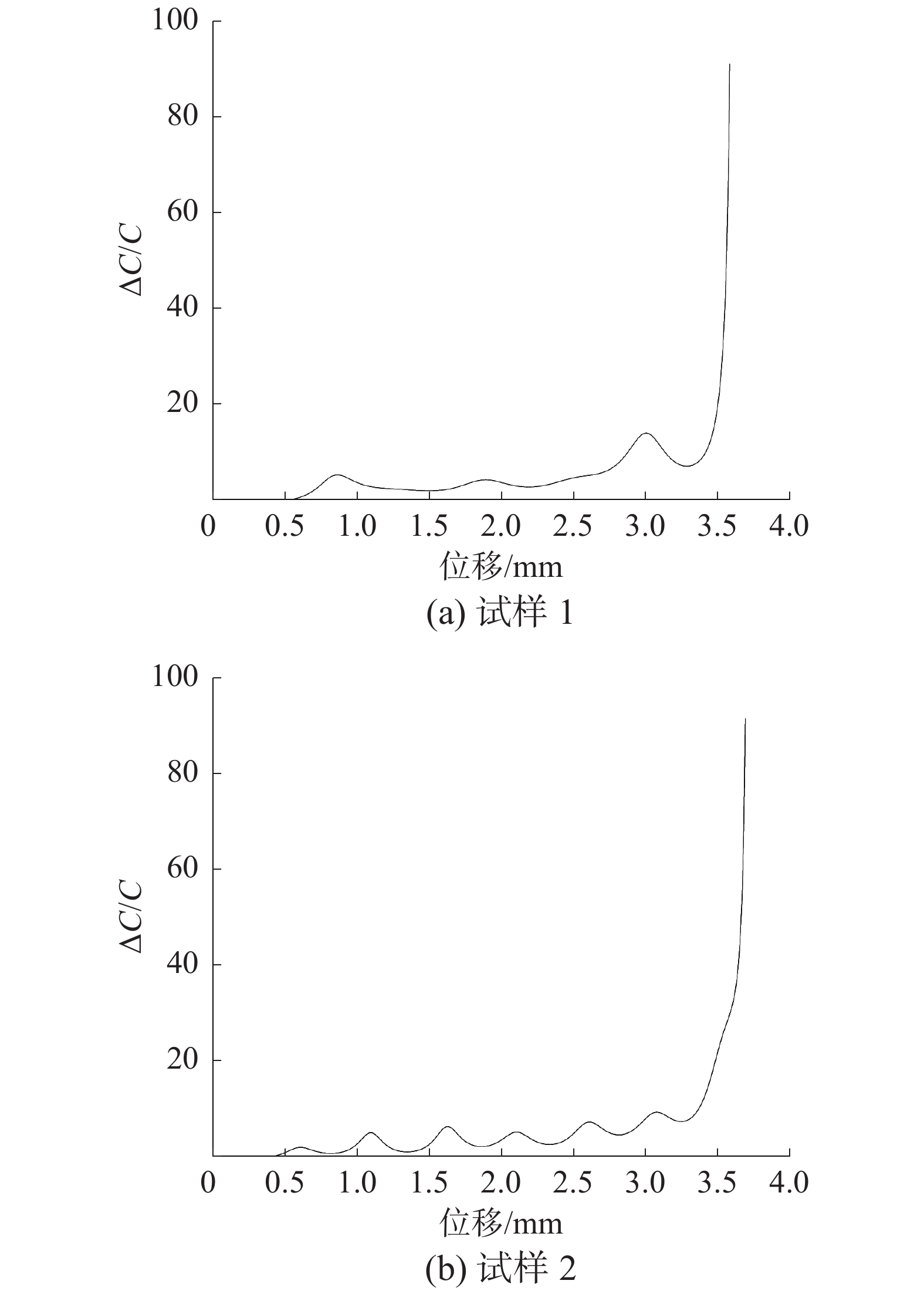
采用柔度变化率法对Q390D载荷位移数据进行处理,可得到图7所示的2个试件的柔度变化率曲线,相关数据列于表2。
|
Download:
|
| 图 7 试样柔度变化率曲线 | |
|
|
表 2 柔度变化率法特征数据 |
通过处理实验结果可知,当载荷尚未达到最大载荷之前便已经出现了裂纹,而该结论和很多已有研究成果相符[12],部分学者通过对比分析韧性材料与脆性材料的实验结果后得出,脆性材料的裂纹产生点多为最大载荷处,但韧性材料的裂纹多产生于最大载荷之前,同时其数据有一定分散性,一般为最大载荷的95%~100%,而相应能量只有最大载荷处能量的八成左右。本次试验所得结果完全符合统计结果,因此可以说明本次所得起裂点准确无误。
2.2 准静态方法求解学者们在研究中发现,材料动态断裂韧性属于加载速率函数[13],即加载速率变化后材料动态断裂韧性也会发生变化。因目前加载技术的最大加载速率有限,需要引入不同测试技术来得出不同加载率下的动态断裂韧性。目前仪器化夏比冲击试验最常用的测试加载速率为100 MPa·m/s量级动态断裂韧性方法,试样起裂时间不得小于其与摆锤冲击系统特征振动周期的3倍,从而才能保证惯性振荡衰减充分且不会对后续断裂发生的识别带来太大影响,然后将所得结果带入到准静态下J积分公式即可。
夏比冲击试样的振动周期的计算公式如下:
| $ \tau = 1.68{\left( {SWEB{C_{{\text{LL}}}}} \right)^{0.5}}/{c_0} $ |
式中:S、B、W、CLL分别为试样跨距、厚度、宽度以及柔度,E与c0分别为弹性模量、波速。
本次试样取S=40 mm,W=10 mm,自振周期计算公式[14]为
| $ \tau = 7 \times {10^{ - 6}}{\left( {EB{C_{{\text{LL}}}}} \right)^{0.5}} $ | (1) |
式中EBCLL为试样的无量纲柔度,表达式为
| $ \left( {EB{C_{{\text{LL}}}}} \right) = 72 \times h\left( {\frac{a}{W}} \right) + 20 $ |
式中h可直接通过式(2)计算得出:
| $ \begin{gathered} h\left( {\frac{a}{W}} \right) = 1.86{\left( {\frac{a}{W}} \right)^2} - 3.95{\left( {\frac{a}{W}} \right)^2} + 116.38{\left( {\frac{a}{W}} \right)^4} - \\ 37.23{\left( {\frac{a}{W}} \right)^5} + 77.55{\left( {\frac{a}{W}} \right)^6} - 128.87{\left( {\frac{a}{W}} \right)^7} + \\ 175.53{\left( {\frac{a}{W}} \right)^8} - 143.96{\left( {\frac{a}{W}} \right)^9} + 66.56{\left( {\frac{a}{W}} \right)^{10}} \\ \end{gathered} $ | (2) |
式中a为预制裂纹长度或缺口深度。
把所得h代入到式(1)中即可得出试样振动周期为0.0982 ms,引入柔度变化率法可得启裂时间为0.5204 ms,因此:
| $ 3\tau = 3 \times 0.0982\;{\rm{ms}}= 0.2946 \;{\rm{ms}} < 0.5204\;{\rm{ms}} $ |
结果显示3倍振动周期值比试样启裂时间要小得多,这意味着本次实验得出的结果满足准静态条件,可用于材料断裂韧性公式。
针对裂纹体而言,J积分比应力强度因子K的使用范围更加广泛,可直接通过裂纹试件试验测定得出J积分值[15],所以本次研究以J积分作为试样断裂韧性测试依据。动态J积分是基于动态加载条件下,通过夏比冲击试验所得出的第I类裂纹J积分值,记作JId。根据前文所述,本次试验不考虑惯性力条件时可视为准静态,因此有:
| $ {J_{{\text{Id}}}} = \frac{{K{W_a}}}{{B(W - a)}} $ | (3) |
式中:
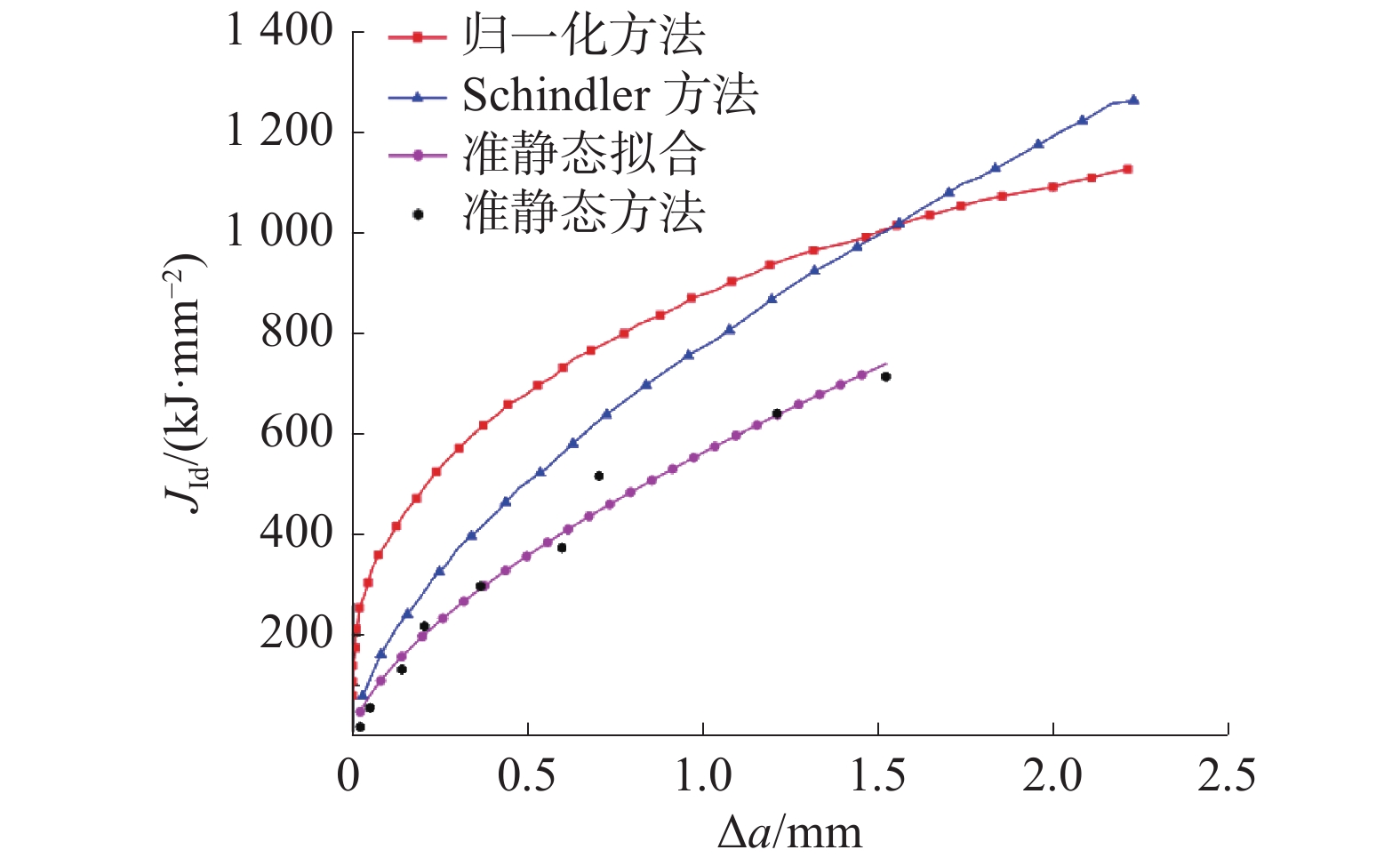
将前文试验中得到的裂纹长度和能量值代入式(3)中,可以得到一系列JId的值,将计算得到的JId值画在坐标轴中,能够拟合成一条裂纹扩展阻力曲线,如图8中紫色曲线所示。
|
Download:
|
| 图 8 3种方法获得的裂纹扩展阻力曲线 | |
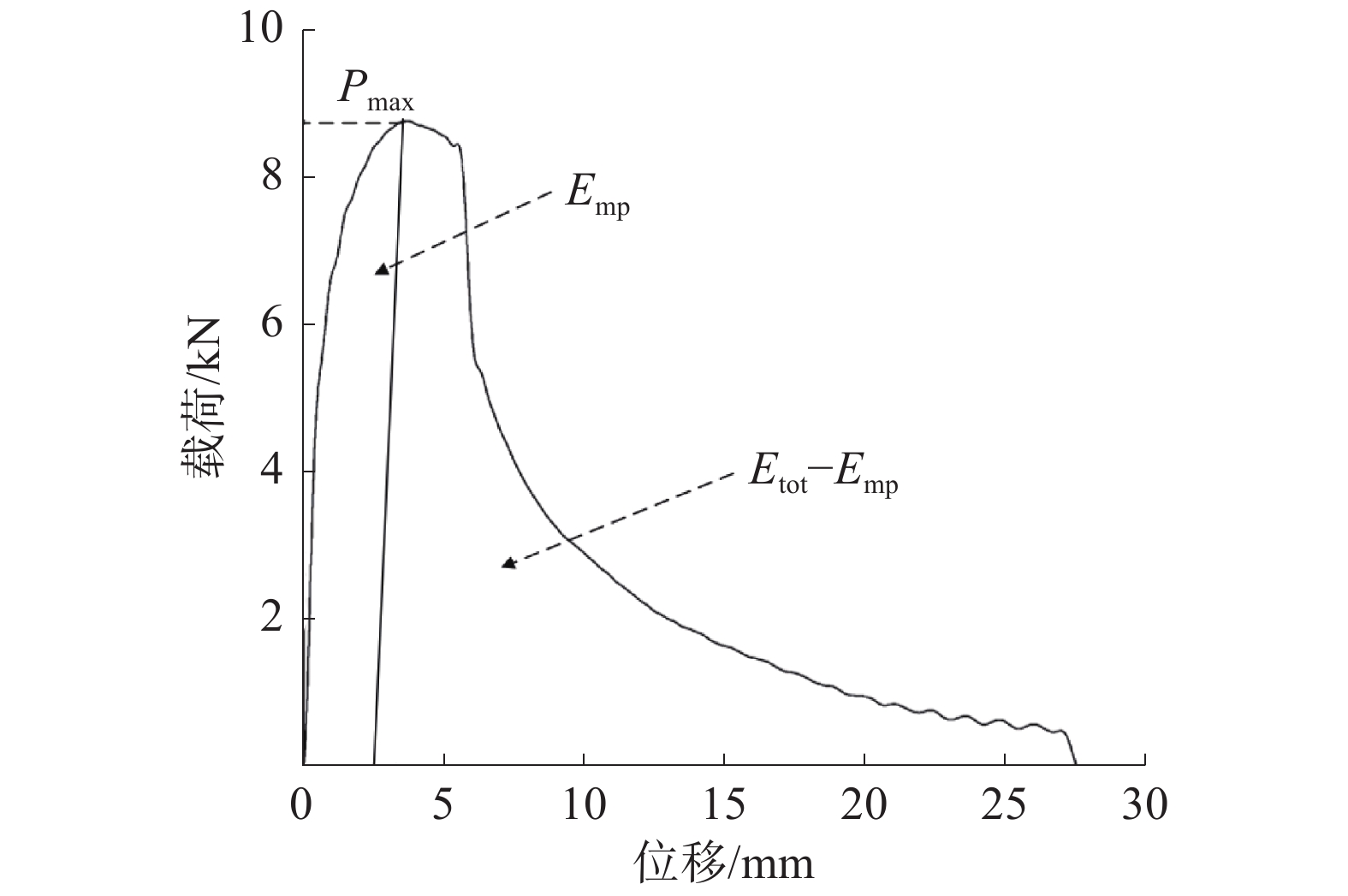
目前对于动态加载条件下的阻力曲线测定难度较大,原因在于无法准确绘制出快速断裂状态下各时刻的裂纹尖端张开位移,Schindler等[16]在研究中提出了一种载荷–位移曲线图,主要用于计算夏比标准试样受到冲击后的动态裂纹扩展阻力曲线函数方程,这一方法已经被很多学者证实可行。在使用Schindler方法时,需要求出冲击试验过程中的冲击总能量Etot和最大载荷处塑性变形能Emp,详情如图9所示。
|
Download:
|
| 图 9 Schindler方法能量示意 | |
Schindler计算动态J-R曲线的表达式为
| $ \left\{ \begin{gathered} J\left( {\Delta a} \right) = C \cdot {\left( {\Delta a} \right)^p}{\text{, }}\left( {\Delta a \leqslant \Delta {a_m}} \right) \hfill \\ J\left( {\Delta a} \right) = {J_{{\text{mp}}}} + S\left[ {\left( {\Delta a - \Delta {a_{\text{m}}}} \right) - {{\left( {\Delta a - \Delta {a_{\text{m}}}} \right)}^2}/2{b_0}} \right], \hfill \\ {\text{ }}\left( {\Delta a > \Delta {a_{\text{m}}}} \right) \hfill \\ \end{gathered} \right. $ | (4) |
式中:
| $ C = {(2/p)^p} \cdot \left[ {\gamma \left( {{a_0}} \right)/B{{\left( {W - {a_0}} \right)}^{p + 1}}} \right]E_{{\text{tot}}}^p \cdot E_{{\text{mp}}}^{1 - p} $ | (5) |
式中
| $ \left\{ \begin{gathered} \gamma = 1.9 - 25.124 \times {\left( {0.275 - \frac{a}{W}} \right)^2},{\text{ }}\left( {\frac{{{a_0}}}{W} < 0.274} \right) \hfill \\ \gamma = 1.859 + 0.03/\left( {1 - \frac{a}{W}} \right){\text{, }}\left( {0.274 < \frac{{{a_0}}}{W} < 0.9} \right) \hfill \\ \end{gathered} \right. $ | (6) |
| $ p = \frac{3}{4}{\left( {1 + {E_{{\text{mp}}}}/{E_{{\text{tot}}}}} \right)^{ - 1}} $ | (7) |
| $ {J_{{\text{mp}}}} = \frac{{\eta {E_{{\text{mp}}}}}}{{B{b_0}}} $ | (8) |
| $ s = 2\gamma \left( {{E_{{\text{tot}}}} - {E_{{\text{mp}}}}} \right)/\left[ {B{{\left( {{b_0} - \Delta {a_{\text{m}}}} \right)}^2}} \right] $ | (9) |
| $ \Delta {a_{\text{m}}} = \frac{{p \cdot {b_0} \cdot {E_{{\text{mp}}}}}}{{2{E_{{\text{tot}}}}}} $ | (10) |
因本次研究中a0/W≈0.4的试样1和试样2两者计算过程完全相同,所以仅对2号试样进行计算分析。以试件2的载荷−位移曲线为例,由式(4)~(10)可以计算出Etot=60.521 J,Emp=20.865 J,p=0.558,Jmp=0.665,C=0.883,
在绘制动态裂纹扩展阻力曲线的过程中,归一化方法基于试验所得的载荷位移曲线数据来进行计算,同时考虑了裂纹扩展的修正,所以其所得结果的准确度高。弹塑性J积分可以写成如下表达式:
| $ {J_{{\text{total}}}} = {J_{\text{e}}} + {J_{{\text{pl}}}} = {K^2}\left( {1 - {v^2}} \right)/E + {J_{{\text{pl}}}} \cdot \xi (a,b) $ | (11) |
式中:
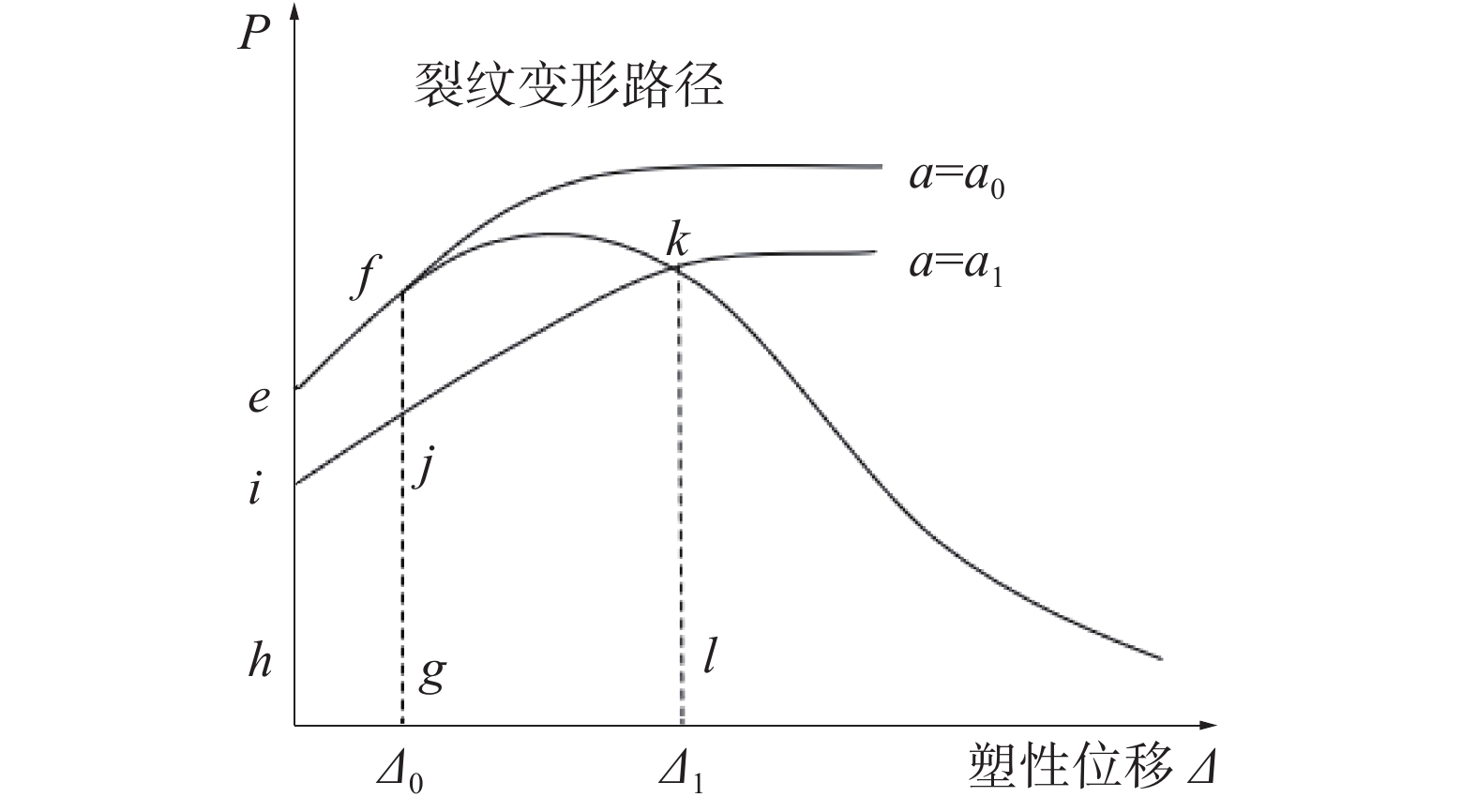
图10给出了常规载荷位移曲线图,图中有2条变形路径:一条是初始裂纹长度a0,另一条是裂纹长度a1。基于塑性形变理论可得出a0对应的J积分值:
| $ {J_0} = \frac{{\eta {U_{efgh}}}}{{\left( {W - {a_0}} \right)B}} $ |
式中:
|
Download:
|
| 图 10 载荷位移曲线示意 | |
裂纹扩展量为a1时的J积分可以写成2部分之和:
| $ {J_1} = J_1^\prime + J_1^{\prime \prime } = \frac{{\eta {U_{ijgh}}}}{{\left( {W - {a_1}} \right)B}} + \frac{{\eta {U_{jklg}}}}{{\left( {W - {a_1}} \right)B}} $ | (12) |
当a0与a1之间的差值足够小时表达式可以改写成:
| $ J_1^\prime = {J_0} + {\left( {\frac{{\partial {J_{{\text{pl}}}}}}{{\partial a}}} \right)_{{\varDelta _0}}}\left( {{a_1} - {a_0}} \right) $ | (13) |
根据塑性形变理论:
| $ {J_{{\text{pl}}}} = \eta {U_{{\text{pl}}}}/(W - a)B $ | (14) |
| $ {\left( {\partial {J_{{\text{pl}}}}/\partial a} \right)_{{\varDelta _{{\text{pl}}}}}} = {\left[ {\partial \left( {\eta {U_{{\text{pl}}}}/(W - a)B} \right)/\partial a} \right]_{{\varDelta _{{\text{pl}}}}}} $ | (15) |
将式(15)右端项展开,求解得:
| $ \begin{gathered} {\left( {{{\partial {J_{{\text{pl}}}}} \mathord{\left/ {\vphantom {{\partial {J_{{\text{pl}}}}} {\partial a}}} \right. } {\partial a}}} \right)_{{\varDelta _{{\text{pl}}}}}} = \frac{\eta }{{\left( {W - a} \right)B}}{\left( {\frac{{\partial {U_{{\text{pl}}}}}}{{\partial a}}} \right)_{{\varDelta _{{\text{pl}}}}}} + \\ \frac{{\eta {U_{{\text{pl}}}}}}{B}\left( {\frac{{\partial \left( {{1 \mathord{\left/ {\vphantom {1 {W - a}}} \right. } {W - a}}} \right)}}{{\partial a}}} \right) + \frac{{{U_{{\text{pl}}}}}}{{(W - a)B}}\frac{{\partial \eta }}{{\partial a}} = \\ \frac{\eta }{{\left( {W - a} \right)B}}{\left( {\frac{{\partial {U_{{\text{pl}}}}}}{{\partial a}}} \right)_{{\varDelta _{{\text{pl}}}}}} + \frac{{\eta {U_{{\text{pl}}}}}}{{{{\left( {W - a} \right)}^2}B}} + \\ \frac{{{U_{{\text{pl}}}}}}{{(W - a)B}}\frac{{\partial \eta }}{{\partial a}} \\ \end{gathered} $ | (16) |
根据J积分形变功率定义[18],有:
| $ {J_{{\text{pl}}}} \equiv - \frac{1}{B} \times {\left( {\frac{{\partial {U_{{\text{pl}}}}}}{{\partial a}}} \right)_{{\varDelta _{{\text{pl}}}}}} $ | (17) |
将式(14)、(17)代入式(16),得:
| $ \begin{gathered} {\left( {{{\partial {J_{{\text{pl}}}}} \mathord{\left/ {\vphantom {{\partial {J_{{\text{pl}}}}} {\partial a}}} \right. } {\partial a}}} \right)_{{\varDelta _N}}} = - \frac{\eta }{{W - a}}{J_{{\text{pt}}}} + \frac{{{J_{{\text{pl}}}}}}{{W - a}} + \frac{{\partial \eta }}{{\partial a}} \cdot \frac{1}{\eta }{J_{{\text{pl}}}}{\text{ }} = \\ - \frac{{{J_{{\text{pl}}}}}}{{W - a}}\left[ {\eta - 1 - \frac{{\partial \eta }}{{\partial a}} \cdot \frac{{W - a}}{\eta }} \right] \\ \end{gathered} $ | (18) |
令:
| $ \zeta = - \left( {\eta - 1 - \frac{{\partial \eta }}{{\partial a}}\frac{{(W - a)}}{\eta }} \right) $ |
则式(18)可写成:
| $ {\left( {\partial {J_{{\text{pl}}}}/\partial a} \right)_{{\varDelta _{{\text{pl}}}}}} = \frac{{{J_{{\text{pl}}}}\zeta }}{{(W - a)}} $ | (19) |
将式(19)代入式(13),得:
| $ J_1^\prime = {J_0}\left( {1 - \frac{\zeta }{{(W - a)}}\left( {{a_1} - {a_0}} \right)} \right) $ | (20) |
同理得:
| $ {J_1}^{\prime \prime } = \frac{{\eta \left( {{U_1} - {U_0}} \right)}}{{\left( {W - {a_1}} \right)B}}\left( {1 - \frac{\zeta }{{(W - a)}}\left( {{a_1} - {a_0}} \right)} \right) $ | (21) |
将式(20)、(21)代入式(12)得:
| $ {J_1} = \left( {{J_0} + \frac{\eta }{{\left( {W - {a_1}} \right)}}\frac{{{U_1} - {U_0}}}{B}} \right)\left( {1 - \frac{{\zeta \left( {{a_1} - {a_0}} \right)}}{{(W - a)}}} \right) $ | (22) |
将式(22)写成增量表达式为
| $ {J_{{\text{pl}}(i)}} = \left( {{J_{{\text{pl}}(i - 1)}} + \frac{\eta }{{\left( {W - {a_i}} \right)}}\frac{{{U_i} - {U_{i - 1}}}}{B}} \right)\left( {1 - \frac{{\zeta \left( {{a_i} - {a_{i - 1}}} \right)}}{{\left( {W - {a_i}} \right)}}} \right) $ | (23) |
联合式(11)和式(23),得积分计算的完整方程表达式为
| $ \begin{gathered} {J_{\left( i \right)}} = \frac{{{K^2}\left( {1 - {v^2}} \right)}}{E} + \\ \left( {{J_{{\text{pl}}\left( {i - 1} \right)}} + \frac{\eta }{{\left( {W - {a_i}} \right)}}\frac{{{U_i} - {U_{i - 1}}}}{B}} \right)\left( {1 - \frac{{\zeta \left( {{a_i} - {a_{i - 1}}} \right)}}{{\left( {W - {a_i}} \right)}}} \right) \\ \end{gathered} $ | (24) |
依据《GBT 38769-2020金属材料预裂纹夏比试样冲击加载断裂韧性的测定》[19],
基于能量吸收角度,Chaouadi等[20]利用载荷位移曲线计算式(24)中的裂纹扩展量,即
| $ {a_i} \approx {a_{{\text{end}}}}{\left( {\frac{{{U_i} - {U_{{\text{start}}}}}}{{{U_{{\text{end}}}} - {U_{{\text{start}}}}}}} \right)^2} $ | (25) |
式中:
这样我们就可以使用式(24)、(25)计算预制裂纹夏比冲击试样的动态裂纹扩展阻力曲线。计算得到的动态裂纹扩展阻力曲线如图10中红色曲线所示。
与Schindler方法计算得到的结果相比较不难看出:当裂纹扩展量达到1.5 mm前,归一化方法求得的J积分值大于Schindler方法求得的J积分值;2种方法得到的裂纹扩展阻力曲线具有相同的增长趋势;归一化方法与Schindler方法得到的阻力曲线吻合性良好。说明使用归一化方法求解是可靠的。
大量研究结果显示,Schindler方法所得出的结果具有一定的准确度,而且整个计算过程十分简单。不过这种方法最大的问题在于所获取的结果过于保守,与实际动态裂纹扩展阻力曲线之间差别较大。总的来说Schindler方法是利用能量间相互关系,并依托半理论半经验计算方式来得出裂纹扩展阻力曲线。不过也正是由于有主观经验夹杂其中,所以在最终结果的准确度上要略有偏差。当然这种方法能够迅速绘制出较为准确的裂纹扩展阻力曲线,同时其结果的保守性特征能够让其为实践工程提供一定的指导。而基于载荷位移曲线的归一化方法对于裂纹扩展阻力曲线的计算将其塑性部分的修正考虑在内,所以这一方法能够得出更加准确的结果。与其他2种方法相比,准静态方法得到的曲线最低,计算结果最为保守。
3 结论本研究主要通过夏比冲击试验得到核用Q390D钢夏比冲击试样的载荷位移曲线,经过对试验结果的处理,得到了如下结论:
1)利用柔度变化率方法确定了核用Q390D夏比冲击试样的起裂点,结果与同类研究的结果相符,起裂点位于极限冲击载荷之前,同时柔度变化率曲线振荡的程度明显,说明裂纹产生会导致试件力学性能发生剧烈变化,因此使用柔度变化率法来确定核用Q390D钢材的起裂点是十分适用的。
2)判断了准静态方法的适用性。利用准静态方法计算了试件断裂过程中的J积分,通过拟合得到了试件的裂纹扩展阻力曲线。
3)分别使用Schindler方法和归一化方法,对含裂纹的核用Q390D夏比冲击试样的裂纹扩展阻力曲线进行求解,结果表明2种方法所求得的曲线趋势相同。经过比分析可知,准静态法由于未考虑动态效应,阻力曲线的计算结果最为保守;Schindler法与归一化方法的相对误差较小,计算过程简单,适用于工程应用。
| [1] |
江洪, 王微. 国内外船舶用钢初探[J]. 新材料产业, 2014(7): 9-14.
( 0) 0)
|
| [2] |
王任甫, 赵彩琴, 蒋颖, 等. 美国舰船用钢板规范的演变与分析[J]. 材料开发与应用, 2012, 27(4): 80-85.
( 0) 0)
|
| [3] |
邵军. 舰船用钢研究现状与发展[J]. 鞍钢技术, 2013(4): 1-4.
( 0) 0)
|
| [4] |
杨乘东, 柳猛, 张茂龙, 等. 不同类型接管安全端焊接接头常温断裂韧性对比研究[J]. 压力容器, 2020, 37(2): 30-36, 50. DOI:10.3969/j.issn.1001-4837.2020.02.005 ( 0) 0)
|
| [5] |
李一磊, 李朋洲, 姚迪, 等. 金属材料裂纹冲击韧性评定方法研究[J]. 核动力工程, 2021, 42(5): 114-118.
( 0) 0)
|
| [6] |
刘志伟, 刘聪, 薛启超. 铁素体钢材韧脆转变温度数值分析[J]. 应用科技, 2021, 48(2): 110-115.
( 0) 0)
|
| [7] |
李荣德, 张新宁, 蒋立鹏, 等. 铁素体球墨铸铁低温冲击断裂行为的影响因素[J]. 机械工程学报, 2016, 52(10): 25-31.
( 0) 0)
|
| [8] |
顾浩洋. 低温下钢结构连接抗剪疲劳和动态断裂韧性试验研究[D]. 北京: 清华大学, 2019.
( 0) 0)
|
| [9] |
何沐阳, 韦家祥, 尹佳静, 等. 基于J-C模型的11MnNiMo钢本构参数标定及验证[J/OL]. 应用科技: 1-6. [2021-06-17]. http://kns.cnki.net/kcms/detail/23.1191.U.20210611.1112.006.html.
( 0) 0)
|
| [10] |
宗秋丽, 孙宏, 汪海燕, 等. GB/T 229-2007金属材料夏比摆锤冲击试验方法简介[J]. 理化检验(物理分册), 2010, 46(3): 190-192. ( 0) 0)
|
| [11] |
KOBAYASHI T, YAMAMOTO I, NIINOMI M. Introduction of a new dynamic fracture toughness evaluation system[J]. Journal of testing and evaluation, 1993, 21(3): 145-153. DOI:10.1520/JTE11763J ( 0) 0)
|
| [12] |
姜风春, 刘瑞堂, 刘殿魁. 船用921A钢动态断裂韧性测试研究[J]. 实验力学, 1999, 14(1): 96-101. ( 0) 0)
|
| [13] |
潘建华, 陈学东, 姜恒, 等. 准静态和动态加载对裂纹扩展阻力曲线的影响及其关系的研究[J]. 高压物理学报, 2015, 29(2): 109-116. DOI:10.11858/gywlxb.2015.02.004 ( 0) 0)
|
| [14] |
赵亚通. 基于仪器化夏比冲击试验的管道钢断裂韧性确定方法研究[D]. 北京: 中国石油大学(北京), 2018.
( 0) 0)
|
| [15] |
孙凯, 刘忆. 断裂力学理论及其研究方法在材料学中的应用[J]. 辽宁工程技术大学学报, 2005, 24(S1): 230-232. ( 0) 0)
|
| [16] |
SCHINDLER H J. Estimation of the dynamic J-R curve from a single impact bending test[C]// 11th European Conference on Fracture. Poitiers, France. 1996.
( 0) 0)
|
| [17] |
NEVALADNEN M, WALLIN K. The effect of crack depth and absolute thickness on fracture toughness of 3PB specimens[C]//Proceedings of the 10th European Conference on Fracture. Berlin, Germany: EMAS, 1994: 997–1006.
( 0) 0)
|
| [18] |
ASTM E. 1820–99 Standard test method for measurement of fracture toughness[S]. [S. l. ]: ASTM Standards, 1999.
( 0) 0)
|
| [19] |
国家市场监督管理总局, 国家标准化管理委员会. GB/T 38769—2020, 金属材料 预裂纹夏比试样冲击加载断裂韧性的测定[S]. 北京: 中国标准出版社, 2020.
( 0) 0)
|
| [20] |
CHAOUADI R. An energy-based crack extension formulation for crack resistance characterization of ductile materials[J]. Journal of testing and evaluation, 2004, 32(6): 469-475. ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


