手势识别技术在非接触式的人机交互中的应用价值广泛，可用于智能家居^[1-2]、虚拟现实^[3]、智能驾驶^[4-5]、游戏控制^[6]等多种应用场景。FMCW毫米波雷达具有硬件成本低，测距、测速方案简单，抗干扰能力强，可全天候工作且不会泄露用户隐私等优点，在手势识别的应用上具有可观的应用前景。

FMCW毫米波雷达是一种可以从目标回波中估计目标的距离、速度、角度信息的一种传感器，文献[7-8]介绍了传统FMCW雷达的调制波形，讨论了FMCW信号的混频和调制原理。基于毫米波雷达的手势识别技术主要通过在回波中提取手势动作的距离、速度甚至角度等信息进行估计后得到特征谱图，然后将特征谱图以图片数据集的形式使用支持向量机(support vector machine, SVM)^[9]或者卷积神经网络^[10-16]等分类器进行识别。谷歌公司在Soli项目^[10-11]中采用了带宽高达7 GHz的毫米波雷达对手势识别进行了研究，利用卷积神经网络将连续时刻的距离–多普勒像逐帧特征提取，再利用循环神经网络对时序特征进行提取后进行手势分类。文献[12]利用短时傅里叶变换(short-time Fourier transform, STFT)对雷达回波信号进行时频分析，得到多普勒谱，并将多普勒谱图像作为卷积神经网络的输入数据实现了手势识别。文献[13]通过对混频后的中频信号进行2维快速傅里叶变换获取手势的距离多普勒图像，以2维距离多普勒像构建数据集，并输入卷积神经网络进行训练。文献[14]通过时频分析和多重信号分类方法估计了手势的距离、速度以及角度信息，构建了多维参数输入的卷积神经网络，对估计的信息进行了分类；文献[15]提出了微动手势的特征提取的最优参数设置准则，利用多特征谱图进行了微动手势识别。靳标等^[16]提出了一种串联式一维神经网络的手势识别方法，该方法对雷达回波直接进行卷积池化，通过1维Inception模块后，利用长短时记忆网络进行分类。本文在距离多普勒图的基础上，提取了距离、速度变化的时序信息并使用全局池化代替扁平层与全连接层构建了双通道的卷积神经网络实现了手势识别。

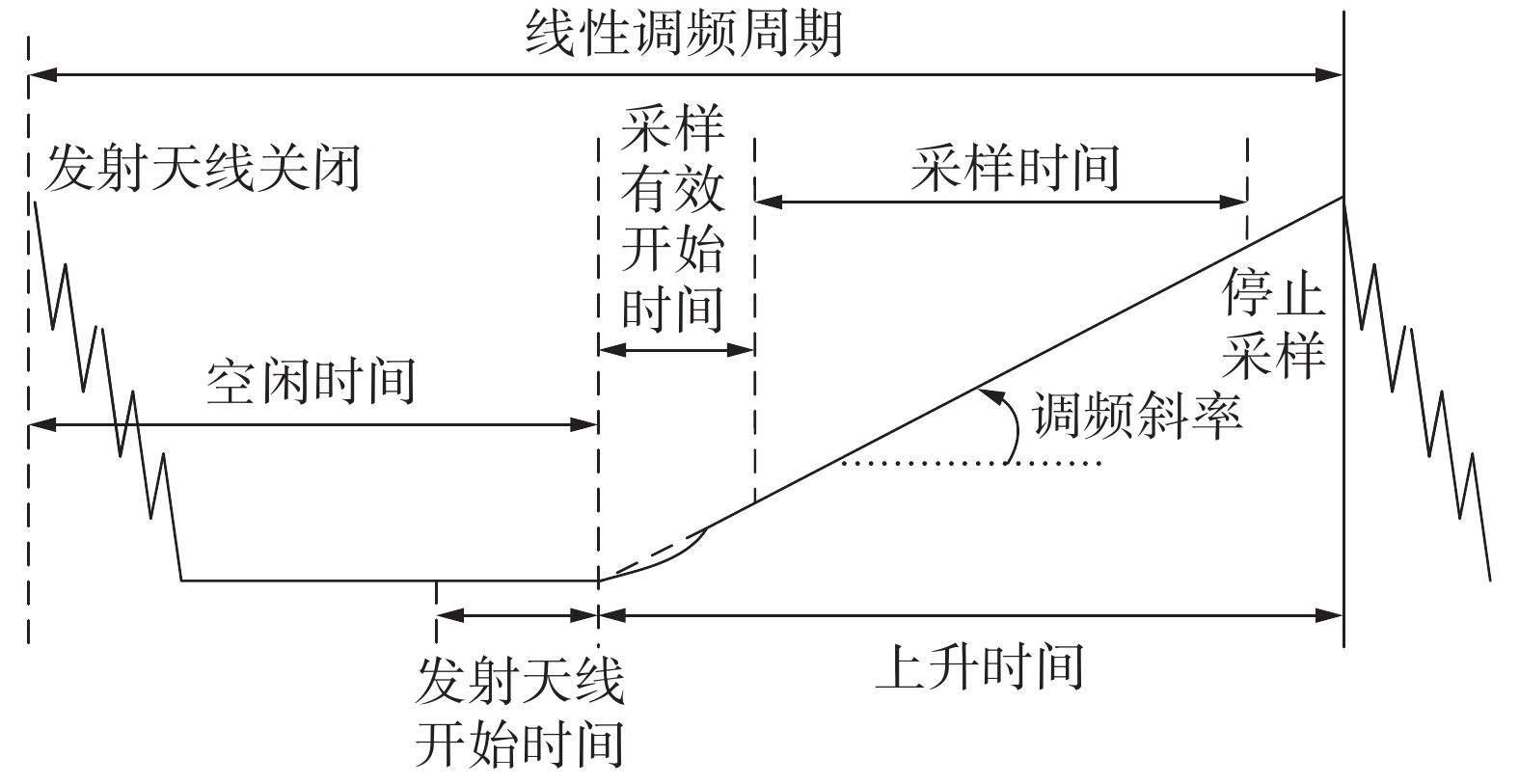
1 FMCW毫米波雷达原理分析 1.1 雷达平台参数设值

本文采用的FMCW毫米波雷达设备为TI公司的IWR1642-BOOST开发板，支持77~81 GHz的调频带宽，在水平方向具有±60°的视场，支持最多2个发射天线4个接收天线。本文仅使用了1个发射天线，仅读取了1个接收天线的数据。波形配置图如图1所示。

从图1可以看出，数模转换器(analog-to-digital converter，ADC)会在上升时间之内的一段时间内进行采样。可以通过配置采样点数 ${N_{{\text{ADC}}}}$ 以及采样率 ${F_{\text{s}}}$ 来计算采样时间 ${T_{{\text{ADC}}}}$ ：

$ {T_{{\text{ADC}}}} = {N_{{\text{ADC}}}}{\text{/}}{F_{\text{s}}}。$

在采样时间确定之后，可以通过设置信号的调频斜率 $ K $ 来得到有效的调频带宽B：

$ B = K \times {T_{{\text{ADC}}}} = K \times {N_{{\text{ADC}}}}{\text{/}}{F_{\text{s}}}。$

在得到有效调频带宽后可求得距离分辨率 ${d_{{\text{res}}}}$ ：

$ {d_{{\text{res}}}} = \frac{c}{{2B}} $

(1)

式中c为光速。

FMCW毫米波雷达会发射M个图2形式的线性调频脉冲帧,根据FMCW毫米波雷达测速原理，可以通过配置图1中的调频周期 ${T_{\text{c}}}$ (chirp cycle time)，求得最大测量速度 ${v_{\max }}$ ：

$ {v_{\max }} = \frac{\lambda }{{4T_{\text{c}}}} $

(2)

式中 $ \lambda $ 为载波频率对应的波长。

可以通过配置每帧的调频脉冲数 ${N_{{\text{chirp}}}}$ 来求得速度分辨率 ${v_{{\text{res}}}}$ ：

$ {v_{{\text{res}}}} = \frac{\lambda }{{2{N_{{\text{chirp}}}}{T_{\text{c}}}}} $

(3)

本文中的雷达参数为：调频起始频率f₀，77 GHz；调频斜率K，66.6 MHz/μs；调频周期T_c，160 μs；ADC采样率，5 MS/s; ADC采样点数，256；帧数，64 f; 每帧脉冲数，128。

结合雷达参数配置，根据式（1）求得距离分辨率：

$ {d_{{\text{res}}}} = \frac{c}{{2B}} = \frac{{{\text{5}} \times {\text{3}} \times {\text{1}}{{\text{0}}^{{\text{14}}}}}}{{{\text{2}} \times {\text{66}}{\text{.6}} \times {\text{256}} \times {\text{1}}{{\text{0}}^{{\text{12}}}}}} \approx {\text{4}}{\text{.40 cm}} $

根据式（2）求得可观测最大速度：

$ {v_{\max }} = \frac{\lambda }{{4{T_{\text{c}}}}} = \frac{{{\text{3}} \times {\text{1}}{{\text{0}}^{\text{8}}}}}{{{\text{4}} \times {\text{160}} \times {\text{1}}{{\text{0}}^{{{ - 6}}}} \times {\text{77}} \times {\text{1}}{{\text{0}}^{\text{9}}}}} \approx {\text{6}}{\text{.09 m/s}} $

根据式（3）求得速度分辨率：

$ \begin{aligned} {v_{{\text{res}}}} & = \frac{\lambda }{{2{N_{{\text{chirp}}}}{T_{\text{c}}}}} = \frac{{{\text{3}} \times {\text{1}}{{\text{0}}^{\text{8}}}}}{{{\text{2}} \times {\text{128}} \times {\text{160}} \times {\text{1}}{{\text{0}}^{{{ - 6}}}} \times {\text{77}} \times {\text{1}}{{\text{0}}^{\text{9}}}}} \approx\\ & \qquad\qquad\qquad\qquad{\text{0}}{\text{.0951 m/s}} \end{aligned} $

1.2 手势成像原理

在一个调频周期内，雷达发射的FMCW信号可以表示为

$ {s_{\text{T}}}(t) = {A_{\text{T}}} \cdot \cos [{{2{\text{π}} }}({f_{\text{c}}}t + \int_0^t {K\tau {\text{d}}\tau )} ] $

式中： $ t $ 为一个调频周期内的快时间索引， ${A_{\text{T}}}$ 为发射信号振幅， ${f_{\text{c}}}$ 为载波中心频率。

由发射信号可以将目标场景反射信号表示为

$ \begin{gathered} {s_{\text{R}}}(t) = {A_{\text{R}}} \cdot \cos {\text{\{ }}2{\text{π}}[({f_{\text{c}}}(t - \Delta t) + \hfill \\ \int_0^t {[K(\tau - \Delta t) + \Delta {f_{\text{d}}}]{\text{d}}\tau ]} {\text{\} }} \end{gathered} $

式中： ${A_{\text{R}}}$ 为接收信号振幅； $ \Delta t $ 为信号飞行时间， $ \Delta t = 2R/C $ ； $ R $ 为目标相对雷达的径向距离； $ K(\tau - \Delta t) $ 为 $ \tau $ 时刻接收信号频率； $\Delta {f_{\text{d}}}$ 为多普勒频移。

接收机将目标场景反射的回波信号与发射信号进行混频和低通滤波后得到中频信号，近似为

$ \begin{aligned} &\qquad\; {{s_{{\text{IF}}}}(t)} = {{f_{{\text{LPF}}}}\{ {s_{\text{T}}}(t){s_{\text{R}}}(t)\} = } \\ & {{A_{\text{T}}} \cdot {A_{\text{R}}} \cdot {\text{cos}}\{ 2{\text{π}}[{f_{\text{c}}}\Delta t + ({f_{_{{\text{IF}}}}} - \Delta {f_{\text{d}}})t]\} } \end{aligned} $

式中 ${f_{{\text{IF}}}} = K\Delta t$ 为 $ t $ 时刻中频信号的频率。所以，得到的中频信号的相位可表示为

$ \phi = {{2{\text{π}} }}[{f_{\text{c}}}\Delta t + ({f_{{\text{IF}}}} - \Delta {f_{\text{d}}})t] $

式中： ${f_{\text{c}}}\Delta t$ 相对于快时间来说为一常量，可认为是初相； ${f_{{\text{IF}}}}$ 只与调频周期内对应的快时间索引有关，由于 ${T_{\text{c}}}$ 很小，通常假定一个调频周期内多普勒频移 $\Delta {f_{\text{d}}}$ 是恒定的，则可通过对快时间域进行快速傅里叶变换求得到与目标距离相关的中频信号频率分布；当不同调频周期的 ${f_{{\text{IF}}}}$ 固定时，即距离相同时， $\Delta {f_{\text{d}}}$ 仅与调频周期之间对应的慢时间索引有关，从而在慢时间域进行快速傅里叶变换可以得到与目标速度相关的多普勒频移分布。

为了实现上述方法，需要将雷达回波处理成为一个矩阵的形式：矩阵的每一列代表快时间方向上 $N{_\text{adc}}$ 个采样点，每一行代表慢时间不同的 $ {N_{{\text{chirp}}}} $ 个脉冲信号的回波在相同快时间处的值。

以帧为单位处理信号，可得到M个 ${N_{{\text{adc}}}} \times {N_{{\text{chirp}}}}$ 的矩阵。对每一个矩阵快时间维做FFT即可得到M个二维距离谱图，后对二维距离谱图进行自相关，抑制背景噪声。假设每帧内的目标距离相同，对得到的每一个二维距离谱图抽取第1列后，按帧拼接，得到距离−时间谱。

对二维距离谱图，在慢时间方向做FFT即可得到距离–多普勒图，将多个距离多普勒图按行累加后转置得到多个列向量，将多个列向量按帧拼接即得到速度–时间谱图。

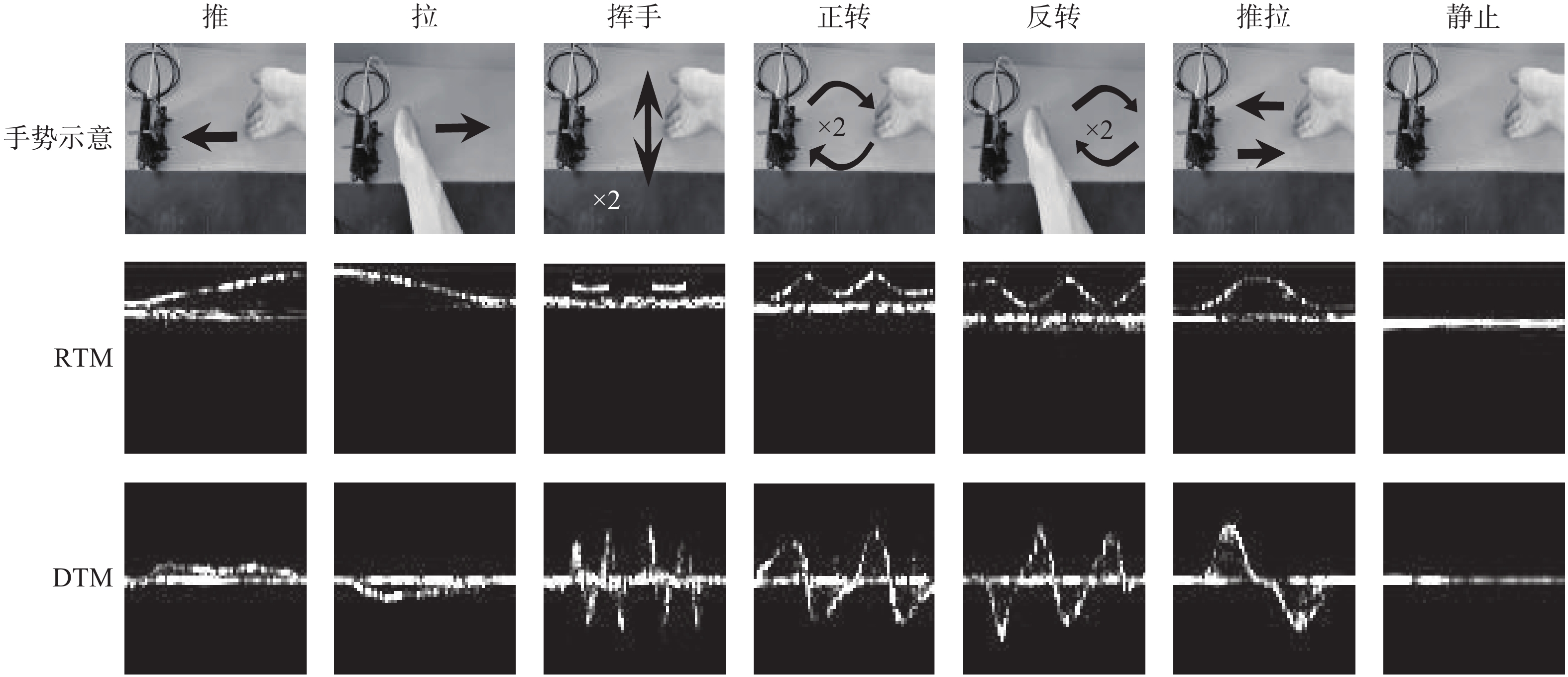
最终得到的手势特征图大小均为64×64。图3给出了手势动作的示意图以及手势动作的回波特征图。本文将雷达前的人也考虑在内，即距离随时间变化图(range-time map，RTM)中距离不变的横线，以及速度随时间变化图(Doppler-time map，DTM)中速度为0的横线。

2 卷积神经网络

在利用上述方法得到特征图后，需要利用卷积神经网络进行学习，在学习前首先需要建立样本集供神经网络训练。本文通过4名志愿者对7种手势进行样本集构建。每种手势200个样本，构建了各有1400个样本的2个数据集RTM、DTM，在此基础上构建了二维的数据集，将其命名为MUL，MUL中每种手势由2个特征图表征。

对于RTM和DTM数据集，本文使用了全局平均池化层来代替扁平层以及全连接层，搭建了3个卷积−池化层的单通道卷积神经网络。本文所使用的单通道卷积神经网络结构如表1所示。

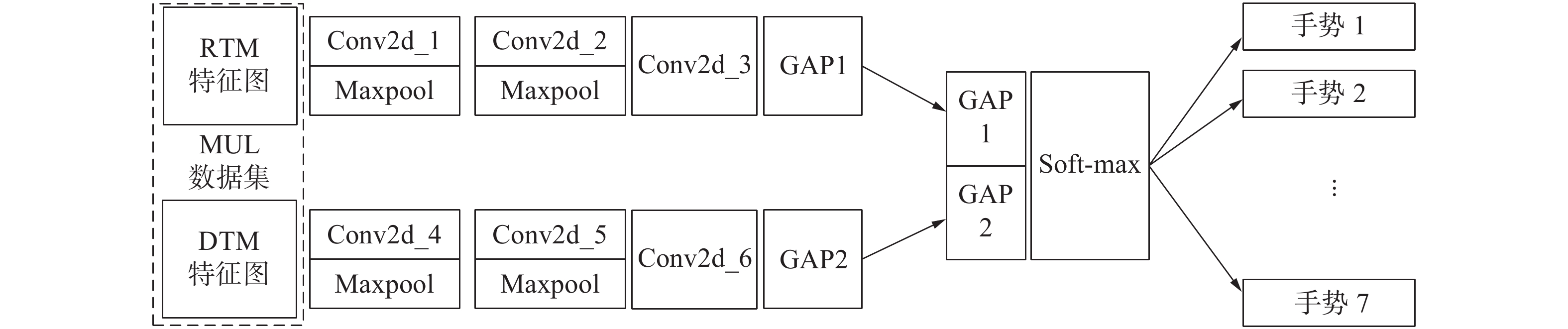
本文使用表1所示的网络分别对由RTM和DTM特征图构建的样本集进行了训练。同时基于表1网络构建了双通道的卷积神经网络，对本文构建的二维手势样本集MUL进行了训练，进而验证双通道神经网络对训练结果的影响。本文所构建的双通道的卷积神经网络结构如图4所示。

3 实验结果 3.1 实验平台

使用了TI公司的DCA1000EVM高速数据采集卡获取毫米波雷达中频信号采样后的ADC原始数据，并经过千兆网口传输到PC端(Windows10 64位操作系统，NVIDIA GeForce GTX 1050显卡)，在Matlab 2020a中进行数据处理，建立数据集后使用Tensorflow2.1深度学习框架搭建了神经网络，并使用本文的样本集对网络进行了学习分类。

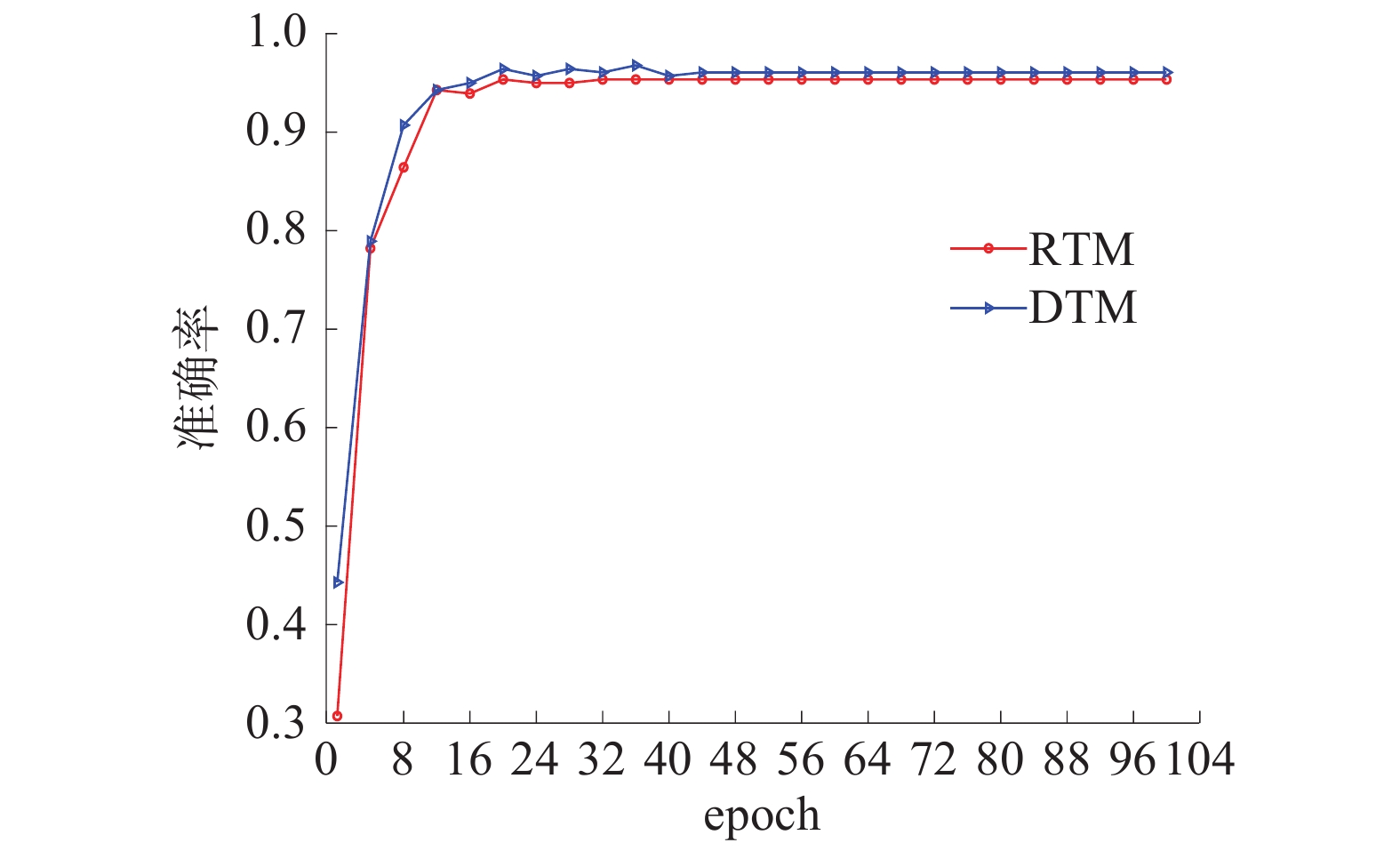
3.2 单通道卷积神经网络验证

在单输入的网络验证中，对RTM与DTM这2种特征图的操作相同。每种数据集具有1120个训练样本以及280个测试样本。使用Adam的优化算法，初始学习率设置为0.001，选取了指数型学习率衰减的方法，使学习率在100个epoch内连续衰减10%，设置的批尺寸为8。从图5中可以看出卷积神经网络训练在测试集的准确率随迭代步数的变化情况。

从图5中可以看出，卷积神经网络对在对本文建立的样本集进行训练的最终识别率达到了95%以上，DTM数据集与RTM数据集的训练结果近似相同，且2种数据集在进行了40个epoch后均达到了收敛。

3.3 双通道卷积神经网络验证

双通道网络同样使用Adam优化算法，初始学习率设置为0.001，选取指数型学习率衰减的方法，使学习率在100个epoch内连续衰减10%，设置批尺寸为8。

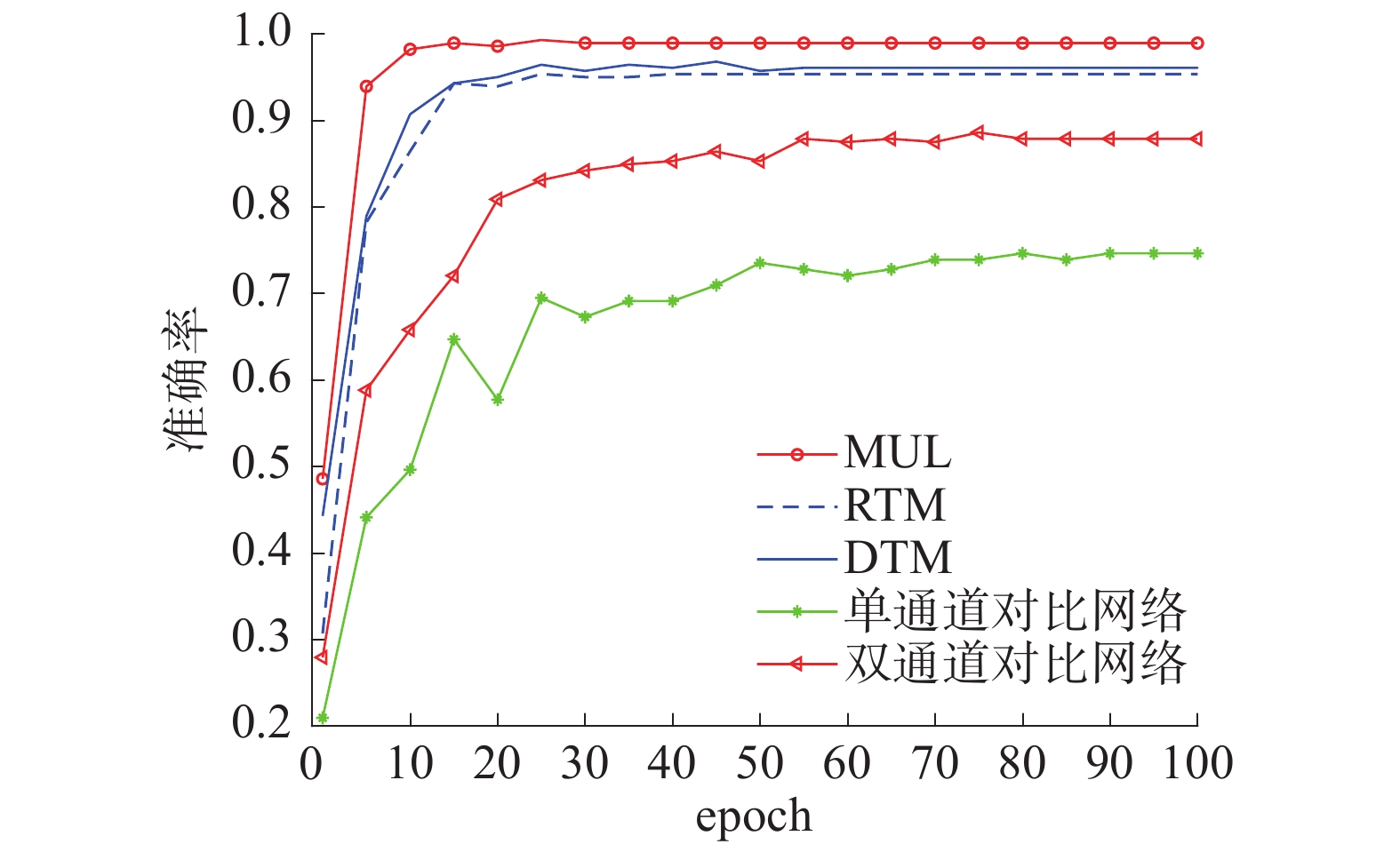
测试集的准确率随迭代步数的变化如图6中MUL所示。

从图6中可以看出，双通道的卷积神经网络结构在测试集上的准确率达到了近99%，相较于单通道神经网络，最终的识别率提升了近4%。由于网络的优化算法、学习率、衰减率等没有改变，所以2种网络的收敛速度几乎相同，只是第2种的网络规模是第1种的2倍，所以在网络训练时多输入网络用的时间是单输入的2倍。本文参考搭建了文献[13]中的单通道的仅两层卷积层的网络模型，并在此基础上搭建了双通道网络模型，2种模型在本文数据集（单通道对比模型使用RTM数据集训练）中的训练结果分别如图6中的单通道对比网络及双通道对比网络所示。

4 结论

本文的FMCW雷达手势识别系统将人体作为参考特征，构建了手势动作的距离–时间、速度–时间特征图，使用全局平均池化层代替扁平层与全连接层的情况下构建了双通道的卷积神经网络。该网络使用本文构建的数据集训练，最终在测试集上达到了99%的识别率，相较于单通道的卷积神经网络，在训练集上的准确率提高了近4%。通过与其他方法对比可以得出：1）网络模型对不同的数据集将会产生不同的结果；2）卷积层数增多会提取到更深层的信息，进而在一定条件下得到更好的拟合结果；3）验证了联合多特征的识别方法优于单特征的识别方法。