无人机路径规划的应用领域正变得越来越广。在军事领域方面无人机可以在战场物资投放、作战资源调度等方面使用[1-5],无人机参与作战可大量减少战争伤亡,大大提高作战效率与成功率。在民用方面使用无人机进行快递配送、救灾物资投放和喷洒田地[6]也成为新的目标,因此在此方面所应用的技术具有巨大的市场潜力。
无人机在以上方面应用所产生的问题都可以归结为无人机路径规划问题,这类问题是一个NP难问题(NP-hard problem),目前使用进化算法可以在这类问题上得到很好的解决[7-8]。文献[2]针对该问题提出了两阶段策略,使用贪心算法与遗传算法作为一、二阶段进行优化;文献[5]使用了单目标进化算法应用于无人机追捕罪犯;文献[9]使用极端拥挤的NSGA-II(EC-NSGA-II)作为第一阶段,求得近似Pareto前沿的极端解作为多目标遗传算法的初始粒子;文献[10]将MOEA/D(基于分解的多目标优化)引入粒子群优化算法中以更好地平衡多个目标函数解;文献[11]将基于集的粒子群优化算法(S-PSO)和综合学习粒子群优化(CLPSO)引入无人机路径规划问题中,其中,使用多目标粒子群优化算法求得的解,其多样性好且收敛速度快,因此在无人机路径规划上表现会更加有前景[12-13]。
1 无人机路径规划问题假设无人机飞行在足够高的上空可以忽略障碍且用户位置不变的条件下,无人机路径规划的多种问题都可以归结为带时间窗的车辆路径规划(vehicle routing problems with time window,VRPTW)问题。在VRPTW问题中的每个实例下,存在一个无人机基地和若干待满足需求的用户,且在固定的位置。每架无人机从无人机基地出发,经过可满足用户后回到无人机基地。当一个路径规划方案可以使所有用户按时得到满足,且无人机可回到无人机基地,则说明路径规划方案可行。
1.1 VRPTW问题的形式化表示VRPTW可以形式化表示为一个完整有向带权图
1)顶点集
2) 边集E:每条边分别表示2个顶点之间的链接,并且有一个距离属性。形式化的表示即在图G中,边集E={
对于每个用户
|
|
表 1 用户细节变量 |
|
|
表 2 无人机基地细节变量 |
设无人机基地的无人机
| $ {a}_{ij}^{r}=\left\{\begin{aligned} & 1{\text{,如果无人机}}{v}_{r}{\text{直接从}}{c}_{i}{\text{到}}{c}_{j}\\ &0{\text{,其他}}\end{aligned}\right.{\text{}} $ | (1) |
二进制决策变量
| $ {b}_{i}^{r}=\left\{\begin{aligned} & 1{\text{,如果用户}}{c}_{i}{\text{由无人机}}{v}_{r}{\text{进行服务}}\\ &0{\text{,其他}}\end{aligned}\right.{\text{}} $ | (2) |
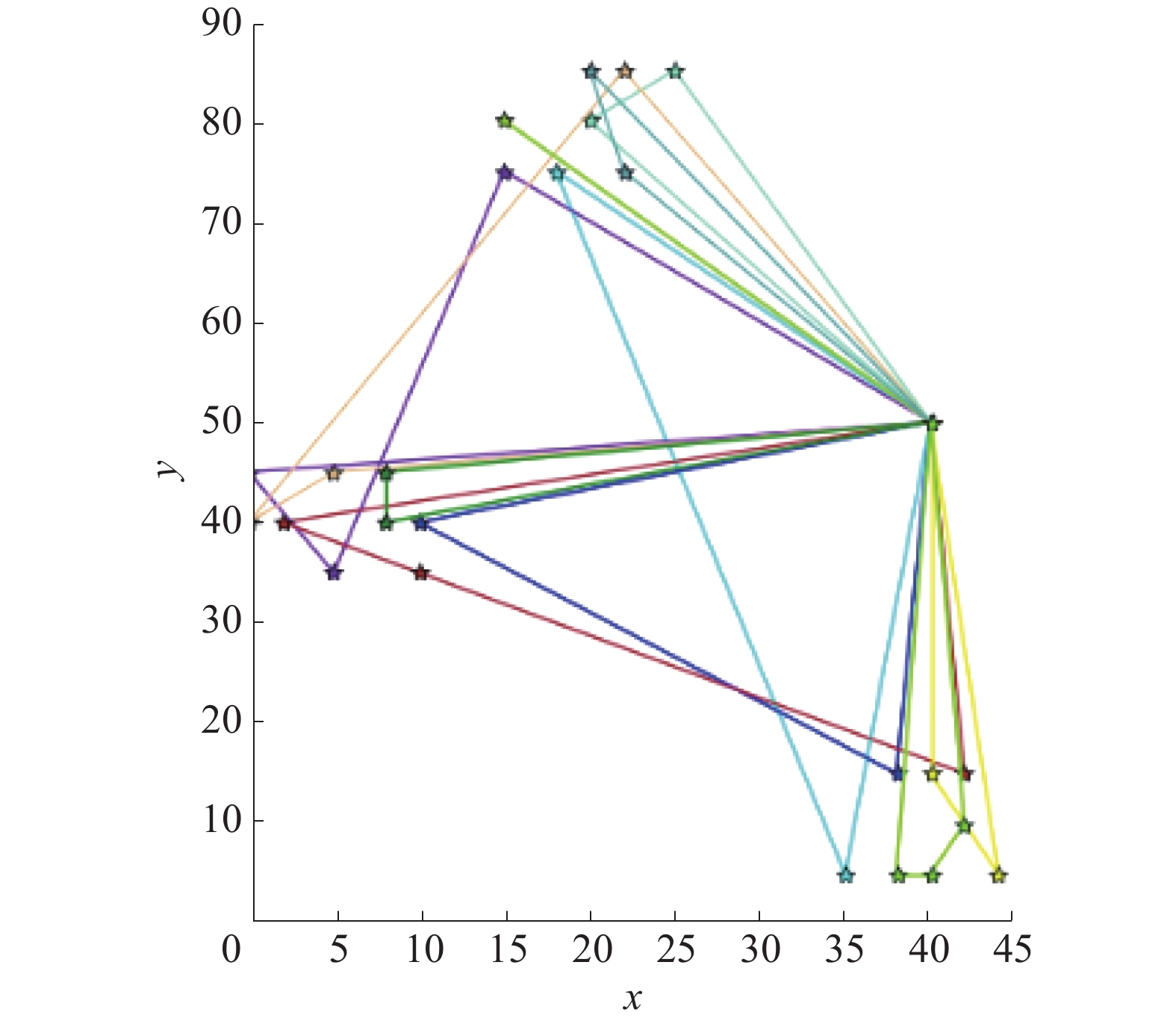
以RC101为例,如图1所示,集中的点代表无人机基地位置,其余点代表用户位置,不同颜色代表不同的无人机出行路线,此图1表明调用了8架无人机完成了此次任务。
|
Download:
|
| 图 1 RC101路径规划图 | |
该问题中顶点集
在使用该算法求解VRPTW时,会得到一组可行解,每个解
|
Download:
|
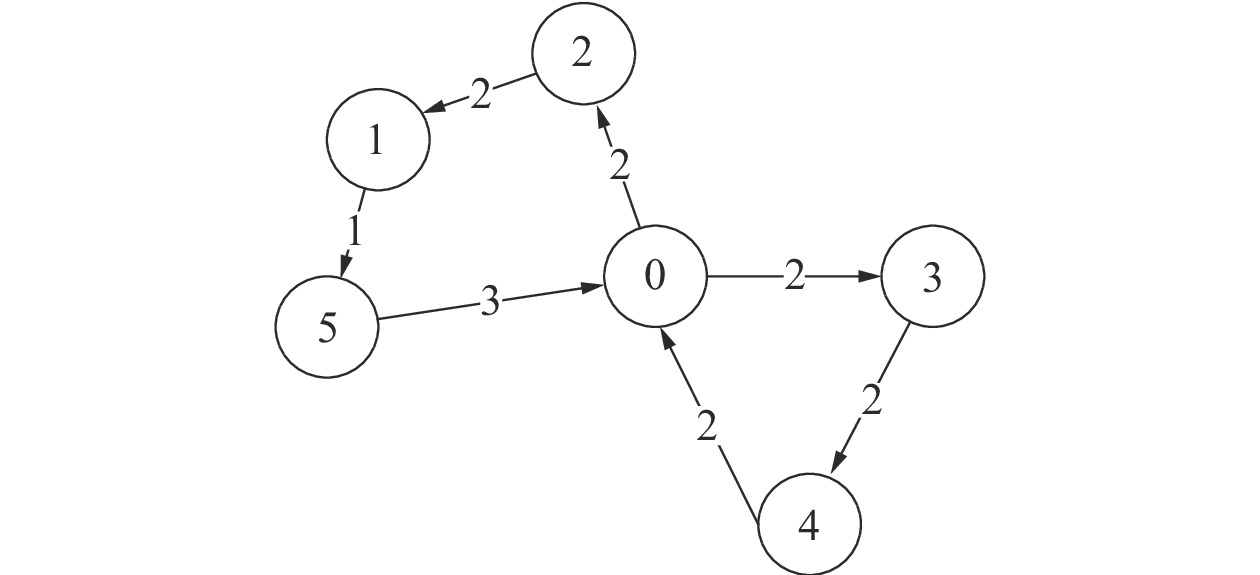
| 图 2 示例有向带权图 | |
|
Download:
|
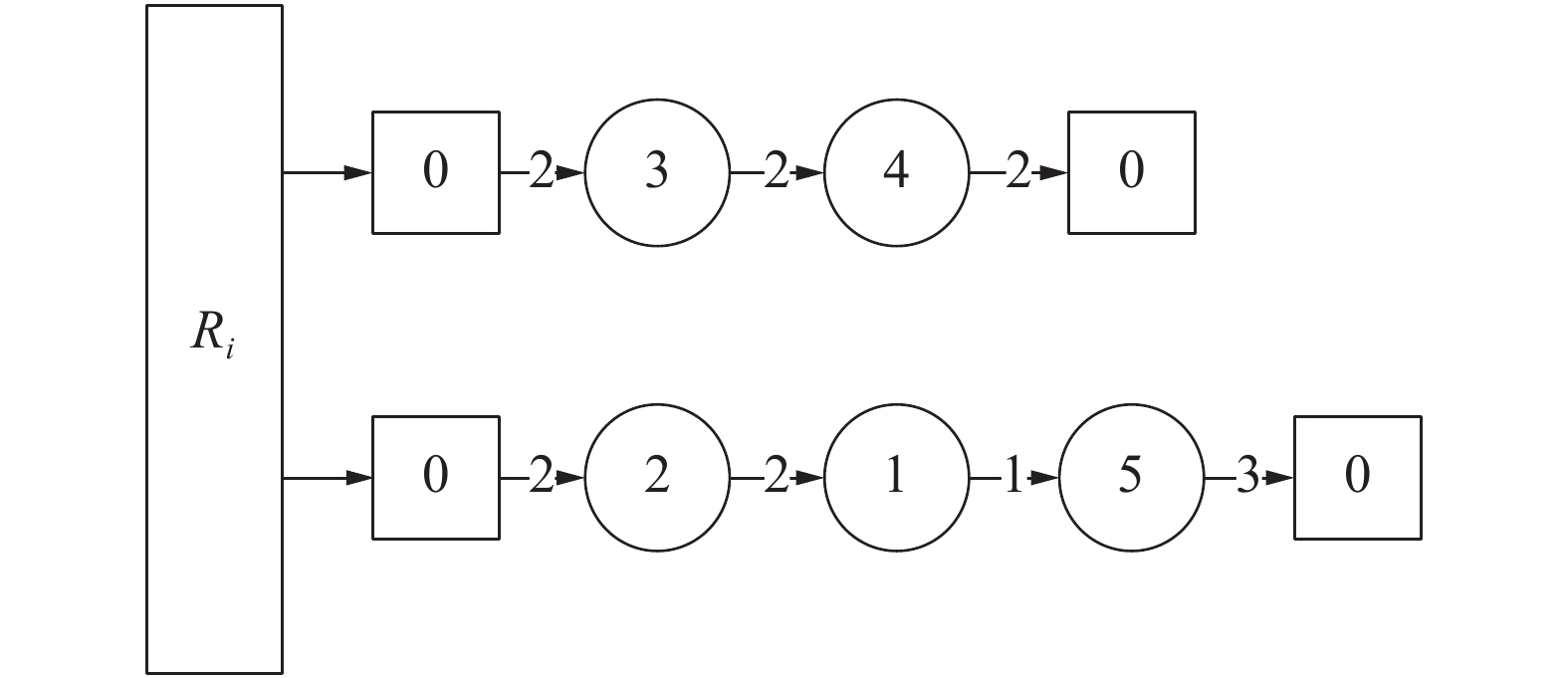
| 图 3 示例邻接图 | |
|
Download:
|
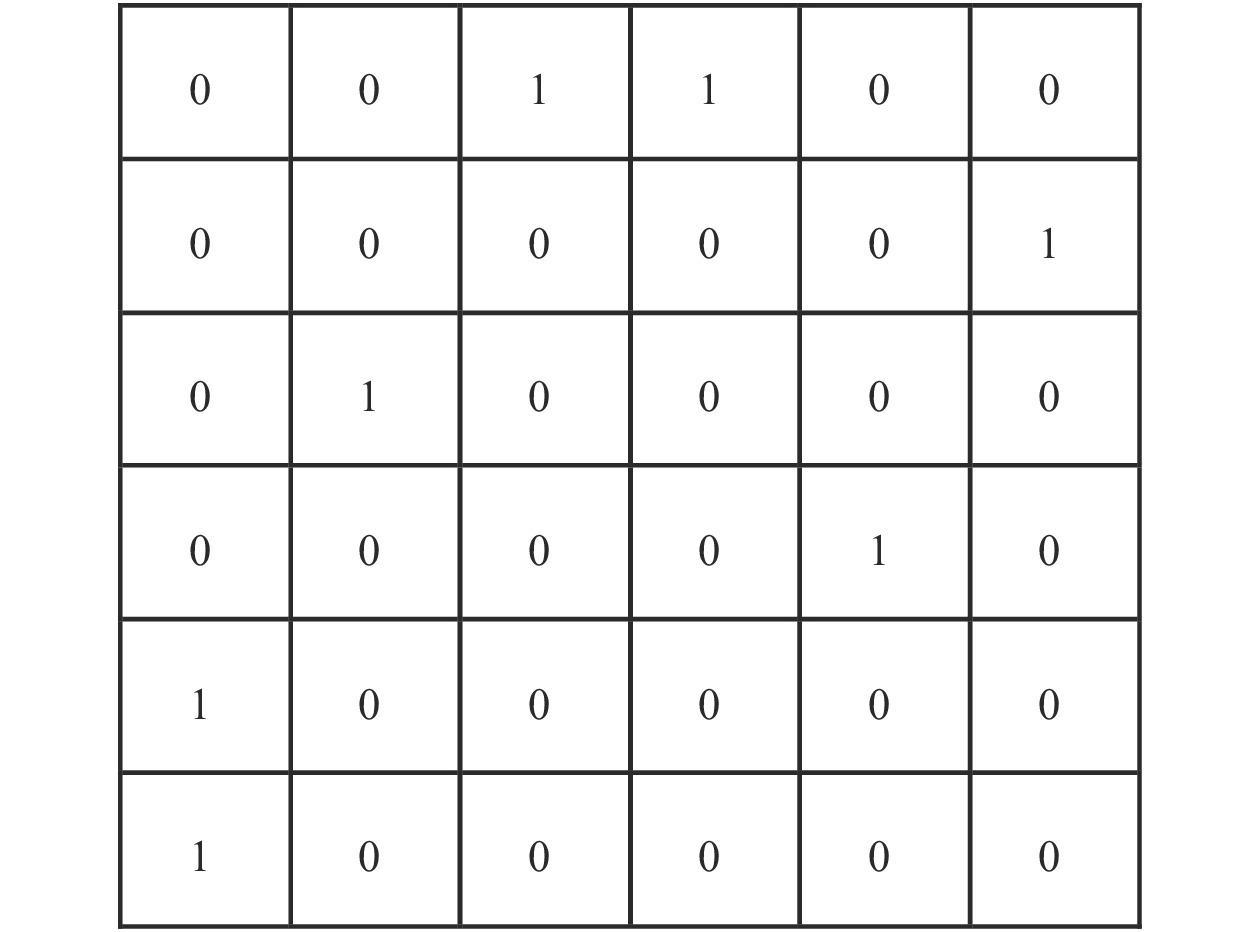
| 图 4 示例邻接矩阵 | |
在VRPTW问题中,有6个约束条件,其中:
1)边与顶点的约束:恰好有一条路径进入和离开与用户相关联的每个顶点,这样后面的公式表示才是成立的。
| $ \begin{aligned} & \sum\nolimits_{i=0}^{n}{a}_{ij}^{r}={b}_{j}^{r}=0|1,\forall r=1,2\cdots ,\left|V\right|,\forall j=1,2\cdots ,n \\ & \sum\nolimits_{j=0}^{n}{a}_{ij}^{r}={b}_{i}^{r}=0|1,\forall r=1,2\cdots ,\left|V\right|,\forall i=1,2\cdots ,n{\text{}} \end{aligned} $ | (3) |
2)每名用户只能使用一架无人机,且所有路线从无人机基地开始。
| $ \begin{aligned} & \sum\nolimits_{r=1}^{\left|V\right|}{b}_{i}^{r}=1,\forall i=1,2\cdots ,n \\ & \sum\nolimits_{r=1}^{\left|V\right|}{b}_{0}^{r}=\left|V\right| {\text{}} \end{aligned} $ | (4) |
(3)无人机总容量约束:表示每架无人机的负载不得超过其承载能力。
| $ \sum\nolimits_{i=0}^{n}{b}_{i}^{r}\times {q}_{i}\leqslant {Q}_{r},\forall r\in 1,2\cdots ,\left|V\right|{\text{}} $ | (5) |
式中
4)无人机工作最长时间约束。
| $ \begin{aligned} & \sum\nolimits_{i=0}^{n}{a}_{ij}^{r}{d}_{ij}+\sum\nolimits_{i=0}^{n}{a}_{ij}^{r}{w}_{j}^{r}+\sum\nolimits_{i=1}^{n}{a}_{ij}^{r}{s}_{i}<{T}_{r} \\ & \forall r\in 1,2\cdots ,\left|V\right|,\forall j=1,2\cdots ,n \\ & {wc}_{j}^{r}=\mathrm{max}\left\{0,{e}_{j}-{t}_{j}\right\},\forall j=1,2\cdots ,n{\text{}} \end{aligned} $ | (6) |
式中:
5)每个用户完成时间的约束。
| $\begin{array}{c} \sum\nolimits_{i=0}^{k}{a}_{ij}^{r}{d}_{ij}+\sum\nolimits_{i=1}^{k}{a}_{ij}^{r}{s}_{j}<{t}_{\mathrm{complete}\;i} \\ \forall r\in 1,2\cdots ,\left|V\right|,\forall j,k=1,2\cdots ,n{\text{}} \end{array} $ | (7) |
式中:
6)每个用户的时间窗约束。
| $ \begin{array}{c} {w}_{cj}^{r}\leqslant {t}_{j}\leqslant {l}_{j} ,\; \forall j=1,2\cdots ,n \\ {t}_{j}={t}_{i}+{w}_{j}^{r}+{s}_{i}+{d}_{ij},\forall i=0,1\cdots ,n\\ \forall j=1,2\cdots ,n,i\ne j \end{array} $ | (8) |
式中:
根据VRPTW的特点,设定了包含冲突的5个目标函数。
1)调用无人机数f1与路线总距离f2。
| $ {{\rm{min}}f}_{1}=\left|V\right|{\text{}} $ | (9) |
| $ {{\rm{min}}f}_{2}=\sum\nolimits_{r}^{\left|V\right|}\sum\nolimits_{i=0}^{n}\sum\nolimits_{j=0}^{n}{a}_{ij}^{r}{d}_{ij}{\text{}} $ | (10) |
式(9)表示调用无人机数,式(10)表示路线总距离,在文献[9]中证明无人机数量与路线总距离成正比,但路线总距离与无人机等待时间为一对冲突函数。
2)路线总时间f3。
| $\begin{array}{c} {{\rm{min}}f}_{3}=\underset{1\leqslant r\leqslant \left|V\right|}{\mathrm{max}}\bigg\{\displaystyle\sum\nolimits_{i=0}^{n}\displaystyle\sum\nolimits_{j=0}^{n}{a}_{ij}^{r}{d}_{ij}+\\ \displaystyle\sum\nolimits_{i=0}^{n}\sum\nolimits_{j=1}^{n}{a}_{ij}^{r}{w}_{j}+\displaystyle\sum\nolimits_{i=1}^{n}\displaystyle\sum\nolimits_{j=1}^{n}{a}_{ij}^{r}{*s}_{j}\bigg\}{\text{}} \end{array} $ | (11) |
式(11)表示路线总时间。总时间与车辆数量在文献[9]中被证明为一对冲突函数。
3)无人机等用户总时间f4与用户等无人机总时间f5。
| $ {\rm{min}}{f_4} = \mathop {{\rm{max}}}\nolimits_{1 \leqslant r \leqslant \left| V \right|} \left\{ \sum\nolimits_{j = 1}^n {\max } \{ b_j^r \times ({e_j} - {t_j}),0\} \right\} {\text{}} $ | (12) |
| $ {\rm{min}}{f_5} = \mathop {{\rm{max}}}\nolimits_{1 \leqslant r \leqslant \left| V \right|} \left\{ \sum\nolimits_{j = 1}^n {\max } \{ b_j^r \times ({t_j} - {e_j}),0\} \right\} {\text{}} $ | (13) |
式中:
式(12)表示无人机等用户总时间,式(13)表示用户等无人机总时间,这2个公式是本文提出的一对冲突函数。
1.5 多目标优化多目标优化问题可以用函数表示为
| $\begin{aligned} \mathrm{min}F\left({{x}}\right)= & \left({f}_{1}\left({{x}}\right),{f}_{2}\left({{x}}\right),\cdots ,{f}_{M}\left({{x}}\right)\right)\\ & {{x}}\in \varOmega ,{f}_{i}\left({{x}}\right)\in {R}^{M},\forall_i=1,2\cdots ,M {\text{}} \end{aligned} $ | (14) |
式中:
在多目标优化问题中,
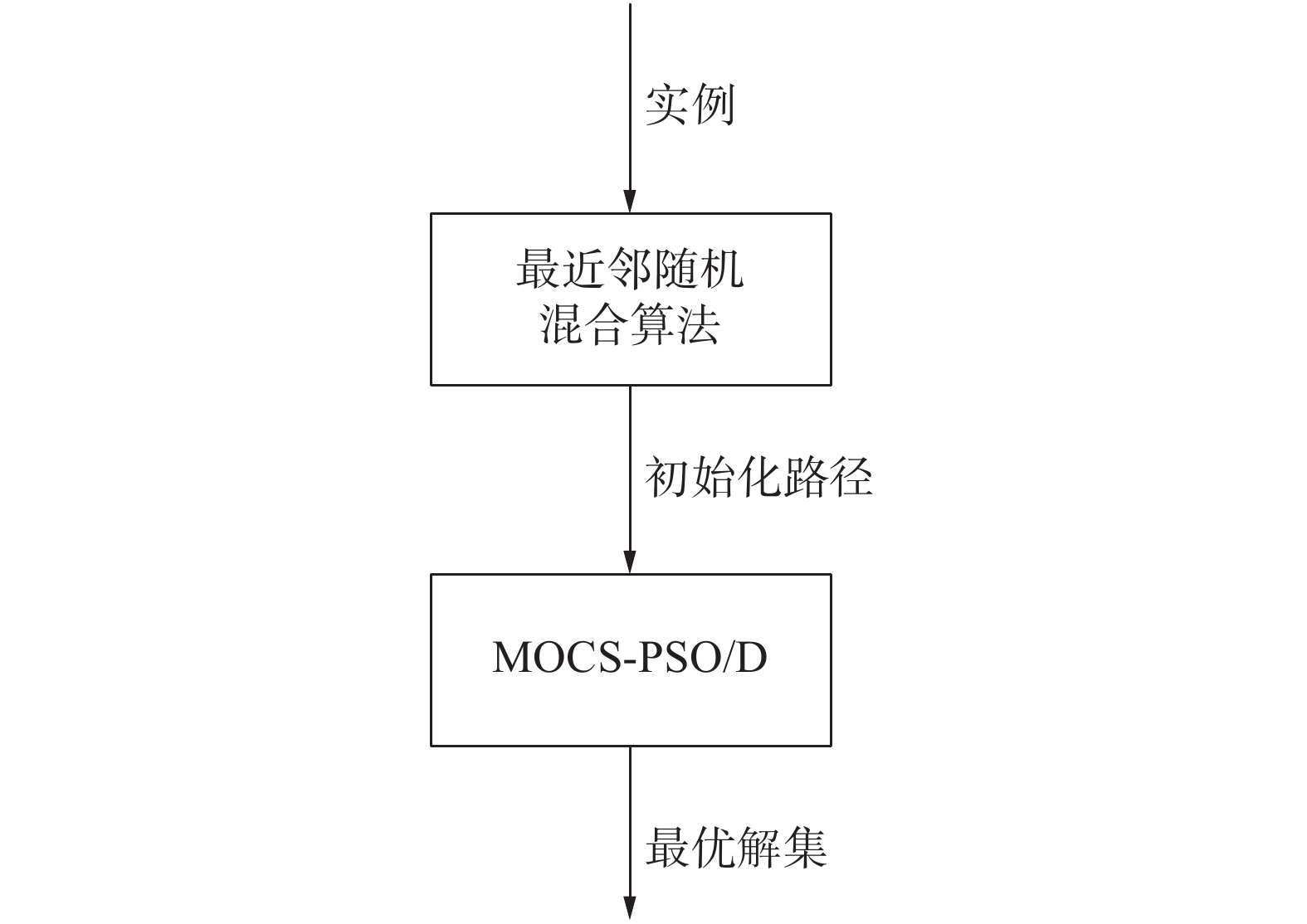
本文提出的MOCS-PSO/D框架是基于MOEA/D的框架,将多个目标函数进行归一化处理,并使用S-PSO来对VRPTW问题的解进行基于集合和概率的表示,同时结合CLPSO来对粒子进行更新。最后,根据实际的应用情况,对局部搜索策略进行调整,以减少调用的无人机架数。
两阶段算法流程如图5所示。
|
Download:
|
| 图 5 两阶段算法流程图 | |
在VRPTW问题中,利用邻接矩阵来表示每个粒子的位置,离散的位置表示方式可以适用于S-PSO的位置更新和速度更新公式中。每个粒子的位置由邻接矩阵表示,粒子
| $ {x}_{k}^{{h}_{\delta }}=\left[\left\langle {c}_{i},\mathrm{\delta } \right\rangle ,\left\langle \mathrm{\delta }{,c}_{j} \right\rangle \right]{\text{}} $ | (15) |
根据每个粒子的位置可以画出一个完整的有向哈密顿圆。其中每个有向哈密顿圆的集合代表要调度的每架无人机在满足约束条件下的出行路线。
速度由边与其出现概率表示,每个粒子的第m维的速度分量用
| $ {u}_{k}^{{h}_{\delta }}=\left\{\frac{\left\langle {c}_{i}{,c}_{j} \right\rangle }{p\left({c}_{i}{,c}_{j}\right)}|\left\langle {c}_{i}{,c}_{j} \right\rangle \in {A}^{\delta }\right\}{\text{}} $ | (16) |
集合
初始化阶段将混合使用最近邻算法和随机算法两种启发式算法进行路径初始化。
NNH是一种贪心的初始化种群候选解的方法,是在实际设计算法时常用的一种方法。将用户集C和无人机基地集D的数据进行读取,利用NNH建立可行解。具体方法如下。
1)初始化从无人机基地开始的路线,递归地将最近的可满足用户添加到路线中,直到不存在可满足用户,则回到无人机基地。已满足的用户移除用户集。
2)如果用户集C不为空,则转到1),否则终止算法。
随机算法将每次选择的用户更改为随机可满足用户即可。也可将2种算法混合使用。
2.3 第二阶段(MOCS-PSO/D算法)本文针对VRPTW问题的MOCS-PSO/D框架将阶段一得到的结果作为初始值进行优化。
MOCS-PSO/D框架的执行详细过程如下。
1)初始化:初始化种群大小Psize、目标函数个数
2)求值和规范化:求得所有粒子以获得目标向量。更新每个目标的上下限。相应地,规范化每个粒子的目标向量。
3)学习者和存档更新:使用粒子的权重向量和其邻域中所有新生成的解以MOEA/D方式更新每个粒子的学习者。使用所有新解基于Pareto优势更新外部存档EP。
4)粒子群更新:对每一个粒子,在CLPSO的速度更新公式中执行基于元素的运算来更新其速度,然后构造一个新的解来更新其位置。
5)局部搜索策略:再对每一个粒子进行局部搜索策略,不断选择用户最少的路线,试图将其中的用户插入其他路线中,依旧可满足约束条件。
6)额外粒子群更新:如果某粒子多次没有进行更新,则对其进行额外粒子群更新策略,使用基于元素的算法运算来更新其速度,然后构造一个新的解来更新其位置。
7)终止:如果满足停止条件,则停止并输出外部储存集EP;否则,转到2)。
2.3.1 速度更新CLPSO算法是PSO算法的一个变种,其采用一种新的速度更新规则来防止解的过早收敛,在每次更新时只采用局部最优解进行更新,而不使用全局最优。用于更新VRPTW的S-PSO算法中每次迭代
| $ {u}_{k+1}^{{h}_{\delta }}=\omega \times {u}_{k}^{{h}_{\delta }} +\sum\nolimits_{i=0}^{n=1}\left({c}_{1}\times {\sigma }_{1}\times ({{{B}}_{{\mathrm{rand}}_{i}}x}_{k}^{{h}_{\delta }}-{x}_{k}^{{h}_{\delta }})\right){\text{}} $ | (17) |
式中:
S-PSO是基于集合和概率定义的,因此将其用于VRPTW问题中需要对其中的运算符进行重新定义。
算子1:权重系数与速度算子相乘由式(18)定义,该公式使用公式(19)确定边
| $ \omega \times {u}_{k}^{{h}_{\delta }} = \left\{\left\langle {c}_{i}{,c}_{j} \right\rangle /p{'}\left({c}_{i}{,c}_{j}\right)|\left\langle {c}_{i}{,c}_{j} \right\rangle \in {A}^{\delta }\right\}{\text{}} $ | (18) |
| $ {p}^{'}\left({c}_{i}{,c}_{j}\right)=\left\{\begin{array}{c}1,\;{\rm{if}}\;w\times p\left({c}_{i}{,c}_{j}\right)>1\\ w\times p\left({c}_{i}{,c}_{j}\right),\;{\rm{其他}}\end{array}\right.{\text{}} $ | (19) |
算子2:位置与位置算子相减由式(20)定义。
| $ {x}_{k}^{{h}_{\delta }}-{x}_{k}^{{h}_{\delta }^{'}}={M}^{\delta }=\left\{\left\langle {c}_{i}{,c}_{j} \right\rangle \right|\left\langle {c}_{i}{,c}_{j} \right\rangle \in {x}_{k}^{{h}_{\delta }}\;{\rm{and}}\;\notin {x}_{k}^{{h}_{\delta }^{'}}{\text{}} $ | (20) |
算子3:
| $ c\times \sigma \times {M}^{\delta }=\left\{\left\langle {c}_{i}{,c}_{j} \right\rangle /p{'}\left({c}_{i}{,c}_{j}\right)|\left\langle {c}_{i}{,c}_{j} \right\rangle \in {M}^{\delta }\right\}{\text{}} $ | (21) |
| $ {p}^{'}\left({c}_{i}{,c}_{j}\right)\left\{\begin{array}{c}1,{\rm{if}}\left\langle {c}_{i}{,c}_{j} \right\rangle \in {M}^{\delta }\;{\rm{and}}\;c\times \sigma >1\\ c\times \sigma ,{\rm{if}}\;\left\langle {c}_{i}{,c}_{j} \right\rangle \in {M}^{\delta }\;{\rm{and}}\;0\leqslant c\times \sigma \leqslant 1\\ 0,{\rm{if}}\;\left\langle {c}_{i}{,c}_{j} \right\rangle \notin {M}^{\delta }\end{array}\right.{\text{}} $ | (22) |
算子4:速度与速度算子相加由式(23)定义,即边
| $ {u}_{k}^{{h}_{\delta }}+{u}_{k}^{{h}_{\delta }^{'}}=\{\left\langle {c}_{i}{,c}_{j} \right\rangle / \mathrm{max}({p}_{k}^{{h}_{\delta }}\left({c}_{i}{,c}_{j}\right),{p}_{k}^{{h}_{\delta }^{'}}\left({c}_{i}{,c}_{j}\right)\left)\right|\left\langle {c}_{i}{,c}_{j} \right\rangle \in {A}^{\delta } {\text{}} $ | (23) |
为了更加清晰的进行表示,用定义算子的应用实例进行说明。假设:
| $ {u}_{k}^{1}=\{\left\langle \mathrm{2,1} \right\rangle /0.5,\left\langle \mathrm{1,3} \right\rangle /0.2,\left\langle \mathrm{4,1} \right\rangle /0.3,\left\langle \mathrm{2,1} \right\rangle /0.1\}\text{} $ |
| $ {x}_{k}^{1}=\{\left\langle \mathrm{5,1} \right\rangle ,\left\langle \mathrm{1,3} \right\rangle \} $ |
| $ {{{B}}_{0}x}_{k}^{1}=\{\left\langle \mathrm{2,1} \right\rangle ,\left\langle \mathrm{1,3} \right\rangle \} $ |
| $ {{{B}}_{1}x}_{k}^{1}=\{\left\langle \mathrm{4,1} \right\rangle ,\left\langle \mathrm{1,3} \right\rangle \} $ |
| $ w=0.7,{c}_{1}=2,{\sigma }_{1}=3 $ |
可以得到
| $ \omega \times {u}_{k}^{1}= \{\left\langle \mathrm{2,1} \right\rangle /0.35,\left\langle \mathrm{1,3} \right\rangle /0.14,\left\langle \mathrm{4,1} \right\rangle /0.21,\left\langle \mathrm{2,1} \right\rangle /0.07\}× $ |
| $ {{{c}_{1}\times {\sigma }_{1}\times ({B}}_{{\mathrm{rand}}_{0}}x}_{k}^{1}-{x}_{k}^{1})=\{\left\langle \mathrm{1,3} \right\rangle /0.6\} $ |
| $ {{c}_{1}\times {\sigma }_{1}\times ({{B}}_{{\mathrm{rand}}_{1}}x}_{k}^{1}-{x}_{k}^{1})=\{\left\langle \mathrm{4,1} \right\rangle /0.6,\left\langle \mathrm{1,3} \right\rangle /0.6\} $ |
最终
| $ \begin{aligned} & {u}_{k+1}^{1}= \omega \times {u}_{k}^{1}+\sum\nolimits_{i=0}^{n=1}\left({c}_{1}\times {\sigma }_{1}\times {{({B}}_{{\mathrm{rand}}_{i}}x}_{k}^{1}-{x}_{k}^{1})\right)=\\ & \{\left\langle \mathrm{2,1} \right\rangle /0.35,\left\langle \mathrm{1,3} \right\rangle /0.6,\left\langle \mathrm{4,1} \right\rangle /0.6,\left\langle \mathrm{2,1} \right\rangle /0.07\} \end{aligned}$ |
通过这个实例可以看出,速度将根据
此外针对综合学习策略的缺陷,设置了额外粒子群更新策略,该策略将学习邻域内的粒子及外部储存集EP中解的信息。其中速度更新策略如式(24)所示
| $\begin{aligned} u_{k + 1}^{{h_\delta }} = & \omega \times u_k^{{h_\delta }} + \sum\nolimits_{i = 0}^{n = 4} {\left( {{c_1} \times {\sigma _1} \times ({{\rm{B}}_i}x_k^{{h_\delta }} - x_k^{{h_\delta }})} \right)} +\\ &\sum\nolimits_{i = 0}^{n = 14} {\left( {{c_2} \times {\sigma _2} \times (E{P_i}x_k^{{h_\delta }} - x_k^{{h_\delta }})} \right)} {\text{}} \end{aligned}$ | (24) |
当粒子位置的边成立时,初始值将设置为[0,1]的随机值,表示可以作为出行路段。位置更新的规则根据式(25)进行完成,这里的‘+’号将根据S-PSO的特点重新进行构造。
| $ {x}_{k+1}^{h}={x}_{k}^{h}+{u}_{k+1}^{h}$ | (25) |
式中:速度
| $ {\rm{Cut}}\left( {u_{k + 1}^h} \right) = \left\{ {\left\langle {{c_i},{c_j}} \right\rangle |\frac{{\left\langle {{c_i},{c_j}} \right\rangle }}{{p\left( {{c_i},{c_j}} \right)}} \in u_{k + 1}^h\;{\rm{and}}\;p\left( {{c_i},{c_j}} \right) \geqslant {\rm{rand}}} \right\}{\text{}} $ | (26) |
式中:rand为[0,1]的随机数,当且仅当
1)对于每架无人机,在
2)为了构造无人机出行路径,该方法将选择一个从无人机基地的可到达点。再依次向后寻找可到达点,直到所有点都不满足,则回到无人机基地。
其中,可到达点的选择将根据以下3个crisp集合依次选择:
| $ {S}_{U}=\left\{{c}_{i}|\left\langle {c}_{i}{,c}_{j} \right\rangle \in {u}_{k+1}^{h},\left\langle {c}_{i}{,c}_{j} \right\rangle {\text{满足约束}}{\Omega }\right\} $ |
| $ {S}_{X}=\left\{{c}_{i}|\left\langle {c}_{i}{,c}_{j} \right\rangle \in {x}_{k}^{h},\left\langle {c}_{i}{,c}_{j} \right\rangle {\text{满足约束}}{\Omega }\right\} $ |
| $ {S}_{A}=\left\{{c}_{i}|\left\langle {c}_{i}{,c}_{j} \right\rangle \in \mathrm{A},\left\langle {c}_{i}{,c}_{j} \right\rangle {\text{满足约束}}{\Omega }\right\} $ |
如果
本文使用的数据是Solomon在1984中介绍的VRPTW的基准数据集,该数据集是基于几个标准路径测试问题数据集生成的;测试使用的RC1类包含随机和集群地理位置用户的混合;实验数据的用户规模为25。其中用户数据集的属性包括用户编号、横纵坐标、需求量、时间窗和服务时间,无人机数据集的属性包括横纵坐标、最大容量和最大工作时间。
3.2 对比实验设置实验都在运行30次取平均值后进行结果统计。
为了对比的公平性,对以下对比算法进行了处理。
1)第一阶段采取最近邻随机混合策略(NNH+RANDOM):取实验的随机15个粒子与其他算法进行比较。
2)第二阶段采取单目标遗传算法(GA)和基于集的单目标CS-PSO(基于集的综合学习粒子群优化算法):取随机15次实验的粒子与其他算法进行比较,该算法使用的单目标适应度函数为
| $ {F\left({x}_{k}^{{h}_{\delta }}\right)=\alpha f}_{1}+\beta {f}_{2} + \mathrm{\gamma }\frac{\left({f}_{4}+{f}_{5}\right)}{{f}_{3}} $ | (27) |
3)第二阶段采取多目标算法MOCS-PSO/D:随机取一次实验的外部储存集解与其他算法进行比较。
3.3 运行时间对比本实验将对4种算法的收敛速度进行对比。如表3所示。
|
|
表 3 4种算法平均一次实验的运行时间 |
该实验数据表明,第一阶段的Rand+NNH算法可以仅消耗少量时间即可以搜索到可行解,为第二阶段的算法提供初始粒子。
GA与CS-PSO算法相比,运行消耗时间相对较长,因此选择对CS-PSO算法进行改进。CS-PSO算法与MOCS-PSO/D算法相比时间消耗较少,但考虑到CS-PSO算法每次实验只能得到1个最优解,而MOCS-PSO/D算法一次实验则可以得到15个最优解,从获得解效率来说,MOCS-PSO/D具有比较大的优势,说明MOCS-PSO/D具有很好的收敛性。
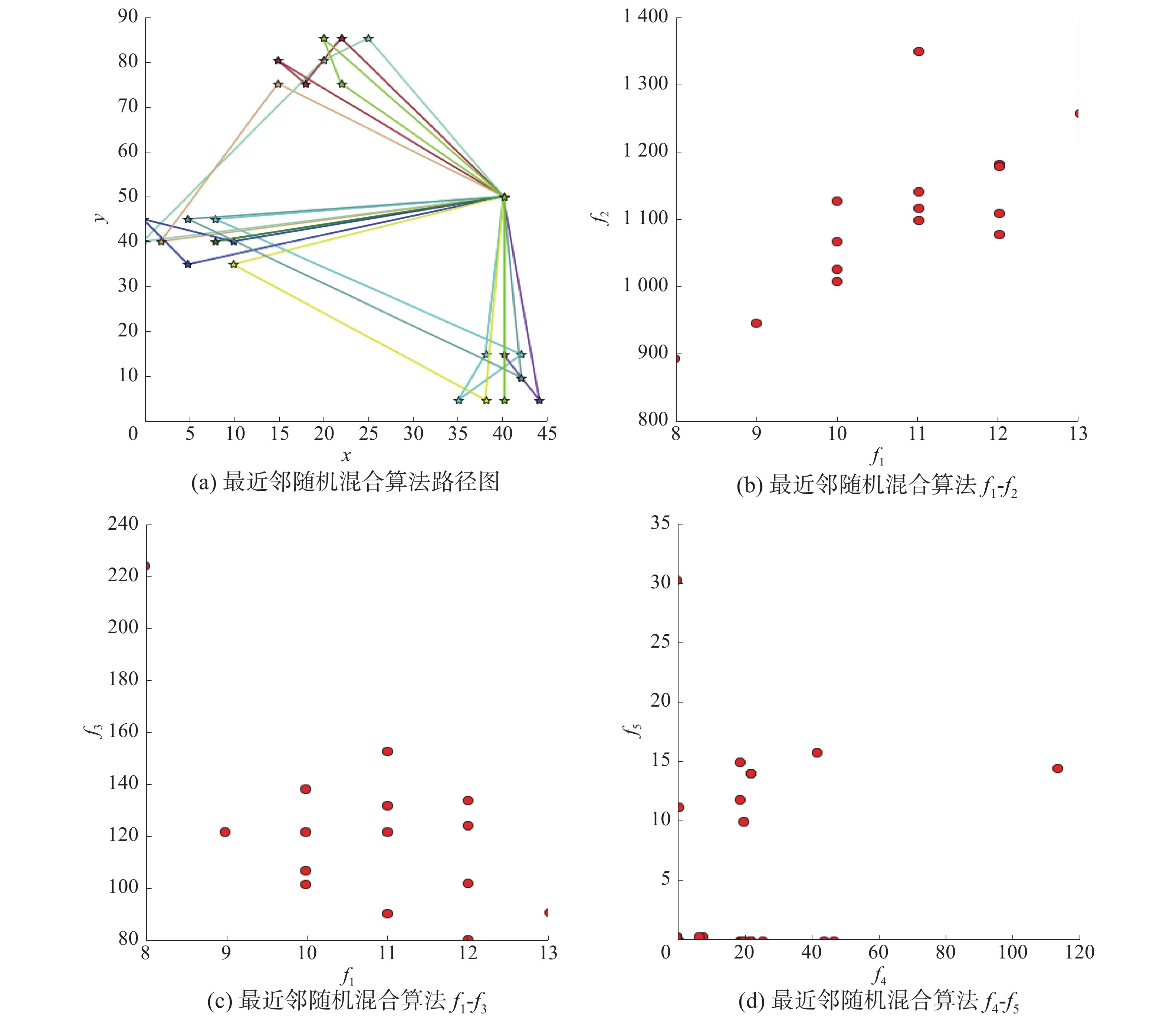
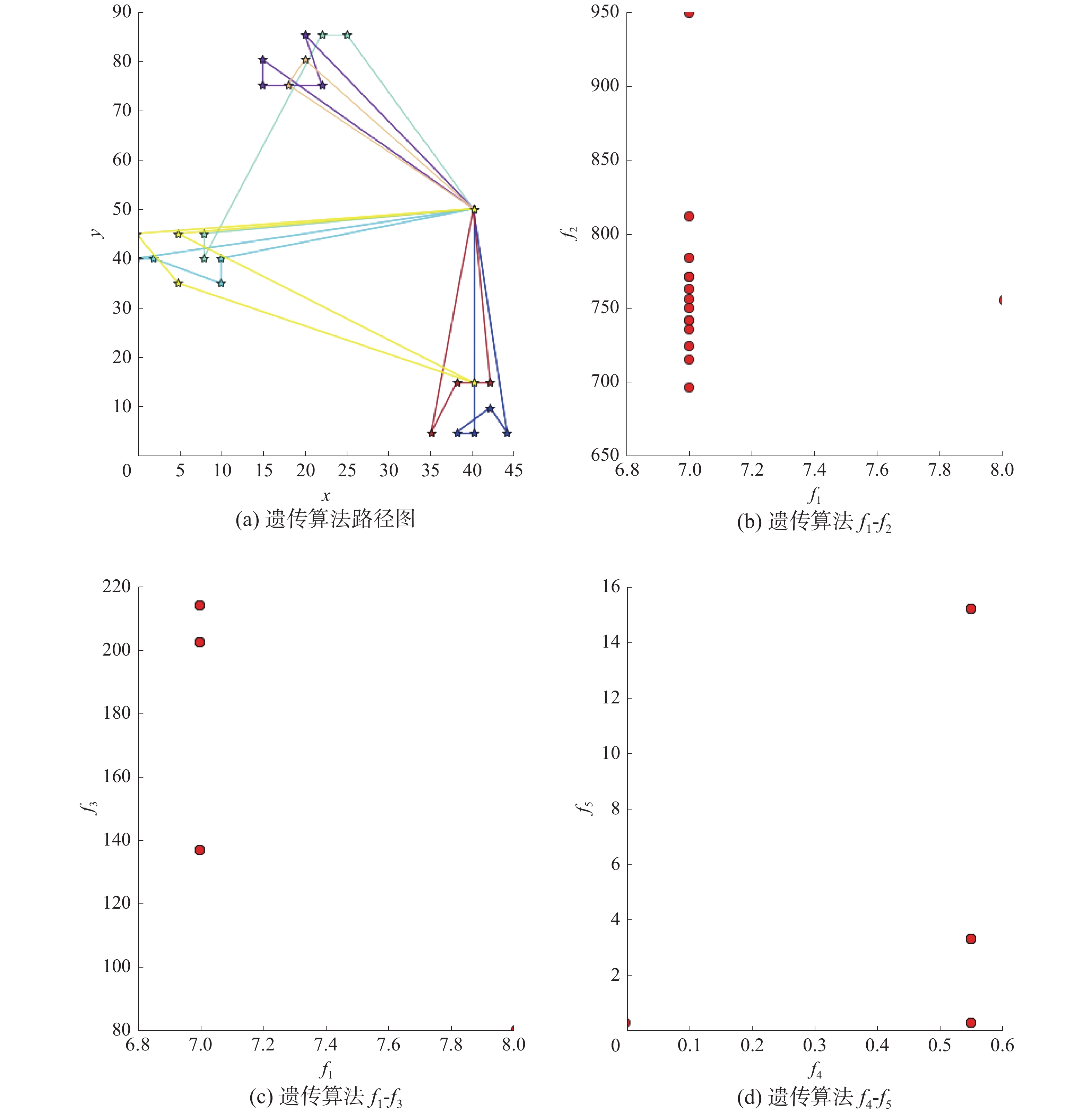
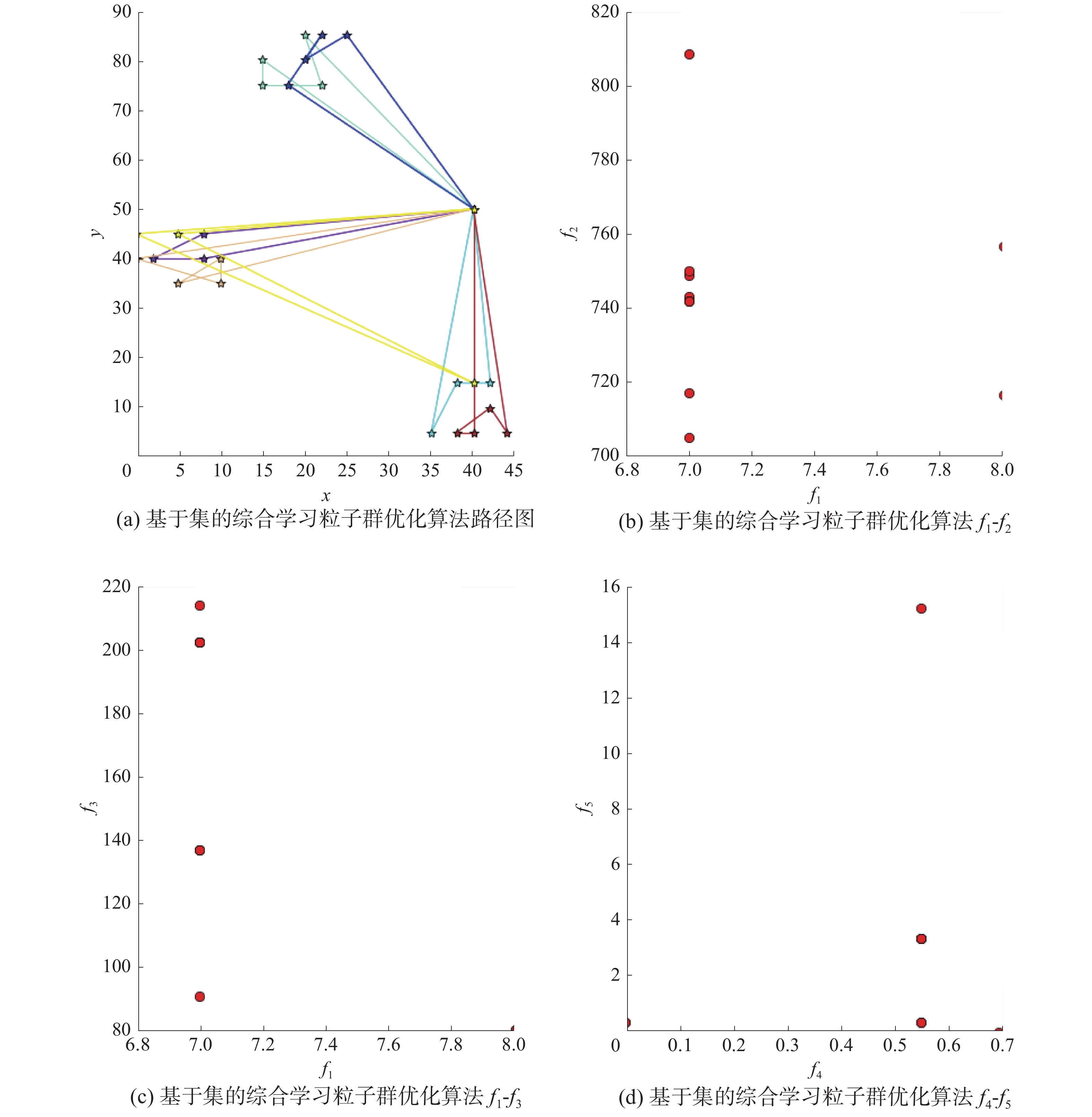
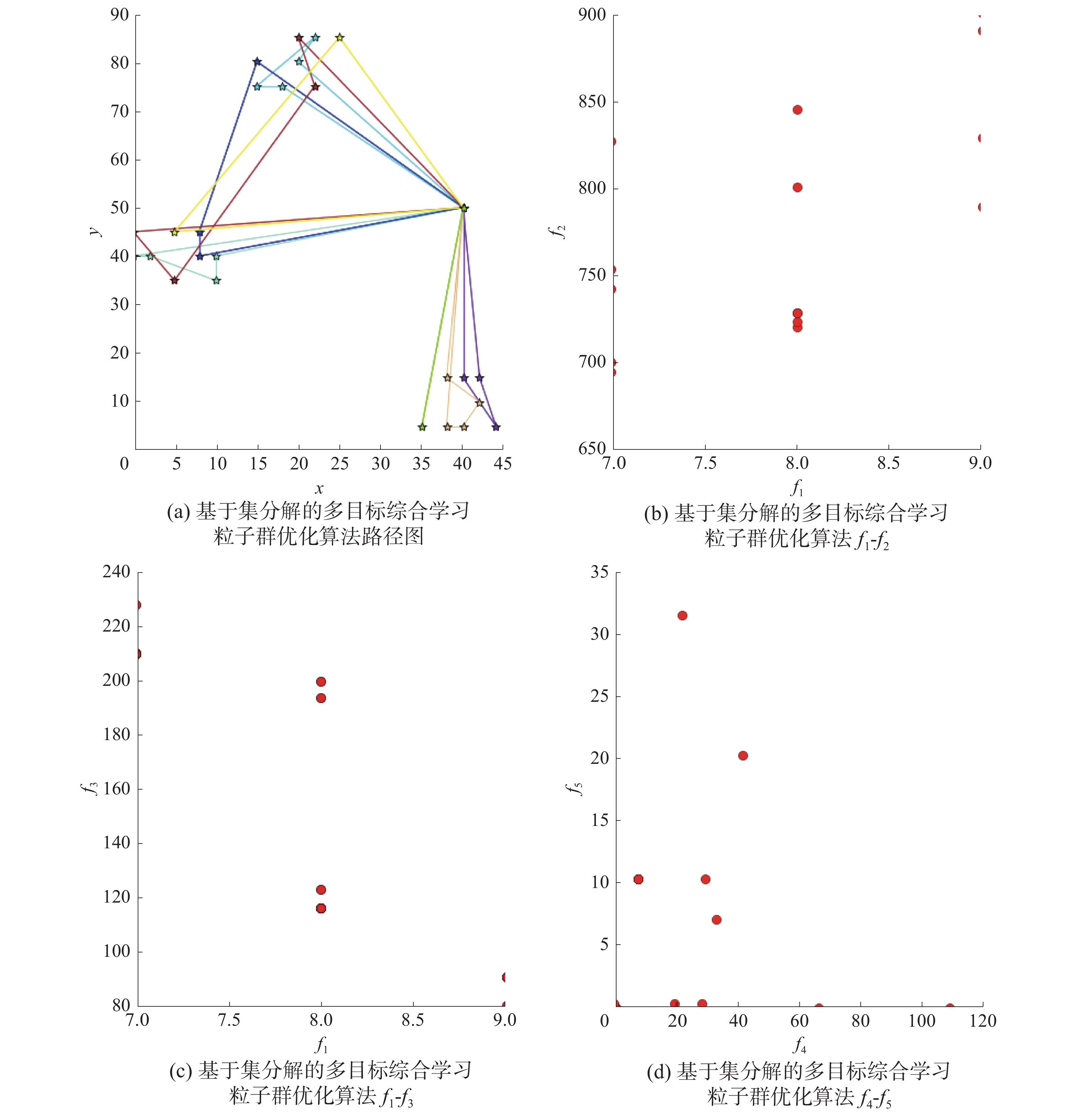
3.4 算法性能对比本实验将从解的多样性方面进行对比。以RC101数据样本为实验数据,图 6—图 9分别为NNH+RANDOM、GA、CS-PSO和MOCS-PSO/D的实验图,其中从左到右依次为其中一个粒子的路径图、3组目标
|
Download:
|
| 图 6 NNH+RANDOM算法结果 | |
|
Download:
|
| 图 7 GA算法结果 | |
|
Download:
|
| 图 8 CS-PSO算法结果 | |
|
Download:
|
| 图 9 MOCS-PSO/D算法结果 | |
由4组实验图的(a)图可以看出,4种算法都可以有效地找到可行路径,且无人机群可以服务全部的25名用户。由4组实验图的(b)图可以看出,GA、CS-PSO和MOCS-PSO/D都可以显著地降低调用无人机数量。同时,可以从MOCS-PSO/D算法中发现
综上,MOCS-PSO/D算法具有很好的多样性,且可以搜索到质量更高的Pareto最优解。
4 结论在面向的无人机路径规划问题中,针对VRPTW问题使用提出的两阶段算法,第一阶段为随机贪心混合策略,第二阶段使用的MOCS-PSO/D算法在CS-PSO算法的基础上增加了MOEA/D框架,改变了CLPSO和PSO的速度更新公式,使其解可以自适应的在5个目标函数上达到均衡,更加符合实际的应用场景,当某路径规划方案不能执行时,可立刻选择其他备选方案。同时,与随机贪心混合策略、GA和CS-PSO相比,在算法收敛速度、解的多样性上都有很好的表现。
但是本文算法的解求得的调用无人机数量依旧较多,由于该目标为主要目标函数,未来将对该方面进行研究。
| [1] |
李绍斌, 姜大立, 付高阳, 等. 战场物资无人机配送研究[J]. 国防科技, 2019, 40(3): 98-104. ( 0) 0)
|
| [2] |
皇甫莹丽, 程威. 灾害救援中无人机资源优化配置仿真研究[J]. 计算机仿真, 2019, 36(2): 55-58. ( 0) 0)
|
| [3] |
PRAG K. Computational Logistics of the Vehicle Routing Problem with Time Windows[D]. University of the Witwatersrand, 2018: 27-64.
( 0) 0)
|
| [4] |
OTTO A, AGATZ N, CAMPBELL J, et al. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey[J]. Networks, 2018, 72(4): 411-458. DOI:10.1002/net.21818 ( 0) 0)
|
| [5] |
庞强伟, 胡永江, 李文广, 等. 多无人机协同侦察任务规划方法研究综述[J]. 电讯技术, 2019, 59(6): 741-748. DOI:10.3969/j.issn.1001-893x.2019.06.020 ( 0) 0)
|
| [6] |
吴柏林. 多目标粒子群优化算法及其应用研究[D]. 成都: 电子科技大学, 2019.
( 0) 0)
|
| [7] |
刘畅, 谢文俊, 张鹏, 等. 多目标群多基地多无人机协同任务规划[J]. 弹箭与制导学报, 2019, 39(1): 119-124. ( 0) 0)
|
| [8] |
杨轻, 杨忠, 许昌亮, 等. 改进PSO算法及其无人机电力巡线规划应用[J]. 应用科技, 2019, 46(3): 80-85. ( 0) 0)
|
| [9] |
YU Xue, CHEN Weineng, GU Tianlong, et al. Set-Based Discrete Particle Swarm Optimization Based on Decomposition for Permutation-Based Multiobjective Combinatorial Optimization Problems.[J]. IEEE Transactions on Cybernetics, 2018, 47(7): 2139-2153. ( 0) 0)
|
| [10] |
ZHENG Yujun, DU Yichen, LING Haifeng, et al. Evolutionary Collaborative Human-UAV Search for Escaped Criminals[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 217-231. DOI:10.1109/TEVC.2019.2925175 ( 0) 0)
|
| [11] |
WANG Jiahai, WENG Taiyao, ZHANG Qingfu. A Two-Stage Multiobjective Evolutionary Algorithm for Multiobjective Multidepot Vehicle Routing Problem With Time Windows[J]. IEEE Transactions on Cybernetics, 2019, 49(7): 2467-2478. DOI:10.1109/TCYB.2018.2821180 ( 0) 0)
|
| [12] |
HUI Y, YUJIA W, QIANG C, et al. Multi - Objective Particle Swarm Optimization Based on Multi - population Dynamic Cooperation[J]. Electronic Science and Technology, 2019, 32(10): 28–33., 2019, 30(2): 28-33. ( 0) 0)
|
| [13] |
JIA Yahui, CHEN Weineng, GU Tianlong, et al. A Dynamic Logistic Dispatching System With Set-Based Particle Swarm Optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(9): 1607-1621. DOI:10.1109/TSMC.2017.2682264 ( 0) 0)
|
 2021, Vol. 48
2021, Vol. 48


