进入21世纪，基于位置服务(location based services, LBS)在诸多领域的需求日益增大。基于位置服务是指由移动通信网络终端、无线局域网等无线通信网络技术进行定位，进而获取待测目标物体的位置信息，所获取的定位信息被用户应用于实现各种位置相关的业务服务。目前从定位场景进行划分可分为室外定位与室内定位。对于室外定位，全球卫星导航系统^[1]完全可以提供较高精度定位结果，当前具有代表性的主要有中国北斗卫星定位系统、欧盟的伽利略卫星导航系统、美国的全球定位系统以及俄罗斯的全球卫星导航系等^[2-5]几大定位系统。室外定位系统主要依靠卫星以及雷达等硬件设备实现，采用以多卫星联合的方式实现户外定位。但将其应用于室内定位就会出现误差较大以及不适用于复杂室内空间环境等问题，主要原因是室内定位时，由于建筑物墙体以及室内环境中各类物体等遮挡的影响，卫星信号的衰落非常明显，使得定位的误差巨大而无法达到较好的定位效果。随着人们在医院、大型商场以及博物馆等环境中的活动日益增多，人们对于复杂空间的室内定位需求越来越大。目前的室内定位技术主要有WIFI定位、蓝牙定位和光纤定位等^[6-8]。

在许多大型商场以及医院中，墙体以及其他物体的遮挡对WIFI信号有较大的影响，定位目标与无线访问节点(access point, AP)之间存在视距(LOS)^[9]与非视距(NLOS)^[10]等交替变换情况，所以，如何保证对异型空间的室内定位的高精度是如今亟需解决的问题。考虑到环境系统的非线性特点，拟采取PF^[11]来做数据融合。但是由于粒子滤波高效率定位仅局限于在高度非线性环境中，对于定位技术的融合无法解决异型空间下的NLOS干扰问题。本文采用基于IMM^[12]的算法，可以有机地将两者信道模型兼用，实现对此类环境中运动物体进行高精度定位。

本文采用交互多模型与粒子滤波相结合的技术，并针对实际的定位环境，提出改进的IMMPF的室内定位算法：首先对运动目标与噪声进行建模，在状态模型更新时利用粒子滤波对于状态以及NLOS/LOS状态参数进行融合；同时对于异型复杂环境中无法表示真实的概率密度函数分布，通过改变粒子权重值向似然函数峰值靠近，有效地增大粒子的有效性，使得采样粒子更接近真实状态，进而可以有效避免NLOS对于定位影响。

1 基于WIFI指纹的定位算法 1.1 基于位置指纹定位原理

在室内某处的WIFI信号，在无外加干扰情况下强度稳定不变。依据这条特性完成建立相应的指纹库。采用指纹库的方式进行定位研究，可以有效避免定位时因为环境原因所产生的多径效应干扰，有效抑制多径效应以及阴影衰落对定位结果带来的影响。定位可以划分为离线指纹采集和在线匹配定位2个阶段。离线阶段主要完成对室内定位空间各处位置信息进行WIFI指纹的采集，对于当前位置WIFI接收信号强度指示(received signal strength indication，RSSI)进行分析提取，作为当前位置的指纹信息存储于指纹库；在线阶段主要完成对于实时接收空间的AP所发射的WIFI信息强度，通过分析WIFI信息中所包含的信息特征与指纹库进行比对匹配，进而得到定位信息。图1为基于位置指纹的模型图。

1.2 WIFI指纹库的建立

本文实验地点为某教学楼的四楼走廊，实验区域内WIFI信号全覆盖，采用华为手机以及传感器进行WIFI信息的采集，在空间内均匀布置6个AP发送设备。AP的服务集标识(service set identifier，SSID)用于区分同一区域所接受的WIFI信号强度。实验环境被分割为1 m×1 m的网格结构，对在进行WIFI信息的采集过程中的人员走动不受限制，同时充分考虑在教学楼内进行实验的人员日常行动习惯以及空气湿度对于WIFI信息采集的影响，分多个时段进行WIFI信息采集。

在室内定位空间内的同一位置测量的WIFI信号强度会因为室内空间的干扰，在指纹库里产生不稳定的波动数据值，这些不稳定值对室内定位的准确性以及误差均存在着干扰。本文通过采用高斯分布模型进行数据筛选，从采集的数据中筛选出高准确率的数据，对所选择数据进行求取几何平均数即可得到高斯滤波结果。

RSSI服从 $\left(0，{\mu }^{2}\right)$ 分布，其概率密度公式如下：

$F\left( {{\rm{RSSI}}} \right) = \frac{1}{{\sigma \sqrt {2{\rm{{\text{π}} }}} }} \cdot {{\rm{e}}^{\frac{{{{\left( {{\rm{RSSI}} - \mu } \right)}^2}}}{{2{\sigma ^2}}}}}$

式中： $\mu $ 为均值， ${\sigma ^2}$ 为方差。

$\mu {\rm{ = }}\frac{1}{N}\sum\limits_{i = 1}^N {{\rm{RSSI}}} $

$\sigma = \sqrt {\frac{1}{{N - 1}} \cdot \sum\limits_{i = 1}^N {{{\left( {{\rm{RSSI}} - \mu } \right)}^2}} } $

针对因为噪声等因素干扰而产生的RSSI值波动，本文对于传统的高斯滤波进行改进，具体步骤如下。

1)输入采集样本值。为了避免噪声的干扰，在进行信息采集时应当进行多次采集。

2)高斯滤波。对于第一部分的样本值引入高斯模型滤波处理，选取概率空间为90%以内。

3)小概率样本值处理。通过高斯滤波技术可以有效地对小概率空间样本值进行剔除，设置小概率空间集合为W，集合空间内的样本数为k：

$W = \left\{ {{\rm{RSS}}{{\rm{I}}_1},{\rm{RSS}}{{\rm{I}}_2}, \cdots ,{\rm{RSS}}{{\rm{I}}_k}} \right\}$

对于集合空间内的样本值进行赋值：

${\rm{RSS}}{{\rm{I}}_j} = \frac{1}{{N - 1}}\sum\limits_{i = 1}^{N - k} {{\rm{RSS}}{{\rm{I}}_i}} $

式中 ${\rm{RSS}}{{\rm{I}}_j}$ 为集合W中的数据， $j = 1,2, \cdots ,k$ 。

4)输出结果降噪。通过滤波技术将小概率空间的数据赋值后，再通过样本选取标准将其汇入大概率空间的样本数据中，最终保存在离线指纹库中。

2 IMMPF的定位算法 2.1 系统模型

为了方便我们研究在NLOS环境中的定位问题，设定系统的状态方程为

${{{X}}_k} = {{A}}{x_{k - 1}} + {{B}}{u_{k - 1}} + {{{\omega }}_{k - 1}}$

式中：X为状态向量；A为转换矩阵，其维数为 $n \times n$ 阶；B为转换矩阵； $\omega $ 为系统噪声输入。

当测量值为Z时，则测量值和状态值之间的关系为

${{{Z}}_k} = {{H}}{{{X}}_k} + {{{v}}_k}$

式中：H为系统的转换矩阵，其维数为 $m \times n$ 阶； ${v_k}$ 为系统的测量噪声。

设V(k)为观测噪声量，对LOS环境以及NLOS环境下的噪声量进行分解，LOS环境下服从 $\left( {0,\sigma _{L,m}^2} \right)$ 分布，NLOS环境下服从 $\left( {\nabla {d_m},\sigma _{N,m}^2} \right)$ ； $\nabla d$ 为距离差变量，其数值大于等于0。则概率密度函数可表示为

${p_{i,m}}(k) = \left\{ \begin{array}{l} \propto \left( {0,\sigma _{L,m}^2} \right),\quad\quad k = 1 \\ \propto \left( {\nabla {d_m},\sigma _{N,m}^2{\rm{ + }}\sigma _{L,m}^2} \right),\quad\quad k = 2 \\ \end{array} \right.$

考虑到多信道模型，本文在其中加入了信道状态量

${{x}}(k) = \left[ {\begin{array}{*{20}{c}} {{{{x}}_i}(k)}&{{{{x}}_{{\rm{LOS}}}}(k)}&{{{{x}}_{{\rm{NLOS}}}}(k)} \end{array}} \right]$

式中： ${{{x}}_i}(k)$ 为运动目标参数向量； ${{{x}}_{{\rm{LOS}}}}(k)$ 和 ${{{x}}_{{\rm{NLOS}}}}(k)$ 分别为对应情况的距离差变量向量，有

${{x}}(k) = {\left[ { {{{{x}}_i}(k)}\quad{{{{x}}_{{\rm{LOS}}}}(k)}\quad{{{{x}}_{{\rm{NLOS}}}}(k),{{{y}}_i}(k)}\quad{{{{y}}_{{\rm{LOS}}}}(k)}\quad{{{{y}}_{{\rm{NLOS}}}}(k)} } \right]^{\rm{T}}}$

通过经验可知，在实际的定位过程中，NLOS环境的量化噪声远远高于LOS环境。所以，对于定位参数的精准设定难以实现。

分别对NLOS和LOS环境测量噪声概率分布均值进行建模

${{{x}}_{{\rm{LOS}}}}(k) = {\left[ {\Delta {{\hat d}_{1,2}}\begin{array}{*{20}{c}} {(k)}&{\Delta {{\hat d}_{1,3}}(k)}& \cdots &{\Delta {{\hat d}_{1,M}}(k)} \end{array}} \right]^{\rm{T}}}$

${{{x}}_{{\rm{NLOS}}}}(k) = {\left[ {\Delta {{\hat d}_{2,2}}\begin{array}{*{20}{c}} {(k)}&{\Delta {{\hat d}_{2,3}}(k)}& \cdots &{\Delta {{\hat d}_{2,M}}(k)} \end{array}} \right]^{\rm{T}}}$

式中 $\Delta {\hat d_{1,M}}(k)$ 为LOS情况中的测量误差均值，在理论上这个数值应当是0，但在实际环境中考虑多径干扰影响，这个数值接近于0，但不是0。

2.2 IMMPF算法

由于实际的复杂空间室内定位运动模式的不确定性，室内运动目标运动状态难以确定。传统的单模型算法在复杂空间的室内定位中无法对定位目标进行实时性跟踪，导致在空间进行跟踪定位时精度较差，难以实现工程应用。多模型(multiple model，MM)算法其核心思想是对室内空间运动目标进行多点运动模式跟踪定位。在多模型算法中，以交互多模型算法为主流。交互多模型算法是具有较高实用价值的代表性算法，其在多模型的基础上，对模型数据集里的模型进行加权，通过设定似然函数和Markov模型转移并结合各个模型进行运算。

交互多模型算法主要分为输入交互、状态滤波、模型概率更新和状态输出这4个模块。交互多模型算法通过采用运动模型集对物体运动模式进行描述，通过计算转移概率模型完成输入交互，在进行输入交互以后进行交互多模型的输入，对概率状态模型进行更新，得到多个模型状态和对应协方差的状态估计值并将结果输出。

假设相应的Markov模型的转移概率矩阵 ${{T}}{\rm{ = }}\left[ {{{\pi} _{ij}}} \right]$ ( $i,j = 1,2, \cdots ,m$ )和各模型概率矩阵 ${{U}}{\rm{ = }}\left[ {u_{i,k}^n} \right]$ ( $i = $ $ 1,2, \cdots , m;n = 1,2, \cdots ,N$ )，其中，m为模型数，N为粒子数。IMMPF的具体运算流程^[13]如下。

1)随机抽取粒子。依据室内定位系统中粒子的状态，设定粒子的状态值和协方差为 $\left\{ {\widehat x_{i,k|k}^n,\widehat p_{i,k}^n} \right\}$ 。

2)输入交互。对系统中的粒子进行交互输入。

$\bar x_{j,k|k}^n = \sum\limits_{i = 1}^m {\hat x_{i,k|k}^n{u_{i|j,k|k}}} $

$\bar p_{j,k|k}^n = \sum\limits_{i = 1}^m {{u_{i|j,k|k}}} \left\{ {\hat p_{i,k|k}^n + \left[ {\begin{array}{*{20}{c}} {\bar x_{i,k|k}^n}&{ - \hat x_{j,k|k}^n} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\bar x_{i,k|k}^n} \\ { - \hat x_{j,k|k}^n} \end{array}} \right]} \right\}$

式中： $u_{i\left| {i,k\left| k \right.} \right.}^n = \displaystyle\frac{1}{{\bar c_j^n}}{\pi _{ij}}u_{i,k}^n$ ； $\bar c_j^n = \displaystyle\sum\limits_{i = 1}^m {{\pi _{ij}}u_{i,k}^n}$ 。

3)模式匹配粒子滤波器。将 $\left\{ {\bar x_{j,k|k}^n,\bar p_{j,k|k}^n} \right\}$ 代入基于第j个概率模型的粒子滤波器，此时我们可以获得相应的粒子状态变量 $\bar x_{j,k{\rm{ + }}1|k{\rm{ + 1}}}^n$ 及其协方差 $\bar p_{j,k + 1|k + 1}^n$ 、残差 $S_{j,k{\rm{ + }}1}^n$ 、似然函数 $\varLambda _{j,k + 1}^n$ 和相应的权值 $\bar \omega _{j,k + 1}^n$ 。

4)概率模型更新。

$u_{j,k + 1}^n = \frac{1}{{{c^n}}}\varLambda _{j,k + 1}^n\bar c_j^n$

式中 ${c^n} = \displaystyle\sum\limits_{j = 1}^m {\varLambda _{j,k + 1}^n\bar c_j^n}$ 。

5)残差重抽样。复制粒子中较大的粒子，以便于减少权值产生新的样本，进而获得高效的计算和较低计算协方差。

6)输出交互。对样本空间中的粒子输出交互：

$\bar x_{j,k{\rm{ + }}1|k{\rm{ + }}1}^n = \sum\limits_{i = 1}^m {\hat x_{i,k{\rm{ + }}1|k{\rm{ + }}1}^n} {u_{j,k{\rm{ + }}1}}$

$\hat x_{j,k + 1|k + 1}^n = \frac{1}{N}\sum\limits_{n = 1}^N {x_{k + 1|k + 1}^n} $

$\begin{array}{c} \hat p_{k + 1|k + 1}^n = \displaystyle\sum\limits_{i = 1}^m {{u_{j + 1,k + 1|k + 1}}\Biggr\{ {p_{i,k + 1|k + 1}^n + } } \\ {\left[ {\begin{array}{*{20}{c}} {\bar x_{j,k + 1|k + 1}^n}&{ - \hat x_{k + 1|k + 1}^n} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\bar x_{j,k + 1|k + 1}^n} \\ { - \hat x_{k + 1|k + 1}^n} \end{array}} \right]} \Biggr\}\hat p_{k + 1|k + 1}^n = \dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^m {\hat p_{k + 1|k + 1}^n} \\ \end{array}$

2.3 对IMMPF进行改进

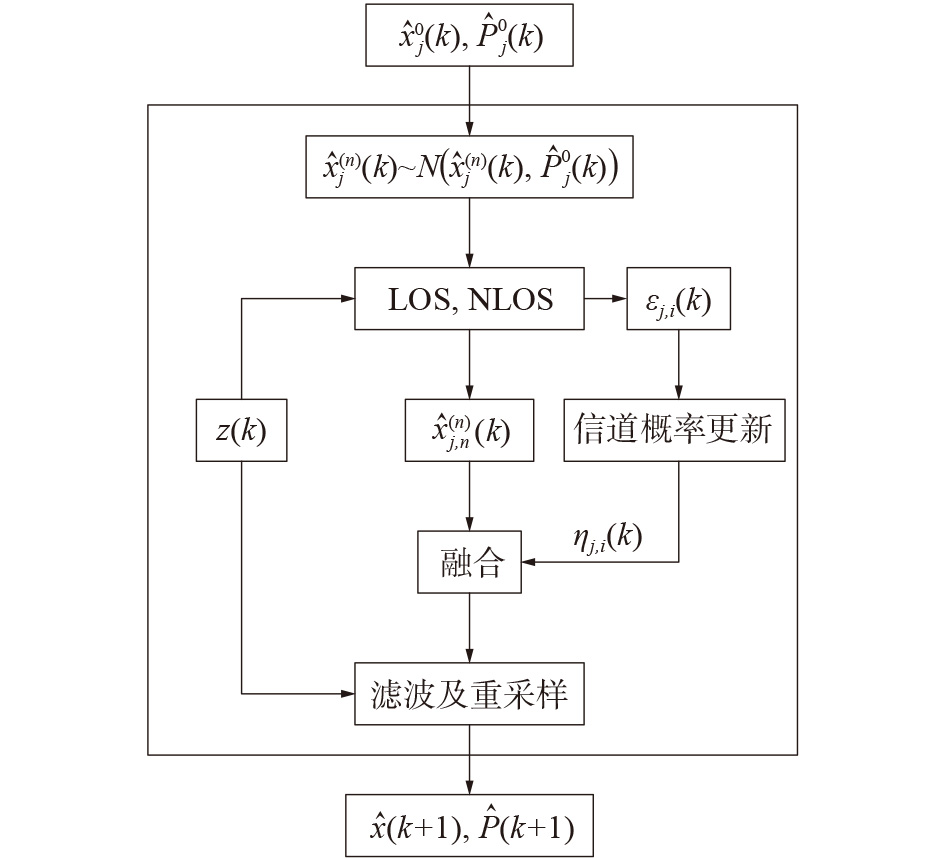
本文提出改进的IMMPF算法，在状态更新中融合了对LOS和NLOS信道参数的估计^[14]，有效地避免了NLOS干扰对于无线室内定位的结果扰动。同时，当定位目标非线性增加时，系统中的噪声会变大，IMMPF算法无法表示真实的概率密度函数分布。本文通过将改变粒子权重值向似然函数峰值靠近，通过改变粒子的权重占比以及增大粒子数目进一步改变粒子的有效性。改变似然函数的分布与粒子的权重值相对应，相对于IMMPF算法就是权值更新做自适应调整。核心算法结构框图如图2所示。

在进行模式匹配滤波器时，在其中融合了对LOS、NLOS信道参数估计，同时考虑对于异型空间室内定位出现墙体等干扰造成的NLOS环境干扰。这样可以有效避免NLOS环境中的定位误差对于定位的干扰，提高异型空间室内定位的精度。主要流程如下。

1)从k时刻初始状态中采集相应的粒子 $\hat x_{i,k|k}^n$ ，根据获得的残差分别计算相应的NLOS、LOS情况下的状态估计及相应的似然函数 $\varLambda _{j,k + 1}^n$ 。

2)根据计算出来的数值对于信道概率与信道模型进行融合

3)将结果分别进行滤波以及重采样，得到相应的目标状态更新。

根据目标运动模型，可知第j种运动模型的预测状态为

$\hat x_j^{(n)}(k + 1) = {f_i}(\hat x_j^{(n)}(k)) + {{{\omega}} _j}(k)$

式中 ${{{\omega}} _j}(k)$ 为系统噪声输入。

再根据距离差可以得到观测噪声误差为

${{e}}_{j,i,m}^{(n)}(k + 1) = {z_m}(k + 1) - {{{h}}_m}\left( {\hat x_j^{(n)}(k + 1)} \right) - \Delta \hat {{d}}_{j,i,m}^{(n)}(k + 1)$

式中： $e_{j,i,m}^{(n)}(k + 1)$ 为第m时刻误差值， ${z_m}(k + 1)$ 为此时刻测量值， ${{{h}}_m}\left( {\hat x_j^{(n)}(k + 1)} \right)$ 为系统预测值， $\Delta d$ 为距离差变量。

由计算测量噪声分布情况可以得到似然概率为

${\varepsilon _{j,i,m}}(k + 1) = N(\nabla {\overline d _{j,i,m}}(k + 1),{\sigma _{j,i,m}}^2(k + 1)\left. {} \right)$

根据IMM算法，由似然概率系数可以分别计算LOS和NLOS信道概率：

${\eta _{j,i,m}}(k + 1) = \frac{1}{{{c_{j,m}}(k)}}\varepsilon _{j,i,m}^{}(k + 1){c_{j,i,m}}(k)$

式中

${c_{j,i,m}}(k){\rm{ = }}\sum\limits_{i = 1}^2 {{\varphi _{j,i}}{\eta _{j,i,m}}} (k)$

其中， ${\varphi _{j,i}}$ 为信道模型的转移概率矩阵中的元素， ${\eta _{j,i,m}}(k)$ 为信道的概率模型。

将不同信道混合并且结合目标运动状态测量方程可以得到新的测量残差及对应的方差：

$S_{j,m}^{(n)}(k + 1) = {z_m}(k + 1) + h_m^{(n)}(k + 1) - \\ \sum\limits_{i = 1}^2 {\eta _{i,j,m}^{}(k + 1)\Delta d_{j,i,m}^{(n)}(k + 1)} $

$\sigma _{j,m}^2(k + 1) = \frac{1}{{{N_p}}}\sum\limits_{n = 1}^N {{{\left| {s_{j,m}^{(n)}(k + 1)} \right|}^2}} $

对粒子进行重采样，此时可以获得重要性权重的似然函数^[15-16]：

$\varLambda _{j,m}^n{\rm{(}}k{\rm{ + 1) = }}\frac{1}{{\sqrt {2{\text{π}} {\sigma _{j,m}}^2(k + 1)} }} \cdot \\ \exp ( - {\left| {s_{j,m}^{(n)}(k + 1)} \right|^2}/2\sigma _{j,m}^2(k + 1))$

对于多径的联合重要性权重：

$s_j^{(n)}(k + 1) = \varLambda _j^{(n)}\prod\limits_{m = 1}^{M - 1} {\varLambda _{j,m}^{(n)}(k + 1)} $

对于重要性权重进行归一化处理以及重采样，可以得到新的状态估计以及误差协方差矩阵。

3 实验与仿真与结果分析

为验证本文所提算法的定位误差，对于IMMPF算法、交互式多模型扩展卡尔曼滤波（interactive multiple model extended Kalman filtering，IMMEKF）算法以及改进的IMMPF算法分别在定位空间内进行仿真实验。这里的匀速模型为

${{F}}\left( {{x_i}} \right) = \left[ {\begin{array}{*{20}{c}} 1&t&0&0 \\ 0&1&0&0 \\ 0&0&1&t \\ 0&0&0&1 \end{array}} \right] \cdot {x_i}$

匀速转弯模型为

${{F}}\left( {{x_i}} \right) = \left[ {\begin{array}{*{20}{c}} 1&{\dfrac{{\sin \omega }}{\omega }}&0&{\dfrac{{\cos \omega - 1}}{\omega }} \\ 0&{\cos \omega }&0&{ - \sin \omega } \\ 0&{\dfrac{{1 - \cos \omega }}{\omega }}&1&{\dfrac{{\sin \omega }}{\omega }} \\ 0&{\sin \omega }&0&{\cos \omega } \end{array}} \right] \cdot {x_i}$

量测模型为

${{{Z}}_k} = \left[ {\begin{array}{*{20}{c}} {\sqrt {x_i^2 + y_i^2} } \\ {\arctan \left( {\dfrac{{{y_i}}}{{{x_i}}}} \right)} \end{array}} \right]$

目标初始的状态向量 ${{{X}}_0} = \left[ {\begin{array}{*{20}{c}} {20}&2&{15}&1 \end{array}} \right]$ ，采样点间隔T=1 s，转弯速率 $\omega $ =0.1 rad/s，粒子总数N=100。第一次实验过程运动整体为匀速运动状态：匀速直线运动和匀速转弯，这里采用2种运动模型进行仿真，仿真图3为在L型空间内定位仿真。

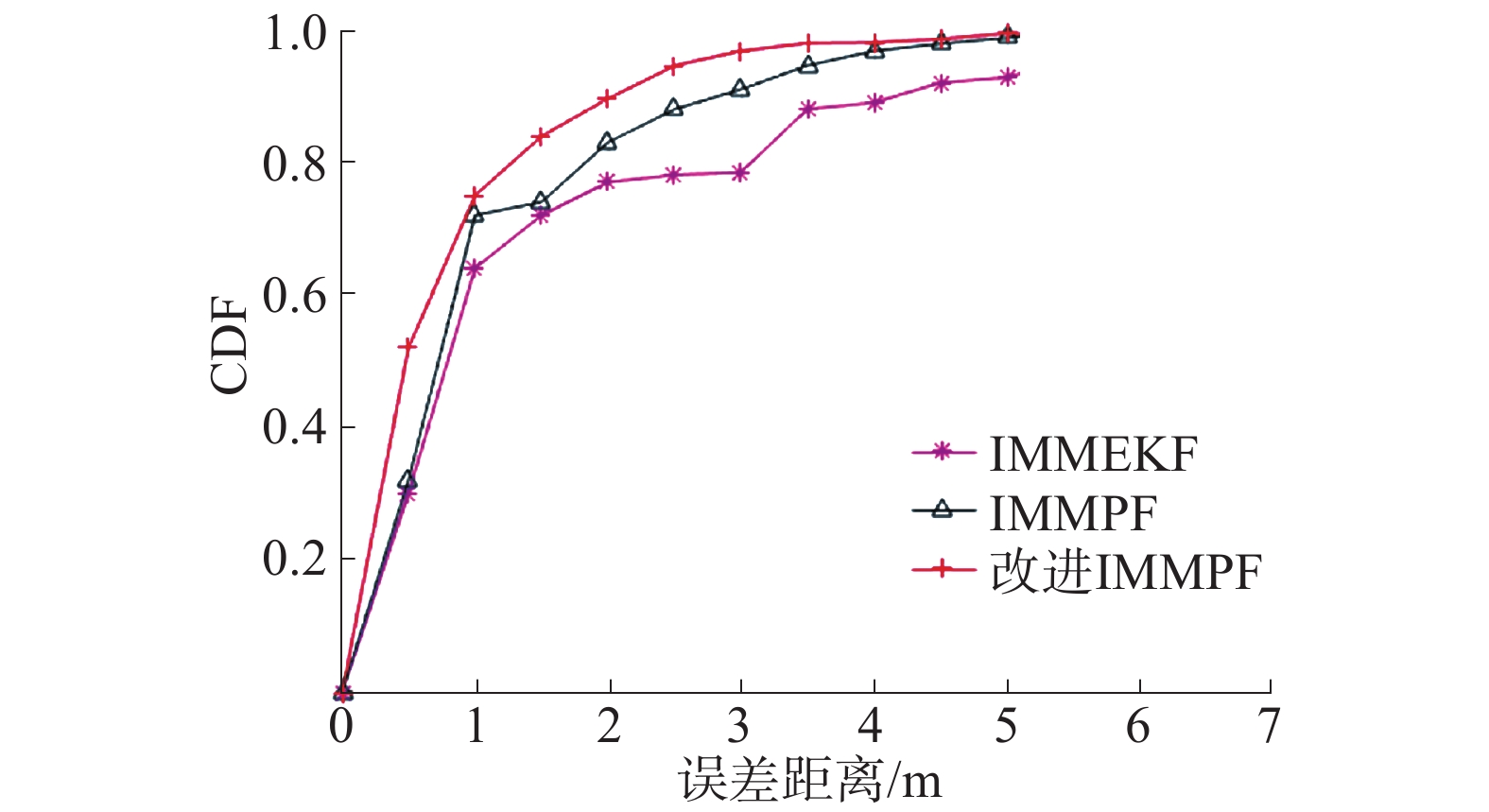
由图3可以得知，在定位的起始点，其定位的波动性比较大，主要是由于定位初期获取信息较少，会出现较大的跟踪误差。随着粒子不断更新，最终误差稳定在1~2 m。针对IMMFP、IMMEKF和改进的IMMFP这3种定位算法，分析每个定位点的位置误差，如图4所示。在各种定位算法中，定位平均误差数据如表1所示。

从表1可以看出，在各种定位算法中，平均定位误差最低的是改进IMMPF融合定位算法，平均误差为1.38 m。平均定位误差的定位精度比传统的IMMPF算法提高26.984%，比传统IMMEKF算法提高了36%，从而证明了该融合算法的有效性。

图5与图6分别为误差累积图以及改变粒子数目的定位误差图。

由图6可以看出，当粒子数目适当增大时，可以通过增大粒子滤波算法执行时间提高定位精度。但是粒子数目不是无限增大的，当粒子数目增大一定数目时，会增加预测时间和粒子的更新时间。

经由上述结果可以得出：对于复杂空间的定位，非视距和多径效应等干扰，传统IMMEKF定位算法不能很好地适用于定位环境中；IMMPF定位算法更适用于多变的环境中，定位精度较高。

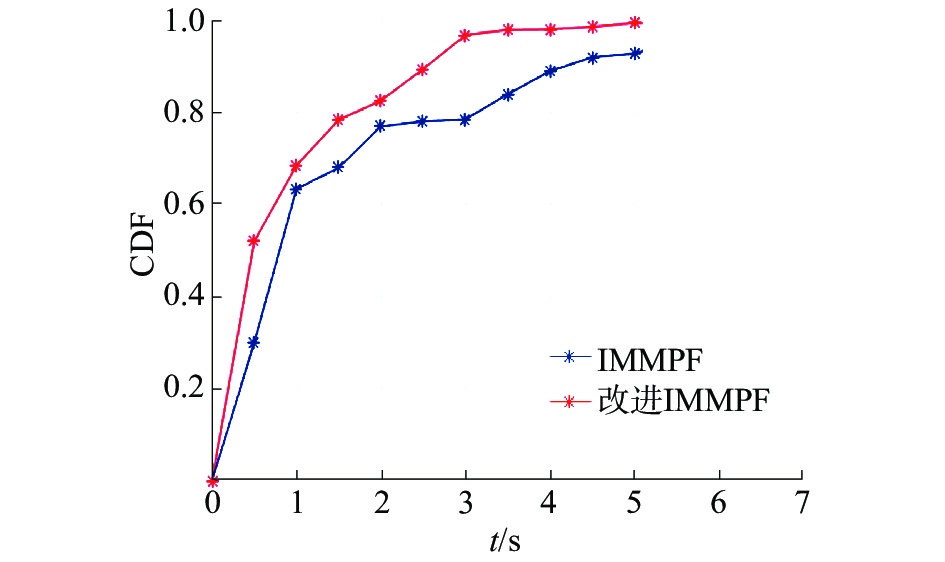
为了进一步验证改进的IMMPF定位算法效果，改变物体的运动模式进行实验验证。保持其他采样条件不变，改变物体的运动模式，先进行匀加速直线运动，转弯；然后进行匀速直线运动，得到定位仿真如图7—图9所示。

4 结论

目前，可以依靠卫星系统等实现室外高精度定位，但由于存在墙体、多径效应以及NLOS干扰问题，卫星系统等无法应用于复杂的室内环境，进而无法应用在室内定位技术中。

1)针对NLOS环境，研究了室内WIFI信号在室内空间的动态变化。基于传统的高斯滤波算法改进得到的滤波算法，可以有效地对RSSI奇异值进行处理，并且可以避免数据丢失对定位的影响，验证了本文所提定位算法的有效性。

2)考虑到复杂空间内定位目标运动的复杂性，在交互多模型中，利用粒子滤波在定位中的实时性更新中混合信道参数同时对于NLOS及其LOS混合信道进行参数估计，同时改变粒子权重值向似然函数靠近，及时通过扩大粒子的权重占比和增大粒子数目，以改变粒子的有效性，这样提高了改进算法的定位准确性。

通过实际环境对改进的IMMPF定位算法进行仿真实验，对于室内目标进行跟踪定位，充分考虑到室内目标运动具有多种模式、复杂环境的NLOS干扰以及粒子枯竭问题。在目标环境较为复杂时，改进的交互多模型粒子滤波算法可以对于定位得到达到次优解中的最优结果。通过实验仿真可以看出，改进的IMMPF算法能够很好地在异型复杂环境中实现高精度定位，且该算法可以在复杂环境实现多种模式跟踪定位，对于无线电监测和管理工作具有重要意义。