随着我国变电站六氟化硫(SF6)充气设备的广泛使用,其SF6气体泄漏检测与维护成为变电站运维的一项重要工作。传统人工检测危险性高、检测效率低、检测效果不稳定[1]。本文研究提出利用先进移动机器人技术开展变电站电流互感器及断路器中SF6气体泄漏的检测。考虑到变电站路面相对狭窄、有台阶障碍、硬质水泥路面或松散砂石路面以及电力设备位置较高的环境条件约束[2],变电站SF6泄漏检测机器人系统采用履带车搭载绝缘云梯、机械臂和检测仪器的方案。履带车具有越障和爬坡性能好的特点,但转向过程中的滑移问题导致其运动精度低,难以快速准确地调整方位。
变电站电流互感器与断路器检测点位置较高,作业范围狭窄。履带车需要频繁地低速小半径转向以靠近作业目标位置,此时其转向滑移误差大,速度不稳定,履带车不能快速准确地到达作业位置,降低了检测效率。因此有必要针对履带车低速小半径转向力学模型进行分析。
基于简化模型的履带车转向模型未考虑履带车的滑移和滑转,精度不高。而考虑滑移和滑转及地面状况的履带车滑移转向地面力学模型[3–8]过于复杂,无解析解,采用数值解法则耗费时间长,不满足控制器实时性要求。中国北方车辆研究所提出了打滑修正系数替代滑移率的方式[9],但解出该打滑系数仍然需要求解超越方程,求解时间长;基于滑移参数实时估计的方法[10–13]解决了短时间内固定转向速度下计算的实时性和精度的问题,但在狭窄区域小半径转向工作状态下速度不稳定,会造成其滑移参数估计误差偏大。陆军装甲兵学院和中国北方车辆研究所[14]使用模糊PID算法等抑制滑移现象,在高速较大半径下轨迹精度较高,但对低速小半径转向下的精度还待研究。本文针对现场实验中履带车实际工况,建立履带车的低速小半径滑移转向运动学模型,利用径向基神经网络拟合任意曲线的特性[15],拟合履带车滑移转向运动模型,实现了基于RBF的履带车正逆运动学建模与求解,最后将该模型应用于变电站检测机器人系统的履带车控制并开展了样机实验。
1 履带车低速小半径滑移转向建模图1所示为变电站环境图。在变电站内,电流互感器检测点位置较高,作业范围狭窄。检测作业过程:履带车移动到作业电流互感器附近;装置被举升到作业高度;检测机械臂带动检测装置环绕电流互感器检测。为完成检测作业,履带车需在复杂,狭窄的环境内移动,需要频繁地低速小半径转向调姿,此工况下机器人转向滑移误差大,速度不稳定,机器人不能准确靠近作业位置,检测效率低。因此有必要针对履带车低速小半径转向模型进行分析。

|
Download:
|
| 图 1 变电站环境图和履带车 Fig. 1 Substation environment and tracked vehicle | |
为了建立硬质地面环境履带车转向模型,进行如下假设:
1) 变电站内机器人低速转向,忽略离心力对履带上载荷分布的影响,不计履带张力变化对接地段压力的影响;
2) 地面被认为是坚实的,忽略履带下沉和相应的横向推土力;
3) 剪应力沿履带纵向的分量构成牵引力,沿横向分量构成履带横向阻力。横向阻力对车体几何中心取矩构成转向阻力矩;
4)履带车在水平面内做匀速转向时,转向中履带机器人行驶阻力系数保持不变。
1.1 滑移转向的运动学建模基于硬质地面力学建模方法[6-8],建立履带式移动机器人的地面力学模型。
履带机器人在硬质地面上转向,可视为平动刚体,建立全局坐标系xoy为,车体形心O初始位置位于全局坐标系的x轴上,转动瞬心Oxoy为全局坐标系坐标原点。履带卷绕速度为vqi (i=1,2)。
机器人转向时内外两侧履带中心线Oi′(i=1,2)处的牵引速度
| ${{v}}'_{{O_i}} = \Bigg({l_{oso}} \pm \frac{B}{2}\Bigg)\dot \theta \begin{array}{*{20}{c}} {}&{(i = 1,2)} \end{array}$ | (1) |
式中:
| $\begin{array}{l} \Bigg({{{l}}_{oso}} - \dfrac{{{B}}}{2} - {{{A}}_1}\Bigg){{\dot \theta}} = {{{v}}_{q1}} \\ \Bigg({{{l}}_{oso}} + \dfrac{{{B}}}{2} + {{{A}}_2}\Bigg){{\dot \theta}} = {{{v}}_{q2}} \\ \end{array} $ | (2) |
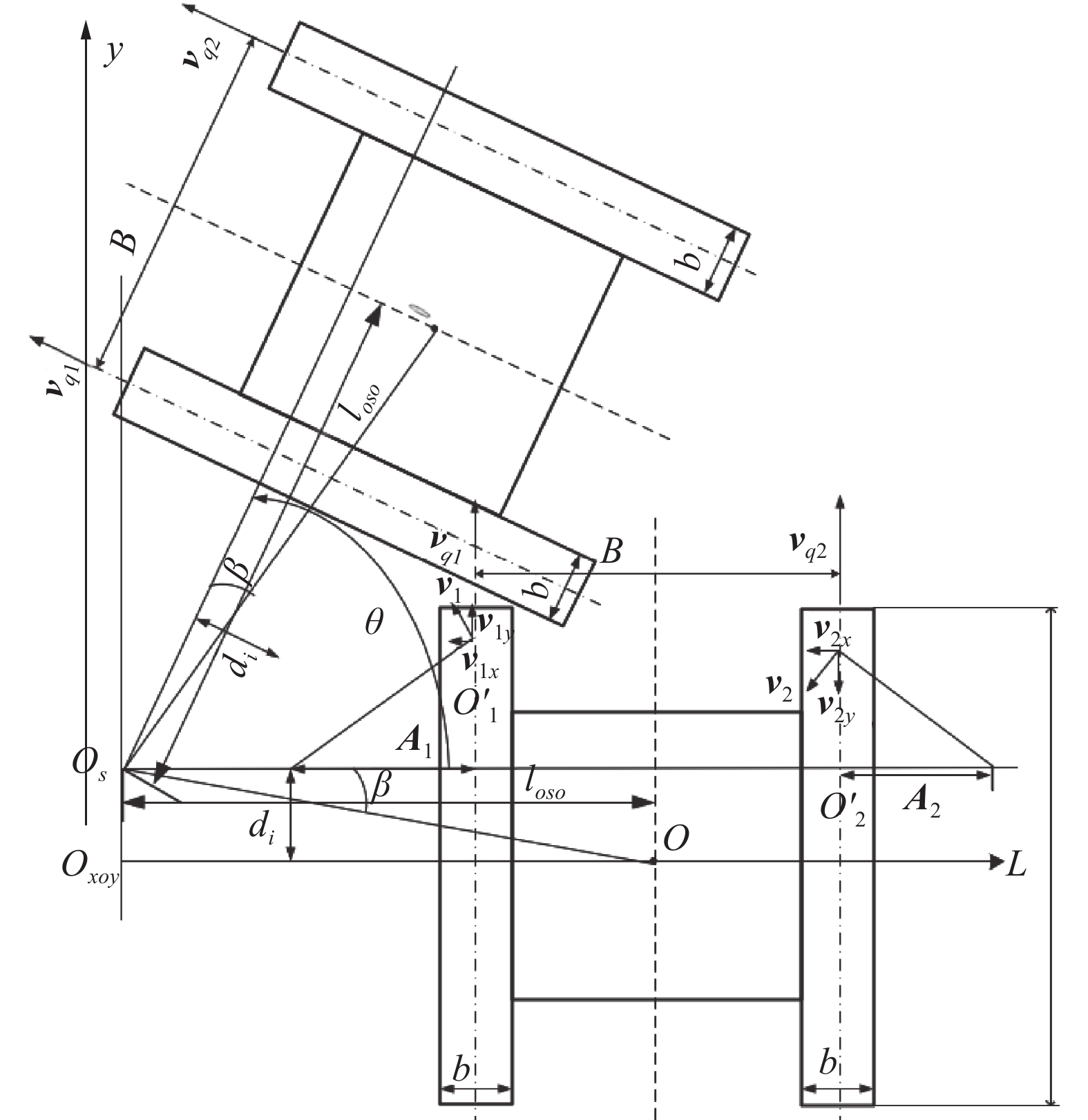
图2给出了低速履带与滑移转向模型。
|
Download:
|
| 图 2 低速履带车滑移转向模型 Fig. 2 Skid steering model of a low speed tracked vehicle | |
根据图2中的运动学关系,可以求履带车在滑移/滑转下实际转向半径:
| ${{R}} = \sqrt {{{l}}_{oso}^2 + d_l^2} $ | (3) |
式中:履带的速度瞬心
| ${{R}} = \sqrt {{{\Bigg(\frac{{({{{v}}_{q2}} + {{{v}}_{q1}})({{B}} + {{{A}}_1} + {{{A}}_2})}}{{2({{{v}}_{q2}} - {{{v}}_{q1}})}} + \frac{{{{{A}}_1} + {{{A}}_2}}}{2}\Bigg)}^2} + d_i^2} $ | (4) |
| ${{\dot \theta}} = \frac{{{{{v}}_{q2}} + {{{v}}_{q1}}}}{{{{B}} + {{{A}}_1} + {{A}}_2}}$ | (5) |
引入滑转率,计算公式为
| ${{{\delta}} _i} = \frac{{{{{v}}_{qi}} - {{{v}}_{O'_i}}}}{{{{{v}}_{qi}}}} = \frac{{{{{A}}_i}}}{{{{{v}}_{qi}}}}{{\dot \theta}} $ | (6) |
基于式(1)~(6),建立履带机器人运动学方程为式(7),其中,
| $\left[ \begin{array}{l} {{{v}}_O} \\ {{{\dot \theta}} } \\ \end{array} \right] = \frac{1}{{{{B}} + {{{A}}_1} + {{{A}}_2}}}{{A}}\left[ \begin{array}{l} {{{v}}_{q1}} \\ {{{v}}_{q2}} \\ \end{array} \right]$ | (7) |
| $\begin{array}{l} {{A}} = \left[ \!\!\!\!\begin{array}{c} \begin{array}{*{20}{c}} {0.5{{B}} + {{{A}}_2}}&{0.5{{B}} + {{{A}}_1}} \end{array} \\ \begin{array}{*{20}{c}} { - 1}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{} \end{array}}&1 \end{array}} \end{array} \\ \end{array} \!\!\!\!\right] \\ {{{A}}_1} = \dfrac{{{{{v}}_O} - {{{v}}_{q1}}}}{{{{\dot \theta}} }} - 0.5{{B}} \\ {{{A}}_2} = \dfrac{{{{{v}}_{q2}} - {{{v}}_O}}}{{{{\dot \theta}} }} - 0.5{{B}} \\ \end{array} $ | (8) |
将履带车的运动学方程更改为关于滑移率的方程,即将式(6)带入式(5)和式(1),可求得
| $\begin{array}{l} {{\dot \theta}} = \dfrac{{{{{v}}_{q2}}(1 - {{\delta} _2}) - {{{v}}_{q1}}(1 + {{\delta} _1})}}{{{B}}} \\ {l_{oso}} = \dfrac{{{{{v}}_{q2}}(1 - {{\delta} _2}) + {{{v}}_{q1}}(1 + {{\delta} _1}){{B}}}}{{{{{v}}_{q2}}(1 - {{\delta} _2}) - {{{v}}_{q1}}(1 + {{\delta} _1})2}} \\ \end{array} $ | (9) |
| $\left[ \begin{array}{l} {{{v}}_O} \\ {{{\dot \theta }}} \\ \end{array} \right] = \left[ \begin{array}{l} \begin{array}{*{20}{c}} {0.5(1 + {\delta _1})}&{0.5(1 - {\delta _2})} \end{array} \\ \begin{array}{*{20}{c}} {\dfrac{{ - (1 + {\delta _1})}}{{{B}}}}&{\dfrac{{(1 - {\delta _1})}}{{{B}}}} \end{array} \\ \end{array} \right]\left[ \begin{array}{l} {{{v}}_{q1}} \\ {{{v}}_{q2}} \\ \end{array} \right]$ | (10) |
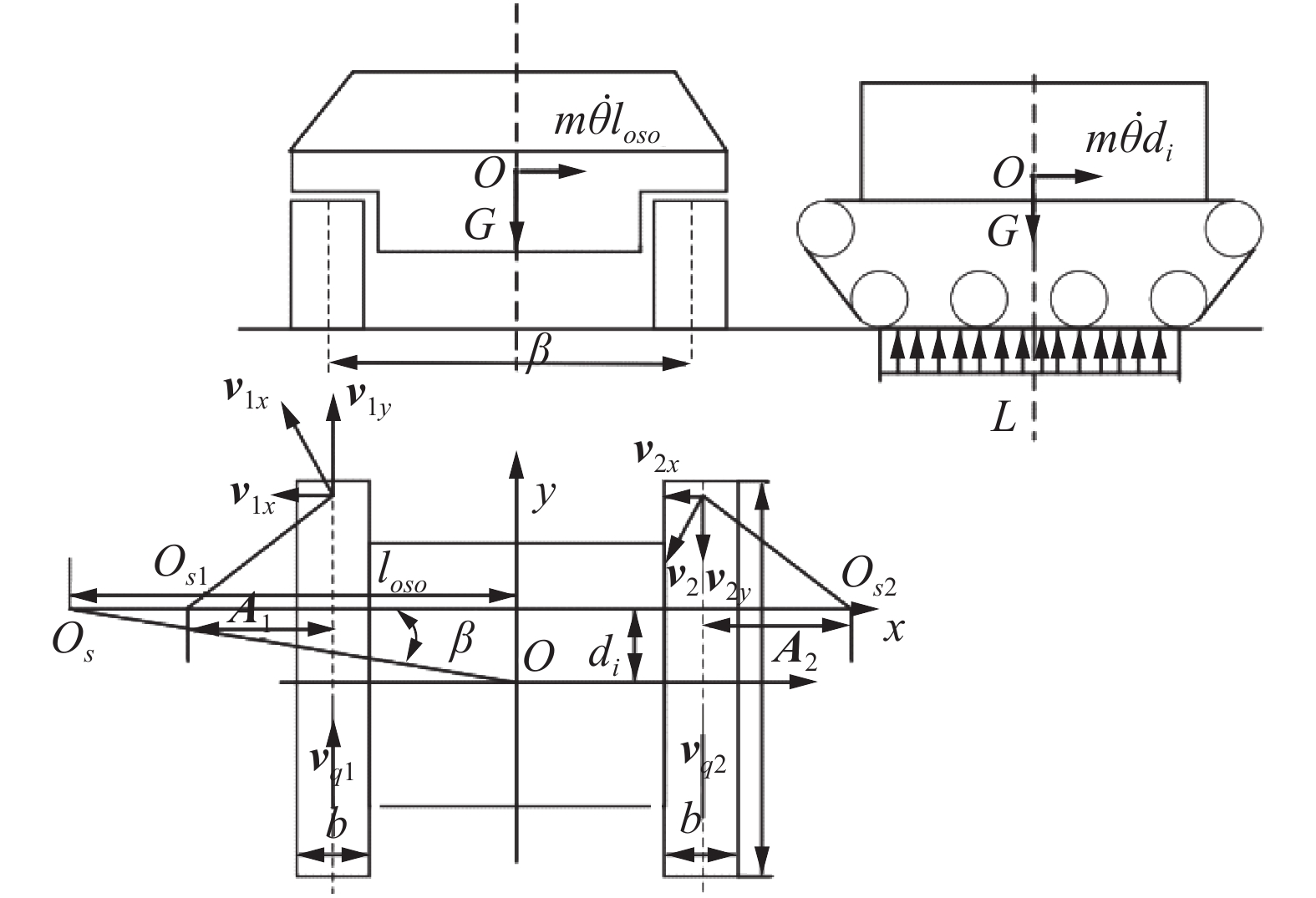
由于忽略离心力对履带上载荷分布的作用,内外履带所受重力大小是一样的。重力载荷在内外履带上呈均匀分布。履带接地段压力分布情况如图3所示。直线运动时,内外两侧履带接地段是静摩擦,相对地面速度是0;转向时,理想情况下内外两侧行走履带接地段的速度瞬心Osi(i=1,2)与该段几何中心瞬心Oi(i=1,2)重合,但实际转向时,由于履带的滑移/滑转使得行走履带接地段的速度瞬心偏离履带接地段的几何中心产生纵向和横向偏移量di和Ai (i=1,2)。实际转向中心为Osi。
|
Download:
|
| 图 3 履带车接地段压力分布情况 Fig. 3 Pressure distribution on the track | |
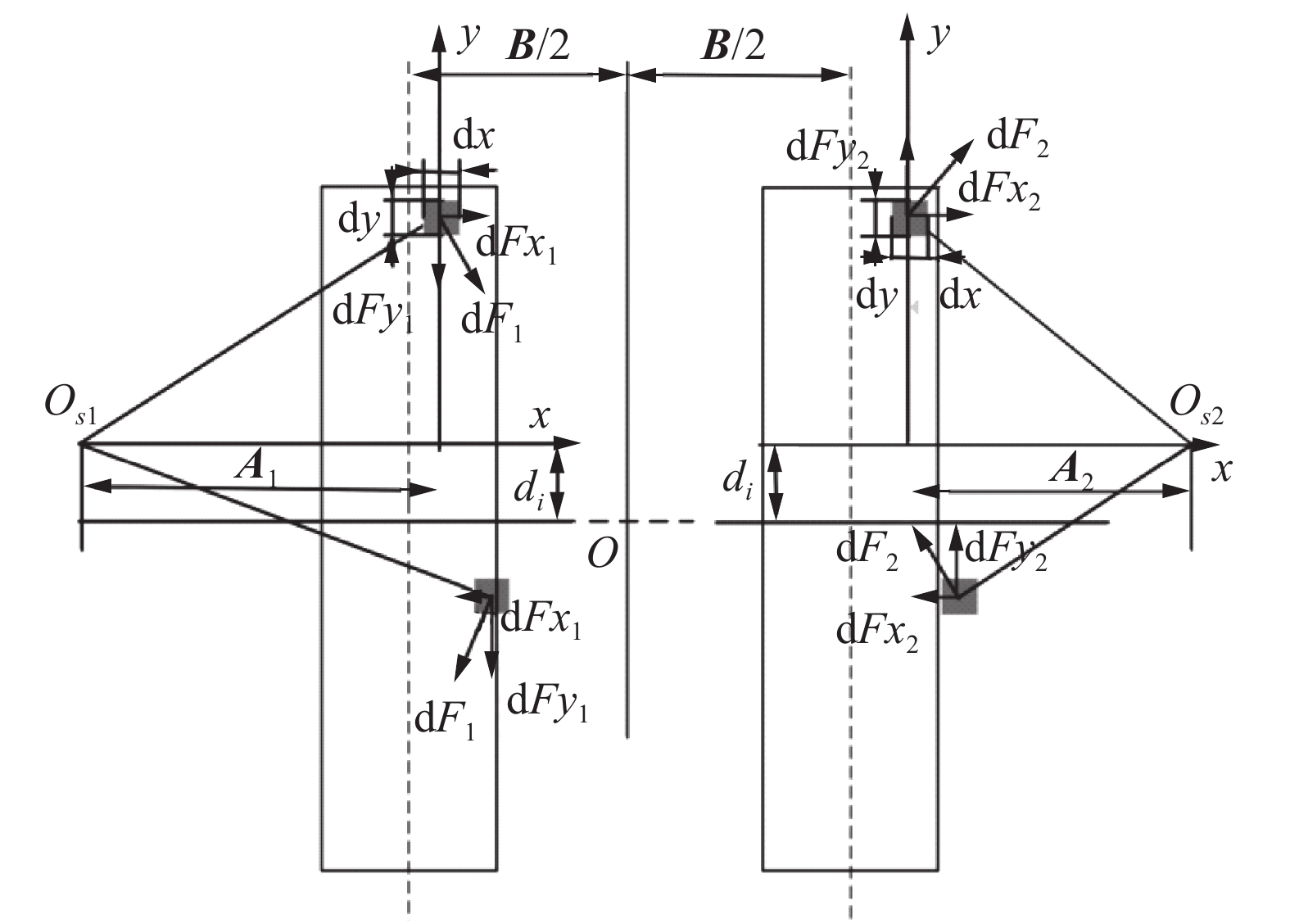
履带车转向过程中受到的阻力主要是地面的摩擦阻力。对内外两侧的履带建立坐标系如图4所示,内外两侧履带接地段dxdy微元内的压力大小为
| $p(x,y) = \frac{G}{{2Lb}}$ | (11) |
式中:L为履带接地段长度;b为履带接地段宽度。由库伦摩擦定律,履带上任一微元所受的剪应力为
| $\begin{array}{l} {\rm{d}}{{F_{X_i}}} = \mu \dfrac{G}{{2Lb}}\dfrac{y}{{\sqrt {{{\Bigg(x \pm {\delta _i}\dfrac{{{{{v}}_{qi}}}}{{{{\dot \theta}} }}\Bigg)}^2}} + {y^2}}}{\rm{d}}x{\rm{d}}y \\ {\rm{d}}{{F_{Y_i}}} = - \mu \dfrac{G}{{2Lb}}\dfrac{{x \pm {\delta _i}\dfrac{{{{{v}}_{qi}}}}{{{\theta}} }}}{{\sqrt {{{\Bigg(x \pm {\delta _i}\dfrac{{{{{v}}_{qi}}}}{{{{\dot \theta}} }}\Bigg)}^2} + {y^2}} }}{\rm{d}}x{\rm{d}}y \\ \end{array} $ | (12) |
|
Download:
|
| 图 4 履带车接地段地面摩擦阻力 Fig. 4 Ground friction resistance on the track | |
对式(12)积分得到履带在横向和纵向方向上的所受的合力为
| $\begin{array}{l} {{F_{X_i}}} = \iint {\mu \dfrac{G}{{2Lb}}}\dfrac{y}{{\sqrt {{{\Bigg(x \pm {\delta _i}\dfrac{{{{{v}}_{qi}}}}{{{{\dot \theta}} }}\Bigg)}^2} + {y^{_2}}} }}{\rm{d}}x{\rm{d}}y \\ {{F_{Y_i}}} = \iint {\mu \dfrac{G}{{2Lb}}}\dfrac{{{\delta _i}\dfrac{{{{{v}}_{qi}}}}{{{{\dot \theta}} }} \pm x}}{{\sqrt {{{\Bigg(x \pm {\delta _i}\dfrac{{{{{v}}_{qi}}}}{{{{\dot \theta}} }}\Bigg)}^2} + {y^{_2}}} }}{\rm{d}}x{\rm{d}}y \\ \end{array} $ | (13) |
积分区域为:
履带微元dxdy上剪应力对履带车的形心O取矩并积分,横向摩擦力取力矩积分得到转向摩擦阻力矩
| $\begin{array}{l} {{{M}}_f} = \iint {(x + {{{d}}_i}})({\rm{d}}F_{x_1} + {\rm{d}}F_{x_2}) \\ {{{M}}_d} = \iint {(0.5B + x){\rm{d}}F_{y_1}} + (0.5B - x){\rm{d}}F_{y_2} \end{array} $ | (14) |
履带车所受的力平衡和力矩平衡方程为
| $\left\{ \begin{array}{l} {{F_{x_1}}} + {{F_{x_2}}} = m{{\dot \theta }^2}l_{oso}^{} \\ {{F_{y_1}}} + {{F_{y_2}}} = m{{\dot \theta }^2}{d_i} \\ {{{M}}_f} - m{{\dot \theta }^2}{d_i}{l_{oso}} = {{{M}}_d} \\ \end{array} \right.$ | (15) |
由履带车运动学模型式(10)可以看出,由规划的
通过MATLAB数值仿真由
径向基神经网络(RBF),是一种前向神经网络,具有全局逼近的性质,不存在局部极小值的问题,网络对于每个输入输出数据对,只需要调整少量的权值,使得它的逼近、分类和学习速度大大优于传统的BP网络。理论上,径向基神经网络作为多层前向网络,能以任意精度逼近任意非线性映射[15-16]。广义回归神经网络(GRNN)和概率神经网络(PNN)作为径向基神经网络的变化形式,同样可以任意精度逼近非线性映射,广泛实用于语音处理、图像识别、电力系统信号处理、神经信号处理等领域[17–23]。但GRNN和PNN隐含层神经元的数目等于输入样本数,导致在拟合样本数据量较大时,其神经元数目过多[23],计算量较大,不利于在嵌入式系统中实现。综上所述,基于RBF实现履带车运动学重建。
履带车质心速度
因此,若需要采用RBF网络重建履带车的正运动学模型,只需要将履带的卷绕速度集作为模型输入样本,履带车质心速度集合作为模型输出样本,用以训练模型,则得到机器人的正向运动学模型重建。反之,将履带车质心速度集作为RBF网络输入样本,履带车相应的卷绕速度集作为RBF网络输出样本进行训练,则得到履带车的逆运动学模型重建。通过RBF重建后的正、逆运动学模型进行计算,相比于实时迭代进行数值求解机器人正、逆运动学,其计算过程简单、计算量小、耗时小,在实际运行时,可有效提高履带车的运动精度。
为提高履带车对不同地面的适应性,可针对不同地面实测摩擦系数范围,按式(1)~(15)建立其地面力学模型并使用RBF分别进行重建。因RBF模型计算量小,可同时编程实现多个模型,根据不同地面情况进行选择,从而提高履带车对不同地面状态的适应性。
3 RBF模型重建实验 3.1 实验设置设定履带车转向时左侧履带的卷绕速度在0~0.4 m·s−1,右侧履带的卷绕速度在0~0.4 m·s−1,保证是左转向的运动状态下,采取精度0.005 m·s−1设立采样点,如此共有6 400个速度对
类似地,使用左侧履带卷绕速度在区间
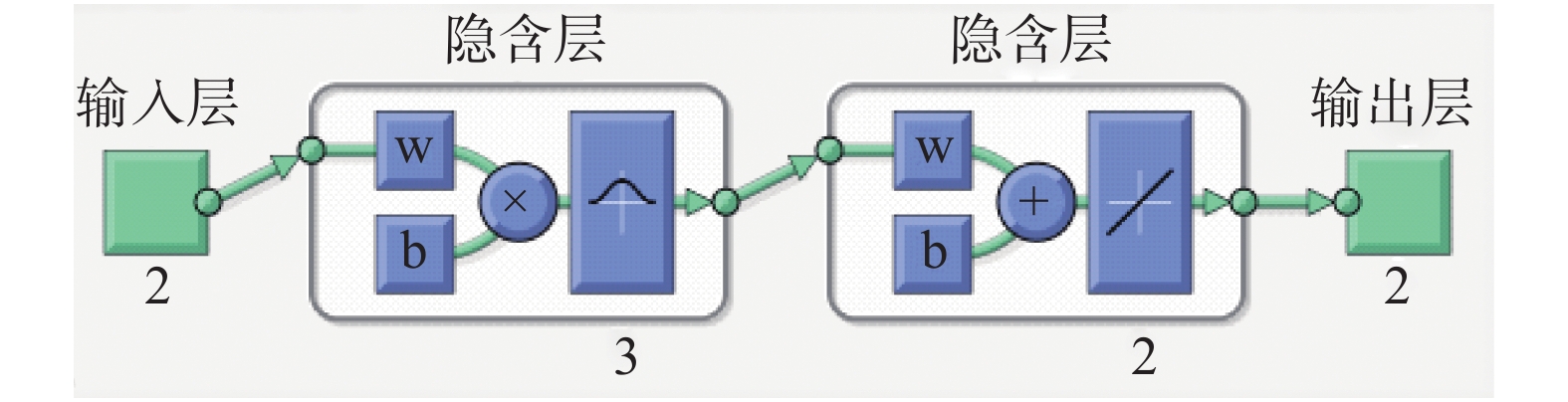
RBF模型重建结果如图5所示。重建后的神经网络结构简单,正逆运动学模型都只有两层,且每层不超过3个神经元,实现简单、计算量小。采用GRNN和PNN网络也可获得相近的精度,但所需的神经元数目为速度曲面上所取速度对的数目,共6 400个。神经元数目过大,计算量过多,不利于嵌入式控制器实现实时计算。
|
Download:
|
| 图 5 RBF正运动学模型的神经网络结构 Fig. 5 Neural network structure of RBF-based forward kinematic model | |
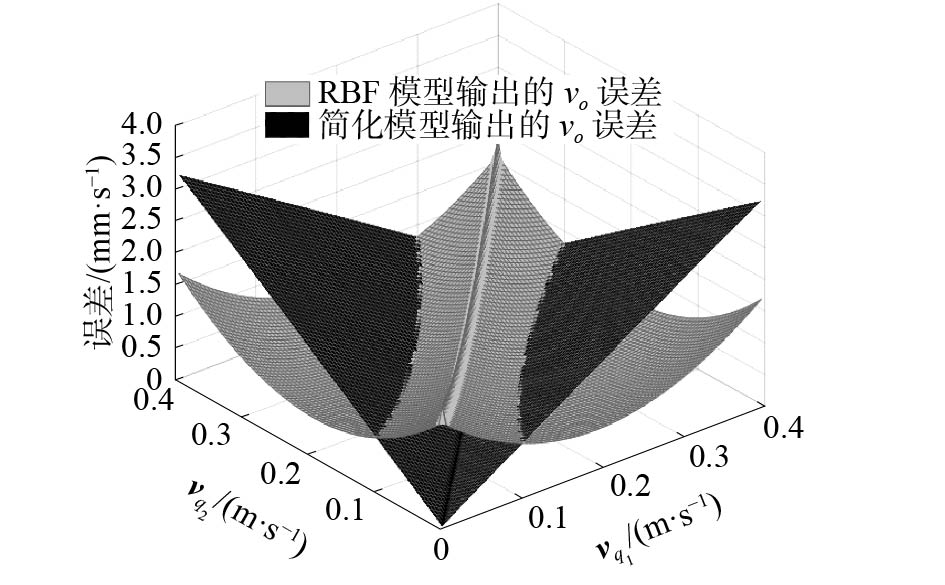
针对RBF重建的正向运动学模型进行测试,实验结果如图6和图7所示。图6中相同输入条件下,简化模型求解得到的正向运动学解
|
Download:
|
|
图 6 RBF模型与简化模型对
|
|
|
Download:
|
|
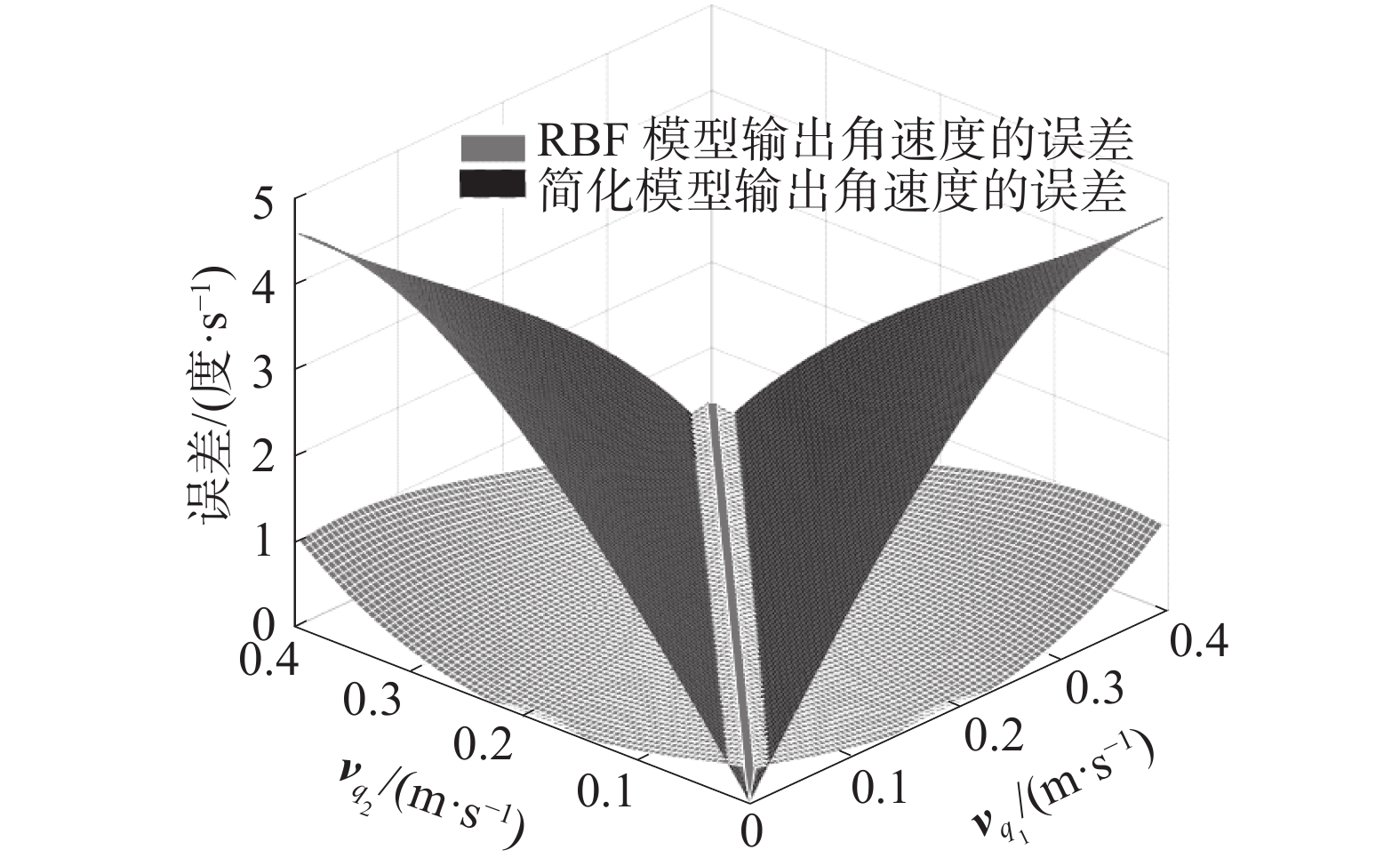
图 7 RBF正运动学模型与简化模型对
|
|
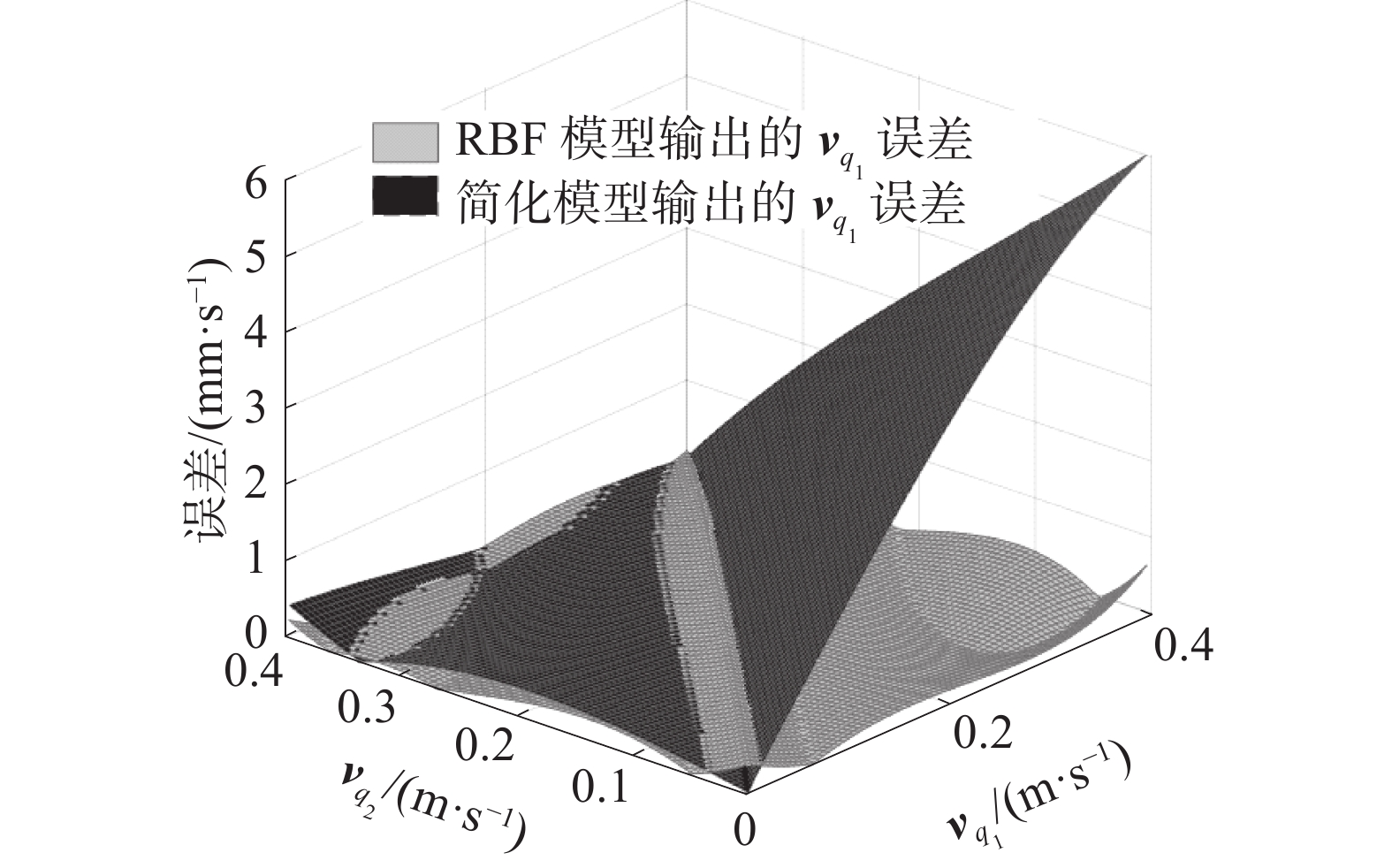
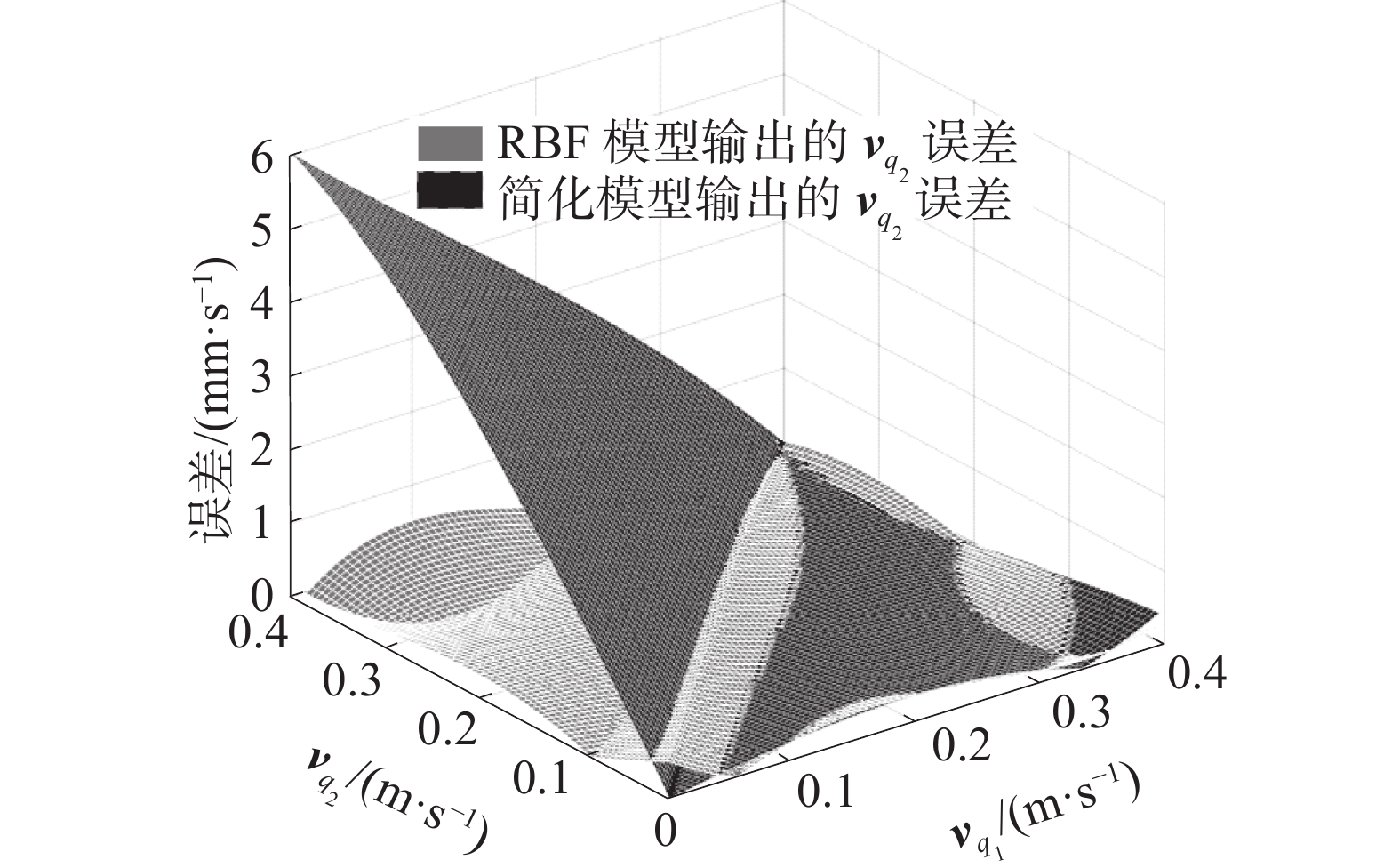
RBF重建的逆运动学模型网络仿真结果如图8、9所示。对测试集,RBF的左右履带转向输出误差也在±1 mm·s−1以内,而简化模型外侧履带(卷绕速度更大的履带)的速度误差则随着履带速度差的增大而增大,且远大于RBF模型的输出误差。与简化模型对比可确定,使用RBF重建机器人运动学模型,相比直接使用不考虑滑移的简化模型,能获得更高的精度。
|
Download:
|
|
图 8 RBF逆运动学模型与简化模型对
|
|
|
Download:
|
|
图 9 RBF逆运动学模型与简化模型对
|
|
在实验过程中,通过MATLAB建立履带车滑移转向运动学和动力学模型,对于模型参数的求解的计算时间较大。为了获得6 400个测试集内的正运动学解,简化传统的MATLAB运动学模型之后,求解时间为13.882 h,但RBF模型训练完成之后对6 400个速度点的计算为0.183 8 s,求解时间极大缩短。同时因为滑移量无法确定,滑移转向模型无法通过求微分和矩阵运算的方式,将式(1)~(15)的方程转变为逆运动学形式,则无法通过所需的履带车质心速度
基于此,采用RBF获得履带车的RBF正逆运动学模型,具有计算耗时小、模型精度高的特点,且RBF网络模型神经元数量小、模型计算所耗费的控制器资源小。
3.3 样机实验图10所示为变电站SF6泄漏检测机器人系统现场实验照片。实验任务目标是检测电流互感器中六氟化硫气体的泄漏状况。为精准检测泄漏量,履带车需进入狭窄的工作区域并快速地调整方位,到达指定的目标位置处,在此过程中,履带车处于低速小半径转向运动状态。

|
Download:
|
| 图 10 样机实验 Fig. 10 The field experiment of prototype | |
分别将前文基于RBF重建的运动学模型以及简化模型应用于现场实验中履带车的运动控制,实验结果表明,基于RBF重建的运动学模型具有求解速度快、精度高的特点,使得履带车能够快速调整方位,高效、准确地运动到目标位置,有效地提高了机器人系统的检测效率。
4 结论面向变电站复杂环境约束及SF6气体泄漏检测实际任务需求,本文针对履带车转向过程中的滑移问题开展研究。建立基于 RBF 重建的运动学模型并与简化模型进行比较分析,仿真和样机实验结果表明:
1)基于RBF的履带车滑移转向运动学重建方法具有计算耗时小、精度高的特点。
2)RBF 网络模型神经元数量小,模型计算所耗费的控制器资源少。
3)该方法应用于变电站 SF6 气体泄漏检测机器人系统的运动控制,有效提高了履带车在低速小半径转向工况下的运动精度,使其能够快速调整方位,高效、准确地运动到目标位置,进而提高了检测作业效率。
| [1] |
梁铁栓. 六氟化硫(SF6)断路器的运转维护和故障处理分析
[J]. 城市建设理论研究:电子版, 2014, 35: 2181. ( 0) 0)
|
| [2] |
高建龙. 变电站智能巡检机器人机械系统设计与巡检技术研究[D]. 北京: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2018: 1–3.
( 0) 0)
|
| [3] |
KITANO M, KUMA M. An analysis of horizontal plane motion of tracked vehicles[J]. Journal of terramechanics, 1977, 14(4): 211-225. DOI:10.1016/0022-4898(77)90035-0 ( 0) 0)
|
| [4] |
吴运耕. 试谈双履带行走装置的转弯理论和功率计算[J]. 工程机械, 1978, 1: 11-29. ( 0) 0)
|
| [5] |
刘国民, 黄海东. 履带底盘转向轨迹的研究[J]. 水利电力机械, 1998, 5: 18-21. ( 0) 0)
|
| [6] |
WONG J Y, CHIANG C F. A general theory for skid steering of tracked vehicles on firm ground[J]. Proceedings of the institution of mechanical engineers, part D: journal of automobile engineering, 2001, 215(3): 343-355. DOI:10.1243/0954407011525683 ( 0) 0)
|
| [7] |
MACLAURIN B. A skid steering model using the magic formula[J]. Journal of terramechanics, 2011, 48(4): 247-263. DOI:10.1016/j.jterra.2011.04.002 ( 0) 0)
|
| [8] |
李雨潭, 朱华, 高志军, 等. 履带机器人通用地面力学模型分析与底盘设计[J]. 哈尔滨工程大学学报, 2015, 36(8): 1126-1130. ( 0) 0)
|
| [9] |
袁艺, 盖江涛, 韩政达, 等. 履带打滑条件下的电驱动车辆转向运动学研究[J]. 车辆与动力技术, 2017, 1: 6-10. ( 0) 0)
|
| [10] |
熊光明, 鲁浩, 郭孔辉, 等. 基于滑动参数实时估计的履带车辆运行轨迹预测方法研究[J]. 兵工学报, 2017, 38(3): 600-607. DOI:10.3969/j.issn.1000-1093.2017.03.025 ( 0) 0)
|
| [11] |
李健, 王小蒙. 基于容积滤波的机器人运动模型估计方法[J]. 内蒙古师范大学学报(自然科学汉文版), 2017, 46(5): 739-743. DOI:10.3969/j.issn.1001-8735.2017.05.030 ( 0) 0)
|
| [12] |
唐思海. 基于履带式移动机器人滑移误差问题的导航修正研究[J]. 通讯世界, 2018, 4: 264-265. DOI:10.3969/j.issn.1006-4222.2018.04.166 ( 0) 0)
|
| [13] |
姜岩, 王琦, 龚建伟, 等. 无人驾驶车辆局部路径规划的时间一致性与鲁棒性研究[J]. 自动化学报, 2015, 41(3): 518-527. ( 0) 0)
|
| [14] |
张舒阳, 张豫南, 宁克焱, 等. 高速重载履带车辆制动滑移控制研究[J]. 火力与指挥控制, 2018, 43(6): 52-56. DOI:10.3969/j.issn.1002-0640.2018.06.010 ( 0) 0)
|
| [15] |
邓春梅, 陈吉红. 径向基神经网络重建自由曲面的探讨[J]. 计算机辅助设计与图形学学报, 2000, 12(10): 782-788. DOI:10.3321/j.issn:1003-9775.2000.10.013 ( 0) 0)
|
| [16] |
卢涛, 陈德钊. 径向基网络的研究进展和评述[J]. 计算机工程与应用, 2005, 41(4): 60-62. DOI:10.3321/j.issn:1002-8331.2005.04.019 ( 0) 0)
|
| [17] |
KHOKHAR S, MEMON A P, KEERIO M U, et. al. A simple methodology for the automatic classification of waveform distortion problems using wavelet transform and pnn-rbf-mlp neural networks[J]. 2014, 10: 2359–2367.
( 0) 0)
|
| [18] |
WU J D, YE S H. Driver identification using finger-vein patterns with Radon transform and neural network[J]. Expert systems with applications, 2009, 36(3): 5793-5799. DOI:10.1016/j.eswa.2008.07.042 ( 0) 0)
|
| [19] |
MIRZAEI M, KADIR M Z A A, HIZAM H, et. al. Comparative analysis of probabilistic neural network, radial basis function, and feed-forward neural network for fault classification in power distribution systems[J]. Electric power components and systems, 2011, 39(16): 1858-1871. DOI:10.1080/15325008.2011.615802 ( 0) 0)
|
| [20] |
PREETHI G, SORNAGOPAL V. MRI image classification using GLCM texture features[C]//2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE). Coimbatore, India, 2014: 1–6.
( 0) 0)
|
| [21] |
NIRMAL J, ZAVERI M, PATNAIK S, et. al. Voice conversion using general regression neural network[J]. Applied soft computing, 2014, 24: 1-12. DOI:10.1016/j.asoc.2014.06.040 ( 0) 0)
|
| [22] |
SANGEETHA P. Brain tumor classification using PNN and clustering[J]. International journal of innovative research science, engineering and technology, 2014, 3:796−803.
( 0) 0)
|
| [23] |
熊鹏文, 雷耀, 李鸣. 基于GRNN的人机交互下遥操作力预测方法[J]. 东南大学学报(自然科学版), 2018, 48(6): 1130-1136. ( 0) 0)
|
| [24] |
王铠, 张彩明. 重建自由曲面的神经网络算法[J]. 计算机辅助设计与图形学学报, 1998, 3: 2-8. DOI:10.3321/j.issn:1003-9775.1998.03.001 ( 0) 0)
|
 2020, Vol. 47
2020, Vol. 47


