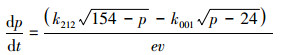阀门在出厂前都已经做过了泄漏率试验,泄漏率必须小于国标对应的要求才能算是合格产品[1]。阀门安装到系统上以后,运行的介质、温度、压力等各不相同,温度、压力经常变化的系统中阀门的密封面容易发生形变[2],而运行介质如果杂质含量较多常常会附着在阀门的密封面上,这两种情况都可能导致阀门的密封面失效,阀门的泄漏率增加,另外如果阀门机械卡涩,也有可能导致阀门操作不到位,同样会导致阀门的泄漏率增加。阀门泄漏率的增加,不仅会导致工厂经济性的下降,如果运行介质是易爆或腐蚀物品,还有导致生产事故的可能性[3]。所以定期在线检查阀门的泄漏率,不仅是经济性的需要,更是安全生产的需要。
阀门出厂前进行泄漏率测试相对比较方便,一旦阀门装在系统上以后,再进行泄漏率的测量就非常不方便,目前在线检查阀门泄漏率的方法主要有声音识别法[4],利用阀门泄漏前后音频不一致的方法,可以发现阀门的泄漏,但是具体的泄漏率不能计算;还有用超声波流量计测量下游管道的流量,这种方法对于小的泄漏率效果不好[5];还有用红外成像测量热管道隔离阀下游温度梯度的方法[6],只能看出该隔离阀泄漏的大小,具体数值也无法计算[7]。
考虑到生产线上都装有很多压力表,我们可以使用压力表来监测阀门的泄漏情况,通过多年的经验积累和方法的不断改进,测量的可靠性和精度不断提高,完全达到了核级阀门泄漏率测量的需要。
1 压力法测量的理论基础 1.1 阀门泄漏和阀门压差的关系在流体力学中关于形阻压降的定义:当流体流径截面突然变化 (突然扩大或缩小) 的局部地区,或者流经弯管、接头、阀门、定位架、孔板等时,会发生由于涡流、碰撞、转向等而造成的集中的不可逆压力损失,称这种不可逆压力损失为形阻压降[8]。阀门泄漏主要是由于密封面故障导致的,比如密封面有缺陷或者密封面上有杂物而导致密封不严等。上述两种情况导致的液体流通通道都比较小且短,所以属于流体流径截面突然变小的工况[9],而这种情况下流体的流量就是我们要测的阀门泄漏率,而加在阀门前后的压差就是该流通截面的形阻压降[10]:
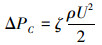 |
(1) |
式中:ζ称为形阻系数;ρ是液体密度;U是液体流速。
由于液体的密度基本不变,液体的流量和液体的流速成正比,液体的流量Q(也就是要计算的泄漏率) 可以用公式Q=ρAU[12]来计算,式中的A是流通截面的截面积,带入式 (1) 可得:
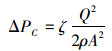 |
(2) |
由式 (2) 可以看出压降和流量的平方成正比,而对于密封面有缺陷或者密封面上有杂物导致密封不严这两种情况,系统压力变化导致的流通截面积的变化不大,可以忽略,所以可以认为ζ、ρ、A是常数,用1/K2表示,则
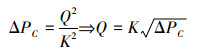 |
(3) |
即阀门的泄漏率和阀门压差的开放成正比。
对于同一个阀门,K参数大小基本不变,所以可以根据阀门设计的压差△Pf和国标要求的泄漏率验收准则Qf,以及试验工况下的阀门压差△Pt,利用式 (4) 计算出试验工况下的泄漏率验收准则Qt[13]:
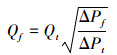 |
(4) |
例如某个阀门设计的压力△Pf是16 MPa,设计的泄漏率Qf是16 ml/h,如果现在阀门的压差△Pt是8 MPa,则现在允许的泄漏率Qt是4 ml/h。
1.2 水的压缩特性压缩系数指物体受到外界压力时体积的变化量,通常认为水不可压缩主要是由于水的压缩系数太小,即受到很大的压力水的体积变化也不大。常温下水的压缩系数是0.000 5/MPa,就是说压力变化1个大气压而水的体积只变化原来的0.000 5,例如一个100 m×100 m,水深2 m的游泳池,如果在游泳池上面增加1个大气压的压力 (当然这个游泳池是密闭刚性的),水的总体积只会减少1 m3,反过来说如果你往这个封闭的刚性池子里注入1 m3的水,则水的压力会增加1个大气压,这就是压力法试验原理。
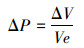 |
(5) |
式中:△P为系统压降;△V为封闭系统体积变化率;V为系统总的体积;e为液体的压缩系数。
2 用压力法测量单个阀门泄漏率 2.1 测量阀门V1的泄漏率图 1是测量阀门V1的示意图,边界阀门V1、V2和T2构成一个封闭系统,压力表可以精确地表征这段封闭系统的压力变化。
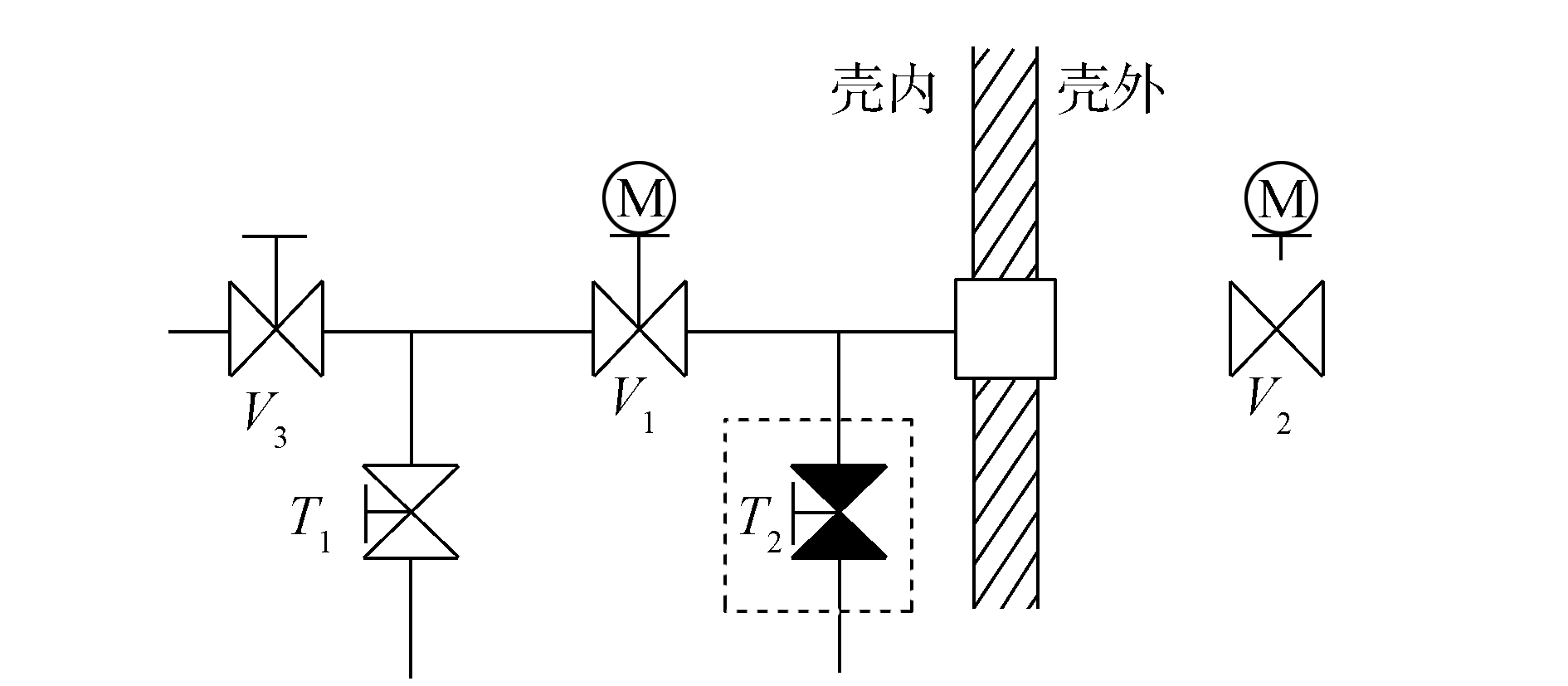
|
| 图 1 单个阀门泄漏率测量方法 |
试验步骤:
1) 在T2接头处连接压力罐,关闭阀门V1、V2,要以系统设计的方式关闭;
2) 利用T2的管线将V1和V2之间的管线施加到试验的压力;
3) 关闭T2,监测一段时间后V1和V2之间压力下降情况,记录数据;
4) 如果压力下降小于允许值,则阀门的泄漏率合格,反之则不合格;
5) 阀门泄漏率和管道允许压降的关系见2.2节。
2.2 利用阀门允许的泄漏率计算允许的压降按照我们的试验方法,因为V1和V2间的管线压力在变,所以阀门V1两侧的压差是变化的,那么V1阀门的泄漏量也是变化的,根据前面得到的形阻公式 (3) 和水的压缩公式 (5),可以列出下面的方程:
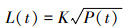 |
(6) |
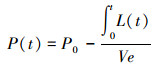 |
(7) |
式中:L(t) 是阀门的泄漏率,是时间的函数,与当时阀门两侧的压差的开放成正比;K是一个常数,与形阻系数、液体的密度以及泄漏截面有关;P(t) 是阀门的压差,也是时间的函数,随着泄漏出去的水越来越多而不断降低;P0是阀门的初始压差,是个已知量;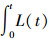
对式 (6)、(7) 求解可得:
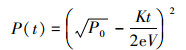 |
(8) |
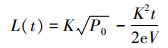 |
(9) |
可以看出压力下降曲线是时间的二次函数,泄漏率曲线是时间的一次函数。
例如某个阀门试验压差1.9 MPa,试验压力下阀门允许的泄漏率是97 ml/h,系统总的体积是719 791 ml。根据初始压差和泄漏率公式 (3) 可以算出K等于0.372,再带入其他已知量得:
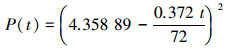 |
(10) |
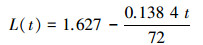 |
(11) |
可以算出30 min后阀门的压降△P从1.9 MPa降到了1.767 MPa,如果V1和V2间管线压力降低了0.133 MPa,这个时候阀门泄漏率刚好合格,就是说如果实际30 min后压力降得比0.133 MPa少,说明阀门的泄漏率是小于97 ml/h,泄漏率肯定是合格的。
需要说明的是如果知道阀门的压降,反过来求阀门的泄漏率也是可以的,可以利用式 (8)、(9) 将K参数求出来,再利用式 (3) 求出某个压差下的阀门泄漏率。
3 两个串联阀门同时泄漏的情况图 2是两个串联阀门同时泄漏的示意图。

|
| 图 2 两个阀门同时泄漏测量方法 |
试验时高压侧处于15.4 MPa,低压侧2.4 MPa,阀门212和阀门001之间压力稳定在4.3 MPa,这个时候212阀门的压降是11.1 MPa,001阀门的压降是1.9 MPa,根据泄漏率公式 (3) 可以计算出L212=K212×10.536,L001=K001×4.359, 如果L212>L001则说明212漏过来的要比001漏出去的多,则212和001之间的压力还会上升,反之则会下降。如果212和001之间的压力会稳定在2.4 ~15.4 MPa之间,在这个压力下两个阀门的泄漏率是相等的,即L212 =L001。
假设测量阀门212和001泄漏率时它们之间的压力稳定在4.3 MPa,根据L212 =L001可得K001=2.4K212。试验过程中还测到212和001之间的压力从2.4 MPa涨到2.9 MPa需要10 min。根据上述条件可以列出下列方程:
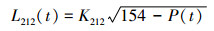 |
(12) |
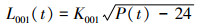 |
(13) |
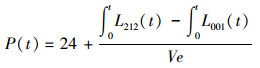 |
(14) |
式中:L212(t) 是阀212的泄漏率,K212为阀门泄漏常数;L001(t) 是阀001的泄漏率,K001为阀门泄漏常数;P(t) 是阀212和阀001之间的压力随时间的变量。
方程 (14) 积分里面带有根号,非常难以求解,将式 (12)、(13) 代入式 (14),然后两边求导,可以得出以下方程:
根据压力最后稳定在4.3 MPa,可以得出K001=2.4K212,根据管道长度和内径可以得出ev=6.42。
因为压力从2.4 MPa涨到2.9 MPa用了10 min,即600 s,将时间分成100个小段,每段6 s,这段时间6 s内认为系统的压力不变,则阀门的泄漏率不变,先假设一个K212的值,然后利用公式可以算出两个阀门各自的泄漏量,然后再算出V212和V001这段管线总水量的变化,最后算出这段管线△P的变化量,然后把这个△P加上这次计算的初始压力作为下次计算的初始压力,再进行下一个6 s的运算,100次计算后可以得出系统总的压力变化量,如果算出来的△P和实测值相比偏高,说明K212值选得偏大,需要减小一点重试,反之则将K212值加大一点,直到计算值和实测值完全一致为止。
表 1是计算两个阀门同时泄漏的部分计算过程,其中时间段0是初始状态,时间段1是第1个6 s的计算结果,时间段2是第2个6 s的计算结果。
| 时间段 | K212 | K001 | P | 212 泄漏量 |
001 泄漏量 |
总的 泄漏量 |
△P |
| 0 | 0.425 | 1.02 | 24 | ||||
| 1 | 0.425 | 1.02 | 24.075 | 11.40 | 0 | 11.4 | 0.07 |
| 2 | 0.425 | 1.02 | 24.147 | 11.39 | 0.27 | 10.12 | 0.07 |
利用EXCEL表格数次尝试后可以求得K212=0.425,K001=1.02,系统正好稳定在4.3 MPa,且系统压力从2.5 MPa涨到2.9 MPa用了10 min,然后可以用式
1) 测量过程要需要系统保持稳定,特别是温度变化对测量结果影响较大,因为温度变化导致液体的密度变化,而密度的变化导致系统体积的变化,最后必然导致系统的压力跟着变化,这样就严重影响检测到的压降结果。
2) 要保证其他边界阀门的严密性,否则也会导致额外的系统压降,导致阀门的测量结果偏大。
3) 压力法测量阀门泄漏率还需要提前算好系统的总容积,越准确越好。
4) 为了保证测量结果的准确性,使用的压力表精度越高越好,测量时间越长越好。
5 结束语利用压力法可以比较精确地测量出阀门的泄漏率,判断阀门的泄漏率是否满足要求,对于2个阀门同时泄漏的情况,经过一定的培训也可以进行检测。考虑因为工艺系统本身就有许多压力表,所以也不需要进行太多的投资,而且可以进行在线检测,不需要系统停运,是一种非常经济、简单、可靠且实用的阀门泄漏检测方法。
| [1] | 同济大学数学系. 高等数学[M]. 7版. 北京: 高等教育出版社, 2014: 294-354. |
| [2] | 合肥通用机械研究所. GB/T12220-1989, 通用阀门标志[S]. 北京: 中国标准出版社, 1990. |
| [3] | 王晓钧, 黄明亚, 林美, 等. GB/T13927-2008, 工业阀门压力试验[S]. 北京: 中国标准出版社, 2009. |
| [4] | 张百麟. 阀门泄漏的原因分析及其设计选型的优化[J]. 石油化工环境保护, 2003, 26(2): 58-61 |
| [5] | 苗雨才. 国内外阀门压力试验标准的比较与分析[J]. 阀门, 2002(6): 28-33 |
| [6] | 董建华, 陈立云. 阀门泄漏量计算方法的探索及检测平台额定研制[J]. 扬州职业大学学报, 2014, 18(1): 40-42 |
| [7] | 袁镇福, 吴骅鸣, 浦兴国, 等. 基于传热原理的电厂阀门泄漏量计算方法[J]. 动力工程, 2004, 24(5): 725-728 |
| [8] | 廖庆斌, 王晓东, 胡必忠. 液体阀门泄漏检测装置的研制及试验研究[J]. 中国机械工程, 2011, 22(3): 295-299 |
| [9] | 高倩霞, 李录平, 饶洪德, 等. 阀门泄漏故障状态与声发射信号特征之间定量关系实验研究[J]. 热能动力工程, 2011, 26(5): 582-587 |
| [10] | 朱绍锋, 刘贵杰, 刘波. 管道阀门泄漏信号仿真分析[J]. 计算机仿真, 2011, 28(3): 393-398 |
| [11] | 贾波. 阀门泄漏量自动检测装置[J]. 阀门, 2006(10): 95-98 |
| [12] | 王同浩. 阀门泄漏检测在石化企业中的应用[J]. 仪器仪表用户, 2013, 20(2): 80-82 |
| [13] | ISO/TC153, 工业用阀泄漏的测量[S]. 2006. |
| [14] | 梁智权. 流体力学[M]. 重庆: 重庆大学出版社, 2002: 112-139. |