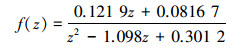收稿日期: 2016-06-25;
网络出版日期: 2017-03-27
基金项目: 国家自然科学基金项目(P041914039)
作者简介:
罗耀华 (1969-), 男, 教授, 博士
三相四桥臂逆变器在传统三桥臂结构的基础上增加了一个桥臂,通过增加一个桥臂来直接控制中性点电压并且产生中性点电流流入负载,这就增加了一个自由度,使得三相四桥臂逆变电源可以产生3个独立的电压,从而使其有能力在不平衡负载下维持三相电压的对称输出。三相四桥臂逆变器具有电路形式简单、体积小、电压利用率高等突出优点。传统的三相四桥臂逆变器常采用的控制策略主要有:第1种方法是在dq0坐标系下用比例积分控制,dq之间存在耦合,需要解耦,因为负序分量的存在,需要用对称分量法才能控制负序分量,这样就会造成控制器数量多,微控制器计算时间紧张,而且三相四桥臂带的是不平衡负载,三相电流不平衡,在dq0坐标下控制,会影响电流环的控制效果[1-3]。第2种方法是在αβ0坐标系下用PR或PI控制,该方法优点是αβ0之间没有耦合,相互之间可以独立控制,但是三相电流也是不平衡电流,在αβ0坐标下,电流环控制效果不好,而且相比abc静止坐标下,带宽也不能达到很大[4-5]。第3种方法是在abc坐标系下,采用三次谐波注入的方法,三相可以独立控制,但是第四桥臂中性电感的耦合没有考虑,实际中需要解耦,解耦会增加控制器的负担,解耦的好坏会影响控制系统性能[6-9]。文献[10]提出了一种基于载波的调制方式,计算简单、便于实际操作,可以提高电压利用率,减少输出电压谐波,而且第四桥臂不需要解耦运算,文中采用这种调制方式。
实际生活中的用电设备大多是非线性负载,产生的谐波含量较大。为了抑制输出电压的谐波含量,文中采用了重复控制器 (repetitive control,RP)。重复控制器的陷波器用于消除谐振峰值,但是同时它也会让重复控制对谐振峰值周围很大一部分频率的谐波增益减小,导致重复控制对一些谐波没有控制效果,导致系统电压的谐波有所提高,为了解决这个问题,文中采用了有源阻尼代替陷波器的方法,这样就可以省去陷波器,同时,为了尽量简化控制器,用有源阻尼代替电流环。
1 abc坐标系下三相四桥臂模型
三相四桥臂逆变器的主电路如图 1。L1到L3为滤波电感;C1到C3为滤波电容;L4是中线电感,第4桥臂的中点和3个电容连接;Z为负载。当带不平衡或者非线性负载时,第4桥臂可以为零序电流的流动提供路径,可以保证三相输出电压的平衡,中线电感可以滤除中线电流的高频分量,根据文献[11],选择中线电感的大小为滤波电感的一半,可以满足体积和滤波的要求。
Vj(j=1、2、3、4) 是2个桥臂之间的电压;ij(j=A、B、C、N) 是电感上的电流;VA、VB、VC是三相输出电压。由图 1可以得到
 |
(1) |
根据式 (1) 可以看出中线电感和前三桥臂在abc坐标系下是耦合的,为了不解耦、减少运算,文中采用类似SVPWM的调制方式,根据文献[10]可得式 (2),第四桥臂电感的电压v4调制方式可以由式 (2) 算出,其中vmax是三相输出电压中最大值,同理,vmin是三相输出电压中最小值。
 |
(2) |
2 三相四桥臂的控制策略
2.1 准比例谐振控制
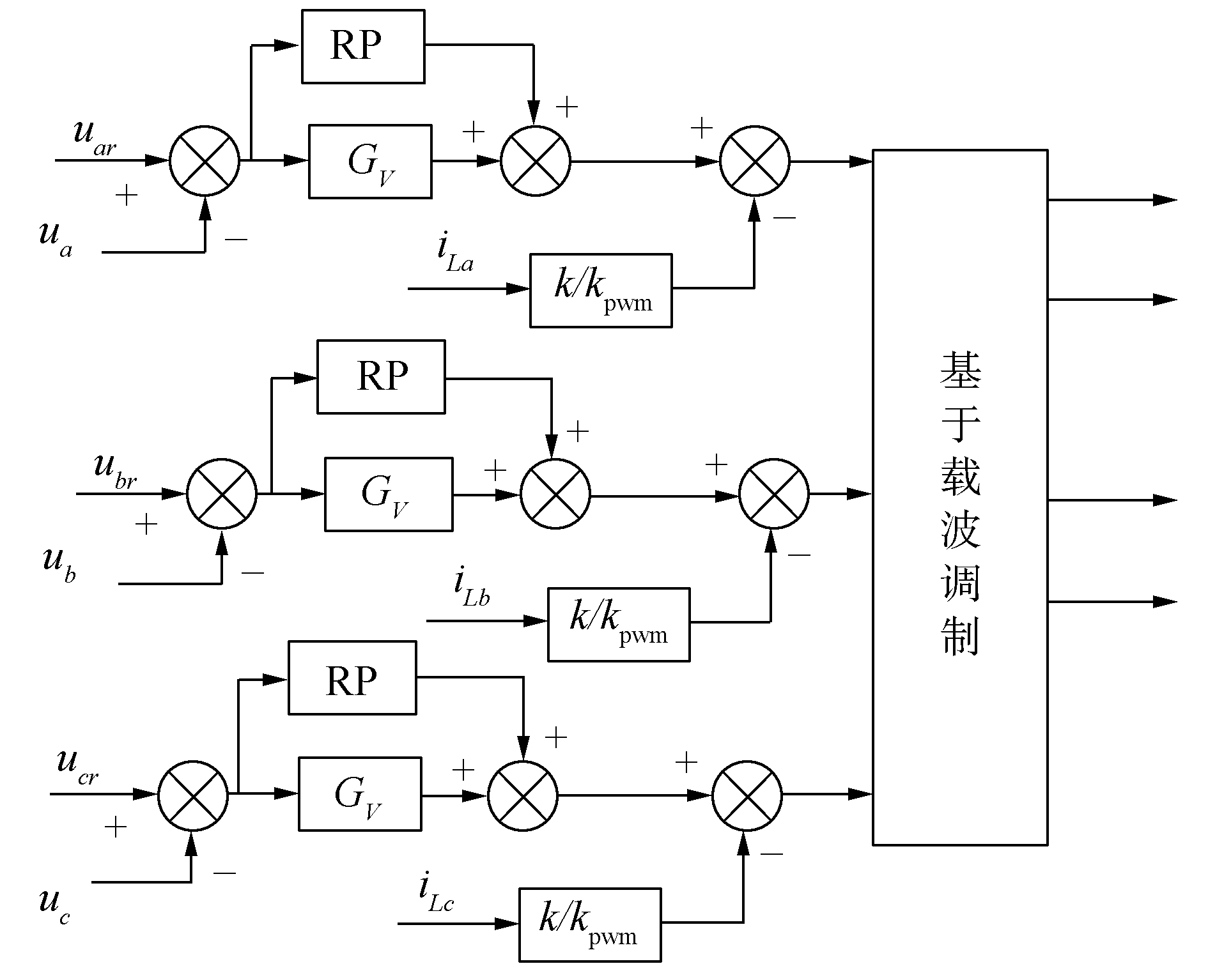
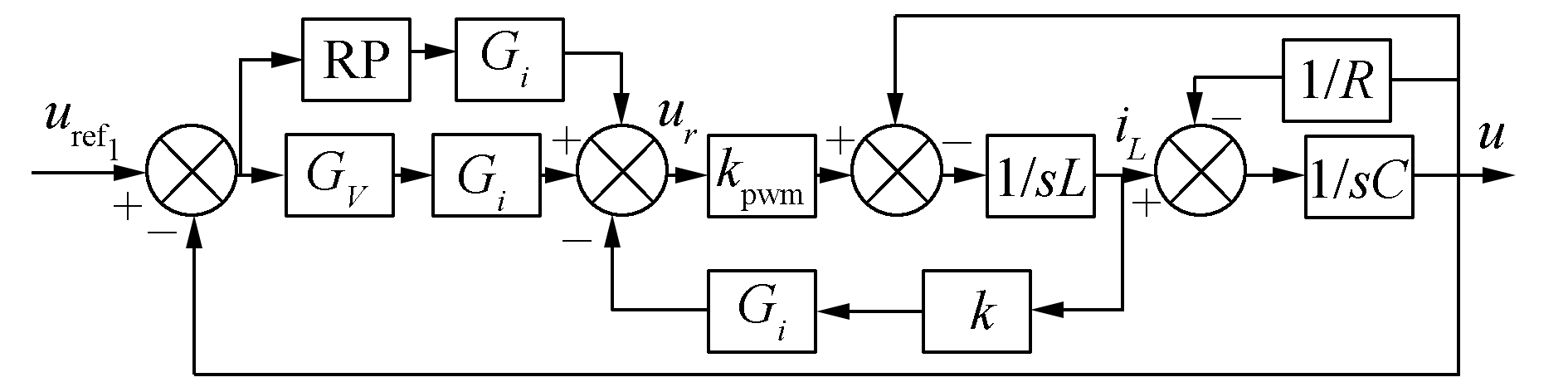
因为在abc坐标系下控制效果最好,我们采用图 2的控制方式。电感的等效电阻非常小,所以文中分析时忽略了电感的电阻,以A相的控制来说明,其他两相也是一样的,电压单环控制框图见图 3,其中:GV是电压环的传递函数;k为有源阻尼;kpwm是逆变桥的比例系数。
因为PI控制交流有稳态误差和相位差,所以采用准比例谐振控制电压环,关于PR控制的形式,我们采用式 (3) 的形式。文献[12]对其进行了说明,其中kp是比例系数;kr是谐振系数;ζ是阻尼系数,ω0为基波角频率。准比例谐振在离散时,基波频率的谐振点位置特别容易偏移,而且离散后系统容易不稳定。为了保证谐振点位置的不变,离散后对基波频率有很大的增益,文献[13]对几种离散方式进行了对比。表 1是几种离散方式的表达式,其中T为采样周期,因为双线性变换法运算简便,而且离散后和离散前的增益及谐振点都一致,因此选用双线性变换离散比例谐振控制器,离散效果比较好,其中PR的比例系数kp取10,谐振系数kr取6 000,阻尼系数ζ取0.01,式 (4) 是离散后的比例谐振。
 |
(3) |
 |
(4) |
2.2 重复控制器
为了控制逆变器带非线性负载时的谐波含量,需要加入额外的谐波控制,对谐波控制的方案主要有以下几种:第1种就是重复控制,第2种是负载电流前馈,即减少电源内阻,使外界的负载扰动对逆变器的输出电压产生的影响降到最低。文献[14-15]提出了另一种方法,但是效果不如重复控制效果好。因此文中决定采用重复控制,补偿器S(z) 见式 (5),补偿器是重复控制器中很重要的部分,它对重复控制器的性能有很大影响,为了有效消除系统的谐波,重复控制器输出的校正量的幅值和相位都必须准确,如果相位补偿的不对,重复控制增益kr就会很小,稍微增大kr,系统就会震荡,所以相位补偿尤其要注意,超前环节的选取决定了相位补偿的程度。二阶低通滤波器f(z) 见式 (6),主要是对滤除高频干扰,增强系统的抗扰动能力,f(z) 的转折频率选择955 Hz,采用零阶保持器离散,采样周期为10 kHz,每个基波周期采样的点数N取200,低通滤波器Q(z) 选择为0.9,重复控制增益kr选择为0.25,超前5个采样周期,k1选择为5。
 |
(5) |
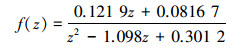 |
(6) |
2.3 基于有源阻尼控制的分析
因为逆变器空载时阻尼较小,系统容易产生震荡,而且为了省去陷波器,因此采用了有源阻尼来消除LC滤波器的的谐振峰值,
为了简化控制器设计,采用有源阻尼代替电流环。电流环的作用是对电压环的增益进行放大,当电流环的采样来自电感电流时,在发生负载短路时,可以有效的进行保护,有电流环时,系统的动态性能也会很好,文献[5]证明了采用有源阻尼代替电流环的可行性。图 3中先忽略重复控制 (RP) 和电压前馈,可以得到系统的输出阻抗Z和闭环电压增益G。
 |
(7) |
 |
(8) |
由式 (7) 可以看出,当有源阻尼k变大时,系统的输出阻抗也会变大,系统应对负载扰动能力减弱,当带非线性负载时,谐波压降会变大,输出电压畸变会更严重。由式 (8) 可以看出随着有源阻尼的变大,系统的闭环电压增益会逐渐变小,为了让逆变器对负载有良好的抗扰动能力,并且电压增益足够大,虚拟电阻取值不可以过大。
 |
(9) |
 |
(10) |
现在分析一下带非线性负载时,重复控制器对系统产生的影响,图 6是双闭环的控制框图,其中的电流环变换了一下位置,其中Gi是电流环的传递函数。
由图 6可以得到
 |
(11) |
由图 3可以得到
 |
(12) |
当逆变器带非线性负载时,负载电流中奇次谐波含量特别多,电感电流中含有大量谐波,会给双环控制中带来大量谐波,从式 (11) 中可以看出重复控制器输出与采样电流做差,然后乘以电流环增益。而式 (12) 中可以看出,电感电流放大了k/kpwm倍,然后重复控制器与放大后的电感电流做差,可见重复控制器的效果明显弱化了,所以我们需要对重复控制器也放大k/kpwm倍。涉及重复控制的文献都会说明放大倍数kr在0~1之间,可见在有源阻尼和重复控制结合的控制器中,最后还要有一个k/kpwm的放大倍数,这样才能对电感电流的谐波进行控制。这就会产生一个问题,见式 (13)。
 |
(13) |
由式 (13) 可以看出,当系统空载的时候,电感电流iL会比较小,电压偏差经过重复控制输出后,与电感电流做差,会减弱有源阻尼消除谐振峰值的作用,甚至会大于电感电流,电感电流的负反馈作用被抵消,导致系统空载震荡,因此既要重复控制充分抑制输出电压谐波,又要有源阻尼充当电流环和陷波器的作用是不可能的,因此我们需要在空载或轻载时不加重复控制。
由式 (13) 可以推算出,负载电流小于多少值时,加上重复控制会震荡。我们来计算出这个电感电流,图 3中先忽略重复控制 (RP),可以得到电压闭环增益见图 7。重复控制器增益见图 8。
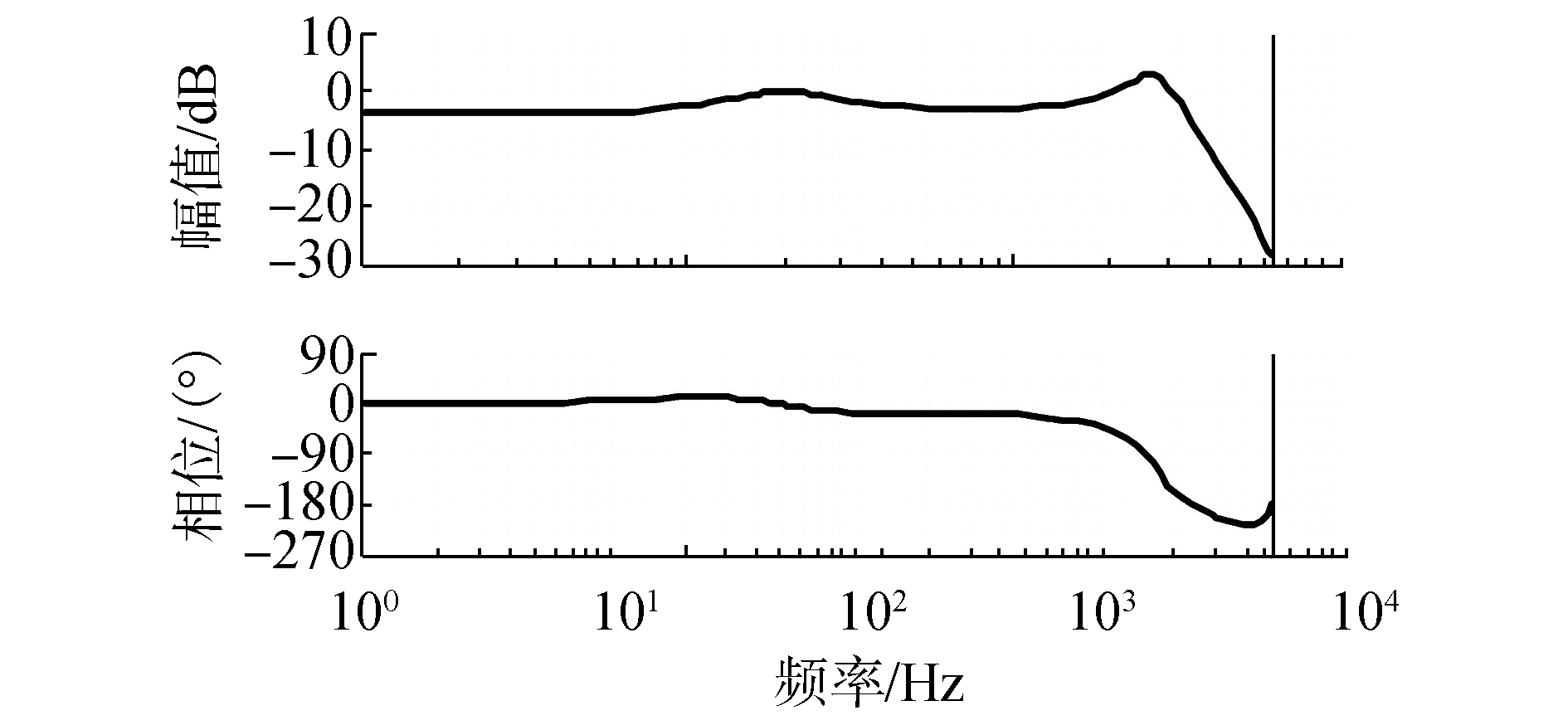
由图 7可以得到在基波频率50 Hz时,闭环电压的放大倍数为-0.054 dB,可以得到输出电压的稳态误差值。LC谐振峰值是在频率为1 130 Hz时。在图 7中可以看出,在900 Hz时重复控制增益较大,并且距离谐振频率点1 130 Hz也较近,因此选择重复控制在900 Hz时的放大倍数作为空载或轻载增益,由伯德图可得2.33 dB,给定电压峰值是311,根据式 (14),可以得到空载或轻载时经过重复控制器输出的控制量峰值为4.1,因此,只要电感电流峰值大于4.1 A时,再加上重复控制器,系统就可以保证稳定。
 |
(14) |
2.4 电压前馈控制
由上面的分析可以知道,电感电流峰值要大于4.1 A,才可以保证加上重复控制时,系统不会产生震荡。为了减小系统震荡的临界值,可以加上电压前馈控制,增大闭环电压增益,也可以改善系统的动态性能,在这里选择参考电压前馈值增益kv为9.7,使电压前馈增益占到系统数字量的0.75,式 (15) 是增加电压前馈后,系统的闭环电压增益,由图 9可以看出加入参考电压前馈后,系统的电压闭环增益变大了。
 |
(15) |
3 仿真验证
为了进一步验证控制策略的可行性,采用SIMUINK进行仿真,搭建了5 kW三相四桥臂仿真平台,仿真参数参照表 2中数据,表 2是系统的参数。比例谐振和重复控制参数都已经在上面给出。图 10是三相空载输出电压。
表 2 系统参数
| 参数 |
数值 |
| 开关频率/kHz |
10 |
| 基波频率/Hz |
50 |
| 滤波电感/mH |
1 |
| 滤波电容/μF |
20 |
| 电感等效电阻/Ω |
0 |
| 直流侧电压/V |
700 |
在图 10中可以看出,空载时三相电压平衡,电压谐波也很小。图 11给出了没加重复控制时,三相电压的波形,其中A相和B相带非线性负载,C相空载,图 12给出了加上重复控制时,三相电压的波形。表 3中第2行给出了图 11对应的电压谐波,表 3中第3行给出了图 12对应的电压谐波。
表 3 输出电压谐波对比
| % |
| A相 |
B相 |
C相 |
| 8.42 |
8.45 |
8.38 |
| 2.29 |
2.52 |
2.44 |
由表 3可以看出,加上重复控制之后,在带非线性负载时,三相输出电压谐波明显减小很多,证明利用有源阻尼代替陷波器的策略可行,系统带非线性负载的能力大大提高。
图 13、14为相突加负载后电压波形和相突加负载后电流波形。由图 (13) 可以看出,A相在0.065 s时突加负载,B相在0.072 s时突加负载,C相在0.078 s时突加负载,由半载到满载,电压降落很小,并且在不到一个基波周期内,三相的输出电压就恢复了,可见系统的动态性能良好。由图 (14) 可以看出,突加负载后,三相电流的波形上升到额定电流大小。因此我们利用有源阻尼代替重复控制和陷波器的控制策略可行。
4 结论
1) 文中提出了带非线性负载的一种控制策略,外环采用准比例谐振控制,为了减少陷波器带来的部分谐波增加,同时减轻微控制器负担,选择有源阻尼功能代替电流环和陷波器,该系统动态性能和稳态性能都很好。
2) 文中提出的控制策略是基于abc坐标系下的,不需要解耦;同时利用类似SVPWM的调制方式,电压利用率高,因为重复控制器的陷波器不用了,这样一个三相四桥臂可以少计算3个陷波器的时间,节约了微控制器的资源,虽然加入了电压前馈,只是加入了3个比例控制,而且系统的动态性能和闭环电压增益都好了。