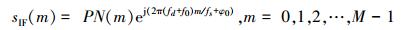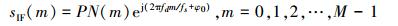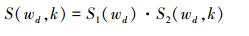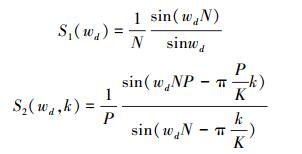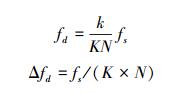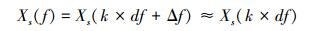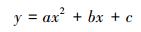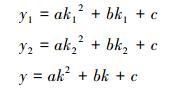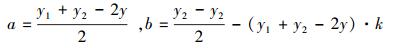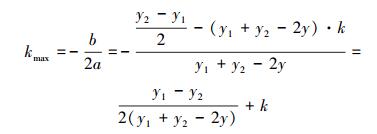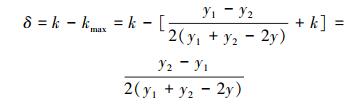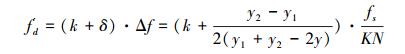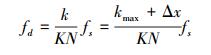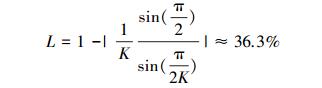直接序列扩频通信系统(direct sequence spread spectrum, DSSS)凭借其独特的优点被广泛应用于军事和民用通信系统中。但是,在高动态环境下由于载体的加速运动,使得扩频信号存在较大的多普勒频移,增大了伪码捕获的难度。传统捕获算法由于捕获时间较长、实时性差等诸多缺点已不再适用,特别是不能补偿大的多普勒频偏。为了快速捕获高动态条件下的扩频信号,现阶段多采用PMF-FFT算法。由于FFT变换存在栅栏效应,导致PMF-FFT系统产生了较大的扇贝损失和多普勒频率估计误差。文献[1]提出采用加窗函数和改进的窗函数校正频率估算误差;文献[2]提出频谱校正法提高PMF-FFT算法的多普勒频偏精度;文献[3]阐述了仅增加少量硬件资源情况下,用三频点线性拟合两轮并行搜索方法提高多普勒频率估计精度。以上方法在提高多普勒频移估算精度方面效果均不足,不能满足现阶段的需求。文中提出采用二次函数内插法补偿校正PMF-FFT算法在高动态环境下多普勒频偏精度估计不足的问题,提高了PMF-FFT系统的性能。
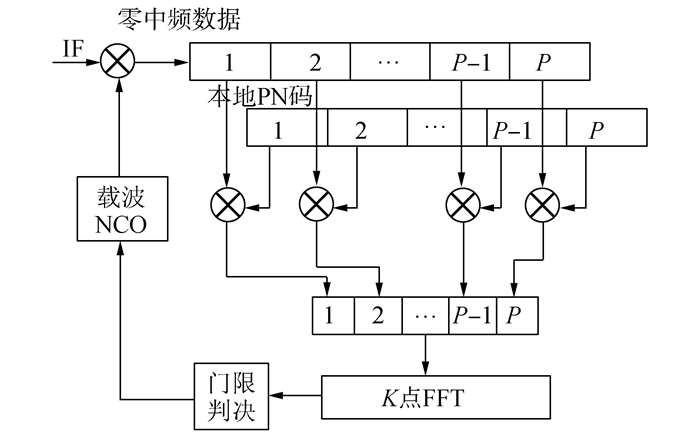
1 PMF-FFT算法原理PMF-FFT算法的系统框图如图 1所示。
|
| 图 1 PMF-FFT算法系统框图 |
设接收端的输入信号为
式中:fs为系统采样频率;fd为高动态产生的大多普勒频移;f0为本地载波频率;M为数据的点数;φ0为相位偏移。解调后得到信号为
由文献[4]知,假定伪码已经同步,系统的幅频响应为
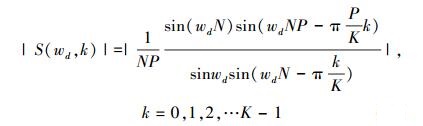 |
(1) |
式中:wd=πfd/fs;P为匹配滤波器的个数;N为匹配滤波器相关长度;K为FFT变换的点数。
由文献[5]可得
式中:
S1(wd)是部分匹配滤波器对系统的贡献,随着多普勒频移的增大,系统输出结果也会随着下降。N=1时,S1(wd)最大值为1,这实质上就是去掉了部分匹配滤波器对系统的影响。S2(wd,k)部分是FFT的输出结果,当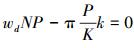
由文中第1章内容中知,要使系统幅频响应输出最大,必须满足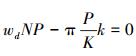

式中:df为系统的频率分辨率;Δf为频率误差。
现阶段多采用加窗法和补零法减小栅栏效应的影响,但都有一定的局限性,只能作为一种辅助手段[7-8]。文中提出通过二次函数函数插值对FFT后的功率谱最大值进行校正,优化最大幅值,提高频率估算精度。
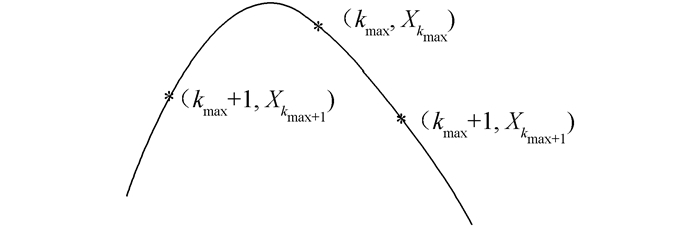
二次函数线性插值算法原理是基于FFT频谱的最大峰值和邻近的两个次最大值进行处理的,具体的实现过程如图 2所示。
|
| 图 2 二次函数内插法求谱峰示意 |
设图中的方程曲线为
式中:k1=k-1;k2=k+1;(k,y)为FFT变化后幅值最大值点的坐标;(kmax,ymax)为栅栏效应所忽略的实际峰值点,也即是内插法所要确定的峰值点;(k1,y1), (k2,y2)为FFT变换后峰值点左右两点次最大值。将(k,y),(k1,y1), (k2,y2)三点坐标代入方程曲线中可得:
解得:
显然,对于开口向下的二次函数而言,最大值点必然是在函数顶点坐标处取得,所以有:
因而有:
所以改进后的多普勒频移估计值为
此时的多普勒频移估计值为
式中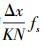
由于二次函数内插法是利用主瓣内最大值和两个次最大值来构造的逼近函数,因而,如果频谱的分辨率越高,栅栏效应的影响越小,二次函数逼近的最大值和次最大值也就越准确,频偏估算的精度也越高。
3 仿真结果及性能分析为了验证改进算法的性能,系统仿真采用的码长为512,数据速率Rb=1 000 b/ps;设抽样速率fs=4.096 MHz,则每个码片被抽样8次,数据总长度为4 096个点。
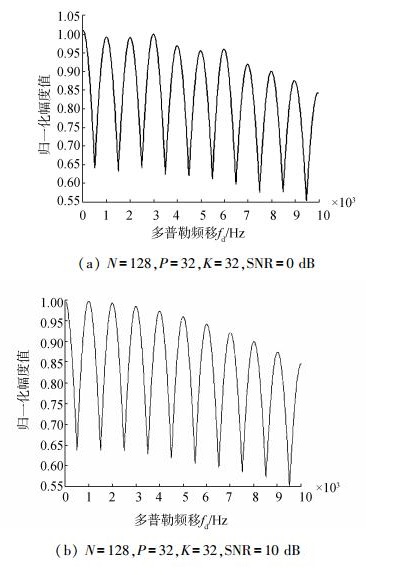
图 3为PMF-FFT系统在不同信噪比的加性高斯白噪声条件下系统幅频响应曲线。
|
| 图 3 PMF-FFT系统幅频响应曲线 |
由图 3可以看出,PMF-FFT系统能够在低信噪比捕获信号的条件下,随着多普勒频移的近一步增大,系统的输出会逐渐下降,同时,在没有做相应补偿的情况下,系统会存在扇贝损失,当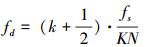
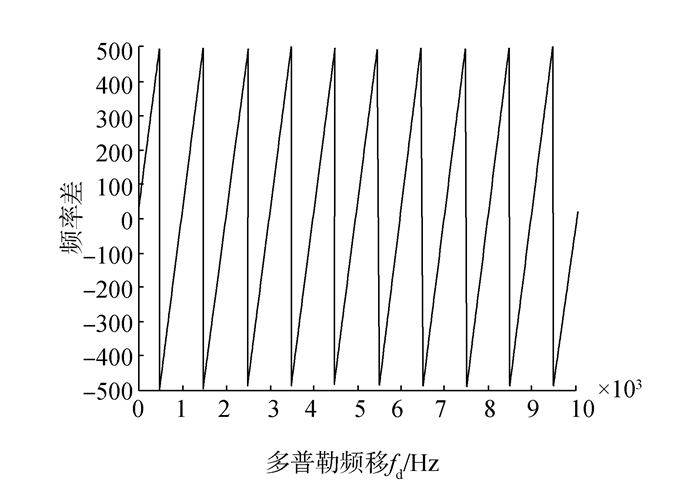
系统频率估计误差可以表示为Δfd=fd-k×fs/KN,k为FFT变换的点数,具体如图 4所示。多普勒频率估计误差仅与谱线的位置k有关,没有做相应的补偿,受噪声影响也较小,因此估计的多普勒频率误差较大[10],最大误差达一个频率分辨率,约为500 Hz。因而,在实际应用中的影响也是不可忽略的。
|
| 图 4 PMF-FFT系统多普勒频率估计误差曲线 |
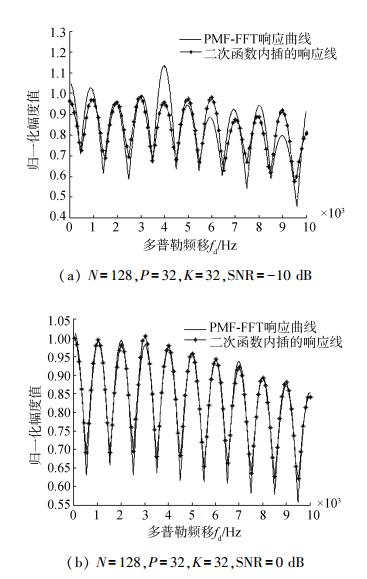
图 5为FFT变换点数为32点,不同信噪比的加性高斯白噪声条件下采用二次函数内插的PMF-FFT系统幅频响应曲线。
|
| 图 5 二次函数内插法系统幅频响应曲线 |
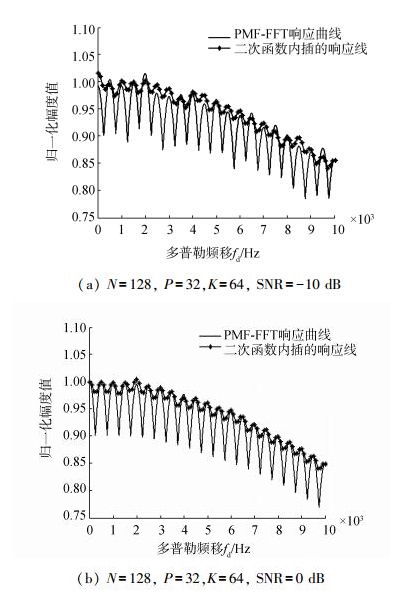
图 5中,采用二次函数内插可以使得系统能够在-10 dB信噪比条件下很好地工作,但在FFT点数较小的情况下对于系统的扇贝损失的性能改善较为局限。为了体现二次函数内插法优越的补偿性能,图 6为在图 5仿真条件的基础上,将FFT变换的点数改为64点。从图 6中可以看出,在低的信噪比条件下,由于噪声的影响较为严重,图形的响应曲线峰值不是依次减小,会出现一些波动,但是,总的趋势也是逐渐变小的。通过对比也可以看出,二次函数内插比原系统更能适应低信噪比。
|
| 图 6 二次函数内插PMF-FFT系统幅频响应曲线 |
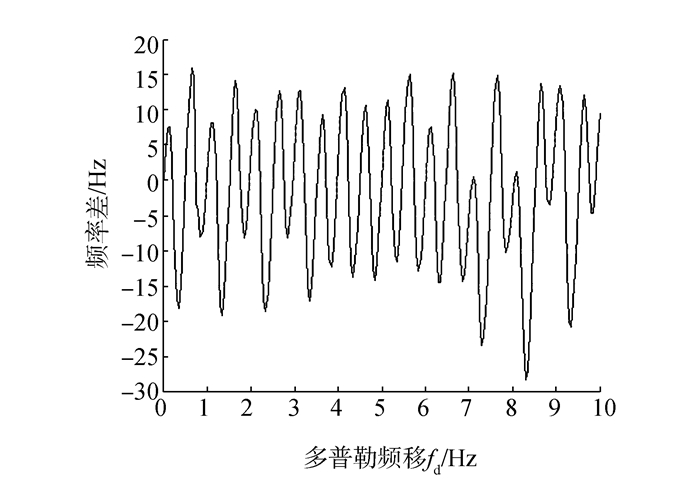
对于采用二次函数内插法,其多普勒频率估计误差为Δfd=fd-k×fs/KN=fd-(δ+k)×fs/KN。图形如图 7所示,其中P=32,N=128,K=64,SNR=0 dB。由于其频率估计误差不仅与谱线的位置k有关,而且与估计的偏移量有关;另一方面,由于估计的偏移量受噪声影响较大,因此相应的误差曲线会出现很大幅度的波动,但估计的多普勒频率误差较原系统有了很大的改善,在K=64时最大的估计误差约为28 Hz,较原系统的500 Hz性能大幅度提升,约为12.5 dB。因此,采用二次函数内插法提高了对多普勒频移的估算精度,较好地克服了原系统存在的扇贝损失问题。
|
| 图 7 二次内插法PMF-FFT系统多普勒频率估计误差曲线 |
文中分析了高动态环境下PMF-FFT算法的系统结构,得出了栅栏效应导致多普勒频谱估算精度不足的结论,提出了基于二次函数内插法的伪码捕获新算法。二次函数内插法在不增加硬件资源的情况下,通过软件算法校正傅里叶变换后的频谱结构,在原算法的基础上,提高了系统的频谱估算精度,在实际的应用中也证明了改进算法的可行性和实用性,具有一定的应用价值。
| [1] | 袁建国, 欧松林. GPS接收机并行捕获算法的研究[J]. 重庆邮电大学学报:自然科学版 , 2013, 25 (4) : 470-474 |
| [2] | 庞统, 张天骐, 刘燕丽, 等. 高动态环境下结合频谱校正的长周期伪码捕获[J]. 计算机应用 , 2010, 30 (8) : 2214-2217 |
| [3] | 何苏勤, 王昊. 一种提高PMF-FFT捕获算法多普勒频偏估计精度的方法[J]. 电子设计工程 , 2012, 20 (12) : 9-12 |
| [4] | 王驰昊, 魏敬法, 寇建辉. PMF-FFT伪码捕获实现与性能分析[C]//第四届中国卫星导航学术年会论文集-S7北斗/GNSS用户终端技术.武汉, 2013: 363-369. |
| [5] | 谢伟. GPS中伪随机码的捕获技术研究[D].合肥:安徽大学, 2007: 33-35. |
| [6] | 黄明军, 王永民. PMF-FFT算法的多普勒频偏估计精度研究[J]. 科学技术与工程 , 2015, 15 (17) : 167-171 |
| [7] | 章兰英, 袁嗣杰, 陈源. 航天扩频测控系统中伪码捕获方法研究[J]. 电子学报 , 2011, 39 (6) : 1471-1476 |
| [8] | 王金刚. GPS数字中频信号仿真及捕获验证[J]. 重庆邮电大学学报:自然科学版 , 2010, 22 (2) : 252-256 |
| [9] | 李文刚, 黄鑫磊, 刘龙伟. 低信噪比环境下的长码捕获新算法[J]. 西安电子科技大学学报:自然科学版 , 2013, 40 (4) : 29-36 |
| [10] | RIFE D, BOORSTYN R. Single tone parameter estimation from discrete-time observations[J]. IEEE transactions on information theory , 1974, 20 (5) : 591-598 DOI:10.1109/TIT.1974.1055282 |