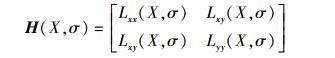近年来,图像拼接受到了人们广泛关注,如将一组相互关联的图像拼接成一幅图像,就要用到图像拼接技术。基于特征的图像拼接中,核心的阶段就是特征提取和特征匹配[1],图像匹配方法的选择将直接影响到最终的拼接效果。
图像匹配分为3个步骤:检测关键点、提取描述向量构造出特征描述子和特征匹配[2]。目前基于特征的研究比较多,如在2004年David G. Lowe提出SIFT算法[3],SIFT算法的优点为对图像尺度不同、亮度不同和旋转不同的图像拼接效果较好以及抗噪声能力强的特点,成为了应用范围普遍的流行算法。2006年Herbert Bay等提出SURF算法[4],这种算法提取的特征具有平移、缩放、旋转的不变性,并且对光照、仿射及投影差异也有相对较好的鲁棒性。随着对特征点匹配速度的要求提高,2011年Ethan Rublee在文献[5]中提出ORB算法,2012年Alexandre Alahi等人在文献[6]中提出FREAK算法。FREAK算法模拟人类视网膜的成像特性来进行采样点的设置和对应点对的选择,利用扫视搜索进行特征向量的匹配,是一种二进制描述子,具有稳定的性能,相对于SIFT、SURF算法更具鲁棒性,并且计算过程要远快过这二者[7],但是它不具备尺度不变性,在图像间场景存在大小尺度差异的状况下,图像间特征点的匹配对的准确度较低。在上述基础之上,文中结合SURF算法对缩放、旋转以及光照不变性的思想[8],对FREAK算法进行改进,并定义为SURF-FREAK算法,经实验比较分析后,该算法在图像特征点匹配准确度上有所提高。
1 FREAK特征点匹配算法 1.1 特征点提取FREAK算法的图像特征点匹配的原理是以FAST算法检测图像特征点。FAST算法基本思想是在待检测的特征点周围邻域范围内的像素点灰度值都与中心待测点灰度值相比较,倘若有像素点灰度值小于或大于中心点像素灰度值,并且这些与中心点一定距离范围中的像素点的数量足够多的话,那么中心点就会被选定成为一个特征点。FAST算法不需要把邻域圆周所有像素点与中心点的差值全都求出,所以运算速度很快,减少了运行的时间,但FAST检测计算的特征点未含有尺度不变性以及旋转不变性的性质。
1.2 FREAK特征点描述子生物学家研究表明,人类视网膜上感受域是能够感知光线的区域,它一般包含中央凹、旁中央凹、远中央凹和周边区4区域。感受域中的神经节细胞的密度和枝状结构的密度随着与中央凹的距离增大而变得越来越小。在图像特征点匹配中,每个区域所完成的功能并不相同:中央凹区能够获得高分辨率的图像,从而对原图像的细节进行识别;周边区则能够获得低分辨率的图像,用于对原图像的轮廓识别。FREAK描述符就是借鉴了人类视觉分区域获取信息的结构而提出的算法。
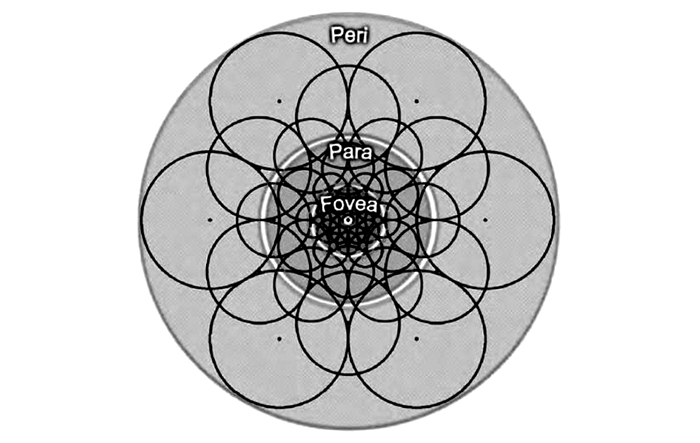
FREAK描述子的采样点的分布与视网膜感受域的结构相似,特征点的位置为中心点,而采样点位置均匀分布在其余圆的圆心上如图 1所示。假设特征点的尺度为σ,则同心圆半径为M1σ,M2σ,…,Mkσ,k表示采样点的层数。与中心特征点间隔越小,采样点越密集;与中心特征点间隔越大,采样点越零散。采样点层数是可选的,随着层数的增多,特征向量的描述能力就增强,计算量也相应的增大。
|
| 图 1 视网膜结构采样模型 |
每个采样点需要进行高斯平滑以去除噪声,周围圆的半径代表高斯核函数的半径。FREAK描述符的形成是通过采样点对的强度比较结果级联组成,属于二进制比特串。假设H是某特征点的FREAK描述符,则:
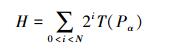 |
(1) |
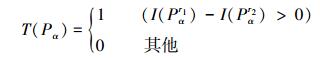 |
(2) |
式中:Pα表示当前采样点的位置;N为特征向量数;I(Pαri)为采样点经高斯平滑后的强度值。
设M为采样点个数,则描述向量共有CM2维生成,其中不是所有的维度都包含很多的图像信息量,有些维度是冗余的,在对比集合中FREAK算法要选择差异性大的部分维度。在图像匹配中,为了保证算法的实用性,只需要针对信息量较大的维度实行保留,细节信息不会严重影响图像匹配的效果。这里通过以下步骤从图像数据中筛选高信息量的维度:
1)建立一个矩阵D,D的每行代表一个FREAK描述符,每一行包含CM2个元素;
2)对D的每一列计算方差,方差越大表示该列携带的信息越多。首先保留方差最大的一列,接着计算其他列与该列的协方差,并选择协方差最小的一列加入到新组成的描述向量中;
3)设置维数上限Nmax,如果达到这个上限则停止,否则继续进行步骤2)。
经上述筛选后,得知FREAK描述符周边的采样区域生成了低维度的描述向量,而FREAK描述符中心的采样区域生成了高维度的描述向量。由此可以证明:目标的基本信息由FREAK算子周边的采样区域提供,对应人眼视网膜结构的周边区,而目标的细节由FREAK算子中央的采样区域提供,对应人眼视网膜结构的中央凹,这表明FREAK算法描述子形成过程与人眼视网膜的成像机理类似。
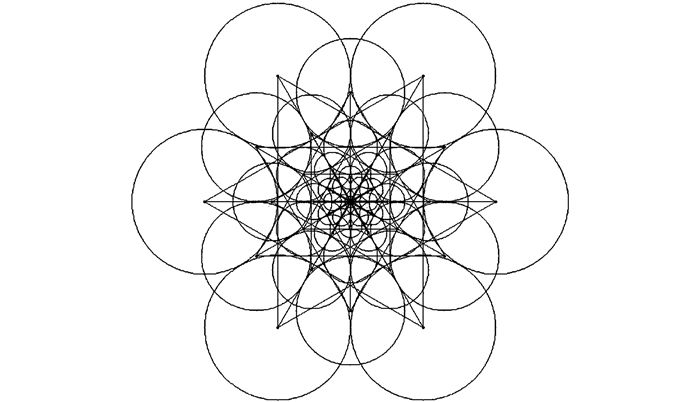
1.3 为特征点分配方向特征点的方向是由上述步骤得到对比集合中差异性较大的部分集合进行局部梯度求和来确定的,一般只将长的、对称的点对提取。对于FREAK算法通常选取45个点对,如图 2所示,然后用式(3)进行角度计算。
|
| 图 2 计算特征点方向的对比对集合 |
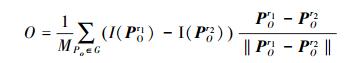 |
(3) |
式中:G是图 2特征点对比点对的集合;M为集合G中点的排列数;I(POr1)是PO的前一位图像像素点的区域灰度均值,对应可分析得到I(POr2)是PO的后一位像素点的区域灰度均值;POr1和POr2分别是PO的前一位和后一位的采样特征点空间坐标的二维向量。
1.4 最近邻算法匹配特征点采用最近邻算法(nearest neighbor,NN)进行配准[9],即采用样本特征点的最近邻特征点与次近邻特征点距离的比值来对特征点进行匹配。利用穷举法找到最精确的最近邻距离,从而达到稳定的匹配。
2 SURF-FREAK算法从上述FREAK算法原理中可以得知:FREAK算法不具有尺度不变性的根本原因是由于检测角点算法FAST,FAST检测计算的特征点未含有尺度不变性的性质,就导致FREAK算法应用于尺度变化的图像匹配效果较差。鉴于SURF算法原理中是构思了多尺度空间理论,从而对图像稳定的特征点检测筛选,再构造SURF描述子来描述取得的特征点促成属于各自图像间的每两个特征点相对应的情况,才使得SURF算法提取的特征保持尺度不变、角度转动不变的性能,除此之外应用于光照差异和透视变换也有良好的鲁棒性。
因而可以借鉴SURF算法原理思维,利用SURF算法的多尺度空间理论提取图像特征点的原理,配合调用FREAK算法使特征点得以描述,构建属于FREAK的描述子,最后使用最近邻算法完成图像间的对齐任务。SURF-FREAK算法解决了FREAK算法不具备尺度不变性的缺陷,同时使算法在对光照变化和旋转变化图像配准的鲁棒性增强。
2.1 SURF算法检测SURF算法检测特征点的思想是基于Hessian矩阵,通过计算得到Hessian矩阵行列式的局部最大值用以定位特征点的位置,并使用积分图像的原理[10]来简化计算,提高速度。
针对原图像I(x, y)中一个像素点I(x, y),位于X处的σ尺度上对应的Hessian矩阵表达式为
式中:Lxx(X, σ)由高斯二阶偏导函数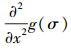
|
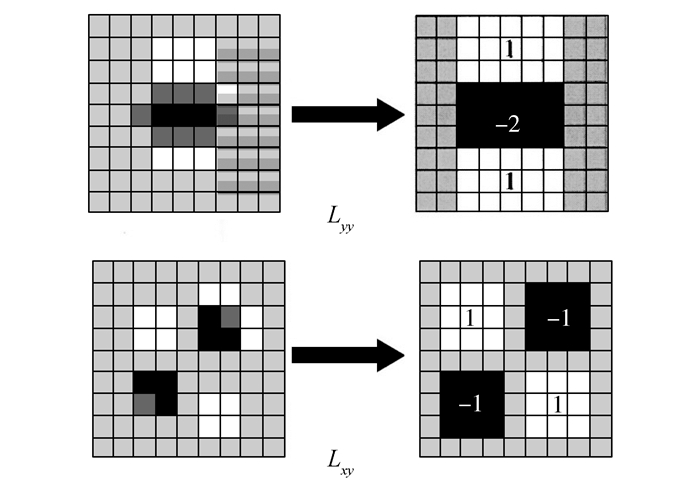
| 图 3 用框状滤波器近似高斯二阶偏导 |
经过实验表明这种框状滤波的近似并没有降低卷积模板的性能。图 3中滤波器模板是σ=1.2的高斯函数通过近似得到的,这构成了对图像进行滤波和斑点检测的最小尺度。将上述改变后的模板与图像卷积结果用Dxx、Dyy、Dxy代换Lxx、Lyy、Lxy可得近似Hessian矩阵Happrox的行列式方法:
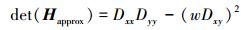 |
(4) |
其中,w是权重系数,主要用来平衡近似误差,一般只取0.9即可。根据式(4)计算原图像X点的响应值,再将对应全部的像素点进行逐个处理,就能够获得相应σ上的响应结果。
2.2 构建尺度空间SURF算法引入了框状滤波模板和积分图像的概念,用不同大小的模板同原始图像在不同方向上做卷积,从而多尺度空间构建完成。尺度空间的最底层由9×9的模板滤波输入得到,对应二阶高斯滤波σ=1.2,此时近似模板的尺度S=σ=1.2。尺度空间的首层是最初始尺度的近似模板同图像做卷积计算结果而来,同理,使用调整尺寸的方式保持模板慢慢增大,之后的尺度层就是在这种情况下用每个尺寸同目标卷积便可形成。每两个距离最近的模板尺寸之差都固定为偶数个像素,从而保证了模板尺寸的奇数性和其中心像素的存在。
每4个模板为1阶(Octave)。每1阶要进行4次滤波,第1阶中相邻的模板尺寸相差6个像素,上1阶第2次滤波模板的大小将作为下1阶最初滤波模板的大小,在第2阶中后1阶滤波模板较前1阶的大小总是增大12,同理第3层每次增加24,以此类推,一般取4阶数就足够了。
SURF算法对于每1个像素点的非极大值抑制要在3×3×3的三维立体空间中进行,与该点上1个尺度对应的9个点、下1个尺度层对应的9个点以及自身周围邻域8个点共26个点比较,只有在达到最大或最小的条件下才选择为特征点,极大值被选定后,采用三维线性插值法得到亚像素级的特征点,同时也去除那些值小于一定阈值的点,最终确定特征点的位置及尺度。
2.3 SURF-FREAK算法总结利用SURF算法中的积分图像的概念简化运算,接着使用Hessian矩阵来确定图像特征候选点并采取非极大值抑制筛选分析,建立图像的尺度空间模型,此时的特征点具备尺度不变数据特性,再针对特征点用FREAK算法采样描述,确立各个特征点矢量方向,最后采用最近邻算法匹配完成图像配准。
3 仿真实验及分析本实验是在Win7系统、Intel(R) Core(TM) i3 CPU、主频为2.26 GHz、内存为4 GB的计算机上运行的,使用Visual Studio 2010进行编程仿真实验。
为了验证SURF-FREAK算法对图像的尺度差异、光照差异以及旋转差异具有良好的鲁棒性的特点,分别以尺度不同、亮度不同和旋转角度不同的测试图像为对象进行实验,并与经典的SIFT算法、SURF算法和FREAK算法进行对比。
3.1 尺度不同对比实验如图 4(a)、4(b)分别为经典SIFT算法和SURF算法对church图像的匹配结果,图 4(c)是采用FAST角点检测的FREAK算法对church图像的匹配结果,图 4(d)为SURF-FREAK算法对church图像的匹配结果。

|
| 图 4 church图像匹配结果 |
为了更直观地比较4种算法对图像的匹配效果,将经典的SIFT算法、SURF算法、FREAK算法和SURF-FREAK算法对church图像的匹配总时间和特征点匹配的准确度用列表反映出来,如表 1。
| 算法 | 匹配总时间/ms | 特征点匹配 准确度/% |
| SIFT算法 | 3 595 | 79.43 |
| SURF算法 | 860 | 77.81 |
| FREAK算法 | 398 | 35.94 |
| SURF-FREAK算法 | 508 | 90.91 |
通过对比数据进行分析,经典的SIFT算法和SURF算法虽然匹配的特征点很多,但是特征点匹配准确度不足80%,而且SIFT算法的匹配总时间较长。由于FREAK算法中FAST特征点检测不具有尺度不变性,使得最终特征点的匹配较为混乱,匹配错误的特征点明显较多,准确度只有35.94%。文中提出的SURF-FREAK算法匹配总时间为508 ms,经典SIFT算法的总时间是它的7.1倍,SURF算法是它的1.7倍,FREAK算法耗时398 ms与文中提出的算法的耗时大致相当。然而文中提出的SURF-FREAK算法在特征点匹配准确度上相对于经典SIFT算法和SURF算法提高约11%,比FREAK算法匹配准确度提高约55%,表明了SURF-FREAK算法克服了FREAK算法不具备尺度不变性的缺陷,同时匹配准确度略高经典SIFT和SURF一筹。
3.2 亮度不同对比实验如图 5(a)、5(b)分别为经典SIFT算法和SURF算法对canal图像的匹配结果,图 5(c)是采用FAST角点检测的FREAK算法对canal图像的匹配结果,图 5(d)为SURF-FREAK算法对canal图像的匹配结果。

|
| 图 5 canal图像匹配结果 |
| 算法 | 匹配总时间/ms | 特征点匹配准确度/% |
| SIFT算法 | 3 526 | 87.8 |
| SURF算法 | 727 | 85.78 |
| FREAK算法 | 164 | 92.23 |
| SURF-FREAK算法 | 594 | 97.06 |
通过对图像亮度不同对比实验结果可知,文中提出的SURF-FREAK算法匹配准确度高于SIFT和SURF约10%,高于FREAK算法约5%;在总时间上SIFT算法是SURF-FREAK算法的5.9倍,SURF算法是SURF-FREAK的1.3倍,FREAK算法时间略少于SURF-FREAK,但是SURF-FREAK算法整体的效果仍然比其他几种算法要好。
3.3 旋转不同对比实验如图 6(a)、6(b)分别为经典SIFT算法和SURF算法对building图像的匹配结果,图 6(c)是采用FAST角点检测的FREAK算法对building图像的匹配结果,图 6(d)为SURF-FREAK算法对building图像的匹配结果。

|
| 图 6 building图像匹配结果 |
| 算法 | 匹配总时间/ms | 特征点匹配 准确度/% |
| SIFT算法 | 4 292 | 80.15 |
| SURF算法 | 1 177 | 85.71 |
| FREAK算法 | 283 | 88.62 |
| SURF-FREAK算法 | 455 | 92.42 |
对比试验结果和数据可知,SIFT算法匹配时间约为SURF-FERAK的10倍,SURF约为SURF-FREAK的2.6倍,FREAK算法略少于SURF-FREAK170 ms;但SURF-FREAK算法的匹配准确度比FERAK提高约4%,比SIFT算法和SURF算法分别提高约12%和7%。
4 结束语结合SURF算法对缩放、旋转以及光照不变性的思想,对FREAK算法进行改进,提出的SURF-FREAK算法有效地解决了FREAK算法不具备尺度不变性的缺陷,并且对光照差异以及旋转差异的图像匹配效果增强。经实验比较分析后,文中提出的算法在图像匹配运算速度上较SIFT、SURF经典算法具有明显优势,图像匹配的准确度相比于SIFT、SURF和FREAK算法都有所提高,更适用于实时性和准确度要求较高和存在尺度变换、旋转变换和光照差异的图像配准中。
| [1] | 阮芹, 彭刚, 李瑞. 基于特征点的图像配准与拼接技术研究[J]. 计算机与数字工程 , 2011, 39 (2) : 141-144 |
| [2] | ZITOV B, FLUSSER J. Image registration methods: a survey[J]. Image and vision computing , 2003, 21 (11) : 977-1000 DOI:10.1016/S0262-8856(03)00137-9 |
| [3] | LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision , 2004, 60 (2) : 91-110 DOI:10.1023/B:VISI.0000029664.99615.94 |
| [4] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer vision and image understanding , 2008, 110 (3) : 346-359 DOI:10.1016/j.cviu.2007.09.014 |
| [5] | RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: an efficient alternative to SIFT or SURF[C]//Proceedings of the 2011 International Conference on Computer Vision. Barcelona, Spain, 2011: 2564-2571. |
| [6] | ALAHI A, ORTIZ R, VANDERGHEYNST P. FREAK: fast retina keypoint[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI, USA, 2012: 510-517. |
| [7] | 王灿进, 孙涛, 陈娟. 基于FREAK特征的快速景象匹配[J]. 电子测量与仪器学报 , 2015, 29 (2) : 204-212 |
| [8] | 阳吉斌, 胡访宇, 朱高. 基于改进SURF算法的遥感图像配准[J]. 电子测量技术 , 2012, 35 (3) : 69-72 |
| [9] | 戚世贵, 戚素娟. 基于特征点的最近邻配准算法[J]. 许昌学院学报 , 2008, 27 (2) : 67-71 |
| [10] | VIOLA P, JONES M. Rapid object detection using a boosted cascade of simple features[C]//Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Kauai, HI, USA, 2001, 1: 511-518. |