温度是一种可以体现物质状态的参数,在工程中为判断部件工作状态提供了重要依据,尤其是在航空工程中显得特别重要。准确测量航空发动机内旋转叶片的温度可以起到对发动机工作状态监测的作用,保证其工作在安全的温度范围内,同时也为发动机部件老化提供预警,最大程度上保障安全。除此之外,温度的测量在国防、农业、医疗等诸多领域中起着非常重要的作用。
目前测量温度主要分为接触法和非接触法。辐射测温的方法是非接触测量法中的一种,它有着延迟时间小、测量精度高、输出信号便于测量、没有测量上限的特点,因而得到了广泛的应用[1]。之前仪器测得的只是物体视在温度(包括亮温,辐射温度等),真实温度的获取还需依靠物体材料的发射率信息,但是物体的发射率是一个十分复杂的因素,它不仅和组分、表面状态有关,温度和波长等因素也对发射率有着很大的影响[2]。多波长测温法利用多条光路的测量信息有效地减小了由于发射率带来的误差。多波长测温法是借助测量的信息,在处理测量数据时,将发射率作为求解的未知量放在方程中,因而在求解得到目标真温的同时材料光谱发射率也会被求解出来,从而减小了测温过程对发射率信息的依赖性,该方法适应性强,近年得到了长足的发展[3]。
在燃气轮机叶片的温度测量等方面,英国、美国等发达国家起步较早,1954年Pyatt首先研制出三波长辐射温度计,但目标的真实温度只有在物体发射率和测量所用波长呈线性关系时才可以获得到;直到20世纪60年代,相对系统的多波长测温的方法和理论才由Reynolds正式提出,为后来多波长的理论研究和工程实践奠定了基础。我国在20世纪90年代,由哈尔滨工业大学戴景民教授与罗马大学著名的教授G Ruffino合作,研制出了三十五波长辐射测温计,并成功测量了物体的实际温度[4];针对高温计得到的数据如何处理,1998年孙晓刚[5]教授提出了利用BP神经网络的算法来实现对数据的处理,但由于需要预先获得材料的发射率模型从而对神经网络进行训练,因此在处理未知材料上仍无法获得很好的效果。孙晓刚[6]教授在2003年提出了基于二次测量的数据处理方法,但是该计算方法需要在一次实验基础上进行多次测量并修正,计算实时性较差,需要多次测量,在工程中并不适用。目前在实时处理依旧采用的是遗传算法。为了获得较高精度的温度,本文利用遗传算法和改进NSGA-Ⅱ算法进行数据处理,通过MATLAB仿真获得实验结果,并对获得的实验结果进行分析比较。
1 测温原理温度在科学研究和工程技术中属于需要测量的参数。1900年,Planck提出了著名的黑体辐射定律揭示了黑体辐射的基本理论,即不同温度下的黑体辐射出射度可表示为
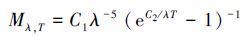 |
(1) |
式中:c1=3.741 8×104 Wμm4/cm2代表第一普朗克系数,c2=1.438 8×10-2 μmK表示第二普朗克系数,Mλ,T表示光谱在温度为T,波长为λ时的单色辐射出射度。
设待测目标真实温度为T,第j路高温计所得到的辐射出射度为Lj,目标的发射率为εj(λ,T)。假设εj(λ,T)=εj(λ)为常量,该目标黑体的出射度为Lbj,则有
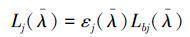 |
(2) |
通过逆函数Lbj-1可以得到高温计所测得的温度,则测量的温度可以表示为
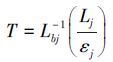 |
(3) |
对于式(3) 在4个不同表面温度下得到模型参数εj(j=1,2,3,4) ,通过使误差方程δ2最小化可得到相应的温度值以及εj(λ)。
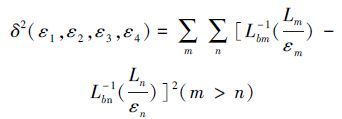 |
(4) |
式中:Lbm-1和Lbn-1分别表示第m路和第n路高温计所测得的温度的逆函数,Lm和Ln代表第m路和第n路得到的物体辐射出射度,εm和εn代表 2路所对应的物体发射率。
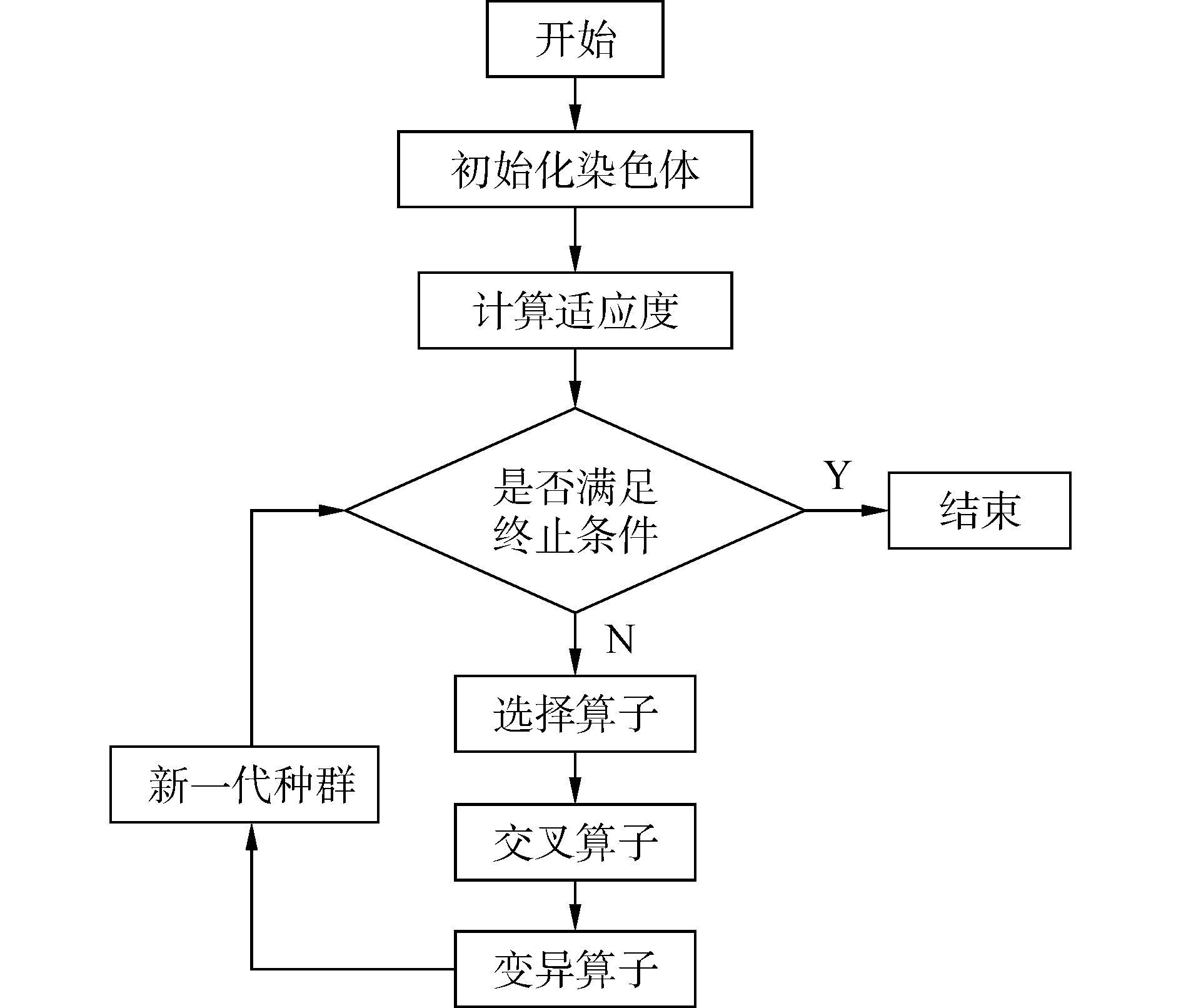
2 改进NSGA-Ⅱ算法原理 2.1 遗传算法遗传算法(genetic algorithm,GA)是一种迭代优化计算模型,它在计算时是通过类似于物种进化的过程,遵循适者生存优胜劣汰的原则来完成对最优解的寻找[7]。遗传算法原理相对简单、结构易与多种实际问题相结合,因此在优化计算方面具有很好的适应性,得到了广泛的应用。此外它还是一种模拟生态进化这种学习过程的计算方法,因此在机器的智能学习领域也有所应用[8]。算法运算流程如图 1所示。
|
| 图 1 遗传算法流程 |
NSGA-Ⅱ算法(non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)是Srinivas和Deb于2000年提出的。虽然它采用了看似复杂的非支配排序和拥挤度比较的方法对解的好坏进行评价,但却具有更低的复杂度。在提升了运行速度的同时,在解的收敛性上也体现出了更好的性能[9]。
2.2.1 快速非支配排序方法在多目标优化问题的求解优化中,一个解在某个目标函数上求解的特性是最好的,但在其他目标上可能就不是最好甚至是比较差的。当2个解x1和x2在所有的目标函数求解上,x1均优于x2,则称解x1支配解x2;若是存在一个解不受其他任何解支配,称该解为非支配解[10]。快速非支配排序的方法就首先从当前种群找出所有的非支配解,并将这些解存入一个空的集合,并赋予一个参数,即其非支配排序的层级,然后从这部分解各自所支配的个体中,再次找出其中非支配的个体,并将其存入另一个集合,赋予新的非支配排序层级,但这个层级要低于之前产生的排序层级。通过不断重复这样的操作对种群中所有的个体进行排序,直到种群中所有个体都被划分了层级才终止之前的排序的操作。这样减小了个体间相互比较的次数,从而使计算复杂度大大的降低。
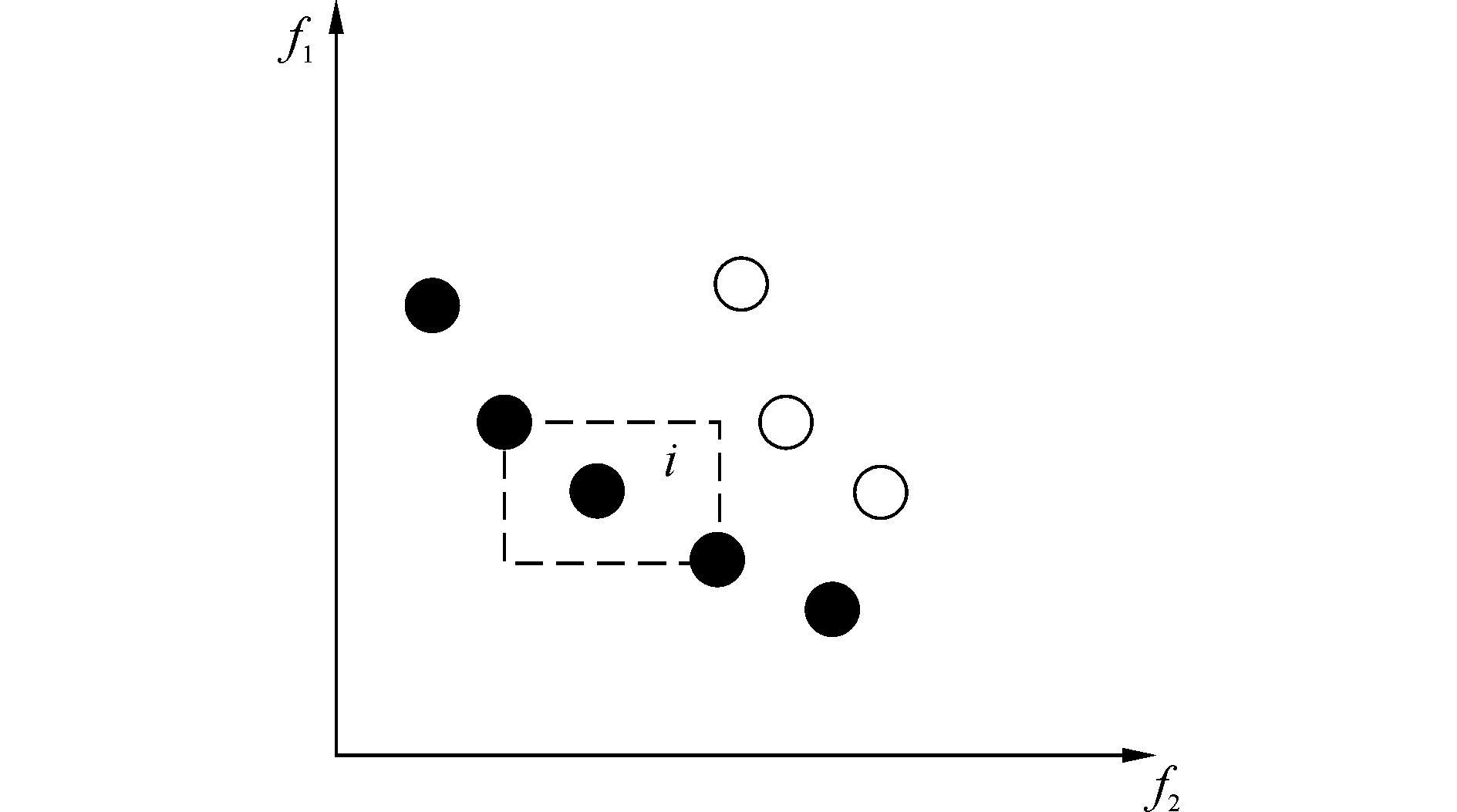
2.2.2 拥挤度和拥挤度比较算子拥挤度是比较解分布特性的参数,在同一非支配层级中,一个个体周围存在其他的个体,拥挤度是指该个体到距离其最近2个个体组成的长方形的面积,个体i拥挤度如图 2所示。
|
| 图 2 拥挤度示意图 |
拥挤度比较算子是在拥挤度和非支配排序层级基础上提出的,是用来比较解的好坏的一种算子。当2个个体非支配层层级不同时,选择非支配层级高的个体作为优秀的解,当2个个体层级数相同时,个体周围不拥挤的视为较好的解。
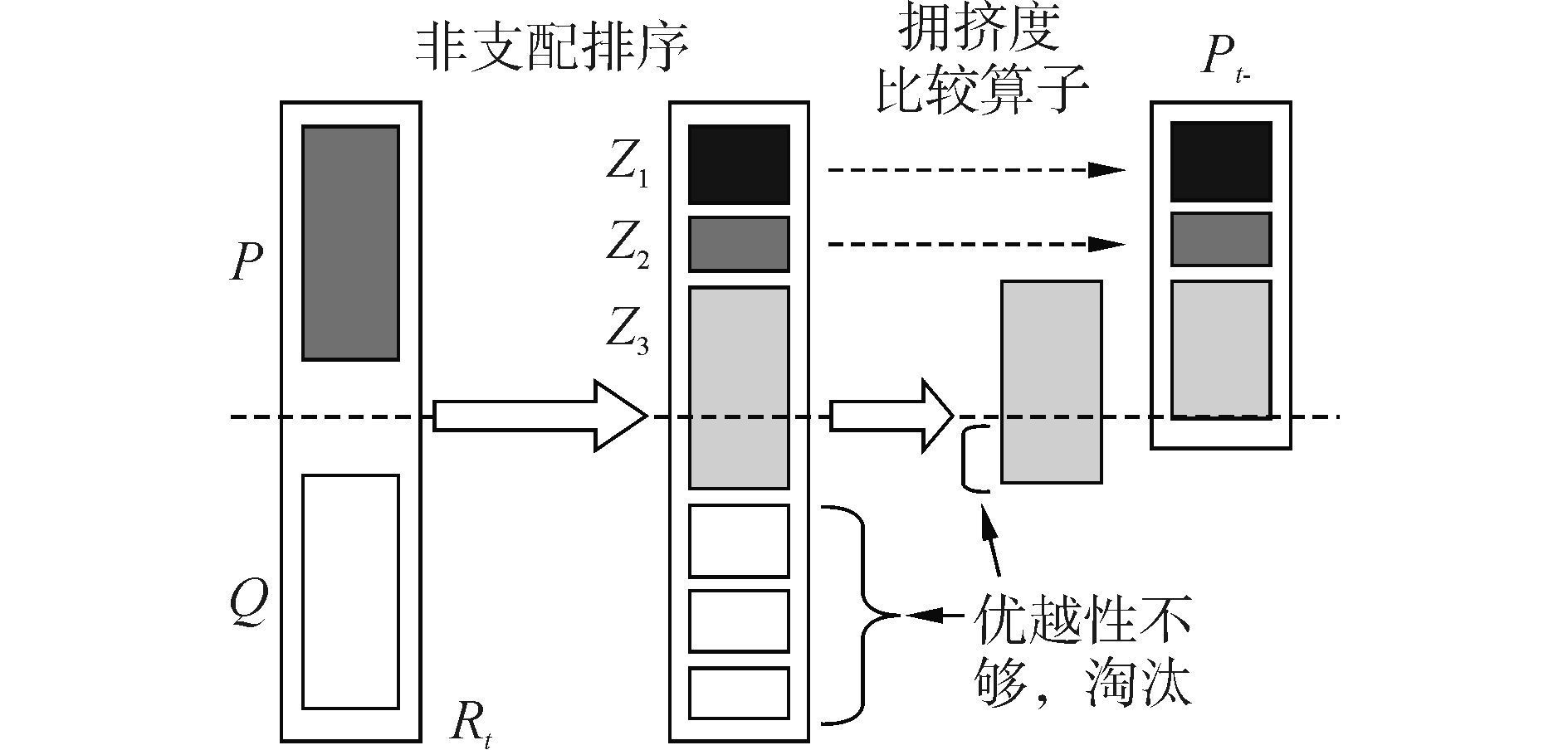
2.2.3 精英策略NSGA-Ⅱ精英策略最大的特点在于父代和子代同时比较,使下一代种群在保留父代中优秀的个体的同时,也加入了子代中优秀的个体,因而保持了种群的多样性[11]。当开始计算时,首先由父代通过遗传操作,交叉变异产生新的种群,并由父代和子代共同组成一个种群规模是之前2倍的新种群。然后通过拥挤度比较算子对种群进行筛选,优先留下非支配级别高的,同一级别时优先保留不拥挤的个体,使种群规模恢复到之前的大小。引入的精英策略,使采样空间变大,搜索的范围更广,有效防止了最佳个体的丢失,提高了算法的运算速度和鲁棒性。NSGA-Ⅱ算法的计算就是在反复执行这种精英策略中进行的,其流程图如图 3所示。
|
| 图 3 NSGA-Ⅱ算法的流程 |
Storn等[12]于1995年提出了差分进化算法(differential evolution,DE),与其他的进化算法相同,DE算法也是通过模拟生物进化的方式来对问题进行求解,通过不断地进行代入运算,求解出问题的近似最优解。DE算法最主要的特点在于其变异策略的不同。初始种群是由一群随机产生的个体组成,差分进化算法随机从种群中选取2个不同的个体,并把这2个个体的差向量与第3个个体以某种运算规则相结合,从而产生新的个体[13]。其变异方式如式(5) 所示:
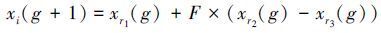 |
(5) |
式中:g表示进化代数,xri表示同一代的不同个体,F为交叉系数,其中i与ri均不相同。
2.4 改进NSGA-Ⅱ算法在保留了NSGA-Ⅱ算法中快速非支配排序的方法和采用了拥挤度和拥挤度比较算子的基础上,主要针对如下几方面进行了相应的改进:
1) 由于NSGA-Ⅱ算法中也存在交叉变异概率,其设定方式与简单遗传算法一致,选择一成不变的交叉变异概率值,存在容易陷入局部最优解和早熟的缺点。这里采用设置2组交叉变异概率,并使之进行动态变化来提高对于最优解的搜索能力。交叉变异概率值设定如式(6) 、(7) :
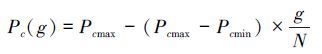 |
(6) |
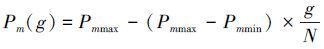 |
(7) |
式中:g表示当前进化的代数,Pc(g)和Pm(g)表示进化到当前代数时交叉变异概率的大小,N表示进化的总代数,Pcmax和Pcmin表示预设的交叉概率上下限的值。Pmmax和Pmmin表示预设的变异概率上下限的值。
计算开始时个体间的差异比较大,在进化初期,进化的代数较小,交叉变异概率较大,算法具有较强的全局搜索能力。随着进化代数的增加,个体间的差异减小,都是较为相近优秀的个体,此时交叉变异概率也动态调整为较小的数值,从而再次寻找更为优秀的个体,增强了在局部寻找最优解的能力。
2) NSGA-Ⅱ算法采用的变异算子与遗传算法相同,在局部寻优时不依赖于种群其他个体信息,具有一定的盲目性,因此采用差分进化算法的变异策略并加以改进,变异算子如式(8) 所示:
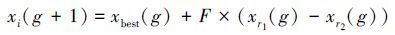 |
(8) |
式中:xbest(g)为第g代中最优秀的个体,其余参数含义均与式(5) 中相同。与传统差分进化算法不同的是,这里是在最优解的个体上加上一定的扰动,保证个体都向着最优解的方向进化的同时,所加上的扰动也能有效减少陷入局部最优解的可能。
3) NSGA-Ⅱ所采用的交叉算子具有确保该算法收敛于全局最优解的特点,保证了子代个体保留了部分父代个体的信息,有利于保留父代良好解的特征,其定义如式(9) :
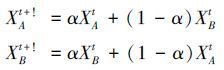 |
(9) |
式中α为一个确定常数。该策略优点在于父代优秀的个体可以遗传给子代,但该策略在全局搜索性能上相对较弱,容易造成有优秀的解过度繁殖,不能很好地保证种群多样性。所以这里,通过重新定义α的值来提高全局搜索能力,尽量留下非支配排序等级高的个体,因此采用非支配排序级别和α相结合的处理方法,在丰富了解的多样性同时,尽量保留下了排序等级高的个体。
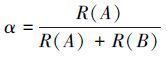 |
(10) |
式中R(A),R(B)分别表示个体A和个体B的非支配排序层,这样处理第一保证了这个参量与之前常数参量的范围保持了一致。第二是将非支配排序级别和α结合了起来,使α可以借助种群中其他个体的信息进行变化,从而让非支配排序级别高的个体在后代中占有的比例提高,提高了下一代种群中个体的质量。
3 仿真实验在本文中,主要针对700~900 ℃进行仿真。选取的4路波长为1.05、1.30、1.425、1.6 μm,为了比较2种算法的求解性能,我们首先假设待测物体温度为800 ℃,物体发射率在各波长下均为0.85,在此条件下比较各个算法的计算精度,比较其计算的性能。本文的仿真实验均是在以下的软件环境下进行的:系统版本为Windows7旗舰版64位系统,处理器为Intel(R) Core(TM) i5-3470 3.20 GHz,安装内存为4.00 GB,仿真软件为Matlab2012a。
3.1 遗传算法仿真结果遗传算法相关参数的设置如表 1、2所示,且实验中所有算法的搜索空间均与表 2相同。
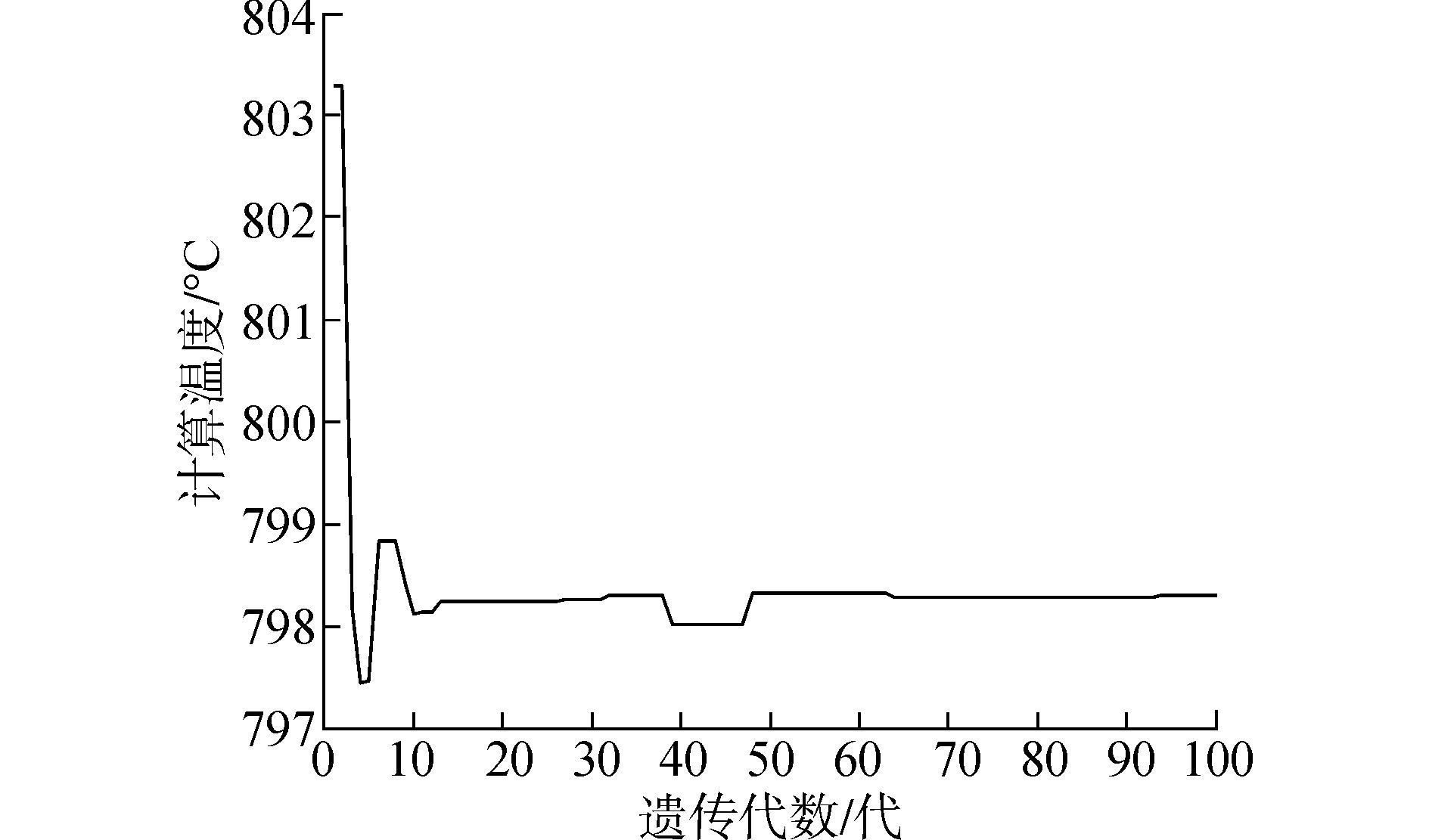
首先通过遗传算法对目标温度进行求解,最优解的变化趋势和最后一代种群特征如图 4、5所示。
|
| 图 4 遗传算法搜索空间 |
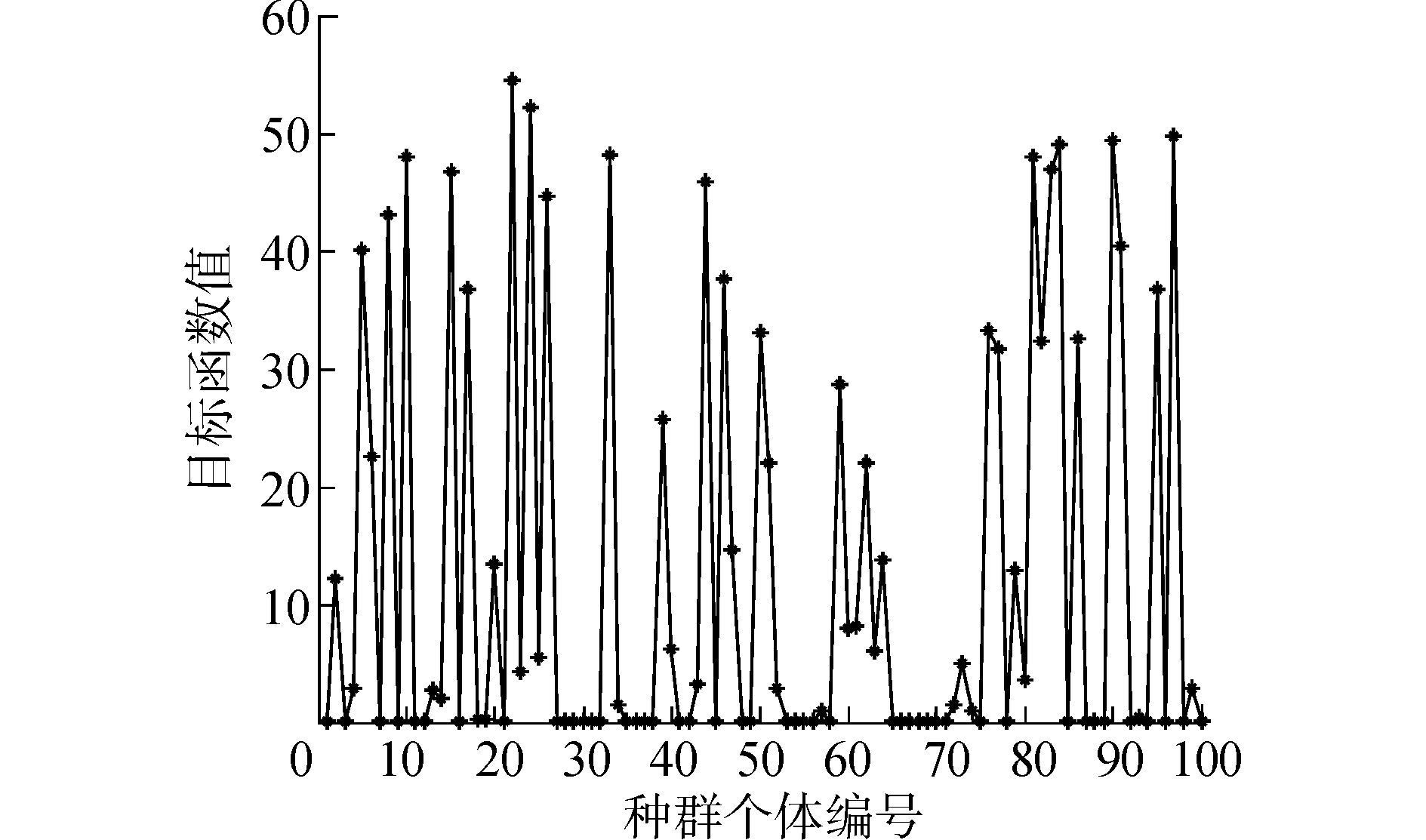
|
| 图 5 最后一代种群特征 |
通过解的变化趋势,我们可以看出解的收敛速度,在多少代的时候最优解的值趋于一个稳定的值。种群解的特征主要体现在种群中个体在求解的目标函数值的大小上。在计算的过程中,目标函数值越小表明解越好,越接近0表明求解的精度越高。每一代计算完成后,种群中目标函数值小的个体所占的比例越多,表明当前种群的解越。当计算完成后,通过比较最后一代的种群中目标函数值小的个体所占的比例,可以观察出好的解是否得到了保留。当目标函数值小的个体比例高的时候,说明求解效果好的个体都保留到了最后一代中,而求解效果差的个体在进化过程已经被淘汰。从图 4、5中发现,遗传算法在求解的过程中在60代左右时收敛,最优解的值趋于稳定。计算完成后,种群个体目标函数值差异较大,最优解的个体较少。
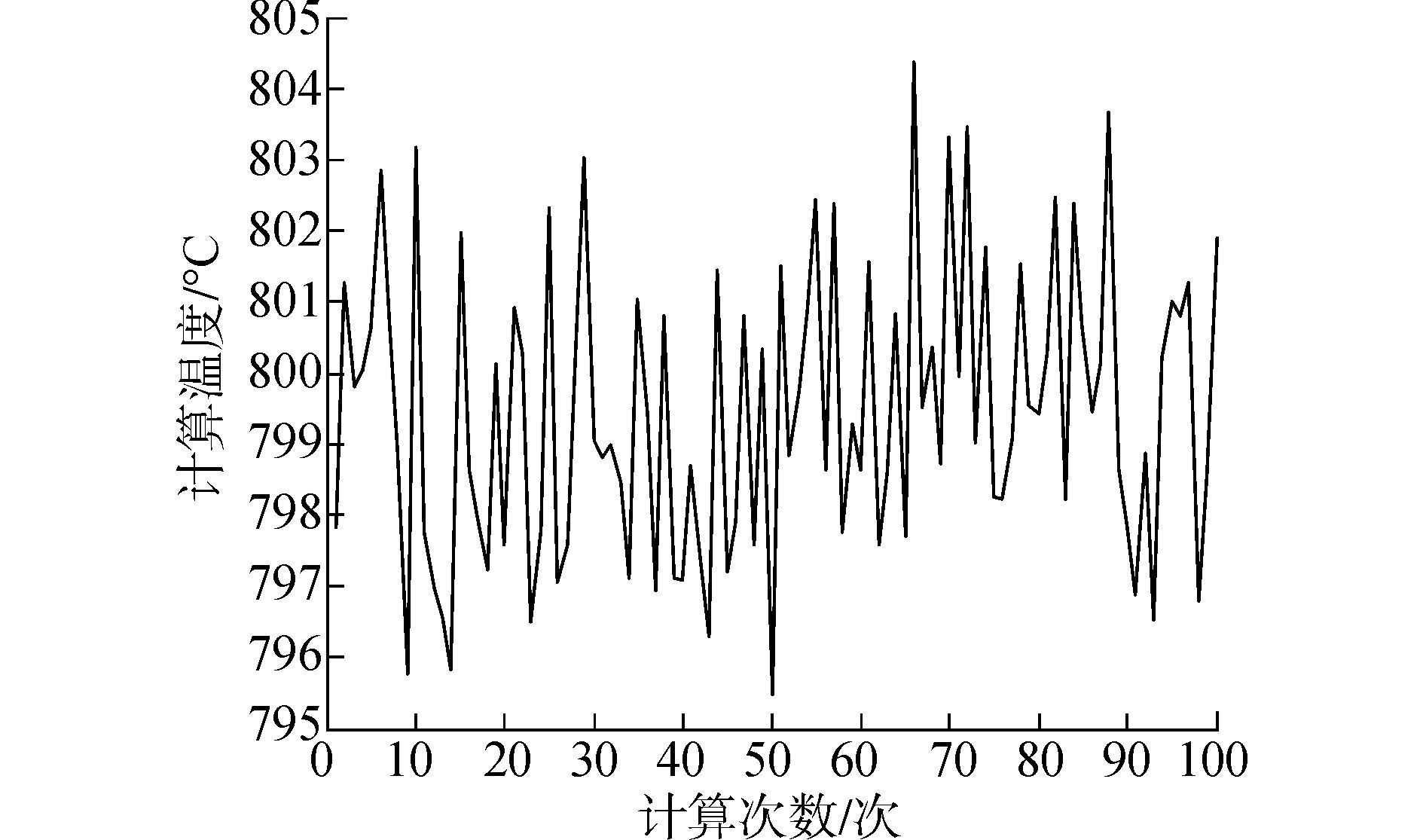
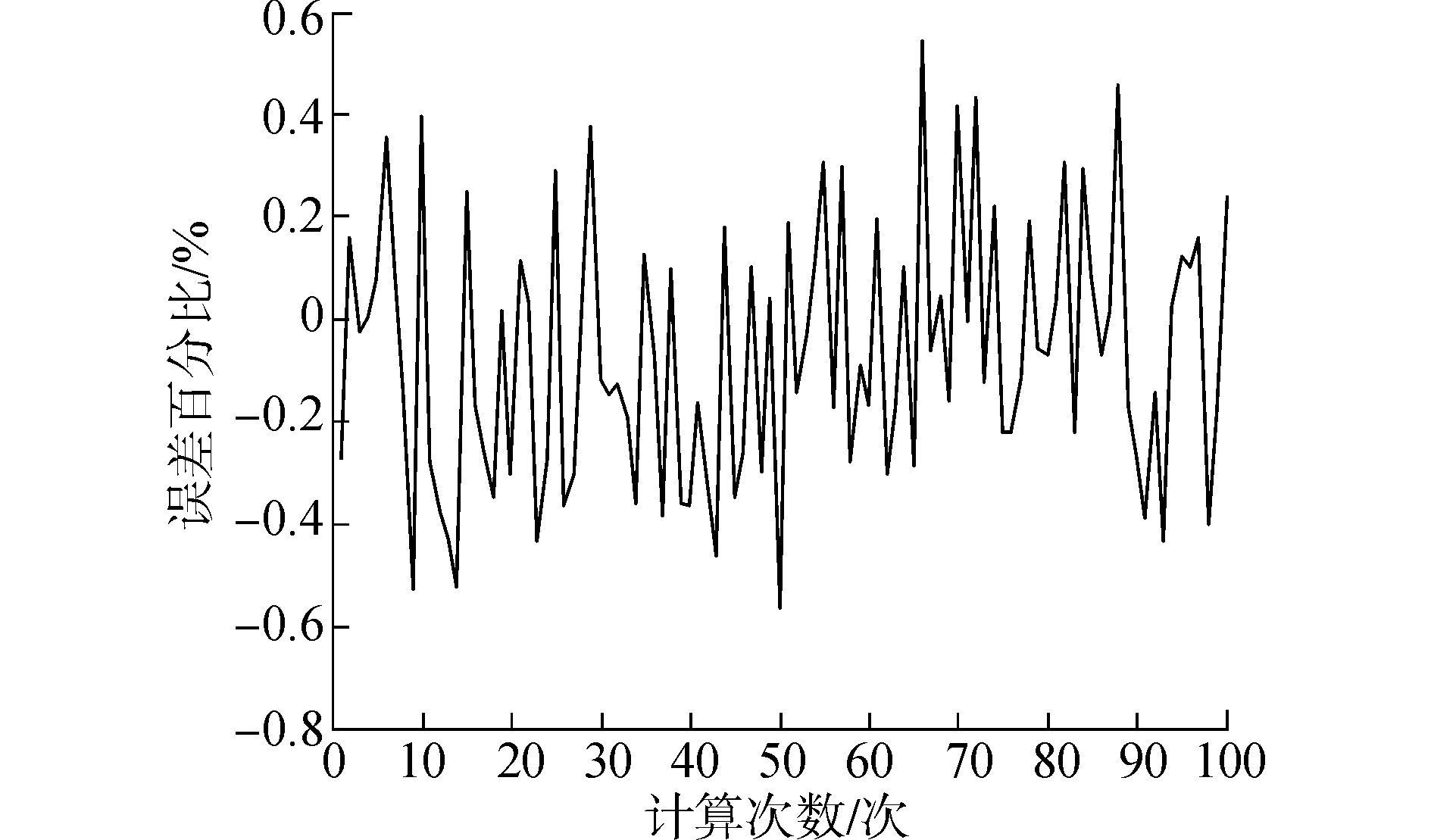
虽然算法的计算具有一定的随机性,但都在一个值左右浮动,为了比较算法的稳定性以及计算误差的大小,我们通过用该算法进行100次计算来比较算法的稳定性以及计算均值的误差大小。遗传算法100次计算结果和误差百分比如图 6、7所示。
|
| 图 6 遗传算法计算100次结果 |
|
| 图 7 遗传算法100次计算误差 |
通过遗传算法进行100次求解,求解的平均温度为799.452 2 ℃,最大计算值为804.368 8 ℃,最小计算值为795.475 0 ℃,最大误差百分比为0.57%。
3.2 NSGA-Ⅱ算法仿真结果NSGA-Ⅱ算法的参数设置如表 3所示。
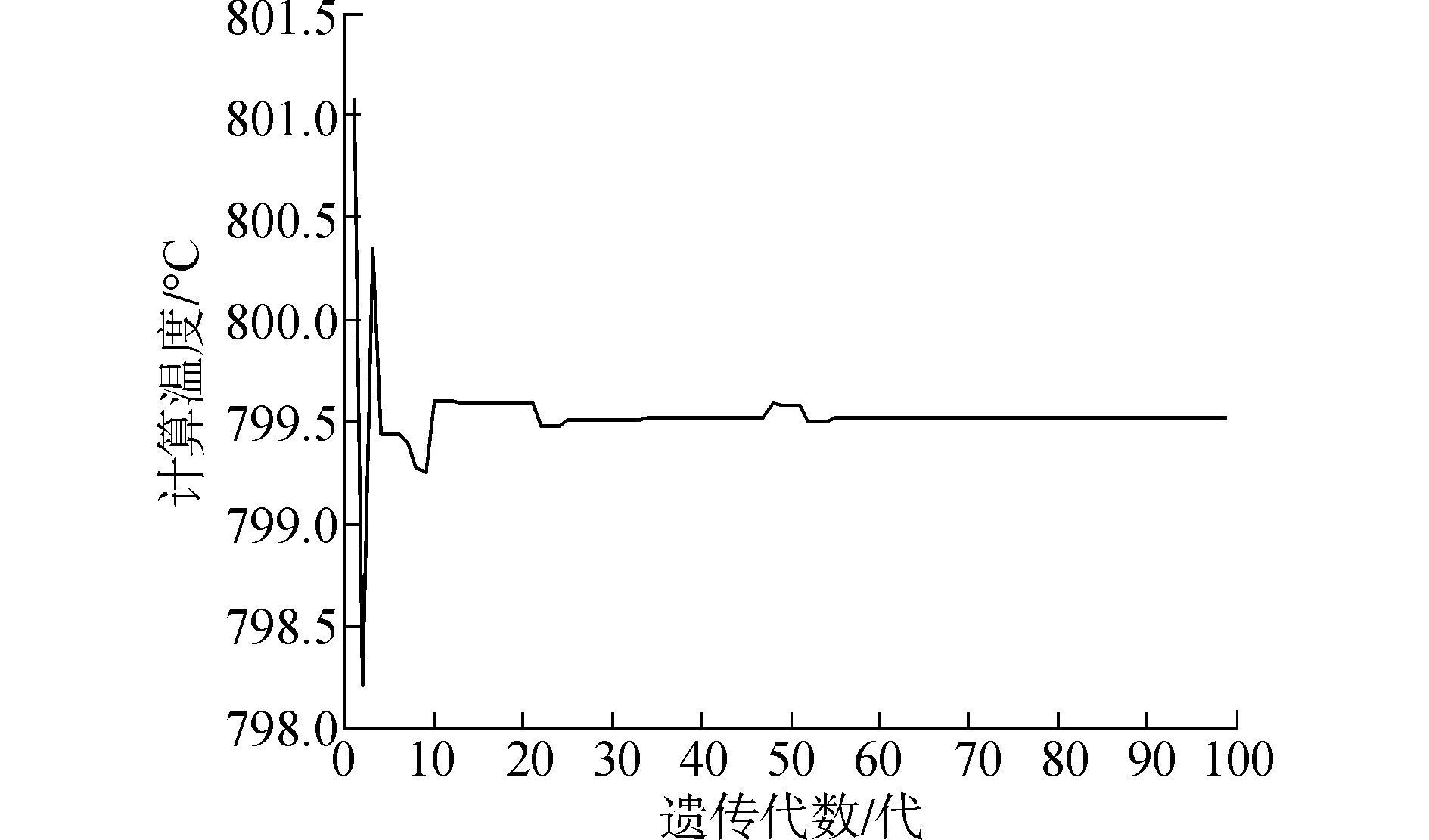
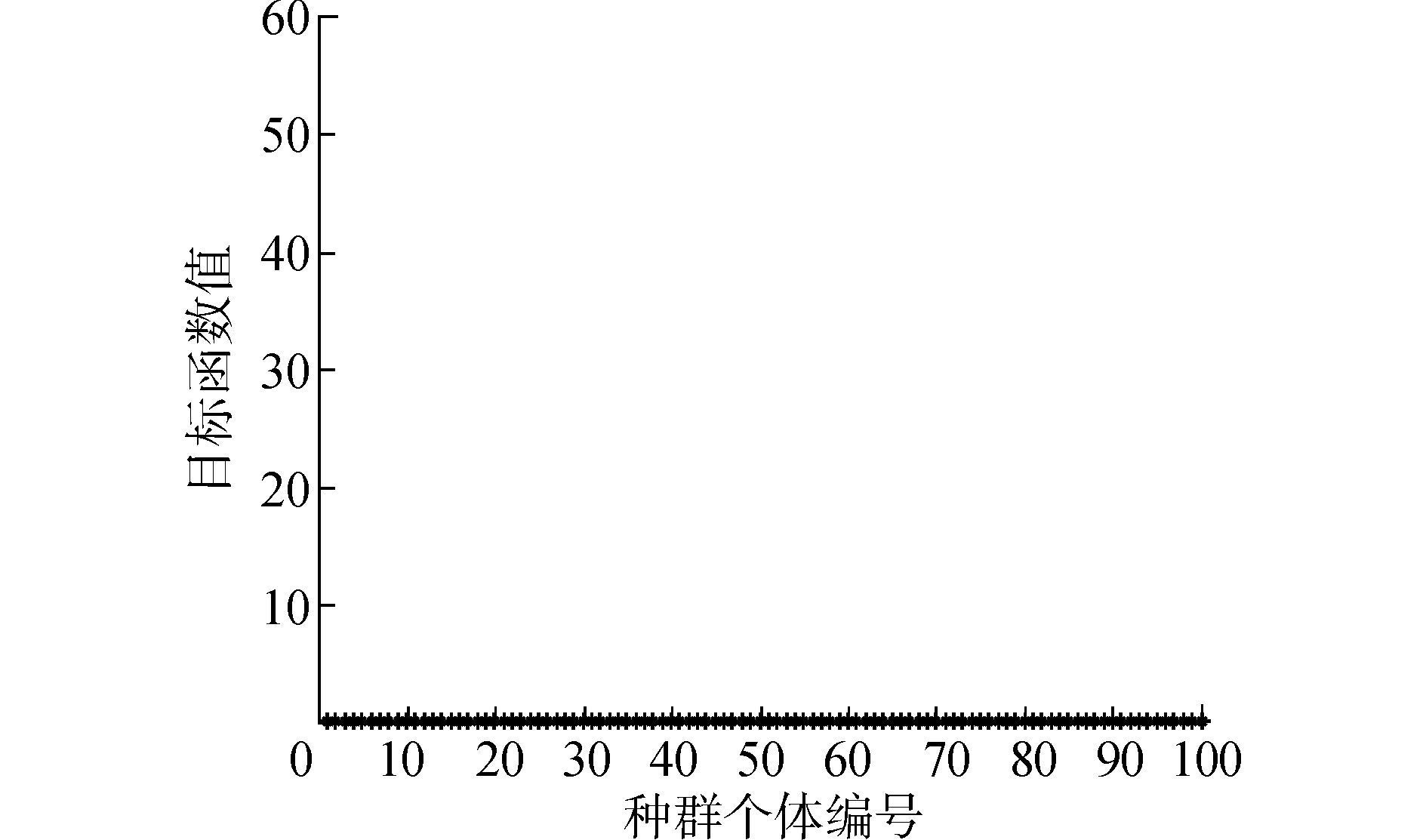
通过NSGA-Ⅱ算法求解的收敛代数以及最后一代解的目标函数值如图 8、9所示。
|
| 图 8 NSGA-Ⅱ算法最优解变化 |
|
| 图 9 最后一代种群特征 |
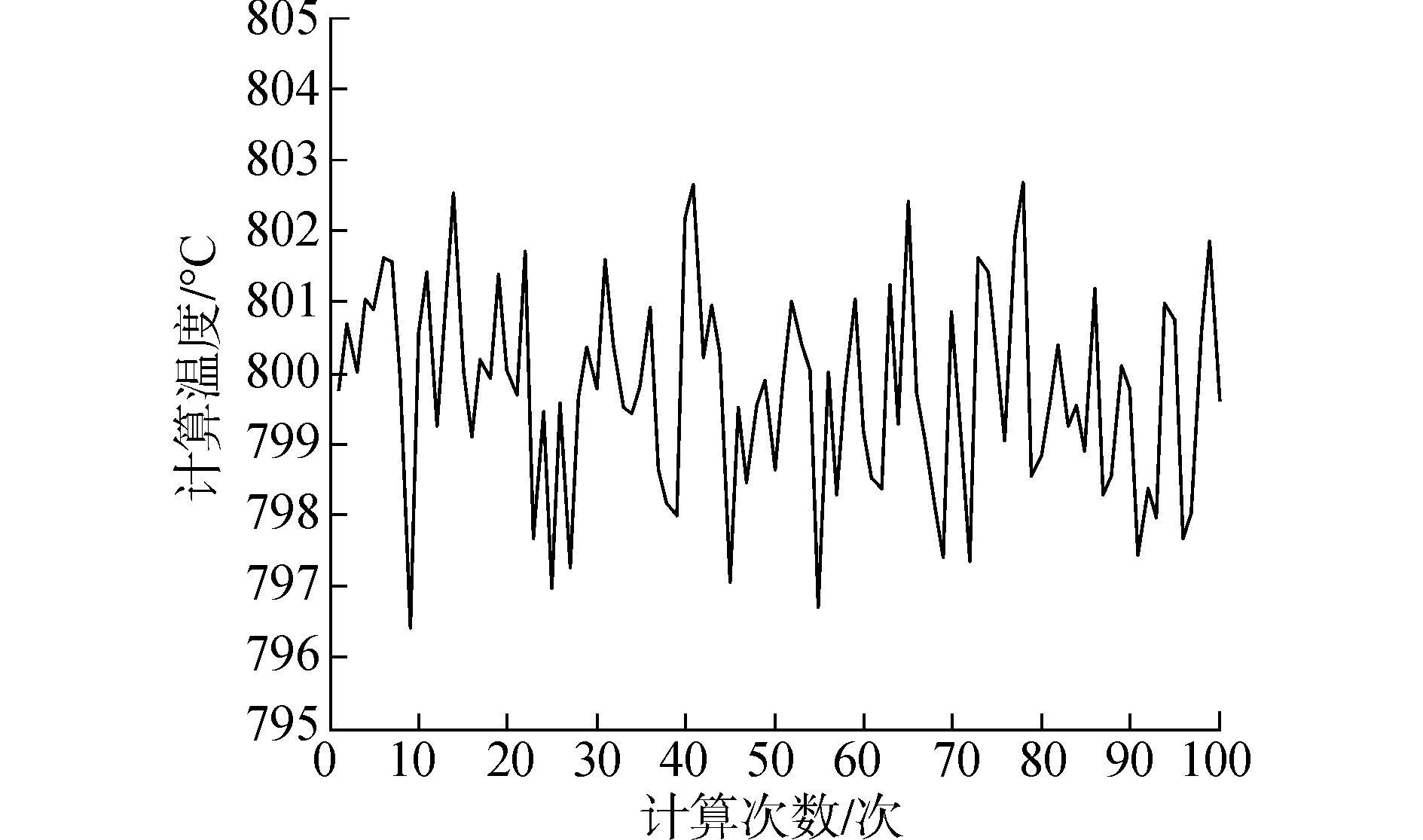
如图 8所示,NSGA-Ⅱ算法计算结果在50代左右收敛,求解的温度值趋于稳定。图 9中,最后一代的种群的个体都趋于最优解,解的分布明显好于遗传算法处理的结果。图 10、11是用NSGA-Ⅱ算法计算100次后的结果和计算的误差百分比。
|
| 图 10 NSGA-Ⅱ算法计算100次结果 |
|
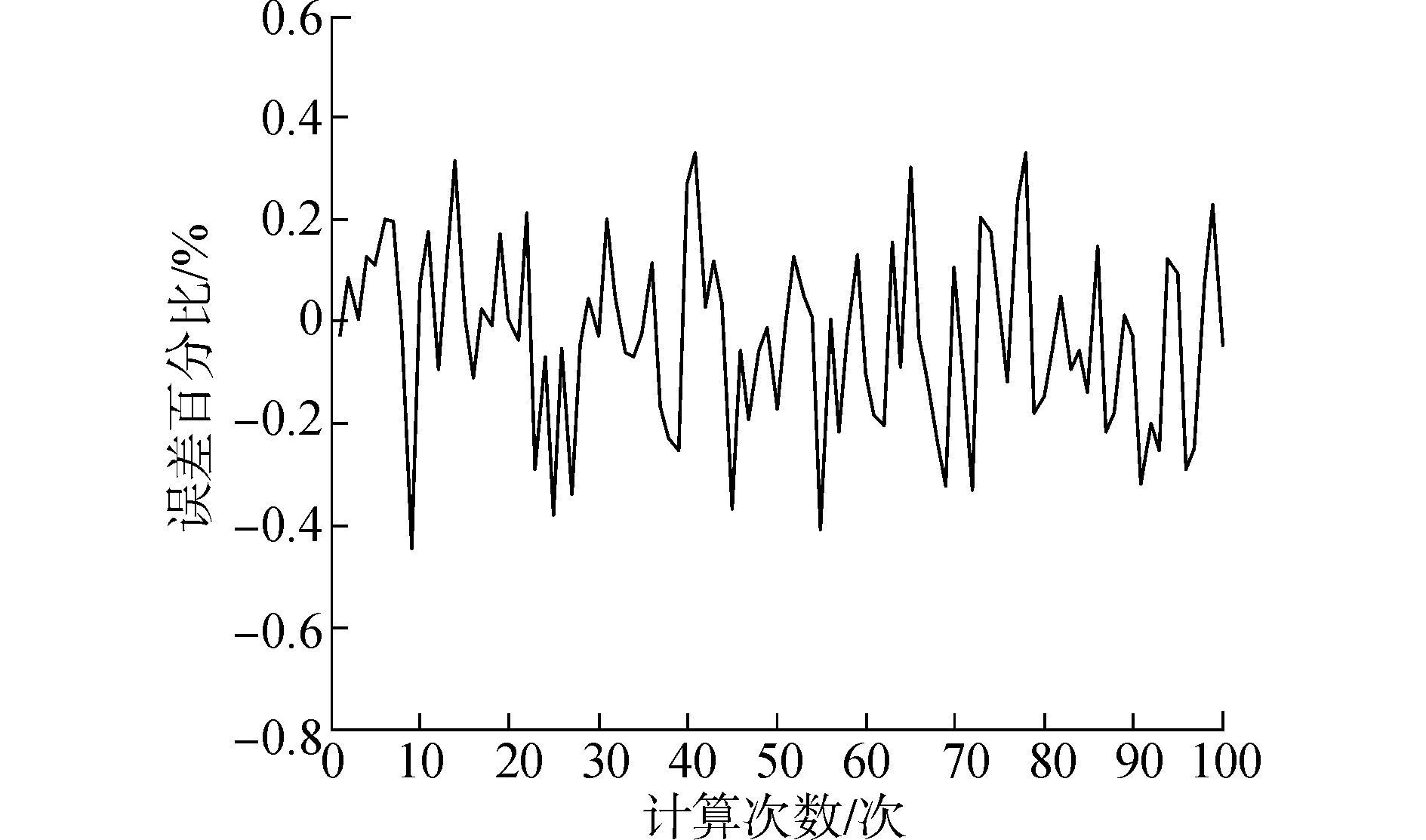
| 图 11 NSGA-Ⅱ算法计算误差百分比 |
100次求解的平均温度为799.763 5 ℃,最大温度为802.668 1 ℃,最小温度为796.420 1 ℃,最大误差百分比为0.44%,100次平均计算的精度高于传统的遗传算法,且在平均值左右浮动的幅度小于遗传算法的波动幅度,具有较好的稳定性。
3.3 改进NSGA-Ⅱ算法仿真结果改进NSGA-Ⅱ算法的参数设置如表 4所示。
通过改进的NSGA-Ⅱ算法对目标温度进行求解,其运算收敛代数以及最后一代解的目标函数值如图 12、13所示。
|
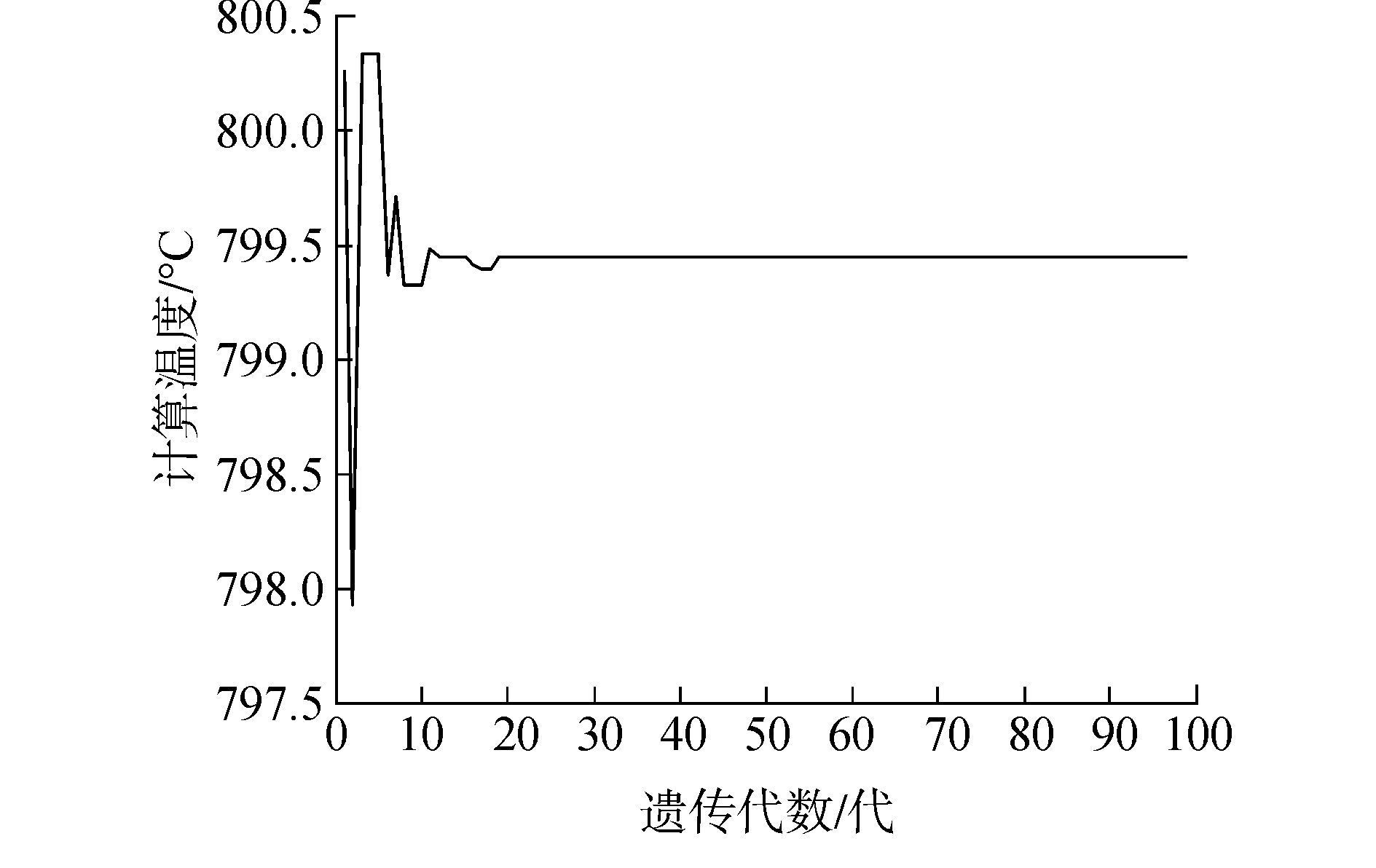
| 图 12 改进NSGA-Ⅱ算法最优解变化 |
|
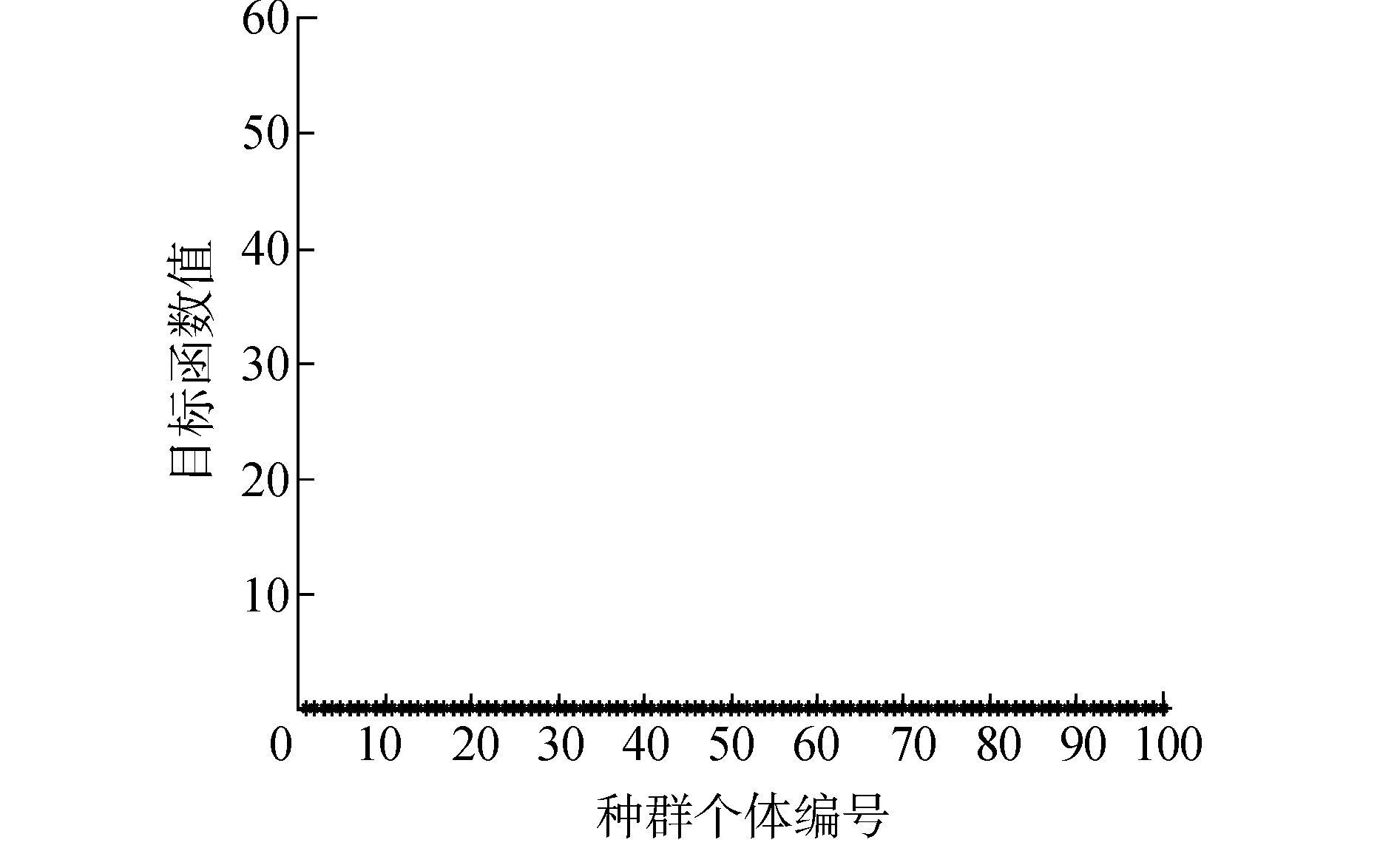
| 图 13 最后一代种群特征 |
如图 12所示,改进的NSGA-Ⅱ算法计算结果在20代左右收敛。图 13显示在最后一代的种群的个体中,所有个体的值都趋于最优解,说明在运算过程中优秀解的个体得到了很好的保留,在改进的过程中保留了传统NSGA-Ⅱ算法的优势,在种群中实现了良好的分布。
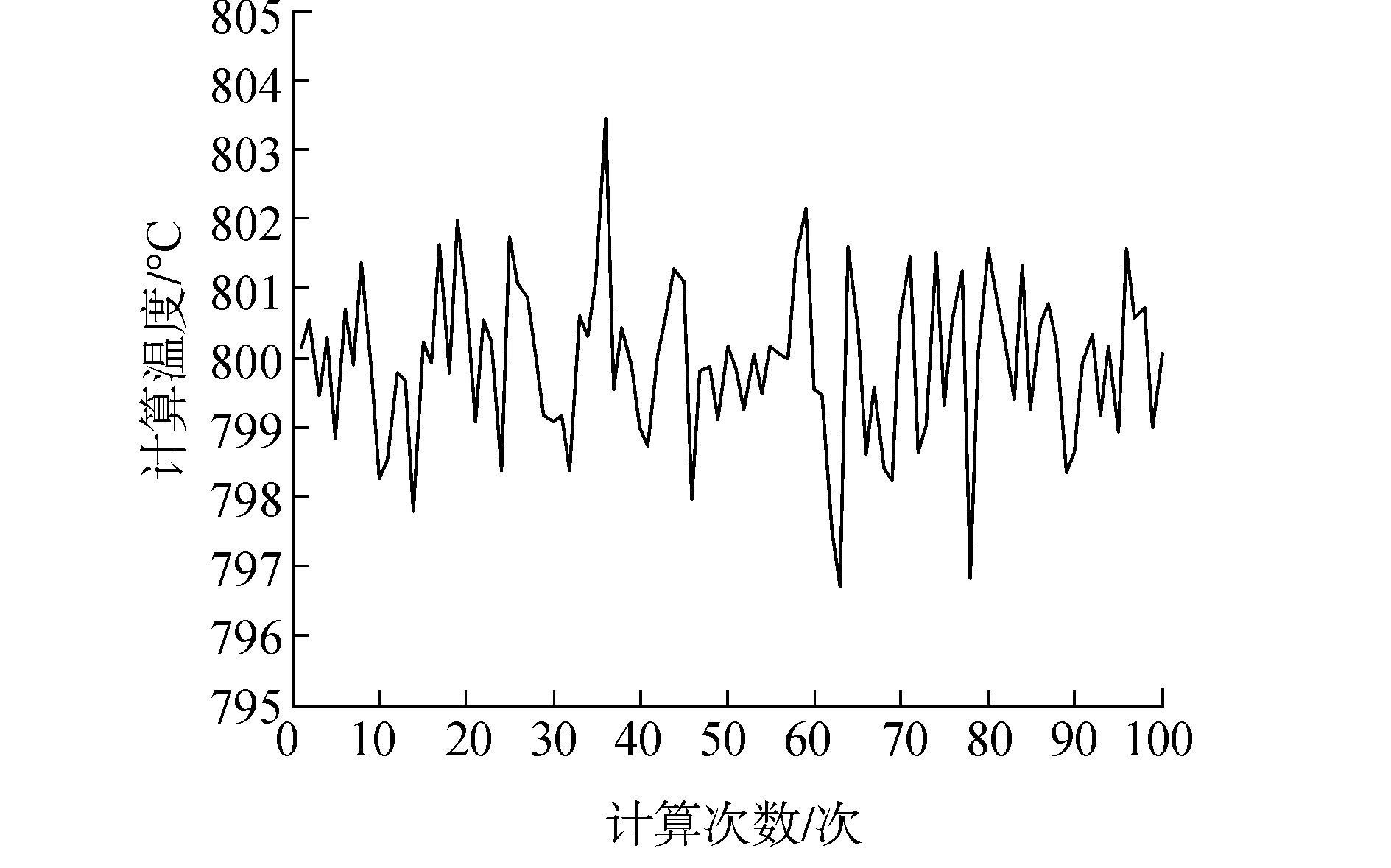
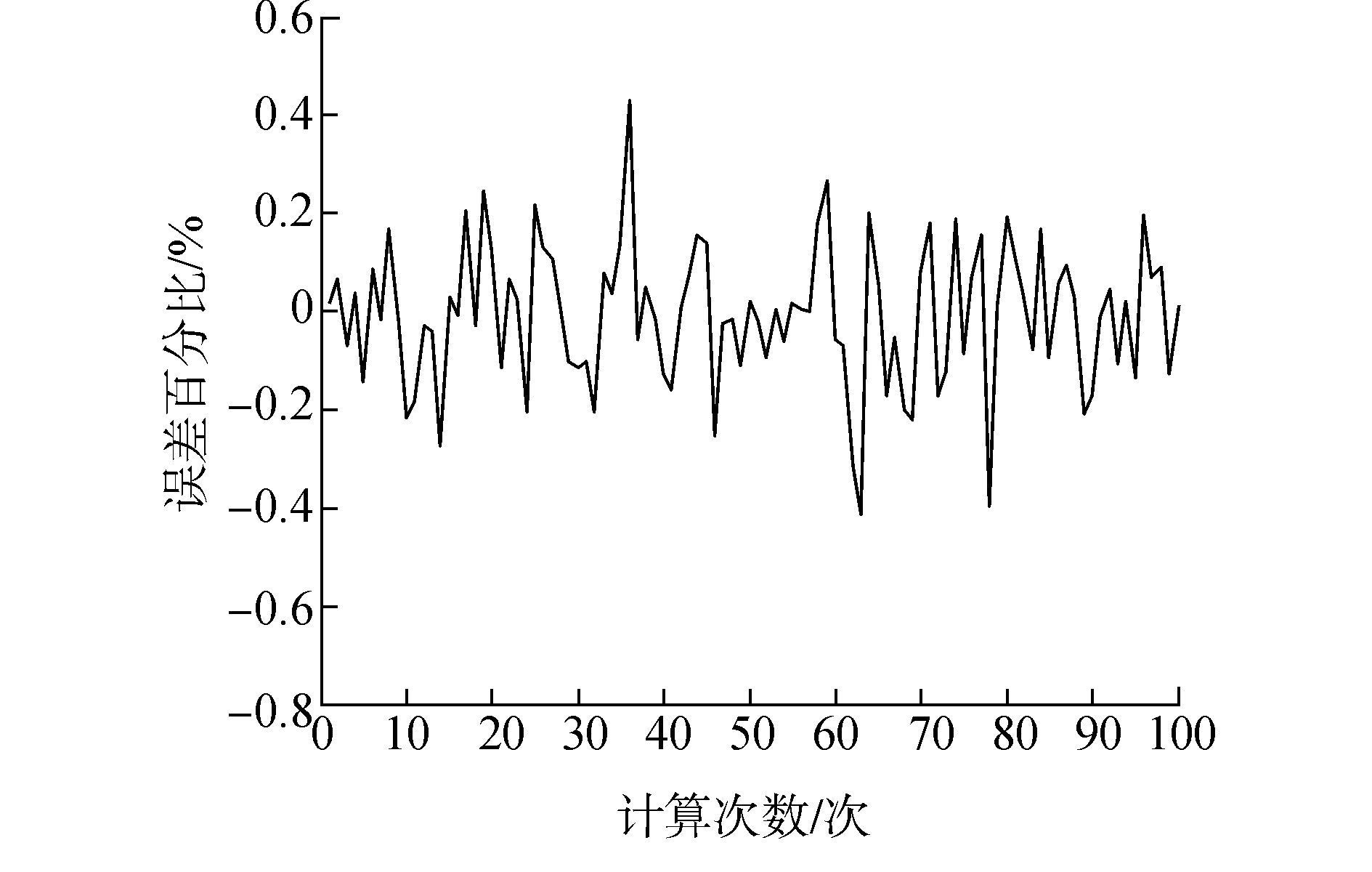
图 14、15是用改进的NSGA-Ⅱ算法计算100次后的结果和计算的误差百分比,100次求解的平均温度为799.935 1 ℃,最大温度为803.441 7 ℃,最小温度为796.696 9 ℃,最大误差百分比为0.41%,100次平均计算的精度高于之前的算法,且在平均值左右浮动的幅度很小,小于传统的NSGA-Ⅱ算法波动幅度,具有更好的稳定性。
|
| 图 14 改进NSGA-Ⅱ算法计算100次结果 |
|
| 图 15 改进NSGA-Ⅱ算法计算误差百分比 |
之前我们比较了算法的性能,在实际的测量过程中,物体发射率的大小对于温度求解的影响很大,因此在仿真过程中加入了不同发射率模型,在不同温度的条件下进行仿真,进一步比较算法求解的精度。
仿真中主要针对以下4种典型发射率模型进行温度求解。
1) A类:灰体材料 ελ=k;
2) B类:线性材料 ελ=kλ+b;
3) C类:对数线性材料 ln ελ=kλ+b;
4) D类:高阶材料 ελ=kλ2+b。
各类发射率材料不同温度下的计算结果如表 5所示,虽然针对不同类型材料误差的大小有所区别,但是相比较而言,改进NSGA-Ⅱ精度绝大部分都高于传统的遗传算法和传统的NSGA-Ⅱ算法,在数据处理上表现出了较好的准确度。
| 材料 | 温度/℃ | GA计算误差/℃ | NSGA-Ⅱ计算误差/℃ | 改进的NSGA-Ⅱ计算误差/℃ |
| 700 | -0.304 4 | 0.455 5 | -0.082 9 | |
| 750 | -0.502 3 | -0.059 6 | 0.006 7 | |
| A类 | 800 | -0.454 4 | -0.449 3 | 0.189 0 |
| 850 | -1.134 9 | -0.651 9 | 0.003 6 | |
| 900 | -0.531 6 | -0.275 0 | -0.111 6 | |
| 700 | -2.722 7 | -1.981 3 | -2.221 0 | |
| 750 | -2.933 2 | -2.359 6 | -2.101 0 | |
| B类 | 800 | -2.847 4 | -2.930 0 | -2.154 2 |
| 850 | -2.877 0 | -2.985 1 | -2.609 7 | |
| 900 | -2.881 9 | -2.992 2 | -2.370 7 | |
| 700 | 2.243 5 | 1.797 2 | 1.977 5 | |
| 750 | 2.453 6 | 1.885 1 | 2.432 9 | |
| C类 | 800 | 2.258 1 | 2.710 5 | 2.644 7 |
| 850 | 2.532 9 | 3.249 0 | 2.391 6 | |
| 900 | -0.397 6 | -2.922 0 | -2.630 2 | |
| 700 | -3.742 7 | -3.816 5 | -3.641 2 | |
| 750 | -3.148 6 | -3.839 1 | -3.639 2 | |
| D类 | 800 | -4.761 7 | -3.949 5 | -4.169 2 |
| 850 | -4.902 9 | -4.793 5 | -4.596 1 | |
| 900 | -5.488 9 | -5.212 3 | -5.094 2 |
4 结论
利用改进的NSGA-II算法对四光谱高温计获得的温度数据进行处理。通过仿真实验发现NSGA-Ⅱ算法虽然相比于遗传算法具有更高的精度和稳定性,但该算法存在参数相对固定,交叉、变异操作相对独立的问题。针对以上问题,做了如下工作:
1) 提出了自适应调整交叉、变异概率的方法解决算法中参数固定的问题,提高了种群动态寻优能力。
2) 利用NSGA-II算法与差分进化算法融合的策略来修改变异操作,避免了以前策略在变异时的盲目性。
3) 修改了交叉操作中的交叉因子,进一步增强了算法在进化过程中与种群信息的结合程度。
改进的NSGA-II算法相比传统的NSGA-II算法有着更好的精度和稳定性,最大误差仅为0.41%,并且改进NSGA-II算法对不同发射率类型的材料都有着很好的计算精度。但是本文使用的算法计算时间相对较长,还有待于进一步提升。
| [1] | 张崇关. 红外辐射温度测量关键技术研究[D]. 哈尔滨:哈尔滨工程大学, 2013:23-25. |
| [2] | SONG Feihu, XU Chuanlong, WANG Shimin, et al. Measurement of temperature gradient in a heated liquid cylinder using rainbow refractometry assisted with infrared thermometry[J]. Optics communications, 2016, 380: 179-185 DOI:10.1016/j.optcom.2016.06.011 |
| [3] | 孙晓刚, 李成伟, 戴景民, 等. 多光谱辐射测温理论综述[J]. 计量学报, 2002, 23(4): 248-250 |
| [4] | 邓兴凯, 杨永军. CCD多光谱辐射测温技术的应用与发展[J]. 计测技术, 2011, 31(1): 45-49 |
| [5] | 孙晓刚, 原桂彬, 戴景民. 基于遗传神经网络的多光谱辐射测温法[J]. 光谱学与光谱分析, 2007, 27(2): 213-216 |
| [6] | 张彩虹. 多光谱温度计的数据处理方法研究[D]. 哈尔滨:哈尔滨工业大学, 2006:30-32. |
| [7] | ABDULHALIM M F, ATTEA B A. Multi-layer genetic algorithm for maximum disjoint reliable set covers problem in wireless sensor networks[J]. Wireless personal communications, 2015, 80(1): 203-227 DOI:10.1007/s11277-014-2004-8 |
| [8] | BETTI M, FACCHINI L, BIAGINI P. Damage detection on a three-storey steel frame using artificial neural networks and genetic algorithms[J]. Meccanica, 2015, 50(3): 875-886 DOI:10.1007/s11012-014-0085-9 |
| [9] | 孟红云. 多目标进化算法及其应用研究[D]. 西安:西安电子科技大学, 2005:34-62. |
| [10] | XU Zhitao, MING X G, ZHENG Maokuan, et al. Cross-trained workers scheduling for field service using improved NSGA-II[J]. International journal of production research, 2015, 53(4): 1255-1272 DOI:10.1080/00207543.2014.955923 |
| [11] | 崔庆勇. 基于改进NSGA-Ⅱ算法的多目标FJSP研究[D]. 昆明:昆明理工大学, 2015:30-35. |
| [12] | PARK S Y, LEE J J. An efficient differential evolution using speeded-up k-nearest neighbor estimator[J]. Soft computing, 2014, 18(1): 35-49 DOI:10.1007/s00500-013-1030-x |
| [13] | KARMAKAR A, GHATAK R, MISHRA R K, et al. Sierpinski carpet fractal-based planar array optimization based on differential evolution algorithm[J]. Journal of electromagnetic waves and applications, 2015, 29(2): 247-260 DOI:10.1080/09205071.2014.997837 |
| [14] | 余廷芳, 王林, 彭春华. 改进NSGA-Ⅱ算法在锅炉燃烧多目标优化中的应用[J]. 计算机应用研究, 2013, 30(1): 179-182 |
| [15] | OKABE M, SHAHRIN M, AOKI H. Network expansion planning using improved controlled NSGA-II[J]. Electrical engineering in Japan, 2015, 193(4): 38-48 DOI:10.1002/eej.2015.193.issue-4 |
| [16] | WANG Long, WANG Tongguang, LUO Yuan. Improved non-dominated sorting genetic algorithm (NSGA)-II in multi-objective optimization studies of wind turbine blades[J]. Applied mathematics and mechanics, 2011, 32(6): 739-748 DOI:10.1007/s10483-011-1453-x |



