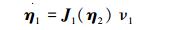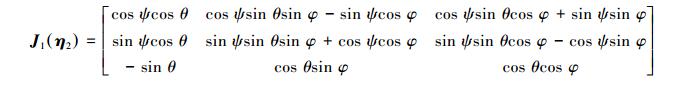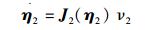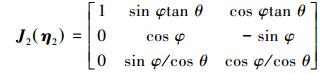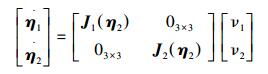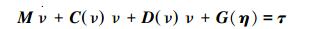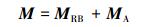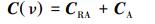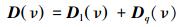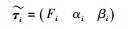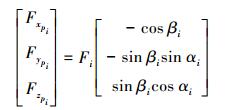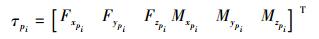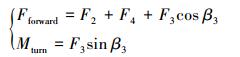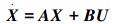2. School of Automation, Beijing Institute of Technology, Beijing 100081, China;
3. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
传统的水下机器人通常由螺旋桨产生前向推力,依靠尾部舵面进行航向控制。为了保证舵面能够产生足够的控制效果,要求水下机器人需以一定的速度运动。矢量喷水推进是一种特殊的推进方式,其推力通过推进水泵喷出水流的反作用力获得,通过调节水泵的推进方向实现水下机器人的操纵。矢量喷水推进器具有常规螺旋桨所不及的一些优点,例如抗空泡能力强、附体阻力小、保护性能好、噪音低、适应变工况的范围大[1-2]。此外,相比于舵面调整,矢量推进的优势还在于在任何航速下,尤其是低速条件下,都可以使水下机器人具有良好的机动性能[3]。因此,矢量推进系统成为业界的研究热点。文献[4]提出了配备三自由度矢量喷水推进器AUV的概念设计;文献[5]提出了一种基于霍尔效应的多通道矢量推进器的概念设计;文献[6]对矢量喷水推进AUV的控制进行了仿真。上述理论探索与实践虽取得一些成果,但仍然存在一些问题,如相关的理论建模、数值仿真和实验验证并不系统和完整,缺乏有力的理论支撑和数据支持,尤其是缺少原理样机的实验验证。文中力图通过矢量喷水推进式水下机器人的建模仿真与验证,改善上述不足。
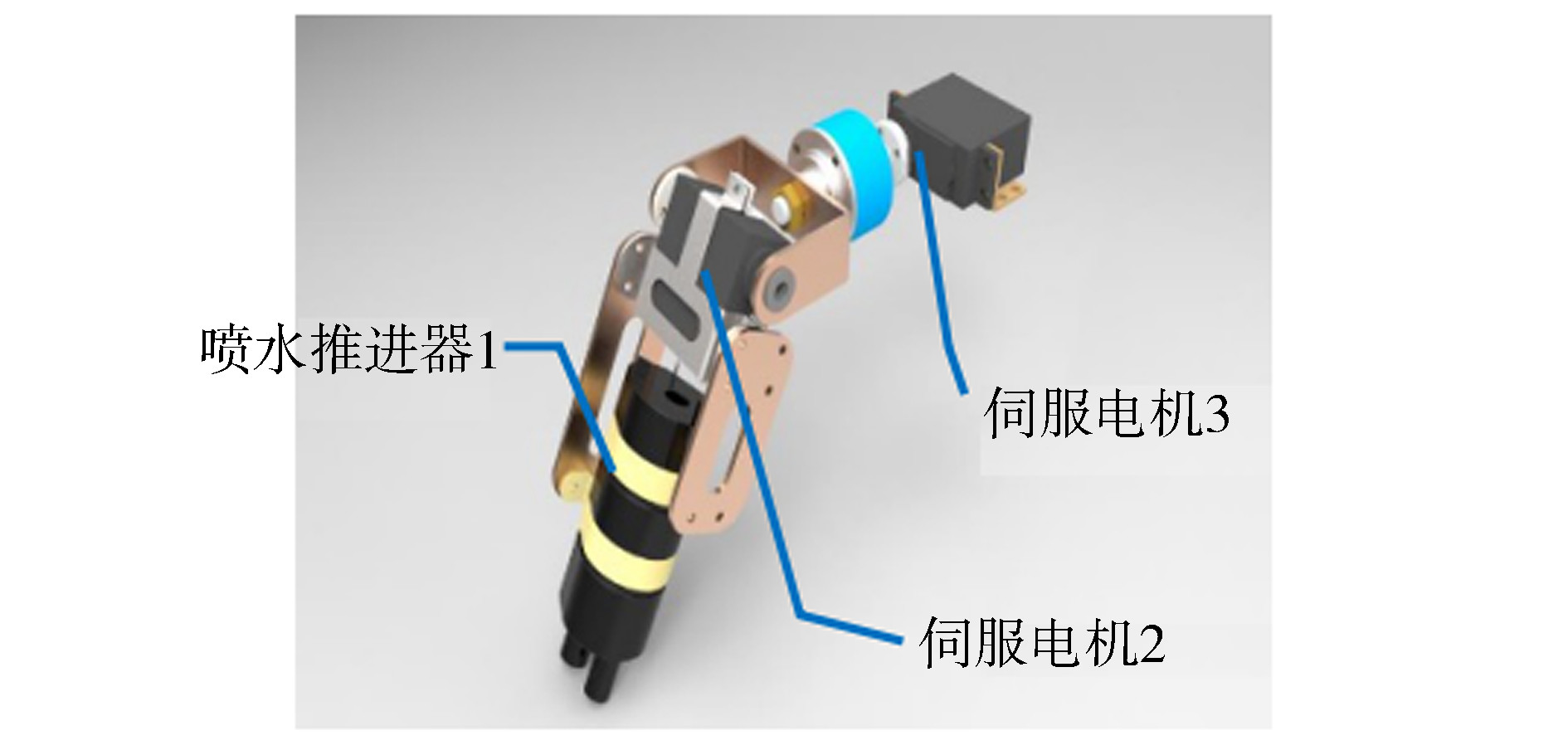
1 多自由度矢量喷水推进式水下机器人系统模型的建立设计了一款矢量喷水推进式水下机器人如图 1。该机器人具有圆盘式外型和4组二自由度推力臂,其特点一是具有多动力均匀对称布局,二是推力臂末端的喷水推进器1通过两个相互正交的电机2和电机3实现在三维空间任意方位的定位[7],如图 2。机器人可通过4条推力臂上喷水推进动力的协调组合来适应不同的运动要求和变化的水下环境。

|
| 图 1 水下机器人实物样机和虚拟样机 |
|
| 图 2 频域脉冲压缩方法框图 |
由于该机器人共有12个自由度,如何协调控制多自由度,实现机器人在水中自由调整运动姿态是设计时必须解决的问题。因而建立水下机器人运动学和动力学模型,提出完整的机器人运动控制方案是十分必要的。为此,首先建立水下机器人推进系统模型,分析矢量推进作用对机器人运动姿态的影响,并提出机器人多自由度协调控制策略,然后采用MATLAB软件进行仿真,指导样机制作,最后进行样机的水中运动实验验证。
1.1 水下机器人的数学模型为了给出水下机器人的运动学和动力学模型,引入固联于地球的大地坐标系E{E-xyz}和固联于机器人的体坐标系S{S-xSySzS},体坐标系原点位于机器人重心处[8]。机器人在大地坐标系下的位置和姿态分别用向量η1=(x, y, z) 和η2=(φ, θ, ψ) 表示。机器人在体坐标系下的线速度和角速度分别用ν1=(u, v, w) 和ν2=(p, q, r) 表示。
1.2 水下机器人的运动学模型根据文献[9],水下机器人的线速度可表示为
式中J1(η2) 是关于欧拉角的转换矩阵:
角速度可以表示为
式中:
从体坐标系到大地坐标系下的转换为
即
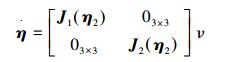 |
(1) |
(1) 即为水下机器人运动学方程。
1.3 水下机器人的动力学模型根据文献[10-11],对水下机器人进行受力分析,列出机器人动力学方程:
式中:M∈R6×6为包括附加质量的机器人惯性矩阵:
式中:MRB为刚体惯性矩阵,MA为附加质量。
C(ν)∈R6×6为科氏力矩阵:
式中:CRA为刚体科氏力,CA为附加质量的科氏力。
D(ν)∈R6×6为阻尼矩阵:
式中:Dl(ν) 为线性阻尼,Dq(ν) 为非线性阻尼。
G(η)∈R6为恢复力和恢复力矩,τ∈R6为推进力和推进力矩。下面根据机器人的系统结构推导τ的具体表达式。
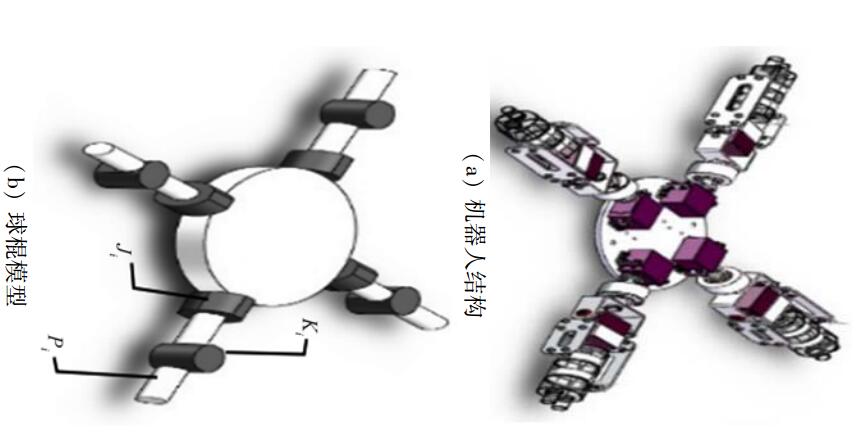
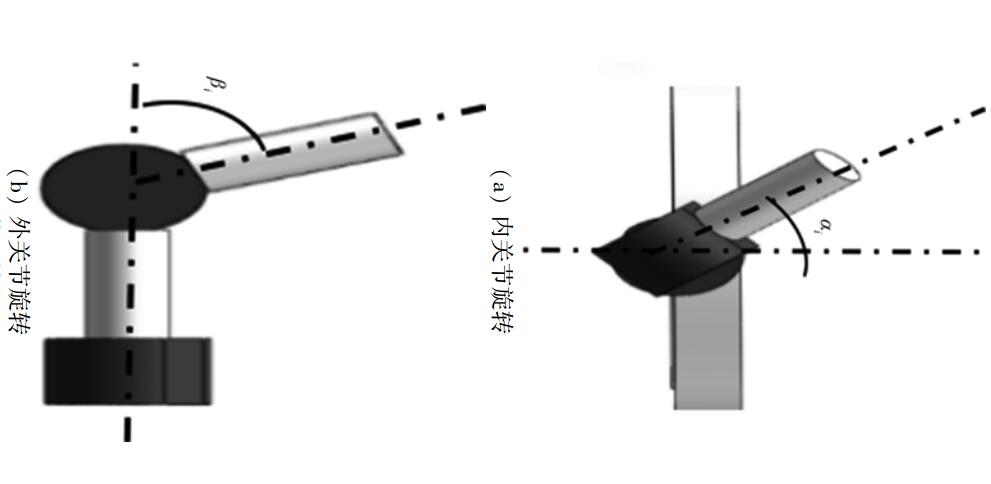
2 矢量喷水推进式水下机器人结构模型 2.1 水下机器人结构模型的简化为了正确表述水下机器人推进系统模型,简化复杂的机械结构,突出各自由度的相互关系,用简明的球棍模型代替,如图 3所示。其中i=1, 2, 3, 4表示推力臂序号,Ji表示内关节,Ki表示外关节,Pi表示喷水推进器喷口,Fi为推力大小,αi为内关节旋转角度,βi为外关节旋转角度,旋转角度方向的定义如图 4所示,由于硬件限制,关节旋转角度满足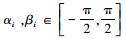
|
| 图 3 机械结构的简化 |
|
| 图 4 关节旋转角度定义 |
为了描述各个推力臂的角度状态,分别引入固联于各个推力臂的坐标系Pi:{Pi-xPiyPizPi},其中i=1, 2, 3, 4,如图 5所示。
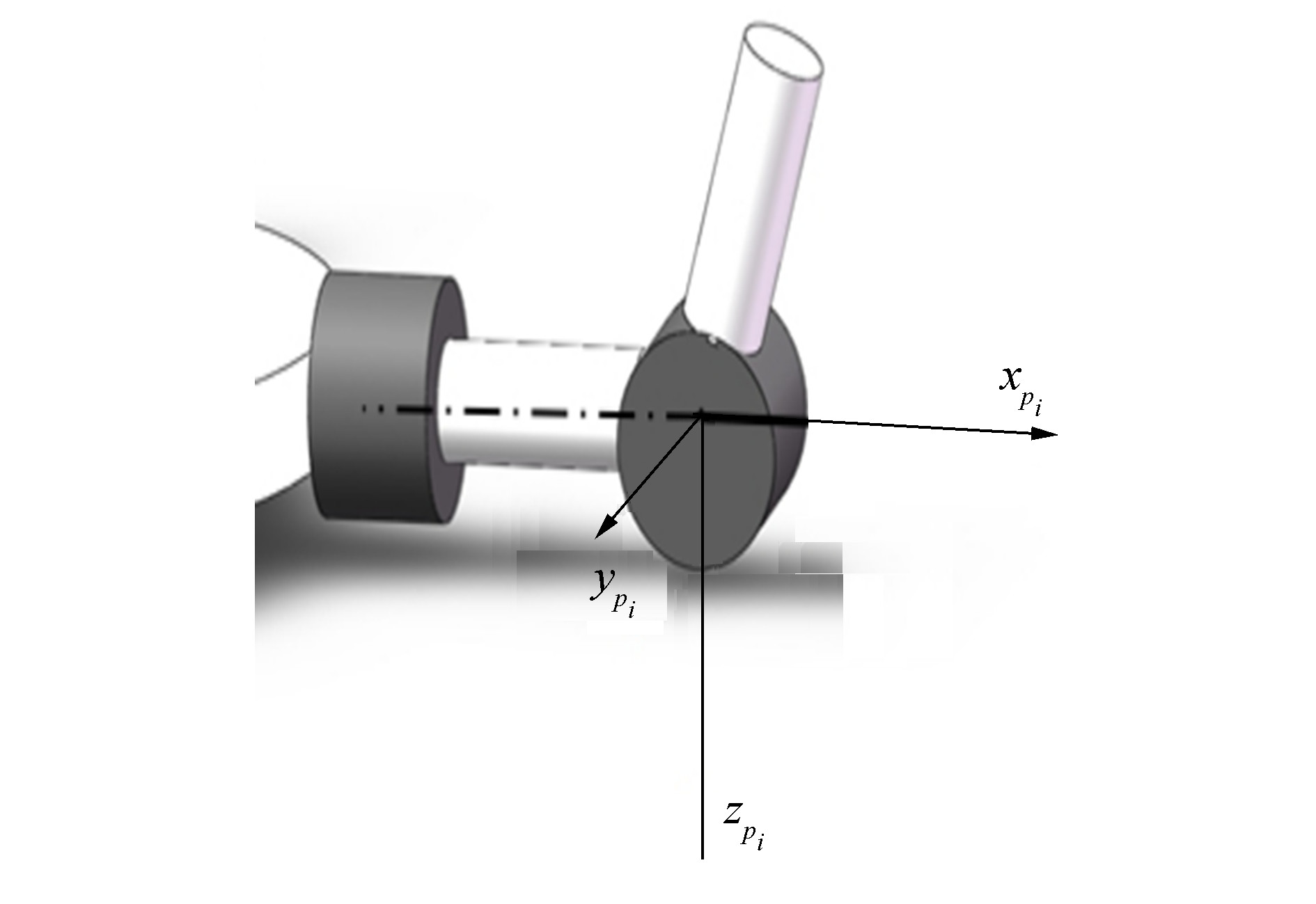
|
| 图 5 推力臂坐标系 |
分别引入固联于各个推力臂的坐标系,各坐标系原点位于各推力臂外关节点 (即推力的等效作用点),xPi的方向沿推力臂中心线方向向外,zPi的方向与zS的方向保持一致。则推力在该坐标系下的分解:
令
得到平移后的推力表达式:τi=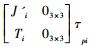
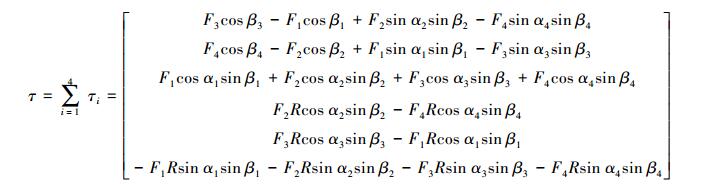 |
(2) |
式 (2) 表达了推进系统对水下机器人的作用,式中包含了机器人推进系统的12个可控自由度。可以看到,推进系统总推力在轴方向分量以及在轴方向扭矩与12个自由度都有联系,这意味着如果分别控制各个自由度,就能控制水下机器人的升沉运动与旋转运动。
3 水下机器人虚拟样机的理论建模与参数分析 3.1 几何模型的建立为方便在ADAMS中进行动力学仿真,用简单几何体建立水下机器人刚体模型。其中机器人上盖、中腰、下盖以及内部结构的质量归入主体,与推进器相关的质量归入喷桶,与外围舵机和支撑架相关的质量归入铰链。主体和铰链之间的相对运动只有转动,故采用revolute-joint进行连接,喷桶与铰链之间并没有相对运动,可采用fixed-joint进行连接。在ADAMS环境中,铰链形式方便修改,为水下机器人复杂动作的仿真创造了条件。
根据对机器人样机实体测量及所用推进器参数给定,得到样机模型各部分尺及动力学参数见表 1。
| 部位名称 | 参数 |
| 机身直径/mm | 310 |
| 机身高度/mm | 150~176 |
| 推力臂长度/mm | 97 |
| 推进器长度/mm | 80 |
| 推力臂扭矩/(N·m) | 40 |
| 推进器推力/N | 34 |
3.2 虚拟样机的水动力设置
要真实模拟水下机器人的运动状态,水动力的影响不可忽视。由文献[14]可知,水下机器人受到的水动力作用可简化为由角速度、线速度和惯性力引起的非线性水阻力及阻力矩。那么可在虚拟样机的质心处设置水阻力和阻力矩,完成水下机器人水动阻力模型的建立。根据文献[10-15],由Morison公式,考虑在XY平面内做平面运动的圆柱体,得到其与运动相反方向的水动阻力大小为
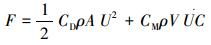 |
(3) |
式中:CD和CM分别为阻力系数和附加质量系数;ρ为水密度;V和A分别为圆柱的体积和截面积,R和L分别为圆柱体的半径和长度,U和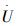
|
| 图 6 水下机器人虚拟样机及实物 |
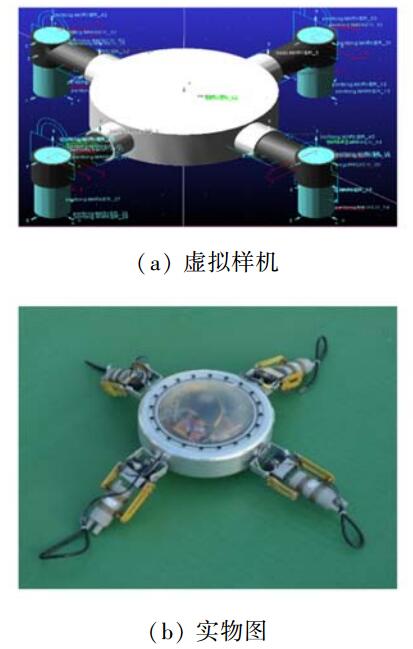
令内关节角度α=90°保持恒定,调节推力大小F与外关节角度β,实现机器人的旋转,如图 7所示。
|
| 图 7 旋转运动控制 |
旋转推力矩大小
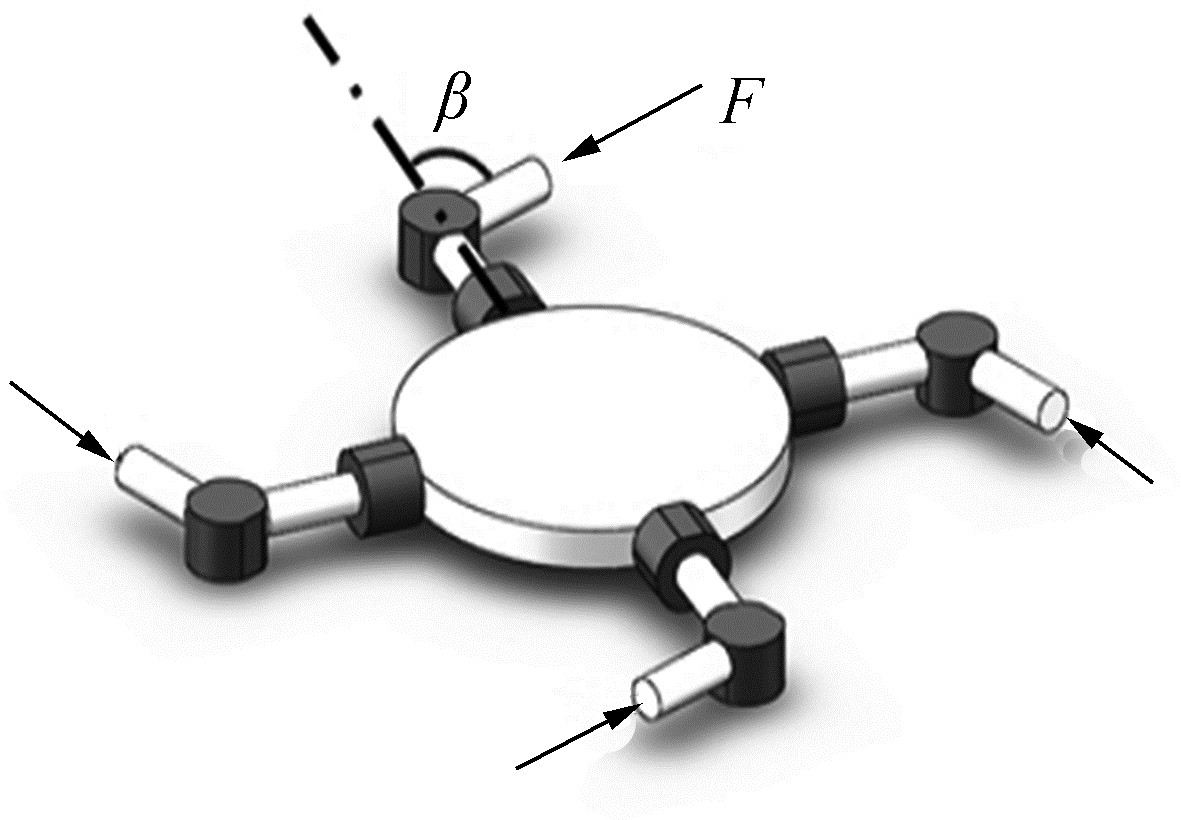
利用虚拟样机对机器人在水下的旋转运动进行仿真可得仿真曲线,如图 8所示。
|
| 图 8 自旋运动过程中姿态变化 |
分析图 8(a)可见,机器人在自旋过程中经过短暂的俯仰角剧烈波动后可以很快恢复为稳定的俯仰角状态,表明所设计的机器人结构可使其完成相应的自旋运动,而不会发生侧翻等情形。分析图 8(b)、8(c)可知机器人在4个喷桶推力的作用下完成稳定的旋转运动,而且由于水动阻力的存在,旋转角速度并不会随时间的增加而剧烈加快,而是逐渐加快,符合实物样机实验的结果。
3.3.2 水平移动控制当机器人水平移动时,希望推力系统提供前进的推力和实现转向的力矩。由于机器人推力臂呈对称分布,当机器人朝某个方向前进时,存在一个推力臂其推力方向与机器人前进方向相反,故在一般情况下该推力臂需要停止工作,只在机器人减速时起制动作用。机器人移动区域和移动方向划分如图 9、10所示。
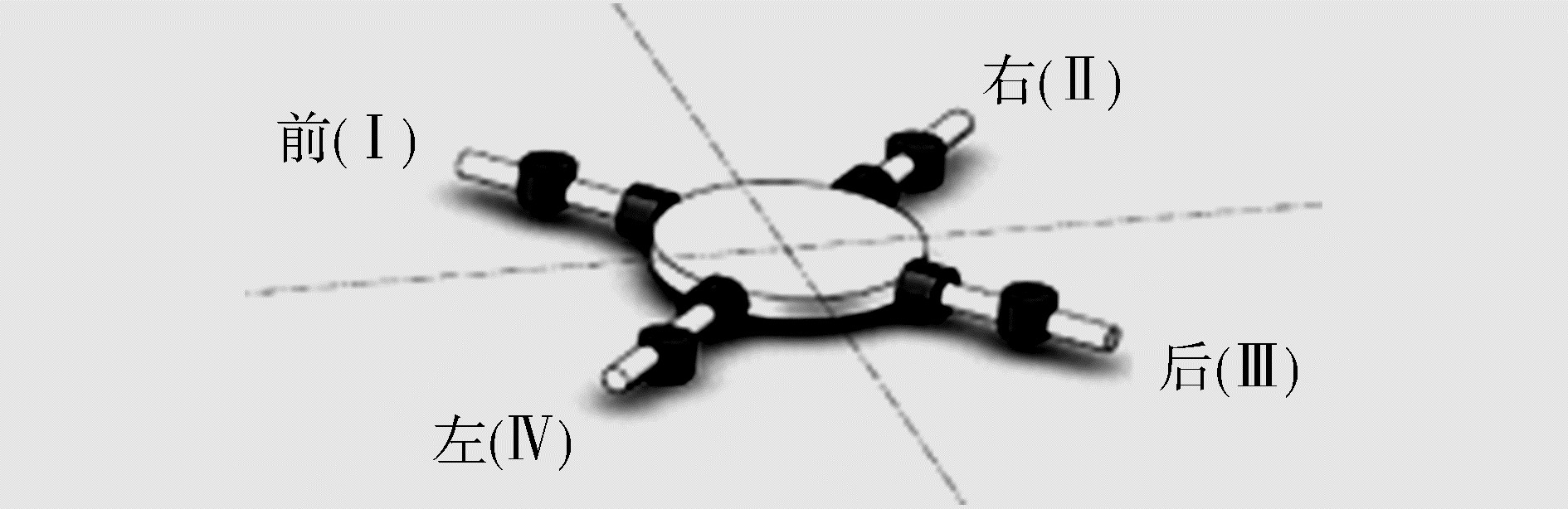
|
| 图 9 水平移动四区域划分 |
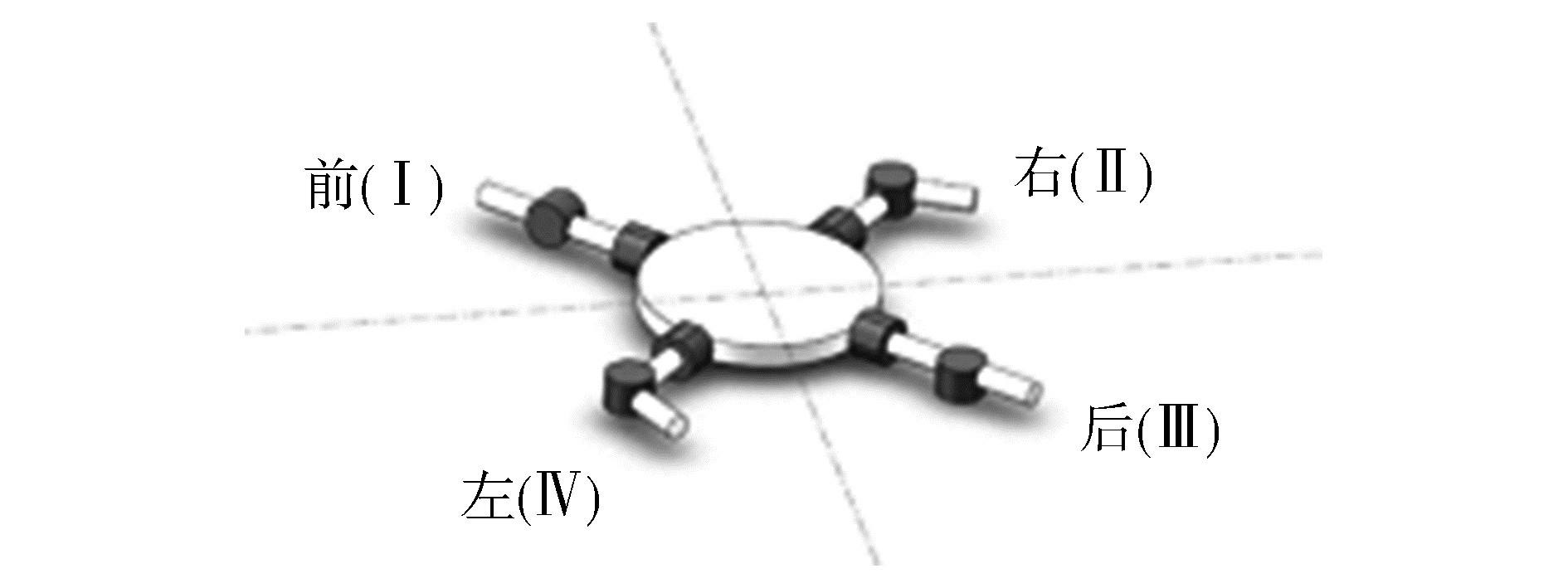
|
| 图 10 机器人向前区某方向移动 |
将上述控制方案代入式 (3),得到机器人前进推力及转矩表达式为
利用虚拟样机对机器人的水平移动进行仿真,可得运动曲线如图 11。
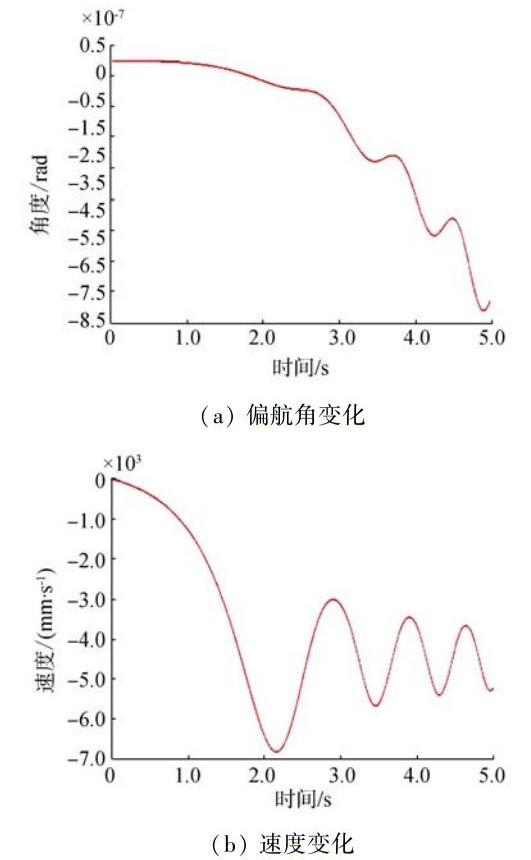
|
| 图 11 水平运动偏航角及速度变化 |
分析图 11(a)可知,在水平运动时,由于结构前后非对称和水动阻力的存在,机器人的运动会产生不超过1°的偏航角,由于其偏航角会逐渐变大,为了确保机器人可靠运动,在运动过程中需对偏航角进行调控。由图 11(b)可知,机器人整体速度虽有波动但总体趋势上是增加的,这和实物样机实验结果是一致的。
3.3.3 快速换向运动控制根据文献[14]可知,在低速条件下,水下机器人模型可近似简化为线性模型。因此在低速时机器人的状态空间模型可简化为
其中,X=[u, v, r]T,A=M-1(CRA+D),B=M-1,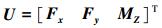
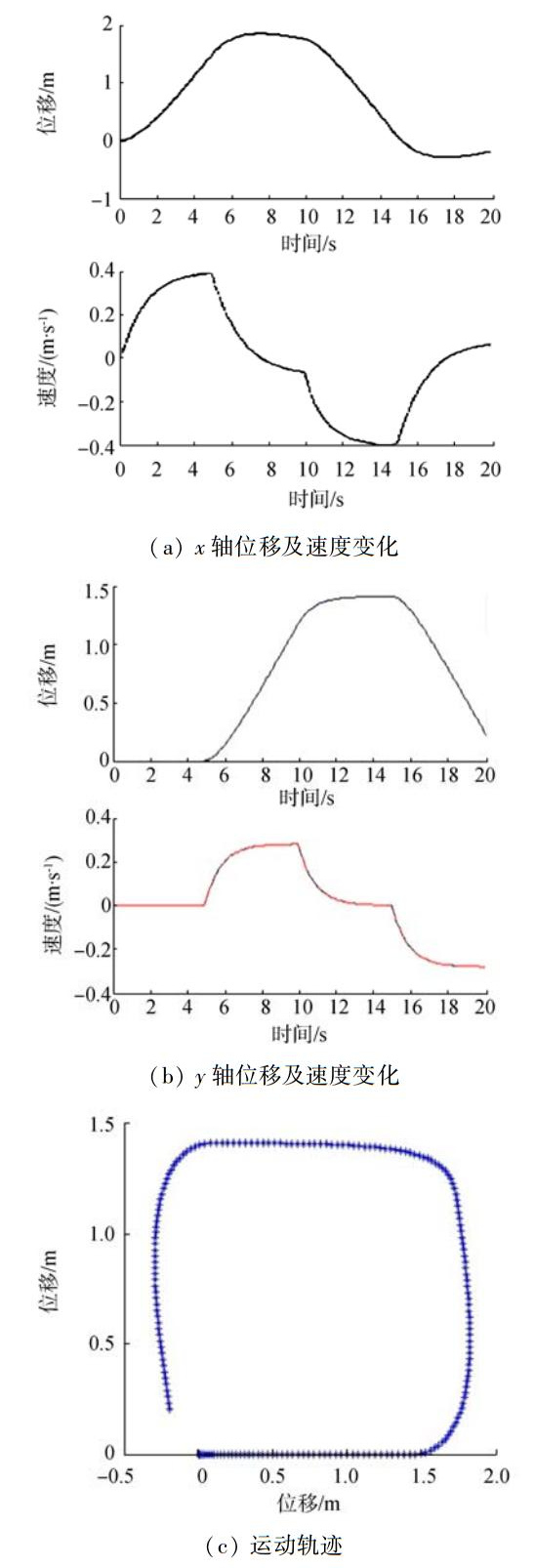
|
| 图 12 MATLAB仿真结果 |
利用虚拟样机在ADAMS中对机器人的快速转向运动进行仿真,得到运动曲线如图 13所示。
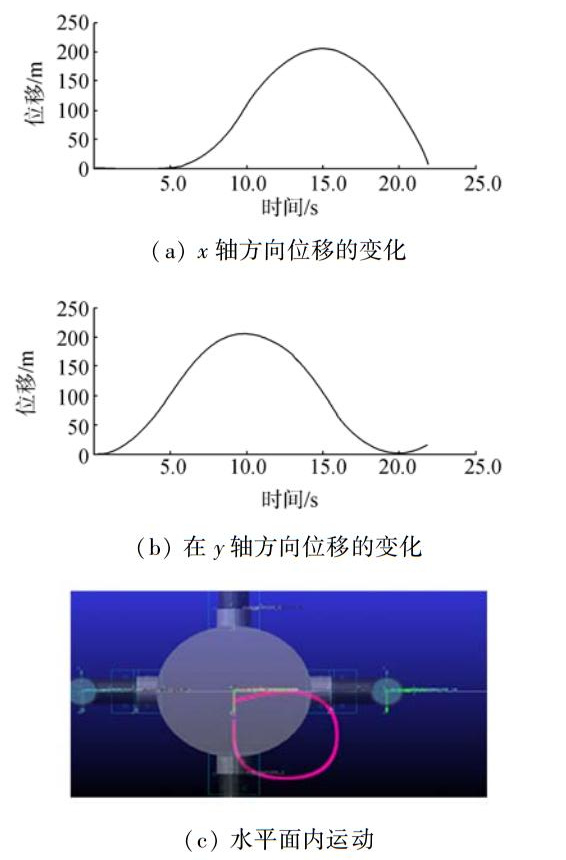
|
| 图 13 机器人运动曲线 |
仿真结果表明机器人在速度小于0.4 m/s的条件下,可以实现快速转向。印证了MATLAB的仿真结果,同时与实物样机实验的结果相符。
4 水下机器人原理样机的实验验证矢量喷水推进式水下机器人原理样机的验证实验在深度为2.0 m的浅水域中进行,机器人各喷水推进器与关节舵机工作正常,通信系统工作正常,用摄像机拍摄水下机器人的运动姿态如图 14所示。实验分别验证了机器人的推力对称运动和推力非对称运动。

|
| 图 14 摄像机镜头拍摄水下机器人的运动姿态 |
由于建模仿真时进行线性简化和水动力参数估计,因此机器人的实验轨迹与仿真轨迹存在一定差别。但从图 15中可以看到,仿真结果仍可真实反映机器人的运动特点,证实该机器人的运动达到理想效果。
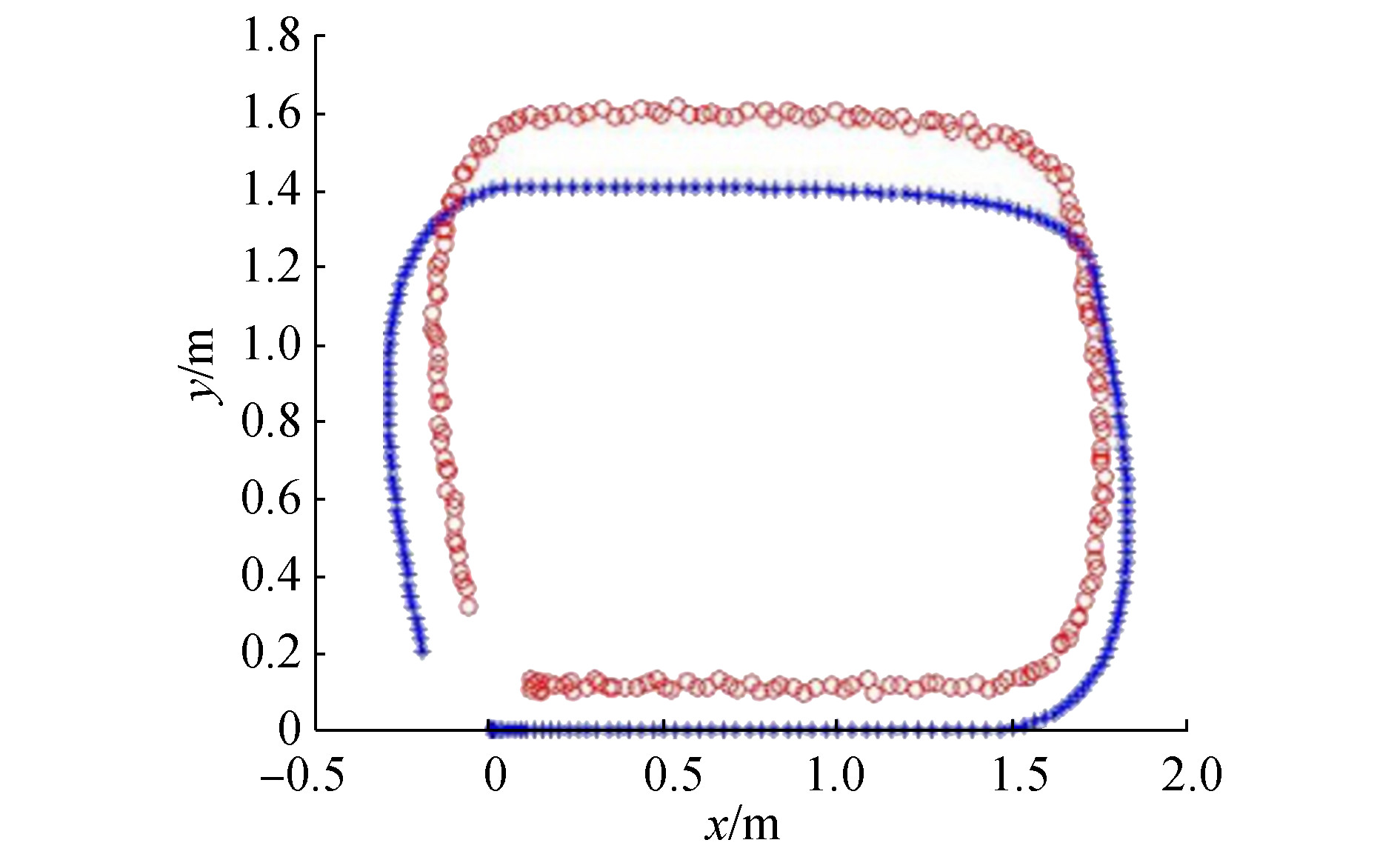
|
| 图 15 仿真轨迹与真实轨迹的比较 |
文中根据多自由度矢量喷水推进系统的特点,导出矢量喷水推力关于自由度的表达式,分析矢量推进作用对水下机器人运动姿态和航行效果的影响,提出机器人多自由度协调控制的策略与方法,以水下机器人多种运动状态的真实表现为研究对象,采用理论建模、数值分析有机结合的方式,验证了矢量喷水推进式水下机器人数理模型的合理性和可靠性。最后,通过机器人原理样机的水中验证实验,分析了机器人在水中的各项运动性能。实验结果与仿真结果高度符合,由此可知研制的矢量喷水推进式水下机器人具有高机动性和高可控性,具有较好的控制水平。
| [1] | 杨波, 方华京. 基于LQG/LTR的水下航行器多变量鲁棒控制[J]. 船海工程, 2008, 37(2): 142-144 |
| [2] | 高剑, 徐德民, 赵宁宁, 等. 一类低速水下航行器的自适应反演运动控制[J]. 系统仿真学报, 2008, 20(7): 1800-1802 |
| [3] | 梁建宏, 郑卫丰, 文力, 等. 两关节仿生水下航行器SPC-Ⅲ的推进与机动性[J]. 机器人, 2010, 32(6): 726-731 |
| [4] | CAVALLO E, MICHELINI R C, FILARETOV V F. Conceptual design of an AUV equipped with a three degrees of freedom vectored thruster[J]. Journal of intelligent and robotic systems, 2004, 39(4): 365-391 DOI:10.1023/B:JINT.0000026081.75417.50 |
| [5] | DUCHEMIN O, LORAND A, NOTARIANNI M, et al. Multi-channel hall-effect thrusters: mission applications and architecture trade-offs[C]//Presented at the 30th International Electric Propulsion Conference. Florence, Italy, 2007: 17-20. |
| [6] | LE PAGE Y G, HOLAPPA K W. Simulation and control of an autonomous underwater vehicle equipped with a vectored thruster[C]//OCEANS 2000 MTS/IEEE Conference and Exhibition. Providence, RI:IEEE, 2000, 3: 2129-2134. |
| [7] | 罗庆生, 魏天骐, 莫洋, 等. 多自由度模块化链节式8足机器人三总线控制系统设计[J]. 北京理工大学学报, 2013, 33(7): 698-703 |
| [8] | 王晓鸣, 王树新, 张宏伟, 等. AUV水下着陆策略研究[J]. 机器人, 2008, 30(4): 346-352 |
| [9] | SMALLWOOD D A, WHITCOMB L L. Model-based dynamic positioning of underwater robotic vehicles: theory and experiment[J]. IEEE journal ofoceanic engineering, 2004, 29(1): 169-186 DOI:10.1109/JOE.2003.823312 |
| [10] | ARSLAN M S, FUKUSHIMA N, HAGIWARA I. Control of an ellipsoidal underwater vehicle with single actuator[C]//Proceedings of 2008 Canadian Conference onElectrical and Computer Engineering.Niagara Falls, ON: IEEE, 2008: 001433-001436. |
| [11] | LI Jihong, LEE P M. A neural network adaptive controller design for free-pitch-angle diving behavior of an autonomous underwater vehicle[J]. Robotics and autonomous systems, 2005, 52(2/3): 132-147 |
| [12] | LIN Xichuan, GUO Shuxiang. Development of a spherical underwater robot equipped with multiple vectored water-jet-based thrusters[J]. Journal of intelligent & robotic systems, 2012, 67(3/4): 307-321 |
| [13] | 陈小龙, 庞永杰, 李晔, 等. 基于极大似然估计的AUV水下地形匹配定位方法[J]. 机器人, 2012, 34(5): 559-565 |
| [14] | 李彦双, 孙健国. 综合飞行/矢量推进系统控制器分离方法[J]. 航空动力学报, 2009, 24(12): 2814-2820 |
| [15] | 王晓鸣, 张宏伟, 王树新. 基于模糊控制的水下自航行器着陆策略分析[J]. 机械工程学报, 2009, 45(3): 84-88 |