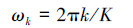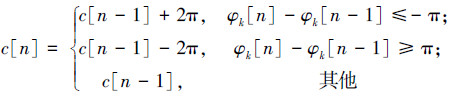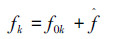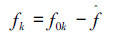现代电磁环境的改变,特别是具有低截获概率特性的脉冲压缩体制雷达的出现,要求数字接收机具有大动态范围、大带宽、实时性、灵活性、高灵敏度等特点,同时要具备处理多个到达信号、完整地保存目标信号的信息和强大的信号处理能力[1]。数字信道化接收机能够很好地满足上述要求,并已经在雷达信号接收、电子对抗、通信侦察等领域得到广泛的应用[2]。脉冲压缩雷达信号的形式复杂多变,多采用频率调制信号、相位编码信号等[3-4]。在后续的信号处理过程需要对脉冲压缩雷达信号进行信号检测和参数估计,其中,频率估计是参数估计的一个经典问题,本文提出了基于数字均匀信道化的调制信号测频方法的实现方案[5-9],即通过中值滤波[10-11]的处理来提高传统测频方法的测频精度。仿真结果表明了该方案的有效性。
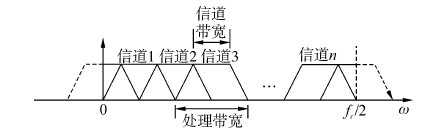
1 数字均匀信道化结构 1.1 信道划分在现实中的信号均为实信号,由于实信号频谱的对称特性,在对实信号进行处理时考虑一半频谱信息即可,在(0,fs/2)(其中fs为采样频率)内实现对信道的均匀划分,为保证整个覆盖带宽内无盲区,在实现信道的均匀划分时,滤波器组采用50%交叠的方式[12],即每个滤波器的处理带宽是信道带宽的2倍,如图 1所示。
|
| 图 1 均匀信道化划分方式 |
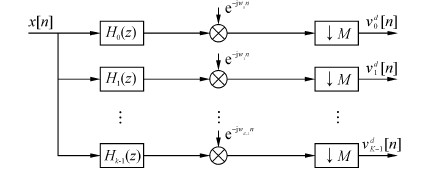
本文采用高效数字信道化结构实现数字信道化[12],首先对其数学模型进行的简单推导如下。传统的数字信道化结构原理框图如图 2所示。
|
| 图 2 传统的数字信道化结构原理框图 |
将带限信号x(t)经高速A/D变换器转换成离散信号x[n],K为划分的信道化数,M为每个信道的抽取倍数。在进行信道的均匀划分时,每个滤波器覆盖相同的频带范围,此时的滤波器组称为均匀滤波器组。将离散信号x[n]序列输入到K个均匀滤波器组,该均匀滤波器组按照图 1进行频带划分实现对相应频带上信号的提取。信道的划分需要采用高效的数字滤波器组,而FIR滤波器具有系统稳定性和可实现线性相位等优点,可以设计多通道的滤波器组,所以采用FIR滤波器来构造均匀滤波器组。其中,H0(z)为FIR低通原型滤波器,Hk(z),k=1,2,…,K-1均可由H0(z)进行相应的频谱搬移得到。接着,将K个均匀滤波器组输出信号分别进行相应的数字下变频,得到相应信道上的基带信号,最后对每个信道上的基带信号进行M倍抽取。在完成均匀信道化处理后即可进行后续的信号检测和参数估计。
在上述传统的数字均匀信道化结构中,首先要设计K个FIR滤波器,当划分较多信道数时计算量较大。其次,在该结构中,M倍的抽取过程在信道化处理的末端,此时前端的处理仍是在较高频率上,因此会导致前端A/D变换器高采样速率与后端信号处理速率不匹配的问题。
为了减少滤波器组计算量,引入多相滤波器组结构,将原型低通滤波器H0(z)表示成多相滤波器结构如下:
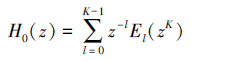 |
(1) |
式中 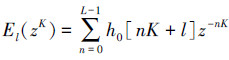
其他信道上的滤波器Hk(z),k=1,2,…,K-1可由原型滤波器进行相应的频谱搬移得到,这里记每个信道的中心频率为ωk(k=1,2,…,K-1),有
则有带通滤波:
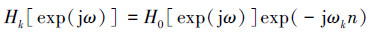 |
(2) |
将原型滤波器的多相滤波结构式(1)代入式(2)化简可得
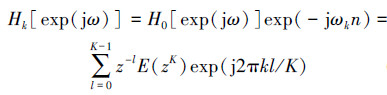 |
(3) |
式(3)为反傅里叶变换的类似结构,则从第2到第K个信道上的带通滤波器可以用一个K点的反傅里叶变换来表示,第一个信道上的原型低通滤波器用多相滤波器结构实现。此时,由原来的要设计K个N阶滤波器组转变为设计一个N阶低通滤波器和一个K点的反傅里叶变换,设计的计算量和复杂度大大降低。
为了解决后端信号的处理速率与前端A/D变换器高采样速率不匹配的问题,将M倍的抽取过程作用在整个信道化结构的最前端,使整个信道化过程的信号处理速率降低为采样频率的1/M倍。经过一系列化简可得到高效数字信道化结构原理框图如图 3所示。上述高效数字信道化接收结构输出v0d[n]和vMd[n]为实数,其他信道输出为复数,并且vld[n]与vK-ld[n](1≤l≤K/2-1)互为共轭形式,即所有信道输出有一半是独立的,所以只考虑前K/2个信道即可。在本文中取K=32,M=16,原型滤波器阶数N=192,则有P=6。即实现32个信道的均匀划分(实际中考虑前16个信道即可),16倍的信号抽取。

|
| 图 3 高效数字信道化接收机结构原理框图 |
在完成信道化处理之后进行信号参数估计,其中信号频率参数信息是后续信号处理部分所必须的,其估计精度将直接影响后续雷达信号处理结果。
本文重点分析针对线性调频信号和相位编码信号采用的测频方法。首先简单介绍瞬时相位差测频,并采用8点相位差平均测频,由于相位编码信号存在相位跳变,在采用瞬时相位差测频时容易产生较大的测频误差,提出在瞬时相位差测频结果的基础上加入中值滤波处理来提高测频精度。
2.1 瞬时相位差法测频在模拟信号中,信号的瞬时频率f(t)为瞬时相位Φ(t)的一阶导数,导数的离散形式为一阶差分[13-14]。故在数字域中,瞬时频率f(n)与瞬时相位Φ(n)的关系为
 |
(4) |
式中Ts为采样周期。式(4)表明,在数字域中频率和相位是一阶差分关系。故只要对均匀信道化结构在相应的信道上输出信号的相位进行一阶差分就可得到信号的频率。
对于常规的雷达信号比如正弦信号,其具有周期性输出,其瞬时相位在[-π,π],并且呈周期性重复出现。例如在正相位斜率情况下φk[n]>φk[n-1]一直成立,可直接用一阶瞬时相位差求信号的频率,当相位信息不连续时,即φk[n] < φk[n-1],就是相位越过了2π的无模糊区间,需要对瞬时相位进行解卷绕[12]。解卷绕算法是在原瞬时相位的基础上,根据相位的后向差分,在瞬时相位差上加一个修正序列c[n],初值c[n]=0。
为了减小噪声对上述一阶相位差瞬时测频结果的影响,可采用多点平均相位差,本文采用8点相位差的平均来减少噪声对测频的影响,则在信号所在信道上输出信号相对于该信道中心频率的偏移频率 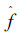
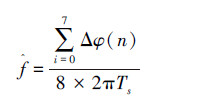 |
(5) |
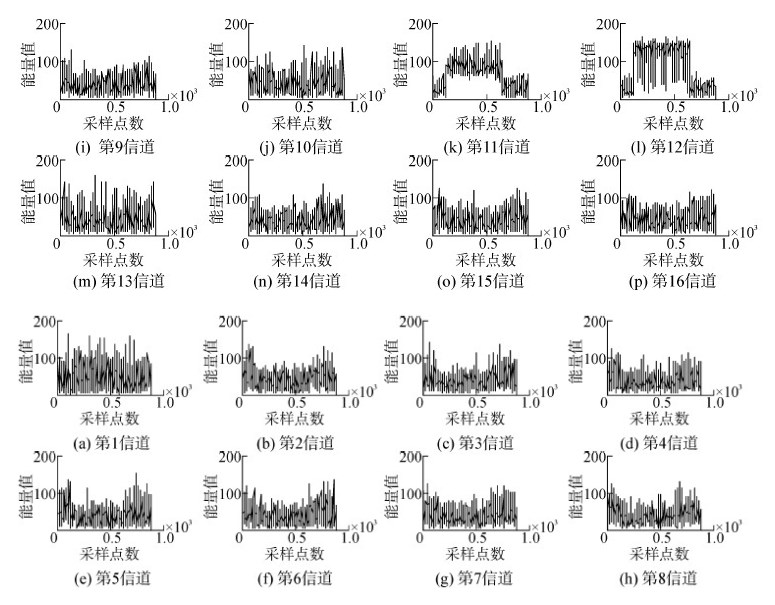
式中Δφ(n)为相位差。最终测得的信号频率fk由该信道的中心频率f0k和由瞬时相位差法所测得的偏移频率 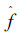
1)当所处理的雷达信号范围在(0,fs/2)时
2)当所处理的雷达信号范围在(fs/2,fs)时
2.2 改进的测频方法针对线性调频信号,其相位信息是连续变化的,不存在相位信息的跳变,采用瞬时相位差法的测频结果在误差允许范围内,不会产生错误的频率信息。而对于相位编码信号,其相位信息存在跳变,采用瞬时相位差法测频时虽然已经进行了相位差的8点平均,但是测频结果仍然会在相位跳变处产生较大的频率波动,甚至产生错误的频率估计结果。为了解决该问题,本文提出在对瞬时相位差测频的结果进行中值滤波处理的测频方法,将由相位跳变引起的测频结果的大幅度跳变滤除,最终得到精度提高的测频结果。
3 计算机仿真及结果分析首先对高效信道化结构进行仿真验证,接着对高效均匀信道化的输出信号进行测频方法对比仿真验证。
3.1 高效均匀信道化结构仿真验证本文将考虑以1 125MHz为中心频率,带宽为500 MHz的宽带雷达调制信号作为输入信号,根据输入调制信号带宽范围0.875~1 375 MHz,中心频率为f0=1 125 MHz,由带通采样定理fs=4f0/(2k+1),k>0,当k=1时,确定A/D变换器采样频率为fs=1.5 GHz。调制信号以线性调频(LFM)信号和二相编码(BPSK)信号为例,按照图 3所示的高效数字信道化结构实现信道化的均匀划分,根据输入信号设置适当的能量阈值,通过每个信道上输出信号的能量与设定阈值的大小比较来判断相应信道上是否有信号输出。
3.1.1 LFM信号通过高效信道化结构仿真验证仿真条件:输入LFM信号,起始频率fl=1 208 MHz,带宽B=20 MHz,脉冲宽度T=8.192 μs,调频斜率K=B/T,加入高斯白噪声,信噪比SNR=5 dB,将该信号通过高效数字信道化结构,其仿真结果如图 4所示。

|
| 图 4 LFM信号通过高效数字信道化结构 |
通过图 4的仿真结果可以看出,在第7信道上输出的信号能量明显大于其他信道上的信号能量。即该LFM信号在第7信道上输出。由于输入调制信号的范围在(fs/2,fs)内,根据信号经带通采样后得到的频谱与基带信号频谱呈反折关系可知该LFM信号所在的信道号为7[15],由此可得仿真结果与理论推导相吻合,验证了仿真结果的正确性。
3.1.2 BPSK信号通过高效信道化结构仿真验证仿真条件:输入调制类型为13位巴克码的BPSK信号,载频f0=1.0 GHz,码元宽度Tb=0.085 μs,加入高斯白噪声,信噪比SNR=5 dB,将该信号通过高效数字信道化结构,其仿真结果如图 5所示。
|
| 图 5 BPSK信号通过高效数字信道化结构 |
从图 5中可以看出,第11信道和第12信道上的信号能量明显大于其他信道上的信号能量,这是因为此时的信号载频正好在第11信道和第12信道上的交界处,而且由于信道的均匀划分是按图 1所示的50%交叠方式实现的,因此该BPSK信号在2个信道上均有信号输出,从图中可以看出第12信道上的信号能量大于第11信道上的信号能量,由此判断该BPSK信号在第12信道上输出。由上述判断LFM信号所在信道号理论可知,该BPSK信号理论上所在的信道号为12,实验仿真结果与理论结果一致。
3.2 测频方法对比仿真验证本文将进行8点相位差平均测频与提出的对8点相位差测频结果进行中值滤波,并对这2种测频方法的测频结果进行对比仿真。
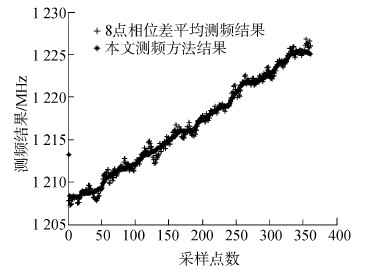
3.2.1 LFM信号测频结果对比仿真对上述输入LFM信号的高效数字信道化结构在第7信道上输出信号进行2种方法的测频结果对比仿真,仿真结果如图 6所示。
|
| 图 6 LFM信号测频结果对比 |
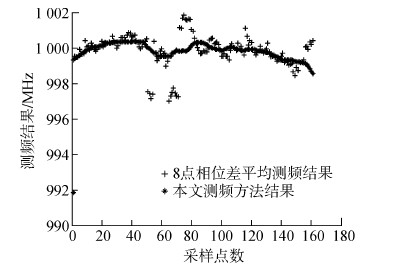
对上述输入BPSK信号的高效数字信道化结构在第12信道上输出信号进行2种方法的测频结果对比仿真,仿真结果如图 7所示。
|
| 图 7 BPSK信号测频结果对比 |
对于LFM信号,从图 6测频对比仿真结果可以看出,这2种方法均正确地测出其起始频率为1 208 MHz,终止频率为1 228 MHz,并且测频结果在一定的误差范围内均呈线性变化,实现了LFM信号的正确测频;对于BPSK信号,该信号的载频为f0=1.0 GHz。从图 7测频对比结果可以看出,8点相位差平均测频结果有较大的测频误差,最大的测频误差可达3 MHz,不满足一般在工程中±1 MHz的测频误差,此时的测频精度不足。而本文的测频方法成功地将这些较大的测频误差点滤除,在一定程度上消除了由相位跳变引起的测频误差,最终实现了测频精度的提高。
4 结论1) 根据能量大小准确地判断通过高效数字信道化结构处理的宽带雷达调制信号所在信道号。
2) 采用8点相位差测频的基础上加上中值滤波处理的方法对相应信道上输出信号进行频率参数估计,提高了测频精度。
3) 在采用传统的相位差测频方法时,由于相位编码信号存在相位信息的跳变,引入不可避免的测频误差,本文提出对8点相位差平均测频的测频结果进行中值滤波处理的测频方法,有效地消除了上述的测频误差。
仿真表明,该方法最终实现了测频精度的提高,对宽带数字接收机后端信号频率测量模块具有一定的工程指导意义。
| [1] | 陈涛, 岳玮. 宽带数字信道化接收机的FPGA实现[J]. 电子设计工程,2011, 19 (3) : 166 –170. |
| [2] | 刘光祖, 王建新, 徐达龙. 数字信道化接收机高效结构的设计与实现[J]. 系统工程与电子技术,2012, 34 (2) : 391 –395. |
| [3] | 李涛, 宿绍莹, 陈曾平, 等. EW接收机中的一种雷达脉内调制实时识别方法[J]. 现代电子技术,2013, 36 (21) : 9 –14. |
| [4] | 李利. 脉压雷达信号的识别和估计算法研究及其实现[D]. 哈尔滨:哈尔滨工程大学, 2009:23-25. |
| [5] | 唐宏. 数字信道化瞬时测频接收技术的研究[D]. 哈尔滨:哈尔滨工程大学, 2006:30-38. |
| [6] | 王杨, 凌万胜. 基于信道化的测频方法研究[J]. 无线电工程,2015, 45 (4) : 50 –52. |
| [7] | 王玉林, 杨书玲, 徐铂韬. 短时数据相位差法测频[J]. 无线电工程,2007, 37 (4) : 48 –50. |
| [8] | KWOK H K, JONES D L. Improved instantaneous frequency estimation using an adaptive short-time Fourier transform[J]. IEEE transactions on signal processing,2000, 48 (10) : 2964 –2972. |
| [9] | LI Yibing, WANG Yanhuan, LIN Yun. Recognition of radar signals modulation based on short time Fourier transform and reduced fractional Fourier transform[J]. Journal of information & computational science,2013, 10 (16) : 5171 –5178. |
| [10] | 邱志祺, 孙铁强. 一种提高图像中值滤波效果的改进算法[J]. 中国科技信息,2014 (22) : 137 –138. |
| [11] | LIANG Yan, GAO Yan. A median filtering algorithm based on selected point in digital image[C]//Proceedings of International Conference on Information Science and Cloud Computing Companion. Guangzhou, China, 2013:757-762. |
| [12] | LIU Heng, ZHOU Ningning. An improved filtering algorithm based on median filtering algorithm and medium filtering algorithm[C]//Proceedings of the Fifth International Conference on Advanced Computational Intelligence. Nanjing, China, 2012:574-578. |
| [13] | 刘旭波. 基于数字信道化接收机LPI雷达信号参数估计与分选[D]. 哈尔滨:哈尔滨工程大学, 2011:11-22. |
| [14] | 李滨玉, 许洁静, 魏波. 基于相位差分的FPGA瞬时测频的实现[J]. 现代电子技术,2013, 36 (18) : 118 –120. |
| [15] | 杨小牛, 楼才义, 徐建良. 软件无线电原理与应用[M]. 北京: 电子工业出版社, 2004 : 11 -14. |