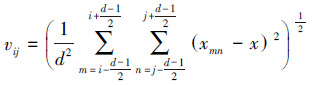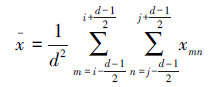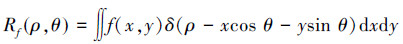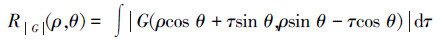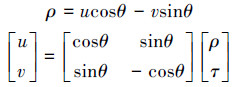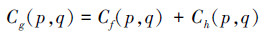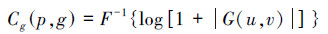图像在生成、传输和处理过程中质量下降的过程被称为图像的退化。其中由于被拍摄物体与成像系统之间产生的相对位移而造成的图像模糊,称之为运动模糊退化,退化模型的关键是点扩散函数。点扩散函数主要涉及对图像模糊角度以及模糊尺度的估计。
目前估计运动模糊参数的方法主要是基于频域上和空域上的估计。在频域上,王秋云[1]通过计算Radon变换值对退化图像频谱分析,检测出退化图像的模糊参数,但由于频谱图的十字亮线影响,会使测得模糊角度为0°或90°;郭红伟等[2]通过建立并分析运动模糊图像的倒频谱,来估计出运动模糊图像的参数,而郭永彩等[3]则是在差分自相关方法用于尺度鉴别理论分析的基础上,利用模糊图像微分图的自相关来估计运动模糊尺度。两种方法在不考虑噪声的情况下,可以很好地完成模糊函数的参数辨识,但存在噪声时,会使参数结果与实际偏差很大;在此基础上,沈瑜等[4]提出模糊图像分块求自相关的算法对图像模糊尺度进行估计,很好地去除了图像自身的相关性,提高了运动参数检测的鲁棒性,但依然没有考虑噪声的影响。在空域上,李均利等[5]将模糊图像的功率谱视为“各向同性的一阶马尔可夫过程”,采用3×3微分算子使模糊角度的估计范围增加,提取运动模糊图像的特征块,鉴定运动角度,但实际应用中并未达到预期的效果;莱文[6]提出Closed-Form自然图像抠图法,通过定义的代价函数求解像素颜色值,但对线条位置敏感;陈佳等[7]采用抠图和隔行扫描透明图的方法辨别模糊参数,但抠图和插值算法都会引入一定误差,进而影响运动变化的分析;吴忠标等[8]将运动模糊图像作为泊松融合技术的局部约束,通过局部模糊运动约束信息,估计模糊图像的参数,但算法复杂度较高,运算量过大。
在现有算法中,往往是以图像中单一人物或物体进行研究分析;而在实际生活中,所拍摄的照片并不能保证所要研究的模糊目标单独存在,往往要伴随其他运动模糊目标,从而影响对研究目标运动模糊参数的鉴别。基于这一点,本文根据运动模糊图像的频谱特性,提出一种基于模糊图像局部方差的运动模糊参数估计算法,其可以在多目标共存的情况下,很好地区分各模糊目标并分别对其进行模糊参数鉴别,并通过数值实验验证该方法的有效性和精确性。
1 运动模糊参数 1.1 图像局部标准差图像局部标准差即图像局部标准差梯度,在局部模糊图像中,其反映了图像在局部区域对比度的变化情况。它可以在未知图像数据结构的情况下,对噪声点进行有效地滤除,并且较为完整地保留了图像的细节以及边缘信息[9]。设f(x,y)为图像中(i,j)位置处像素的灰度值,图像大小为M×N,W为以(i,j)为中心,大小为d×d的局部区域,d为奇数且d>1,计算局部均值梯度vij为
式中:i、j≥0,m≤M-1,n≤N-1。x为窗口W中所有像素灰度平均值,定义如下:
局部标准差在一定程度上反映了图像局部灰度对比度的变化情况。在标准差较小的区域,图像灰度变化较小,图像边缘的出现机率也相应较小;反之,则图像边缘的出现机率相应较大。所以可以根据图像的局部标准差把图像的可能边缘区域很好地划分出来。
1.2 Radon变换被拍摄目标与成像系统之间的相对运动会造成像的运动模糊在极短曝光时间内,可以看作匀速运动。假设在曝光时间t、物体运动速度为v、沿水平方向角度θ条件下,运动模糊的点扩展函数h(x,y)为
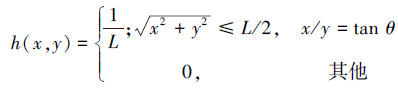 |
(1) |
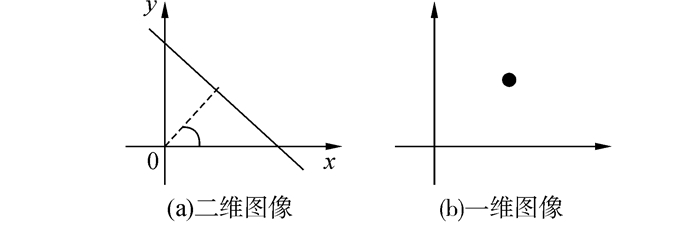
由式(1)可知,当模糊角度θ与模糊尺度L确定时,即可得到确定的点扩散函数。在二维图像中,Radon变换可以看成图像f(x,y)沿与x轴夹角的积分线的一维投影,由此可根据函数在平面内所有直线上的积分值来鉴定图像方向。
一条直线在二维空间可表示为[10]
式中ρ表示积分线到坐标原点的距离。对|G(u,v)|求Radon变换有:
在频率坐标系(u,v) 内,积分斜线方程可表示为
|
| 图 1 Radon变换示意图 |
图像g(x,y),其倒谱的计算公式为[11]
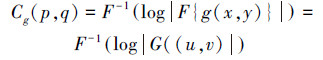 |
(2) |
式中:G(u,v)是图像g(x,y)的傅里叶变换,F表示傅里叶变换,F-1为傅里叶逆变换。
在忽略噪声的情况下,根据模糊图像退化模型,倒频谱可表示为[12]:
运动模糊退化函数为可以通过倒谱域图像分析出运动模糊参数信息的可分离函数[13]。模糊图像在时域为原图像和模糊核的卷积,变换到倒谱域之后为原图像的倒谱与PSF的倒谱之和。空间域的卷积在倒谱域变成了加法,能够真实地分离出模糊信息。当G(u,v)=0时,为使式(2)有意义,实际应用中图像的倒谱通常表示为[14]
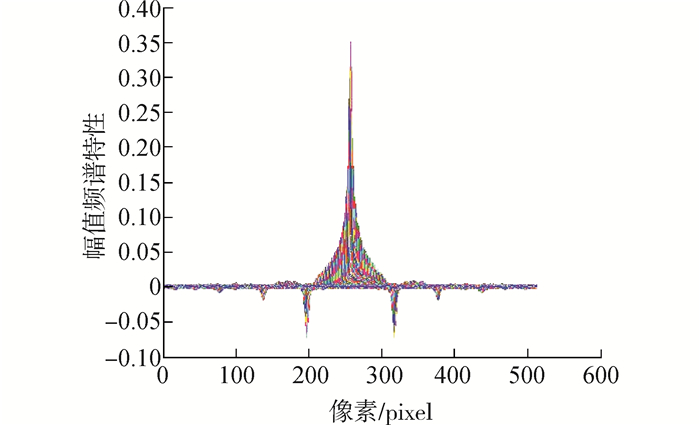
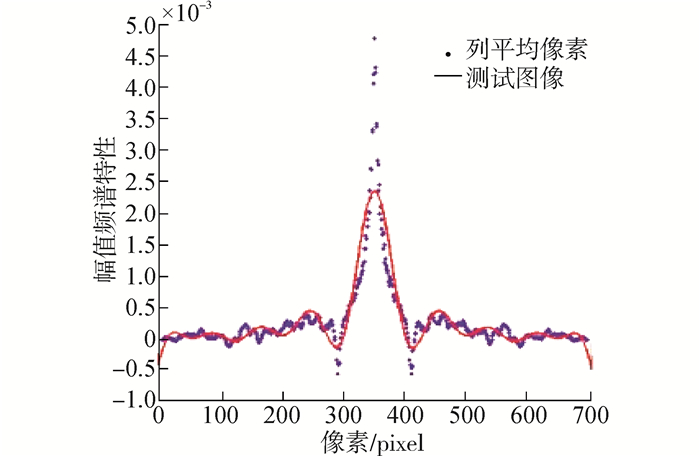
为了更清楚地显示运动模糊后的图像特性,这里采用512 pixels×512 pixels的Lena测试图像,对该图像进行模糊尺度60 pixels的模糊处理。图 2给出了无噪情况下的倒谱图,它由两部分组成:在运动模糊方向上,一部分是高幅值成分,它反映了原始图像特性;另一部分是低幅值成分,它反映了模糊系统的特性。两部分构成完整的模糊图像。其中2个最高负峰值的距离即为运动模糊尺度的2倍。然而在实际情况中,由于噪音等因素影响,倒谱的低幅值成分往往并不能明显地突显出来,使计算模糊尺度产生误差,造成极大干扰,图 3、4分别给出了测试图像在无噪与有噪情况下倒谱域的列平均像素拟合曲线。
|
| 图 2 Lena图像频谱 |
|
| 图 3 无噪倒谱域图像 |
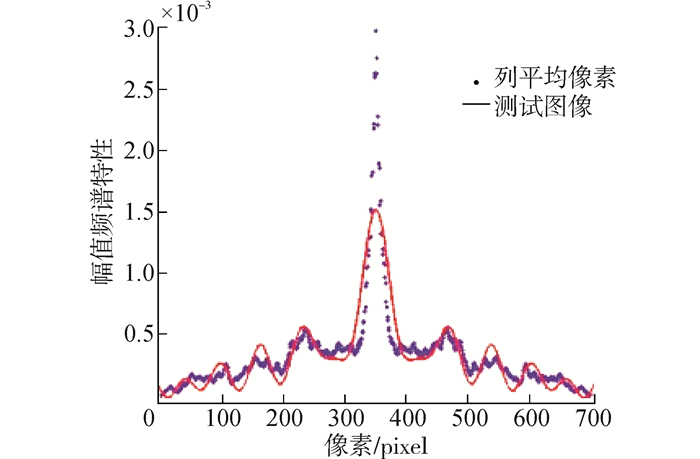
|
| 图 4 有噪倒谱域图像 |
考虑在多目标模糊图像中,各目标区域对比度反差大的特点,通过提取图像边缘梯度值大的图像块,并对各图像块加以分析研究,进而获得各目标模糊参数。本文采用5×5窗口标准差滤波器对模糊图像进行梯度处理,选取梯度值较大的图像块,分别对其进行标记,并返回原图,观察各图像块在原图中所在位置,剔除与目标图形无关以及目标重叠的图像块。根据图像目标位置,对余下的图像块进行筛选、归类。并分别对其退化模型应用Radon变换及改进倒谱法求取模糊角度和模糊尺度。
由于边缘截断效应的存在,Radon变换会在每个角度投影方向上产生一定的线性积分值[15],对模糊参数的估计的精确性产生影响,使得Radon投影模糊化严重,从而导致所提取图像块测量角度会产生近于水平或垂直角度离散值[16],使测量失真。本文对各图像块所求模糊角度进行升序排列,剔除离散值,有效地减缓噪声和十字亮线对测量结果的影响。可知,在升序角度值中,其趋于中间数值往往更接近真实模糊角度,因此为进一步精确角度,本文采用(1,2,…,n-1,n,n-1,…,2,1)×10-1(n>0且n∈N)似金字塔式权值,对所求角度进行加权求平均,获取模糊角度。
在拟合曲线最大值两侧,离其最近的两极小值点即为倒谱图两负峰值。因此,首先对倒谱域的列平均像素值离散点进行拟合曲线处理,求得图像最大值横坐标x0,以x0为分界点,分别对两侧拟合曲线求极小值,左侧选取极小值的横坐标最大值x1,右侧选取极小值的横坐标最小值x2,所求模糊尺度d即为 d=(x2-x1)/2。为进一步精确结果,依然对模糊尺度测得结果采用似金字塔权值进行加权求平均。本文算法过程如下:
1)对模糊图像进行预处理得到图像g(x,y),并构造5×5窗口标准差滤波器对模糊图像进行梯度处理。求得图像各像素点梯度值a1,a2,…,am。
2)对图像梯度值每行按升序排列,选取梯度值矩阵后n列,从n列矩阵中随机抽取m个值,并标记它们所在原图中的位置a1,a2,…,am。
3)以a1,a2,…,am为中心标记出m个图像块p1,p2,…,pm,剔除所在非目标区域以及目标重叠区域的x个图像块。
4)采用Radon算法及改进倒谱法分别对m-x个图像块进行模糊角度和模糊尺度的鉴别。
5)将所求得模糊角度与尺度分别进行加权求平均值,即为所求模糊参数。
3 实验分析为了验证算法的准确性和通用性,以典型图像Lena、Baboon作为实验对象1、2,以卡西欧数码相机EX-ZR400所拍实物图作为实验对象3和4加以验证,CCD尺寸为1/2.3英寸,影像原尺寸2 976 pixels×3 968 pixels,因尺寸过大其会影响测量效果,本文将影像尺寸设定为600 pixels×600 pixels,镜头焦距24~300 mm,快门速度1/640 s。首先分别对512 pixels×512 pixels像素的标准图像实验对象1和2进行随机生成不同模糊角度、尺度,在均值为0.1、方差为0.001的高斯噪声下的10组运动模糊参数的模糊处理,应用本文算法对其分别进行参数鉴别,然后与传统Radon变换及倒谱法进行对比。
表 1、2分别为实验对象1、2模糊参数对比表。其数据表明,由于噪声等因素影响,传统模糊角度算法产生较大误差,特别是在0°、90°附近。传统倒谱法在无噪、0°情况下,可以较为精确测量模糊尺度,但在噪音影响下以及角度的不精确测量,致使模糊尺度测量造成极大误差。其中传统算法极个别较为精确数据并不能说明算法准确性。而本文算法可使模糊角度误差控制在2~3°,模糊尺度误差控制在3~4 pixels,能够较好地抑制噪音等因素干扰,提高参数准确率。
| 原始 角度/ (°) | 分块 Radon 变换 | Radon 变换 | 原始 尺度/ pixel | 改进 倒谱法 | 倒谱法 |
| 9 | 10.62 | 0 | 65 | 68.41 | 57.28 |
| 57 | 56.18 | 50.48 | 43 | 46.57 | 50.61 |
| 29 | 29.70 | 31.61 | 41 | 43.28 | 33.95 |
| 85 | 87.54 | 90.00 | 22 | 19.06 | 17.75 |
| 16 | 14.92 | 25.58 | 57 | 58.43 | 69.82 |
| 32 | 33.19 | 28.32 | 15 | 12.62 | 11.21 |
| 44 | 44.10 | 40.36 | 19 | 18.83 | 10.54 |
| 61 | 60.97 | 57.52 | 70 | 72.12 | 79.56 |
| 48 | 47.28 | 44.63 | 59 | 60.37 | 64.43 |
| 25 | 26.15 | 30.56 | 32 | 31.69 | 42.14 |
| 原始 角度/ (°) | 分块 Radon 变换 | Radon 变换 | 原始 尺度/ pixel | 改进 倒谱法 | 倒谱法 |
| 48 | 46.81 | 42.25 | 38 | 40.17 | 30.23 |
| 28 | 27.65 | 21.93 | 47 | 46.54 | 39.63 |
| 76 | 78.22 | 70.56 | 69 | 70.20 | 88.41 |
| 11 | 12.23 | 0 | 30 | 28.85 | 29.72 |
| 29 | 30.00 | 32.27 | 56 | 58.31 | 64.67 |
| 87 | 88.35 | 90.00 | 12 | 10.33 | 255.00 |
| 63 | 62.15 | 64.55 | 19 | 18.65 | 30.24 |
| 23 | 23.31 | 30.17 | 70 | 71.89 | 80.23 |
| 15 | 17.26 | 27.11 | 23 | 19.56 | 26.17 |
| 47 | 45.63 | 42.43 | 31 | 31.13 | 34.25 |
表 3、4分别为实验对象1、2模糊参数鉴别精度对比表。从表中可知,分块Radon变换角度最大误差在2°左右,最小可精确至0.03°,平均误差不超过2°,均方误差可控制在1°以内,而传统Radon算法角度最大误差超过10°,均方误差达到3°。倒谱法平均误差在7 pixels左右,均方误差甚至超过5 pixels,而本文算法最小误差可精确至0.1 pixels,平均误差在2 pixels以内,均方误差达到1 pixels左右;并且不会出现奇异值,在精确度上较倒谱法大大提高(为精确对比测量结果,倒谱法在鉴别精度时未包括奇异值)。
| 鉴别精度 | 角度/(°) | 尺度/pixel | ||
| 分块Radon 变换 | Radon 变换 | 改进 倒谱法 | 倒谱法 | |
| 最大误差 | 1.70 | 9.58 | 3.57 | 12.82 |
| 最小误差 | 0.03 | 2.61 | 0.17 | 3.79 |
| 平均误差 | 1.00 | 5.13 | 2.00 | 7.56 |
| 均方误差 | 0.69 | 2.32 | 1.12 | 2.66 |
| 鉴别精度 | 角度/(°) | 尺度/pixel | ||||
| 分块Radon 变换 | Radon 变换 | 改进 倒谱法 | 倒谱法 | |||
| 最大误差 | 2.26 | 12.11 | 3.44 | 19.41 | ||
| 最小误差 | 0.31 | 1.55 | 0.13 | 0.28 | ||
| 平均误差 | 1.21 | 5.96 | 1.57 | 7.93 | ||
| 均方误差 | 0.62 | 3.19 | 0.89 | 5.29 | ||
图 5给出表 1中第3组数据的相关参数图。表格中其他示例模糊参数谱图类似,不一一列出。
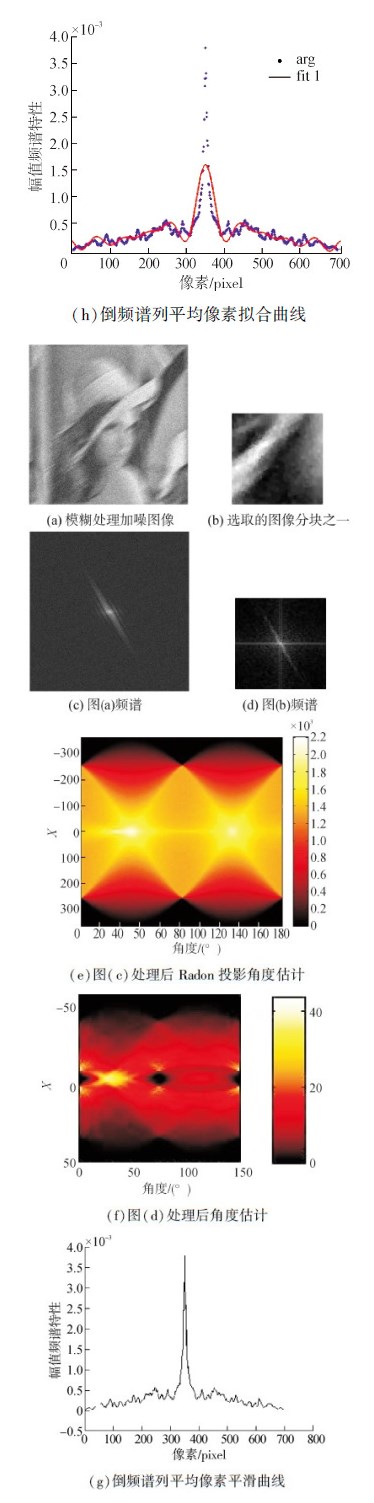
|
| 图 5 测试图 |
在提高测量模糊参数精确性的同时,针对目前只能对单一目标进行研究分析的缺点,本文算法能够对单幅图像多目标分别进行模糊参数鉴别。图 6、7分别为实验对象3、4经过梯度处理,分块返还到原图的图像。

|
| 图 6 实验对象3双风扇分块返还到原图的图像 |

|
| 图 7 实验对象4双车分块返还到原图的图像 |
实验对象3为双风扇在转动时所拍摄模糊图像,以灰色记号标记与背景距离较远的风扇,黑色记号标记与背景距离较近风扇,其中灰风扇(已使用一年)标定转速600 r/min,风扇旋转中心距离标定圆框圆心约11 cm。焦距为35 mm,焦距与灰风扇相距140 cm,两风扇相距35 cm。由于扇叶较多,为准确测得两风扇模糊参数,提取梯度值较大的大小为40 pixels×40 pixels图像块20个,并对其标记进行筛选、归类。其中7个特征块在黑风扇扇叶所在的1号框中,7个特征块在灰风扇扇叶所在2号框中,3个特征块在灰风扇扇叶所在3号框中,舍去其中与目标无关以及两风扇扇叶退化图形共存的图像块,虽然扇叶不同部分线速度不同,但角度相同,所以可用本文算法分别对3个框中图像块进行模糊角度计算,算取扇叶模糊角度。再通过圆框中线速度相同的模糊特征块求取扇叶模糊尺度,由相似三角形定理,求得风扇的旋转速度。
虽然实验对象4只有双目标,但因背景更加复杂,目标与目标之间、目标与背景之间梯度变化更加多样化,因此提取20个40 pixels×40 pixels图像块进行参数处理。距离焦距较远货车可标记模糊图像块9个,距离焦距较近黑色轿车标记图像块7个。相机焦距为55 mm,城市道路车道宽约3 m,由图可估算,两车右侧面相距约3.5 m。焦距距离两车分别为6、9.5 m,通过本文算法从而测得两车车速。因为实验对象4主要测量目标的尺度,相机成像边缘与车近乎平行,因此忽略对车辆角度测量。
测得实验结果,实验对象3中1号框中扇叶角度为71.83°,2、3号框中扇叶角度分别为136.79°、48.25°,灰风扇扇叶模糊尺度为17.31 pixels,扇叶所在圆框圆心附近线速度为627.38 cm/s,即转速为18.15 π/s。实验对象4中测得货车模糊尺度13.21 pixels,轿车模糊尺度为18.23 pixels,车速分别为为27.62、21.53 km/h。
4 结论1) 将图像局部标准差与Radon变换、倒谱法相结合,分别对模糊角度与尺度进行估计,从而可以达到同时测出一幅图像中多运动模糊目标的模糊参数的目的。
2) 采用对倒频谱列像素进行曲线拟合的方法求取模糊尺度,并通过仿真实验验证了该方法的有效性及精确性。
3) 引入似金字塔式权值对测量结果进行进一步的精确,结果验证了该方法的有效性及精确性。
由以上实验分析表明,基于运动模糊图像的多目标参数估计算法不但可以确保模糊参数估计的精度,并且可以同时对单幅图像多目标分别进行模糊参数与速度的估计。同时,该算法也存在一定缺陷,如背景更加复杂、被测目标过多等,都会对测量结果带来一定误差,仍需进一步研究实验。
| [1] | 王秋云, 王轶群. 基于Lucy-Richardson算法的运动模糊图像复原研究[J]. 自动化与仪器仪表,2013 (2) : 13 –14. |
| [2] | 郭红伟, 付波, 田益民, 等. 实拍运动模糊图像的退化参数估计与复原[J]. 激光与红外,2013, 43 (5) : 459 –464. |
| [3] | 郭永彩, 丁小平, 高潮. 基于差分自相关的运动模糊图像尺度参数识别[J]. 光电工程,2011, 38 (6) : 134 –140. |
| [4] | 沈瑜, 任恩恩, 党建武. 一种运动模糊参数估计算法[J]. 兰州交通大学学报,2012, 31 (3) : 116 –119. |
| [5] | 李均利, 储诚曦. 方向微分分块统计的运动模糊方向鉴别[J]. 中国图象图形学报,2013, 18 (7) : 776 –782. |
| [6] | LEVIN A, WEISS Y, DURAND F, et al. Efficient marginal likelihood optimization in blind deconvolution[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI, 2011:2657-2664. |
| [7] | 陈佳, 吴洁明. 基于透明度的单幅运动模糊图像运动参数估算方法研究[J]. 玉林师范学院学报:自然科学版,2013, 34 (2) : 139 –142. |
| [8] | 吴忠标, 方贤勇, 阚未然, 等. 一种运动模糊图像的鲁棒运动估计策略[J]. 计算机应用与软件,2013, 30 (7) : 66 –70. |
| [9] | SAEEDI J, MORADI M H, FAEZ K. A new wavelet-based fuzzy single and multi-channel image denoising[J]. Image and vision computing,2010, 28 (12) : 1611 –1623. |
| [10] | 廖永忠, 蔡自兴, 何湘华. 基于Radon变换的运动模糊图像恢复[J]. 计算机应用,2014, 34 (7) : 2005 –2009. |
| [11] | 王秋云. 基于倒谱特性的运动模糊图像PSF参数估计[J]. 自动化与仪器仪表,2014 (12) : 180 –183. |
| [12] | OPPENHEIM A V, SCHAFER R W. From frequency to quefrency:a history of the cepstrum[J]. IEEE signal processing magazine,2004, 21 (5) : 95 –106. |
| [13] | 董超, 毛凯, 赵文飞. 基于倒谱的运动模糊图像参数估计方法[J]. 海军航空工程学院学报,2014, 29 (5) : 435 –439. |
| [14] | 谢伟, 秦前清. 基于倒频谱的运动模糊图像PSF参数估计[J]. 武汉大学学报:信息科学版,2008, 33 (2) : 128 –131. |
| [15] | 孔勇奇, 卢敏, 潘志庚. 频谱预处理模糊运动方向鉴别的改进算法[J]. 中国图象图形学报,2013, 18 (6) : 637 –646. |
| [16] | 乐翔, 程建, 李民. 一种改进的基于Radon变换的运动模糊图像参数估计方法[J]. 红外与激光工程,2011, 40 (5) : 963 –969. |